航空声呐浮标(下文简称浮标)是航空反潜的主要搜潜装备,航空反潜时,通过空投浮标,依据水下目标在海洋环境条件下的特征,对目标进行搜索、识别、定位和跟踪,并为攻潜武器的使用提供目标指示。战场环境瞬息万变,浮标水中释放的效率,在很大程度上决定了航空探潜的效率和精度,直接影响到作战部署的准确性[1-2]。目前,国内关于浮标水中释放过程的研究较少,有必要开展相关工作,为高效率地使用浮标提供理论支撑。
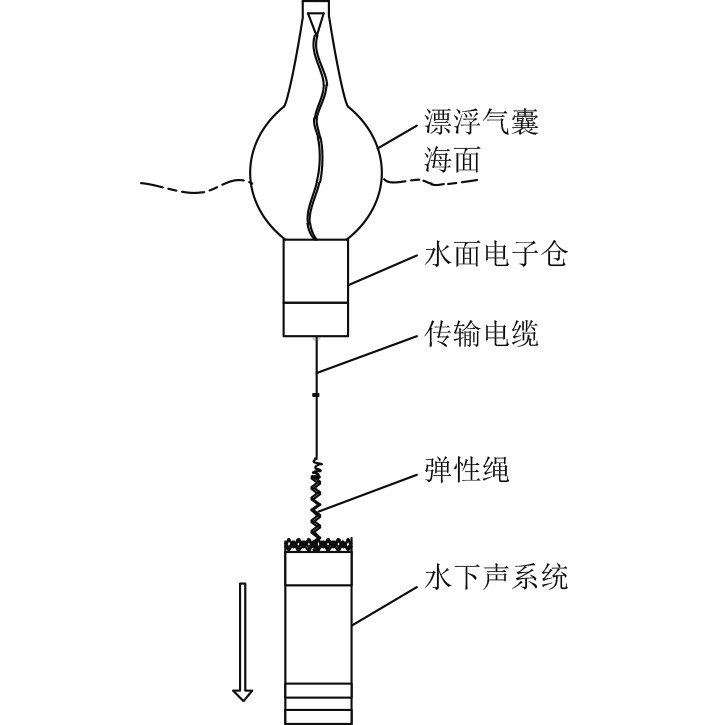
浮标空投入水后,漂浮气囊及水面电子仓保持直立姿态漂浮于海面,水下声系统及约束筒带着传输电缆和弹性绳向下运动。传输电缆线径较小,释放过程中的牵引力几乎为0,对水下声系统的干扰可以忽略。水下声系统随约束筒一起下降,先加速运动,再匀速运动,接近浮标设置的工作深度时,弹性绳开始拉伸,水下声系统开始减速运动[3]。图1为声呐浮标入水后释放过程示意图。
|
图 1 浮标释放过程示意图 Fig. 1 Schematic diagram of buoy deployment process |
浮标入水后,水下声系统在惯性力的作用下先加速运动,设位移
| $ M\ddot{y}+\frac{1}{8}\text{π} \rho {C}_{D}{D}^{2}{\dot{y}}^{2}=mg 。$ | (1) |
式中:
求解二阶常系数非线性微分方程(1),得到:
| $ {y\left(t\right)=\alpha }^{-1}\mathrm{ln}\frac{{{e}^{\sqrt{\alpha \beta }t}+e}^{-\sqrt{\alpha \beta }t}}{2},$ | (2) |
| $ v\left(t\right)=\dot{y\left(t\right)=}\sqrt{\mathrm{\beta }{\mathrm{\alpha }}^{-1}}\frac{{e}^{2\sqrt{\alpha \beta }t}-1}{{e}^{2\sqrt{\alpha \beta }t}+1}。$ | (3) |
式中:
浮标水下声系统在水中变速运动时,会带着周围的水体一起运动,从而受到水体的反作用力,该力大小与运动系统加速度成正比,该力与加速度之比称为附加质量。若是水下声系统在水中质量为
| $ {m}_{a}={C}_{a}\rho \text{π} {D}^{2}L/4。$ | (4) |
式中:
关于圆柱体的附加质量,于肖宇等[7]开展了薄壁圆筒结构附加质量的实验研究,通过对圆柱结构和圆筒结构附加质量的测量,得出了两者之间的比例常数。倪宝玉等[8]基于势流理论开展了弹体落水过程中附加质量变化影响研究,得出附加质量的变化主要取决于弹体形状和湿表面积的变化。冯双双等[9]基于相对运动原理得出了在无限流体域中不同长细比圆柱的附加质量,给出了附加质量系数与长细比之间的关系。
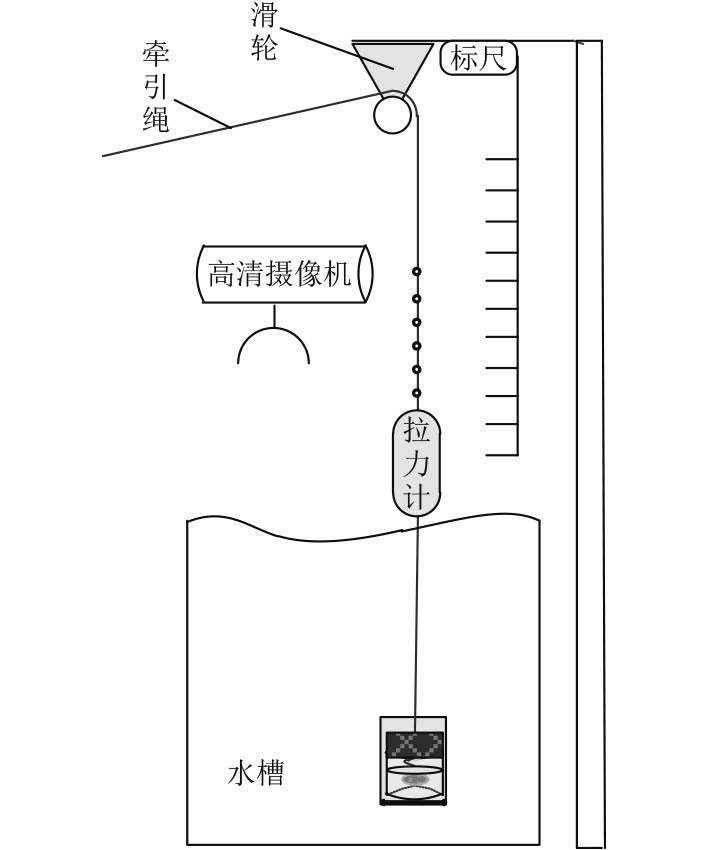
参照上述文献,结合浮标水下声系统结构特点,研究声呐浮标水下声系统释放过程时,忽略海洋水文条件的影响,认为水下声系统在未展开时为圆柱体质量块,沿中心轴线运动。浮标水下声系统在无限域中非定常运动时可以按照图2所示的示意图进行测量,将运动系统放置在水槽内,通过牵引绳带动运动系统移动,使用高清摄像机记录牵引绳上标志点位移变化,近似计算出标志点移动时的速度和加速度,同时记录从拉力计上读出的流体总阻力。结合运动系统定常移动时的阻力,根据流体总阻力与定常移动阻力之差,可以得到附加质量。
|
图 2 附加质量测量方法示意图 Fig. 2 Schematic diagram of added mass measurement |
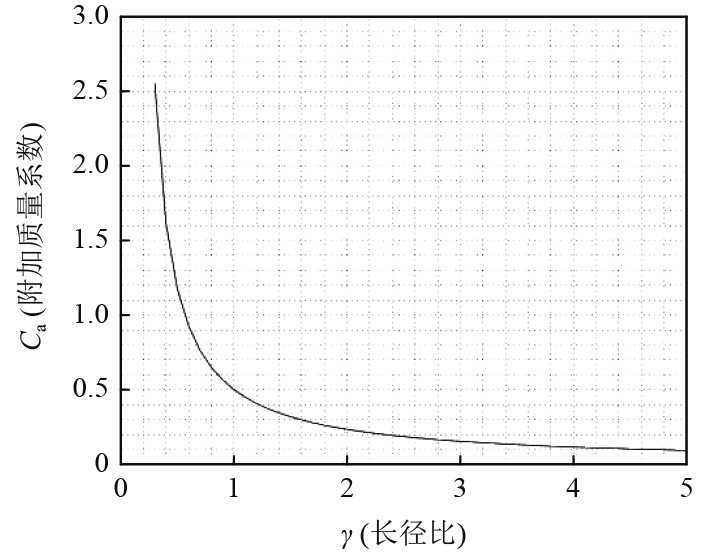
测量长度与直径之比不同的圆柱体变速运动时的总阻力,减去对应速度下定常移动的阻力,可以得到多组附加质量,拟合附加质量系数
|
图 3 附加质量系数随长径比变化曲线 Fig. 3 Curve of added mass coefficient with ratio of length to diameter |
通过查询图3中的圆柱体长径比对应的附加质量系数,可以求出不同类型浮标的水下声系统变速运动过程中的附加质量。
2 匀速运动阶段浮标水下声系统加速运动时,随着速度增加,受到的非线性阻尼力也在增加,经过一段时间后达到受力平衡,水下声系统开始以匀速
| $ y\left(t\right)={V}_{0}t。$ | (5) |
浮标水下声系统匀速下降到接近预先设置的工作深度时,弹性绳开始拉伸,随着弹性绳拉伸,水下声系统开始受到弹性力,弹性力的大小与弹性绳的拉伸量有关,减速阶段的运动方程为:
| $ M\ddot{y}+\frac{1}{8}\text{π} \rho {C}_{D}{D}^{2}{\dot{y}}^{2}+ky=mg,$ | (6) |
在弹性力作用下,产生近似简谐运动。解微分方程(6)比较复杂,可以将非线性阻尼力等效为线性阻力,等效线性阻力系数为
| $ M\ddot{y}+R\dot{y}+ky=mg ,$ | (7) |
求解式(7),得到位移表达式:
| $\begin{aligned} y\left(t\right)=&\frac{mg}{k}+\left({C}_{1}{{\rm{cos}}}\left(\frac{\sqrt{4kM-{R}^{2}}}{2M}t\right)+\right.\\ &\left. {C}_{2}{{\rm{sin}}}\left(\frac{\sqrt{4\mathit{kM}-{R}^{2}}}{2M}t\right)\right){e}^{-\frac{R}{2M}t}。\end{aligned}$ | (8) |
式中:
在简谐运动中,假定运动系统实际的非线性阻力与等效线性阻力在每个周期内所产生的能量损失相等[10-11],若是简谐运动记作
| $ {E}_{1}={\int }_{0}^{T}\frac{1}{8}{C}_{D}\rho \text{π} {D}^{2}{\dot{x}}^{2}\dot{x}{\rm{d}}t= \frac{{C}_{D}\rho \text{π} {D}^{2}{A}^{3}{\omega }^{2}}{3},$ | (9) |
| $ {E}_{2}={\int }_{0}^{T}R\dot{x}\dot{x}{\rm{d}}t={R\text{π} A}^{2}\omega 。$ | (10) |
令
已知某型浮标水下声系统的尺寸和水中质量,直径
浮标入水后,水下声系统先是加速运动,加速运动阶段速度变化如下式:
| $ {v}_{1}\left(t\right)=\sqrt{9.1{{C}_{D}}^{-1}}\frac{{e}^{2\sqrt{8.4{C}_{D}}t}-1}{{e}^{2\sqrt{8.4{C}_{D}}t}+1}。$ | (11) |
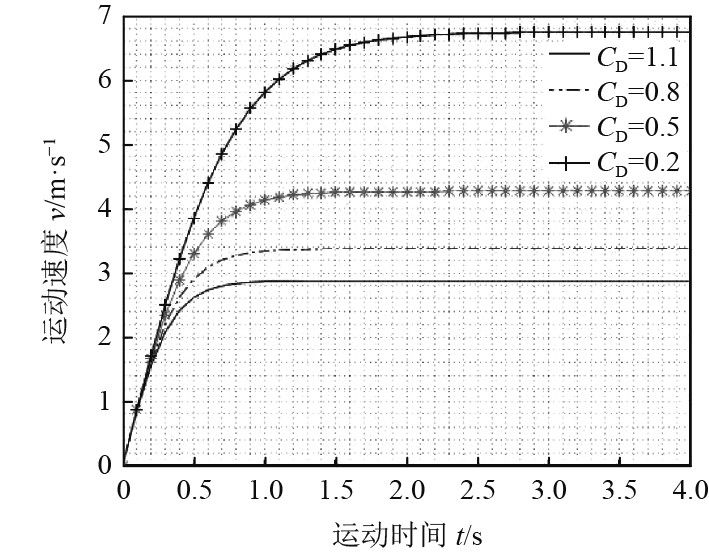
水下声系统加速阶段的速度变化曲线如图4所示。可以看出,加速时间与阻力系数
|
图 4 加速阶段速度变化 Fig. 4 Speed vs time during accelerated phase |
结合典型声呐浮标水下声系统的形状尺寸,选取阻力系数为
水下声系统加速阶段位移变化函数如下式:
| $ {y}_{1}\left(t\right)=1.3{{\rm{ln}}}\frac{{{e}^{2.6t}+e}^{-2.6t}}{2}。$ | (12) |
当阻力系数
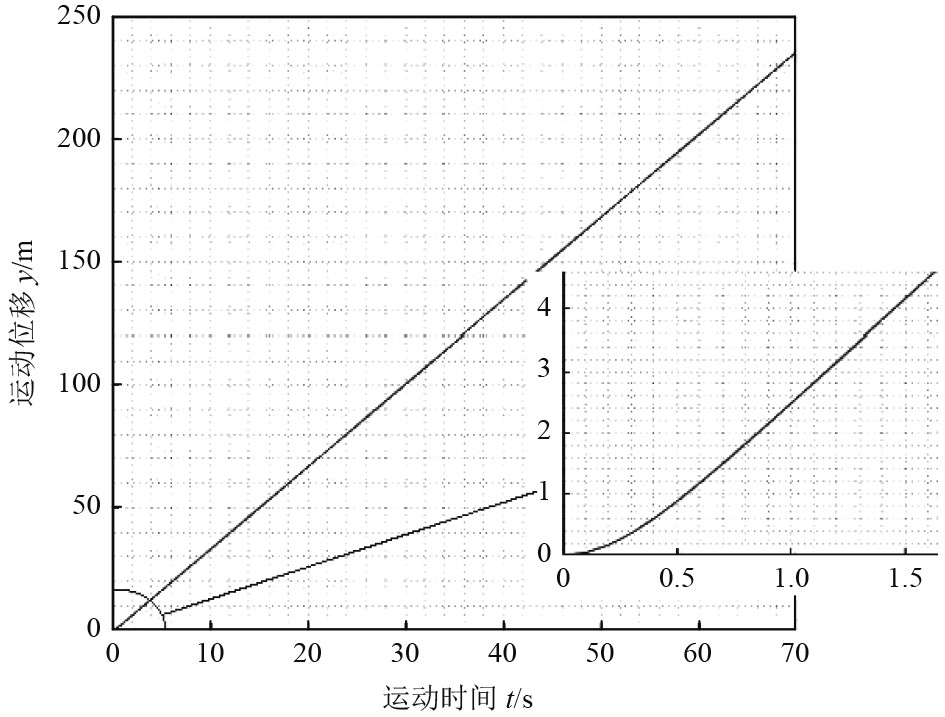
|
图 5 加速阶段位移变化 Fig. 5 Displacement vs time during accelerated phase |
选取浮标弹性绳的弹力系数
| $ {{y}}_{2}\left({t}\right)=6.125-(6.125\mathrm{cos}\left(0.54{t}\right){+5.893\mathrm{sin}\left(0.54{t}\right))\mathrm{e}}^{-1.07{t}} 。$ | (13) |
减速阶段位移变化曲线如图6所示。从数值分析来看,弹性绳第一次拉伸到最大位移后,若是不考虑海洋环境带来其它激励力,该系统很难再次振动起来。弹性绳拉伸
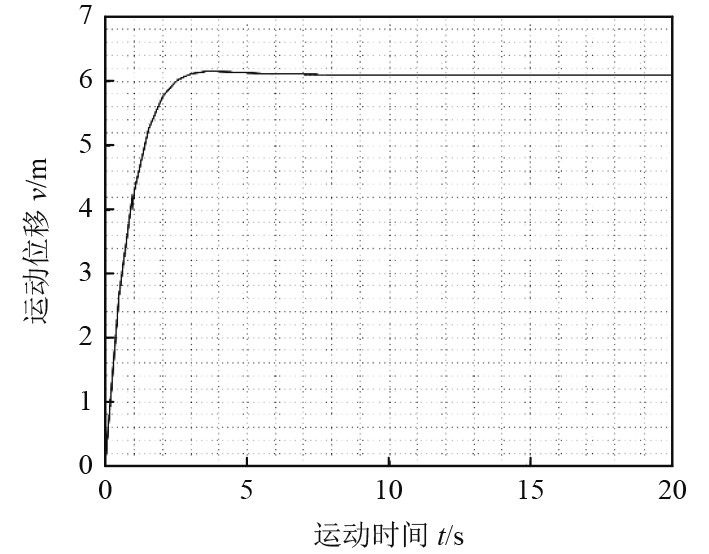
|
图 6 减速阶段位移变化 Fig. 6 Displacement vs time during decelerated phase |
浮标水中释放时,水下声系统的加速阶段和减速阶段的时间都很短暂,花费时间较长的是匀速运动阶段。根据浮标预设工作深度,可以计算出浮标布放时间。假定浮标的工作深度设置为
| $ \Delta t={t}_{1}+{t}_{2}+(H-{y}_{1}-{y}_{2})/{V}_{0}。$ | (14) |
若是浮标预设工作深度为
根据实际使用流程,将浮标的水中释放过程分为加速阶段、匀速阶段和减速阶段。分析加速阶段的受力情况,建立加速运动方程,求出水下声系统加速过程中的位移和速度变化函数;介绍附加质量的求解方法,分析减速阶段的受力情况,建立减速运动方程,将减速运动方程进行简化,求出减速阶段位移变化函数;介绍非线性阻尼力等效为线性阻力的方法,给出了匀速阶段位移变化函数。选取典型浮标的运动参数进行数值分析,推导出了浮标水下声系统的加速时间、加速阶段速度变化曲线、加速阶段位移变化曲线、减速阶段的位移变化曲线。根据声呐浮标设置的工作深度,可以求出水中释放时间。所使用的分析方法能够评估出更多型号的声呐浮标水中释放时间,为作战流程的设计提供依据。
| [1] |
程浩, 饶炜, 赵海潮. 空投声呐浮标空中运动轨迹研究[J]. 舰船科学技术, 2022, 44(11): 146-150. DOI:10.3404/j.issn.1672-7649.2022.11.030 |
| [2] |
周宏坤. 航空声纳浮标用矢量水听器及其悬挂技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2016.
|
| [3] |
程浩. 声呐浮标漂浮性能分析[J]. 声学与电子工程, 2020(3): 26-28. |
| [4] |
GU Hanbin, STANSBY P, STALLARD T, et al. Drag, added mass and radiation damping of oscillating vertical cylindrical bodies in heave and surge in still water[J]. Journal of Fluids and Structures, 2018, 82: 343-345. DOI:10.1016/j.jfluidstructs.2018.06.012 |
| [5] |
匡建平, 吴训涛, 王虹旋. 细长圆柱体水中无约束运动的附加质量计算方法探析[J]. 四川兵工学报, 2014, 35(6): 113-114. |
| [6] |
茅春浦. 流体力学[M]. 上海: 上海交通大学出版社, 1995.
|
| [7] |
于肖宇, 张继革, 顾卫国, 等. 薄壁圆筒结构附加质量的实验研究[J]. 水动力学研究与进展, 2010, 25(5): 655-657. |
| [8] |
倪宝玉, 孙士丽, 孙龙泉, 等. 弹体落水过程中附加质量变化影响研究[J]. 振动与冲击, 2012, 31(14): 171-172. DOI:10.3969/j.issn.1000-3835.2012.14.035 |
| [9] |
冯双双, 魏晓娟, 孙磊, 等. 流场中沿轴向运动圆柱的附加质量计算[J]. 计算机辅助工程, 2015, 24(2): 42-44. |
| [10] |
GUAN Guan, GENG Jiahong, WANG Lei. Dynamic calculation for sonobuoy suspension heave reduction system with experimental correction[J]. Ocean Engineering, 2020, 201: 107141. DOI:10.1016/j.oceaneng.2020.107141 |
| [11] |
CHAPMAN D MF, KEZELE D BA. Sinusoidal vertical motion of a sonobuoy suspension: experimental data and a theoretical model[R]. Canada: Defence R&D Canada- Atlantic, 2008, TM2008-121.
|
 2023, Vol. 45
2023, Vol. 45
