0 引　言

甚低频(VLF, 3~30 kHz)频段的电磁波波长较长，具有传播损耗小、幅度和相位较为稳定的特点，长期以来一直用于远距离通信和导航。此外，VLF波由于趋肤效应能渗透进入一定深度的海水中而被接收，是目前广泛用于水面舰艇和潜艇通信的无线电波。通常用于军事方面通信的地面电磁波发射台所占面积巨大，投入成本很高，且辐射效率较低，在战时容易被破坏且修复时间很长，因此需要对其他形式的VLF发射装置进行研究。地基大功率短波发射机能有效将高频段(HF, 3~30 MHz)的电波注入到电离层中，与电离层中等离子体相互影响，使各项电参数变化而发生非线性过程。随着研究的进展，相关研究者提出了利用高频波调制加热电离层，通过人工调制加热电离层的电急流振荡来辐射VLF波的设想。该方法能极大减少发射成本，可通过调节加热区域减小辐射源与舰艇的通信距离，有着广泛的应用前景，因此利用HF波人工调制加热电离层产生VLF辐射源的研究成为热点。

利用地基高频加热机调制加热电离层属于欧姆加热，引起加热区域内电子温度和电子密度变化，从而引起电离层中的电导率等参数产生扰动，电离层中的自然电流也产生振荡。Gurevich^[1]回顾了苏联对电离层中非线性过程的研究，通过无线电波改变等离子体电离成分的密度、电子和离子温度等电参数，产生复杂等离子体湍流的过程。Barr等^[2-4]通过高频波X模式加热电离层，在电离层中形成的辐射源电流可理想化为一个偶极子，在150 MW X波的加热条件下能有效辐射出ELF/VLF信号，计算了偶极子在波导中产生的场强，并在后续的实验中实现了人工调制电离层产生ELF/VLF辐射源，偶极子的高度位于最大霍尔电流高度处^[5]。Papadopoulos等^[6]使用极性电喷流调制控制地面HF功率转化为ELF/VLF功率，在夹角为35°的锥形区域内，加热速率以快于冷却速率扫描该区域时能将HF到ELF/VLF辐射的功率转换效率提高2个数量级以上。在国内，也广泛开展了电离层加热产生VLF辐射源的研究。黄文耿等^[7-8]构造了大功率电波对电离层加热产生电急流的自洽理论模型，从基本磁离子理论出发，简化了在加热过程中对电子温度、电子密度、电导率等各项电参数变化的计算，所产生的振荡调制电流可以作为ELF/VLF电波的辐射源。汪枫等^[9]采用ELF/VLF调幅HF电波加热电离层，在加热区域产生周期性振荡电流，以此等效产生ELF/VLF波的电离层虚拟天线，低纬地区人工调制电离层主要发生在90 km以下。随着研究的进行，地面大功率加热设备不断完善，其中最大的高频加热设备是位于Alaska的HAARP加热装置，研究发现通过调制极区电急流, 可以辐射出频率0.1 Hz～40 kHz的ELF/VLF波。

本文采用全波解研究VLF波传播，该方法是从Helliwell^[10]的研究开始发展，Nygren^[11]采用新的全波解方法解决了垂直波数虚部过大导致结算不稳定。Li等^[12]将不均匀的电离层进行了水平分层处理，利用全波解和传播矩阵的方法，对VLF波向下传播进行了数值计算。李凯等^[13]通过对特征波的计算得到了星载的VLF发射天线在海面上产生场。

本文受对电离层加热产生VLF偶极子源的启发，从电子能量方程出发，分析电离层中各参数随加热变化，计算该辐射源的偶极矩。若同时对多个区域进行加热可产生多个电偶极子，若电偶极子首尾相连可形成一个磁偶极子，即虚拟的VLF环形天线，以此作为本文辐射VLF波的磁流源。随后研究该源辐射的VLF波在低电离层中向下传播问题，利用全波解的方法对传播过程进行数值计算，求出电离层中的辐射源在海面上的场强，并讨论电子温度和地磁场对场强的影响。

1 理论模型及计算方法 1.1 调制加热电离层产生VLF磁流源

电离层调制加热首先是入射高频电波损失的能量被电离层等离子体中的电子吸收，并在电场作用下被加速，导致温度上升，在低电离层中的碰撞频率很大，通过碰撞又损失电子能量，温度降低。由于离子质量远大于电子质量，离子的加热可忽略不计。在对低电离层调制加热过程中，电子能量方程中的对流项、压缩项和热传导率几乎为0，因此可以忽略^[14]，则电子能量方程可表示为^[15]：

$\dfrac{3}{2}K{N_e}\dfrac{{\partial {T_e}}}{{\partial t}} = Q - L 。$

(1)

式中： $K$ 为Boltzmann常数； ${N_e}$ 为电子密度； ${T_e}$ 为电子温度； $Q$ 和 $L$ 分别为单位体积内的电子的吸收能流密度^[16]和损失能流密度^[17-18]。在加热过程中电子温度达到饱和的时间远小于电子密度达到饱和的时间，且加热周期远小于电子密度达到饱和时间，很难引起电子密度变化，因此在计算过程中忽略 ${N_e}$ 的变化。电离层中的电导率是关于电子、离子密度和碰撞频率的函数，周期的加热将使电导率张量中的各分量产生扰动，其各分量可表示为：

${\sigma _P} = \dfrac{{e{N_{\text{e}}}}}{B}(\dfrac{{{\omega _e}{\upsilon _e}}}{{{\omega _e}^2 + {\upsilon _e}^2}} + \dfrac{{{\omega _i}{\upsilon _i}}}{{{\omega _i}^2 + {\upsilon _i}^2}})，$

(2)

${\sigma _H} = \dfrac{{e{N_{\text{e}}}}}{B}(\dfrac{{{\omega _e}^2}}{{{\omega _e}^2 + {\upsilon _e}^2}} - \dfrac{{{\omega _i}^2}}{{{\omega _i}^2 + {\upsilon _i}^2}}) ，$

(3)

${\sigma _{//}} = \dfrac{{e{N_{\text{e}}}}}{B}(\dfrac{{{\omega _e}}}{{{\upsilon _e}}} + \dfrac{{{\omega _i}}}{{{\upsilon _i}}})。$

(4)

式中： ${\sigma _P}$ ， ${\sigma _H}$ ， ${\sigma _{//}}$ 分别为Pedersen电导率、Hall电导率、平行电导率， $e$ 为单位电子所带电量； ${\omega _e}$ 和 ${\omega _i}$ 分别表示为电子和离子的回旋角频率； ${\upsilon _e}$ 和 ${\upsilon _i}$ 分别为电子与中性大气粒子、离子与中性大气粒子的碰撞频率，可由经验公式^[19]给出。

$\begin{aligned} {\upsilon _e} =& 1.7 \times {10^{ - 11}}n({N_2}){T_e} + 3.8 \times {10^{ - 10}}n({O_2}){T_e}^{0.5} + \\ & 1.4 \times {10^{ - 10}}n(O){T_e}^{0.5}，\end{aligned}$

(5)

$\begin{aligned} {\upsilon _i} =& ( 4.34 \times {{10}^{ - 10}}n({N_2}) + 4.28 \times {{10}^{ - 10}}n({O_2}) +\\ & 2.44 \times {{10}^{ - 10}}n(O) )\dfrac{{{T_i}}}{{300}}。\end{aligned}$

(6)

在自然电场 ${E_0}$ 的作用下电流产生了振荡，随时间变化的电流能辐射处电磁波，等效于在电离层中产生一个辐射VLF波的电偶极子，其偶极矩的可表示为^[6]：

$M = IL = \Delta {\kern 1pt} J\Delta z{L^2} 。$

(7)

式中： $\Delta {\kern 1pt} z$ 为有效加热电离层在高度上的范围； $L$ 为调制区域的线性大小； $\Delta {\kern 1pt} J$ 为电流的变化。以Hall电流为例可表示为：

$\Delta {\kern 1pt} {J_H} = ({\sigma _H}(\max ) - {\sigma _H}(\min )){E_0}。$

(8)

若同时对n个区域进行加热，可产生n个偶极矩大小相等、方向不同的电偶极子。假设n个电偶极子均为水平电偶极子且水平尺度足够小，在电离层中组成一个正n边形，当n足够大时可近似成一个小电流环，并以此作为辐射VLF波的垂直磁偶极子。当n为偶数时，该辐射源的磁偶极矩大小可表示为：

$m = IS = I \times \dfrac{{\text{π} {L^2}}}{{4{{\sin }^2}(\pi /n)}}。$

(9)

1.2 电磁波传播模型

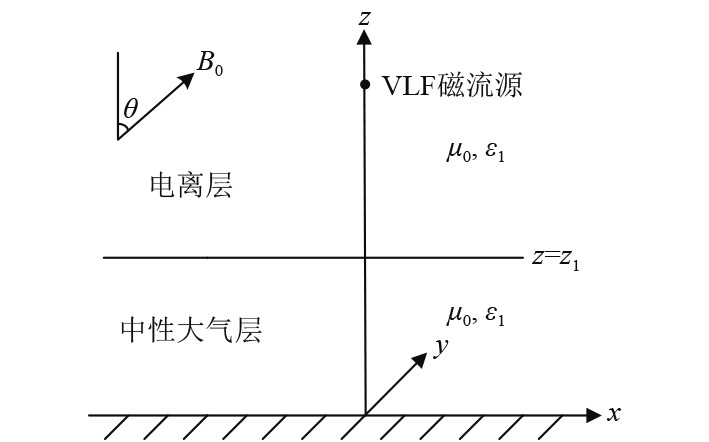
为方便计算分析，将电离层理想化为均匀锐边界各向异性的等离子体，计算选取的笛卡尔坐标系如图1所示。

选取 $x$ 轴使地磁场在 $x - z$ 平面内，并把地磁场 ${B_0}$ 与 $z$ 轴的夹角记为 $\theta$ ，其中电离层与中性大气层的分界面在 $z = {z_1}$ 处，VLF辐射源位于 $({\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {z_0}{\kern 1pt} )$ 处。电离层的介电常数在地磁场影响下是一个张量，VLF频率又远高于离子回旋频率，可忽略离子的影响，因此可表示为：

$\hat \varepsilon = {\varepsilon _0}(I + M)。$

(10)

式中： ${\varepsilon _0}$ 为真空中的介电常数(F/m)； $I$ 为3×3的单位矩阵； $M$ 为电离层的电极化率矩阵。

$\begin{aligned} & M = - \dfrac{X}{{U({U^2} - {y^2})}}\times\\ & \left[ \begin{gathered} {U^2} - {m_B}^2{y^2}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i{n_B}Uy{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - {m_B}{n_B}{y^2} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - i{n_B}Uy{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {U^2}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i{m_B}yU \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - {m_B}{n_B}{y^2}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - i{m_B}Uy{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {U^2} - {n_B}^2{y^2} \\ \end{gathered} \right] 。\end{aligned}$

(11)

式中： $X = {\omega _0}^2/{\omega ^2}$ ， ${\omega _0}$ 为电子的等离子体角频率， $\omega$ 为电波角频率； ${\kern 1pt} {\kern 1pt} U = 1 + i\upsilon /\omega$ ， $\upsilon$ 为电离层中电子的碰撞频率； $y = {\omega _H}/\omega$ ， ${\kern 1pt} {\kern 1pt} {\kern 1pt} {\omega _H}$ 为电子的回旋角频率， ${m_B}$ 和 ${n_B}$ 为地磁场在轴上的方向余弦。

1.3 计算方法

设场的时谐因子取为 ${e^{ - i\omega t}}$ ，则任意指向辐射源在介质中的电磁波满足Maxwell方程组：

$\left\{ \begin{gathered} \nabla \times E = i\omega {\mu _0}H + m\delta (x)\delta (y)\delta (z - {z_0}) \times (x\hat x + y\hat y + z\hat z) ，\\ \nabla \times H = - i\omega \hat \varepsilon E。\\ \end{gathered} \right.$

(12)

式中： $x{\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} y{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} z$ 为辐射源的方向余弦； ${\mu _0}$ 为自由空间的磁导率。

由于辐射源为垂直磁偶极子，则 $x = y = 0$ ， $z = 1$ 。通过傅里叶变换对Maxwell进行展开并消去 $z$ 方向上的分量，可得矩阵形式的方程组：

$\dfrac{{{\text{d}}W}}{{\text{d}}} = - i{k_0}TW + f\delta (z - {z_0})。$

(13)

式中： $W = {[{e_x},{e_y},{h_x},{h_y}]^{\rm{T}}}$ ； $f = \dfrac{m}{{4{\text{π} ^2}}}{[{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0,0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \dfrac{{{k_x}}}{{{k_0}}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \dfrac{{{k_y}}}{{{k_0}}}]^{\rm{T}}}$ ； ${k_0}$ 为自由空间的波数， ${k_x}$ 和 ${k_y}$ 为水平方向波数， $T$ 为特征矩阵。

$\begin{array}{l}T= \left[ {\begin{array}{*{20}{c}} {\dfrac{{{k_x}{M_{zx}}}}{{{k_0}(1 + {M_{zz}})}},}&{\dfrac{{{k_x}{M_{zy}}}}{{{k_0}(1 + {M_{zz}})}},}\\ { - \dfrac{{{k_x}{k_y}}}{{k_0^2(1 + {M_{zz}})}},}&{\dfrac{{k_x^2}}{{k_0^2(1 + {M_{zz}})}} - 1}\\ {\dfrac{{{k_y}{M_{zx}}}}{{{k_0}(1 + {M_{zz}})}},}&{\dfrac{{{k_y}{M_{zy}}}}{{{k_0}(1 + {M_{zz}})}},}\\ {1 - \dfrac{{k_y^2}}{{k_0^2(1 + {M_{zz}})}},}&{\dfrac{{{k_x}{k_y}}}{{k_0^2(1 + {M_{zz}})}}} \end{array}} \right.\\ \left. {\begin{array}{*{20}{c}} {{M_{yx}} - \dfrac{{{M_{yz}}{M_{zx}}}}{{1 + {M_{zz}}}} + \dfrac{{{k_x}{k_y}}}{{k_0^2}},}&{1 + {M_{yy}} - \dfrac{{{M_{yz}}{M_{zy}}}}{{1 + {M_{zz}}}} - \dfrac{{k_x^2}}{{k_0^2}},}\\ {\dfrac{{{k_y}{M_{yz}}}}{{{k_0}(1 + {M_{zz}})}},}&{ - \dfrac{{{k_x}{M_{yz}}}}{{{k_0}(1 + {M_{zz}})}}}\\ { - 1 - {M_{xx}} + \dfrac{{{M_{xz}}{M_{zx}}}}{{1 + {M_{zz}}}} + \dfrac{{k_y^2}}{{k_0^2}},}&{ - {M_{xy}} + \dfrac{{{M_{xz}}{M_{zy}}}}{{1 + {M_{zz}}}} - \dfrac{{{k_x}{k_y}}}{{k_0^2}},}\\ { - \dfrac{{{k_y}{M_{xz}}}}{{{k_0}(1 + {M_{zz}})}},}&{\dfrac{{{k_x}{M_{xz}}}}{{{k_0}(1 + {M_{zz}})}}} \end{array}} \right]。\end{array}$

(14)

当介质为有耗介质时，矩阵 $T$ 的4个特征值均为复数，其中2个虚部为正，对应特征波为下行波，2个虚部为负，对应特征波为下行波，则磁偶极子产生的场的傅里叶变换式可表示为：

$\begin{gathered} \tilde W = [{D_1}{W_1}{e^{i{k_0}{\lambda _1}(z - {z_0})}} + {D_2}{W_2}{e^{i{k_0}{\lambda _2}(z - {z_0})}}]u({z_0} - z) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [{U_1}{W_3}{e^{i{k_0}{\lambda _3}(z - {z_0})}} + {U_2}{W_4}{e^{i{k_0}{\lambda _4}(z - {z_0})}}]u(z - {z_0})。\\ \end{gathered}$

(15)

式中： ${\lambda _{{\kern 1pt} 1,2}}$ 对应下行波， ${\lambda _{{\kern 1pt} 3,4}}$ 对应上行波， ${W_{(j)}}(j = 1,2,3,4)$ 为各特征值对应的特征向量。将式(11)代入式(9)可求出激励系数 ${D_1}$ ， ${D_2}$ ， ${U_1}$ ， ${U_2}$ 。

波在电离层与中性大气层分界面存在反射，因此当 ${z_1} \lt z \lt {z_0}$ 时，电离层的场傅里叶变换式为：

$\begin{split} W = &{D_1}{W_1}{e^{i{k_0}{\lambda _1}(z - {z_0})}} + {D_2}{W_2}{e^{i{k_0}{\lambda _2}(z - {z_0})}} + \\ &{R_1}{W_3}{e^{i{k_0}{\lambda _3}(z - {z_1})}} + {R_2}{W_4}{e^{i{k_0}{\lambda _4}(z - {z_1})}}，\\ \end{split}$

(16)

式中， ${R_1}$ 和 ${R_2}$ 为电离层与中性大气层分界面反射系数。在 $z = {z_1}$ 处满足电磁场分量连续的边界条件，将电离层和中性大气层场的傅里叶变换式的对应水平分量进行联立，可求出 ${R_1}$ 和 ${R_2}$ 。海面上场的傅里叶变换式在准纵近似下时，通过傅里叶反变换可得到磁场的表达式为：

$\begin{gathered} {H_\rho }(\rho ,\phi )\left| {_{z = 0} = - \dfrac{{imP{\rm{sign}}({n_b})}}{{2\text{π} k_0^2\eta }}} \right. \cdot {e^{i{k_0}{\lambda _1}(d - {z_0})}}\sum\limits_{j = 0}^\infty \dfrac{{\rho {e^{i{k_0}{R_j}}}}}{{R_j^3}}\times \\ \quad\quad\quad\left[ {(\dfrac{3}{{R_j^2}} - \dfrac{{3i{k_0}}}{{{R_j}}}} \right. - k_0^2) + \dfrac{{{{[(2j + 1)d]}^2}}}{{R_j^2}}( - \dfrac{{15}}{{R_j^2}} + \dfrac{{15i{k_0}}}{{{R_j}}} + \\\quad\quad\;\;6k_0^2 - ik_0^3{R_j}) + \left. {k_0^2(1 + {\rm{sign}}({n_b}))( - \dfrac{1}{{R_j^2}} + \dfrac{{i{k_0}}}{{{R_j}}})} \right]，\end{gathered}$

(17)

${H_\phi }(\rho ,\phi ) \left| {_{z = 0}} \right. = \dfrac{{mP{\rm{sign}}({n_b})}}{{2\text{π} \eta }} \cdot {e^{i{k_0}{\lambda _1}(d - {z_0})}} \sum\limits_{j = 0}^\infty {\dfrac{{{e^{i{k_0}{R_j}}}}}{{{R_j}}}} ( - \dfrac{\rho }{{R_j^2}} + \dfrac{{i{k_0}\rho }}{{{R_j}}})。$

(18)

其中： ${R_j} = \sqrt {{{(2j + 1)}^2}{d^2} + {\rho ^2}}$ ， ${R_j} = \sqrt {{{(2j + 1)}^2}{d^2} + {\rho ^2}}$ ， $\eta = \sqrt {{\mu _0}/{\varepsilon _0}}$ ， ${\rm{ sign}}({n_b})$ 为 ${n_b}$ 的正负符号。

2 模拟结果分析 2.1 VLF磁流源

计算中背景电离层电子、离子的温度及密度由国际参考电离层模型(IRI-2016)确定，中性大气密度和温度由NRLMSISE-00大气模型确定。加热时间和地点分别为2021年7月21日12:00LT，武汉(地理坐标30.6°N, 114.3°E)。地磁场强度B₀= 5×10⁻⁵ T，电离层中自然电场强度E₀= 25 mV/m，设电离层下边界z₁= 65 km。加热调制波为方波，调制深度为1，调制频率f_VLF= 5 kHz，采用半波幅度调制。用于调制加热电离层的发射机入射X模式高频波频率和功率分别为7 MHz和200 MW。

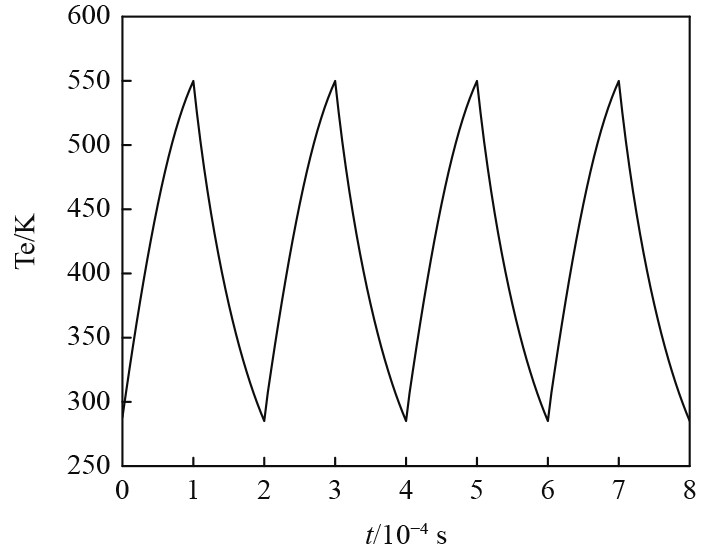
图2为当调制频率f_VLF= 5 kHz时电离层加热过程中电子温度的周期变化，温度最大值相对于初始温度增加了264.8 K。在调制过程中前半个周期( $Q \ne 0$ )是加热过程，后半个周期( $Q = 0$ )是冷却过程，由于调制时间小于电子温度达到饱和的时间，电子温度在一个周期内没有充分加热就开始冷却。因此当调制频率越小，调制周期越大，电离层的加热更加充分，电子温度的扰动更大，在温度最大值附近的变化更平缓。加热功率也能影响电子温度的扰动，通常功率越大，温度变化越明显。

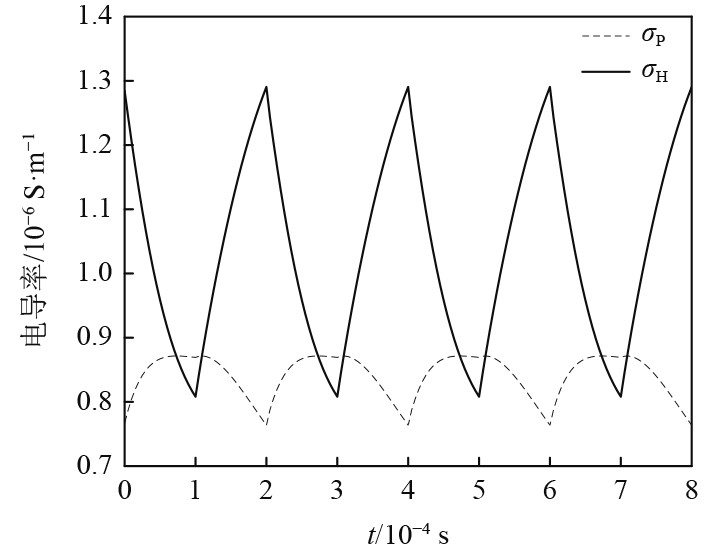
电离层中的自然电流产生振荡的直接原因是电导率的扰动，在自然电场的作用下使电流发生变化。由于磁力线近似于等位线，平行电场很小，因此可忽略平行电导率的作用。电子温度的周期变化影响了电导率，图3为电离层75 km高度处Pedersen电导率和Hall电导率的周期变化。在低电离层，2种电导率相位相反，且Hall电导率在调制中占主导位置。通过式(8)可计算电流变化大小，产生的振荡电流可对空间辐射出5 kHz的电磁波。当对电离层中多个区域进行加热，可使产生的多个电偶极子组成一个磁偶极子辐射源，假设L=1 km，可根据式(9)可得到该VLF辐射源的磁偶极矩。

2.2 传播特性

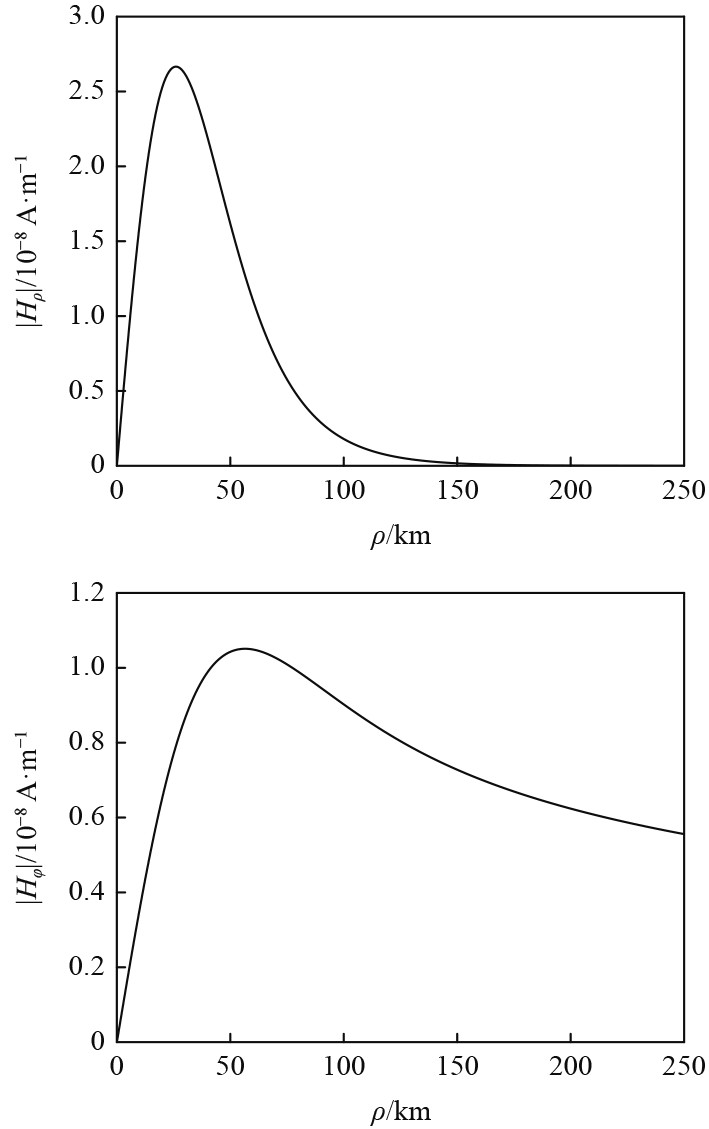
在电离层中的VLF磁流源可向下激励出特征波，其中寻常波是衰减波，对应的特征值具有很大的虚部，衰减很大，非寻常波对应的特征值虚部很小，能有效在电离层中向下传播，且只有垂直或接近垂直方向的电磁波(即水平方向波矢量几乎为0)才能透射到中性大气层，否则会产生全反射^[21]。图4给出了当电磁波接近垂直向下传播，T_e=288 K，f_VLF= 5 kHz， $\theta = 30^\circ$ 时海面上激起的场强。可以看出，在磁偶极子正下方激起的场为0，之后随着 $\rho$ 的增大而增大，在40 km附近场强达到最大值，其强度为 ${10^{ - 8}}{\rm{A/m}}$ 量级，在强度达到最大值后又逐渐减弱。

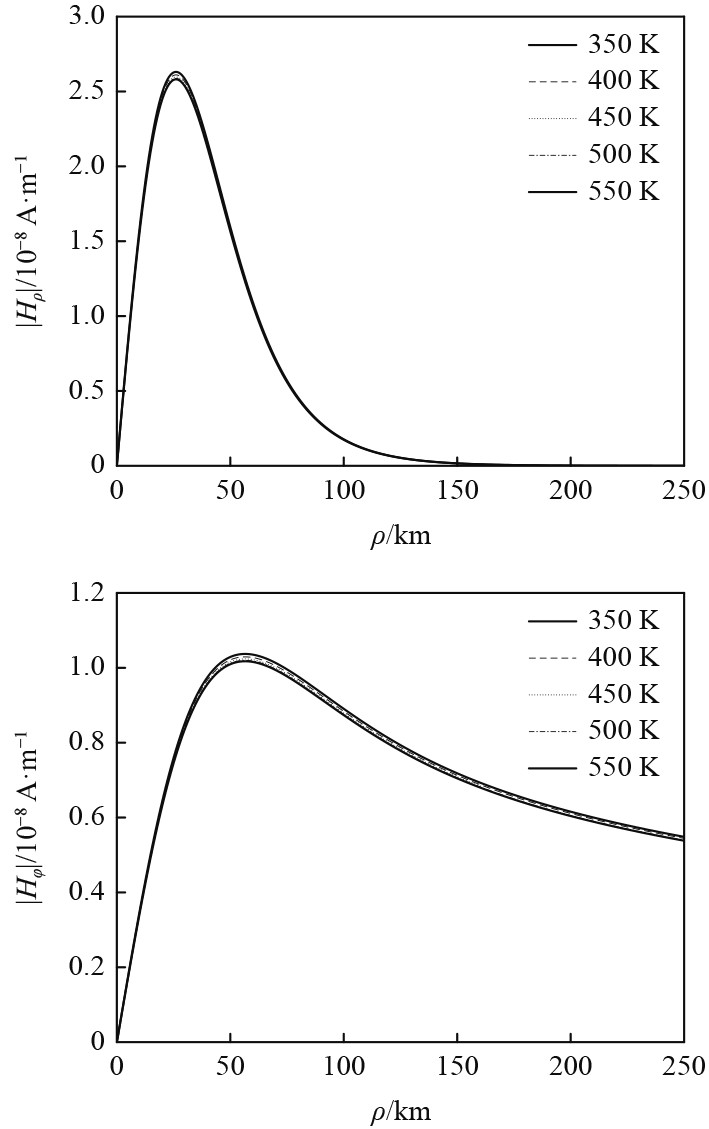
由于在加热过程中，区域内的电子温度进行周期变化，与温度有关的参数(如U, $\nu$ 等)也发生变化，进而会对电磁波的传播产生影响。图5给出了不同温度下磁流源在海面上的场强，可以看出，磁流源在海面上激起的磁场幅度随温度的升高而减小，但衰减不明显，仅在峰值附近有较大差距，因此加热电离层的过程中温度的变化对该磁流源辐射的电磁波传播影响较小，VLF磁流源较为稳定。

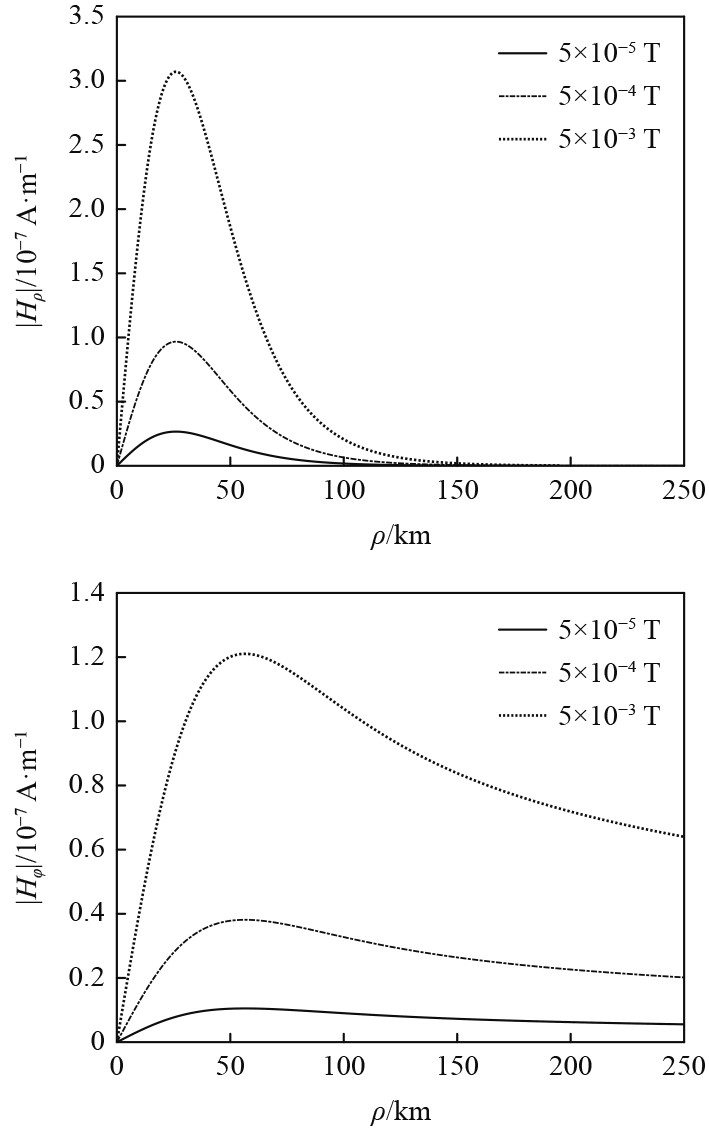
用于加热电离层的地基大功率发射机可建在不同地理位置，不同位置的地磁场强度也不同，因此讨论不同的地磁场强度对VLF波向下传播的影响。当 $\theta = 30^\circ$ 不变，计算地磁场强度分别为5×10⁻⁵ T，5×10⁻⁴ T，5×10⁻³ T时海面上的磁场强度。如图6所示，不同条件下所产生的场有相似变化趋势，地磁场强度越大，所产生的磁场强度也越大，其中地磁场强度每提高10倍， $|{H_\rho }|$ 和 $|{H_\varphi }|$ 的最大值都可提高5 dB左右。这可能是地磁场强度增大，电子回旋频率也增大，影响了由于碰撞损失的能量。

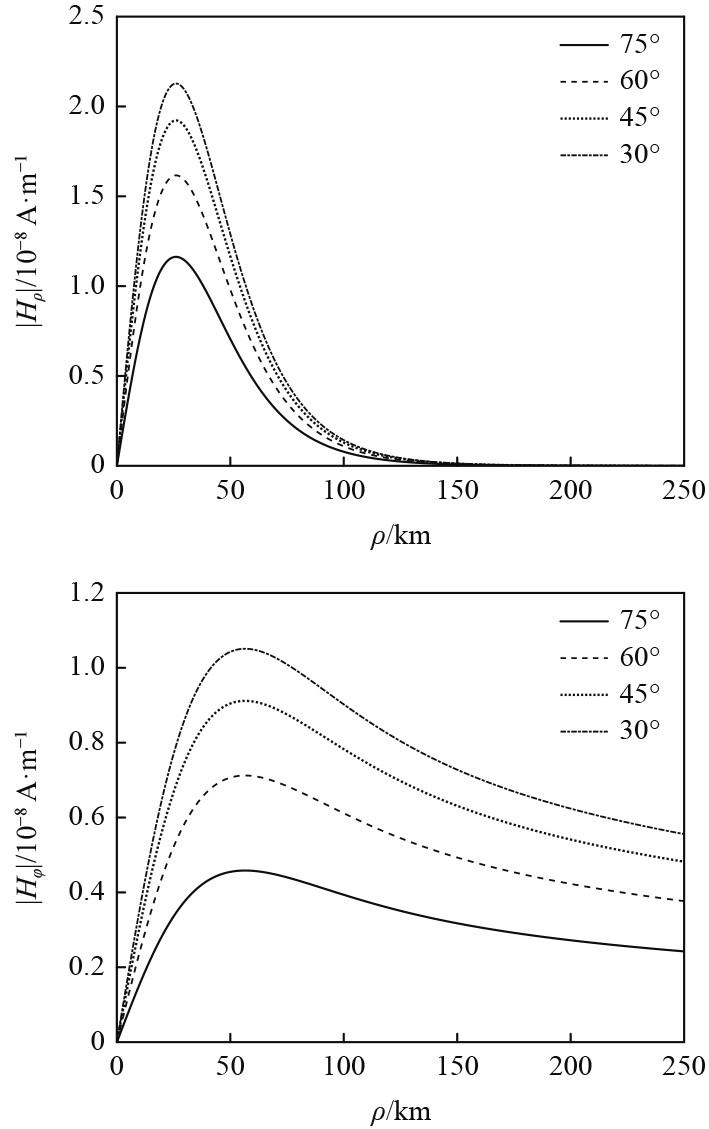
当地磁场强度为5×10⁻⁵ T，计算 $\theta$ 分别为30°，45°，60°，75°时VLF磁流源在海面上的场强。其中夹角 $\theta$ 不断增大，表示所在地理位置的纬度越来越低。由图7可见，高纬度地区的场强幅度明显大于低纬度地区的场强幅度，以 $\left| {{H_\rho }} \right|$ 为例，当 $\theta$ 从 $75^\circ$ 增大到 $30^\circ$ 时，场强的幅度可提高3 dB左右。这主要是因为 $\theta$ 影响了低电离层对电磁波的吸收衰减，夹角越小，电离层的吸收作用越强烈。

3 结　语

本文建立人工调制加热电离层模型，对加热过程中电离层各参数的变化和VLF磁流源的形成过程进行计算和分析。进一步建立电离层中磁流源的模型，利用全波解的方法对该源辐射的电磁波在低电离层中的传播进行求解，得到了海面上的磁场强度，并利用该模型研究不同电子温度和不同地磁场参数条件下对海面上激起场强的影响，得出以下结论：

1）VLF磁流源的形成主要是由于电子温度的改变使电离层中的电导率发生了扰动，从而自然电流产生振荡辐射电磁波。在VLF频段，调制频率越低，调制周期越长，可使电子温度加热更充分，从而产生更大的自然电流振荡，增大磁偶极矩。加热功率越大，电子温度上升越高，也能增大磁偶极矩。

2）调制加热电离层过程中电子温度上升，对电磁波在低电离层中的传播衰减几乎没有影响，其在海面上的场强只在最大值附近有较大变化，说明VLF波传输损耗较小，该VLF磁流源较为稳定。

3）地磁场强度和 $\theta$ ，对电磁波的传播衰减有较大的影响，其主要影响低电离层对电磁波的吸收。因此当研究电磁波在电离层的传播时，必须考虑地磁场参数的影响。通常纬度越高，地磁场越大，衰减越小，则VLF波能更有效进行传播。

本文建立的磁流源模型较理想化，忽略了振荡电流方向的影响，需进一步进行改进。此外在地磁场参数的分析中，没有考虑高度、纬度等的影响，需通过地磁场模型完善研究内容。