0 引　言

在石油、天然气等可再生资源日益减少的今天，电力驱动船等新能源船舶的开发成为一种行业的趋势，电力驱动船舶的电力通常来自于柴油发电机，柴油发电机将化石燃料的内能转换为电能，进而驱动电动机和螺旋桨，使船舶产生前进的动力。进入21世纪，电力驱动船舶的吨位不断提高，由此对电力驱动系统的负载要求也在日益增加，主要体现在两方面，一是对于电力驱动系统的功率要求更高，常规的小兆瓦级别柴油发电机的功率已经难以满足；二是对于柴油发电机系统的稳定性有更高要求，这就要求柴油发电机具有良好的转速控制技术。

本文建立船舶柴油发电机的函数模型，介绍柴油发电机调速系统工作原理，基于PID控制理论和液压伺服控制技术，优化了船舶柴油发电机的转速控制系统。

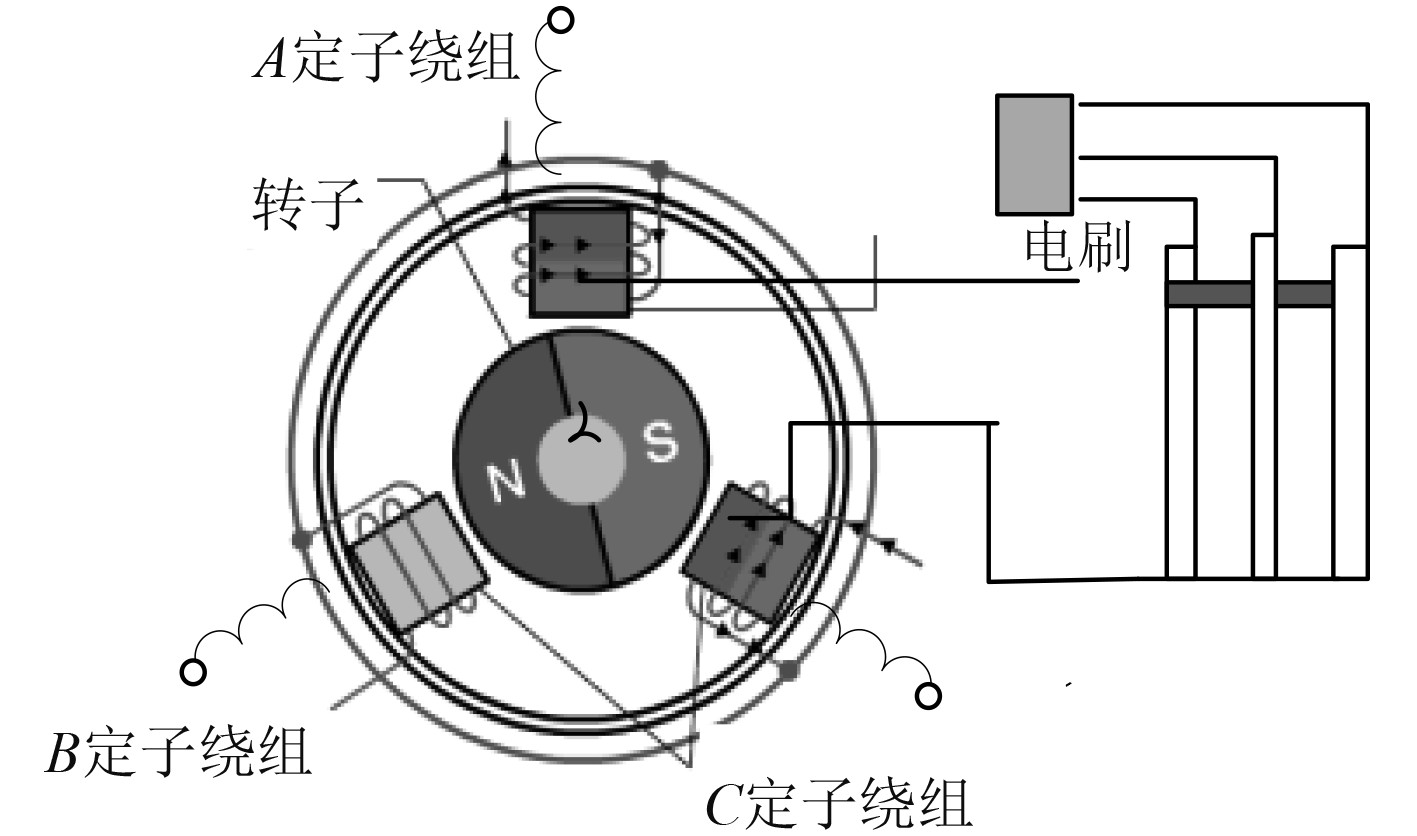
1 三相永磁柴油发电机的数学模型

大多数电力驱动船舶的电力来源是三相永磁柴油发电机，其模型如图1所示。

三相永磁柴油发电机的坐标系由静止坐标系A-B-C及旋转坐标系a-b-c组成，坐标系的转换是发电机控制策略优化的关键环节，建立三相永磁柴油发电机坐标变换方程如下式：

$\left[ {\begin{array}{*{20}{c}} {{f_a}} \\ {{f_b}} \\ {{f_c}} \end{array}} \right] = \sqrt {\displaystyle\frac{2}{3}} \left[ {\begin{array}{*{20}{c}} {\cos \theta }&{\cos ( - \displaystyle\frac{{2\text{π} }}{3})}&{\cos (\theta + \displaystyle\frac{{2\text{π} }}{3})} \\ { - \sin \theta }&{\sin ( - \displaystyle\frac{{2\text{π} }}{3})}&{ - \sin (\theta + \displaystyle\frac{{2\text{π} }}{3})} \\ {\sqrt {\displaystyle\frac{1}{2}} }&{\sqrt {\displaystyle\frac{1}{2}} }&{\sqrt {\frac{1}{2}} } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{f_A}} \\ {{f_B}} \\ {{f_C}} \end{array}} \right] \text{，}$

$\left[ {\begin{array}{*{20}{c}} {{f_A}} \\ {{f_B}} \\ {{f_C}} \end{array}} \right] = \sqrt {\displaystyle\frac{2}{3}} \left[ {\begin{array}{*{20}{c}} {\cos \theta }&{ - \sin \theta }&{\sqrt {\displaystyle\frac{1}{2}} } \\ {\cos (\theta - \displaystyle\frac{{2\text{π} }}{3})}&{ - \sin ( - \displaystyle\frac{{2\text{π} }}{3})}&{\sqrt {\displaystyle\frac{1}{2}} } \\ {\cos (\theta + \displaystyle\frac{{2\text{π} }}{3})}&{ - \sin (\theta + \displaystyle\frac{{2\text{π} }}{3})}&{\sqrt {\displaystyle\frac{1}{2}} } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{f_a}} \\ {{f_b}} \\ {{f_c}} \end{array}} \right] 。$

其中， ${\left[ {{f_a},{f_b},{f_c}} \right]^\text{T}}$ 为三相永磁柴油发电机在静止坐标系下的电流、电压和磁链变量。 ${\left[ {{f_A},{f_B},{f_C}} \right]^\text{T}}$ 为三相永磁柴油发电机在旋转坐标系下的电流、电压和磁链变量。

建立三相永磁柴油发电机绕组电压表达式为：

$u = R{l^2} + pLi = R{i^2} + p\psi 。$

其矩阵形式为：

$\left[ {\begin{array}{*{20}{c}} {{u_1}} \\ {{u_2}} \\ {{u_3}} \\ {{u_4}} \\ {{u_5}} \\ {{u_6}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{R_1}}&0&0&0&0&0 \\ {}&{{R_2}}&0&0&0&0 \\ {}&{}&{{R_3}}&0&0&0 \\ {}&{}&{}&{{R_4}}&0&0 \\ {}&{}&{}&{}&{{R_5}}&0 \\ {}&{}&{}&{}&{}&{{R_6}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{i_a}} \\ {{i_b}} \\ {{i_c}} \\ {{i_d}} \\ {{i_e}} \\ {{i_f}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\psi _A}} \\ {{\psi _B}} \\ {{\psi _C}} \\ {{\psi _D}} \\ {{\psi _E}} \\ {{\psi _F}} \end{array}} \right] 。$

其中： ${u_1} - {u_6}$ 为三相永磁柴油发电机定子绕组电压值； ${i_a} - {i_f}$ 为三相永磁柴油发电机转子绕组电流； ${R_1} - {R_6}$ 为电阻； ${\psi _A}$ - ${\psi _F}$ 为发电机的磁势^[1]。

三相永磁柴油发电机的机械损耗会影响发电机的整体效率，考虑机械损耗的船舶柴油发电机运动模型可用下式表示：

${T_i} = {T_l} + \frac{J}{{{n_p}}}pw + \frac{D}{{{n_p}}}w + \frac{K}{{{n_p}}}{\theta _{_R}} 。$

式中： ${T_l}$ 为发电机输出转矩； ${n_p}$ 为发电机的转速； $J$ ， $D$ ， $K$ 分别为刚度系数，弹性系数和阻尼系数； $w$ 为发电机的角速度； ${\theta _{_R}}$ 为旋转角度。

2 船舶柴油发电机转速控制系统的开发设计 2.1 柴油发电机的液压调速器原理与建模

本文研究的船舶柴油发电机以中速四冲程柴油发电机为主，作为电力驱动船舶的能量来源，发电机要在负载变化时保持转速恒定，进而确保输出的电压和频率恒定。当电力驱动船舶的用电负载明显增加时，柴油发电机的转矩会低于所需转矩，此时如果不进行发电机的调速控制，增加柴油机供油量，柴油发电机就会因为转矩不平衡出现停车。与此同时，当船舶发电机的负载出现明显的减小时，如果不及时减小循环供油量，控制发电机的转矩，机组就会出现转速的异常升高。

由于柴油发电机本身不具有调速功能，因此要想实现柴油发电机的稳定控制，必须要增加调速器，设计对应的速度控制系统。

调速器可以分为电子式、液压式、机械式调速器等多种，针对船舶柴油发电机较为恶劣的工作环境，本文选择液压式调速器进行柴油发电机的速度控制。

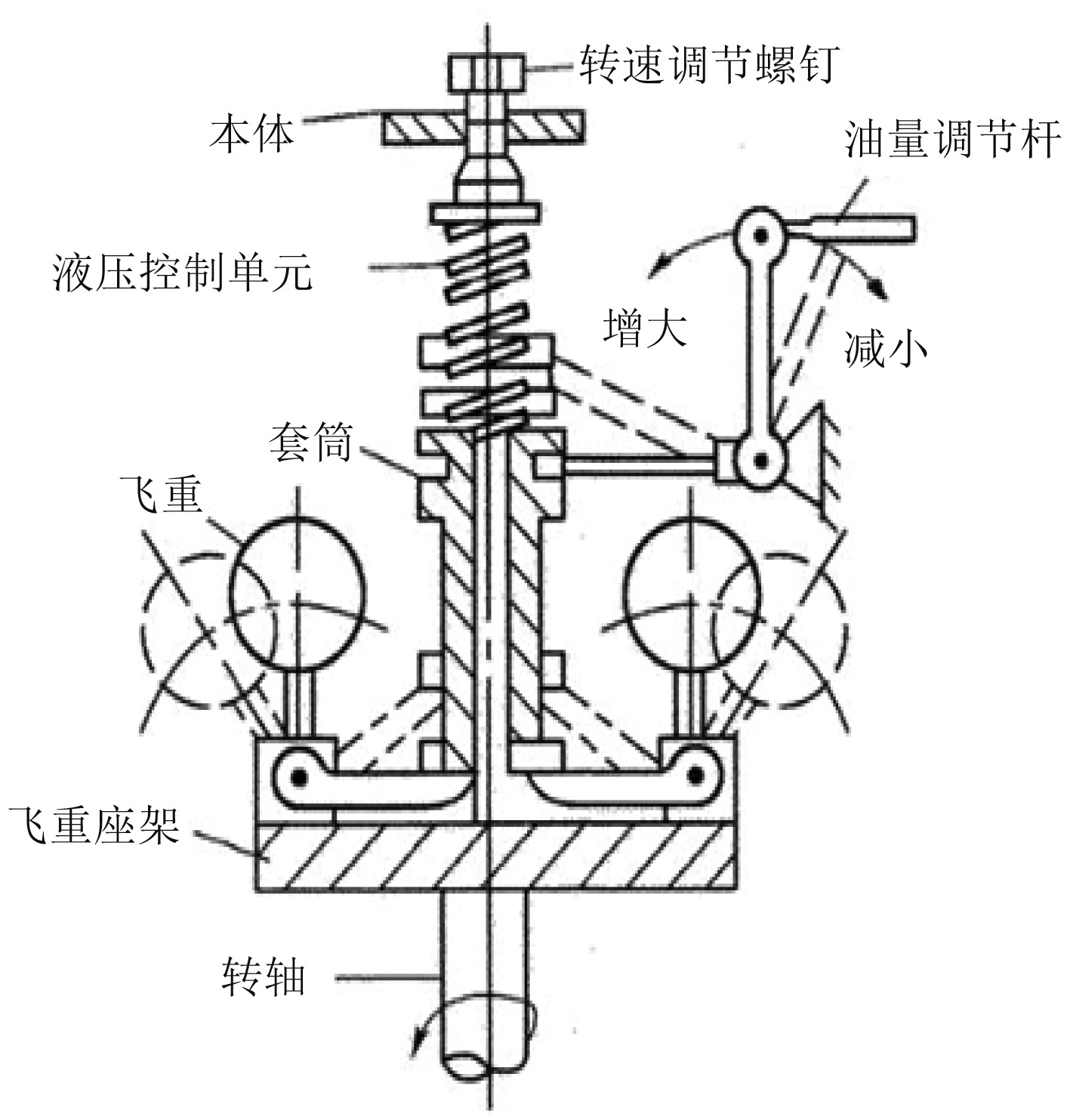
图2为液压式柴油发电机的调速器原理图。

基于液压调速器的控制理论，对调速器的液压执行机构进行数学建模，包括流量、压力等。

1）控制阀

在液压调速执行机构中，控制阀的负荷流量 ${Q_L}$ 与压力 ${p_L}$ 和位移 ${x_r}$ 互相关联，即

${Q_L} = f\left( {{x_r},{p_L}} \right) \text{，}$

该非线性关系可以用泰勒公式进行展开^[2]，拟合出较为准确的函数，即

${Q_L} = \Delta {Q_{L1}} + {\left. {\frac{{\partial {Q_L}}}{{\partial {x_r}}}} \right|_1}\Delta {x_r} + {\left. {\frac{{\partial {Q_L}}}{{\partial {p_L}}}} \right|_2}\Delta {p_L} + ... \text{，}$

忽略阶段分量，可简化为：

${Q_L} = {\left. {\frac{{\partial {Q_L}}}{{\partial {x_r}}}} \right|_L}\Delta {x_r} + \left. {\frac{{\partial {Q_L}}}{{\partial {p_L}}}} \right|\Delta {p_L} 。$

2）流量增益

${K_q} = \frac{{\partial {Q_t}}}{{\partial {x_v}}} 。$

3）压力增益

${K_p} = \frac{{\partial {p_L}}}{{\partial {x_r}}} 。$

4）流量-压力系数

${K_c} = - \frac{{\partial {Q_L}}}{{\partial {p_L}}} 。$

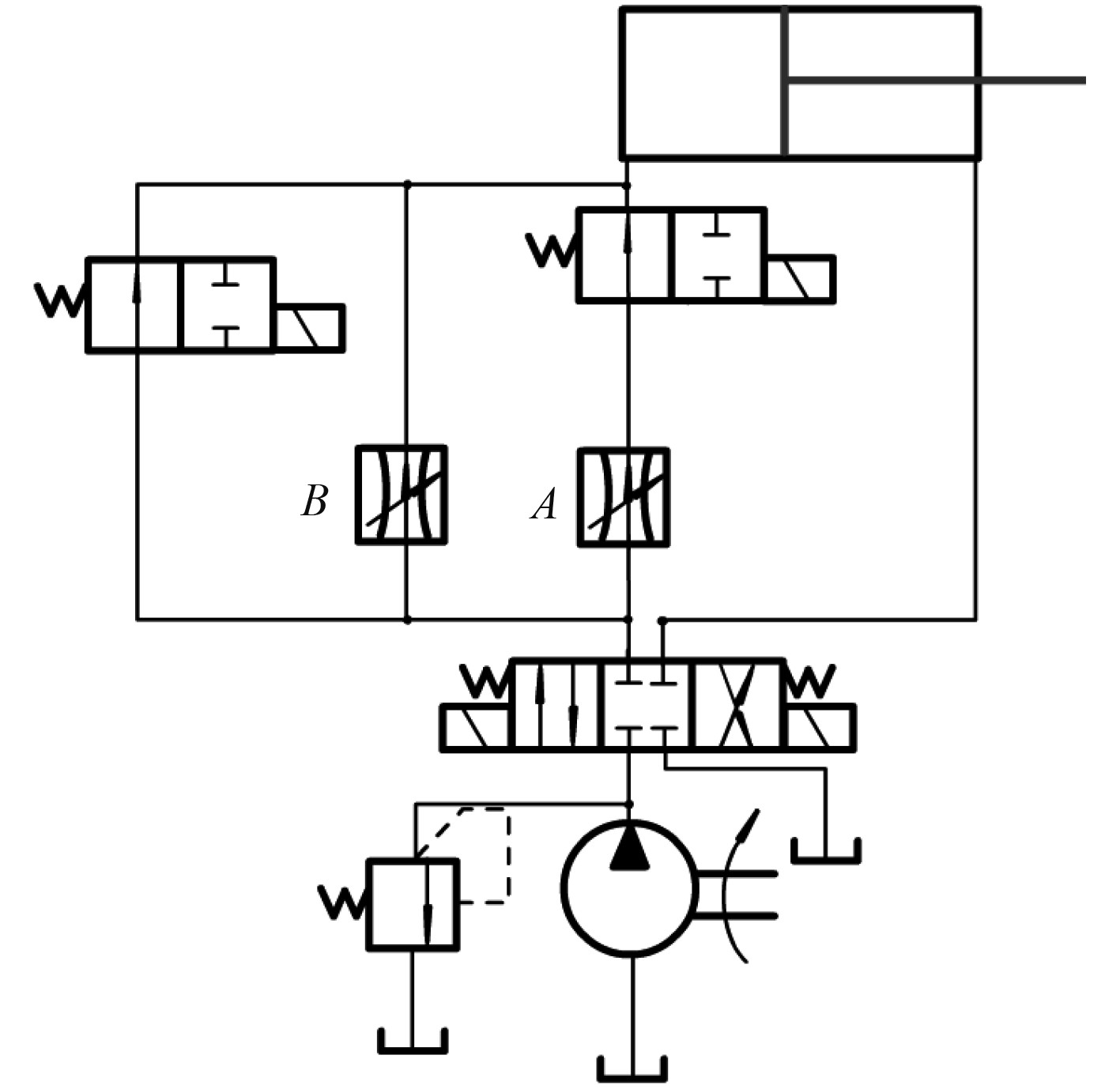
柴油发电机调速器的液压执行机构原理图如图3所示。

2.2 基于PID控制器的船舶柴油发电机转速控制系统设计

为了提高船舶柴油发电机转速控制系统的性能，引入PID控制算法^[3]。这种算法作为一种负反馈算法，在电动机、发电机控制领域有广泛应用。

PID控制算法的模型可以写为：

$u(t) = {K_P}\left[ {e(t) + \frac{1}{{{T_i}}}\int_0^t e (t){\rm{d}}t + {T_b}\frac{{\text{d}e(t)}}{{\text{d}t}}} \right] \text{。}$

其中： $e(t)$ 为输入与输出的偏差量； ${K_P}$ 为比例系数； ${T_i}$ 为算法的积分系数； ${T_b}$ 为算法的微分系数。

PID算法的传递函数为：

$G(s) = \frac{{U(s)}}{{E(s)}} = {K_p}\left( {1 + \frac{1}{{{T_f}s}} + {T_b}s} \right) 。$

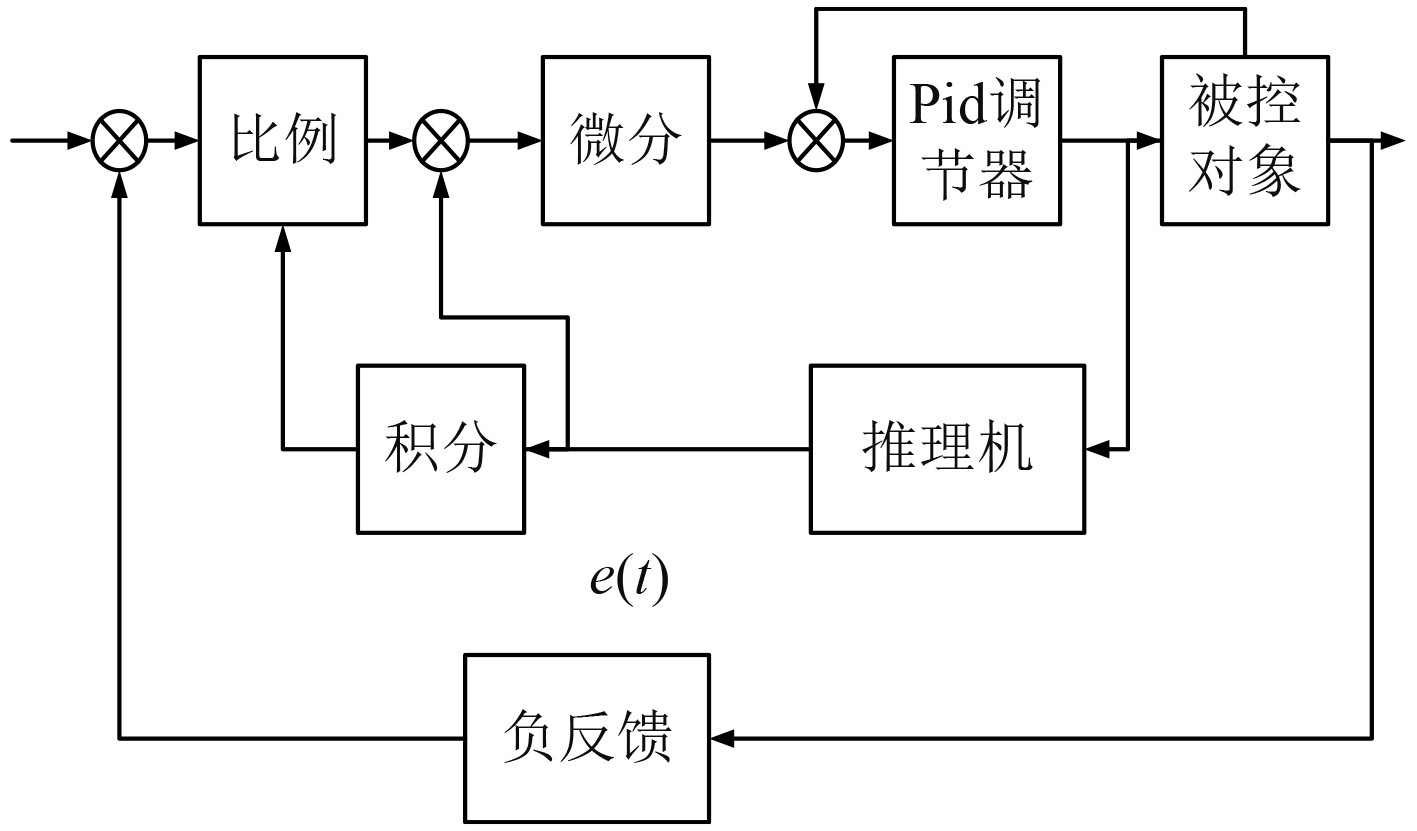
图4为PID控制算法的原理图。

PID算法的核心为3个环节。

1）比例环节

比例环节表征了系统输入信号与输出信号的偏差比例关系，决定了控制系统的响应速度，比例系数越大，系统的响应速度越快。但同时，比例系数过大会影响系统的稳定性，造成系统震荡。

2）积分环节

积分环节对于降低系统的静态误差有主要的作用，积分系数越大，纠偏能力就越强。

3）微分环节

微分环节有利于解决控制系统的动态变化，具有一定的预测性。

采用数字PID控制器进行柴油发电机的转速控制，数字PID的时域模型为：

$u(kT) = {K_p}\left\{ {e(kT) + \frac{T}{{{T_i}}}\sum\limits_{j = 0}^k {e(jT) + \frac{{{T_d}}}{T}\left[ {e(kT) - e(kT - T)} \right]} } \right\} 。$

式中：T为采样周期；k为采样序列号，k=0，1,2…；经z变换之后，得

$U(z) = {K_p}\left\{ {E(z) + \frac{{TE(z)}}{{{T_i}(1 - {z^{ - 1}})}} + {T_d}\left[ {E(z) - {z^{ - 1}}E(z)} \right]/T} \right\} \text{，}$

PID数字调节器的z传递函数为：

$D（z）=\frac{U(z)}{E(z)}={K}_{p}+{T}_{i}\frac{1}{1-{z}^{-1}}+{T}_{d}(1-{z}^{-1}) \text{。}$

可以看出，PID调节器的控制品质的优劣取决于 ${K_{\text{p}}}$ ， ${T_i}$ ， ${T_d}$ 三个参数的选择。

2.3 基于PID控制器的转速控制系统仿真

基于Simulink软件的模块化程序^[4]，对船舶柴油发电机的调速控制进行仿真，试验采用的发电机模块是软件平台Simpower模块库^[5]中的三相永磁同步发电机模块。

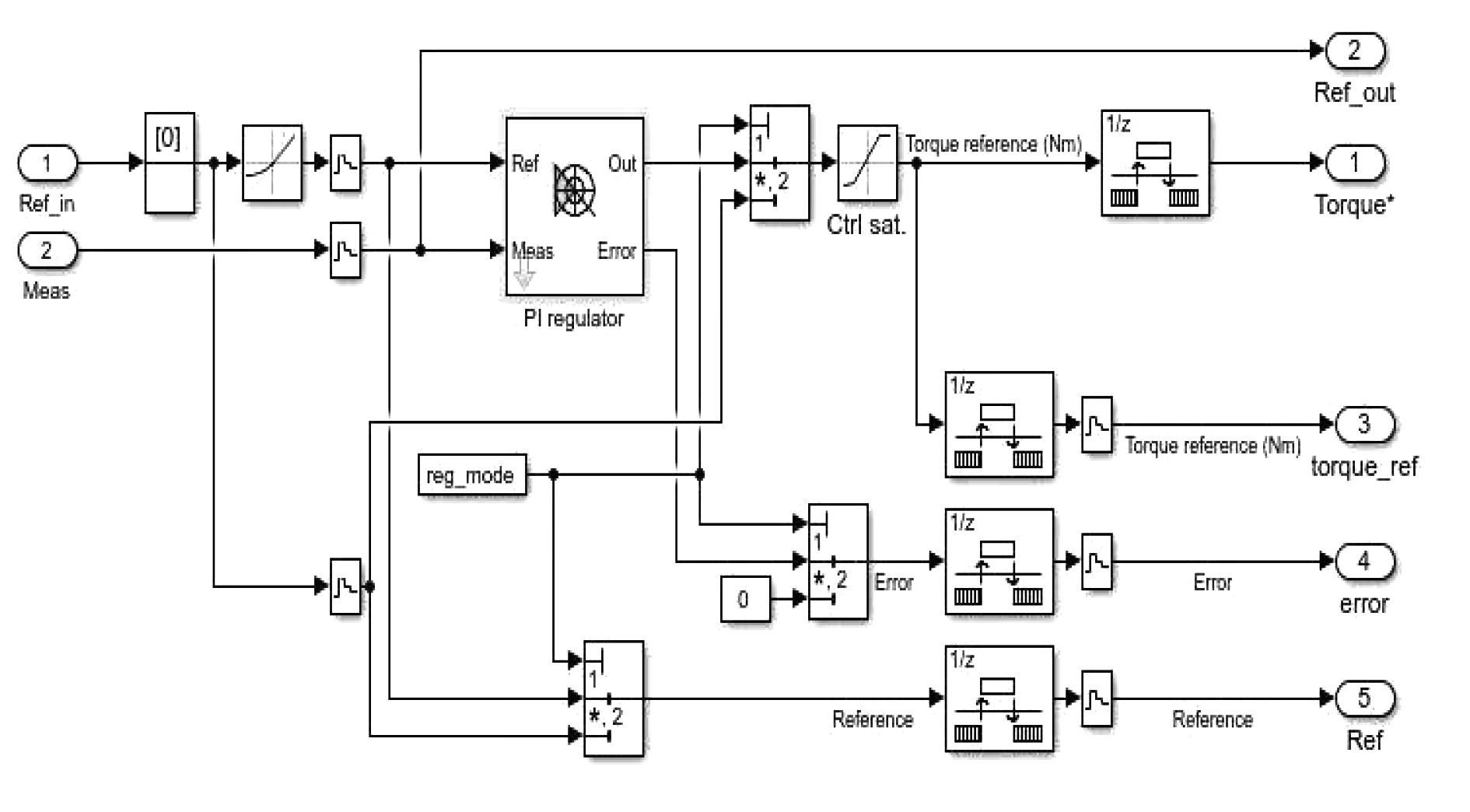
搭建的柴油发电机速度控制simulink仿真程序如图5所示。

船舶柴油发电机关键参数包括定子和转子电阻、电感、互感等^[4]，表示如下：

$p = \left[ {{p_1},{p_2},{p_3},{p_4}} \right]\text{。}$

其中： ${p_1} = \displaystyle\frac{1}{{{T_i}}}$ ； ${p_2} = \displaystyle\frac{{{L_m}}}{{{T_i}}}$ ； ${p_3} = \displaystyle\frac{{{R_a}{L_m}^2}}{{\delta {T_i}}}m$ ； ${T_i}$ 为平均输出转矩； ${L_m}$ 为电感； ${R_a}$ 为电阻； $\delta$ 为功率因数。仿真使用的船舶柴油发电机参数如表1所示。

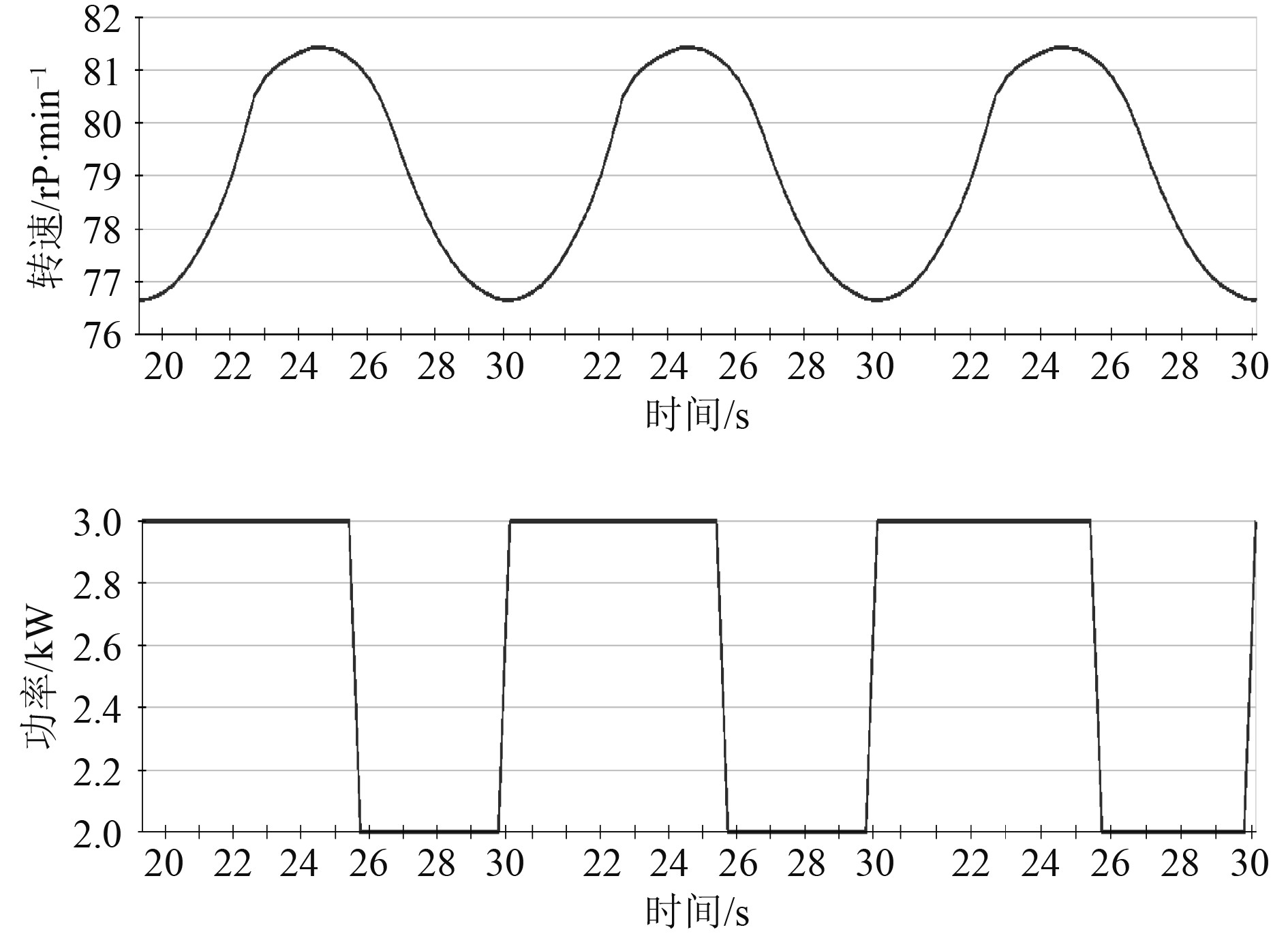
图6为船舶柴油发电机转速-功率仿真曲线，可以发现在转速变化时，船舶柴油发电机的输出功率保持稳定，这也保证了船舶电力供应的高度稳定性^[6]。

3 结　语

为了保障柴油发电机的负载-转速稳定性，本文结合柴油发电机的数学模型，开发了基于PID控制算法的船舶柴油发电机转速控制系统，并利用simulink平台进行了转速控制系统的仿真。结果表明，转速变化时，输出功率保持稳定。