随着大数据分析技术的不断发展,面向船舶主机分析与应用已经成为船舶行业的研究热点。智能船舶采集的大量实船数据为主机的性能分析、故障诊断预测以及维护提供可靠的依据,可以利用大数据分析、人工智能、机器学习等先进技术分析出每艘船每个主机每个工况下的运行特点,从而提供合理的主机性能评估结果,依据评估结果能够有效地制定因船制宜的维护方案。
大数据分析先进技术进行工况分析已经在交通运输行业广泛应用。秦大同等[1]利用K-均值聚类算法构建了城市循环工况,从而更好地反映实际交通道路状况。肖权[2]以船舶低速柴油机为研究对象,应用神经网络算法构建故障诊断及趋势预测系统。李添翼[3]利用小波神经网络算法对船舶主机进行分析。张嘉琦等[4]结合高斯混合模型(GMM)和深度神经网络来预估大型船舶的主机输出功率。目前国内外对船舶主机的研究主要集中在主机的故障分析和预测上,对如何识别不同的工况,从而根据不同工况进行故障分析的研究较少。船舶主机的工况状态识别是故障分析的基础,划分合理的船舶主机运行工况为确定船舶污染物排放量、预估燃油消耗量、评估主机性能评估以及主机关键设备故障诊断预测等方面奠定基础,为船舶设备管理和维护提供参考依据[5]。
本文以某船为例,综合考虑实船采集到的各特征参数之间的相关性,确定主机工况划分的主要特征参数,引入置信区间找出目标船主机在主要营运要求下的转速范围,结合GMM算法构建主机工况划分方法,并对各个工况设备参数进行特征值分析。研究结果表明,基于GMM算法的工况划分方法可以对复杂的主机运行数据进行有效划分,能够很好地反映目标船主机的运行特点。
1 主机运行工况构建方案本文构建主机工况的主要流程分为实船数据处理、特征参数选取以及工况划分3个部分。
实船数据处理:根据目标船主机特性对实船数据进行分析处理,确定目标船舶在正常营运期间的主机功率、转速分布范围。剔除主机非正常运行的实际数据,得到符合目标船营运规律的实船数据。实船数据主要包含GPS、航速、风速风向、主机油耗以及主机关键参数等数据。
特征参数选取:对实船采集的多个特征参数进行分析,计算各个特征参数和主机功率的相关性程度,选择相关性最高的特征参数作为工况划分的特征值。
工况划分:引入置信区间对筛选后的实船数据进行主要营运范围计算,得到常见营运下的实船数据范围,结合GMM聚类算法,划分出主机正常营运下的各个工况。
基于GMM聚类算法的主机工况构建总体流程如图1所示。

|
图 1 主机工况划分框架 Fig. 1 Construction framework of main engine working conditions |
实船数据主要包含:经纬度数据、吃水数据、航行数据、气象数据、主机转速、主机功率以及主机其他关键参数。各设备以秒为时间单位输出实时数据,将未处理的秒级数据存入数据库之后,剔除各设备传输的异常数据,如空值等。在确保数据准确性的基础上根据各类数据特征将实船数据进行预处理,计算出小时级船舶实时数据。
为了确保划分出的工况可靠性,在工况划分之前,需对船舶数据进行初步筛选,获得船舶稳定运行期间的各类主要数据,主要筛选条件如下式:
| $ \left\{ {\begin{array}{*{20}{l}} {Rp{m_i} \gt 0.5Rp{m_{\max }}} ,\\ {V{s_i} \gt 0.5{V_{design}}} ,\\ {|Rp{m_i} - Rp{m_{i + 1}}|/Rp{m_i} \leqslant 0.05} ,\\ \begin{gathered} |Rp{m_i} - Rp{m_{i + 2}}|/Rp{m_i} \leqslant 0.05 ,\\ |Rp{m_{i + 2}} - Rp{m_{i + 1}}|/Rp{m_{i + 1}} \leqslant 0.05 。\\ \end{gathered} \end{array}} \right. $ | (1) |
式中:Rpmi为i时刻的主机转速,Rpmmax为主机最大转速,Vsi为i时刻的对水航速,Vdesign为设计航速。
选取的目标船主机最大转速76 r/min、设计航速15 kn,提取14个月的实船数据,约12000条小时级数据,根据式(1)的限制条件进行初步筛选后得到约8100条可用于后续研究的数据。
3 GMM算法GMM假定所有数据都是从有限数据的高斯分布与未知参数的混合中生成的,这是一种基于最大似然估计的概率模型。可以将高斯混合模型由k个单一高斯机率密度函数组合而成,每个有相应的均值和协方差,以合并有关数据协方差结构以及潜在高斯中心的信息[6]。其表达式如下式:
| $ p(x) = \sum\limits_{k = 1}^K {{\text{π} _k}N(x|{\mu _k},{\Sigma _k})}。$ | (2) |
式中:N(x|μk,Σk)为第k个子模型的高斯分布密度函数;μk为第k个子模型的样本均值,Σk为第k个子模型的协方差;πk为第k个高斯分布所占的权重,且满足式(3)约束条件。
| $ {\displaystyle \sum _{k=1}^{K}{\pi}_{k}}=1,\begin{array}{ccc}& & {\pi}_{k}\in \end{array}\left\{0\text{,}1\right\}。$ | (3) |
高斯概率密度分布函数表示为下式:
| $ N(x|{\mu _k},{\Sigma _k}) = \frac{1}{{\sqrt {{{(2\pi_k )}^d}|{\Sigma _k}|} }}\exp [ - \frac{1}{2}{(x - {\mu _k})^\text{T}}{\Sigma ^{ - 1}}(x - {\mu _k})] ,$ | (4) |
式中,d为数据的维度。
假设θk={μk,Σk},对应的GMM似然函数为下式:
| $ p(x|{\theta _k}) = \sum\limits_{k = 1}^K {{\pi _k}N(x;{\theta _k})} ,$ | (5) |
设θ={Π1, Π2, ..., Πk;θ1, θ2, ..., θk}, 则θ为GMM中待估计的参数。应用期望最大算法(EM)求解式(5),输入变量数据xi(i=1,...,N),步骤如下:
步骤1 随机初始化模型参数θ的初始θ0。
步骤2 开始E步算法,根据当前模型参数,计算分模型k对数据xj的响应度。
| $ \gamma ({Z_{nk}}) = \frac{{{\pi _k}N({x_n}|{\mu _k},{\Sigma _k})}}{{\displaystyle\sum\limits_{j = 1}^K {{\pi _j}N({x_n}|{\mu _j},{\Sigma _j})} }} 。$ | (6) |
步骤3 迭代更新模型的参数。
| $ \mu _k^{new} = \frac{1}{{{N_k}}}\sum\limits_{n = 1}^N {\gamma ({Z_{nk}})} {X_n} ,$ | (7) |
| $ \Sigma _k^{new} = \frac{1}{{{N_k}}}\gamma ({Z_{nk}})({X_n} - \mu _k^{new}){({X_n} - \mu _k^{new})^\text{T}} ,$ | (8) |
其中,
步骤4 估算对数似然函数的值。
| $ \ln p(X|\mu ,\Sigma ,\pi ) = \sum\limits_{n = 1}^N {\ln \{ \sum\limits_{k = 1}^K {{\pi _k}N({X_n}|{\mu _k},{\Sigma _k})} \} } 。$ | (9) |
重复步骤2、步骤3步直至算法收敛。
4 特征参数选取与GMM聚类分析 4.1 特征参数选取在运行过程中,船舶主机输出功率受多个变量参数的影响,选择适当的特征参数进行分析,不但可以提高工况划分的可行度也能减少聚类分析的运算时间。
实际分析时,相关系数被用来量化随机变量之间的相关性。选取船舶对水航速Vs、主机转速RPM、平均吃水Draft、遭遇真风速Vw、对地航速Vg、主机扫气箱平均温度Tscav、主机气缸排气出口温度Tge、主机气缸缸套冷却水出口温度Tcfw、主机气缸活塞滑油出口温度Tpco共9个特征参数,计算各参数与主机功率之间的相关性,最终提取出相关性最大的变量。相关系数r计算公式如下:
| $ r = \frac{{\displaystyle\sum\limits_{i = 1}^n {({x_i} - x)({y_i} - y)} }}{{\sqrt {\displaystyle\sum\limits_{i = 1}^n {{{({x_i} - x)}^2}\displaystyle\sum\limits_{i = 1}^n {{{({y_i} - y)}^2}} } } }} 。$ | (10) |
式中,x和y分别为2个特征参数的平均值。
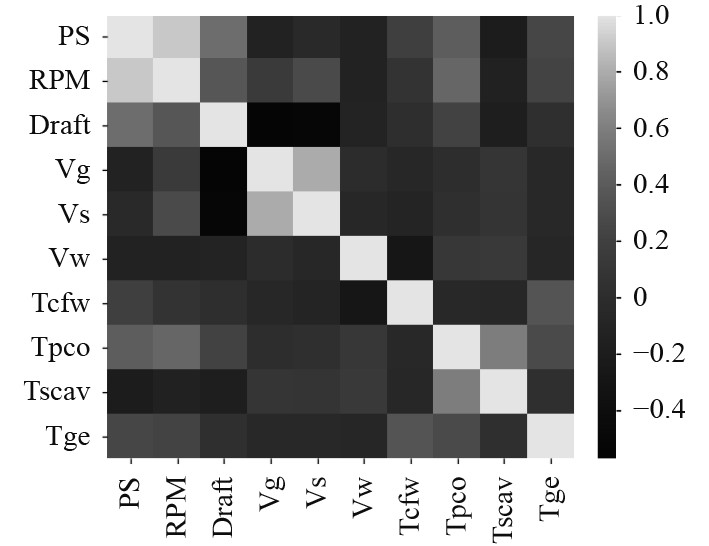
各参数之间的相关系数如图2所示,其中RPM与功率的相关系数大于0.9,为极强相关,因此确定RPM、功率为主机工况划分的2个特征参数。
|
图 2 特征参数相关性分析展示图 Fig. 2 Display of characteristic parameter correlation analysis |
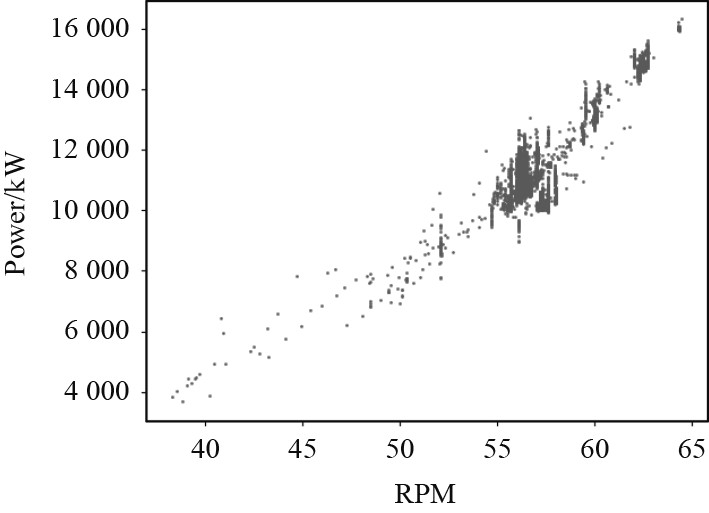
根据章节2的数据预处理结果,目标船在正常营运期间主机转速范围集中在[55,62]之间,如图3所示。绝大多数的主机转速分布在[55,58]之间,有一小部分聚集在62附近。此外,图中存在的大部分离散点主要是非正常营运期间的船舶主机参数,如RPM在40~54之间的散点数据。
|
图 3 初步筛选后的主机转速-功率分布散点图 Fig. 3 Scatter diagram of engine speed and power distribution after preliminary screening |
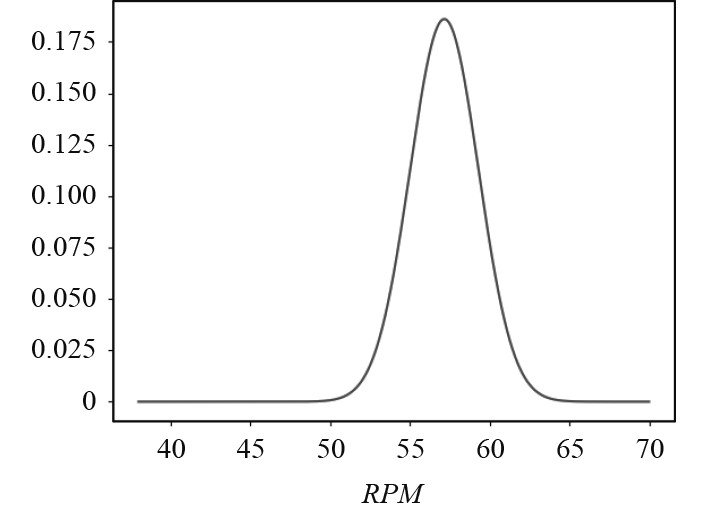
因此,引入置信区间对实船数据进行二次筛选,从而剔除影响工况划分的主机转速功率离散点。图4为利用置信区间计算的主机转速概率分布图。
|
图 4 主机转速概率分布图 Fig. 4 Probability distribution diagram of engine speed |
选取75%的置信区间,得到转速在[54.8,58.2]范围之间,因此进一步缩减转速范围划分主机工况。
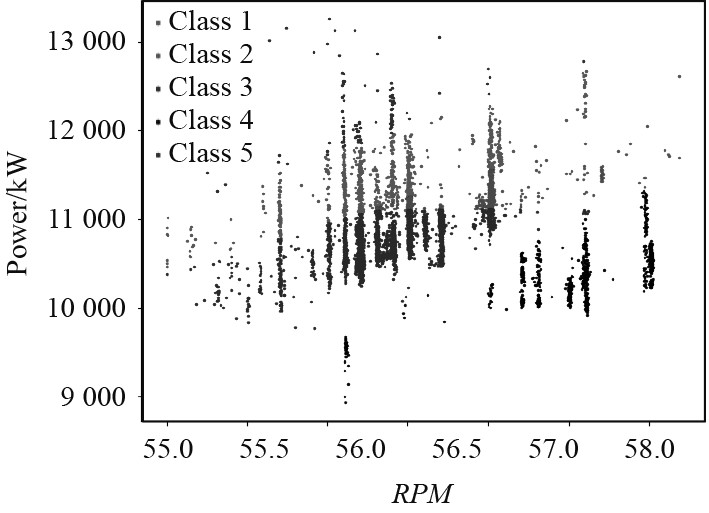
4.3 基于GMM算法的主机工况特征分析将[54.8,58.2]范围之间的数据划分成5个数据簇,图5为基于GMM的聚类分析结果,图中每个点都代表一个工况的转速和功率。最终,在这个转速范围下,船舶主机主要运行期间由5个工况组成。图5可以清楚展现基于GMM的聚类算法对主机运行产生的复杂数据进行的划分,特别是数据簇1、簇2、簇3、簇5组成的复杂集合,基于GMM的聚类算法能够将这一大簇的数据进行有效切分。
|
图 5 基于GMM算法聚类分析的主机工况划分图 Fig. 5 Scatter diagram of main engine working condition based on GMM algorithm |
对5个工况下的转速、功率数据进行特征提取,分别提取5个工况下的转速平均值、转速标准差、功率平均值以及功率标准差,如表1所示。可以看出,工况5的占比最高,达到62.3%,工况3的占比最低1.6%;转速平均值最大的是工况4,为57.5转,同转速平均值最小的工况3相比,高了1.3转。由转速标准差可知,工况1的分布最为广泛,工况3相对集中;工况3的平均功率最大为12205 kW,工况4的平均功率最小为10334.8 kW,相差了将近1900 kW;由功率标准差可知,工况3的功率分布较为广泛,工况2的功率分布较为集中。
|
|
表 1 5种主机工况转速、功率特征值对比表 Tab.1 Comparison of characteristic values of speed and power under five working conditions of main engine |
对5个工况下主机4个设备参数(Tscav,Tge,Tcfw,Tpco)进行特征分析,主要分析4个参数的主要特征值:最小值xmin、最大值xmax、平均值xavg、标准差xstd以及峰值因子C,其中峰值因子的计算公式如下式:
| $ C = \frac{{x{}_{\max }}}{{\sqrt {\tfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {x_i^2} } }}。$ | (11) |
式中,xmax为工况中最大值,n为工况中数据组数目。
表2的数据表明,5个工况下,除了Tge最大值、平均值和标准差在各个工况有较大波动,其他主机设备参数的特征值基本都在一个稳定范围内变化,特别是C的计算结果表明,5个工况下的主机设备参数稳定性很好,可以将5个工况下计算后的C值作为评估指标,监测主机设备故障情况。
|
|
表 2 5种主机工况下设备主要参数特征对比表 Tab.2 Comparison table of main parameter characteristics of equipment under five main engine working conditions |
在工况划分之前,对船舶数据进行初步筛选,获得主机稳定运行期间的实船数据。计算实船数据中各个特征参数之间的相关性,确定与功率相关性最高的主机转速作为主机工况划分的特征参数,并基于RPM的75%置信区间进一步确定工况划分数据范围。利用基于GMM的聚类算法对筛选后的实船数据进行工况划分,确定划分数据簇为5个,最终得到各个工况下的主要设备参数特征值。该方法所需的输入参数较少,工况划分精度和分析效率较高,可以对主机运行数据进行特征提取,并有效地从复杂数据中提取出可用的设备参数特征数据。
| [1] |
秦大同, 詹森, 漆正刚, 等. 基于
K
-均值聚类算法的行驶工况构建方法
[J]. 吉林大学学报(工学版), 2016, 46(2): 383-389. |
| [2] |
肖权. 基于数据驱动的船舶低速柴油机的故障诊断及趋势预测[D]. 南京: 南京航空航天大学, 2017.
|
| [3] |
李添翼. 船舶柴油主机状态监测中故障诊断方法研究[J]. 舰船科学技术, 2018, 40(24): 91-93. |
| [4] |
张嘉琦, 苏伟, 张久文, 等. 基于高斯混合模型和深度神经网络的大型船舶主机功率预测(英文)[J]. 船舶力学, 2021, 25(12): 1623-1634. |
| [5] |
WANG K, YAN X, YUAN Y, et al. Real-time optimization of ship energy efficiency based on the prediction technology of working condition[J]. Transportation Research Part D Transport & Environment, 2016, 46(7): 81-93. |
| [6] |
甄荣, 石自强. 一种基于高斯混合模型的船舶航迹聚类方法[J]. 船舶工程, 2021, 43(11): 139-143. DOI:10.13788/j.cnki.cbgc.2021.11.24 |
 2023, Vol. 45
2023, Vol. 45
