0 引　言

轴流压气机设计体系对燃气轮机的设计周期和性能有着重要影响^[1]。目前常用的压气机喘振工况分析预测方法^[2]可以归纳为3 类：三维数值方法^[3]、试验方法和经验模型方法。其中，三维数值方法通过仿真等数值计算手段建立虚拟的物理模型，但是由于受到模型精度、计算方法和网格划分数量等其他因素影响，所建立的物理模型只能在一定程度上反映压气机的内部工况，需针对具体情况具体分析，难以推广使用。利用试验方法^[4]直接探究压气机喘振边界是目前最准确最基本的方法。这种方法受限于成本、周期和环境因素的干扰难以实现。经验模型方法^[5-6]依赖于设计者工程经验，利用现有的试验数据和实测值多维辅助预判，是目前最为简单有效的方法。此类方法需利用压气机运行时采集的传感器信号，但是压气机运行时传感器采集的一维信号并不能完全体现压气机多维、复杂的运行特点。因此，此时就需要将采集到的一维信号升高到高维上来体现其实际的运行状态。经验模态分解（EMD）是一种自适应的处理非线性、非平稳信号的方法^[7]。EMD方法是基于复杂信号的局部特征时间尺度，把原始信号分解为有限个本征模态函数（IMF），每个IMF所包含的频率成分不仅与采样频率有关，还会随原始信号本身的变化而变化^[8]。通过对一维信号的EMD分解可以把数据的维数进行一定的升高，但是高维数的数据不一定是原信号的本质信号，所以必须采用一定的降维方法把数据降到信号的本征维数上，此时的信号才可以从本质上代表原始信号^[9]。而样本熵作为近似熵的改进算法，其反映了信号的混乱相似程度，可以客观反映故障与正常状态的不同^[10]。本文利用样本熵对喘振和正常工况进行了识别，结果表明此方法可以有效地区分2种工况。

1 数据处理方法 1.1 经验模态分解（EMD）

经验模态分解（EMD）是由Huang等^[11]在1998年提出的一种新的进行时频分析方法。EMD分解通过平稳化处理时间序列，逐级分解原始输入信号中不同尺度的波动或趋势，从而得到一系列不同特征尺度的数据序列，这些序列称为固有模态函数(intrinsic mode function，IMF)。IMF分量必须具备2个特征：一是其极点数和零点数相同(或最多相差一个)；二是其上下包络线关于时间轴局部对称。其具体的分解过程为：

步骤1　求解输入信号的所有局部极值点，再基于三次样条曲线分别连接所有局部极大值和极小值点，最终形成上下包络线，上下包络线的平均值记为m₁，求出：

$ \mathit{x}\left(\mathit{t}\right)-{\mathit{m}}_{1}={\mathit{h}}_{1} 。$

(1)

如果 $ {h}_{1} $ 满足IMF的2个特征，那么其就是 $ x\left(t\right) $ 的第一个IMF分量。

步骤2　如果 $ {h}_{1} $ 不满足IMF的2个特征，则把 $ {h}_{1} $ 作为输入信号，重复 $ k $ 次步骤1，得到 $ {h}_{1(k-1)}-{m}_{1k}= {h}_{1k} $ ，使得 $ {h}_{1k} $ 满足IMF特征。记 $ {c}_{1}={h}_{1k} $ ，将 $ {c}_{1} $ 作为信号 $ x\left(t\right) $ 的第一个满足IMF特征分量。

步骤3　将 $ {c}_{1} $ 从信号 $ x\left(t\right) $ 中分离出来得到：

$ {r}_{1}=x\left(t\right)-{c}_{1} 。$

(2)

将 $ {r}_{1} $ 作为原始信号重复步骤1、步骤2，得到 $ x\left(t\right) $ 的第2个满足IMF特征的分量 $ {c}_{2} $ ，重复循环 $ n $ 次，得到信号 $ x\left(t\right) $ 的 $ n $ 个满足IMF特征的分量 $ {r}_{1},{r}_{2},{r}_{3}\cdots {r}_{n} $ ，当 $ {r}_{n} $ 成为一个单调函数时，不能再从中提取满足IMF特征的数据系列时，结束循环，得到信号 $ x\left(t\right) $ 的EMD分解。

$ x\left(t\right)={\sum }_{j=1}^{n}{c}_{j}+{r}_{n} 。$

(3)

$ {r}_{n} $ 代表了信号的趋势，而 $ {c}_{j} $ 中包含有不同频率的成分并且是非等宽的。这一点正体现了EMD分解的自适应性。

1.2 样本熵

样本熵是由Richman^[12]提出的一种新的时间序列复杂性测度方法，函数形式为 $ SampEn(m,r,N) $ ，其中数据长度为 $ N $ ，相似容限为 $ r $ ，维数为 $ m $ 及 $ m+1 $ 。其具体的计算步骤如下：

设原始信号为 $ x\left(1\right),x\left(2\right),x\left(3\right)\cdots x\left(N\right) $ ，共 $ N $ 个点。

步骤1　将原始信号按顺序排列组成 $ m $ 维矢量，即

$ X\left(i\right)=\left[x\right(i),x(i+1),\cdots x(i+m-1\left)\right] \text{，} i=1\sim N-m-1 。$

(5)

步骤2　定义 $ X\left(i\right) $ 与 $ X\left(j\right) $ 之间的距离 $ d\left[X\right(i),X(j\left)\right] $ 为两者对应元素中差值最大的一个，即

$ d\left[X\right(i),X(j\left)\right]=\underset{k=0~m-1}{max}[\left|x(i+k)-x(j+k)\right| 。$

(6)

步骤3　给定阈值 $ r $ ，对每一个 $ I $ 统计 $ d\left[X\right(i),X(j\left)\right] $ 小于 $ r $ 的数目及此数目与距离总数 $ N-m $ 的比值，记作 $ {B}_{i}^{m}\left(r\right) $ ，即

$ \begin{split}&{B}_{i}^{m}\left(r\right)=\frac{1}{N-m}\left\{d\right[x\left(i\right),x\left(j\right)] < r的数目\} \text{，} \\ &i=1\sim N-m+1,i\ne j 。\end{split}$

(7)

则有：

$ {B}^{m}\left(r\right)=\frac{1}{N-m+1}{\sum }_{i=1}^{N-m+1}{B}_{i}^{m}\left(r\right) ，$

(8)

再将维数加1，即对于 $ m+1 $ 点矢量，得到 $ {B}_{i}^{m+1}\left(r\right) $ ，即 $ {B}^{m+1}\left(r\right) $ 。

步骤4　求解出该序列的样本熵：

$SampEn(m,r)=\underset{N\to \infty }{lim}\{-\mathit{ln}[{B}^{m+1}(r)/{B}^{m}(r\left)\right] ，$

(9)

$ N $ 为有限值时，则上式可以写为

$ SampEn(m,r，N)=-\mathit{ln}[{B}^{m+1}\left(r\right)/{B}^{m}\left(r\right) 。$

(10)

$ SampEn $ 的值显然与 $ m $ ， $ r $ 的取值有关。由文献[8]可以得知， $ m $ =1或2， $ r=0.1SD~0.25SD $ （ $ SD $ 为原始数据的标准差）计算得到的样本熵具有合理的统计特性。因此，本文选取 $ r=0.2SD $ ， $ m=2 $ 。

1.3 数据降维

实际上压气机的运行是一个多维的运行状态，有很多因素对它的运行状态产生影响。通过传感器测量的一维时间序列可以理解为压气机高维复杂的空间运动向一维空间的投影。然而压气机运行状态的本质维数并不一定是一维的，所以在投影的过程中，会受到很多其他因素的影响造成原本能够表征压气机运行状态的一些本质特征在向一维投影的时候发生变化、被削弱甚至消失，即微弱故障难以提取。这一现象导致在分析所测得的一维数据时很有可能造成特征提取错误、特征难提取等问题。因此，首先对采集到的信号进行EMD分解，使得信号的维数升高，然而一维数据升高到高维并不一定可以表征压气机实际运行的本质，并且还会有维数灾难的出现，不利于分析。因此，通过对压气机本征维数进行估计，对EMD分解后的高维数据进行降维，使其降到本征维数从而可以反映出压气机的本质运行状态。对高维数据降维处理是提取复杂多成分原始信号特征值，去除噪声最常用的手段，具体优势体现在以下方面^[13]：

1）对原始数据进行有效压缩以节省存储空间；

2）可以消除原始数据中存在的噪声；

3）有利于提取原始信号中的特征值，为后续的分类或识别提供基础；

4）将高维信号投影到二维或三维空间，有利于信号可视化处理。

本文采用线性降维的主成份分析（PCA）的方法进行降维。

2 试验装置

本试验压气机为三级轴流压气机，在一级、二级之间以及三级处各安装有一个高频动态压力传感器，用于实时采集三级轴流压气机动态压力信号的变化。设置排气节流阀的开口流量模拟实际压气机的运行环境，将采集的数据存储在计算机上。

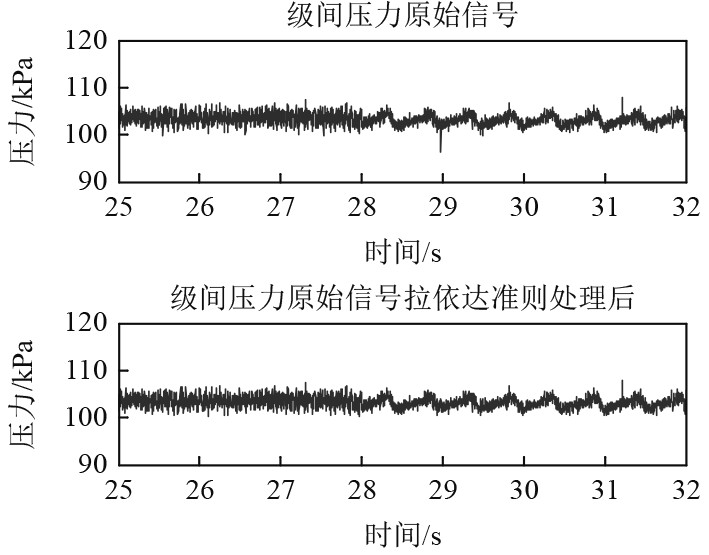
3 数据处理

通过调节排气节流阀的开度改变压气机的工况，发现当排气阀的开度调节到20°时，压气机在9 600 r/min时出现喘振，因此对喘振前后的级间压力、三级出口处的压力信号进行处理。由于在采集的过程中信号会受到电气干扰，在处理之前首先采用拉伊达准则对原始信号进行处理消除电器干扰的影响。图1为9 600 r/min时喘振前后级间压力原始信号以及经过拉依达准则处理后的信号。

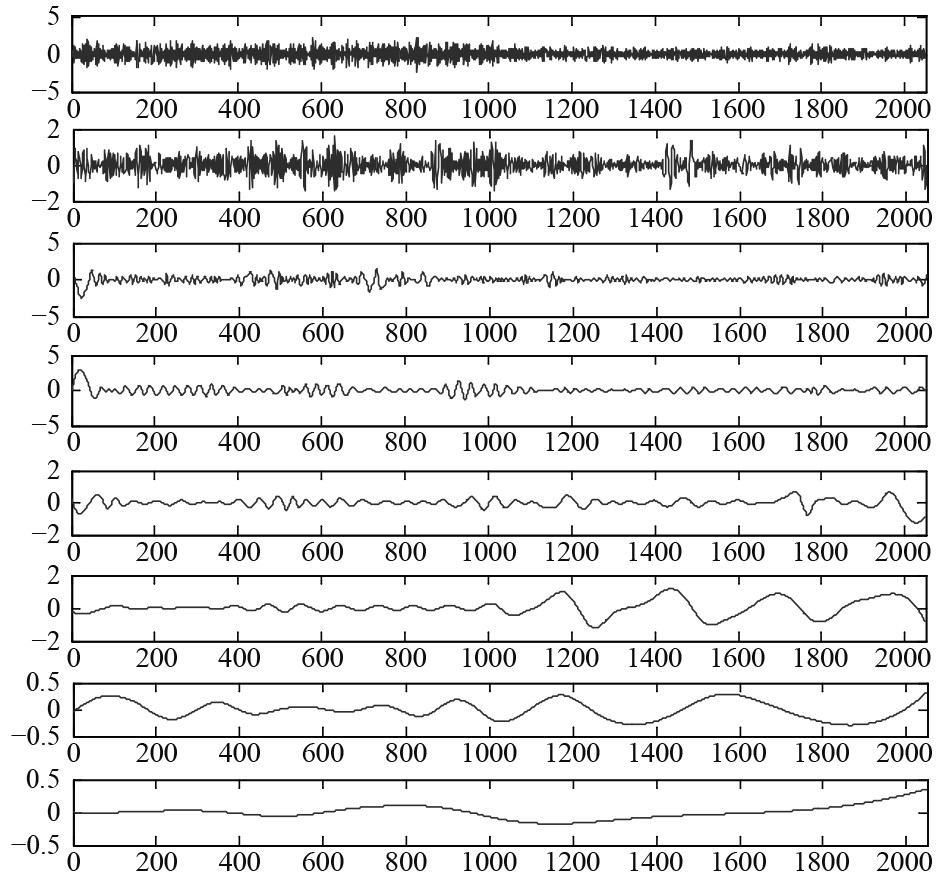
对处理后的信号进行EMD分解，其前8个IMF如图2所示。

可以看出，第6个IMF分量可以反映出压气机喘振时出现的波动。

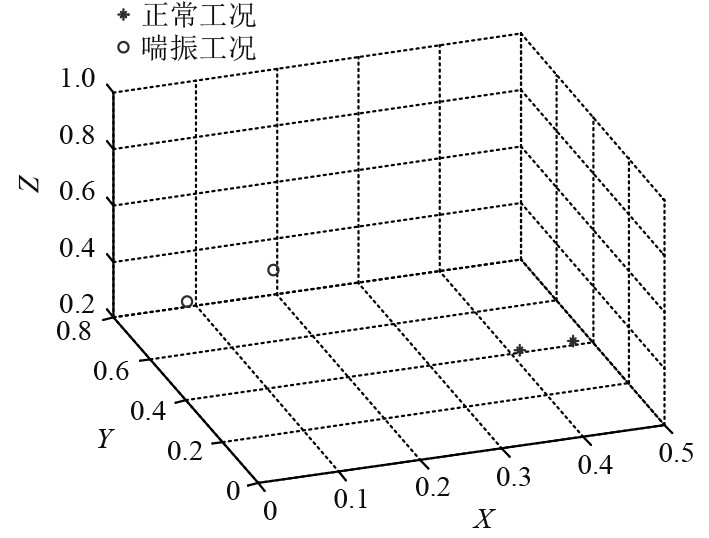
因此，通过记录的时刻得知在28 s时压气机发生了喘振，对级间压力和三级出口压力分别取发生喘振前2 s的数据以及发生喘振后2 s的数据。进行EMD分解，并且对分解的信号选择主成份分析（PCA）方法进行数据降维，在对本征维数的估计基础上把维数降到三维，计算各个的样本熵。表1和表2列出了级间压力以及三级出口压力在喘振前后的样本熵。样本熵三维图如图3所示。

由计算结果可以得知，在三维图中喘振工况和正常工况分别聚集在一起，具有良好的聚类效果，说明利用样本熵的方法可以对2种工况进行区分，证明此方法可以对压气机的2种工况进行判断，用于压气机喘振的实时监测。

4 结　语

通过EMD分解使得传感器采集的一维信号可以在高维来体现压气机的实际运行状态。但是在高维时并不是所有的维数都起作用，有的维数会相当于“噪声”从而影响本质运行状态的体现。因此，采用降维的方法把高维的数据降到可以表征压气机运行状态的本质维数上，再通过样本熵把压气机正常工况与喘振的工况区分开，为压气机的监测提供了一定的理论基础。