0 引　言

无人船被广泛应用在水面和水下环境监测、海上作战、对敌侦察等领域，随着无人船技术的发展，对无人船的航行稳定性、降噪性以及续航能力等都提出了更高的要求^[1]。发动机是无人船的核心部件，无人船发动机前端附件驱动系统的振动可能会导致发动机的输出失稳，导致无人船的航行稳定性和续航能力降低，需要构建优化的无人船发动机前端附件驱动系统横向振动性能分析模型，结合对发动机的系统结构分析和振动信号分析方法，提高振动监测能力，从而提高无人船发动机的输出稳定性^[2]。

对无人船发动机前端附件驱动系统横向振动性能分析建立在对振动信号特征分析基础上，结合对振动负荷加载特征分析，实现对无人船发动机的动态特征参数分析，提高输出稳定性。当前对力学性能和结构性能参数分析是通过结构部件特征分析以及振动强度和刚度分析，实现对无人船发动机前端附件驱动系统横向减振控制，但传统方法在进行无人船发动机前端附件驱动振动特征性分析的刚度解耦和阻尼振荡抑制能力不好。

针对上述问题，本文提出基于动力学和结构可靠性分析的驱动系统横向振动分析模型，并分析其性能。

1 信号模型和特征分析 1.1 前端附件驱动系统横向振动信号模型

为了实现无人船发动机前端附件驱动系统横向振动性能动态监测分析，结合振动信号特征分析方法，通过分析横向振动和纵向振动的动态特性，提出基于多策略动态计算和自适应滑模控制的方法^[3]。建立无人船发动机前端附件驱动控制的滑模减振模型，实现对系统横向振动控制模型设计。结合模型参数和运动学参数分析，采用特征量提取传感信息融合的方法，建立无人船发动机前端附件驱动系统横向动力学参数分析模型。通过重力势能和锚线系统的机构模型分析，进行振动信号检测，得到无人船发动机前端附件驱动系统横向振动性能分析的总体结构如图1所示。

根据图1的总体结构模型，在机舱中安装主动作动器，采用动态振动特征分析方法，实现对无人船发动机前端附件驱动系统横向振动的运动空间进行联合规划识别^[4]，构建无人船发动机前端附件驱动系统横向振动的空间坐标系为 $O{x_3}{y_3}{z_3}$ 、传动装置坐标系 $O{x_1}{y_1}{z_1}$ 、弹性驱动坐标系 $O{x_2}{y_2}{z_2}$ 和地面坐标系 $Axyz$ 。在各级坐标系中，通过气动-水动-结构-TMD-HMD 耦合控制方法，得到混联机构FAST 和耦合模型。采用高频振动峰值调节，得到振动信号采集模型如图2所示。

1.2 振动信号特征分析

无人船发动机前端附件驱动系统横向振动的双轮质心为坐标系原点 $O$ ，速度坐标系 $O{x_3}{y_3}{z_3}$ 该坐标系原点 $O$ 取在无人船发动机前端附件驱动系统横向振动的质心上，用载荷引起的应变信号特征分析方法，提取前端附件驱动系统横向振动信号模型。设置世界坐标系原点 O 在W 的 X 轴，体坐标系 $O{x_1}{y_1}{z_1}$ 与无人船发动机前端附件驱动系统横向振动耦合，载荷时域特性分布特征点分布在原点 $O$ 的质心上，θ₁ 和 θ₂分别为二系垂向减振器在 L₁，L₂ 和 L₃ 上的动力矩，垂向减振器对应的载分量满足T ₁ = A₁，T ₂ = A₁A₂，由此构建前端附件驱动系统横向振动的动力学的数学模型：

$ \left\{ {\begin{aligned} & {{J_s}({{\ddot \theta }_s} + {{\ddot \theta }_c}) = {T_s} + \sum\limits_{n = 1} {{F_{Eyn}}{r_s}} }，\\ & {{J_r}({{\ddot \theta }_r} + {{\ddot \theta }_c}) = \sum\limits_{n = 1} {{F_{lyn}}{r_r} - {k_{\theta r}}\left( {{\theta _r} + {\theta _c}} \right)} }，\\ & {({J_c} + N{m_p}r_c^2){{\ddot \theta }_r} = {T_c} - \sum\limits_{n = 1} {({F_{lyn}}\cos {\alpha _s} + {F_{lyn}}\cos {\alpha _r}){r_c}} }，\\ & {{J_{pn}}{{\ddot \theta }_{pn}} = {F_{Eyn}}{r_{pn}} - {F_{lyn}}{r_{pn}}}。\end{aligned}} \right. $

(1)

式中： $ {J_s} $ 为偏移大小与曲线半径的相关性分布旋转力矩， $ {T_s} $ 为轴箱减振器的啮合刚度， $ {F_{Eyn}} $ 为对抗蛇行减振器的啮合阻尼， $ {r_s} $ 为最大载荷位置对应的刚度， $ {J_r} $ 为载荷幅值的转动力矩， $ {J_c} $ 为减振器载荷的变动幅值传动力矩， $ {J_{pn}} $ 为垂向减振器载荷的中心线和驱动中心动力矩， $ {T_c} $ 为传动系统减振力矩， $ {F_{lyn}} $ 为垂向减振器的振动衰减， $ {F_{Eyn}} $ 为垂向减振器的无功衰减， $ {k_{\theta r}} $ 为变动幅值的传动惯量， $ {m_p} $ 为减振器载荷的有效频率衰减， $ N $ 为减振器载荷的幅值谱分布特征量， $ {\theta _r} $ 和 $ {\theta _c} $ 均为各阶固有频率。

由此建立无人船发动机前端附件驱动系统横向振动参数传感特征分析模型，采用频带的敏感特性特征分析，进行轴箱垂向减振控制和振动特性监测。

2 振动性能动态监测 2.1 驱动系统横向振动信号幅频特征分析

对发动机前段的轴箱垂向减振器、二系垂向减振器进行联合特征分析，对减振器的速度和加速度进行惯性特征分析和信号幅频特征检测^[5]，得到幅频检测方程为：

$ A = \left[ {\begin{array}{*{20}{c}} {{f_{{x_1}}}}&{{f_{{x_2}}}} \\ {{g_{{x_1}}}}&{{g_{{x_2}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{r_1}(1 - \displaystyle\frac{{2{x_1}}}{{{N_1}}} - \displaystyle\frac{{{\sigma _1}{x_2}}}{{{N_2}}})}&{ - \displaystyle\frac{{{r_1}{\sigma _1}{x_1}}}{{{N_2}}}} \\ { - \displaystyle\frac{{{r_2}{\sigma _2}{x_2}}}{{{N_1}}}}&{{r_2}(1 - \displaystyle\frac{{{\sigma _2}{x_1}}}{{{N_1}}} - \displaystyle\frac{{2{x_2}}}{{{N_2}}})} \end{array}} \right] 。$

(2)

式中：x₁和x₂为减振器载荷和载荷-速度融合参数， $ {N_1} $ 和 $ {N_2} $ 为蛇行减振器载下的振动模态数， $ {\sigma _1} $ 和 $ {\sigma _2} $ 为载荷循环和载荷幅值构成的载倍频参数， $ {r_1} $ 和 $ {r_2} $ 为减振器载荷的最大驱动参数， $ {f_{{x_1}}} $ 和 $ {f_{{x_2}}} $ 为减振器腔室阻尼力参数， $ {g_{{x_1}}} $ 和 $ {g_{{x_2}}} $ 为高通功率谱密度。

假设振动系统状态 q 完全可测，得到最大的频率范围内的特征量 $ m\left( A \right) $ 满足：

$ m\left( A \right) = \left\{ {\begin{aligned} &{\frac{{\displaystyle\sum\limits_{ \cap {A_i} = A} {\prod\limits_{1 \leqslant i \leqslant n} {{{m'}_i}\left( {{A_i}} \right)} } }}{{1 - K}}{\text{ }}，A \ne \emptyset } ，\\ & {0，{\text{}}A = \emptyset } 。\end{aligned}} \right. $

(3)

$ K = \sum\limits_{ \cap {A_j} = \emptyset } {\prod\limits_{1 \leqslant i \leqslant n} {{{m'}_i}\left( {{A_j}} \right)} } 。$

(4)

式中： $ K $ 为耦合模型的相关输出， $ {A_i} $ 为最优机舱 TMD减振的子频带， $ m' $ 为高频振动峰值的减振惯性参数。令 $ A\in {C}^{n\times n}(n\times n维复数空间) $ 表示颤振弱敏感性频带，通过对驱动系统横向振动信号幅频特征分析，实现对驱动系统的横向振动控制和抑制。

2.2 横向振动反馈控制和优化调节

为了提高对驱动系统高频振动抑制能力，通过求解无人船发动机前端附件驱动系统的运动学规划模型，采用高频振动峰值减振率误差补偿的方法，得到扰动抑制的反馈控制函数为^[6]：

$ \left\{ \begin{gathered} a({H_{ac}}) = 1 - \frac{{{H_{ac}}}}{{\max ({H_{ac}}) + l}} ，\\ \max ({H_{ac}}) = {\log _2}k 。\\ \end{gathered} \right. $

(5)

式中： $ {H_{ac}} $ 为第 i 个驱动系统横向振动惯性特征量在X方向的子带信号， $ k $ 为低频振动峰值的减振惯性参数， $ l $ 为第 i 个频带能量。

构建耦合动力学模型，得到驱动系统横向振动的附加应变能和离心刚度为：

$ {x_i}(n) = \sum\limits_{j = 1}^M {{h_{ij}}{{(n)}^{\rm{T}}}} {s_j}(n) + {v_i}(n) ，$

(6)

$ {y_j}(n) = \sum\limits_{i = 1}^P {{f_{ij}}} {(n)^{\rm{T}}}{x_i}(n) 。$

(7)

式中： $ {h_{i{\text{j}}}} $ 代表各个截面的位置伺服运动系数， $ {s_j}(n) $ 为频带重构相干振动动态参数， $ {v_i}(n) $ 为无人船发动机前端附件驱动系统绕 x轴、y轴、z 轴的转动的自由度， $ {x_i}(n) $ 为运动副位置的限制特征量， $ {f_{ij}} $ 为施加主动控制约束的旋转惯性参数，表示无人船发动机前端附件驱动系统横向振动的敏感性特征量， $ {f_{ij}}(n) $ 为支链中运动副的对应关联特征量， $ P $ 为漂浮式风力机沿 X 轴的摆振角度数。

根据信号幅频特征提取结果以及振动惯性参数检测结果，实现对驱动系统横向振动性能动态分析，如图3所示。

3 仿真测试

通过仿真测试验证本文方法在实现无人船发动机前端附件驱动系统横向振动状态监测的应用性能，设定振动信号采样长度为2400，频率为12 kHz，变增益状态反馈系数为0.34，发动机轮毂平均风速为4.5 rad/s，自由衰减状态参数为0.13 dB，驱动系统构件几何参数如表1所示。

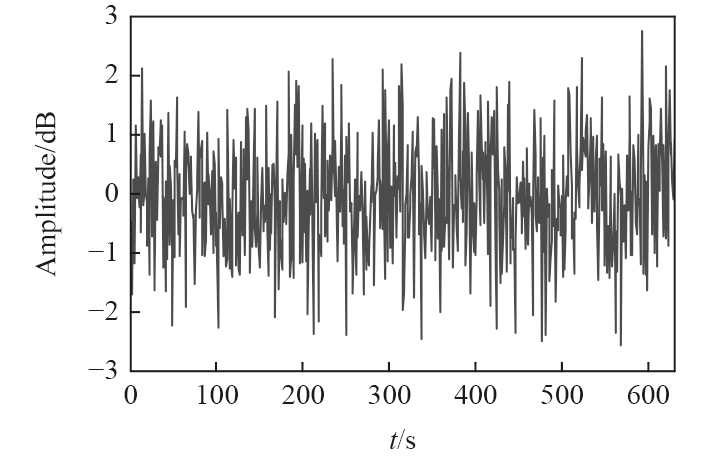
根据上述参数设定，进行无人船发动机前端附件驱动系统横向振动特性分析。使用L3G4002D二自由度陀螺仪实现对无人船发动机前端附件驱动系统振动信号检测，得到原始信号如图4所示。

以图4 振动信号为测试对象，采用本文方法进行振动特征提取，得到幅频特征检测结果如图5所示。分析可知，本文方法对无人船发动机前端附件驱动系统横向振动的幅频检测性能较好，对振动控制的收敛性较好。

测试不同方法进行无人船发动机前端附件驱动系统横向振动抑制的误差，得到对比结果如表2所示。分析可知，本文方法进行无人船发动机前端附件驱动系统横向振动抑制的误差较小。

4 结　语

构建优化的无人船发动机前端附件驱动系统横向振动性能分析模型，结合对发动机的系统结构分析和振动信号分析方法，提高振动监测能力。本文提出基于动力学和结构可靠性分析的驱动系统横向振动分析模型，建立无人船发动机前端附件驱动控制的滑模减振模型，通过对驱动系统横向振动信号幅频特征分析，实现对驱动系统的横向振动控制和抑制。分析可知，本文方法能有效实现对振动的幅频特征检测，提高振动抑制能力。