0 引　言

海上原油运输主要风险是海上溢油事故，原油泄漏不仅严重影响了海洋生态和环境，也造成严重的经济损失^[1]。

因此，提高海上船舶溢油事故的评估能力，及早对溢油事故进行预防，并建立合理的船舶溢油风险评估方法非常必要。本文系统分析海上原油运输船舶的溢油风险和要素，结合灰色理论模型建立船舶溢油风险评估方法，对于改善当前原油运输船舶的安全性，降低船舶溢油风险有重要意义。

1 船舶溢油风险因素分析

结合行业内大量的统计数据，将原油运输船舶的溢油风险因素划分为人为因素、海况因素、船型因素和其他因素这4个维度，并针对每个溢油风险维度的特点进行了详细介绍。

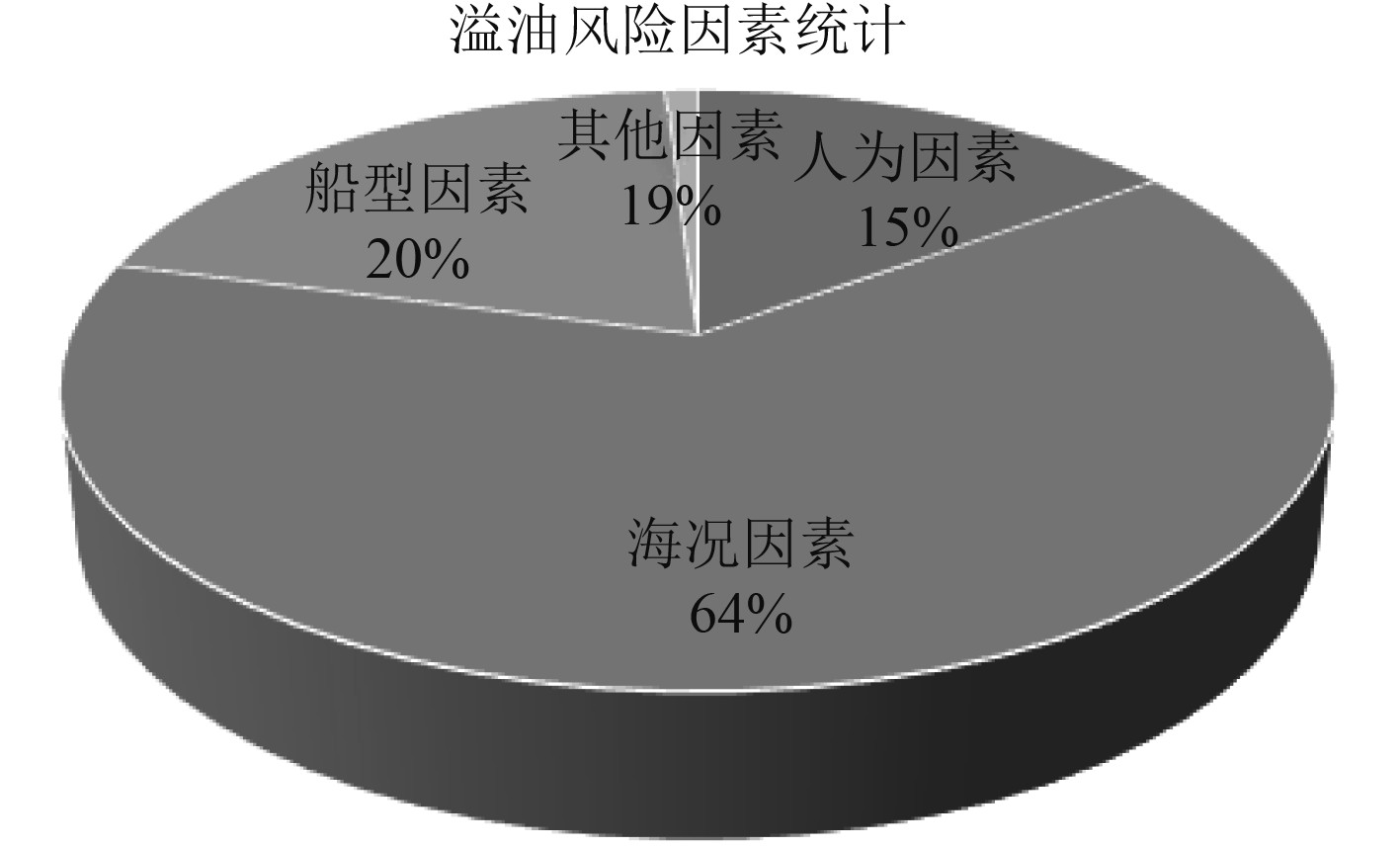
图1为船舶溢油风险要素的整体占比情况图。

1）海况因素

海况因素是导致船舶发生溢油事故的最主要原因，海况因素又包括风浪流等自然条件因素和航道条件等硬件因素。

①自然条件因素

海上自然条件非常恶劣，尤其是远洋和深海区域。一方面，剧烈的海风、海浪可能导致船舶结构的破坏，产生严重的燃油和货物油泄漏；另一方面，剧烈的风浪会诱发和加剧船舶溢油事故造成的破坏作用，对海洋环境的破坏性推波助澜。

②航道条件等硬件因素

港口、内河航道等硬件条件的限制也可能导致船舶出现溢油事故，比如航道内水深、礁石等因素导致的船舶搁浅事故。此外，良好的导航设备和系统也是保障船舶航行安全的重要措施，能够从船舶避碰策略、传感器等方面提升船舶航运安全。

2）船型因素

从港口及航道统计数据分析得知，船型因素在船舶溢油事故中占据的比例仅次于海况因素，船型因素又包括船舶的类型，比如单壳船还是双壳船、船舶的吨位等。通常，单壳船由于撞击等事故很容易发生船体破损，导致燃油泄漏，双壳船甚至多壳船当发生事故时具有一定抗破坏能力，发生溢油事故的风险会明显低于单壳船。

船舶的吨位与燃油泄漏事故也是呈正相关的关系，随着船舶吨位的增加，船舶的吃水深度更深，船舶方向改变、速度控制等灵活性都会降低，从而使船舶整体的操作性较差，在港口、内河航道等水域内发生事故的概率更高。

3）人为因素

主要是指船舶操作人员因为误操作或者疏于职守等原因，导致船舶未按照合理的航线行驶，发生搁浅事故。或者在船舶会遇过程中，操作人员转向或减速不及时，造成船舶碰撞事故，进而导致船舶燃油的泄漏^[2]。

4）其他因素

造成船舶溢油风险的其他因素包括交通密度等因素，随着交通密度的增加，船舶发生碰撞事故的概率也在不断增加。统计数据表明，海事事故的发生与距离海岸的距离存在正相关。

图2表示为不同离岸距离下不同风险因素造成的船舶溢油事故统计。

2 基于灰色理论的船舶溢油风险评估方法 2.1 灰色理论建模

20世纪80年代初，邓聚龙等率先提出灰色系统理论，该理论将客观事物理解为不断变化且相互关联，并根据客观事物的未知性将系统分为灰色、黑色和白色系统3种。其中，灰色系统理论主要针对不确定性问题的分析，这种应用场景通过对原始数据序列的建模，从离散的数据中寻找数据序列相互关联的规律，进而进行非线性系统的建模和预测。

灰色系统模型从数学原理角度上讲是一种非线性的数列模型，在利用灰色系统理论进行系统的分析时，首先需要对系统的原始数据进行转化，将数据转换为n阶矩阵。

在工业控制系统中存在着许多非线性因素，这些因素会不同程度的影响系统的控制精度。采用灰色系统理论并通过定义非线性系统的灰导数等，可以有效对控制系统的变量进行转化，因此，灰色系统理论的应用范围很广。

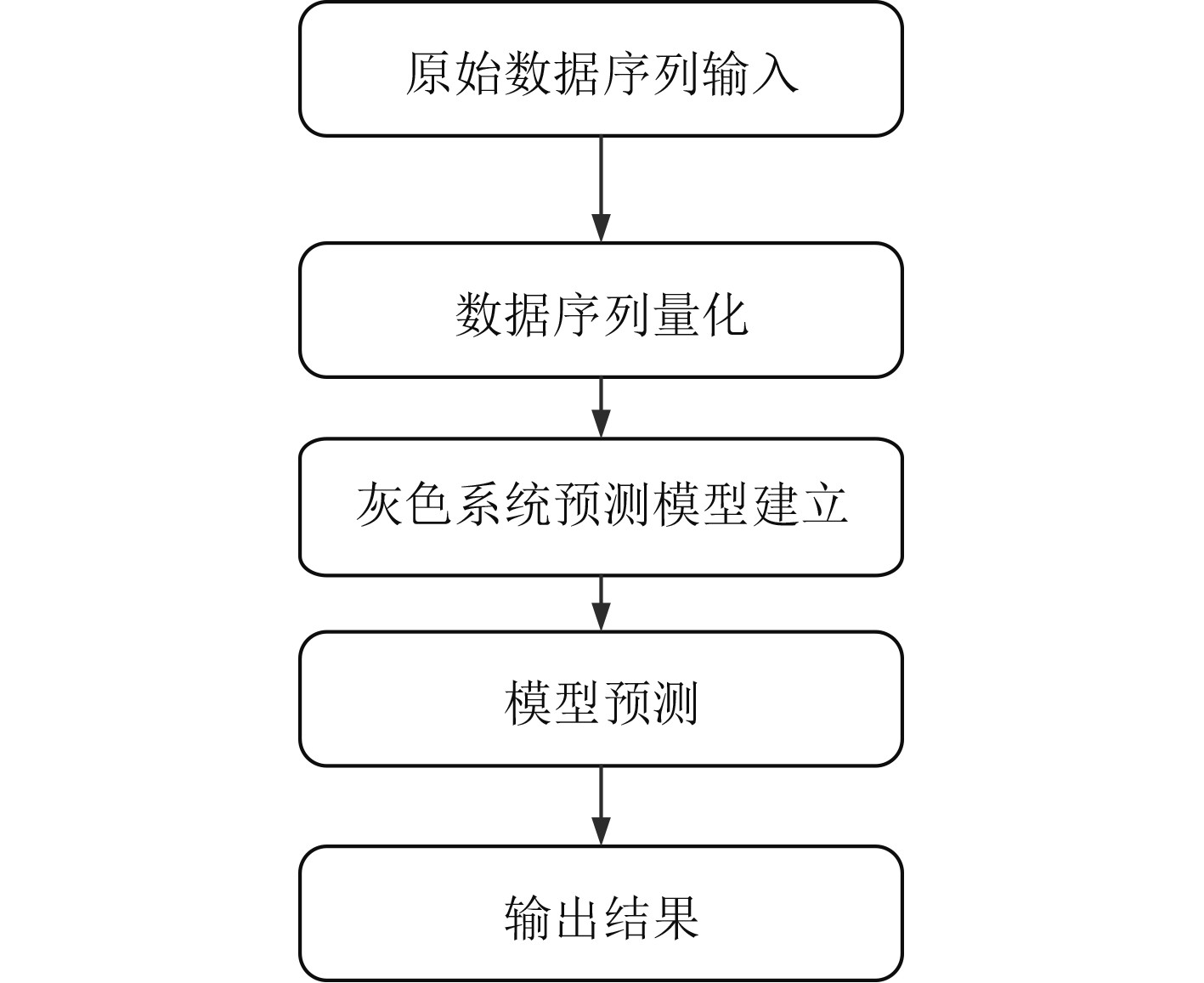
灰色系统理论的通用工作流程如图3所示。

灰色理论系统建模过程如下：

1）结合不确定系统的输入信息，建立原始数列^[3]：

$ \left[ {\begin{array}{*{20}{c}} {{X^{\left( 0 \right)}}\left( 1 \right),..,{X^{\left( 0 \right)}}\left( i \right)} \\ {...} \\ {{X^{\left( i \right)}}\left( 1 \right),..,{X^{\left( i \right)}}\left( i \right)} \end{array}} \right]。$

2）定义系统的灰导数为：

$ {F_n} = \sum\limits_{i = 1}^n {{X^{\left( 0 \right)}}\left( i \right)} ,\;\;\;\;\left( {i = 1,2,...,n} \right) 。$

3）建立灰色理论模型微分方程为：

$ {F_n} + \frac{1}{k}G(i) = h \text{，} $

其中， $ G(i) = \displaystyle\frac{1}{3}{X^{\left( 0 \right)}}\left( i \right) + \displaystyle\frac{1}{2}{X^{\left( 0 \right)}}\left( {i - 1} \right) $ ，k为0.1-0.6的调节系数，得到微分方程的解为：

$ M = \left[ {\begin{array}{*{20}{c}} { - {G^{\left( 1 \right)}}(1)} \\ { - {G^{\left( 2 \right)}}(2)} \\ { - {G^{\left( i \right)}}(i)} \end{array}} \right] 。$

4）将微分方程的解集转化为时间序列，从而得到理论模型为：

$ \tilde X\left( i \right) = \left( {\left( {{X^{(0)}}(1) - \frac{{G(0)}}{a}} \right) + b} \right) \text{。} $

式中：a，b为理论模型的因数。

2.2 船舶溢油风险评估的灰色理论模型建模

在使用灰色理论对船舶溢油风险进行评估时，根据系统的初始输入，分别建立系统的因素集和评价集^[4]如下：

1）因素集

$ {\boldsymbol{U}}{\text{ = }}\left( {{U_1},{U_2},...,{U_n}} \right) \text{，} $

其中， $ {U_1},{U_2},...,{U_n} $ 分别为人为因素、海况因素、船型因素和其他因素。

2）评价集

$ V{\text{ = }}\left( {{V_1},{V_2},...,{V_n}} \right) \text{，} $

$ {V_1},{V_2},...,{V_n} $ 分别为船舶溢油风险指标的等级，如 $ {V_1} = \left( {{V_{p1}},{V_{q1}},...} \right) $ ，表示溢油风险的可能性在10%，20%等。

设溢油评估系统因素集 $ {\boldsymbol{U}}{\text{ = }}\left( {{U_1},{U_2},...,{U_n}} \right) $ 中， $ {u_{ij}} $ 表示因素 $ {U}_{i} $ ， ${U}_{j} $ 的相对重要性，得到如下判断矩阵：

$ {\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {{u_{11}}}&{{u_{12}}}& \ldots &{{u_{1j}}}& \ldots &{{u_{1n}}} \\ {{u_{21}}}&{{u_{22}}}& \ldots &{{u_{2j}}}& \ldots &{{u_{2n}}} \\ \ldots & \ldots & \ldots & \ldots & \ldots & \ldots \\ {{u_{i1}}}&{{u_{i1}}}& \ldots &{{u_{ij}}}& \ldots &{{u_{in}}} \\ \ldots & \ldots & \ldots & \ldots & \ldots & \ldots \\ {{u_{n1}}}&{{u_{n2}}}& \ldots &{{u_{nj}}}& \ldots &{{u_{nn}}} \end{array}} \right] \text{，} $

矩阵的特性包括：

$ {u_{11}} = 1 \text{，} $

$ {u_{ij}} = 1/{u_{ji}} \text{，} $

$ {u_{ij}} = {u_{ik}}/{u_{jk}}({{i}},{{j}},{{k}} = 1,2, \ldots ,{\text{n}}) 。$

建立溢油风险评估矩阵为：

$ \begin{split}& {{\boldsymbol{f}}_i} = {{\boldsymbol{A}}_i} \cdot {{\boldsymbol{R}}_i} = \left( {{\omega _1},{\omega _2}, \ldots {\omega _m}} \right) \cdot \left[ {\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}& \ldots &{{r_{1n}}} \\ {{r_{21}}}&{{r_{22}}}& \ldots &{{r_{2n}}} \\ \ldots & \ldots & \ldots & \ldots \\ {{r_{m1}}}&{{r_{m2}}}& \ldots &{{r_{mn}}} \end{array}} \right]，\\ & {\text{i}} = 1,2, \ldots ,{{n}} 。\end{split}$

式中： $ {{\text{A}}_i} $ 为指标权重； $ {{\text{R}}_i} $ 为隶属度。

将因素集和评价集矩阵视为时间t的连续函数，建立灰色系统理论模型：

$ B \cdot \frac{{{\rm{d}}{f_i}\left( t \right)}}{{{\rm{d}}t}} - {\alpha _0} \cdot {f_i}\left( t \right) = 603.7 \text{。} $

式中： $ {\alpha _0} $ 为模型的平滑性控制参数； $B = \left\{ \displaystyle\frac{1}{2}{f_1}\left( 1 \right) + \displaystyle\frac{1}{2}{f_1}\left( 1 \right) + \cdots \displaystyle\frac{1}{2}{f_1}\left( n \right) \right\}$ 。得到船舶溢油风险评估的响应模型为：

$ S(k) = \left( {{f_i}(t) + \frac{B}{{603.7}}} \right){e^{0.036}} - \frac{B}{{603.7}} 。$

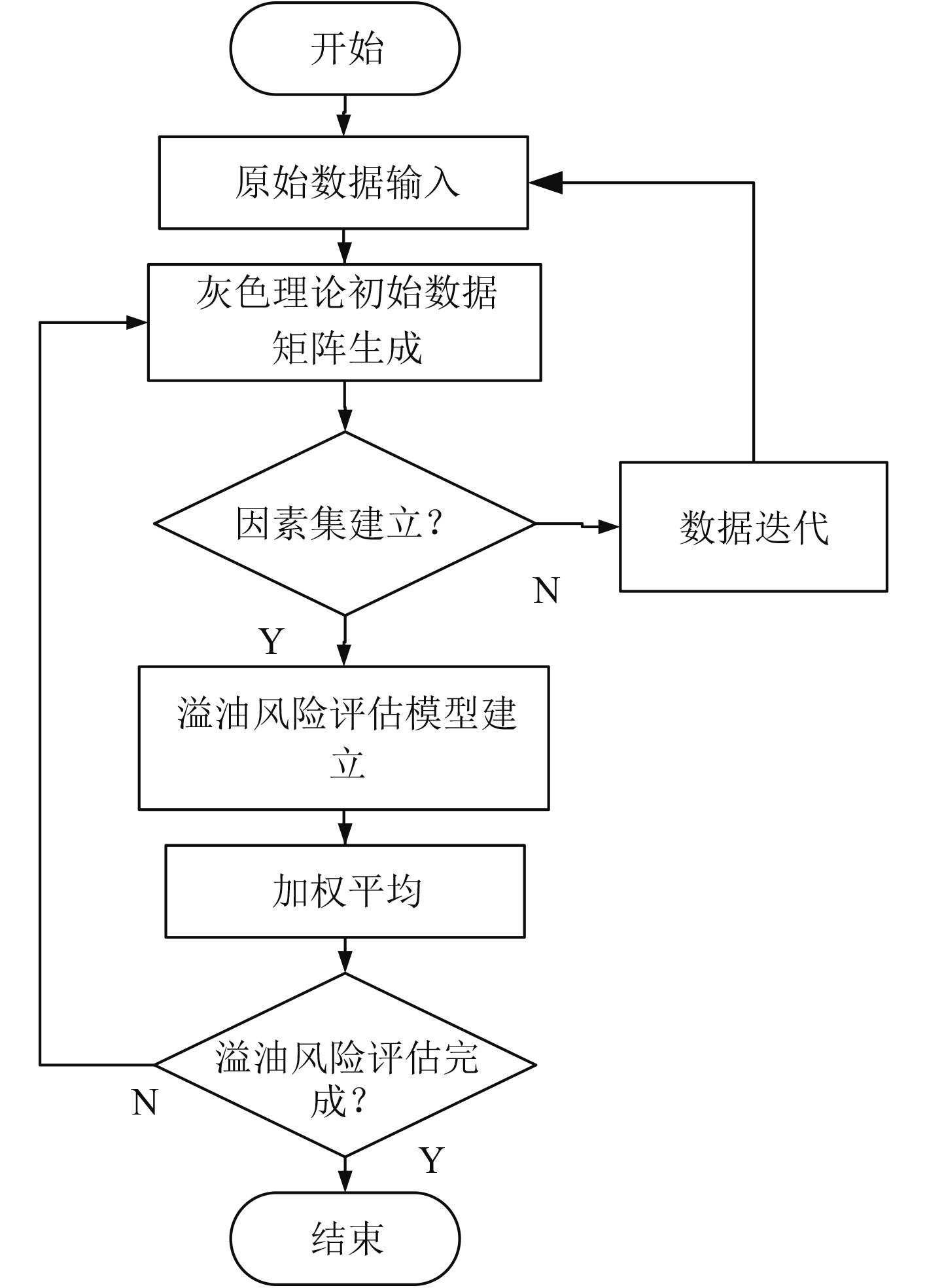
图4为基于灰色理论的船舶溢油风险评估过程。

2.3 船舶溢油风险评估与预测

为了验证本文开发的船舶溢油风险评估方法的准确性，以大连海区的统计数据为基础，假设大连海区内的船舶碰撞、搁浅等事故符合二项概率分布^[5]，大连海区溢油事故统计历史数据如表1所示。

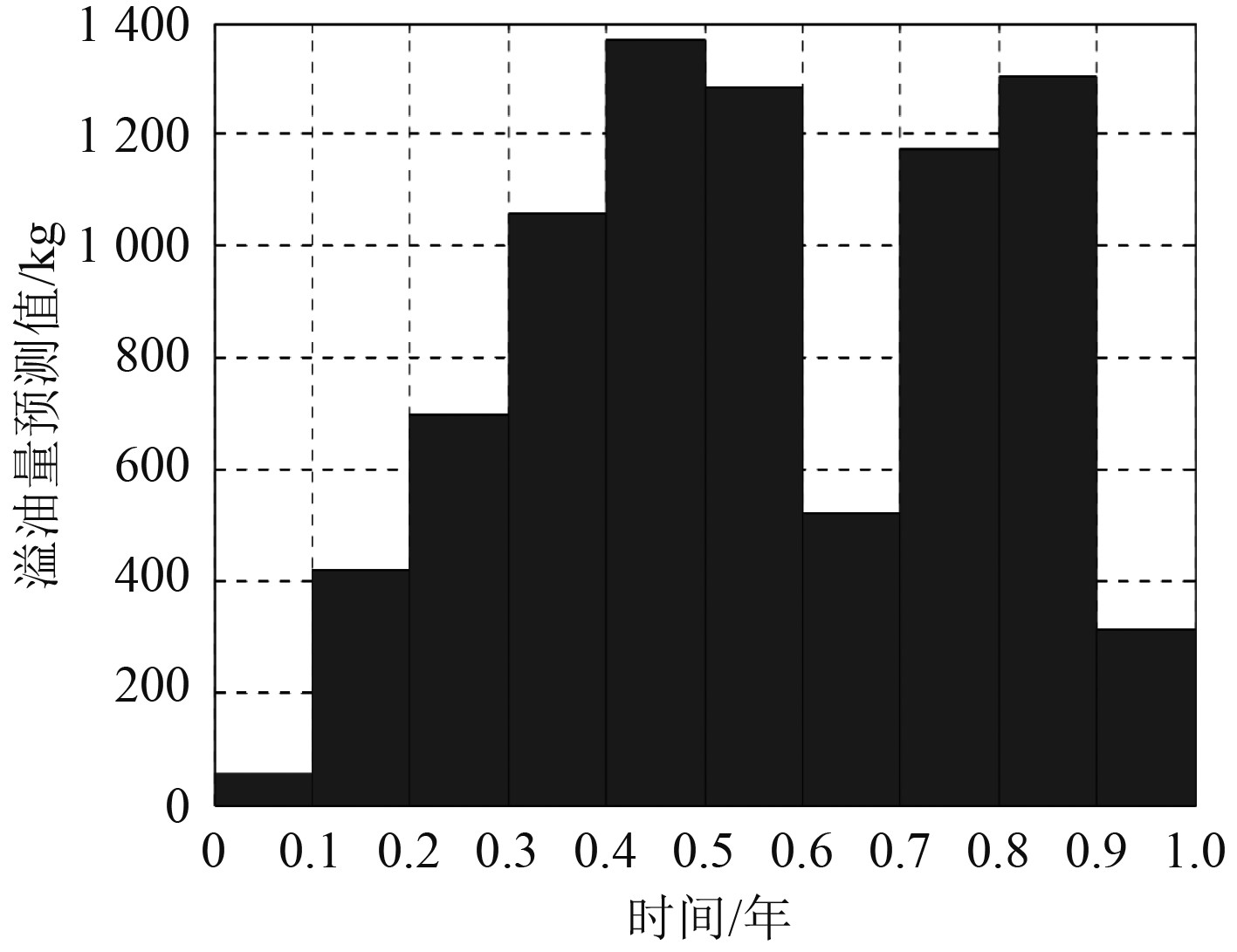
本文得到基于灰色理论模型的一年内海域内船舶溢油量的预测数据如图5所示，可以发现预测结果和实际溢油的误差在可接受范围内，因而本文建立的模型具有一定的应用价值。

3 结　语

海上船舶的溢油事故对海洋环境有严重破坏作用，也不利于船舶的航运安全，本文结合灰色理论原理，建立一种船舶溢油风向评估方法，介绍了评估原理和过程，并针对大连海区的溢油风险进行了预测。