在舰船编队作战和调度中,需要结合舰船的空间方位信息进行路径规划设计,采用分布式的编队控制技术,结合对舰船目标信息估计和方位参数分析,构建舰船编队的分布式组网控制模型,结合路径规划方法,实现对舰船编队的三维路径规划设计,提高舰船的作战规划能力。在进行舰船的三维路径规划设计中,需要通过对舰船的刚体平移和旋转性参数分析,结合控制器设计和中心节点分布设计,实现对舰船三维路径规划设计[1]。
目前,对舰船三维路径规划方法主要有粒子滤波算法、点跟踪识别算法、Kalman滤波估计方法等,通过路径动态检测方法[2],根据舰船编队的空间分布数据进行动态加权和最短路径寻优控制,建立舰船三维路径规划模型,实现舰船三维路径规划[3]。但传统方法进行舰船三维路径规划的实时性不好,为此,本文提出基于改进粒子群优化算法的舰船三维路径规划方法。首先采用视点模型跟踪方法实现对舰船三维路径移动任务规划设计,然后通过改进粒子群仿生算分获取虚拟刚体状态约束特征值,结合方位信息编队移动分布情况,实现对目标舰船编队的形成、保持与跟踪识别,通过对舰船目标三维参数估计结果实现对舰船的路径规划。最后,进行仿真测试。
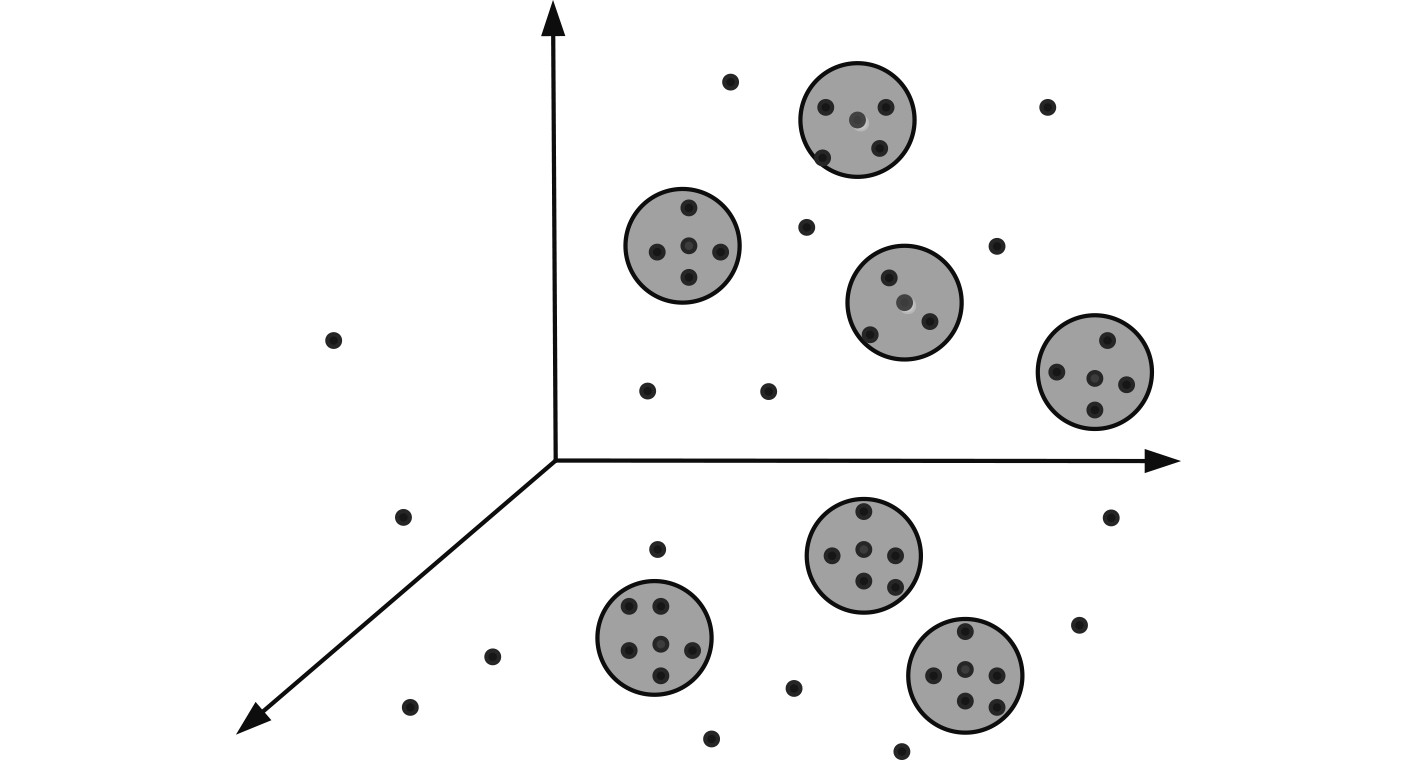
1 舰船三维路径移动任务参数分析 1.1 舰船三维路径视点模型跟踪为了实现改进粒子群优化算法的舰船三维路径规划,首先采用视点模型跟踪方法实现对舰船三维路径移动任务规划设计。将舰船编队目标视为一个刚体结构[4],舰船三维路径规划问题为一个具有未知扰动的二阶模型参数分析问题,通过构建时变编队控制策略,采用误差的收敛性判断与编队系统规划设计的方法[5],获取虚拟刚体状态约束特征值,得到舰船三维路径视点模型和刚体分布模型如图1所示。采用粒子群规划方法,构建集中式编队控制模型,得到系统中某几个机体的虚拟位置参数信息,采用一阶、二阶模型参数识别,得到机体感知动态参数为lc。
|
图 1 舰船三维路径视点模型和刚体分布模型 Fig. 1 3D path viewpoint model and rigid body distribution model of ships |
将舰船的动力学模型描述为一个二阶微分方程,得到惯性坐标系下的姿态旋转矩阵,第
| $ {l_{ci}} = {l_{c{\rm{Min}}}} + {\text{(}}{l_{c{\rm{Max}}}} - {l_{c{\rm{Min}}}}{\text{)}} \times {\left( {i/s} \right)^\alpha }。$ | (1) |
式中:
采用方位信息对期望队形进行自适应控制,得到系统动力学模型梯度分布函数为:
| $ {[\nabla F(x)]_j} = \frac{{\partial F(x)}}{{\partial {x_j}}} = 2\sum\limits_{i = 1}^N {v_i^{}(x)\frac{{\partial {v_i}(x)}}{{\partial {x_j}}}} 。$ | (2) |
式中:
| $ Edge = \left\{ {StartID,EndID,{c_a},{x_a},{t_a}} \right\} 。$ | (3) |
式中:
根据舰船路径分布点的方位信息,用
| $ E = \{ {e_1},{e_2},{e_3}\cdots {e_M}\} ,$ | (4) |
式中:
采用大范围搜索和小范围组合控制,得到舰船三维路径的空间规划函数为:
| $ {t_a} = t_a^0\left[ 1 + J(x_a/({c_a} - {x_a})) \right] 。$ | (5) |
式中:
由此构建了舰船三维路径视点模型跟踪模型,根据粒子群跟踪识别方法,进行路径寻优。
1.2 舰船的方位信息及编队任务分布通过大量的像素点融合和方位信息估计,得到粒子群状态参数为
| $ \begin{split} & \Delta T = \left( {{T_1} - {T_0}} \right)/n,\\ & \Delta U = \left( {{U_1} - {U_0}} \right)/n,\\ & \Delta V = \left( {{V_1} - {V_0}} \right)/n,\\ & \Delta x = \left( {p_x^1 - p_x^0} \right)/n ,\\ & \Delta y = \left( {p_y^1 - p_y^0} \right)/n,\\ & \Delta z = \left( {p_z^1 - p_z^0} \right)/n 。\\ \end{split} $ | (6) |
式中:
选择不同的指标权重,得到场景非结构化融合机制下的粒子群寻优参数
| $ {T_i} = \left[ {\begin{array}{*{20}{c}} {c{\theta _i}}&{ - s{\theta _i}}&0&{{a_{i - 1}}} \\ {s{\theta _i}c}&{c{\theta _i}c}&{ - s}&{ - {d_i}s} \\ {s{\theta _i}s}&{c{\theta _i}s}&{c}&{{d_i}c} \\ 0&0&0&1 \end{array}} \right] 。$ | (7) |
式中:s 表示执行闭环检测的定位误差,c表示全局特征描述符,
建立舰船编队的多串联点分布式寻优模型,结合方位信息编队移动分布情况,实现对目标舰船编队的形成、保持与跟踪识别,得到最短路径寻优的目标方位参数估计值为:
| $ \left\{ \begin{aligned} & A = \frac{{{\partial ^2}}}{{\partial {f^2}}}\left[ {{D_s}\left( {f,\mu } \right)} \right]_{\begin{subarray}{l} f_{0k},\\ {\mu_{0k}} \end{subarray}}\\ & B = \frac{{{\partial ^2}}}{{\partial {\mu ^2}}}\left[ {{D_s}\left( {f,\mu } \right)} \right]_{\begin{subarray}{l} f_{0k},\\ {\mu_{0k}} \end{subarray}}\\ & C = \frac{{{\partial ^2}}}{{\partial f\partial \mu }}\left[ {{D_s}\left( {f,\mu } \right)} \right]_{\begin{subarray}{l} f_{0k}\\ {\mu_{0k}}。\end{subarray}} \end{aligned} \right. $ | (8) |
式中:
以最短路径为寻优目标函数,得到分布式目标个数分布为
| $ {d_i} = \sum {_j} {a_{ij}}。$ | (9) |
式中:
| $ \hat x_k^{} = \sum\limits_{i = 1}^N {w_k^i} x_k^i 。$ | (10) |
式中:
| $ {x_i}(k + 1) = {x_i}(k) + s\left(\frac{{{x_j}(k) - {x_i}(k)}}{{\left\| {{x_j}(k) - {x_i}(k)} \right\|}}\right) 。$ | (11) |
式中:
由此构建了舰船方位信息估计模型,结合方位信息编队移动分布情况,实现对目标舰船编队的形成、保持与跟踪识别。
2.2 路径规划粒子群优化算法采用粒子群路径规划方法,结合离散时间间隔采样,得到粒子群寻优节点
| $ {x_i}(t + 1) = {x_i}(t) + {v_i}(t + 1)。$ | (12) |
式中:
采用零均值的复值闭合参数分析的方法,得到舰船的方位及路径寻优的动态函数为:
| $ A = {({a_{ij}})_{n \times n}}E\left[ {{\boldsymbol{b}}\left( {\boldsymbol{k}} \right){{\boldsymbol{b}}^{\boldsymbol{H}}}\left( {\boldsymbol{k}} \right)} \right] 。$ | (13) |
式中:
初始化粒子种群,根据对舰船的实时动态信息参数估计,实现对舰船三维路径规划。
3 仿真测试对舰船三维路径规划的仿真实验中,给出舰船编队有32个阵元组成,相邻舰船的间隔为
|
|
表 1 舰船编队路径的空间节点分布 Tab.1 Spatial node distribution of ship formation paths |
据参数设定,进行舰船三维路径规划设计,初始舰船方位分布如图2所示。

|
图 2 舰船目标初始方位分布 Fig. 2 Initial azimuth distribution of ship targets |
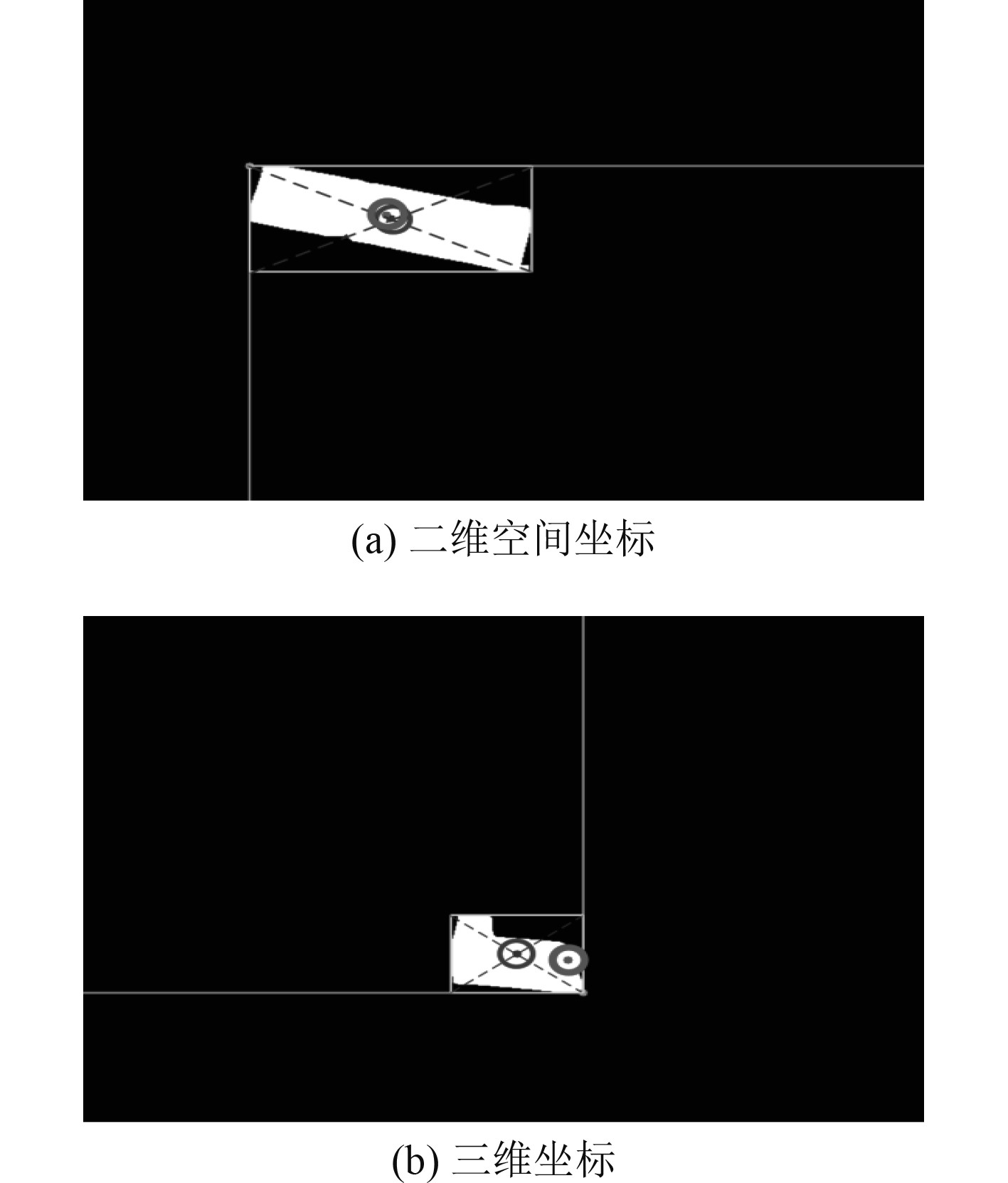
采用本文方法进行三维路径规划,首先对舰船目标的空间位置进行估计和跟踪识别,如图3所示。
|
图 3 舰船目标空间位置估计和跟踪识别 Fig. 3 Estimation and tracking recognition of ship target spatial position |
根据对空间方位估计结果,进行三维路径规划,如图4所示。
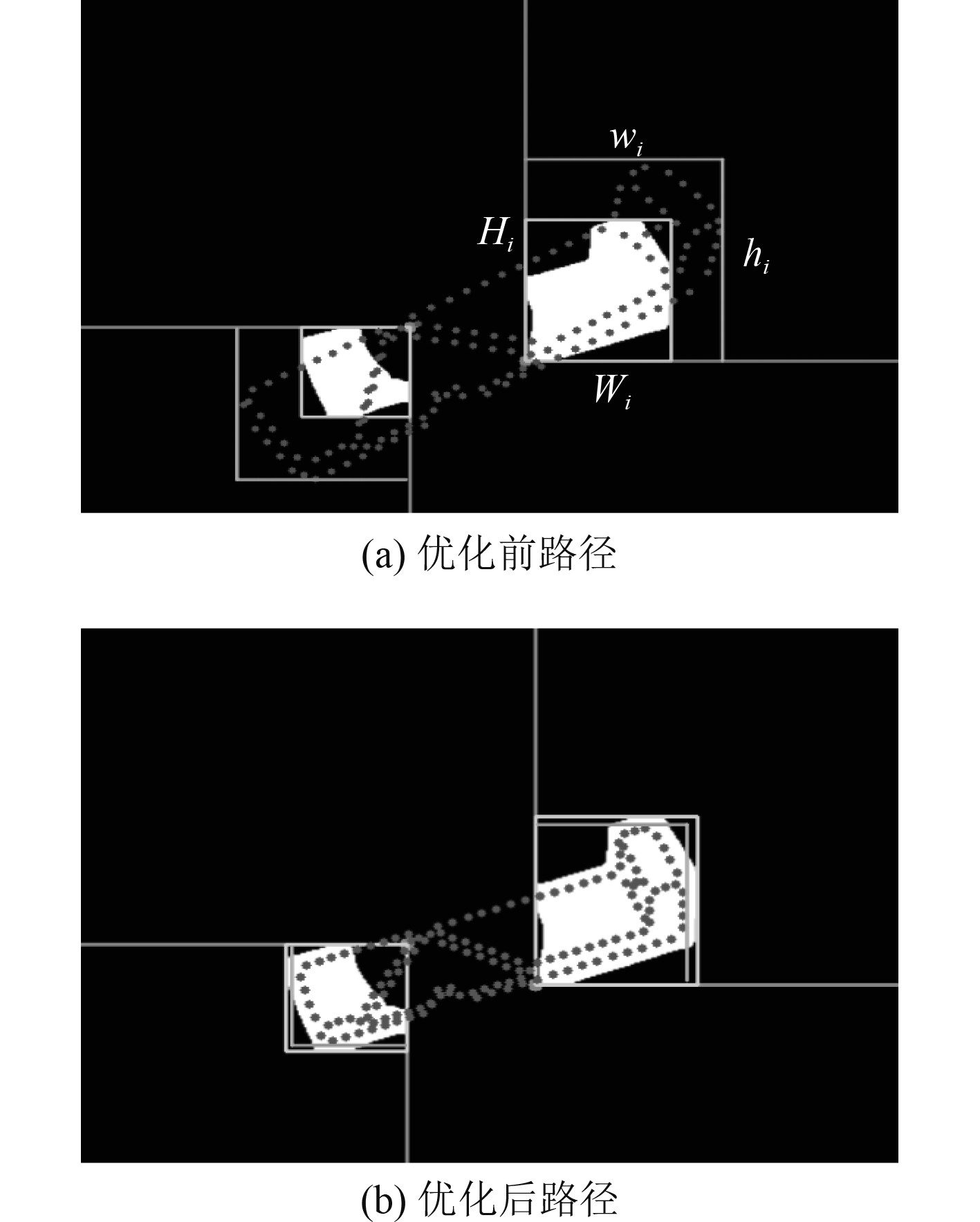
|
图 4 舰船三维路径规划 Fig. 4 3D path planning for ships |
分析可知,本文方法对舰船三维路径规划的空间分布定位能力较好,能准确估计舰船位置和空间方位信息,测试舰船目标定位精度,对比结果见表2。分析可知,本文方法实现舰船路径规划,定位精度较高。
|
|
表 2 舰船方位估计误差对比 Tab.2 Comparison of ship azimuth estimation errors |
本文结合对路径规划方法,实现对舰船编队的三维路径规划设计,提高舰船的作战规划能力。提出基于改进粒子群优化算法的舰船三维路径规划方法,构建时变编队控制策略。采用误差的收敛性判断与编队系统规划设计的方法,获取虚拟刚体状态约束特征值。建立舰船编队的多串联点分布式寻优模型,结合方位信息编队移动分布情况,实现对目标舰船编队的形成、保持与跟踪识别。分析可知,本文方法对舰船三维路径规划的空间分布定位能力较好,能准确估计舰船位置和空间方位信息。
| [1] |
黄磊, 李慧, 张媛. 基于网络感知信息的船舶航迹规划智能避障方法[J]. 舰船科学技术, 2022, 44(3): 71-74. HUANG Lei, LI Hui, ZHANG Yuan. Intelligent obstacle avoidance method for ship trajectory planning based on network perception information[J]. Ship Science and Technology, 2022, 44(3): 71-74. DOI:10.3404/j.issn.1672-7649.2022.03.014 |
| [2] |
张香竹, 张立家, 宋逸凡, 等. 基于深度学习的无人机单目视觉避障算法[J]. 华南理工大学学报(自然科学版), 2022, 50(1): 101-108+131. |
| [3] |
张果, 曹立佳, 卢天秀, 等. 基于收缩理论的多无人机姿态自适应同步控制[J]. 信息与控制, 2020, 49(2): 170-176, 187. |
| [4] |
李聪, 王勇, 周欢, 等. 多无人机编队分组决策与一致性[J]. 电光与控制, 2017, 24(10): 12–16.
|
| [5] |
郑重, 熊朝华, 党宏涛, 等. 时变通信延迟下的无人机编队鲁棒自适应控制[J]. 中国惯性技术学报, 2016, 24(1): 108–113. ZHENG Zheng, XIONG Chaohua, DANG Hongtao, et al. Robust adaptive control of unmanned aerial vehicle formation under time-varying communication delay [J]. Chinese Journal of Inertial Technology, 2016, 24(1): 108–113 |
 2023, Vol. 45
2023, Vol. 45
