2. 东莞小豚智能技术有限公司,广东 东莞 523830
2. Dongguan Xiaotun Intelligence Technologies Co., Ltd., Dongguan 523830, China
随着无人驾驶技术、计算机技术等先进技术的发展,无人船已成为未来船舶发展的一个重要分支。因为其较强的灵活性与较高的可扩展性,无人船无论是在军用还是在民用领域都有着广泛的应用。随着无人船的快速发展,航向的控制问题得到了重点关注。目前传统的航向控制方法主要为PID控制、模糊PID控制[1],张晨等[2-4]基于不同类型的滑模控制设计无人船航向控制器,并通过仿真证明控制器的优越性。但上述这些方法多数较为复杂,调参困难,对计算资源要求较高,难以在工程应用中实现。
Tzeng等[5-6]提出利用一阶 Nomoto 模型和内模控制思想设计船舶首向控制器。杨吉[7]基于内模控制设计航向控制器,并实船验证航向内模控制器的可行性。但传统内模控制器在系统稳定后存在静态误差。近年来,国内外专家提出二自由度控制方式[8],许多学者根据不同的对象或控制方式设计了二自由度内模控制器,具有较好的跟踪性能和抗负载干扰特性[9-10]。本文以二自由度内模控制器原理为基础,结合线性Nomoto船舶模型,提出一种改进的二自由度内模航向控制器。消除了静态误差,通过建模仿真,证明该控制器具有良好的控制效果。
1 船舶模型建模目前对于无人船数学模型的描述,由于水动力模型建模复杂,而响应型模型需要考虑的因素较少,反映了无人船航向角随时间的变化规律,所以在工程上响应型模型应用广泛。响应型模型可以直观地显示模型输入输出关系,非常适合无人船航向控制器的设计,可通过实验获得输入输出数据辨识参数。
线性Nomoto模型已具有较高的精度,将船舶的纵向运动从三自由度操纵运动方程中解耦,忽略掉纵向运动,得到仅考虑船舶的2个自由度横漂速度v和转艏角速度r,船舶动力学的方程如下:
| $ \left\{ \begin{aligned} & (m - {Y_{\dot v}})\dot v - {Y_v}v = {Y_\delta }\delta - (m{x_G} - {Y_{\dot r}})\dot r - (m{u_0} - {Y_r})r ,\\ & (m - {N_{\dot v}})\dot v - {N_v}v = {N_\delta }\delta - ({I_z} - {N_{\dot r}})\dot r - (m{x_G}{u_0} - {N_r})r 。\end{aligned} \right. $ | (1) |
为得到无人船转首角速度与舵角之间的关系,将式(1)中的横向速度v消掉即可得到一个描述操纵舵角对首摇的二阶线性响应模型,即
| $ {T_1}{T_2}\ddot r + ({T_1} + {T_2})\dot r + r = K\delta + K{T_3}\dot \delta 。$ | (2) |
式中:K及
| $ r = \dot \psi ,\;\; \dot r = \ddot \psi 。$ | (3) |
采用野本谦作[11]提供的线性模型,可得航向角
| $ {G_{\psi \delta }}(s) = \frac{K}{{s(Ts + 1)}}。$ | (4) |
式(4)为船舶操纵运动方程,也称Nomoto模型。本文采用Thor I. Fossen书中货船的航向模型参数,
| $ {G_{\psi \delta }}(s) = \frac{{0.185}}{{s(107.3s + 1)}}。$ | (5) |
考虑实际工程中的应用,需要在离散系统中实现,对船舶模型进行离散化可得:
| $ {G_{{\text{hat}}}}({z^{ - 1}}) = \frac{{B({z^{ - 1}})}}{{A({z^{ - 1}})}}。$ | (6) |
其中:
| $ \left\{ \begin{gathered} A({z^{ - 1}}) = 1 + {a_1}{z^{ - 1}} + {a_2}{z^{ - 1}},\\ B({z^{ - 1}}) = {b_0}{z^{ - 1}},\\ {a_1} = {a_2} - 1 ,\\ {a_2} = \frac{{ - T}}{{T + Ts}},\\ {b_0} = \frac{{K \cdot Ts}}{{T + Ts}} 。\\ \end{gathered} \right. $ | (7) |
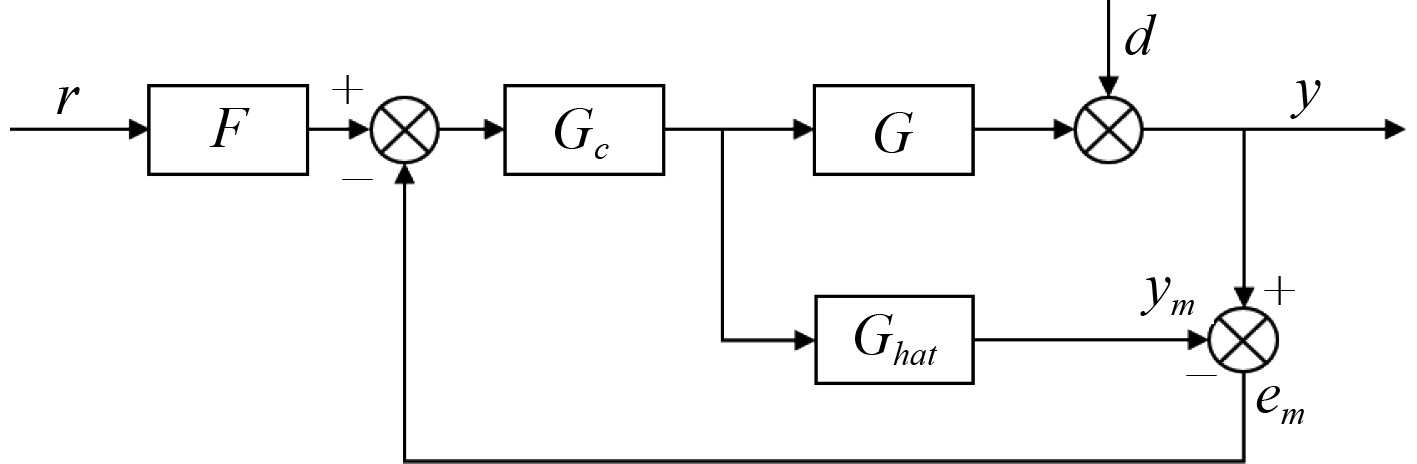
内模控制(IMC)是一种采用被控对象的内部模型和反馈修正的预测控制,作为Smith预估控制的扩展,因为其控制系统设计简单、可调参数少,且性能良好,使得参数整定较为简单,方便工业现场的调试。传统的内模控制器结构如图1所示。
|
图 1 传统内模控制器结构图 Fig. 1 Structure diagram of traditional internal model controller |
图中,
根据内模结构原理可得出系统对应的传递函数为:
| $ \begin{split} y(s) =& \frac{{{G_c}(s)G(s)}}{{1 + {G_c}(s)\left[ {G(s) - {G_{hat}}(s)} \right]}}r(s) + \\ & \frac{{1 - {G_c}(s){G_{hat}}(s)}}{{1 + {G_c}(s)\left[ {G(s) - {G_{hat}}(s)} \right]}}d(s) 。\end{split}$ | (8) |
当实际被控无人船与所建立的船舶模型达到匹配时,即
| $ y(s) = {G_c}(s)G(s)r(s) + [1 - {G_c}(s){G_{hat}}(s)]d(s) 。$ | (9) |
航向输出值与航向期望值之间的差值为:
| $ e(s) = \frac{{1 - {G_c}(s){G_{hat}}(s)}}{{1 + {G_c}(s)[G(s) - {G_{hat}}(s)]}}[r(s) - d(s)G(s)] 。$ | (10) |
内模控制器
由于期望航向输入一般为阶跃信号,需要对输入的期望航向进行柔化,为了物理可实现引入低通滤波器结构
| $ {G_c}(s) = G_{_{hat - }}^{ - 1}(s)F(s),$ | (11) |
式中,
| $ F(s) = \frac{1}{{{{(\tau s + 1)}^n}}} 。$ | (12) |
式中:n为滤波器的阶次,一般n的选择要保证内模控制器的正则性。由图1可以看出,传统内模控制方法可调节参数非常少,只有一个滤波器参数
式(4)为内模控制系统中被控对象数学模型
| $ {G_{\text{c}}}(s) = \frac{{s(Ts + 1)}}{K} \cdot \frac{1}{{{{(\tau s + 1)}^n}}}。$ | (13) |
对IMC控制器
| $ {G_c}({z^{ - 1}}) = {G_{hat}}^{ - 1}({z^{ - 1}})F({z^{ - 1}})。$ | (14) |
对滤波器
| $ F(s) = \frac{{Y(s)}}{{U(s)}} = \frac{1}{{\tau s + 1}}。$ | (15) |
使用反向差分整理可得低通滤波器离散形式为:
| $ F({{\text{z}}^{ - 1}}) = \frac{{D({z^{ - 1}})}}{{C({z^{ - 1}})}} = \frac{{1 - \alpha }}{{1 + ( - \alpha ){{\text{z}}^{ - 1}}}}。$ | (16) |
其中:
| $ \alpha = \frac{1}{{1 + \dfrac{\tau }{{{T_s}}}}} 。$ | (17) |
将式(6)和式(16)代入式(14)可得离散形式
| $ G_c(z^{-1})=\frac{A(z^{-1})}{B(z^{-1})}\cdot \frac{D(z^{-1})}{C(z^{-1})}\cdot \frac{D(z^{-1})}{C(z^{-1})}。$ | (18) |
传统的一自由度内模控制或是二自由度内模控制方法,无论无人船模型建立是否准确,在扰动传递函数中,都存在不稳定的极点
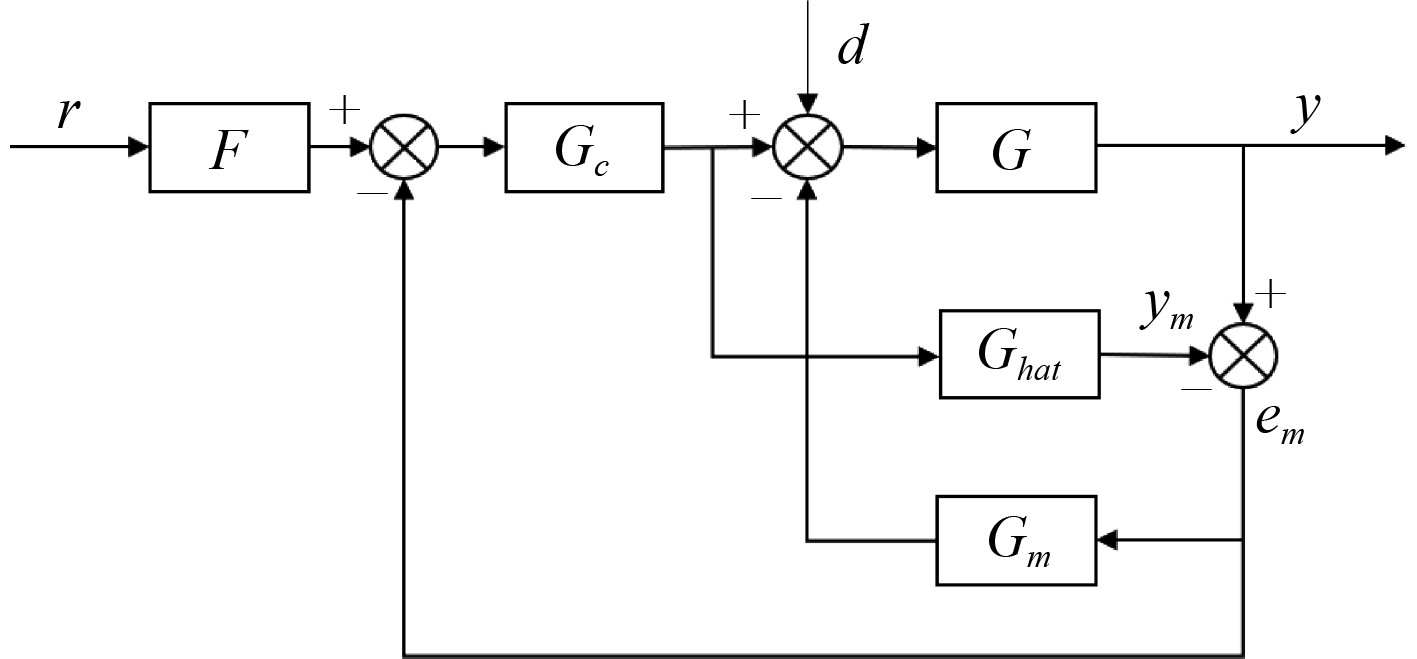
在无人船实际工程应用中,在安装船舵时,由于机械误差或是人工安装误差,使得船舵存在一定程度的偏差,这样的偏舵作为负载干扰,使得传统的内模控制方法即使在系统达到稳定后,总存在一定的静态误差,造成无人船航向存在一定的偏差。这一点在仿真中也证实存在。本文介绍一种改进的二自由度内模控制结构,通过零极点对消的方法,使得控制器稳定,从而消除静态误差与镇定控制对象。改进的二自由度内模控制结构,如图2所示。
|
图 2 改进的二自由度内模控制结构图 Fig. 2 Improved two degrees of freedom internal model control structure diagram |
该结构改进之处在于它是在传统内模控制的基础上增加一个预稳定控制器
该结构另一个优点在于将输入的期望航向值响应和负载干扰响应实现解耦控制,使控制器的设计如传统内模控制方法设计一样简便,且控制器内的参数有各自的意义,控制器
由图2可得系统的输出y的传递函数为:
| $\begin{split} y(s) =& \frac{{{G_c}(s)G(s)\left[ {1 + {G_{hat}}(s){G_m}(s)} \right]}}{{1 + {G_c}(s)\left[ {G(s) - {G_{hat}}(s)} \right] + G(s){G_m}(s)}}r(s) + \\ & \frac{{G(s)\left[ {1 - {G_c}(s){G_{hat}}(s)} \right]}}{{1 + {G_c}(s)\left[ {G(s) - {G_{hat}}(s)} \right] + G(s){G_m}(s)}}d(s)。\end{split}$ | (19) |
当无人船模型建立准确时,即
| $ y(s) = {G_c}G(s)r(s) + \left[\frac{{G(s)\left[ {1 - {G_c}(s){G_{hat}}(s)} \right]}}{{1 + G(s){G_m}(s)}}\right]d(s) 。$ | (20) |
上式中输入干扰
| $ {T_d} = \frac{{G(s)}}{{1 + G(s){G_m}(s)}} 。$ | (21) |
可以看出其是一个闭环系统,通过调节控制器
由式(19)可以看出,
设预稳定控制器
| $ {G_m} = \frac{{{K_c}(Ts + 1)}}{{\beta s + 1}}。$ | (22) |
式中:
| $ \beta=\frac{\dfrac{\text{π}}{2}}{A_{m} K K_{c}}-\theta。$ | (23) |
式中:
| $ \dfrac{{\dfrac{\text{π} }{2} - 1}}{{\theta {A_m}K}} < {K_c} < \dfrac{{\dfrac{\text{π} }{2}}}{{\theta {A_m}K}} 。$ | (24) |
对于无人船,舵机的时滞常数
改进的二自由度内模控制方法总共有3个可调参数,但
为在离散系统中实现,将式(22)进行离散化:
| $ G_{m}\left(z^{-1}\right)=\frac{f_{0}+f_{1} z^{-1}}{e_{0}+e_{1} z^{-1}}=\frac{F\left(z^{-1}\right)}{E\left(z^{-1}\right)},$ | (25) |
| $ \frac{u_{c}(k)}{e_{m}(k)}=\frac{F\left(z^{-1}\right)}{E\left(z^{-1}\right)}=\frac{K_{c} \alpha_{2} /\left[\begin{array}{ll} 1 & -\alpha_{1} \end{array}\right]}{\left[\begin{array}{ll} 1 & -\alpha_{2} \end{array}\right]} 。$ | (26) |
其中:
| $ \begin{split} &\alpha_{1}=\dfrac{T}{T+T s} ,\\ &\alpha_{2}=\dfrac{\beta}{\beta+T s}。\end{split} $ | (27) |
无人船航向作为被控对象,使用改进的二自由度内模控制器对航向进行控制,通过Matlab/Simulink仿真平台,针对式(5)船舶航向模型,期望值分别在
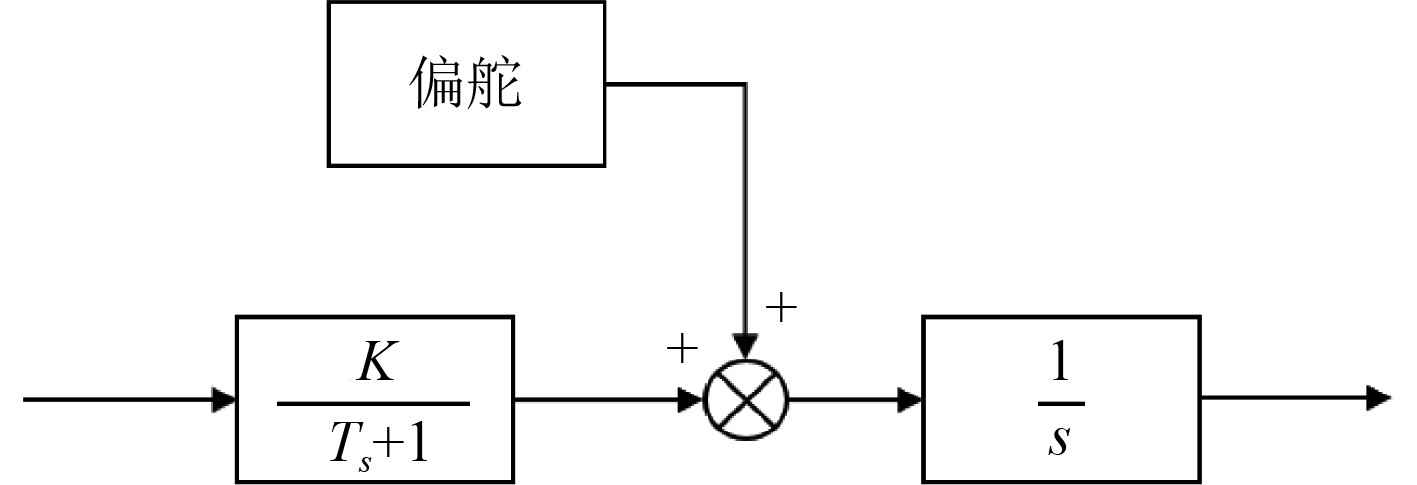
为模拟实际工程中由于船舵的安装误差及设备误差导致的偏舵问题,在Matlab/Simulink仿真软件中,对船舶机理模型对象中加入偏舵干扰,一般取0.02~0.05 rad/s之间较为符合实际工程中的情况。仿真中偏舵取0.02 rad/s,结构如图3所示。
|
图 3 偏舵干扰模型结构 Fig. 3 Rudder interference model structure |
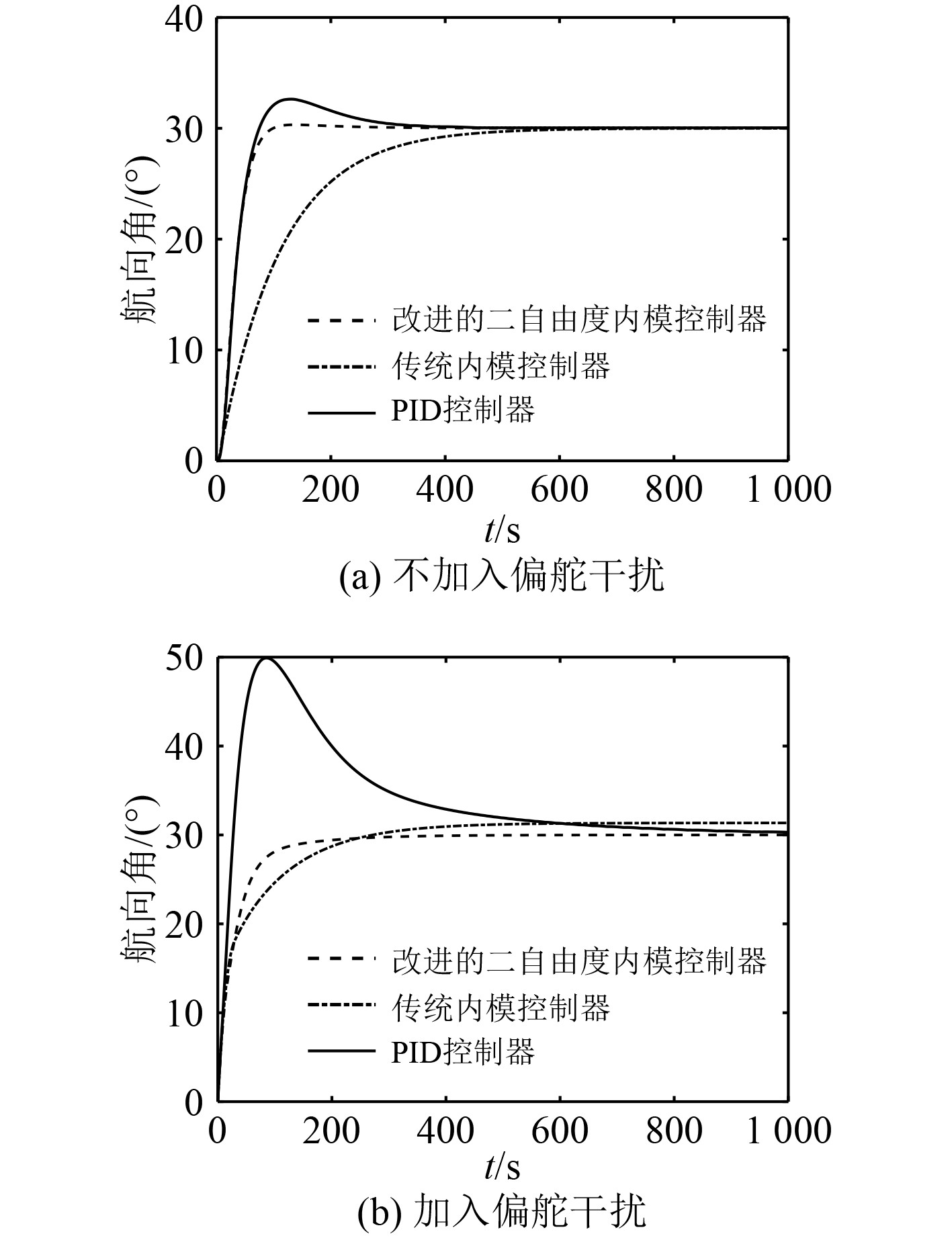
开展不同航向值以及偏舵干扰影响下的航向控制仿真。仿真实验结果如图4~图6所示。图4~图6中加入偏舵的仿真结果总结于表1。
|
图 4 30°时航向控制算法对应的航向角变化 Fig. 4 Change of heading angle corresponding to heading control algorithm at 30° |
|
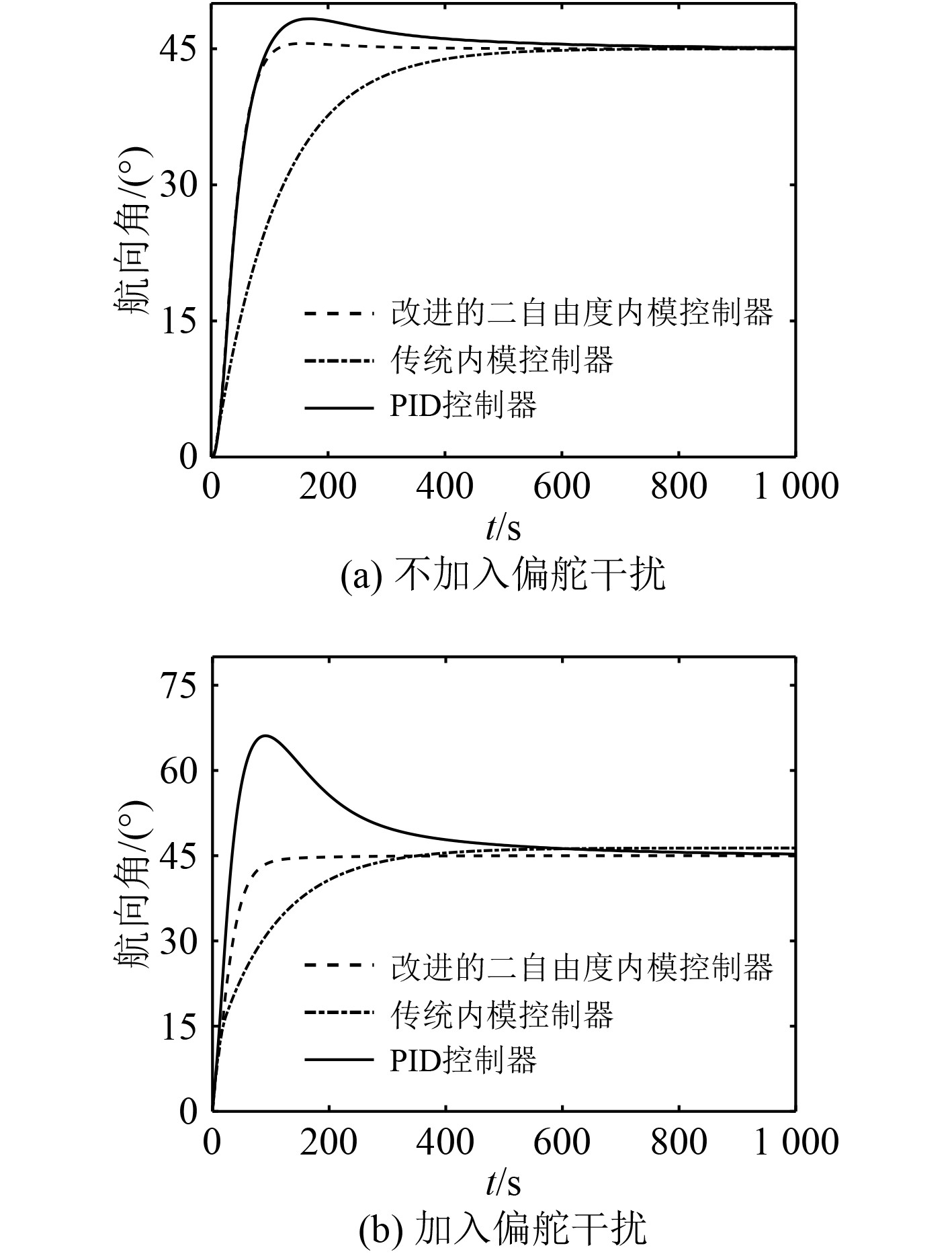
图 5 45°时航向控制算法对应的航向角变化 Fig. 5 Change of heading angle corresponding to heading control algorithm at 45° |
|
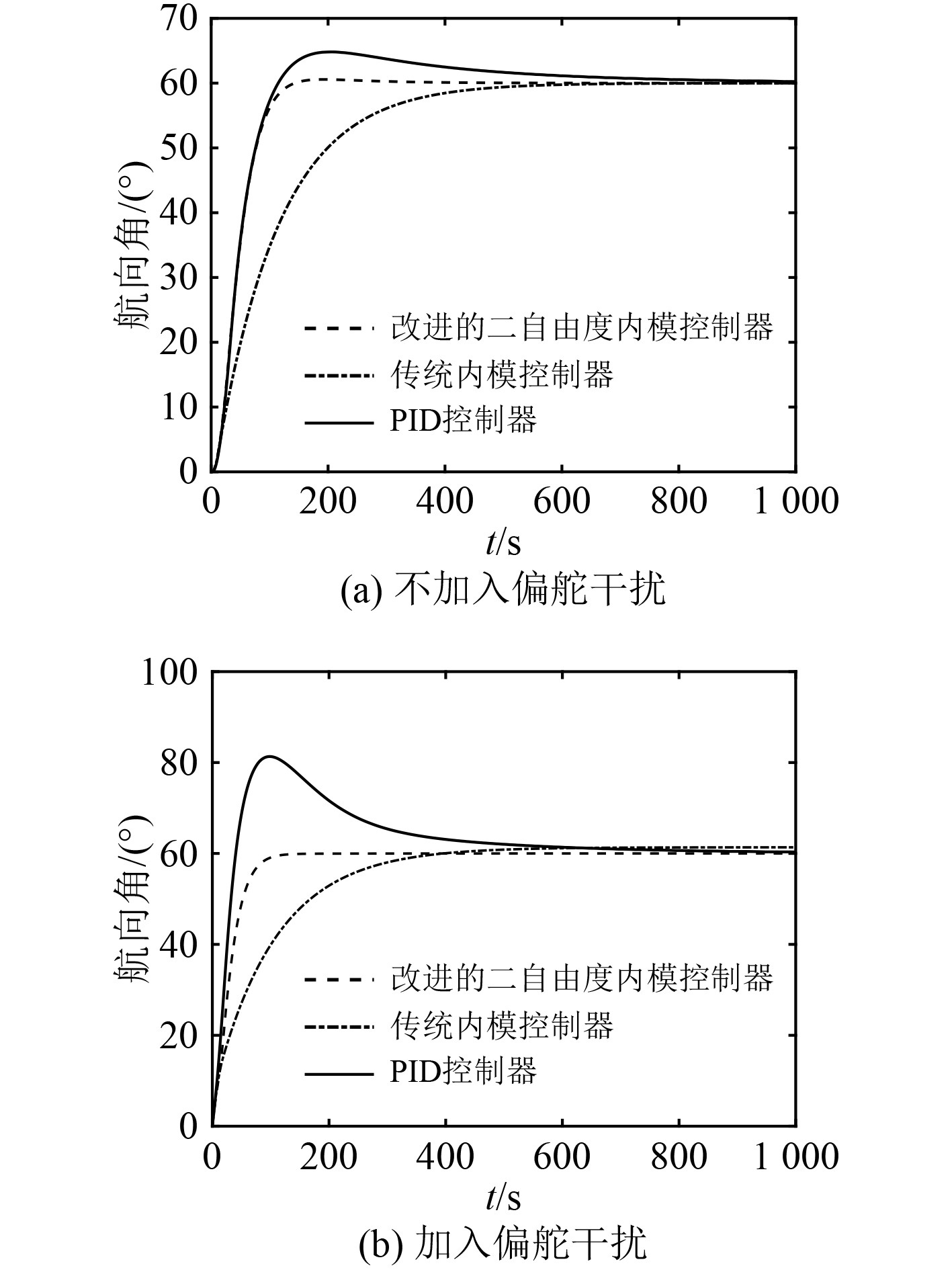
图 6 60°时航向控制算法对应的航向角变化 Fig. 6 Change of heading angle corresponding to heading control algorithm at 60° |
|
|
表 1 各航向控制算法仿真结果对比 Tab.1 Comparison of simulation results of each heading control algorithm |
由数据分析可以看出,传统内模控制器和PID控制器,2种控制方法均存在不同程度的静态误差,传统内模控制方法静差最大,而本文方法则消除了静态误差。传统PID控制器在偏舵干扰下,超调量显著增加,而改进的二自由度内模控制方法与传统内模控制方法均无超调。相较于另外2种控制器,本文提出的方法具有更短的稳定时间,并且该控制器控制性能不会因为初始航向角的不同而产生较大的偏差,说明该系统具有良好的控制性能和鲁棒性。
4 结 语本文针对无人船航向控制Nomoto线性系统,设计一种改进二自由度内模航向控制器,实现单独设计和调节跟踪性能和抗负载扰动性能,相比传统航向控制方法相比可调参数少,仅有一个可调参数,且整定简单。当无人船模型参数确定后,整套控制系统即确定,为实现自适应控制提供控制方法。通过Matlab/Simulink将该控制器与传统内模控制器、PID控制器相比,改进的二自由度内模控制器消除了静态误差,对于航向的控制没有超调量,同时拥有更短的稳定时间。
| [1] |
张雪飞, 袁鹏, 谭俊哲, 等. 基于模糊PID的无人帆船航向控制方法[J]. 中国舰船研究, 2019, 14(6): 15−21.
|
| [2] |
张晨, 薛文涛. 新型幂次趋近律的无人艇航向的终端滑模控制方法[J]. 电光与控制, 2017, 24(8): 29−32+60.
|
| [3] |
陈霄, 周德超, 刘忠, 等. 欠驱动无人船自适应滑模航迹跟踪控制[J]. 国防科技大学学报, 2018, 40(3): 127−134.
|
| [4] |
D MU, WANG G, FAN Y, et al. Modeling and identification of podded propulsion unmanned surface vehicle and its course control research[J]. Mathematical Problems in Engineering, 2017, 1−13.
|
| [5] |
TZENG C Y, LIN K F. Adaptive ship steering autopilot design with saturating and slew rate limiting actuator[J]. IFAC Proceedings Volumes, 1998, 31(30): 5-14. DOI:10.1016/S1474-6670(17)38410-0 |
| [6] |
LEE S D, YU C H, HSIU K, et al. Design and experiment of a small boat track-keeping autopilot[J]. Ocean Engineering, 2010, 37(2-3): 208-217. DOI:10.1016/j.oceaneng.2009.11.005 |
| [7] |
杨吉. 基于吊舱推进的无人船自适应运动控制研究[D]. 武汉: 武汉理工大学, 2018.
|
| [8] |
张井岗. 二自由度控制[M]. 北京: 电子工业出版社, 2012.
|
| [9] |
吴延凯, 张伟. 基于GA的二自由度PID在火电机组的应用[J]. 电力科学与工程, 2018, 34(10): 68−73.
|
| [10] |
冷月, 杨洪耕, 王智琦. 一种基于二自由度内模控制的牵引网低频振荡抑制方法[J]. 电网技术, 2017, 41(1): 258−264.
|
| [11] |
NOMOTO K, TAGUCHI K, HONDA K, et al. On the steering qualities of ships[J]. Journal of Zosen Kiokai, 1956(99): 75-82. DOI:10.2534/jjasnaoe1952.1956.99_75 |
| [12] |
宰文姣. 一类非自衡对象的改进两自由度内模控制[D]. 成都: 四川大学, 2006.
|
 2023, Vol. 45
2023, Vol. 45
