2. 中国船舶研究设计中心,湖北 武汉 430064
2. China Ship Development and Design Center, Wuhan 430064, China
为灵活调控声波的透射和损耗,在单层板、双层板、加筋板的基础上,多层均匀材料复合结构受到广泛关注,研究其声反射和透射特性具有重要意义。
对于板结构的声学计算,学者们已提出了多种方法,包括模态分析法、统计能量分析法、波传递法等[1]。此外,传递矩阵方法也是研究多层介质声学特性的一种主要理论方法[2-4],以上这些方法对于结构形式简单的平板结构是方便可行的,但也存在局限性,如板结构的外形变得复杂或者边界条件有了改变时,以上这些方法很可能不再适用。近年来,随着计算机技术的迅速发展,数值方法得到广泛应用,即采用有限元法和边界元法计算板结构的声学特性。赵洪等[5]利用数值解法研究了由弹性薄板、弹性板及消声材料组成的多层复合结构,在斜入射时反射系数、透射系数的频率响应和角分布特性。使用数值方法计算板结构的声学特性具有很多优点,对于结构外形与边界条件适用性很强,并且能够同时考虑多个因素对声学参数的影响规律等[6-7]。仿真方法也存在不足,对于大型结构,当计算频率较高时耗时过长,但随着计算机技术的发展,关于计算效率的问题已不是一个主要的障碍[8]。
1 基本理论 1.1 声学有限元仿真对于弹性体的声学分析是一个流固耦合问题,弹性体在流体载荷作用下将会发生变形和运动,与此同时固体的形变等反过来也将对流体产生影响。在流体域中,声压的分布满足下式:
| $ \dfrac{1}{{c_0^2}}\dfrac{{{\partial ^2}p}}{{\partial {t^2}}} - {\nabla ^{\rm{T}}}(\nabla p) = 0 。$ | (1) |
式中:c 0
式(1)称为Helmholtz积分公式,是求解结构声学特性的理论基础。根据变分原理,上述连续计算域可被离散为多个小的计算域,也就是完成了单元离散,此时原有的积分公式被转换为了线性方程组,通过数值方法求解表征结构声学特性的各个参数。
在弹性结构中,位移及其导数也需要满足结构的振动方程:
| $ \left[ {{{\boldsymbol{M}}^s}} \right]\{ \ddot {\boldsymbol{\delta }}\} + \left[ {{{\boldsymbol{K}}^s}} \right]\{ {\boldsymbol{\delta}} \} = \{ {{\boldsymbol{F}}^S}\} + \{ {{\boldsymbol{F}}^P}\} 。$ | (2) |
式中:
| $ \begin{split} & {[{{\boldsymbol{M}}^s}] = \displaystyle\sum\limits_e {\iiint\limits_{V_s^e} {{{[{{\boldsymbol{B}}_\delta }]}^{\rm{T}}}[{\boldsymbol{D}}][{{\boldsymbol{B}}_\delta }]{\rm{d}}V}} } ,\\ & {[{{\boldsymbol{K}}^s}] = {\rho _s}\displaystyle\sum\limits_e {\iiint\limits_{V_s^e} {{{[{{{N}}_\delta }]}^{\rm{T}}}[{{\boldsymbol{N}}_\delta }]{\rm{d}}V}} } 。\end{split} $ | (3) |
其中:
对于无限大平板问题(厚度为d,密度为
| $ R = \dfrac{{H({Z_2} - {Z_1}) + i(({G^2} - {H^2}){Z_1} - {Z_2})}}{{H({Z_2} + {Z_1}) + i(({G^2} - {H^2}){Z_1} + {Z_2})}},$ | (4) |
| $ T = \dfrac{{2G{Z_2}}}{{H({Z_2} + {Z_1}) + i(({G^2} - {H^2}){Z_1} + {Z_2})}} 。$ | (5) |
其中:G和H为传递矩阵中相应的元素;
在计算声学问题时,利用Comsol中的声学模块,可以模拟声学物理场的状态,将压力声学与结构力学2个物理场进行耦合,准确地模拟出弹性体声学分析的流固耦合力学问题,再利用Comsol声学模块中压力声学模块的频域接口对Helmholtz方程进行求解,得到反射声压pra和透射声压pta,进一步根据反射系数与透射系数的定义式(6)和式(7)求得反射透射系数。
| $ {r}_{p}=\dfrac{{p}_{ra}}{{p}_{ia}} ,$ | (6) |
| $ {t}_{p}=\dfrac{{p}_{ta}}{{p}_{ia}}。$ | (7) |
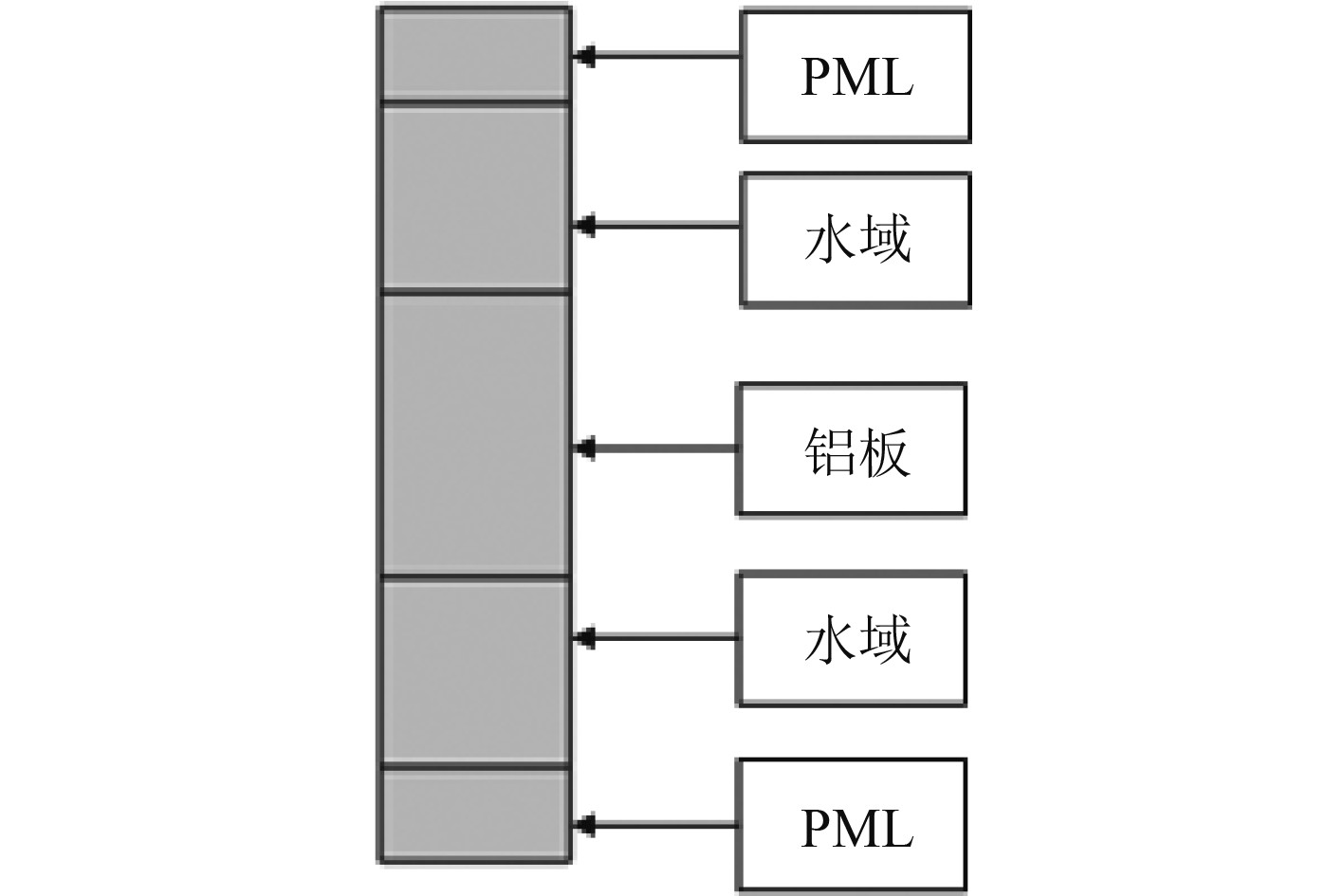
本文利用Comsol进行计算分析,为了验证本文计算所使用的计算模型以及有限元软件的有效性,将利用Comsol对单层金属板声强透射系数计算结果与理论解进行对比验证。有限元计算模型中平面波沿Y轴负方向入射,其结构如图1所示。该单元从上至下被分为5层,最上层为完美匹配层(PML层),其厚度设置为10 mm;第2层为厚度为20 mm的水域,第3层为厚度为30 mm的铝板,第4层同样为厚度为20 mm的水域,最下层为厚度为10 mm的PML层。其中水域的密度设置为1000 kg/m3,声速设置为1500 m/s。铝板的材料参数为:泊松比
|
图 1 验证模型结构示意图 Fig. 1 Schematic Diagram of the verification model’s structure |
|
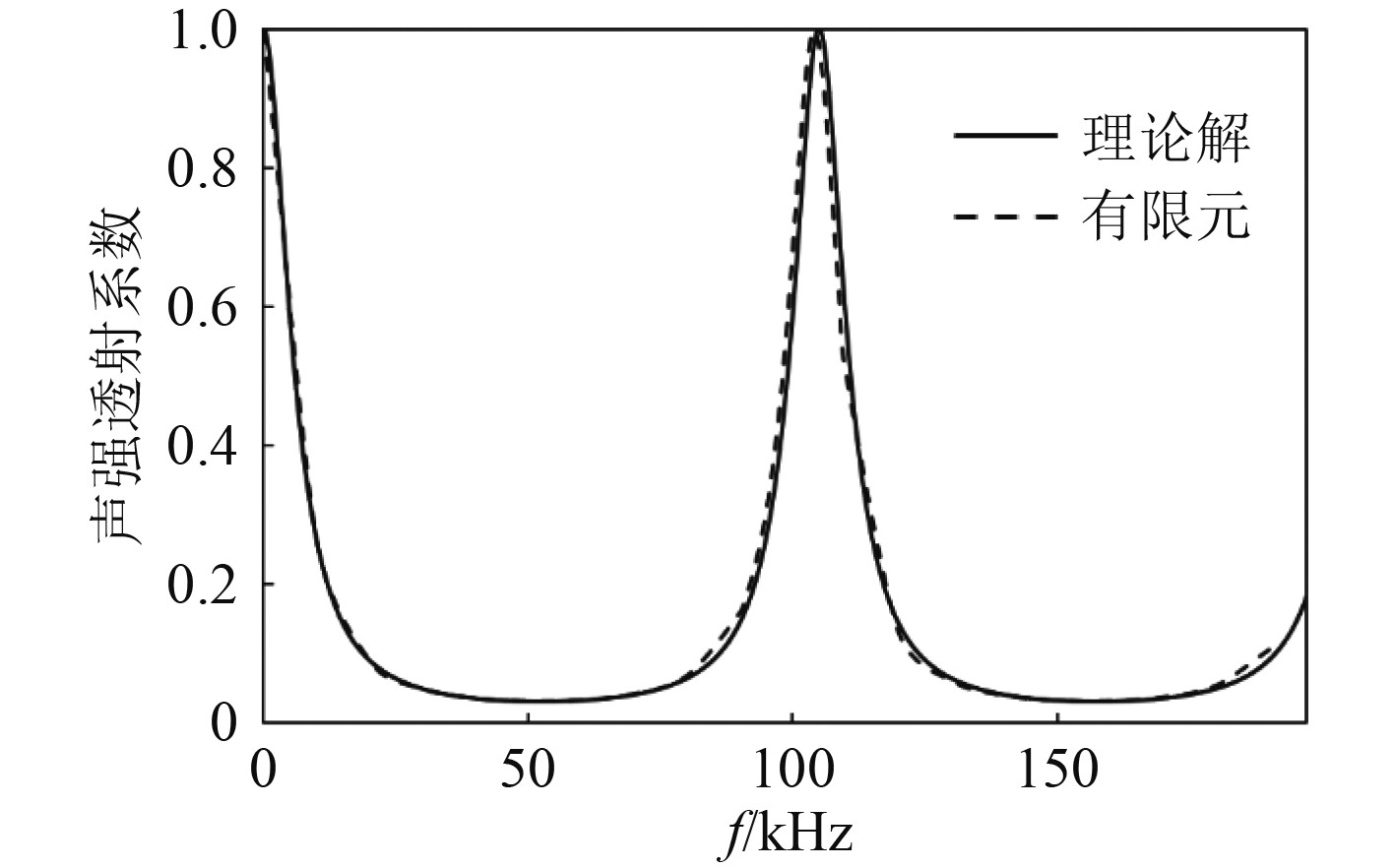
图 2 铝板声强透射系数仿真结果与解析结果对比 Fig. 2 Comparison between simulation and theoretical results |
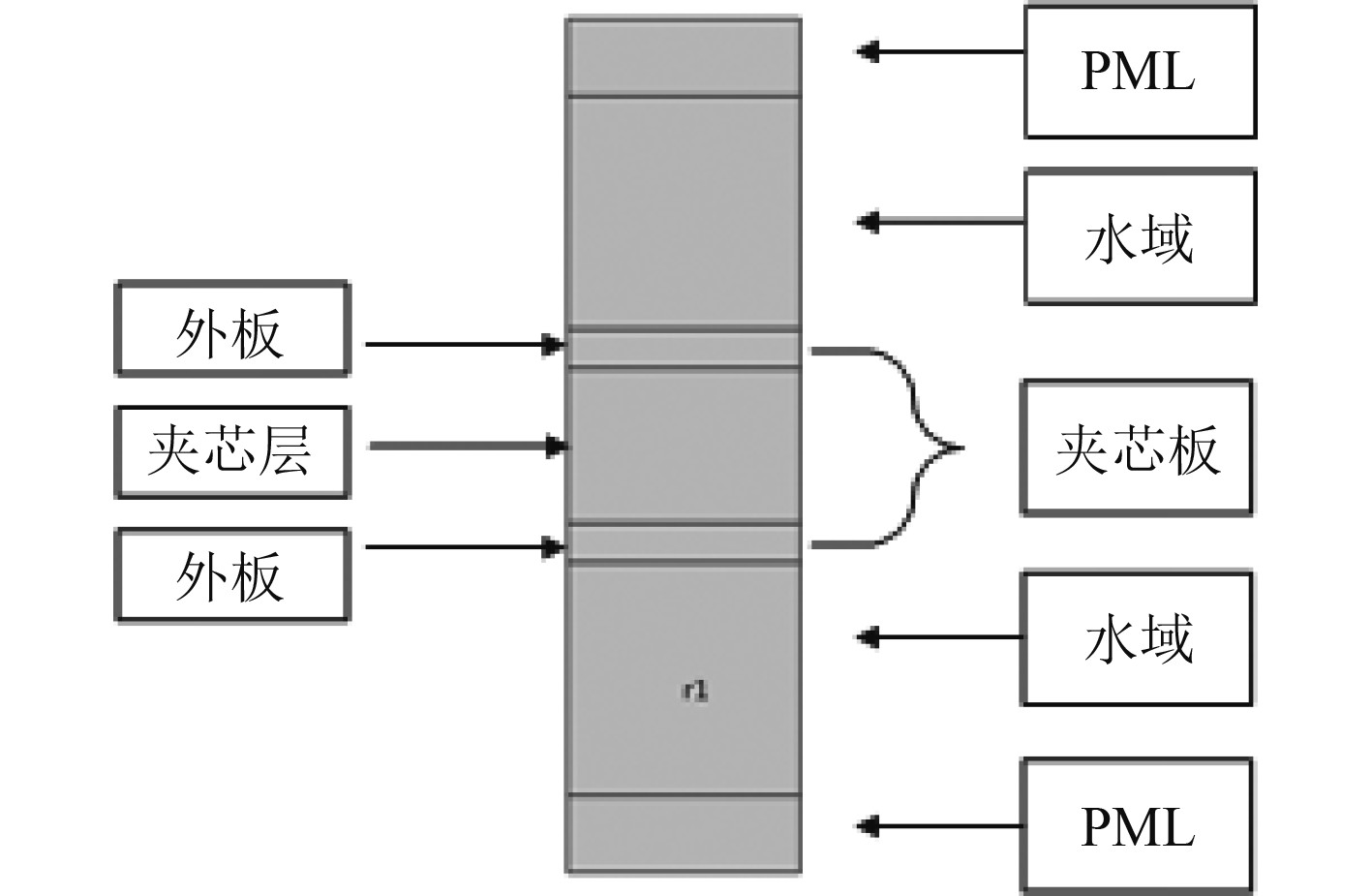
利用Comsol对于无限大三明治夹芯板的声学反射以及透射系数进行仿真计算,夹芯板计算模型的结构与有限元模型结构相似,仅仅将铝层替换为夹芯板。夹芯板的结构见图1,包括3层:厚度为30 mm的中间芯层,以及芯层两侧厚度为5 mm的面板。各层的材料参数如表1所示,其中
|
|
表 1 夹芯板各层材料参数 Tab.1 Sandwich plate′s material parameters |
|
图 3 夹芯板计算模型示意图 Fig. 3 Schematic diagram of the sandwich plate′s compute model |
本文主要探讨夹芯层的厚度、材料属性的变化对于夹芯板反射透射特性的影响规律,这主要是考虑到夹芯层的改变对于整体特性的影响较大。从芯层厚度与材料属性2个方面给出夹层板声学特性(反射与透射)的仿真结果,从中可见2个要素的影响规律。
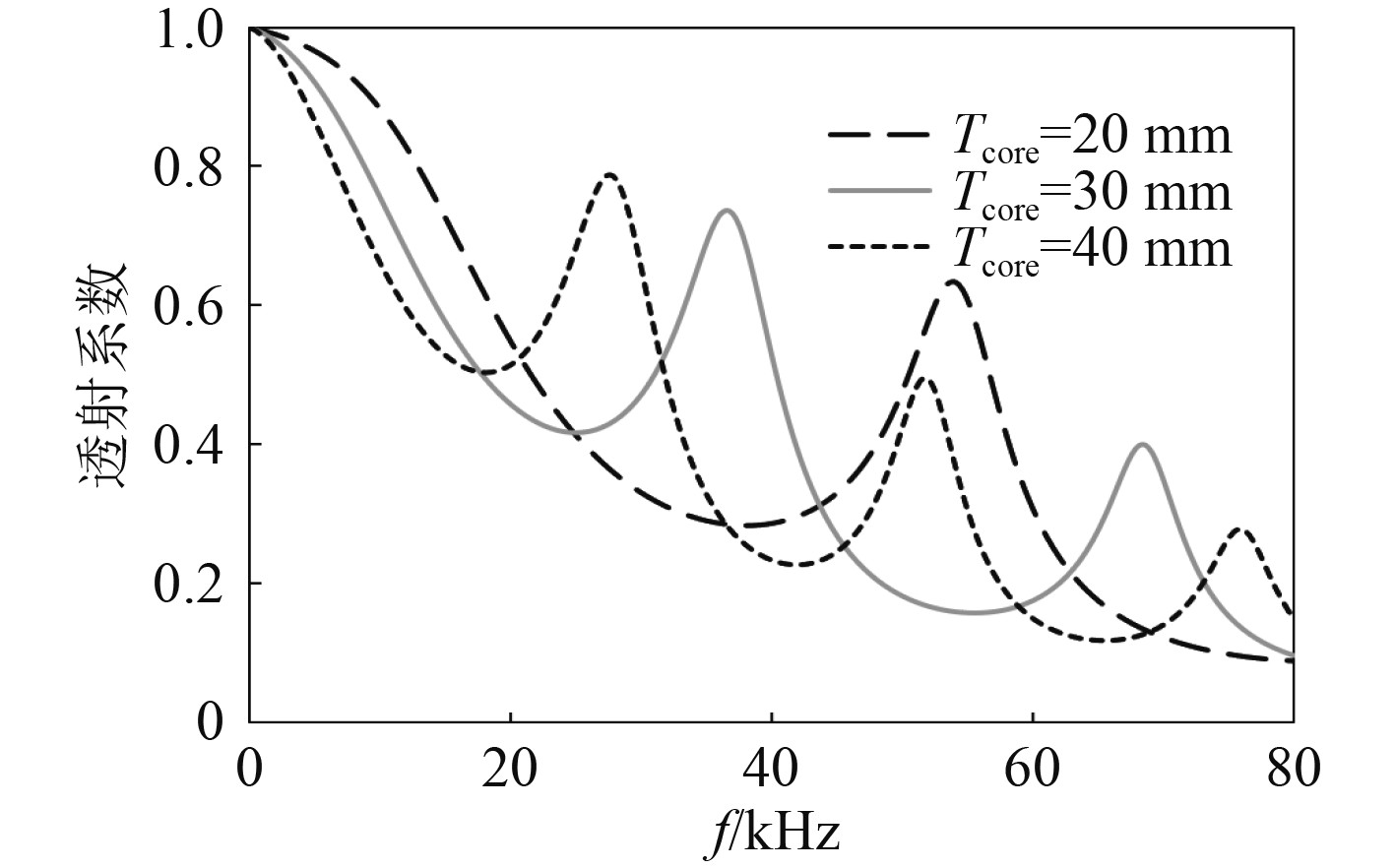
2.1 芯层厚度的影响研究夹芯层厚度的改变对于结构的反射透射系数的影响,芯层厚度分别取为20 mm,30 mm和40 mm。从图4可以看出,随着夹芯层厚度的增加,夹芯结构的透射系数在0~20 kHz频段下有明显下降,且随着芯层厚度的增加,结构透射系数峰值对应的频率不断向低频移动且幅值有明显增加。从图5可以看出,随着夹芯层厚度的增加,在0~20 kHz频段下夹芯结构的反射系数会逐渐增大,且随着芯层厚度的增加,结构反射系数峰值对应的频率不断向低频移动且幅值逐渐降低。对这种现象的解释,可以类比考虑均匀中间层的情况,根据已有结论,最大透射发生时其入射波波长正比于中间层的厚度,也就是说中间层厚度增加,其对应的入射波波长也增加,或者说对应频率将下降。
|
图 4 不同夹芯层厚度下的透射系数 Fig. 4 The transmission coefficient under different thickness of the core |
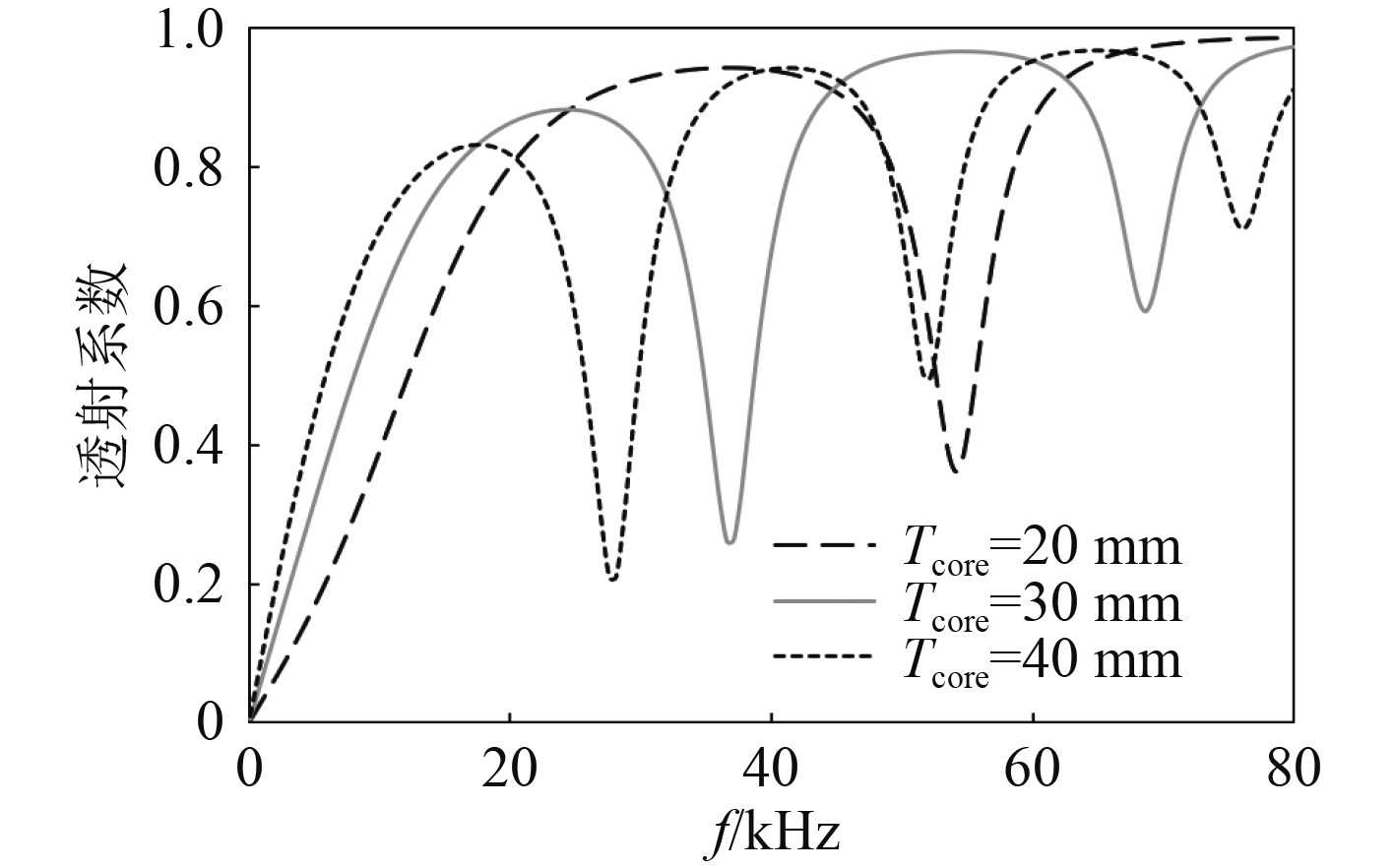
|
图 5 不同夹芯层厚度下的反射系数 Fig. 5 The reflection coefficient under different thickness of the core |
研究夹芯层材料杨氏模量改变对于结构的反射透射系数的影响。从图6可以看出,随着夹芯层材料杨氏模量的增加,结构透射系数峰值对应的频率不断向高频移动且峰值逐渐降低。从图7可以看出,随着夹芯层材料杨氏模量的增加,结构反射系数的峰值对应的频率不断向高频移动且峰值逐渐升高。芯层的材料弹性模量变化主要通过杨氏模量的改变,这里杨氏模量分别取为0.45 GPa,0.55 GPa和0.65 GPa。对这种现象的解释,同样可以类比考虑均匀中间层的情况。因为当中间层发生最大透射时,其波数与厚度乘积为一常数,所以当中间层的厚度不变,而改变材料属性进而影响纵波波速时,为保持波数不变,其对应的频率将发生相应改变。杨氏模量增加导致波速增加,此时对应的峰值频率也要增加。
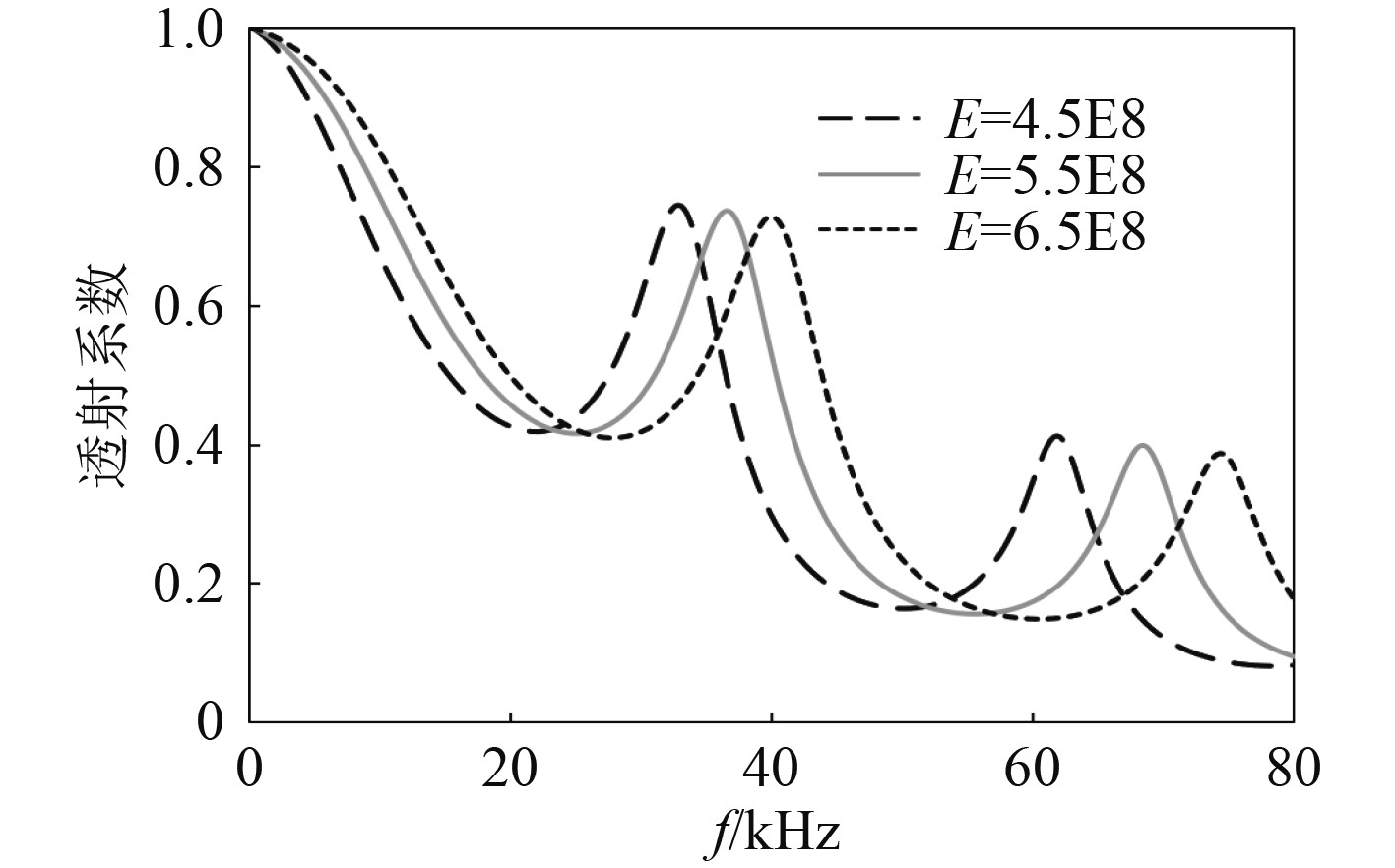
|
图 6 不同夹芯层杨氏模量情形下的透射系数 Fig. 6 The transmission coefficient under different Young′s modulus of the core |
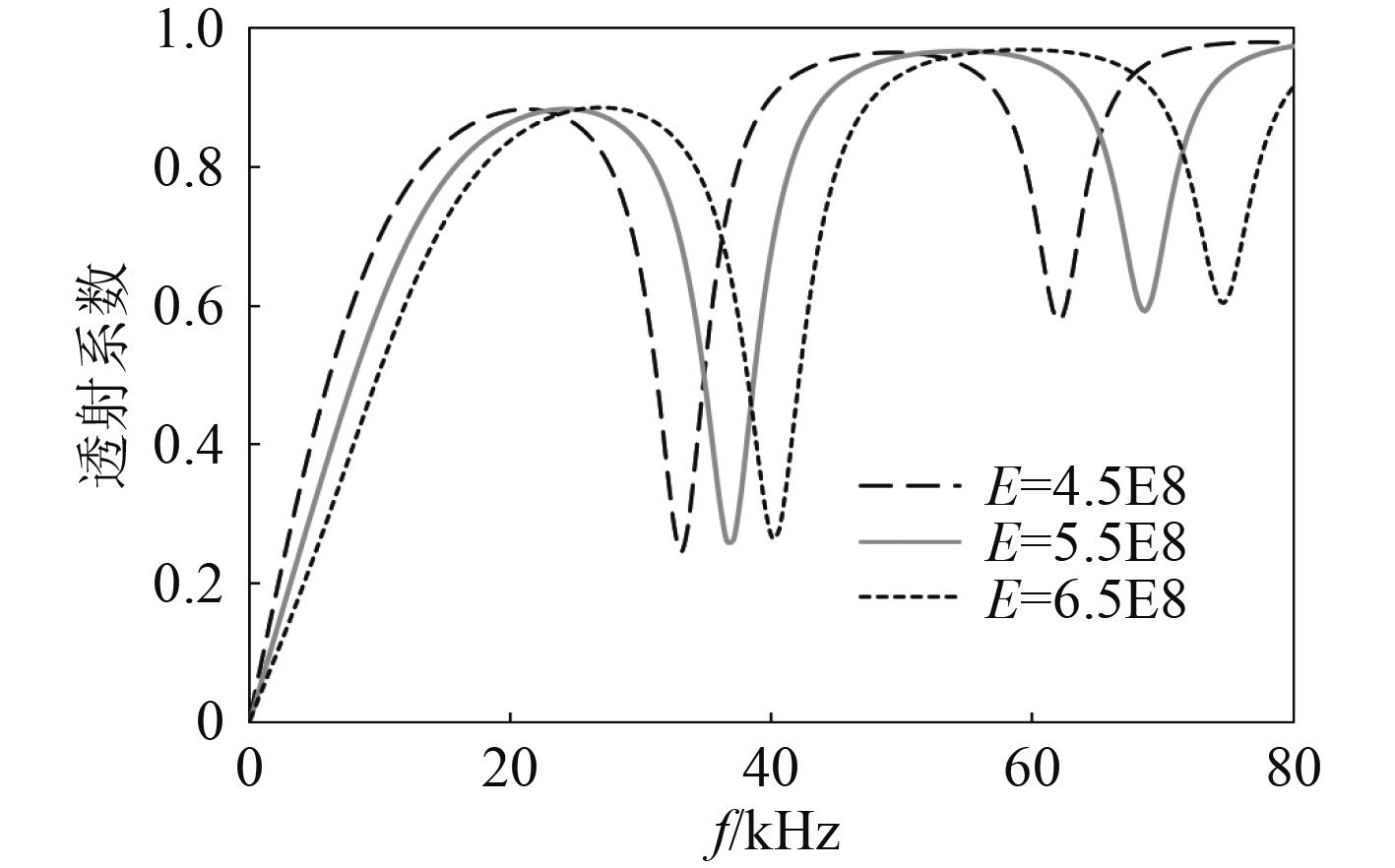
|
图 7 不同夹芯层杨氏模量情形下的反射系数 Fig. 7 The reflection coefficient under different Young′s modulus of the core |
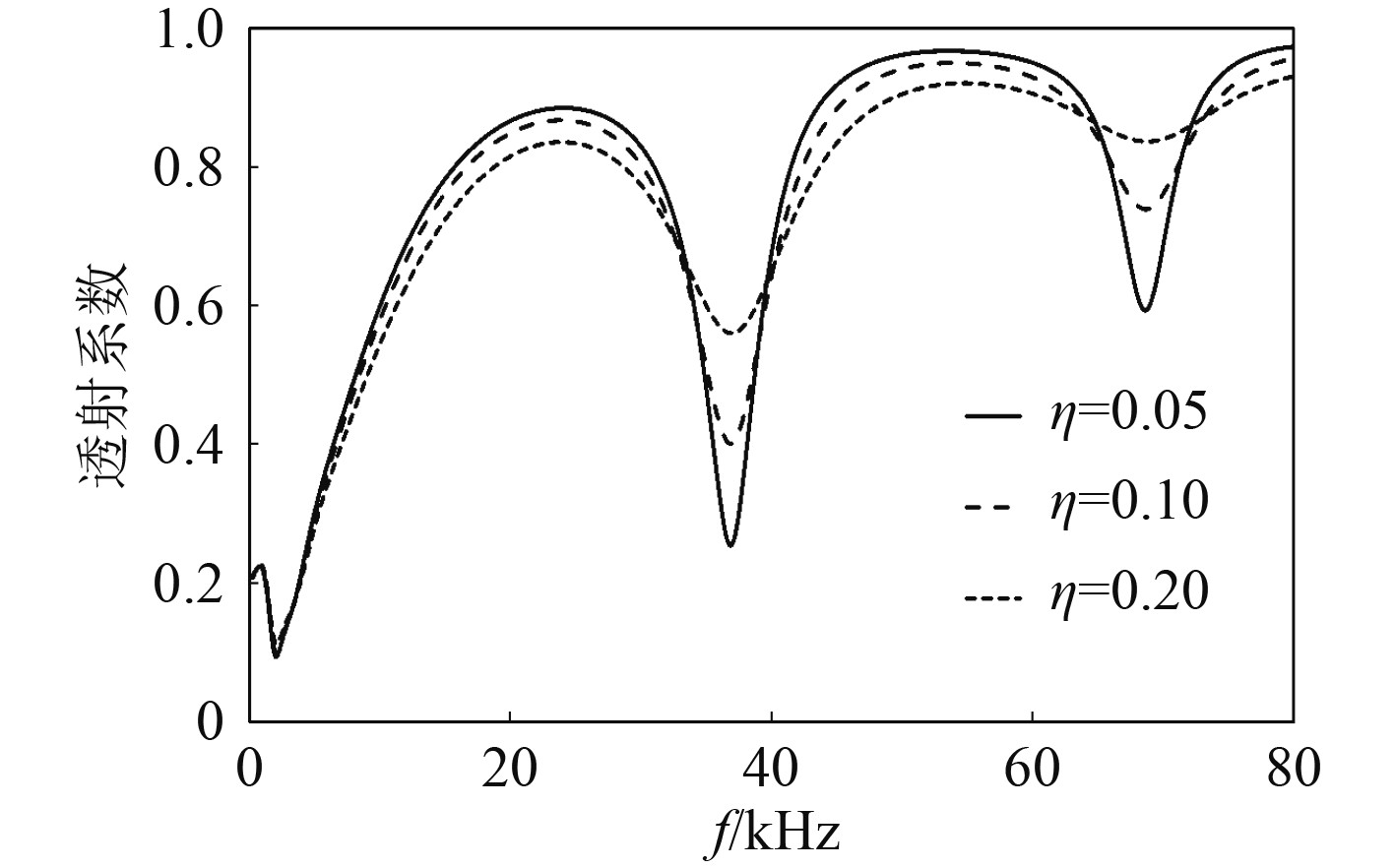
研究夹芯层材料损耗因子的改变对于结构反射透射系数的影响,芯层材料的损耗因子分别取为0.05,0.1,0.2,得到结构的透射和反射系数分别如图8和图9所示。从图8可以看出,随着夹芯层材料损耗因子的增加,结构透射系数峰值不断降低,而对应频率未发生明显改变。从图9可以看出,随着夹芯层材料损耗因子的增加,结构反射系数峰值不断升高,对应频率未发生明显改变。对于这种现象的解释,仍然可以类比考虑均匀中间层的情况,结构的损耗因子增大,会对结构的共振产生抑制,从而导致峰值的改变,而损耗因子的改变对共振频率的影响不大,故曲线峰值对应频率未发生明显偏移。
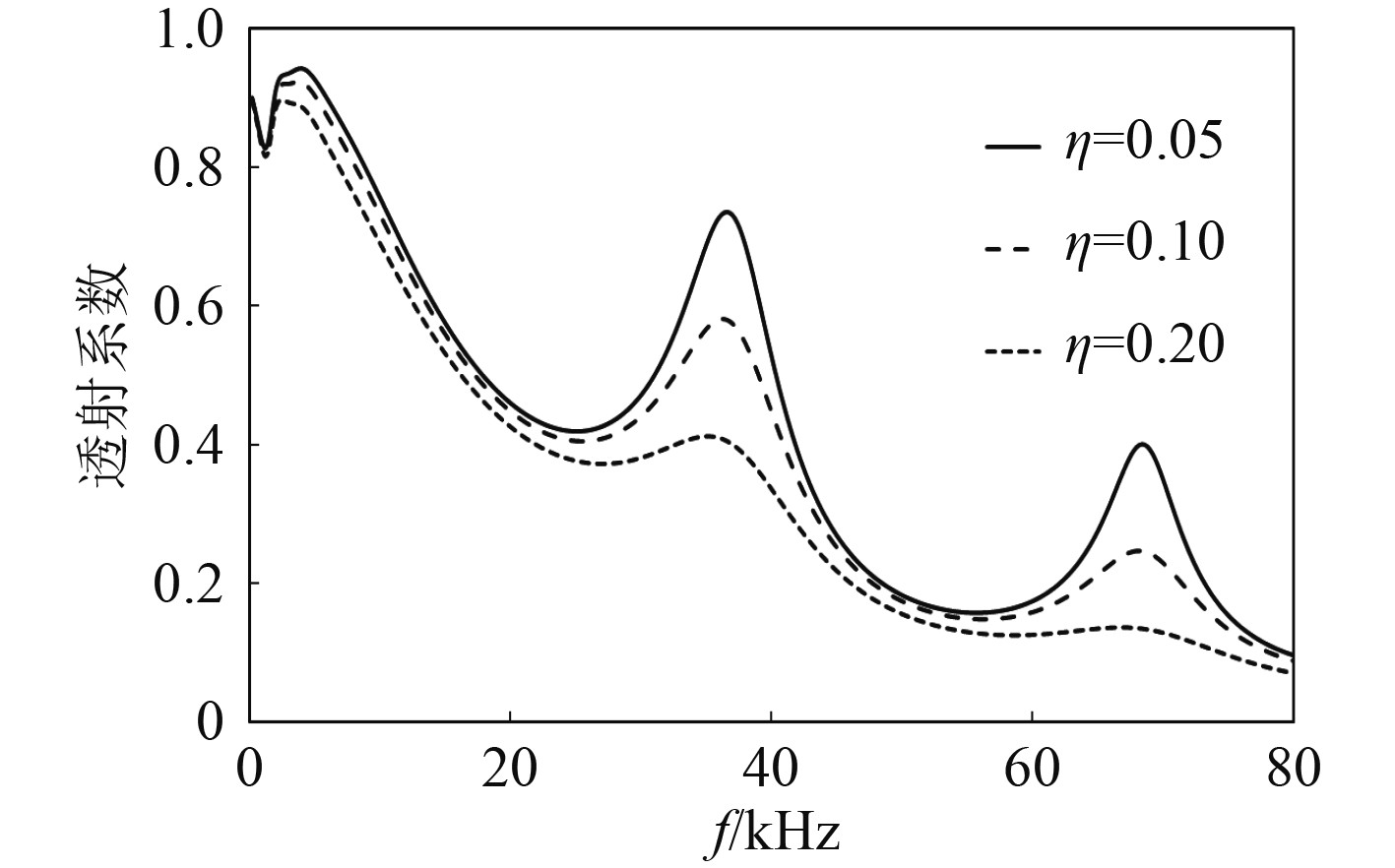
|
图 8 不同夹芯层损耗因子情形下的透射系数 Fig. 8 The transmission coefficient under different loss factor of the core |
|
图 9 不同夹芯层损耗因子情形下的反射系数 Fig. 9 The reflection coefficient under different loss factor of the core |
本文针对三明治夹芯平板结构,根据平面波正入射基本理论,利用有限元软件Comsol开展声学特性仿真分析,研究三明治夹芯平板在声波正入射下的结构声学特性,具体包括反射系数与透射系数。首先通过与单一平板结构理论解的对比,验证了该仿真模型的准确性;讨论了正入射条件下,平板厚度与平板材料参数等变化对于三明治夹芯平板反射性能与透射性能的影响。该方法同样适用于斜入射的情况,相关研究将在后面的工作中开展,总之,声学有限元方法对于研究结构的声学特性是方便可行的。
| [1] |
刘冬冰. 垂直/斜入射阻抗管吸隔声测量仪的设计与仿真[D]. 吉林: 吉林大学, 2018.
|
| [2] |
布列霍夫斯基赫Л М. 分层介质中的波[M ]. 北京: 科学出版社, 1985.
|
| [3] |
杨雪, 王源升, 余红伟. 多层高分子复合结构斜入射声波吸声性能[J]. 复合材料学报, 2006, 23(6): 21-29. DOI:10.3321/j.issn:1000-3851.2006.06.004 |
| [4] |
陈卫松, 邱小军. 多层板的隔声特性研究[J]. 南京大学学报:自然科学版, 2005, 41(1): 91-98. |
| [5] |
赵洪, 徐海亭. 水下多层均匀材料的声特性[J]. 应用声学, 1999, 18(4): 8-12. DOI:10.3969/j.issn.1000-310X.1999.04.003 |
| [6] |
孙丽萍. 船舶结构有限元分析[M]. 哈尔滨: 哈尔滨工程大学出版社, 2013.
|
| [7] |
STEFFEN M, BODO N. Computational Acoustics of noise propagation in fluids: Finite and Boundary Element Methods. Springer, 2008.
|
| [8] |
张海澜. 计算声学[M ]. 北京: 科学出版社, 2021.
|
 2023, Vol. 45
2023, Vol. 45
