水下航行器的隐蔽性决定了其战斗力与生命力。为了提高其隐蔽性以及有效躲避水下声学探测,水下航行器往往需要采用各种不规则路径航行。开展面向收发合置声呐探测模式下水下航行器任意航行路径的时域回波特征研究,突破运动中水下航行器目标时域回波计算方法,是当前水下航行器隐蔽路径规划以及对运动中水下航行器探测等课题中亟需解决的问题。
有限元−完美匹配层联合仿真计算方法有着适用频率范围广、计算精度高、计算方法成熟等优点,是当前处理声学散射问题常用的数值计算方法。随着入射信号频率的增大,以及目标与声波发射接收点距离增加,为了提高计算精度,需要的有限元体网格数量将成倍增加,采用上述计算方法需要大量的计算资源。为了能够有效提高中高频声学散射问题的计算效率,克服高频计算量大的问题,范军[1]、郑国垠等[2]提出并改进了板块元方法。该方法基于Kirchhoff近似原理,将目标表面用剖分平面板块元网格的方法近似模拟,最终目标的总散射声场由所有的平面板块散射声场叠加而得。经过验证,该方法具有较高的计算精度。贾波等[3]基于传统板块元方法,运用切比雪夫多项式插值实现了水下目标宽带回波特征的快速计算。孙乃葳[4]基于改进板块元法,利用Gordon积分方法,同时考虑了优化后的模型中面元遮挡计算流程,完成了潜艇目标强度的仿真计算,建立了基于改进板块元方法的潜艇目标强度快速预报模型。冯奇等[5]基于板块元法,研究了近场高频情况下水下复杂目标声目标强度方向特性。
对于水中动态目标的回波特征,国内外学者已经进行了一定研究。其中,周华等[6]通过研究目标回波信号模型理论,结合目标强度理论得到了圆柱体简单目标近场目标强度计算公式,并推导了动态圆柱体目标回波理论。潘明等[7]基于板块元法分析了潜艇回波在直线运动状态以及不同距离条件下的亮点结构分布及其特点。
上述文献基于板块元法研究了水下目标的动态回波特征,但仍存在以下不足:1)缺乏实测验证;2)研究的水下目标外形或者运动状态单一,无法推广到一般情况;3)未对水下多目标同时运动的回波特征进行研究探讨。本文从工程应用角度出发,考虑单个或多个水下航行器以任意路径航行的情况,通过构建水下航行器几何模型,采用基于频域间接法的板块元方法对其回波特征进行研究。最后,通过水下声散射试验测试对预报结果进行了验证。
1 基于频域间接法的板块元基本原理Kirchhoff近似原理基于如下2个基本假设[8]:假设1,散射表面可以分成产生声波的散射的被照亮区域,即亮区,以及不产生声波散射的未被照亮区域,即影区;假设2,亮区反射面的每个局部都可以看成是平面,波的反射特性服从局部平面波反射规律。
如图1所示,S为整个散射体外表面,
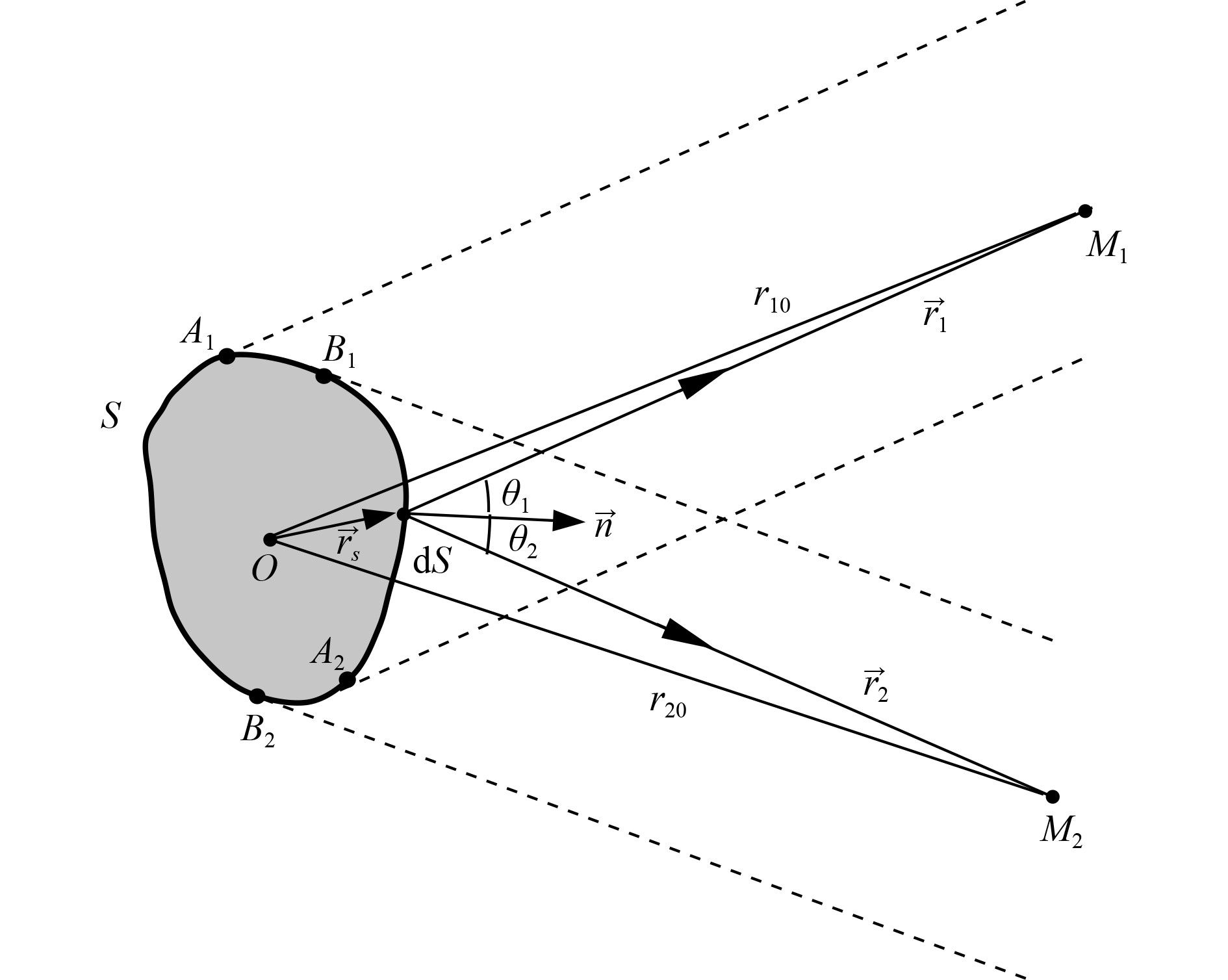
|
图 1 推导Kirchhoff近似的示意图 Fig. 1 Schematic for deriving Kirchhoff approximation |
在收发合置情况下,
| $ {\varphi }_{s}\left(\overrightarrow{r}\right)=-\frac{ikA}{2{\text π} }{\int }_{S}\frac{{e}^{ik2r}}{{r}^{2}}\mathrm{cos}\theta {\rm{d}}S ,$ | (1) |
其中,
| $ {\varphi }_{s}\left(\overrightarrow{r}\right)=-\frac{ikA}{2{\text π} }\frac{{e}^{ik2{r}_{0}}}{{{r}_{0}}^{2}}{\int }_{S}{e}^{ik2\Delta r}\mathit{{\rm{cos}}}\theta {\rm{d}}S ,$ | (2) |
因为远场中声程差可以近似为
| $ {\varphi }_{s}=-\frac{A}{2{\text π} }\underset{S}{\overset{}{\int }}{e}^{i2kr}V\left(\theta \right)\left(\frac{ikr-1}{{r}^{3}}{\rm{cos}}{\theta }_{1}\right){\rm{d}}S 。$ | (3) |
考虑入射波势函数
目标时域回波
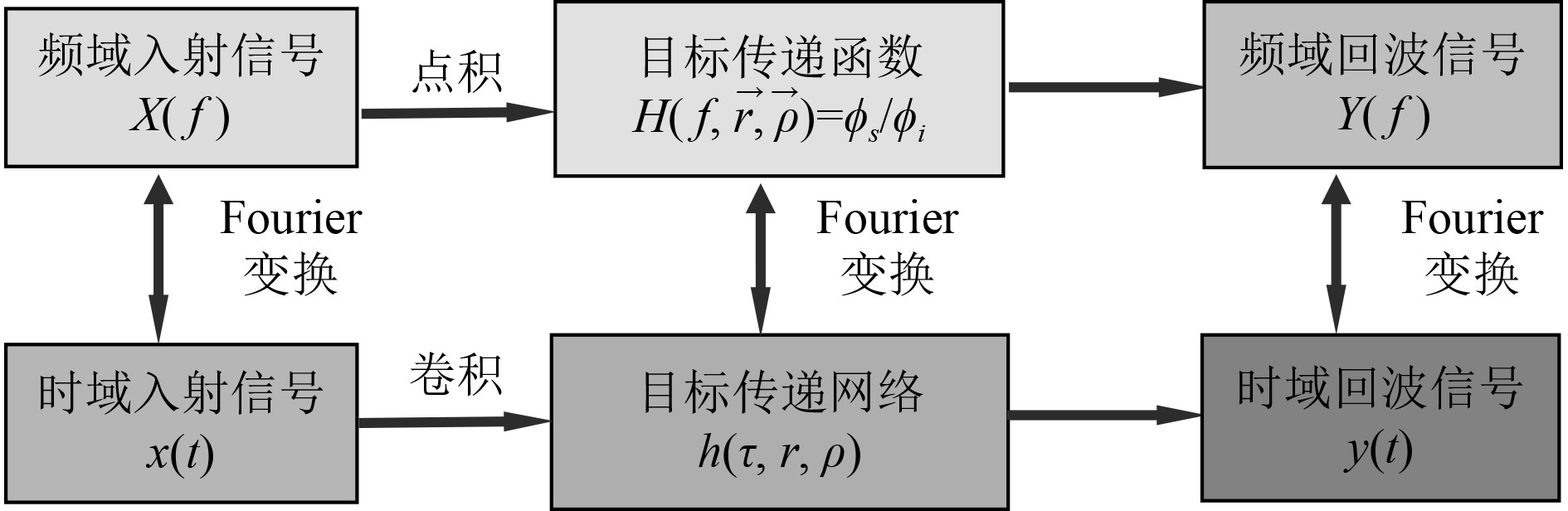
|
图 2 时域回波信号传递网络模型 Fig. 2 Time-domain echo signal transmission network model |
| $ y\left(t\right)=x\left(t\right)\otimes h(\tau ,\overrightarrow{r},\overrightarrow{\rho }) 。$ | (4) |
其中,
| $ Y\left(f\right)=X\left(f\right)\cdot H(f,\overrightarrow{r},\overrightarrow{\rho }) ,$ | (5) |
且有:
| $ X\left(f\right)=F\left[x\left(t\right)\right] ,$ | (6) |
| $ y\left(t\right)={F}^{-1}\left[Y\left(f\right)\right] 。$ | (7) |
其中,F和F−1分别为傅里叶变换和逆变换。因此,根据上述公式辅以快速傅里叶变换和逆变换,就可以间接求出目标瞬态时域回波。
2 任意路径时域回波特征计算根据基于频域间接法的板块元基本原理,计算水下航行器目标回波特征需要获得水面舰板块元网格。水下航行器总长3.20 m,主艇体(不包含尾部推进器)长3.00 m,最大直径为0.39 m。首部为椭球的一半,椭球半长轴为0.38 m。尾部十字舵最前端距首部2.57 m,高0.21 m。尾部导管长0.16 m,最大直径为0.36 m,螺旋桨由6个相同的叶片组成。利用几何三维建模软件,建立水下航行器三维几何模型模型,如图3所示。在网格剖分软件中剖分三角形面网格,每个小板块的尺寸满足
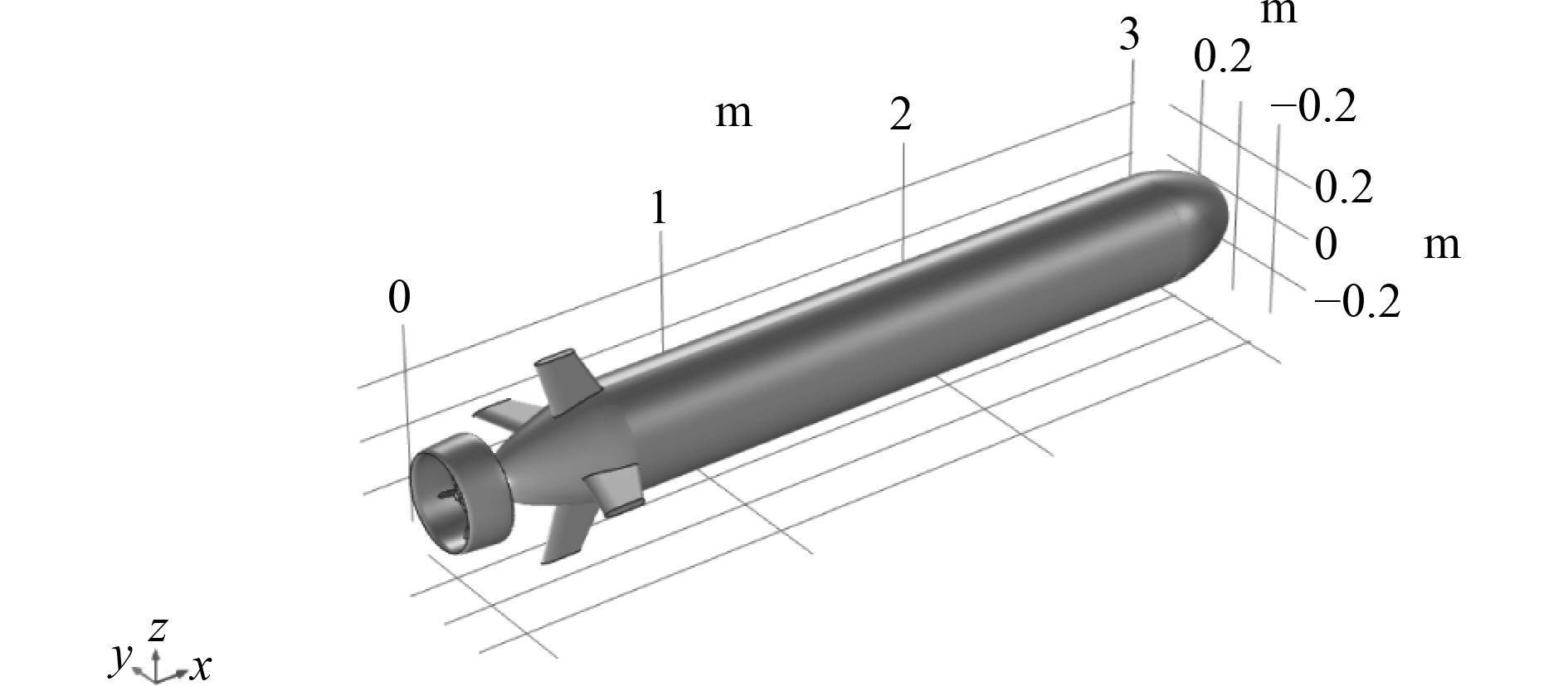
|
图 3 水下航行器几何模型 Fig. 3 Geometric model of underwater vehicle |
如图4所示,计算时规定水下航行器在长60
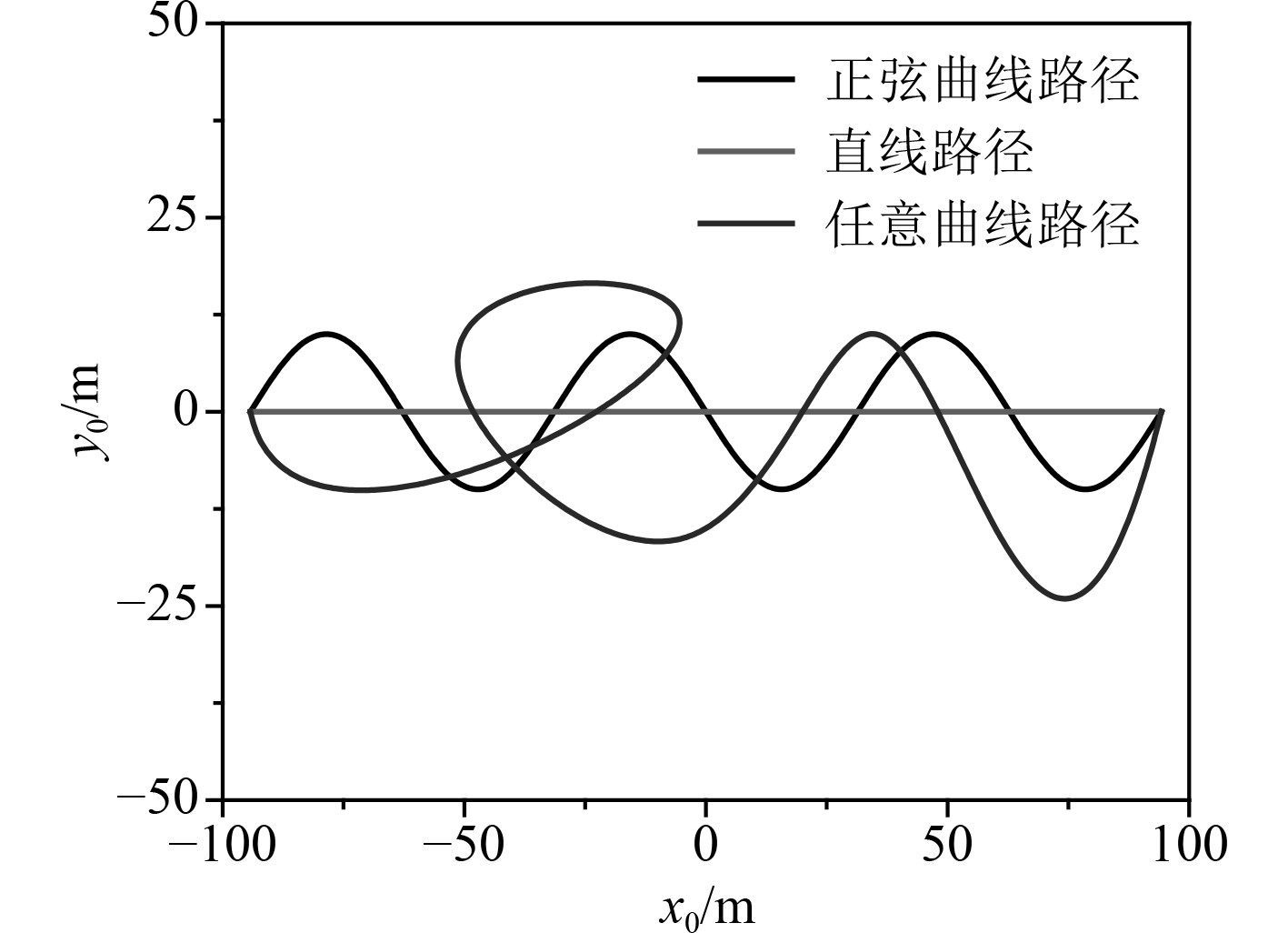
|
图 4 航行路径 Fig. 4 Navigation path |
如图5所示,以随机路径航行为例,使用COMSOL软件在航行范围内随机画一条开放曲线,将该曲线剖分若干数量的边网格,从而获得该航行路径曲线上x0-y0-z0坐标系下的n个点坐标信息,将n个点按照航行经过的先后顺序编号为1~n,当水下航行器航行到任意点k时(k≠n),以k点为原点建立新的x-y-z坐标系,定义k到k+1的方向为x轴的正方向,假设k点在原始x0-y0-z0坐标系下坐标为(xk,yk,0),k1坐标为(xk+1,yk+1,0),则x轴正方向单位向量i可表示为:
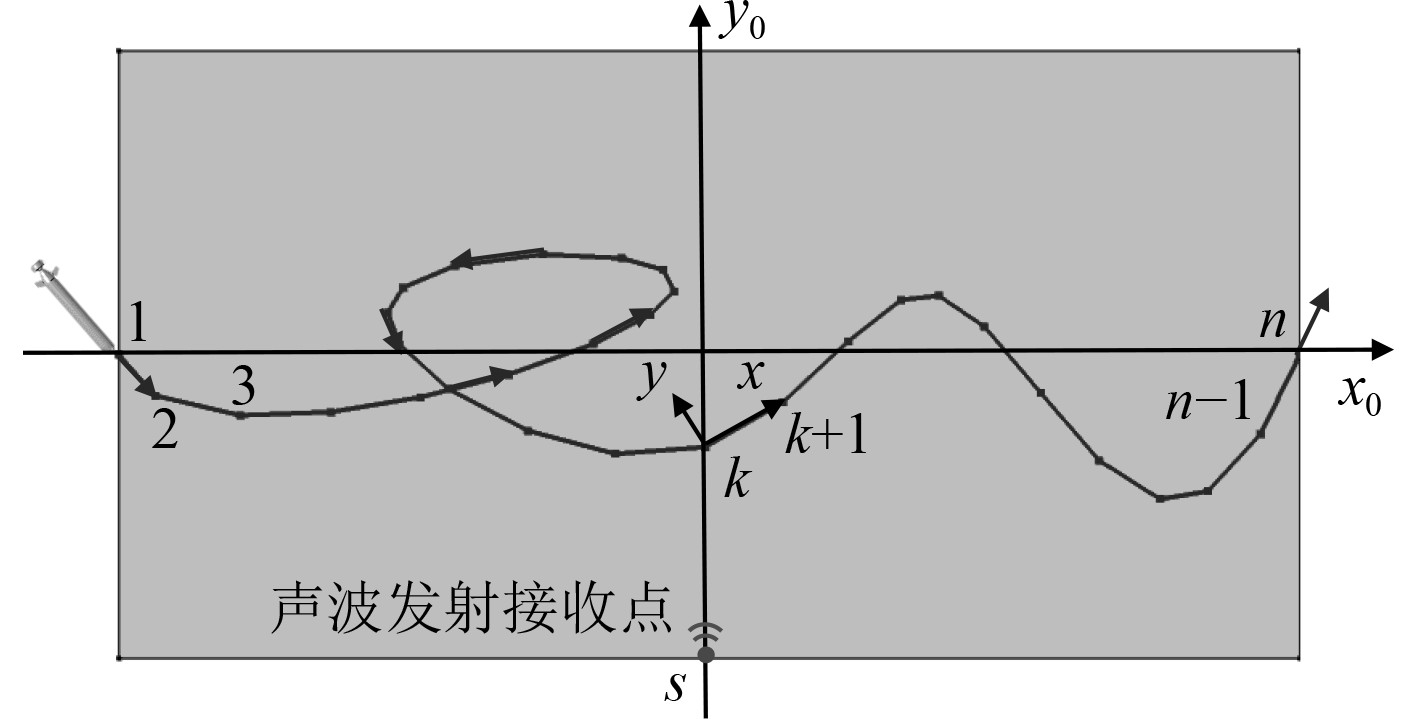
|
图 5 任意路径航行回波特征计算示意图 Fig. 5 Schematic diagram of calculation of navigation echo characteristics in arbitrary path |
| $ \mathit{i}=({x}_{k+1}-{x}_{k},{y}_{k+1}-{y}_{k},0)/\sqrt{{({x}_{k+1}-{x}_{k})}^{2}+{({y}_{k+1}-{y}_{k})}^{2}} ,$ | (8) |
z轴正方向垂直于x-y平面向外,可得z轴正方向单位向量为k=(0,0,1)将x轴正方向和z轴正方向单位向量叉乘,得到y轴正方向的单位向量为:
| $\begin{aligned} & \mathit{{\boldsymbol{j}}}=\mathit{{\boldsymbol{i}}}\times \mathit{{\boldsymbol{k}}}=({y}_{k+1}-{y}_{k},-{x}_{k+1}+{x}_{k},0)/ \\ & \sqrt{{({x}_{k+1}-{x}_{k})}^{2}+{({y}_{k+1}-{y}_{k})}^{2}},\end{aligned} $ | (9) |
设声波发射接收点s在原始x0-y0-z0坐标系下坐标为(p,q,0),则k点到s点的方向向量为:s=
| $\begin{split} & {S}_{k} =\left(\begin{array}{l} \left({x}_{k+1}-{x}_{k}\right)\left(p-{x}_{k}\right)+\left({y}_{k+1}-{y}_{k}\right)(q-{y}_{k}),\\ \left({-x}_{k+1}+{x}_{k}\right)\left(p-{x}_{k}\right)+\left({y}_{k+1}-{y}_{k}\right)\left(q-{y}_{k}\right),0\end{array}\right)/ \\ & \sqrt{{({x}_{k+1}-{x}_{k})}^{2}+{({y}_{k+1}-{y}_{k})}^{2}} 。\\[-15pt]\end{split}$ | (10) |
根据Sk的坐标计算出新x-y-z坐标系下声波发射接收点与水下航行器在k点的相对位置,从而求得目标在该点的瞬态时域回波,循环计算每一个航行点的瞬态回波即可获得目标在整个航行路径上的时域回波特征。当航行到最后一个点n,即k=n时,目标航行方向与点n-1一致。
计算中,每个航行路径都剖分600条边网格,即最终航行路径可由601个航行运动点来表示,声波发射接收点在x0-y0坐标系下初始坐标为(0,50)。发射信号为60 ~70 kHz的线性调频信号,脉宽0.5 ms,采样频率为1.75E5。
为了提高输出信号的信噪比并获得比较精细的距离分辨率,对目标的回波信号做匹配滤波,最终计算结果分别如图6所示。
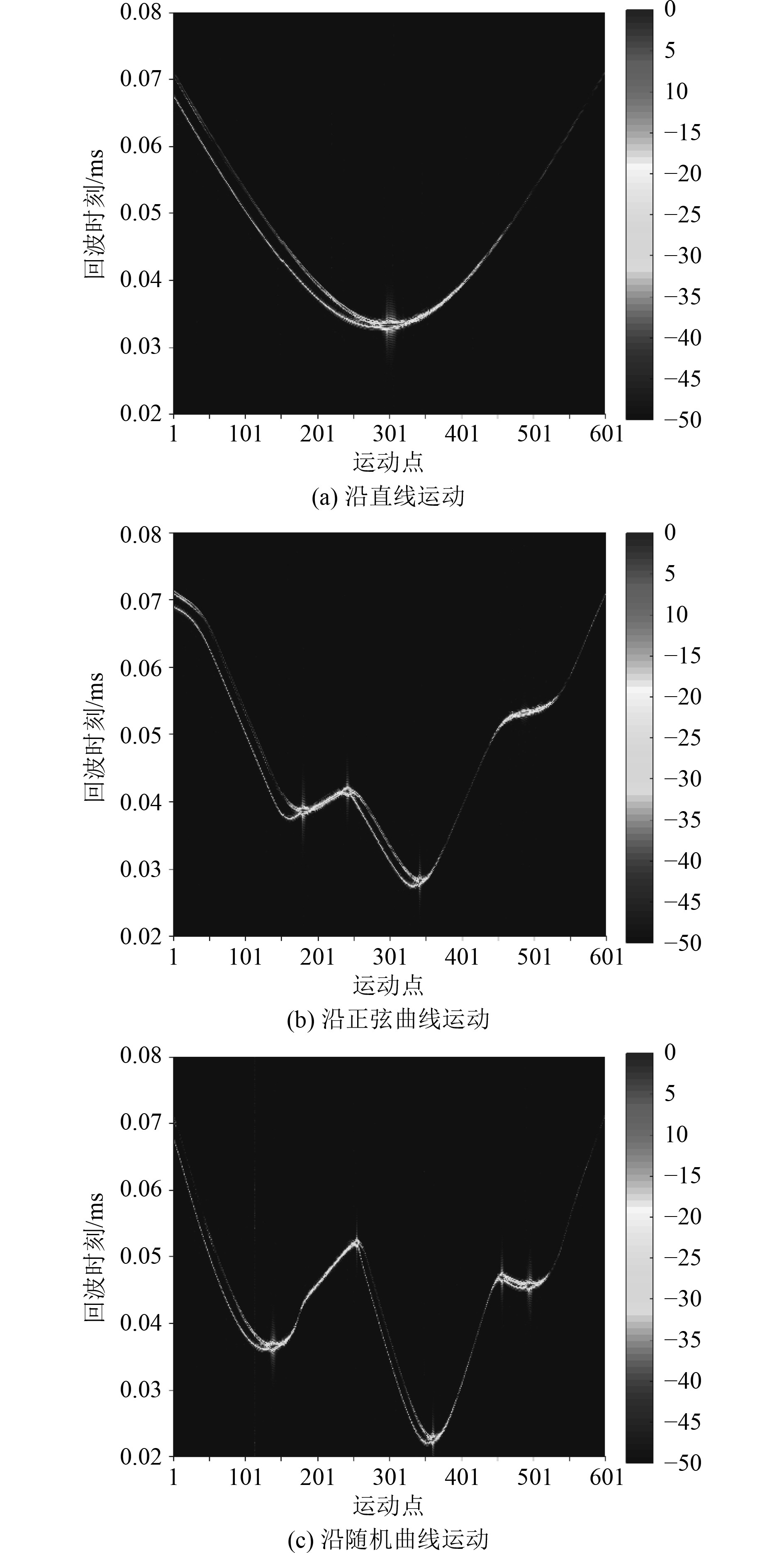
|
图 6 不同运动路径下水下航行器时域回波特征 Fig. 6 Time-domain echo characteristics of underwater vehicle under different moving paths |
由图6可知,水下航行器沿直线运动时,其回波特征由2条U型曲线构成,在运动到第301航行点附近时,该航行器回波强度最大,航程过半以后U型曲线由2条变为1条。这是因为当航行器运动到第301个点时整个航行器航行方向正好与声波发射方向垂直,此时回波强度最大,且航程过半以后,声波发射点矢径与航行方向夹角大于90°,声波无法照射到航行器首部,失去了航行器的首部亮点。
根据上述规律,不难发现,沿正弦曲线方向航行时,航行器分别在序号为175,251,351和501的点附近航行方向与声波发射方向垂直,此时回波强度较大,也是探测到该航行器最容易的区域。当序号在201~251范围内,沿正弦曲线运动的航行器回波强度都很强,说明在该区间内,航行器航行方向与声波发射方向之间夹角变化不大,一直在90°附近。同理,沿随机曲线运动时,航行器在序号为125,251,351,451和501的点附近回波强度较大,此时航行方向与声波发射方向垂直,容易探测。
为了研究水下多目标同时运动的回波特征,将上述3种航行路径的时域回波相干叠加,经过匹配滤波后,最终计算结果如图7所示。可知,当沿3种不同路径的水下航行器同时航行时,其时域回波包含了单个航行器航行的所有回波特征。
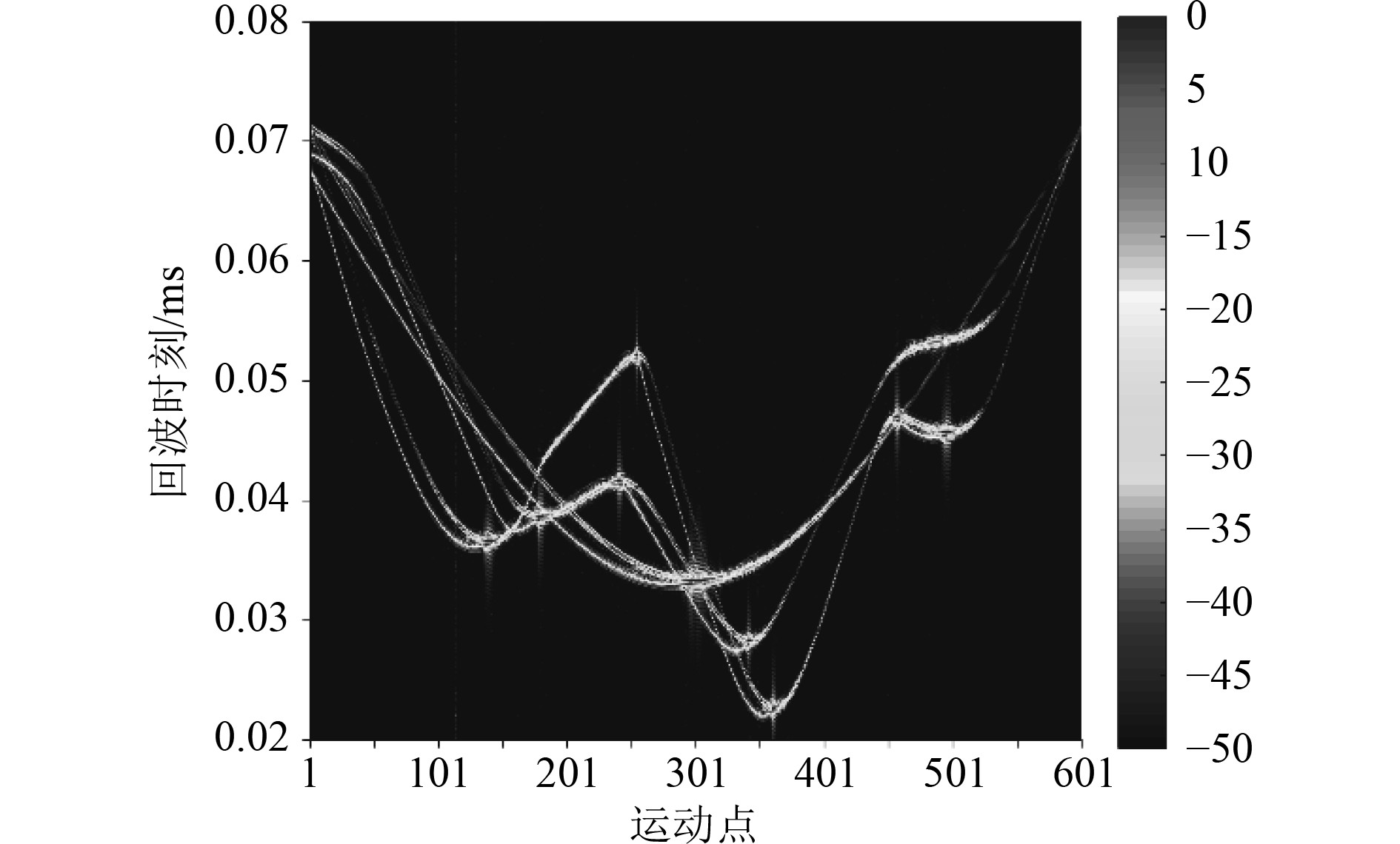
|
图 7 三路径同时航行时水下航行器回波特征 Fig. 7 Echo characteristics of underwater vehicle under three paths simultaneous navigation |
为了验证上述回波特征计算的正确性开展回波特性水下声散射试验。
试验模型为1∶20缩比的单壳体Benchmark潜艇,壳体厚度为3 mm,材料为不锈钢,其长度为3.2 m。在试验过程中,按照图8对试验装置进行布置。
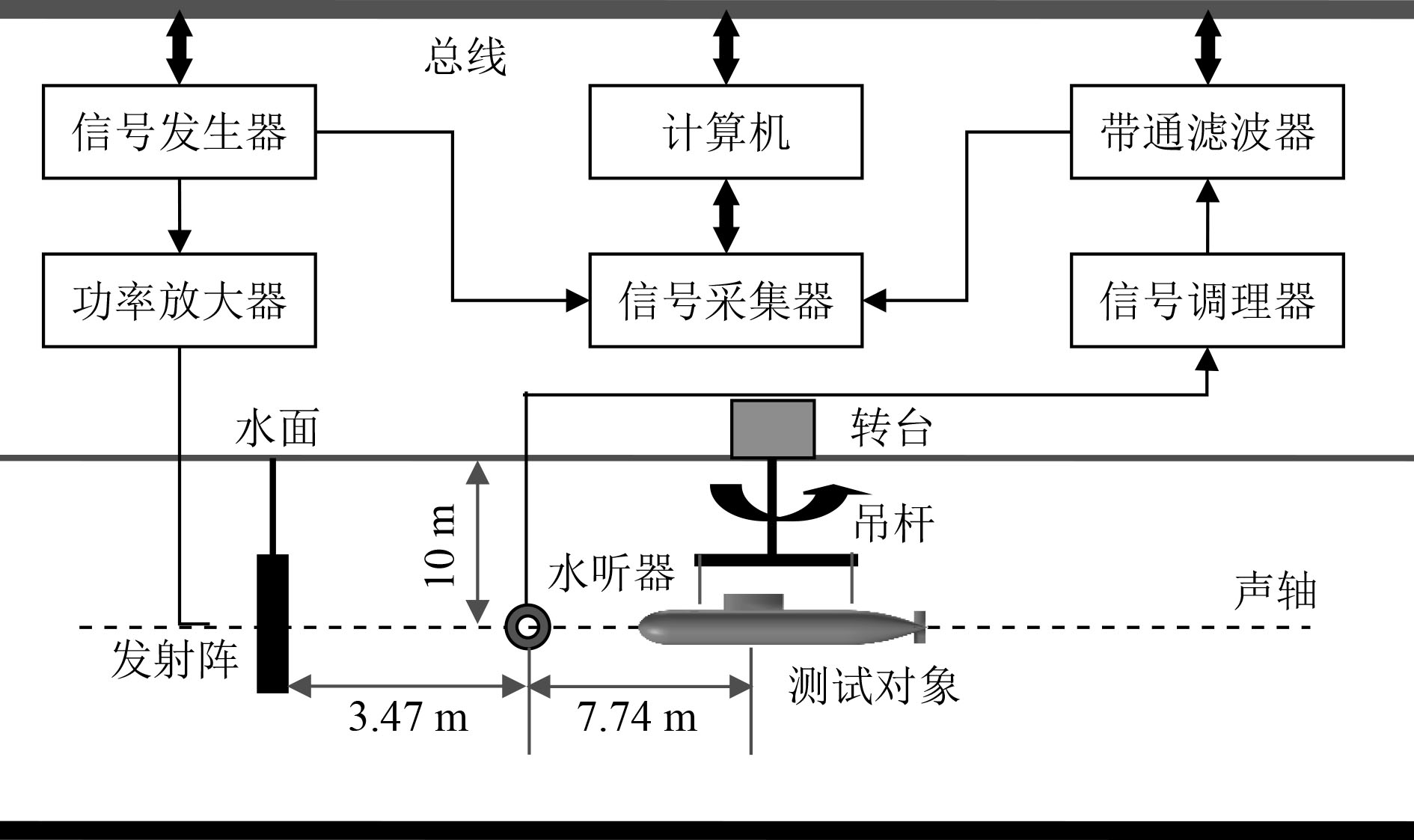
|
图 8 试验设备布置图 Fig. 8 Layout of test equipment |
试验开始时转台匀速旋转,信号发生器信号经功率放大器放大后由发射阵发出。发射阵直达波和目标散射回波由水听器接收后经过信号调理器和带通滤波器的补偿与限制,最终由信号采集器同步采集获得,最后经过分析计算即可得到1∶20缩比的Benchmark潜艇回波特性。
对于水下航行器任意路径时域回波预报的正确性,关键在于对任意声波入射角度下水下航行器时域回波的准确计算。经试验测得的Benchmark潜艇在0°~180°(尾部到首部)声波入射角度范围内,60 ~100 kHz频段时域回波特征实测结果与仿真结果对比如图9所示。
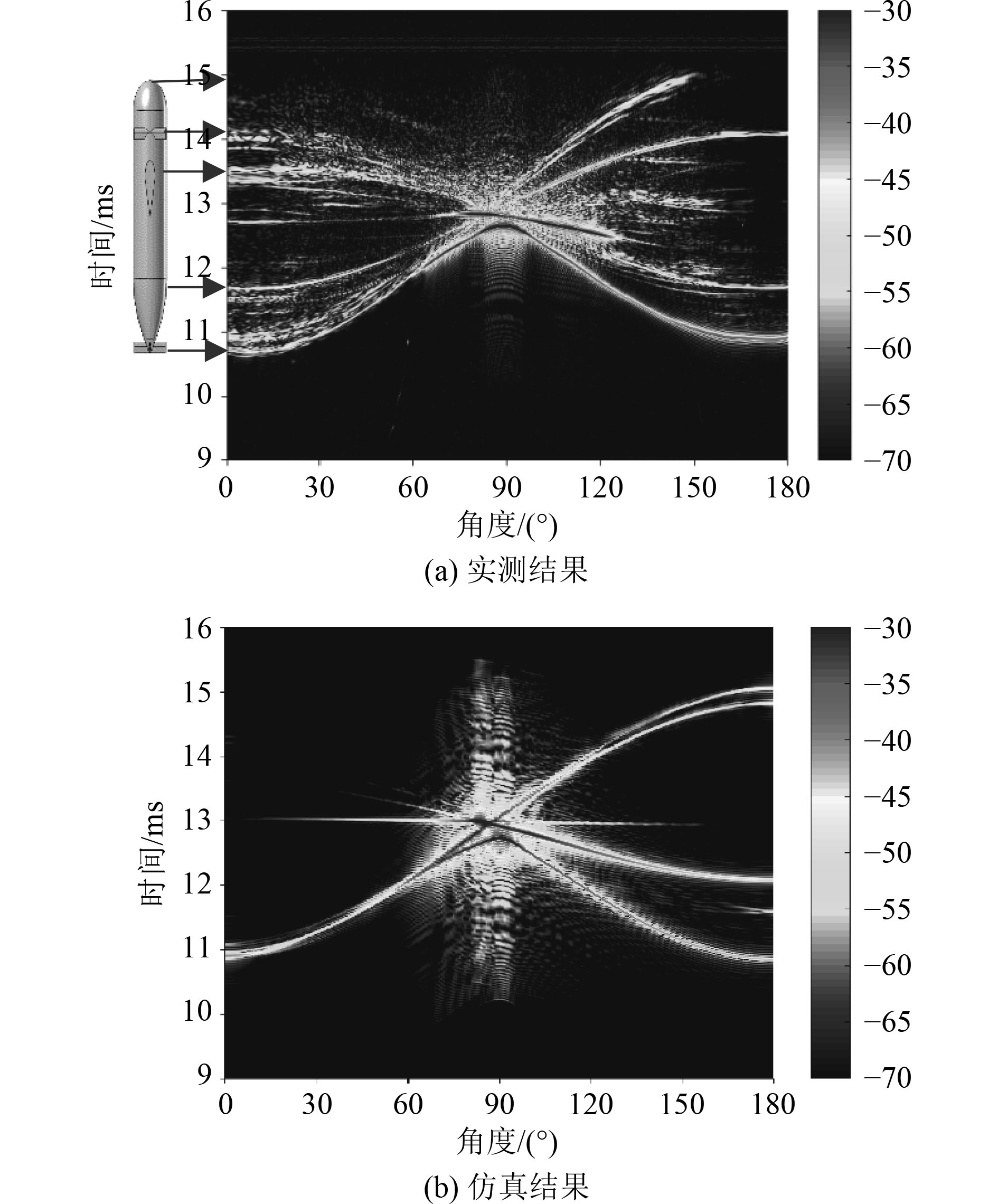
|
图 9 潜艇缩比模型回波特征试验和仿真结果对比 Fig. 9 Comparison of echo characteristics test and simulation results of submarine scaling model |
由图9可知,1∶20缩比的Benchmark潜艇尾部、首部以及围壳的回波特征在实测结果和仿真结果都清晰可见,且特征十分相似。由此可以确定,利用板块元法能够较准确预报以任意路径航行的水下航行器时域回波特征。但实测结果在首部平衡舵以及尾部锥体部位明显比仿真结果多出1~2条曲线特征,实测结果与仿真结果仍然存一定误差。经过分析认为,这有可能是潜艇旋转时吊放绳索的回波特征。仿真计算时潜艇壳体考虑为刚性壳体,但潜艇实际材料为不锈钢,这也是实测结果比仿真结果回波特征更丰富的原因之一。
4 结 语本文简要阐述基于频域间接法的板块元基本原理。在此基础上,提出了以任意路径运动的水下航行器回波特征预报方法。进一步,通过开展1∶20缩比的Benchmark潜艇回波特性水下声散射试验,验证了上述预报方法的准确性。得出以下几个主要结论:
1)利用板块元法能够较准确预报以任意路径航行的水下航行器时域回波特征;
2)通过对3种不同路径航行的水下航行器回波的仿真分析,可以确定航行方向与声波发射方向垂直时回波强度最大,也是探测到该航行器最容易的区域;
3)对于给定的航行路径,可以通过本文的仿真方法获得该路径水下航行器最容易探测的区域,这对水下运动目标的探测与识别有一定意义。
| [1] |
范军, 汤渭霖, 卓琳凯. 声呐目标回声特性预报的板块元方法[J]. 船舶力学, 2012, 16(Z1): 171-180. |
| [2] |
郑国垠, 范军, 汤渭霖. 考虑遮挡和二次散射的修正板块元算法[J]. 声学学报, 2011, 36(4): 377-383. |
| [3] |
贾波, 王斌, 范军, 等. 水下目标宽带回波特征的快速计算方法[J]. 上海交通大学学报, 2017, 51(2): 224-228. |
| [4] |
孙乃葳, 李建辰, 万亚民, 等. 基于改进板块元法的潜艇目标强度预报仿真[J]. 鱼雷技术, 2016, 24(4): 254-259. |
| [5] |
冯奇. 基于板块元法的水下复杂目标强度预报[J]. 鱼雷技术, 2010, 18(4): 258-262+267. |
| [6] |
周华. 水下动态目标回波特征研究[J]. 自动化与仪器仪表, 2016(8): 6-7. |
| [7] |
潘明, 邓伟. 运动状态下Benchmark潜艇回波特征仿真研究[J]. 舰船电子工程, 2019, 39(5): 75-77+100. |
| [8] |
汤渭霖, 范军, 马忠成, 等. 水中目标声散射[J]. 声学学报, 2018, 43(5): 873. |
 2023, Vol. 45
2023, Vol. 45
