0 引　言

复合材料构件具备高比强度/比刚度的力学性能，能够很好地满足船舶工程领域的应用需求^[1]。夹层结构由于其独特的力学性能，也引起了学者们的关注^[2-4]。复合材料夹层结构的研究对象主要有波纹夹层结构、蜂窝夹层结构、泡沫夹层结构、点阵夹层结构^[5-7]。

周磊等^[8]设计了一种双向的波纹夹层结构，开展了压缩、弯曲和剪切试验，分析了破坏模式和失效机理。张丰辉等^[9]在蜂窝夹层结构中引入波纹结构，并在面板和波纹上分别进行微穿孔制备了复合材料波纹结构，在声学方面有突出性能。李宗权等^[10]综述了蜂窝夹层结构冲击试验及仿真研究进展，研究了各项参数对仿真计算的影响。徐学宏等^[11]研究不同缝合方式和缝合密度对泡沫夹层结构的拉伸、弯曲、剪切性能的影响。赵兴辰等^[12]采用3D打印技术制备点阵夹层结构，开展了压缩吸能实验与有限元仿真，揭示了结构损伤失效的原理。

本文制备复合材料波纹夹层结构，开展三点弯曲试验与有限元仿真计算，研究相对密度对弯曲性能的影响，借助数值仿真，拓展计算了芯层几何构型对复合材料波纹夹层结构弯曲性能的影响。

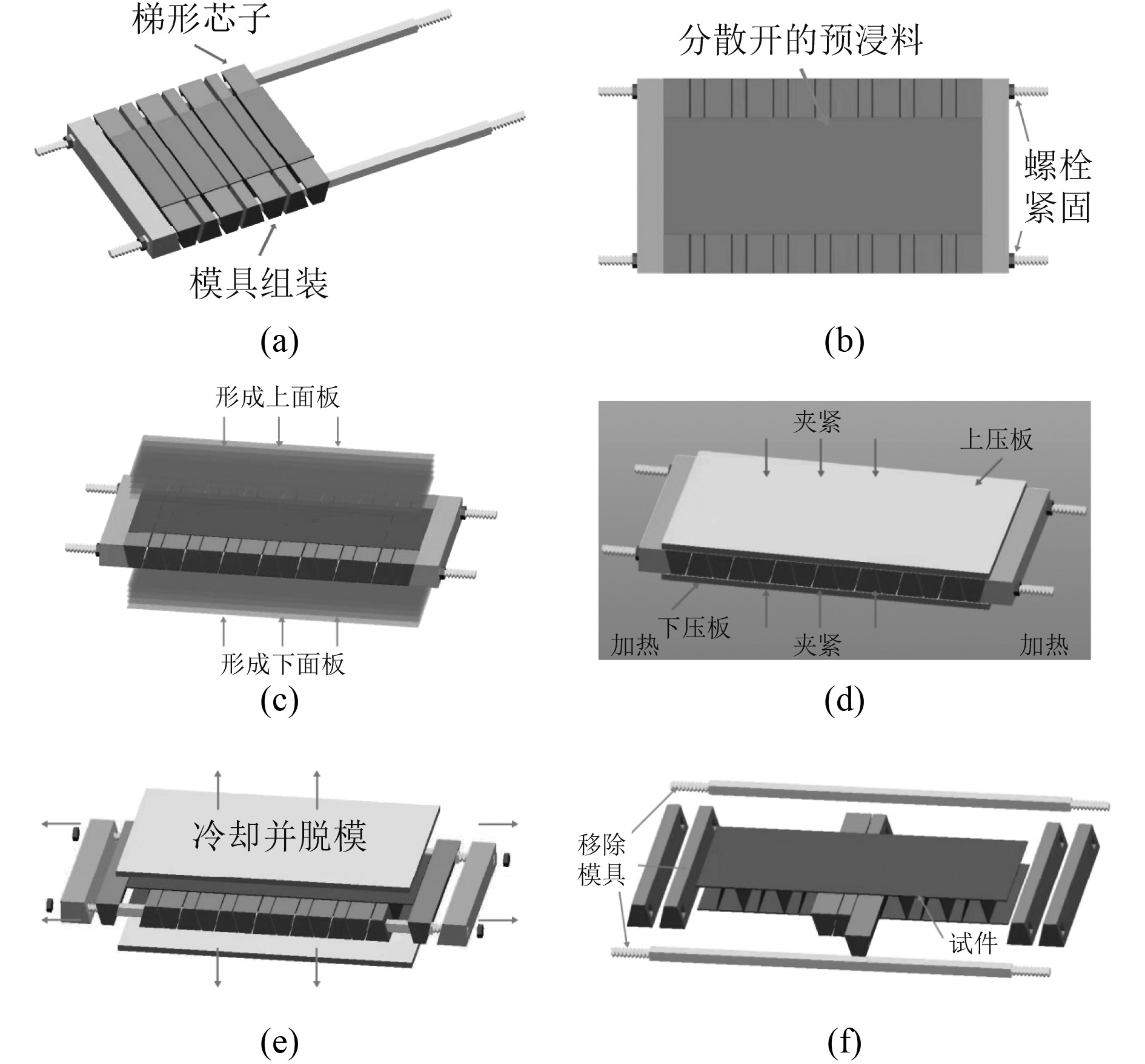
1 试件制备

3种不同相对密度的波纹夹层结构试件所用到的碳纤维预浸料层数分别为6层、10层和14层，试件的制备工艺流程如图1所示。相对密度（RD） $ \bar \rho $ 计算公式为：

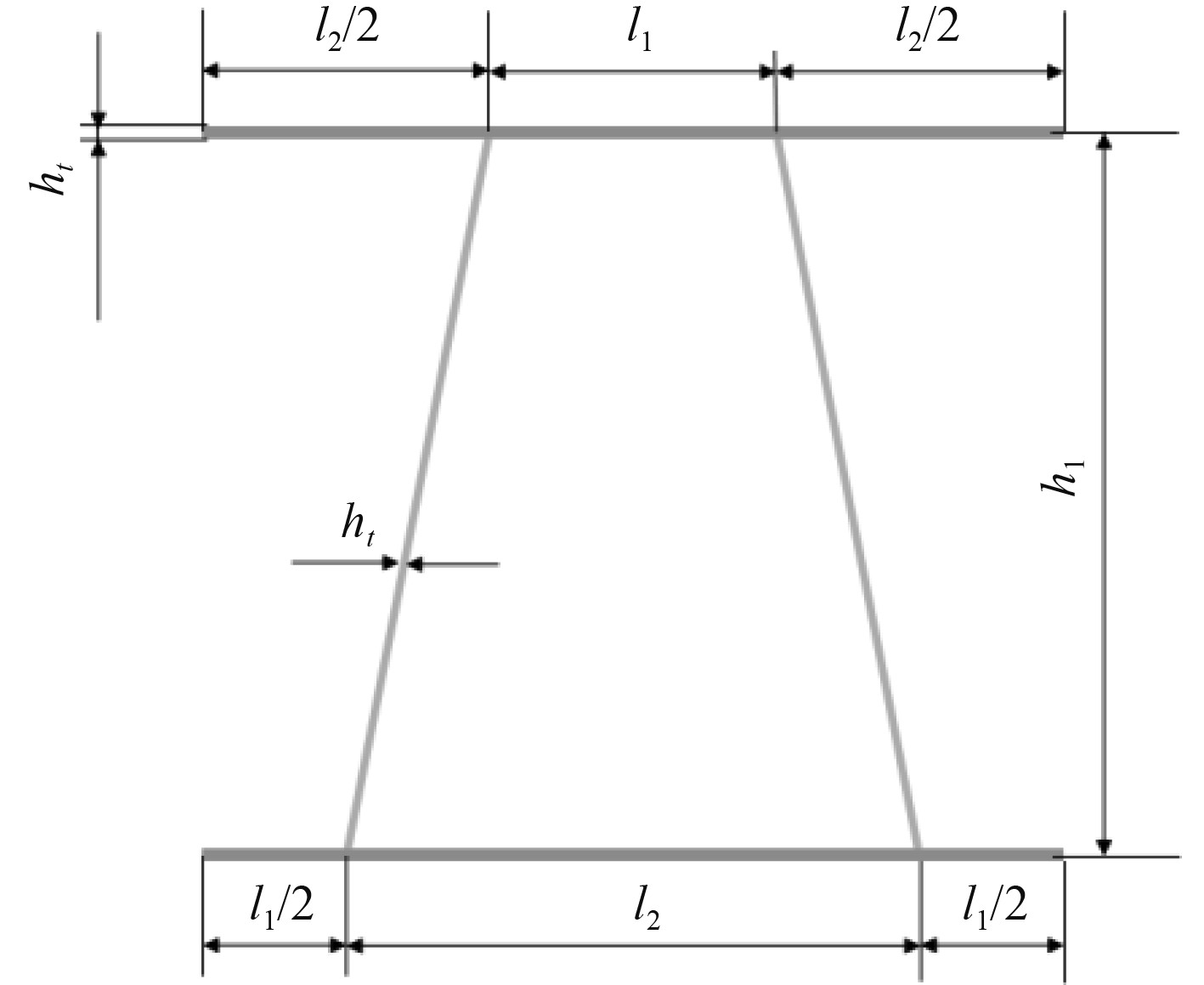
$ \bar \rho = \frac{{\left( {{l_1} + {l_2}} \right) \times 2{h_t} + {h_1} \times 2{h_t}}}{{\left( {{h_1} + 2{h_t}} \right) \times \left( {{l_1} + {l_2}} \right)}} 。$

(1)

式中： $ {l_1} $ 为单胞短边长； $ {l_2} $ 为单胞长边长； $ {h_1} $ 为单胞高； $ {h_t} $ 为层厚。

图2为计算相对密度时的单胞示意图，1层碳纤维预浸料的厚度为0.1 mm，单胞尺寸 $ {l_1} $ =10 mm， $ {l_2} $ =20 mm， $ {h_1} $ =20 mm，计算可得3种试件的相对密度分别为9.55%，15.34%，20.72%。3种不同相对密度的波纹夹层结构铺层顺序分别为[0°/90°/0°]_s，[0°/90°/0°/90°/0°]_s和[0°/90°/0°/90°/0°/90°/0°]_s。单向碳纤维预浸料的力学性能见表1，如图3所示，试件整体尺寸250 mm×90 mm×22 mm。

2 试验方法

压载头截面尺寸15 mm $ \times $ 20 mm，支撑结构直径20 mm，跨距230 mm。弯曲试验压载头的作用位置为中间单胞处，加载速度为2 mm/min。此外，为保障波纹夹层结构在两端的受力条件，加工制造了一对铝制夹具，用于夹持试件。

3 试验结果 3.1 载荷-位移曲线

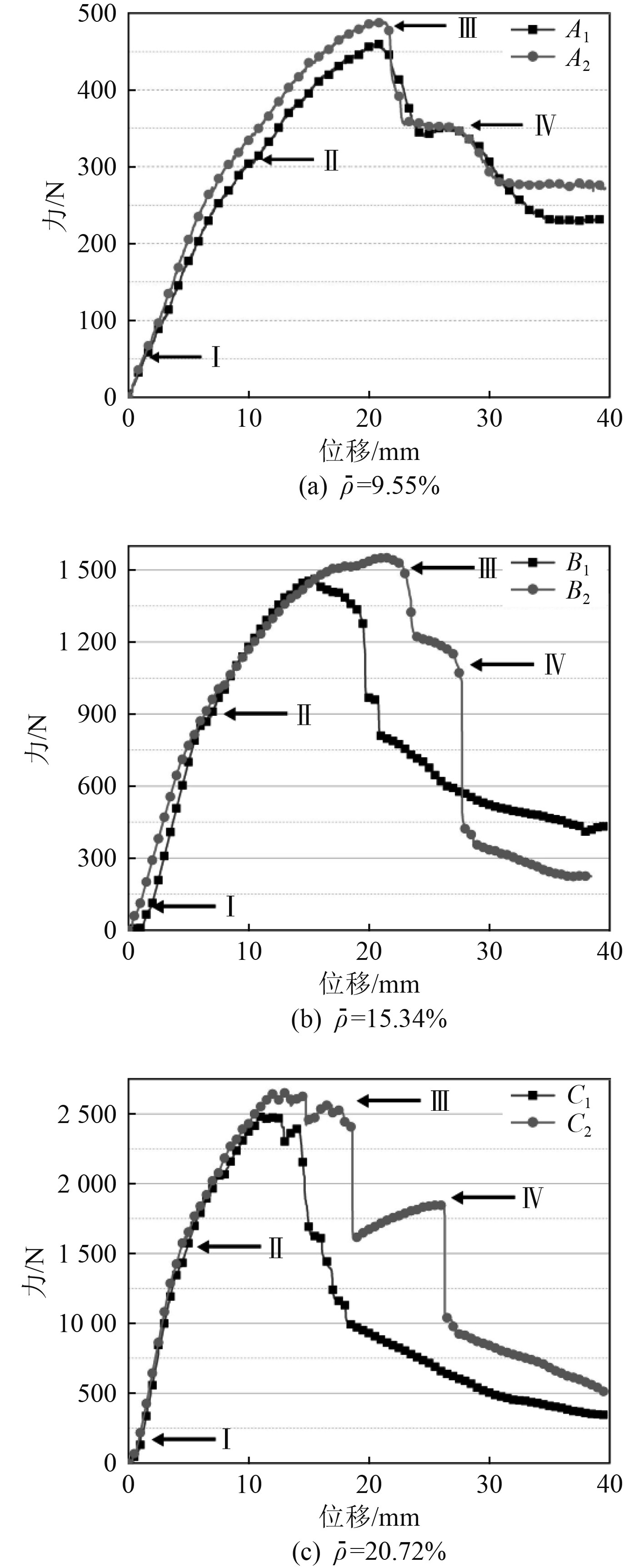
图3为不同相对密度试件的载荷-位移曲线。每一种试件均制作了2个，并对试件进行了三点弯曲性能测试。

曲线可分为4个阶段。在第1阶段，载荷-位移曲线直线上升，这一阶段试件承载能力良好；在第2阶段，载荷-位移曲线仍在上升。但上升速度较第1阶段有所下降，这一阶段试件逐步开始受损；在第3阶段，曲线出现陡降，承载能力大幅降低；在第4阶段，载荷缓慢下降后，又一次出现陡降，波纹夹层结构已经失去了承载能力。

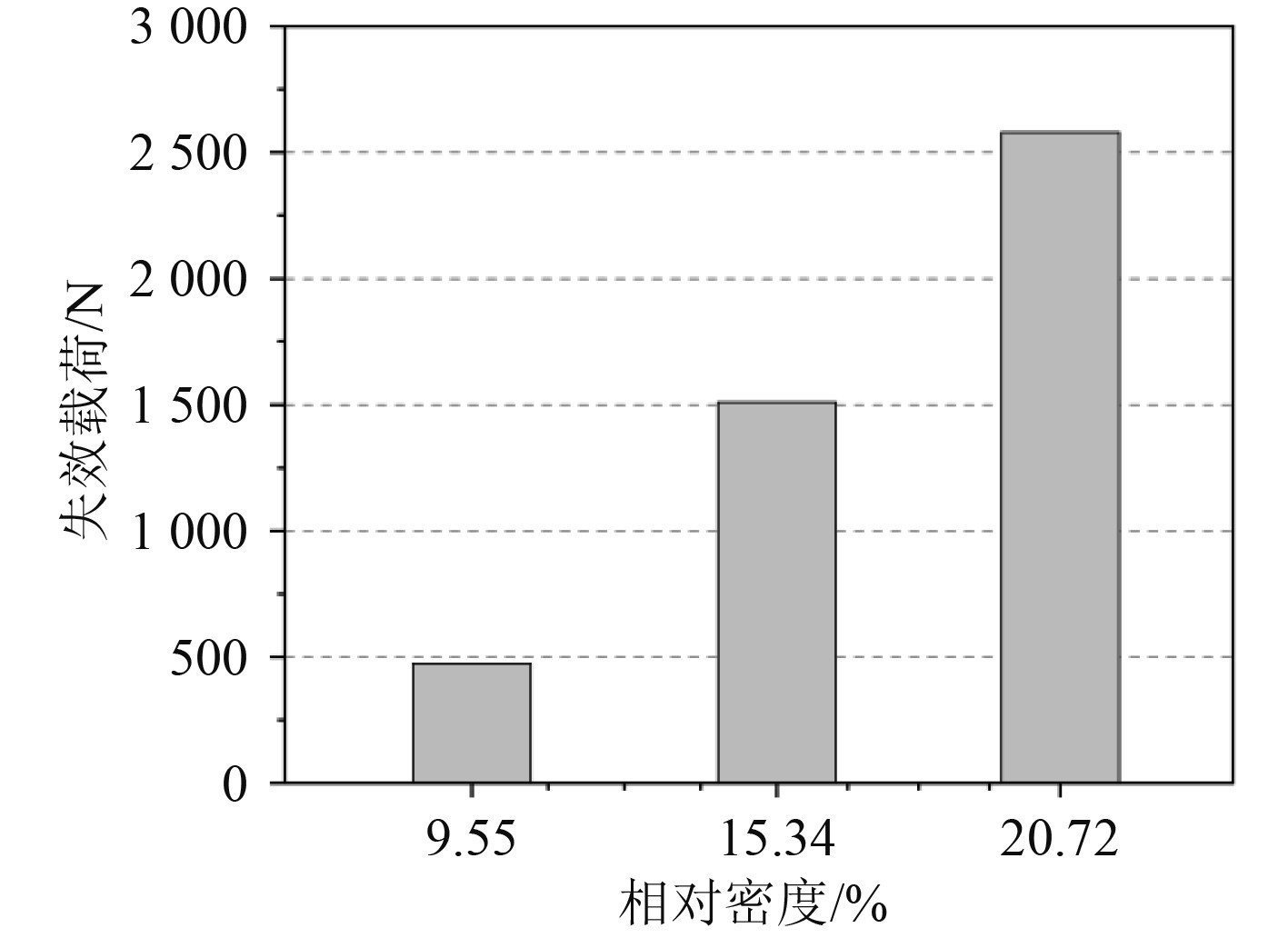
在弯曲试验过程中，从第1阶段到第4阶段，试件在抵抗弯曲变形的过程中逐步失去承载能力。图4为不同相对密度试件的失效载荷，其值取自载荷-位移曲线的最大值，由2次测试结果的平均值计算得到。当相对密度从9.55%增加至15.34%时，极限载荷增加了1035.7 N，当相对密度从15.34%增加至20.72%时，极限载荷增加了1070.2 N，波纹夹层结构的失效载荷随着相对密度的增大而增大。

3.2 失效模式

为了分析波纹夹层结构受弯曲载荷时的失效机理，选取不同加载阶段、不同相对密度的试件的失效。模式如图5所示。

图5(a)给出了相对密度为9.55%的弯曲试件的失效模式，在第1阶段，试件平滑变形，弯曲载荷由整个试件共同承担；在第2阶段，单胞靠内的转角处承载，出现了一定的变形；在第3阶段，试件上层出现分层，对应曲线出现陡降；在第四阶段，试件上表面出现纤维断裂，完全失去了承载能力。图5(b)、图5(c)分别给出了相对密度为15.34%，20.72%的波纹夹层结构的失效模式，其失效模式与相对密度为9.55%的弯曲试件相近，但随着相对密度的增加，更多的表现出了“脆性”，即在弯曲载荷加载过程中，其脆性断裂更明显。

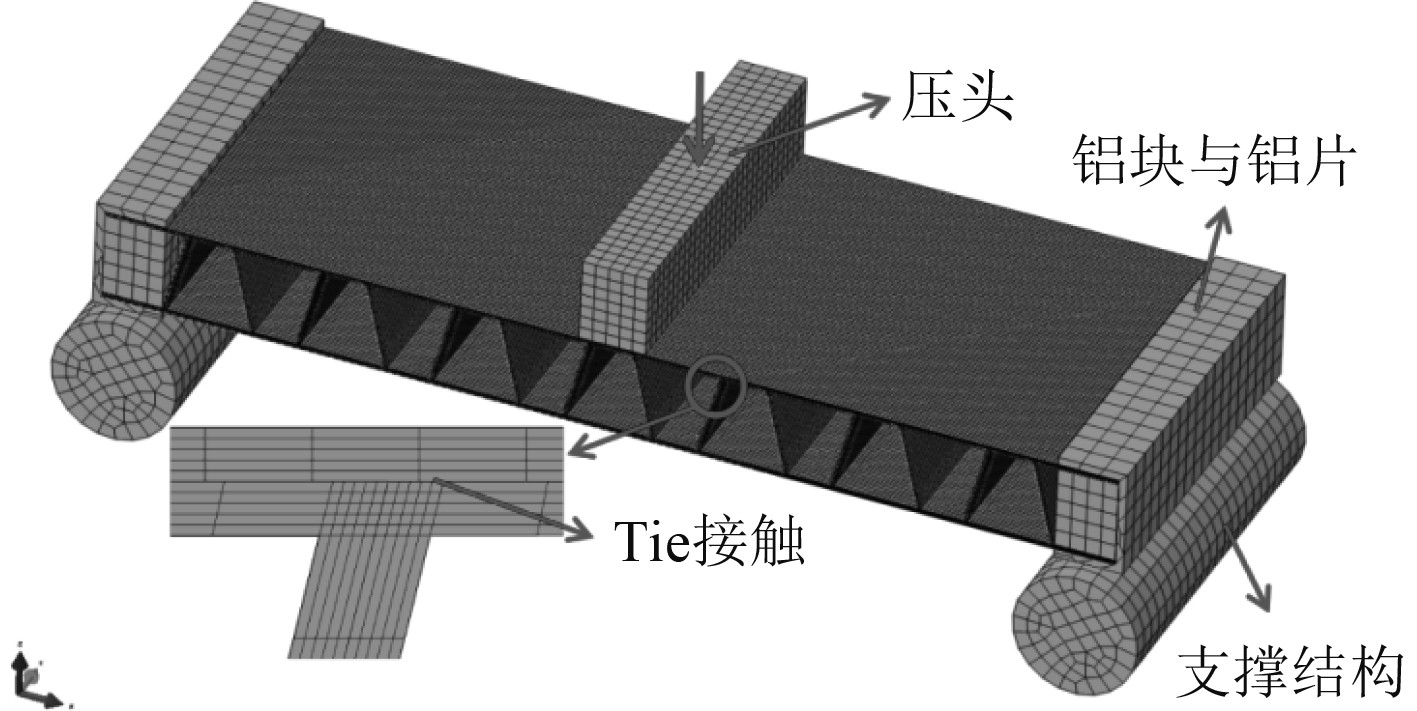
4 有限元仿真 4.1 有限元模型

图6为计算三点弯曲作用的试件的有限元分析模型，该计算模型根据试件尺寸建立，并依次构建铺层，计算过程所用的材料参数以表1为准。压头与支撑结构不是研究的主体，故设置为刚体。波纹结构两端夹持件材料为铝，其材料密度 $ \bar \rho $ =2.7×10⁻⁹ t/mm³，杨氏模量E=70 GPa，泊松比μ=0.3。压头沿图7所示方向向下运动施加载荷，其加载速度为2 mm/min。两支撑结构被完全固定，各个方向的运动均被限制。压头与波纹夹层结构、波纹夹层结构与铝块、U型铝片与支撑结构均设置通用接触，其中法线方向设置硬接触，切线方向设置摩擦系数0.1^[13]。面板与单胞间采用刚性绑定。由于涉及到材料的失效和接触，为了保障计算收敛，采用Abaqus/Explicit进行分析计算^[14]。

依渐进损伤模型，编写用户自定义子程序VUMAT，预报波纹夹层结构弯曲失效行为。该子程序中定义了5种失效模式^[15-17]，这5种不同的失效模式对应有5个失效因子，5个失效因子表达式具体如下：

纤维拉伸失效因子

$ R_{ft}^2 = {\left( {\dfrac{{{\sigma _{11}}}}{{{X_T}}}} \right)^2} + {\left( {\dfrac{{{\sigma _{12}}}}{{{S_{12}}}}} \right)^2} + {\left( {\dfrac{{{\sigma _{13}}}}{{{S_{13}}}}} \right)^2},{\sigma _{11}} > 0 ，$

(2)

纤维压缩失效因子

$ R_{fc}^2 = {\left( {\dfrac{{{\sigma _{11}}}}{{{X_C}}}} \right)^2},{\sigma _{11}} < 0 ，$

(3)

基体拉伸失效因子

$\begin{aligned} & R_{mt}^2 = {\left( {\dfrac{{{\sigma _{22}} + {\sigma _{33}}}}{{{Y_T}}}} \right)^2} + \dfrac{{\sigma _{23}^2 - {\sigma _{22}}{\sigma _{33}}}}{{S_{23}^2}} +\\ & {\left( {\dfrac{{{\sigma _{12}}}}{{{S_{12}}}}} \right)^2} + {\left( {\dfrac{{{\sigma _{13}}}}{{{S_{13}}}}} \right)^2},\left( {{\sigma _{22}} + {\sigma _{33}}} \right) \geqslant 0 ，\end{aligned} $

(4)

基体压缩失效因子

$\begin{aligned} & R_{mc}^2 = \left[ {{{\left( {\dfrac{{{Y_C}}}{{2{S_{23}}}}} \right)}^2} - 1} \right]\left( {\dfrac{{{\sigma _{22}} + {\sigma _{33}}}}{{{Y_C}}}} \right) + \left( {\dfrac{{{\sigma _{22}} + {\sigma _{33}}}}{{2{S_{12}}}}} \right) +\\ & {\left( {\dfrac{{\sigma _{23}^2 - {\sigma _{22}}{\sigma _{33}}}}{{{S_{23}}}}} \right)^2} + {\left( {\dfrac{{{\sigma _{12}}}}{{{S_{12}}}}} \right)^2} + {\left( {\dfrac{{{\sigma _{13}}}}{{{S_{13}}}}} \right)^2},\left( {{\sigma _{22}} + {\sigma _{33}}} \right) < 0 ，\end{aligned}$

(5)

分层失效因子

$ R_{ld}^2 = {\left( {\dfrac{{{\sigma _{23}}}}{{{Z_T}}}} \right)^2} + {\left( {\dfrac{{{\sigma _{13}}}}{{{S_{13}}}}} \right)^2} + {\left( {\dfrac{{{\sigma _{23}}}}{{{S_{23}}}}} \right)^2},{\sigma _{33}} \geqslant 0 。$

(6)

式中：X_T和X_C分别为沿纤维方向的拉伸和压缩强度；Y_T和Y_C分别为垂直于纤维方向的拉伸强度和压缩强度；S₁₂，S₁₃和S₂₃为3个方向的剪切强度；Z_T为厚度方向的拉伸强度。上述5个失效因子中，任意一个值大于等于1，则材料发生对应的失效。

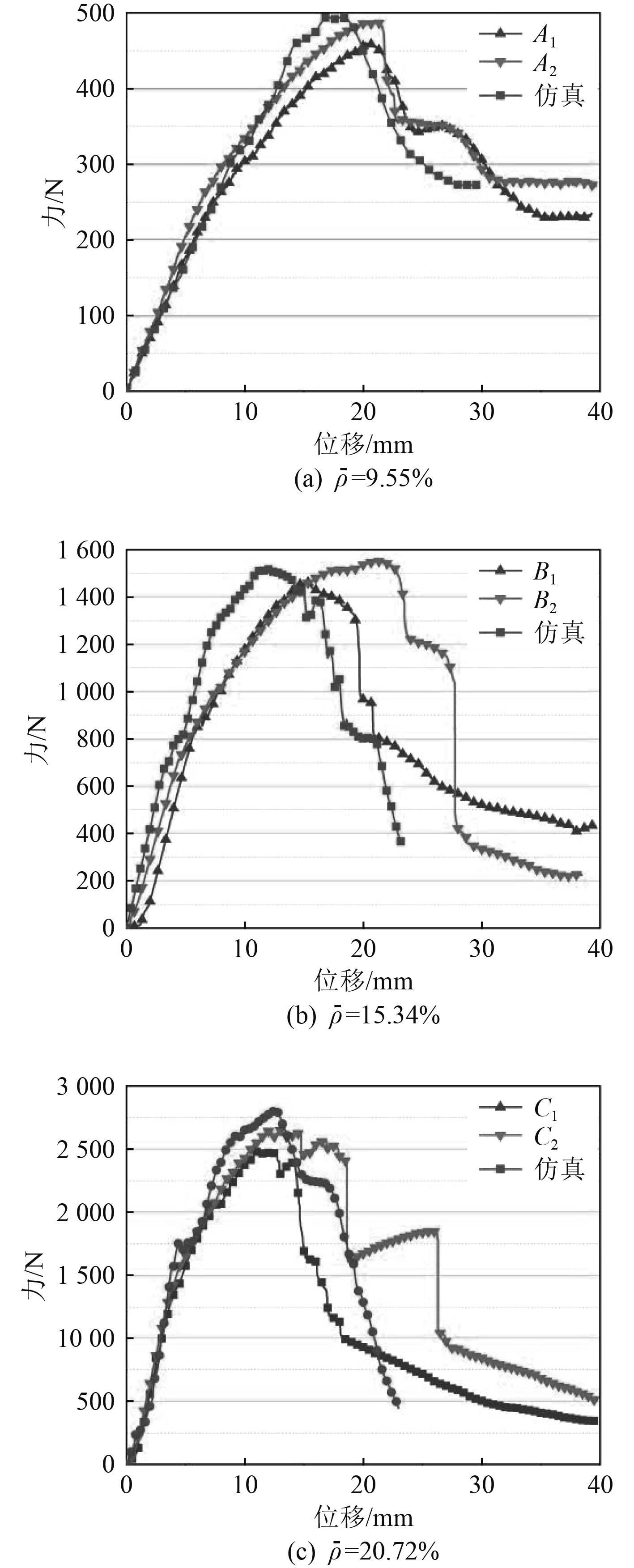
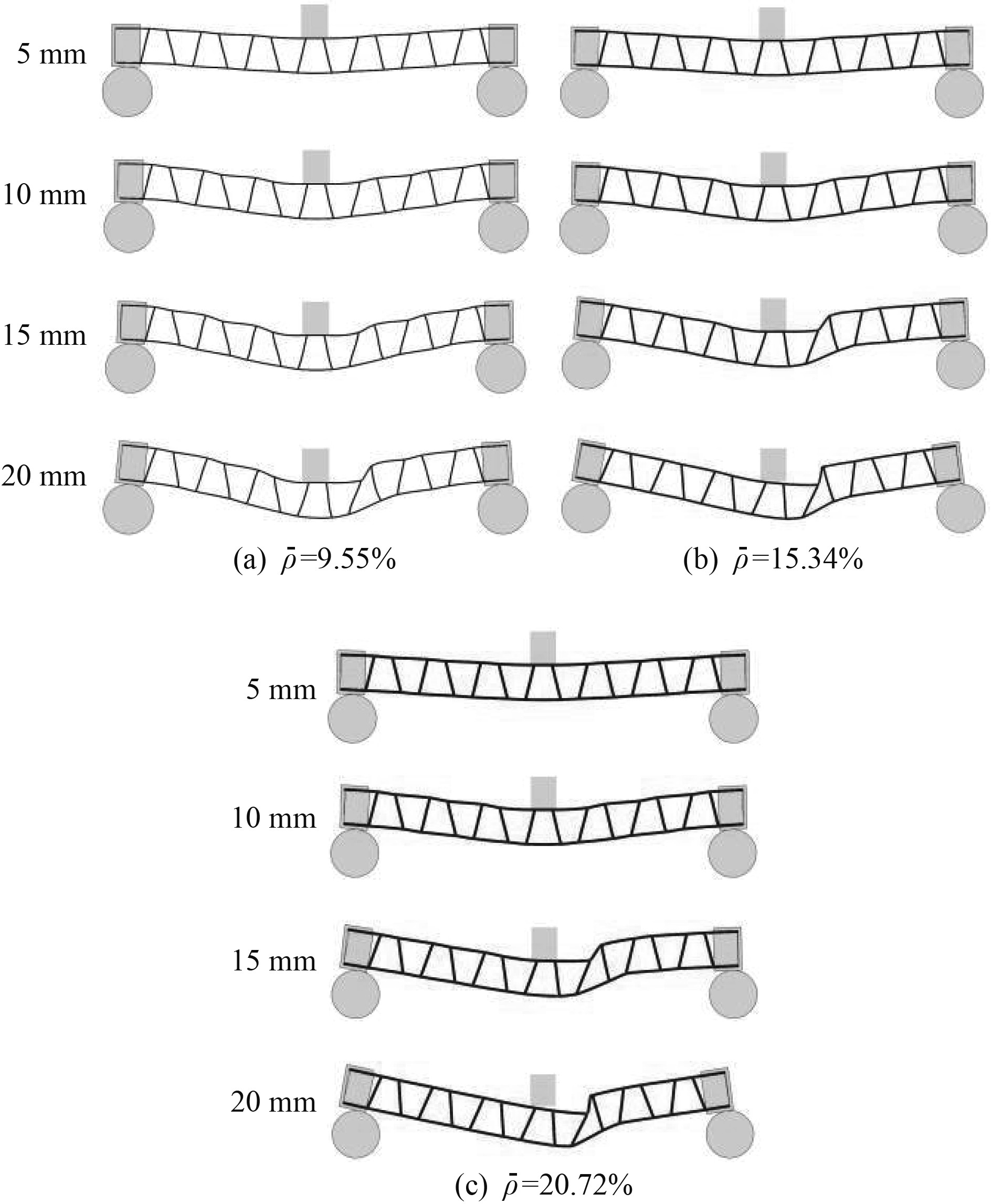
4.2 数值仿真结果与分析

图7为数值计算得到的载荷位移曲线。计算得到的曲线特征与试验测试得到的曲线相似，第1阶段曲线上升斜率相近，失效载荷较为一致。图8为数值计算得到的试件在弯曲过程中的失效云图，反映了随中心挠度的增加，夹层结构损伤演化的过程。数值计算结果与试验结果吻合较好。

4.3 芯层几何构型对弯曲性能的影响

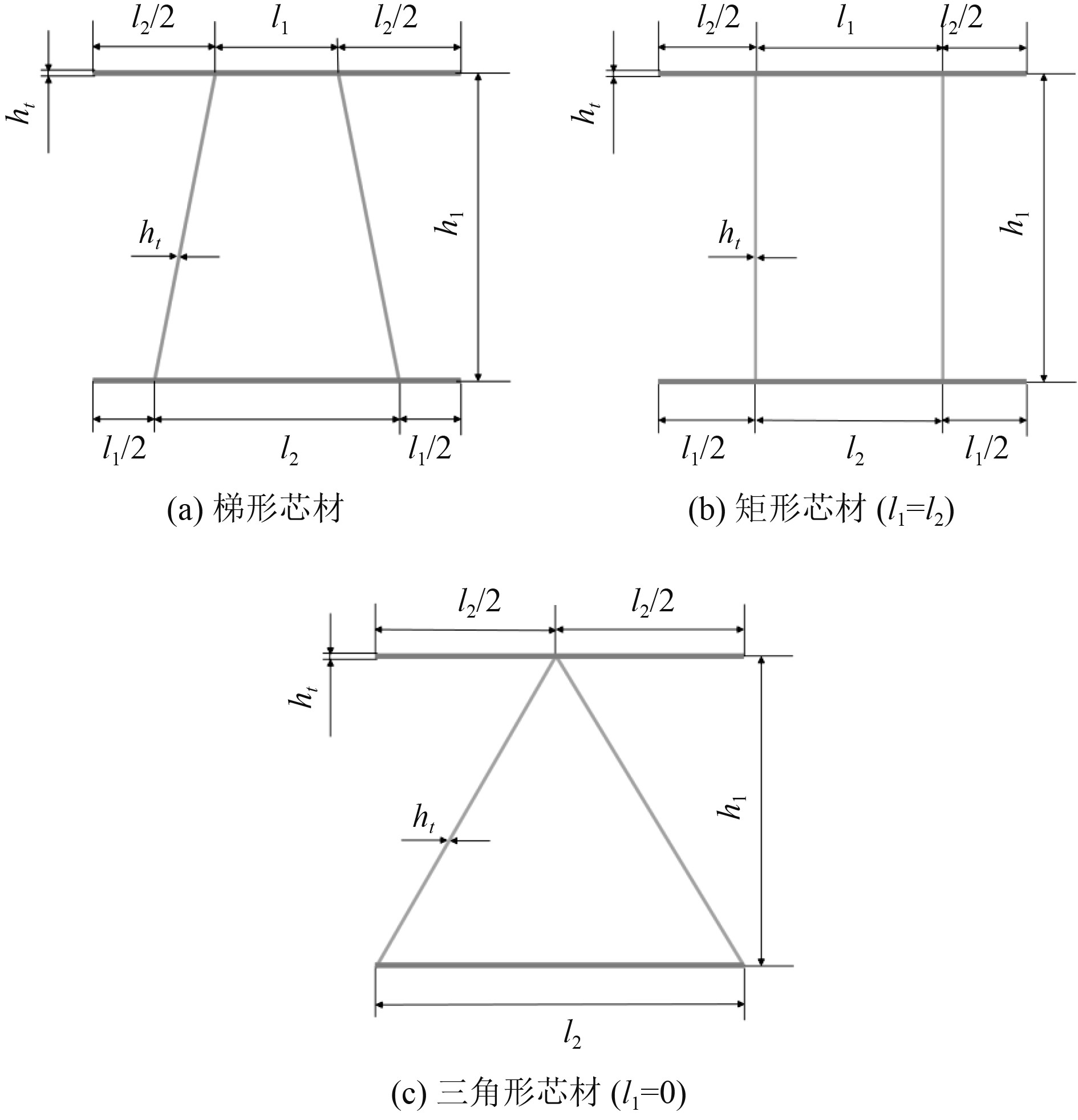
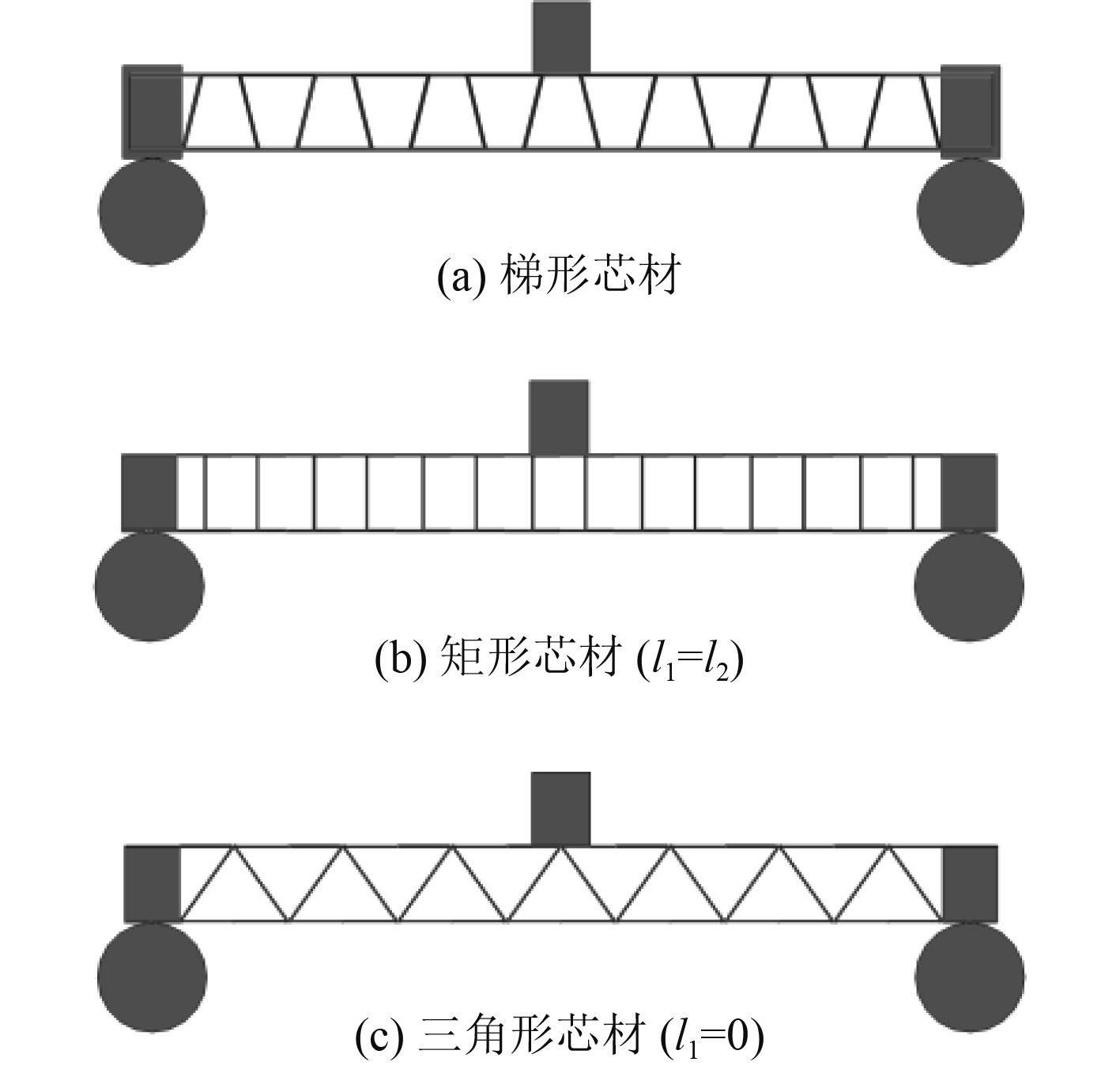
在确定有限元分析的有效性后，为对比不同芯层几何构型对弯曲性能的影响，设计3组不同类型的试件，图9为不同芯层几何构型的单胞示意图，图10为不同芯材的的波纹夹层结构的三点弯曲仿真计算示意图。对芯层结构计算截面积时以平行四边形计算，在保证l₁+l₂不变的情况下，3种夹层结构的相对密度不变。为提高计算效率，均选取相对密度ρ=9.55%，考察l₁=l₂与l₁=0两种特殊情况，对比其弯曲性能。

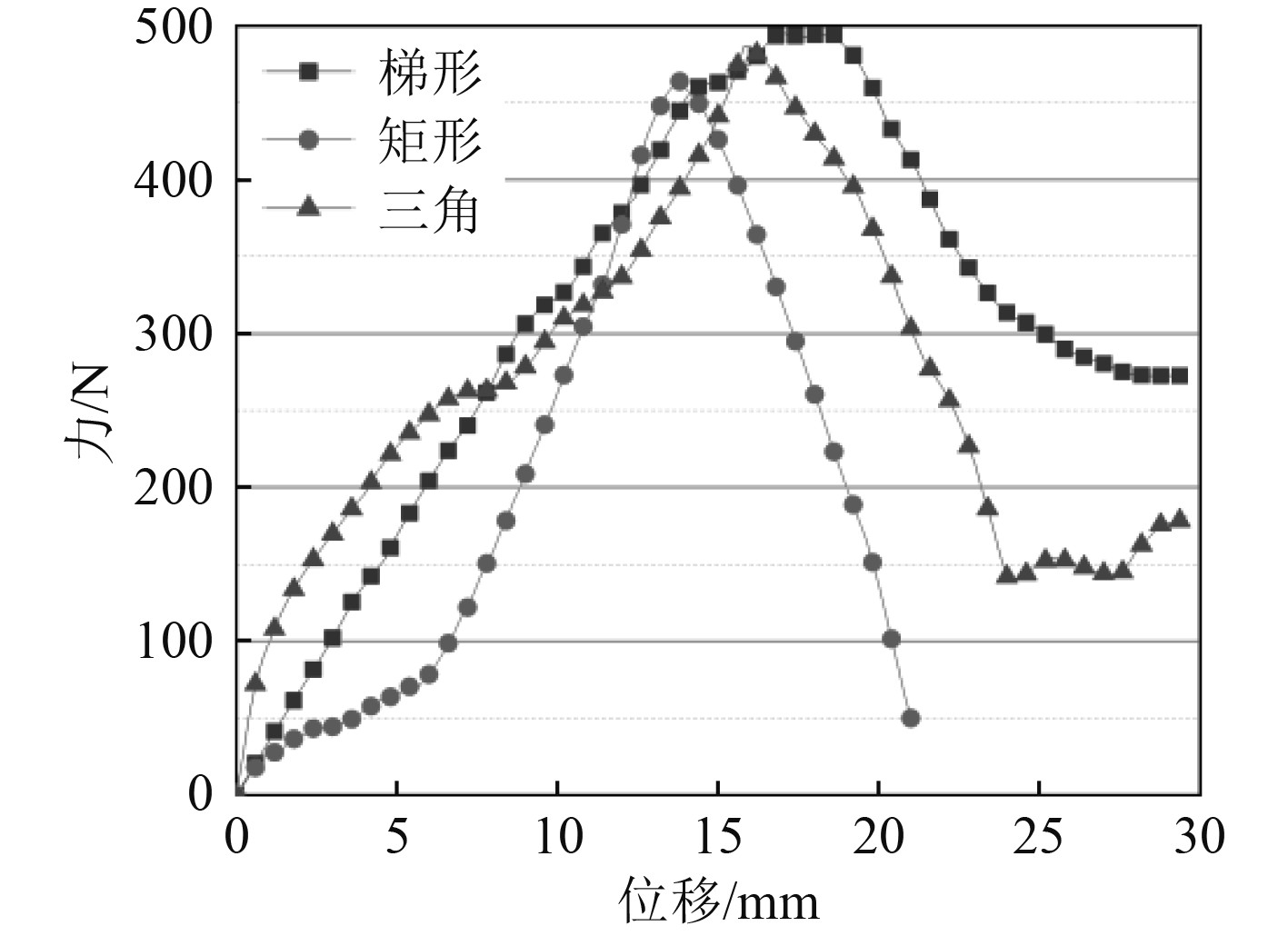
图11为数值计算得到的不同芯材试件的载荷位移曲线。可知，在相同面密度的情况下，梯形芯材的波纹夹层结构承受弯曲载荷的能力比矩形芯材的承载能力提高6.87%，比三角形芯材的承载能力提高1.84%。

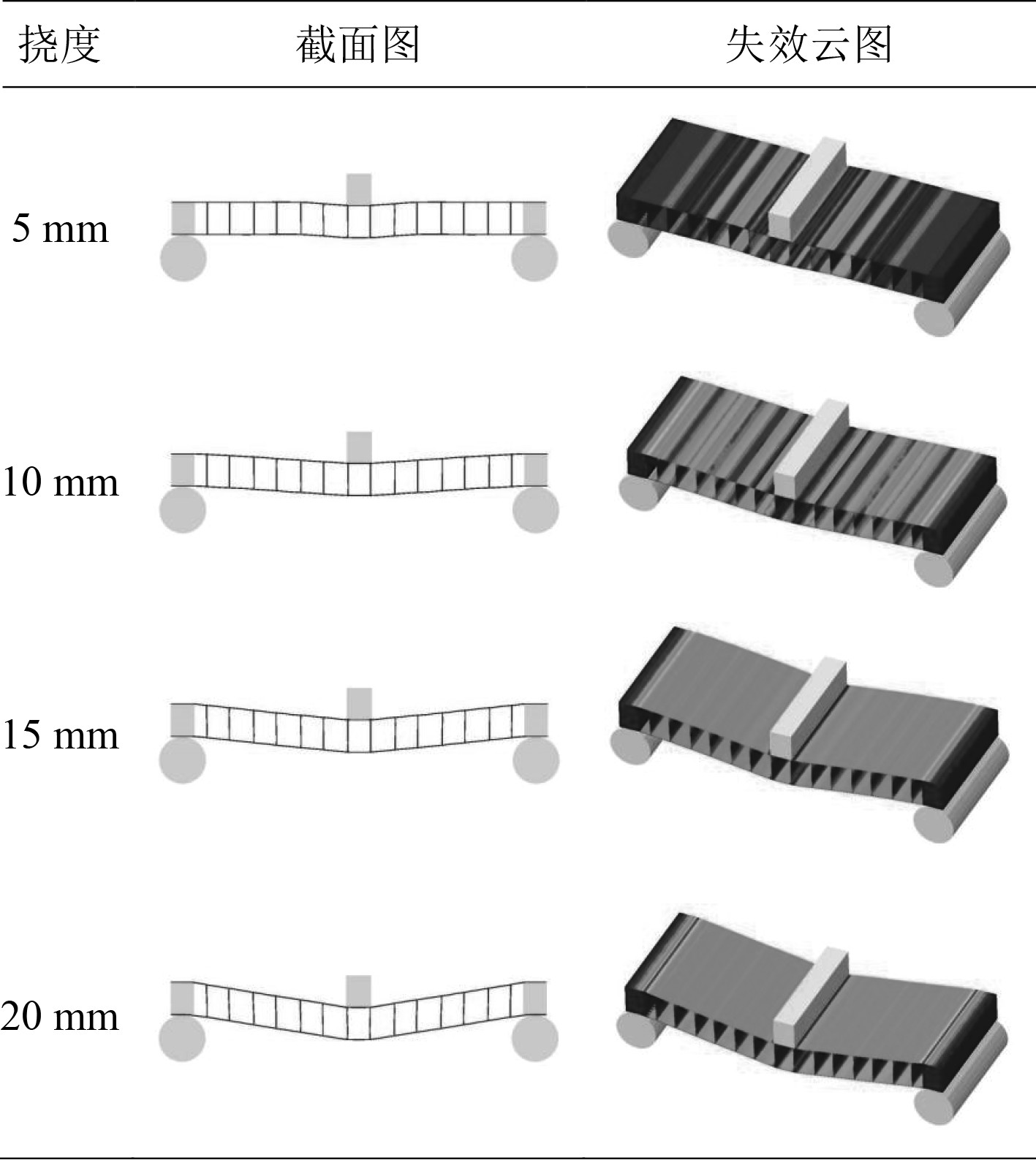
图12为梯形芯材复合材料波纹夹层结构弯曲失效的数值仿真图。图13为矩形芯材（l₁=l₂）的复合材料波纹夹层结构弯曲失效的数值仿真图。其前半段的失效模式与梯形芯材相近，但在后半段时，失效部位出现在了端部的上表面。

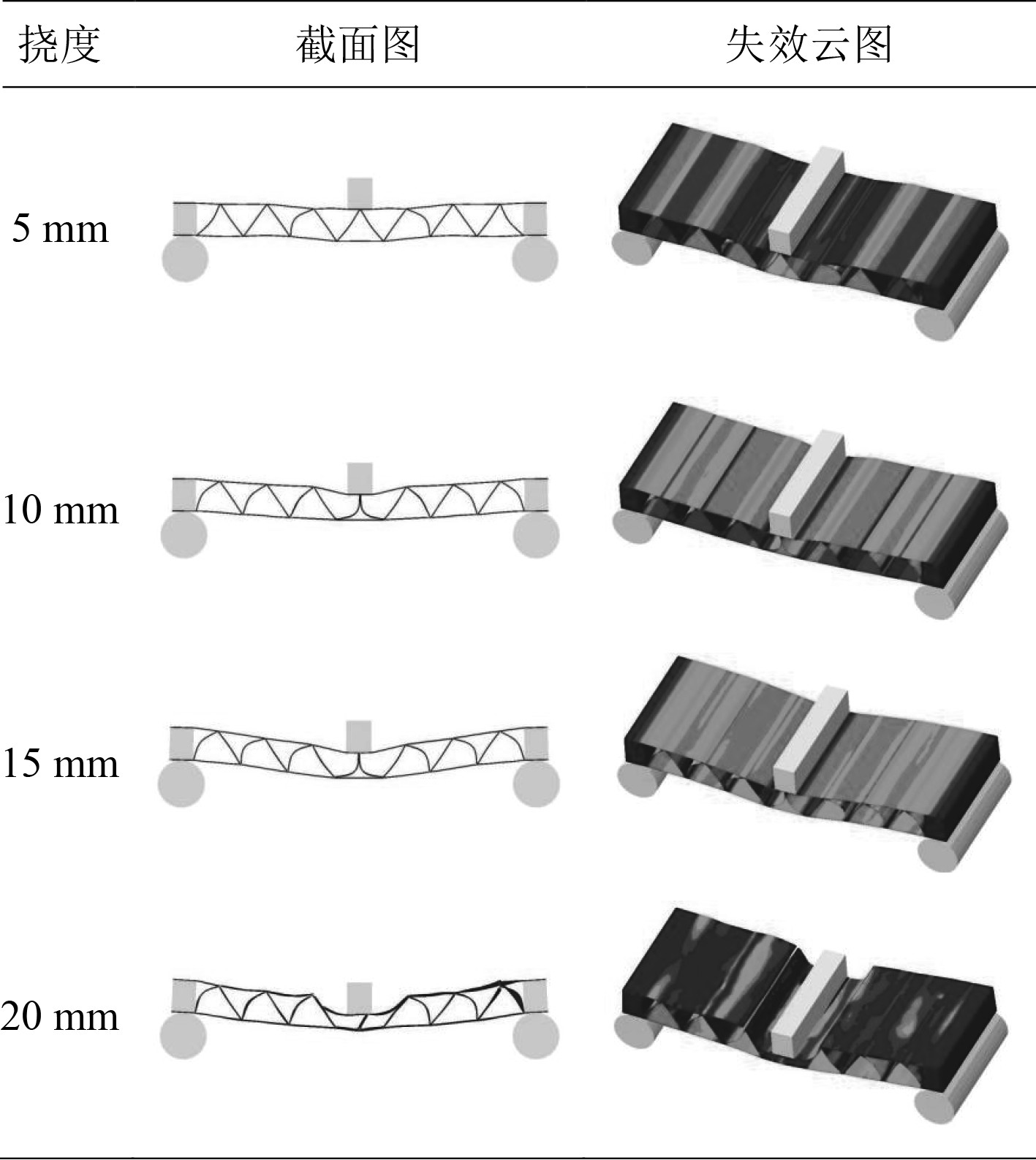
图14为三角形芯材（l₁=0）的复合材料波纹夹层结构弯曲失效的数值仿真图。在第1阶段的失效模式与梯形芯材相近，在第2阶段，中心单胞出现内凹现象，载荷-位移曲线出现一小段平滑现象，这表明波纹夹层结构发生局部的损伤；在第3阶段，两侧的单胞出现外凸现象，载荷-位移曲线进一步上升，但是斜率有所下降，表明损伤进一步发生；在第4阶段，上面板出现纤维断裂，中心单胞完全失效，复合材料波纹夹层结构失去承受载荷的能力。

5 结　语

本文制备复合材料波纹夹层结构，对其开展三点弯曲试验，研究了相对密度对极限载荷的影响。建立有限元计算模型，研究了不同芯层几何构型对弯曲性能的影响，结论如下：

1）复合材料波纹夹层结构在弯曲承载过程中，依次出现了局部损伤、分层失效和纤维断裂3种失效模式。当相对密度从9.55%增加至15.34%时，极限载荷增加了1035.7 N，当相对密度从15.34%增加至20.72%时，极限载荷增加了1070.2 N。

2）建立有限元计算模型，对比数值计算结果与实验结果，其线性阶段斜率、极限载荷、失效模式均吻合较好。

3）研究不同芯层几何构型对波纹夹层结构弯曲性能的影响，在相对密度一致的前提下，梯形芯材的波纹夹层结构承受横向载荷的能力比矩形芯材的承载能力高6.87%，比三角形芯材的承载能力高1.84%。