因为非均匀有理B样条(NURBS)在形状定义方面具有很好的造型能力,因此已被广泛地用于图像处理等诸多学科。已经开展了大量的关于把NURBS与产品外观设计结合起来的研究,使得NURBS的使用范围不断扩大。
但在采用NURBS表示产品外形时,因为数据点在网格中分布的较为松散,且点与点之间的几何联系不明确,从而难以有效处理数据,为外形设计工作造成了很大困难[1-3]。为了解决这个问题,本文提出一种改良的NURBS表达方法,将数据进行重新组织,经过一系列操作后,通过结果中数值的符号来判定所设计的产品外型是否符合特定的外型要求,从而判定设计结果的合理性。
1 NURBS在某一具体的NURBS模型中,需要满足某些几何限制,而每一点都要有一个数值区间[4-5],本文介绍B样条基函数以及NURBS曲面。
1.1 B样条基函数定义B样条基函数,设U={u0,u1,…,um}是一个单调不减的实数序列,以ui为节点,得出如下函数:
| $ {N}_{i0}\left(\mu \right)=\left\{\begin{aligned} 1,&\;\;{\mu }_{i}\leqslant \mu < {\mu }_{i+1},\\ 0,&\;\;{\rm{otherwise}}。\end{aligned}\right. $ |
| $ {N_{i,{{p}}}}(\mu ) = \frac{{\mu {\text{ - }}{\mu _{{i}}}}}{{{\mu _{{{i}} + {{p}}}}{\text{ - }}{\mu _{{i}}}}}{N_{i,{{p - 1}}}}(\mu ) + \frac{{{\mu _{{{i}} + {{p}} + {\text{1}}}}{\text{ - }}\mu }}{{{\mu _{{{i}} + {{p}} + {\text{1}}}}{\text{ - }}{\mu _{{{i}} + {\text{1}}}}}}{N_{i + 1,{{p - 1}}}}(\mu ) \text{。} $ |
NURBS曲面与非有理B样条基函数在本研究中具有相似性,其定义如下式:
| $ \begin{split}P\left( {{{u}},{{v}}} \right) =& \frac{{\displaystyle\sum\nolimits_{{{i}} = 0}^{{m}} {\sum\nolimits_{{{i}} = 0}^{{u}} {{{{w}}_{{{ij}}}}} } {P_{{{ij}}}}{N_{{{i}},p}}(u){N_{{{j}},q}}(v)}}{{\displaystyle\sum\nolimits_{{{i}} = 0}^{{m}} {\sum\nolimits_{{{i}} = 0}^{{n}} {{{{w}}_{{{ij}}}}{N_{{{i}},p}}(u){N_{{{j}},q}}(v)} } }} =\\ &\sum\nolimits_{{{i}} = 0}^{{m}} {\sum\nolimits_{{{j}} = 0}^{{n}} {{P_{{{ij}}}}{R_{{{i}},p:}}_{{{j}},q}(u,v),u,v} } \in \left[ {0,1} \right] \text{,}\end{split} $ |
| $ {R_{{{i}},p:}}_{{{j}},q}(u,v) = \frac{{wijN_{i,p}^{}(u){N_{j,q}}(v)}}{{\displaystyle\sum\nolimits_{{{r}} = 0}^{{m}} {\sum\nolimits_{\delta = 0}^{{n}} {{W_{rs}}{N_{r,p}}} } (u){N_{s,q}}(v)}} \text{。} $ |
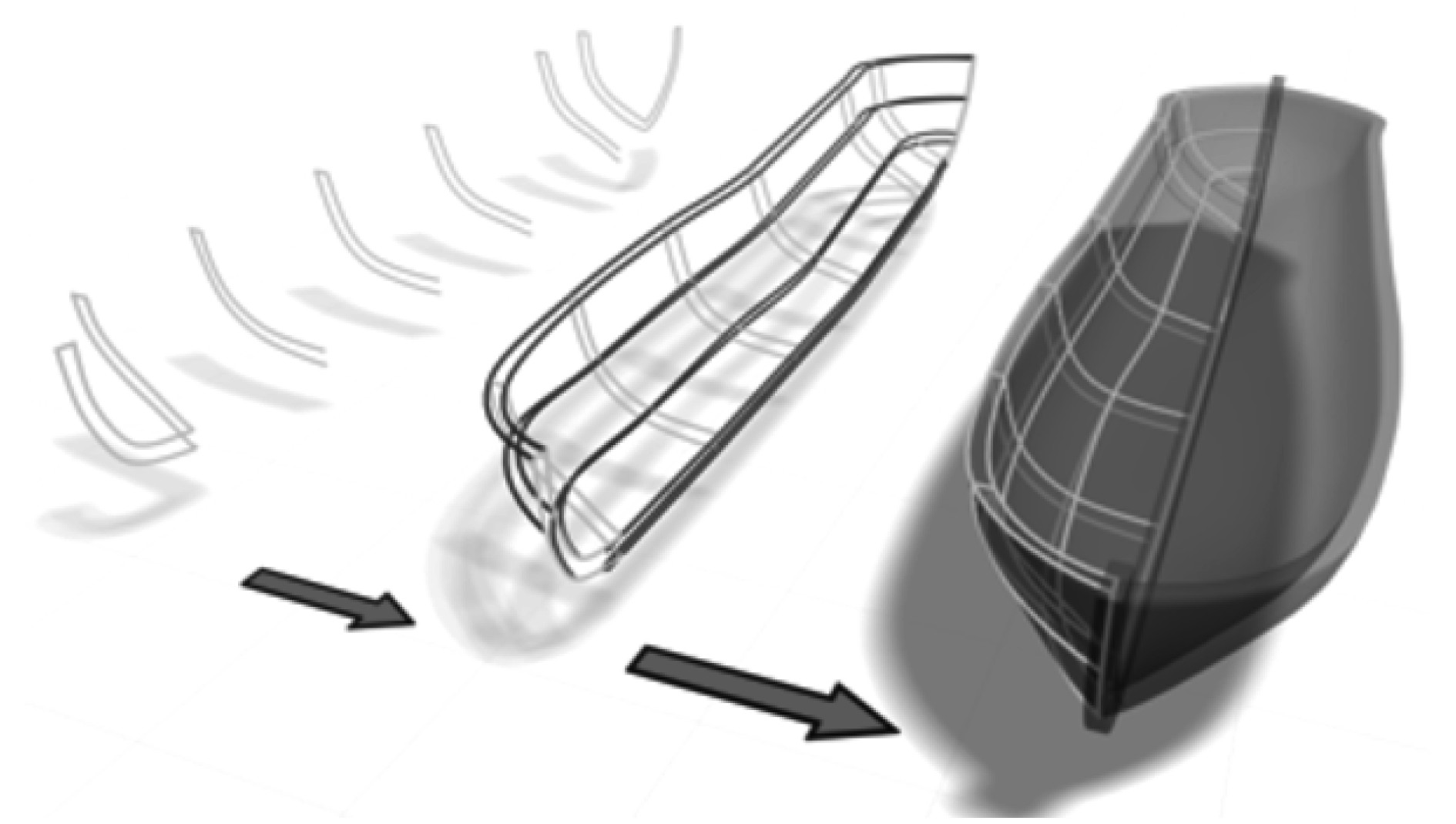
在非参数化交互船体设计软件中,利用分布规则的型值点对其进行表面插值计算可以获得曲面,但其难度很大,由于对边界条件的处理比较繁琐,即使获得曲面,也难以达到设计需求。在此情形下,一般采用曲线内插方法获得各剖面线,再将各平面线当作剖面线,采用“蒙皮法”获得船舶曲面,若船舶曲面较简单,则采用中纵剖线、水线或桥面线等做为脊线或引线,从而获得船舶曲面。然而,由于大部分船舶的首尾外形十分复杂,因此很难用一个表面来表示完整的船身,这时必须采用表面分割的方法,根据连接点的几何连续性,将曲面片光顺地连在一起,形成一种新的曲面,即曲面拼接法。蒙皮法简单曲面如图1所示。
|
图 1 蒙皮法简单曲面 Fig. 1 Skin method simple surface |
船舶垂向参数设计是在水线附近布置具有特定用途的船型,以满足某项特定要求。在进行垂向参数设计时,应根据船型特点,对参数进行优化计算。由于船舶水动力学模型较为复杂,所以在进行垂向参数设计时,首先应进行简化处理。
一般情况下,通过对船体运动分析,可以得到船舶水动力学模型中的关键参数,如纵摇、横摇、垂荡等。对于不同类型的船型,在进行参数设计时所考虑的因素也不同,应根据具体船型的性能要求进行参数优化计算。
首先根据已知条件进行初始参数优化计算,得到初始参数优化结果后,继续进行验证与分析,并将初始参数优化结果与该船的性能要求进行比较分析,若不能满足要求则继续对该船的初始参数优化结果进行验证与分析。对于满足要求的船体型线可以直接利用该方法进行垂向参数设计。
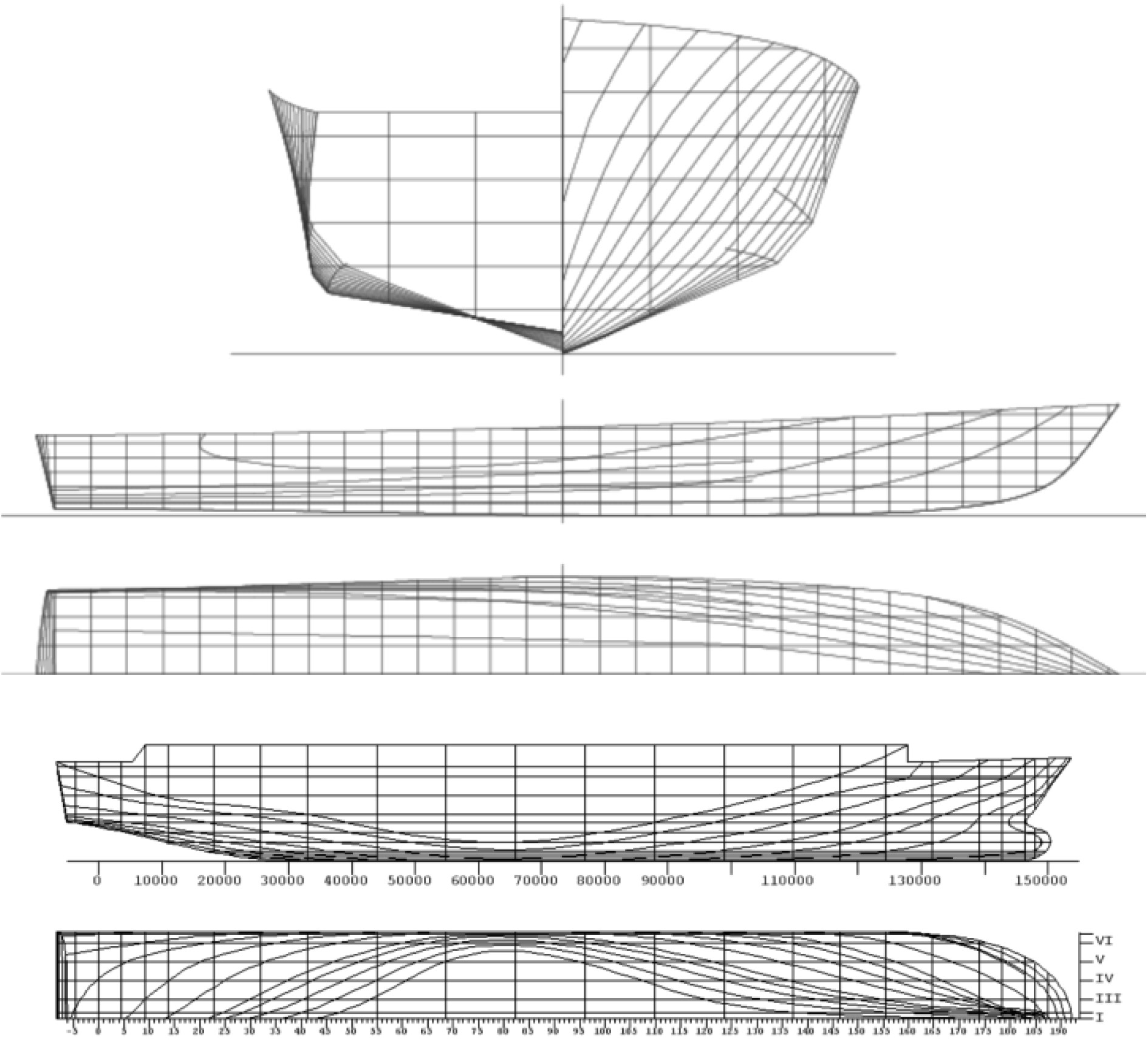
船体曲面特征线如图2所示,在采用NURBS曲面构造垂向参数时,应根据船体型线的特点选取合适的NURBS曲面构造方法。经对比发现,基于NURBS曲面构造船体型线具有良好的可设计性及灵活性。
|
图 2 船体曲面特征线 Fig. 2 Hull surface feature lines |
水线的特征点是水线的起点和终点,也是直线部分的起点和终点,而直线部分的起点和终点又可以用其他的特征点来定义,如头部和尾部等高线、边缘等。在最初的设计阶段,弧度的直径可以通过拉力功能来预先确定。此外,由于前、后2个船身在外形上具有相似性,因此还可以建立一个参数化的联合优化设计模型。为此,把坐标系统的起点设置在船首的横剖面和中纵剖线的交叉点上:将中纵剖面和基面的交叉点确定为X轴,并将指向船首和船尾2个方向的方向确定为正值;Y轴是船体的横切面和船体基面的相交,当朝向船体左侧时,即为正确坐标;Z轴是中纵线和下横线的交叉点,并在上方表示为正值。在这个坐标系统中,给出水线前面的特性参数。
首先确定NURBS曲线逼近首位轮廓线,以此来满足精确性和灵活度,将水线前体控制点分为四大类:1)边界控制顶点;2)切矢控制顶点;3)形状控制顶点;4)尾封板平面控制顶点。
接下来确定参数,之后对其进行调整,从而获得符合设计要求的头尾等高线。在确定了首、尾等高线之后,再决定所要设计的水线特性参数。
以圆舭型为例,对其最大横截面进行计算,结果如下式:
| $ B{wf}\left({z}\right)=\left\{\begin{aligned} &B/2\text{,} R\leqslant {z}< T,\\ & \sqrt{2R{{z-z}}^{2}}+\left(B/2\right)\text-R\text{,}0\leqslant {z}< R。\end{aligned}\right. $ |
式中:B为型宽,T为设计吃水深度。
直线段的长度对船舶外形光滑度的影响很小,在初始设计时,可以将直线段的长度作为外形参数,表达式为:
| $ \begin{split}{L_{{{pf}}}}\left( {{z}} \right) = &{L_{{{pf}}0}} + 0.5\left( {{L_{{{pfd}}}}{{ - }}{L_{{{pf}}0}}} \right)\times \\ &\left( {3\left( {{\text{z}}/T} \right) - 2{{\left( {{\text{z}}/T} \right)}^3} + {{\left( {{\text{z}}/T} \right)}^4}} \right) \text{。} \end{split}$ |
式中:Lpf0直线段的中体长,Lpfd设计水线的中体长,在进行平面图的设计时,可根据计算结果绘制平面图,并逐步进行平面图的修正,使平面图达到设计的目的。
船体模型中的垂向函数公式如下:
| $ {{i}}\left( {{z}} \right) = {{{c}}_1} + {{{c}}_{\text{2}}}\left( {{{z}}/T} \right) + {{{c}}_{\text{3}}}{\left( {{{z}}/T} \right)^2} \text{。} $ |
确定系数c1,c2,c3为形状控制参数,T=2×J (J=1,2,3)。
圆弧半径r的三次多项式方程如下:
| $ {{r}}\left( {{z}} \right) = {{{c}}_1} + {{{c}}_{\text{2}}}\left( {{{z}}/T} \right) + {{{c}}_{\text{3}}}{\left( {{{z}}/T} \right)^2} + {{{c}}_{\text{4}}}{\left( {{{z}}/T} \right)^3} \text{。} $ |
其水线面系数为:
| $ {{{C}}_{{{wf}}}}\left( {{z}} \right) = {{{c}}_1} + {{{c}}_{\text{2}}}\left( {{\text{z}}/T} \right) + {{\text{c}}_{\text{3}}}{\left( {{\text{z}}/T} \right)^2} \text{。} $ |
最后,基于以上计算所得参数,对水面系数进行归一化处理,最终得出公式:
| $ {{C}_{{{bf}}}} = \int_0^{{r}} {\frac{{2{C_{{{wf}}}}\left( {{z}} \right){L_{{{wf}}}}\left( {{z}} \right){{{B}}_{{{wf}}}}\left( {{z}} \right)}}{{{L_{{{p}}pf}}{{BT}}}}} {\rm{d}}z \text{。} $ |
将每个参数组成一个N维列向量:
| $ \begin{split} {\boldsymbol{x}} =& {[x_1^{\rm{T}},x_2^{\rm{T}}, \cdots ,x_N^{\rm{T}}]^{\rm{T}}} = \\ & \left[ {\begin{array}{*{20}{c}} {{S_1}(\theta )}&0& \cdots &0 \\ 0&{{S_2}(\theta )}& \cdots &0 \\ \vdots & \vdots & \ddots & \vdots \\ 0&0& \cdots &{{S_N}(\theta )} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{a_1}} \\ {{a_2}} \\ \vdots \\ {{a_N}} \end{array}} \right] = S(\theta )a \text{。} \end{split} $ |
上式为分布式参数处理阵列,其中
首先通过NURBS曲面进行船体主尺度的计算,再利用NURBS曲面的控制点信息和三角面方程,通过约束条件得到船体各舱室的垂向参数以及结合船体曲面特征,然后对首位轮廓线控制点的参数和最大横剖面的参数进行分析,通过研究能发现船体各舱室的垂向参数之间存在几何上的耦合关系,结合上述方程式,垂向参数和横向线条曲线间的几何关系可通过NURBS曲面进行表达,因此可利用NURBS曲面生成船舶垂向参数曲面。
在基于NURBS曲面进行垂向参数设计时,可以根据不同类型的船舶及其典型垂向参数设计流程,选取相应的船体主尺度及垂向线条曲线。当船舶主尺度及垂向线条曲线变化较大时,需要采用不同的垂向线条曲线。其中,对于长宽比较大、尺度较大的船舶,可采用具有较小长宽比、较短上甲板宽度和较多的垂向线条曲线;而对于长宽比较小、尺度相对较小的船舶则可采用具有较大长宽比、更多横向线条曲线。
3.1 算例分析基于NURBS曲面的方法,对船舶典型垂向参数进行设计,对不同垂向参数下上层建筑高度展开分析,并与基于曲面曲线方法的设计结果进行比较。
本文选取一艘运输船作为案例,其排水量约为7 000 t,将统计结果导入系统后,经实践可知,本次研究的船舶垂向参数设计方法在实际应用中符合本次的设计预期,具体结果如表1所示。
|
|
表 1 控制顶点坐标对比分析 Tab.1 Comparative analysis of control vertex coordinates |
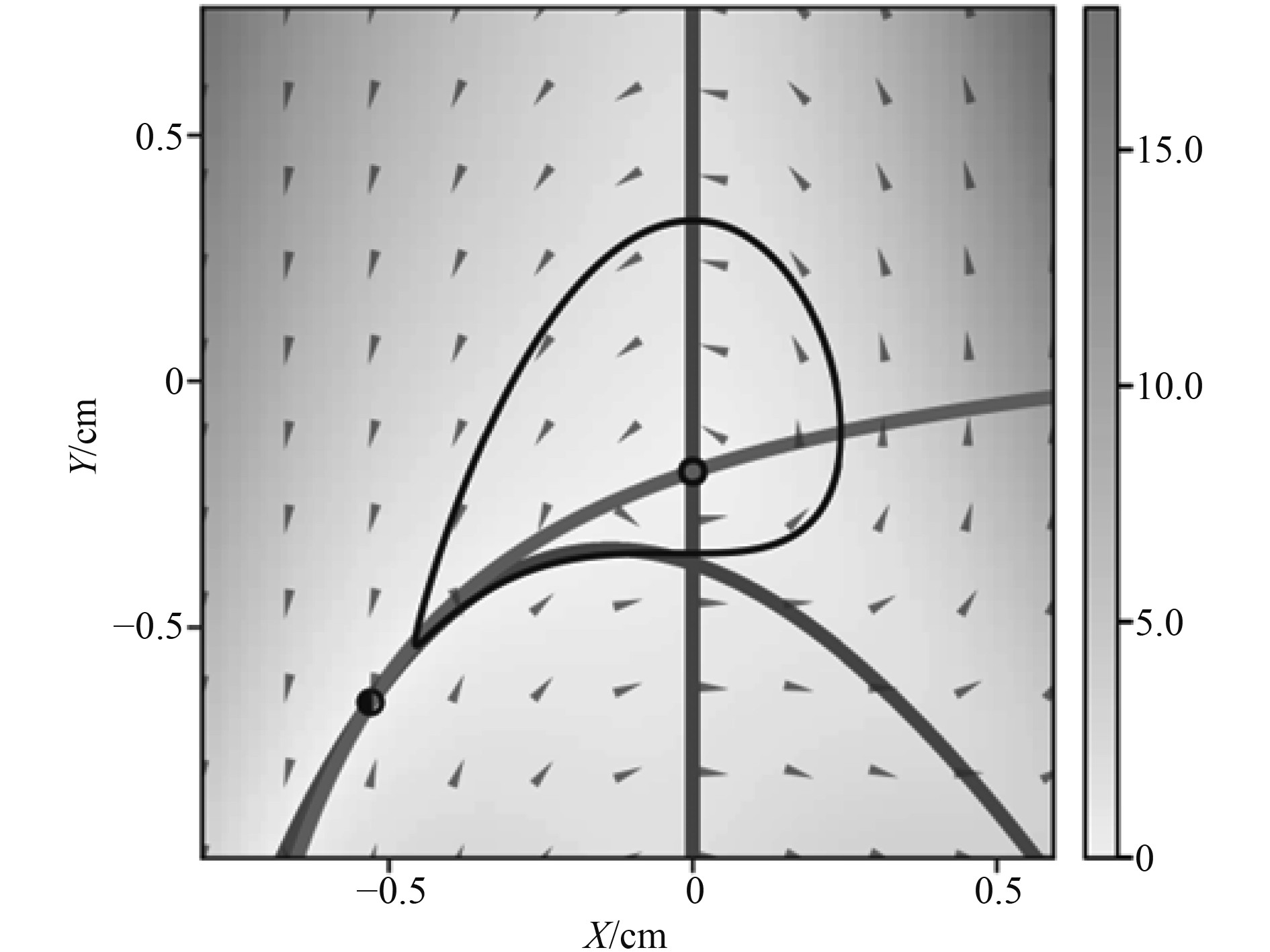
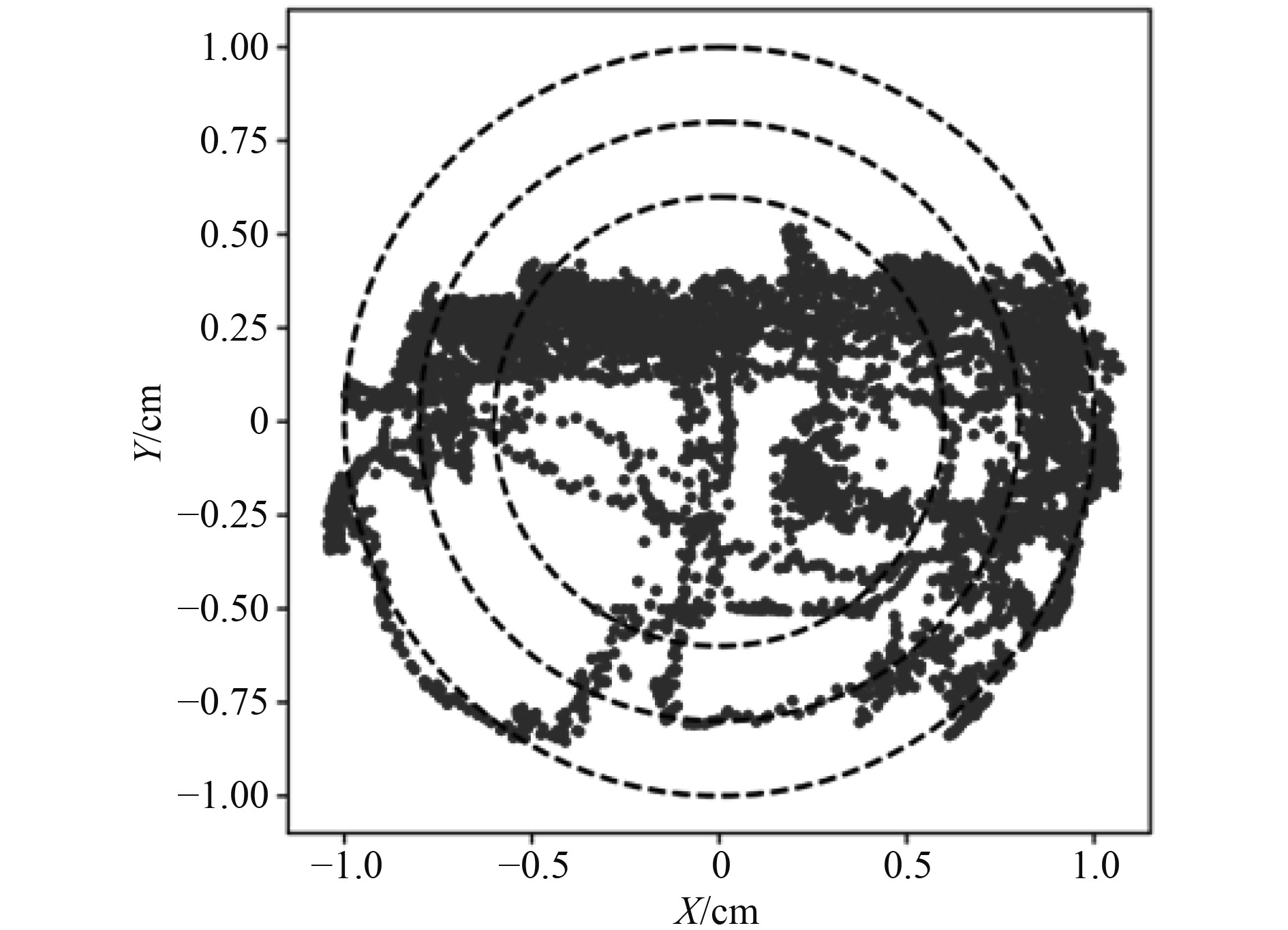
通过以上对比分析可知,本研究思路在数据呈现上符合船舶工程精度,经过归一化的数学计算后,可以得到船舶加工过程中的相对控制精度分布,如图3所示。曲面检测点的分布如图4所示。说明本次船舶垂向参数设计流程具有一定的实操性。
|
图 3 相对控制精度分布图 Fig. 3 Relative control accuracy distribution chart |
|
图 4 曲面检测点的分布图 Fig. 4 Distribution map of surface inspection points |
该垂向参数曲面具有以下优点:
1)该垂向参数曲面通过NURBS曲面构造方法,能更加精确地表示船舶垂向参数的形状。
2)该垂向参数曲面不需要任何中间过渡面,避免了由于过渡面所带来的几何误差。
3)由于垂向参数曲面构造过程中引入了NURBS曲面的参数化表达方式,所以能够在参数化表达过程中不受任何约束,且无需进行各种计算。
4)该垂向参数曲面能方便地与其他船型参数化表达方式结合。通过实例验证表明,基于NURBS曲面的垂向参数设计方法具有较高的效率和精度,能更好地满足设计要求。
4 结 语本文基于NURBS曲面构造了船舶典型垂向参数的设计方法,并以某运输船为例对该方法进行验证,结果表明:
1)该方法能够快速准确地进行船舶垂向参数设计,并能较好地满足实船要求。
2)该方法与基于曲面曲线的设计方法相比,不仅可以更好地满足实船的使用要求,还能更好地实现对线型的追求。
3)由于该方法没有涉及曲面曲线,因此在设计过程中不需要了解复杂的曲面曲线理论,从而具有更高的实用性和通用性。
| [1] |
李尧, 陈仲铭, 严谨, 等. 复杂船体曲面的一种草图重叠建模法[J]. 机械工程与自动化, 2018(5): 54-55+58. LI Yao, CHEN Zhong-ming, YAN Jing, et al. A sketch overlay modeling method for complex hull surfaces[J]. Mechanical Engineering and Automation, 2018(5): 54-55+58. |
| [2] |
王梦莹, 景旭文, 周宏根, 等. 基于时空约束的船体曲面分段车间调度方法研究[J]. 现代制造工程, 2017(9): 96-101. WANG Meng-ying, JING Xu-wen, ZHOU Hong-gen, et al. Research on segmented workshop scheduling method for hull curved surface based on space-time constraints[J]. Modern Manufacturing Engineering, 2017(9): 96-101. |
| [3] |
周宏, 蒋志勇, 罗宇, 等. 材料热物理性能对高频感应船体曲面弯板成型的影响研究[J]. 中国造船, 2015, 56(4): 101-108. ZHOU Hong, JIANG Zhi-yong, LUO Yu, et al. Research on the influence of material thermophysical properties on forming of high-frequency induced hull curved plate[J]. China Shipbuilding, 2015, 56(4): 101-108. |
| [4] |
董明海, 陈倩清, 李攀, 等. 船体曲面分段余量补偿及精度过程控制方法研究[J]. 中国水运(下半月), 2015, 15(10): 6-8. DONG Ming-hai, CHEN Qian-qing, LI Pan, et al. Research on segmented margin compensation and accuracy process control method of hull surface[J]. China Water Transport (Second Half Month), 2015, 15(10): 6-8. |
| [5] |
安艳平, 易鹏飞, 丘宏俊. 一种基于NURBS的曲面表达方法及其应用[J]. 中国制造业信息化, 2008(7): 41-44. AN Yan-ping, YI Peng-fei, QIU Hong-jun. A NURBS-based surface expression method and its application[J]. China Manufacturing Informatization, 2008(7): 41-44. |
 2023, Vol. 45
2023, Vol. 45
