2. 深海技术科学太湖实验室,江苏 无锡 214082
2. Taihu Laboratory of Deep Sea Technology and Science, Wuxi 214082, China
船舶在航行过程中,燃油消耗的成本占总成本的45%~65%,而燃油消耗获得的能量则主要用于克服船体表面的摩擦阻力[1]。因此,减小船舶阻力,尤其是摩擦阻力成为降低船舶营运成本的关键因素。
目前减小摩擦阻力的方法包含以下几类:1) 疏水材料减阻法[2]。该方法主要是在船舶表面加工设计具备疏水性质的表皮,利用材料的疏水特性将船体表面流体“抬升”,从而达到减小阻力的目的。2)柔性蒙皮减阻法[3]。该方法是利用柔性表皮的被动变形来达到缓解流体冲击,减小边界层内的能量消耗来达到减阻的目的。3)气泡减阻法[4]。该方法主要是通过向船体底部喷注气泡,在水线面与船体底部之间形成一层保护膜来达到减小流动阻力的目的。上述减阻技术已通过大量数值计算和模型试验对其可行性进行了验证,并且在实船上也进行了应用。
除上述减阻技术外,模仿鱼类表层微型凹槽的仿生沟槽减阻技术得到较少的关注[5]。本文利用数值模拟技术开展仿生沟槽对平板阻力性能的影响研究,系统分析沟槽剖面形状、特征尺寸对减阻性能的影响,阐明沟槽减阻的内在机制。本文研究成果可为新一代水下航行体减阻增效提供水动力学技术支撑。
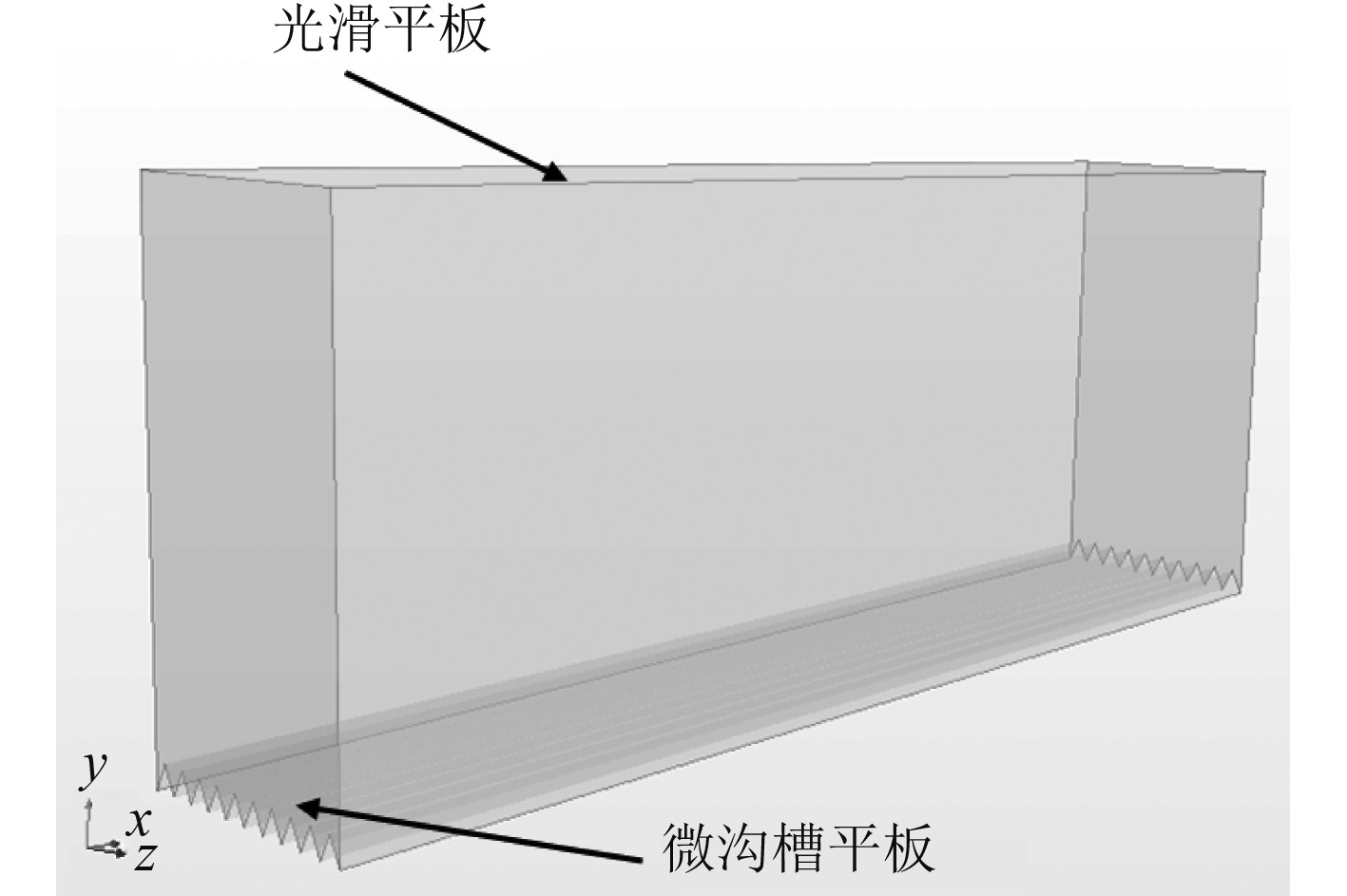
1 计算模型及网格本文计算模型如图1所示,图中X向、Y向和Z向分别表示流向、垂向、展向方向。本文展向长度设置为Z=1 mm,垂向高度设置为y = 50 mm。原因如下:为了削除壁面对水动力性能的影响,计算域高度至少大于边界层厚度的10倍,其中湍流边界层厚度表达式为
|
图 1 计算模型 Fig. 1 Diagram of computation model |
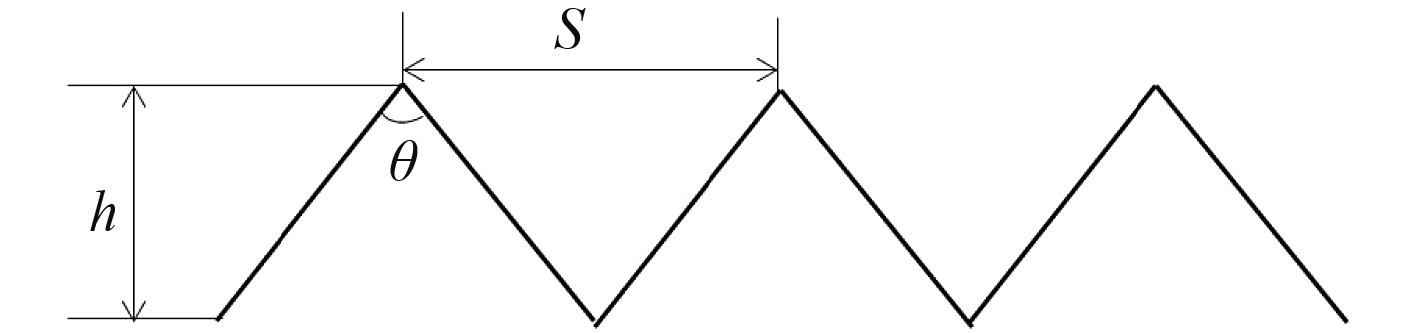
选取的微沟槽表面为典型的V型表面,其具体形态如图2所示。其中h和s分别为垂向高度和横向间距。研究表明,当垂向高度h和横向间距s的无量纲尺寸h+ ≤25, s+ ≤30时可具备减阻效果,h+和s+定义如下:
|
图 2 仿生沟槽表面的形态组成 Fig. 2 Morphological composition of biomimetic groove surface |
| $ {h^ + } = h\frac{{{u_\tau }}}{\nu },{\text{ }}{s^ + } = s\frac{{{u_\tau }}}{\nu } ,$ | (1) |
| $ {u_\tau } = 0.172 \cdot {U_0}{(\frac{{{U_0}x}}{\nu })^{ - 0.1}} ,$ | (2) |
联立式(1)和式(2)可得:
| $ {h^ + } = 0.172\frac{{h \cdot {U_0} \cdot {{{Re} }_x}^{ - 0.1}}}{\nu },{\text{ }}{s^ + } = 0.172\frac{{s \cdot {U_0} \cdot {{{Re} }_x}^{ - 0.1}}}{\nu } 。$ | (3) |
来流速度取为5 m/s,雷诺数
选取的计算域为长方体计算域,具体尺寸为(x, y, z)= (400 mm, 50 mm, 1 mm)。边界及边界条件设置如下:
1)质量流进口边界
给定质量流大小和方向,湍流强度和湍流粘度比分别设为5%和10%;流体介质为水,质量流量为0.25 kg/s。
2)压力出口边界
计算域出口处设为压力出口边界条件。
3)壁面
计算域上侧为光滑平板,下侧为带沟槽的平板,平板上施加无滑移壁面条件。
4)侧面
计算域左右两个平面设置为对称边界条件。
采用Gambit软件进行网格划分,全局采用结构化网格划分,并对平板近壁区采用网格加密的方法(第1层网格高度满足y+ ≤ 1)。以 Re x= 2×106为例,全局网格共计120万左右。带沟槽平板附近网格划分放大图如图3所示。

|
图 3 带沟槽平板附近网格 Fig. 3 Grid near a grooved flat plate |
采用RANS方程作为流体运动的控制方程:
| $\begin{aligned} \nabla \cdot {\boldsymbol{u}} =& 0,\\ {\text{ }}\frac{{{\rm{\partial}} {\boldsymbol{u}}}}{{{\rm{\partial}} t}} + ({\boldsymbol{u}} \cdot \nabla ){\boldsymbol{u}} =& - \frac{1}{\rho }\nabla p + \frac{\mu }{\rho }{\nabla ^2}{\boldsymbol{u}}。\end{aligned}$ | (4) |
式中:u为流体速度;μ为流体动力粘性系数;p为压力;ρ为流体密度。
采用有限体积法对控制方程(3)进行离散,湍流模型采用SST k – ω两方程模型,基于压力求解器采用标准壁面函数对近壁面流动进行处理,通过通用流体计算软件包Ansys Fluent对离散化的方程进行求解。
2.2 精度验证进行数值方法精度验证,以平板为例,其摩擦阻力系数Cf的解析解可按普朗特经验公式(5)计算得出。表1给出了不同雷诺数下数值模拟结果与经验公式计算结果对比。可以看出,采用k-ω SST 湍流模型计算得到的平板阻力系数值与经验公式的结果吻合较好,验证了k-ω SST 模型的精度。
|
|
表 1 初始计算参数设置 Tab.1 Initial calculation parameter settings |
| $ {C_f} = \frac{{0.074}}{{{{({Re} )}^{0.2}}}} ,$ | (5) |
开展沟槽减阻的内在机理研究。沟槽形状设置为V形,几何尺寸为s = h = 0.1 mm。
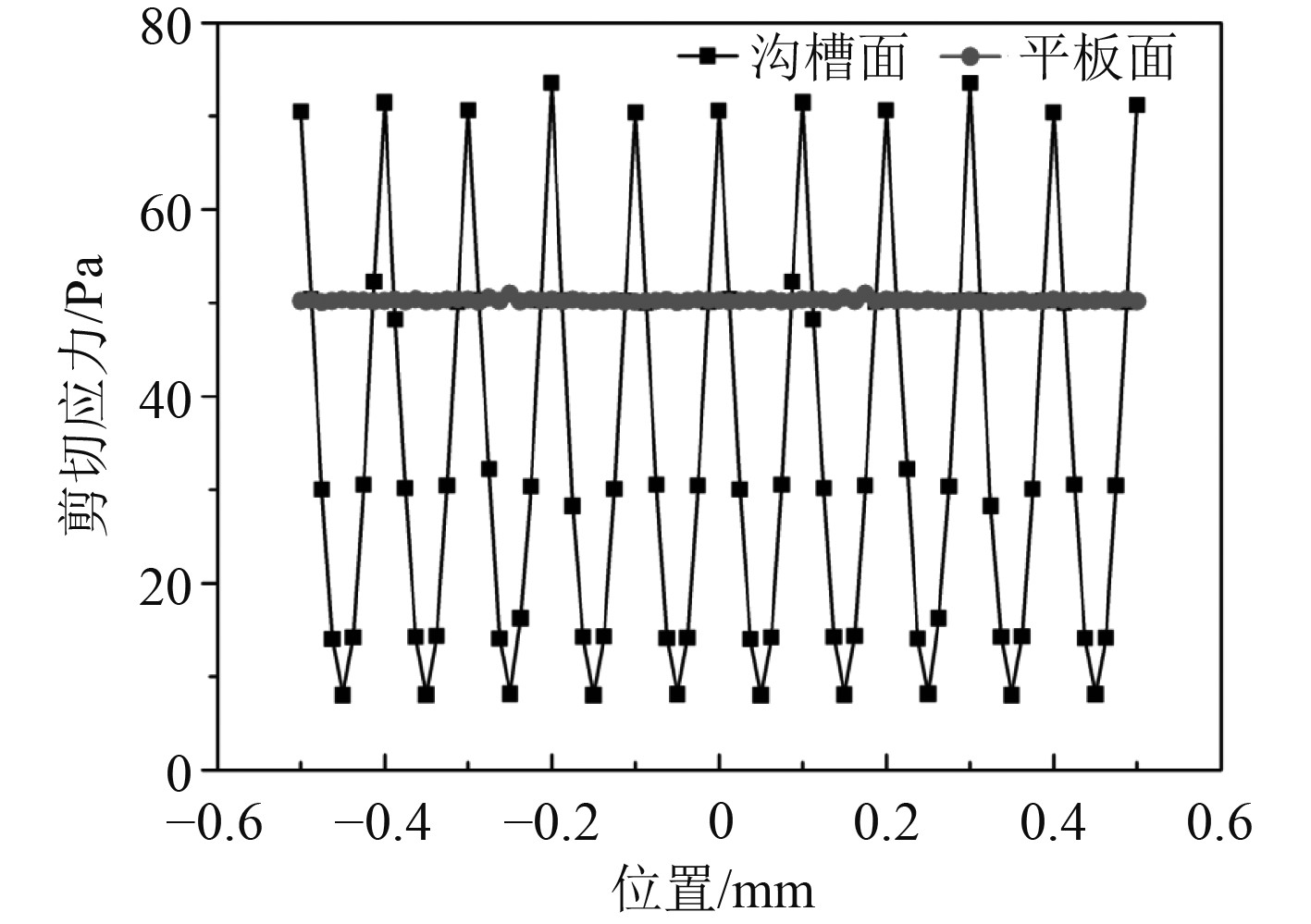
图4为沟槽平板和光滑平板剪切应力曲线图。可以看出,沟槽平板表面剪切应力分布与其几何形状较为类似。整体来看沟槽底部剪切应力远小于沟槽顶部剪切应力值,说明沟槽底部流动较为平缓,速度梯度小,而沟槽顶部则存在剧烈的动量交换且速度梯度值较大。此外沟槽大部分位置的剪切应力值低于平板,仅顶部剪切应力值略高于平板相应位置处的剪切应力值,不难判断沟槽平板表面平均剪切应力值低于光滑平板的剪切应力值。因此,可定性说明沟槽平板可起到减阻的效果。
|
图 4 沟槽平板和光滑平板剪切应力曲线图 Fig. 4 Shear stress curves of grooved and smooth flat plates |
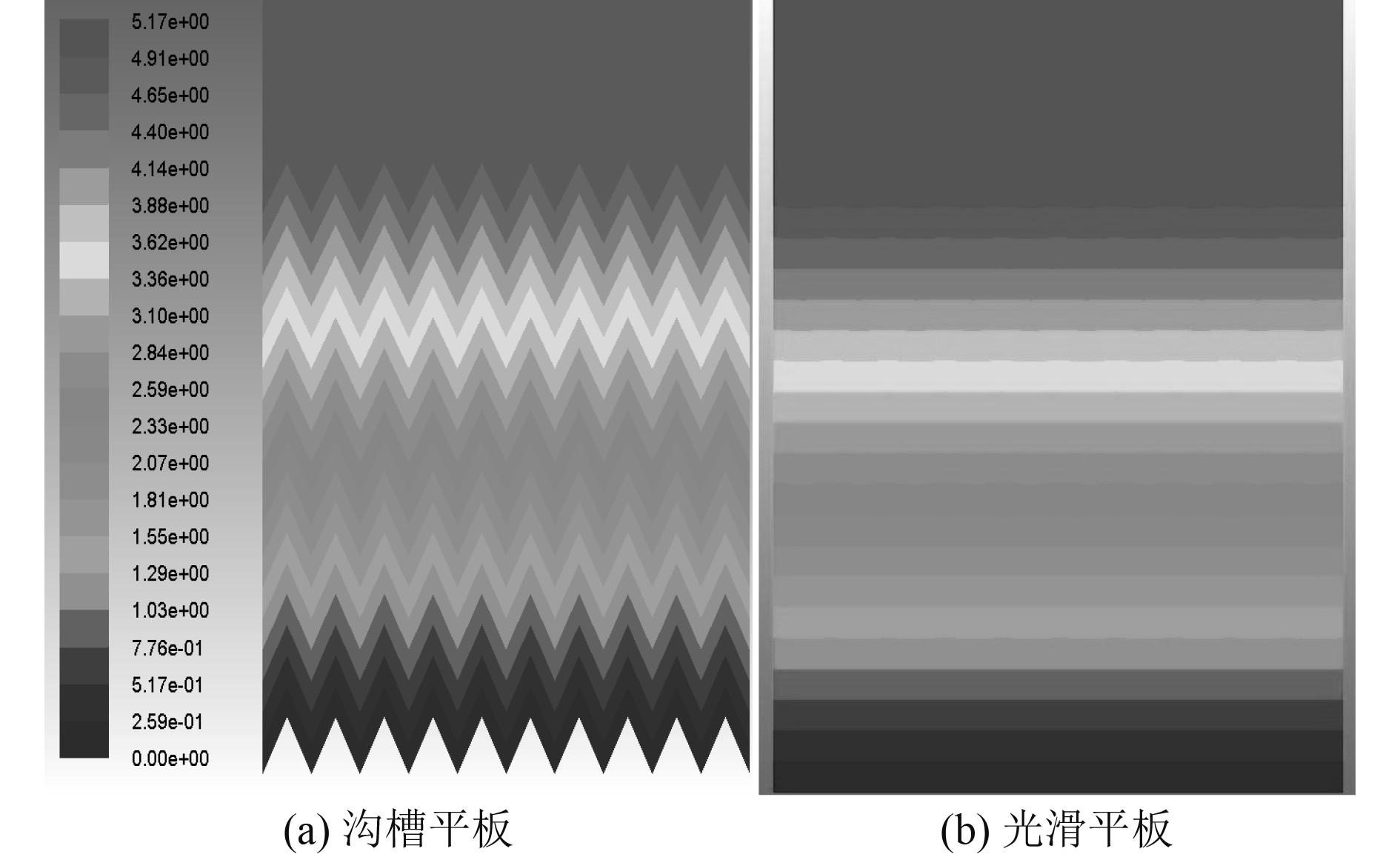
图5为光滑平板和带沟槽平板表面的流向速度云图。结合图5可以看出,带沟槽平板底部的流速大幅减小,且垂向速度梯度也得以降低。这就意味着,带沟槽平板底部的流体较为“安静”,对应的能量消耗较少,因此阻力值得以降低。
|
图 5 沟槽平板和光滑平板附近流向速度云图 Fig. 5 Flow velocity cloud map near grooved and smooth flat plates |
V形沟槽表面可起到减阻的作用,详细研究其形状参数对减阻效果的影响。考虑到V形沟槽的主要形状参数h和s对减阻效果的影响较大,选取自定义的V形角 θ 研究形状参数对减阻效果的影响。
图6为不同V形角下平板阻力系数以及减阻率变化曲线(来流速度固定为5m/s,沟槽间距s固定为0.1 mm)。其中CD为阻力系数,ζ为减阻率。其具体表达式为:

|
图 6 不同V形角下平板阻力系数和减阻率变化曲线 Fig. 6 Variation curve of plate resistance coefficient and drag reduction rate under different v-shaped angles |
| $\begin{aligned} {C_D} =& \frac{D}{{0.5 \cdot \rho \cdot {V^2} \cdot {L_0}^2}} , \\ \zeta =&\frac{{D}_{光滑平板}\text-{D}_{凹槽平板}}{{D}_{光滑平板}}\times 100\text{%} 。\end{aligned}$ | (6) |
其中:L0为特征长度,L0=400 mm;V为特征来流速度,V=为5 m/s;ρ为流体介质速度,ρ=998.2 kg/m3。
可以看出,沟槽平板的阻力系数随着V形角度的增加呈现出逐渐增大的趋势,对应的减阻率则随着V形角度的增加则逐渐减小,这意味着V形角度过大不利于减小流动阻力。
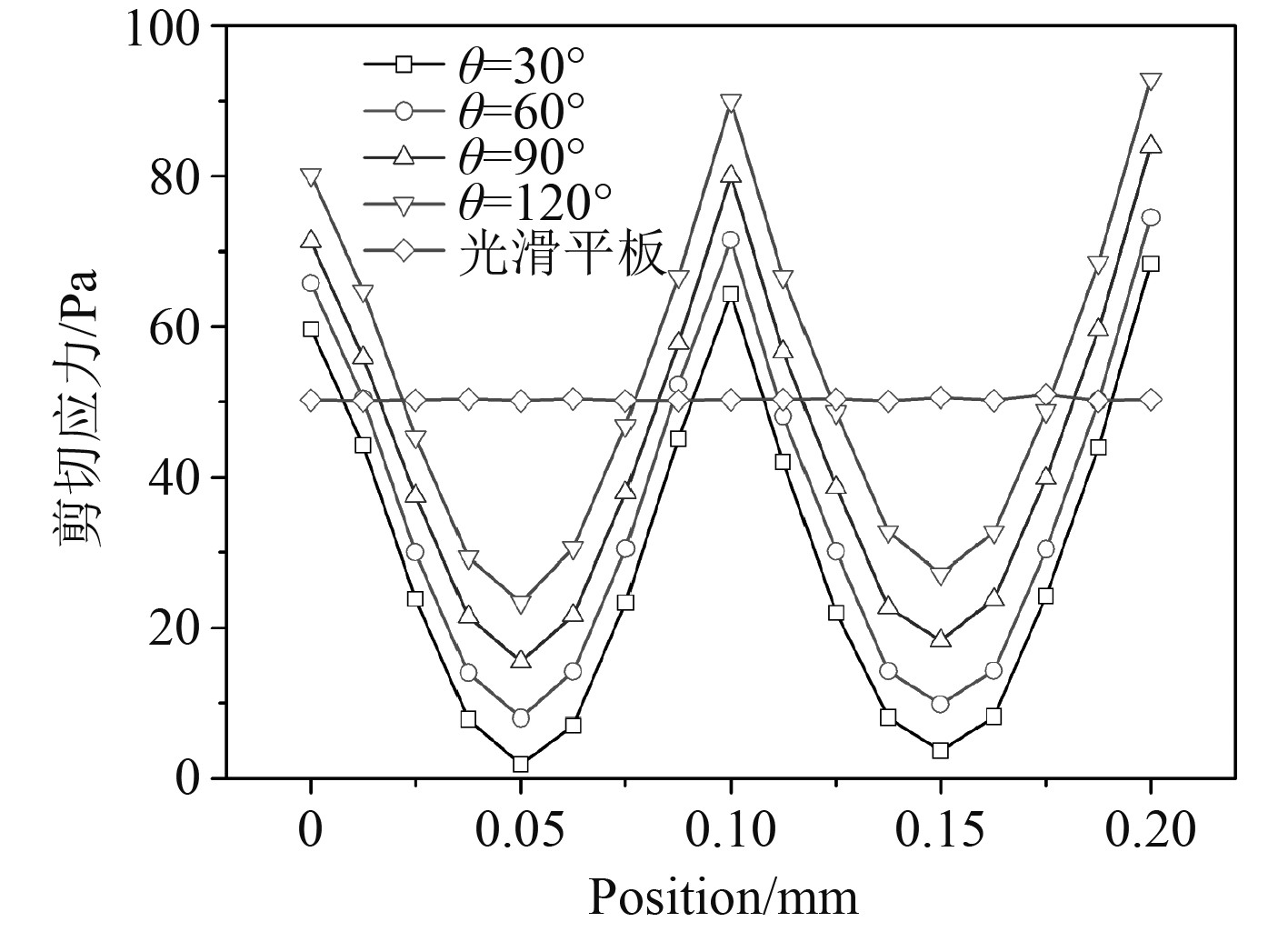
图7 为不同角度下带沟槽平板表面的剪切应力云图,可以看出不同V形角下平板表面剪切应力变化趋势与几何形状是一致的,即在谷顶取得剪切应力的最大值,在谷底取得剪切应力的最小值。不同之处在于V形角越大,剪切应力值亦呈现逐渐增大的趋势,对应的凹槽底部的低应力趋于亦逐渐增加,因此总的阻力呈现逐渐增大的趋势。
|
图 7 不同V形角下平板剪切应力变化曲线 Fig. 7 Shear stress variation curve of flat plate under different V-shaped angles |
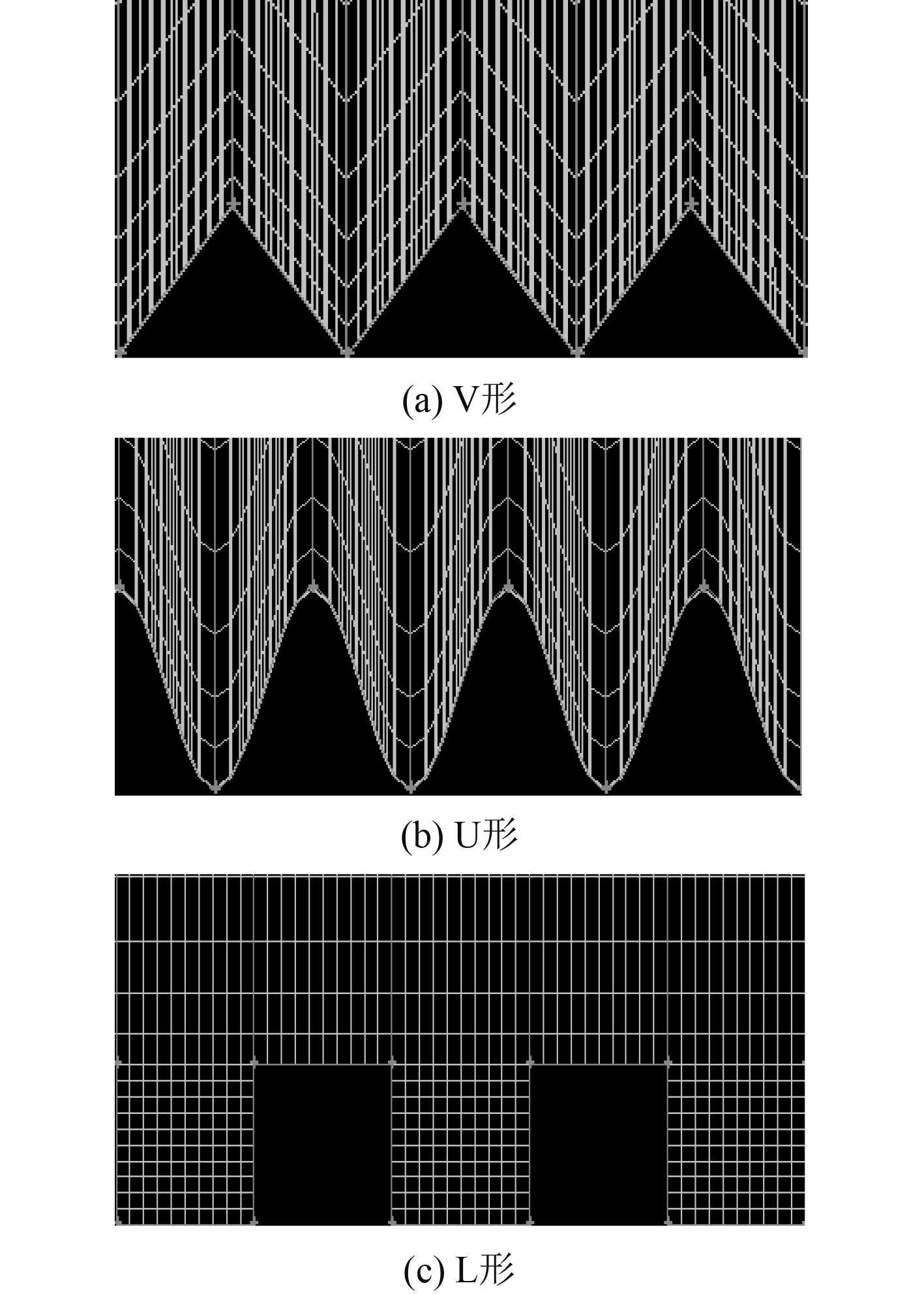
分别选取V形、U形和L形3种不同沟槽形状下的平板进行数值模拟,用于探讨不同沟槽形状下沟槽平板的减阻特性。3种沟槽的几何形状以如图8所示,沟槽深度和高度值相同,即s = h= 0.1 mm。
|
图 8 三种沟槽剖面示意图 Fig. 8 Schematic diagram of three types of groove profiles |
取相同的网格划分参数(y+ = 1)和边界条件, 不同来流速度下3种沟槽形状的平板阻力系数值如表2所示。可以看出,3种不同沟槽形状的平板在不同来流速度下均起到了减阻的作用且V形的减阻效果最优,L形减阻效果最差。
|
|
表 2 不同来流速度下3种沟槽形状的平板阻力系数值 Tab.2 Numerical values of resistance coefficients for three different groove shapes of flat plates under different inflow velocities |
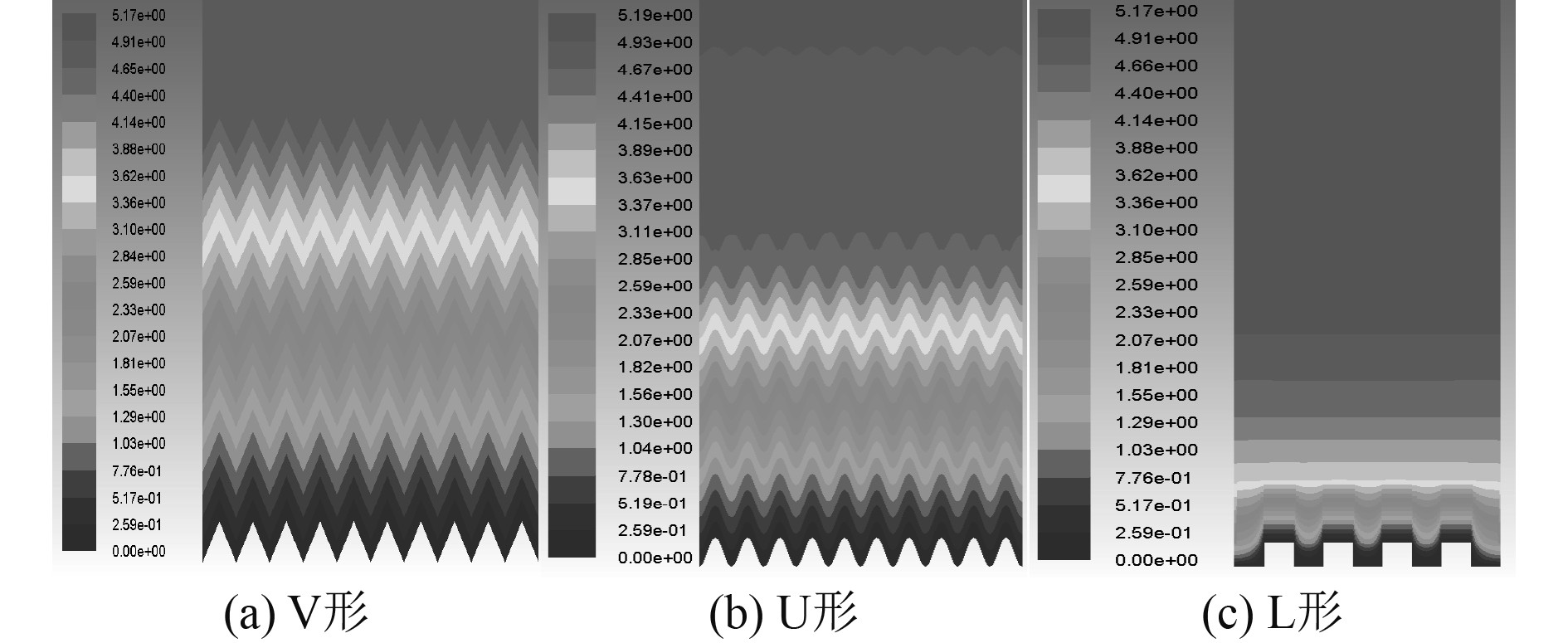
图9为不同剖面形状微沟槽平板附近的剪切应力云图。可以看出,沟槽平板几何形状为V型时,其剪切应力值最小,因此减阻性能最优。对于L 形表面和U形表面,U形沟槽表面的剪切应力区域要比 L形沟槽大,因此U形沟槽表面的阻力性能要优于L形沟槽。
|
图 9 三种不同沟槽形状平板附近流向速度云图 Fig. 9 Cloud images of flow velocity near three different groove shapes of flat plates |
本文借助Ansys开展平板仿生沟槽表面减阻性能数值模拟研究,相关结论如下:
1)微沟槽表面的平板可以起到减阻的作用。其减阻机理在于沟槽表面的引入有助于降低平板表面的速度梯度,且边界层厚度亦有所增大,因此阻力值有所减小。
2)通过对比分析3种不同沟槽形状的平板的减阻性能发现V形沟槽的减阻性能较U形和L形减阻性能更优,在后续设计中可考虑V形沟槽。
| [1] |
许春晓. 壁湍流相干结构和减阻控制机理研究[J]. 力学与实践, 2015, 37(3): 460-467. |
| [2] |
陈瑞芳, 江志东, 吴嘉. 高分子减阻流场湍流结构试验研究[J]. 大连理工大学学报, 1998, 38(5): 525-529. |
| [3] |
刘宝胜, 吴为, 曾元松. 鲨鱼皮仿生结构应用及制造技术综述[J]. 塑性工程学报, 2014, 21(4): 56-62. DOI:10.3969/j.issn.1007-2012.2014.04.012 |
| [4] |
黄乐萍, 范宝春, 董 刚. 槽道湍流壁面展向周期振动减阻机理研究[J]. 南京理工大学学报(自然科学版), 2010, 34(3): 361-366. |
| [5] |
葛铭纬. 基于近壁相干结构的湍流减阻主动控制研究[D]. 北京: 清华大学, 2011.
|
 2023, Vol. 45
2023, Vol. 45
