为保证设备正常运行,航行器在水下运动过程中会利用冷却水吸收设备运行所产生的热量,冷却水排出后形成热射流[1-4],并与环境流体掺混换热。
国内外学者对热射流相关特征进行了大量的实验及仿真研究。张旭升等[5]系统分析了航行器附体结构运动、热射流排放流量、热射流排放速度、环境流体温度分层、盐度分层、热射流排放温度等初始运动结构参数对水下航行器热射流温度扩散及浮升特性的影响。来庆志等[6]对仿真计算壁面条件的差异进行了分析。在不同壁面条件下的水下航行器热射流在浮升扩散过程中,不仅浮升高度不同,浮升扩散的速度也不一样。刘洋等[7]通过研究发现,热射流扩散过程中,存在涡动特性,运动产生的涡流会对热射流水面红外特征产生明显影响。仿真结果表明,热射流在排放过程中,不仅有由于热量传递所产生的温度特征,还有在热射流掺混运动过程中造成的水动力特征。周哲等[8]采用了不同于来流法的温度差值法计算热射流温度变化特征,对比了不同工况下热射流温度衰减特征的差异,结果表明温度插值法可以精确得到尾流的细微变化,仿真精度更高。从上述研究可知,有关热射流特征及变化过程的研究十分完善,但未对排放口结构在热射流特征中的影响进行深入探讨。
一般来说,水下航行器热射流排放口为圆形结构,圆形排放口制造简单,经济实用,但不同结构排放口是否对热射流特征产生影响,相关研究尚不充足。与单孔排放口相比,多孔结构可以使得单股热射流分为多股热射流,加强热射流与环境流体掺混换热效果。肖洋等[9]通过Fluent模拟计算得到当多孔射流孔间距增大时,位于后方的射流速度损失较小,与环境流体掺混效果越快。高猛等[10]对多孔射流的分叉及融合现象进行了详细研究,阐述了多孔结构排放口射流问题的特点。但上述研究对多孔结构分孔形状没有进行深入考虑,对分孔分布位置考虑简单。朱科铃等[11]采用PIV技术对小间距多孔射流流场特性进行了研究,区别于间距较大射流,当多孔射流之间孔间距较小时,射流雷诺数发生变化。郑亚男等[12]对平板多孔射流形成的旋涡结构特征进行了研究,结果表明,多孔射流的发展变化产生强脉动特性,壁面边界层出现尾迹涡结构。但该研究未对射流温度特性展开探讨。本文重点围绕排放口结构,对排放口数量及分布方式进行设计,得到最有利于抑制热射流红外特征的排放口结构,为工业设计制造提供理论研究思路。
1 物理方程及模型流体运动的复杂性由流体本身特性所决定,流体的惯性、流体的可压缩性、流体的黏性等使得如何描述、测量流体运动变得较为困难。再加上流体运动是否为定常或非定常流动,有旋或无旋流动,层流或湍流流动等,这些流动特点同样导致了流体运动的复杂性。根据流体运动的物理特性,数学家和物理学家们以数学表达的形式建立了流体运动的相关方程组用以描述流体运动。
1) 质量守恒方程
| $ \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_j}k} \right)}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _{\text{k}}}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k}{\kern 1pt} {\kern 1pt} + {G_b} - \rho \varepsilon。$ | (1) |
2)动量守恒方程
| $\begin{aligned} & \rho \frac{{\partial {u_i}}}{{\partial t}} + \rho {u_j}\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial p}}{{\partial {x_i}}} - \left( {{\rho _0} - \rho } \right){g_i} =\\ & \frac{\partial }{{\partial {x_j}}}\left[ {\mu \left( {\frac{{\partial {u_i}}}{{\partial{u_j}}} + \frac{{\partial {u_j}}}{{\partial {u_i}}}} \right)} \right] - \frac{2}{3}\frac{\partial }{{\partial {x_i}}}\left( {\mu \frac{{\partial {u_j}}}{{\partial {x_j}}}} \right)。\end{aligned}$ | (2) |
式中,ρ0为环境流体密度。
3)能量守恒方程
| $ \rho {c_p}\frac{{\partial T}}{{\partial t}} + \rho {c_p}{u_j}\frac{{\partial T}}{{\partial {x_j}}} = {u_j}\frac{{\partial p}}{{\partial {x_j}}} + \frac{\partial }{{\partial {x_j}}}\left( {\lambda \frac{{\partial T}}{{\partial {x_j}}}} \right)。$ | (3) |
式中:
受温度影响,环境水体密度状态方程为:
| $ \rho (T) = - 6.71 + 9.119T - 0.02645{T^2} + 2.399 \times {10^{ - 5}}{T^3},$ | (4) |
选择Realizable k-ε模型将湍流的脉动值附加项与时均值联系起来。
湍动能k方程:
| $ \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_j}k} \right)}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _{\text{k}}}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k}{\kern 1pt} {\kern 1pt} + {G_b} - \rho \varepsilon,$ | (5) |
耗散率ε方程:
| $ \begin{split} \frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_j}\varepsilon } \right)}}{{\partial {x_j}}} =& \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _{{\varepsilon }}}}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \rho {C_1}S\varepsilon -\\ &\rho {{{C}}_{\text{2}}}\frac{{{\varepsilon ^2}}}{{k + \sqrt {\nu \varepsilon } }} + {{\text{C}}_{{{1\varepsilon }}}}\frac{\varepsilon }{k}{C_{3\varepsilon }}{G_b}。\end{split} $ | (6) |
式中:
| $ {{\text{C}}_{{{1\varepsilon }}}}{\text{ = 1}}{\text{.44}} \text{,} {{\text{C}}_{\text{2}}}{\text{ = }}1.9\text{,}{\sigma _k}{\text{ = }}1.0\text{,}{\sigma _{{\varepsilon }}}{\text{ = }}1.2。$ |
| $\begin{split} & {C_1} = \max \left[ {0.43,\frac{1}{{\eta + 5}}} \right]\text{,}\eta {\text{ = }}S\frac{k}{\varepsilon }\text{,}\\ & S = \sqrt {2{S_{ij}}{S_{ij}}} \text{,}{C_{3\varepsilon }} = \tanh \left| {\frac{v}{u}} \right|。\end{split}$ | (7) |
式中:v为平行于重力矢量的速度分量;u为垂直于重力矢量的速度分量。
| $ {\mu _t} = \rho {C_\mu }\frac{{{k^2}}}{\varepsilon }。$ | (8) |
式中:
| $ {C_\mu } = \frac{1}{{{A_0} + {A_s}\frac{{k{U^*}}}{\varepsilon }}} 。$ | (9) |
式中:
| $ {{\text{A}}_{\text{0}}} = 4.04,{A_s} = \sqrt 6 \cos \varphi,{U^*} \equiv \sqrt {{s_{ij}}{s_{ij}} + {{\tilde \Omega }_{ij}}{{\tilde \Omega }_{ij}}},$ |
| $\begin{aligned} & \varphi = \frac{1}{3}{\cos ^{ - 1}}\left( {\sqrt 6 W} \right),W = \frac{{{s_{ij}} + {s_{jk}} + {s_{ki}}}}{{{{\tilde s}^3}}},\\ & W = \frac{{{s_{ij}} + {s_{jk}} + {s_{ki}}}}{{{{\tilde s}^3}}},{s_{ij}} = \frac{1}{2}\left( {\frac{{{\rm{\partial}} {u_j}}}{{{\rm{\partial}} {x_i}}} + \frac{{{\rm{\partial}} {u_i}}}{{{\rm{\partial}} {x_j}}}} \right)。\end{aligned} $ |
式中,
流体计算域长宽高为8 m×1.1 m×0.5 m,水下航行器距离流体计算域左侧来流面100 mm,距离右侧出流面7000 mm,距离底部100 mm,距离顶部300 mm(距离水面200 mm),距离后部300 mm,距离前部700 mm。采用非结构化网格进行划分,在局部尺寸上,对排放口、航行器表面以及局部加密实体区域进行限制,网格类型采用多面体混六面体网格类型。网格划分完成后如图1所示。

|
图 1 流体计算域网格划分示意图 Fig. 1 Schematic diagram of fluid computing domain grid division |

|
图 2 单孔及多孔排放口网格划分 Fig. 2 Single discharge port and multiport discharge port meshing |
在边界条件的设置上,排放口(hot)为速度入口边界条件(velocity-inlet);航行器表面(wall)为非计算边界条件(dead);来流面(in)为速度入口边界条件(velocity-inlet);出流面(out)为压力出口边界条件(pressure-outlet);流体计算域顶部(top)为压力出口边界条件(pressure-outlet);流体计算域其余面(wallw)为对称边界条件(symmetry)。来流面设置环境流体来流温度293 K,来流速度0.1 m/s;排放口设置热射流初始温度333 K,热射流初始速度0.3 m/s。
在求解设置中,考虑到水下航行器热射流水面红外特征,在流体计算域中划分出空气层,对气液交界层采用VOF流体体积函数进行追踪,水面上的空气层厚度为100 mm。采用基于有限体积法思想的SIMPLE算法,Solver类型为Pressure-Based,时间属性上采用Transient。同时将重力作用对流体运动的影响体现在求解过程中。关于计算求解的可靠性要求体现在对各参数收敛残差的限制上,能量残差的收敛数量级要小于10−7,其余各参数残差的收敛数量级要小于10−4。计算过程中达到残差收敛要求可认为计算求解结果可靠。
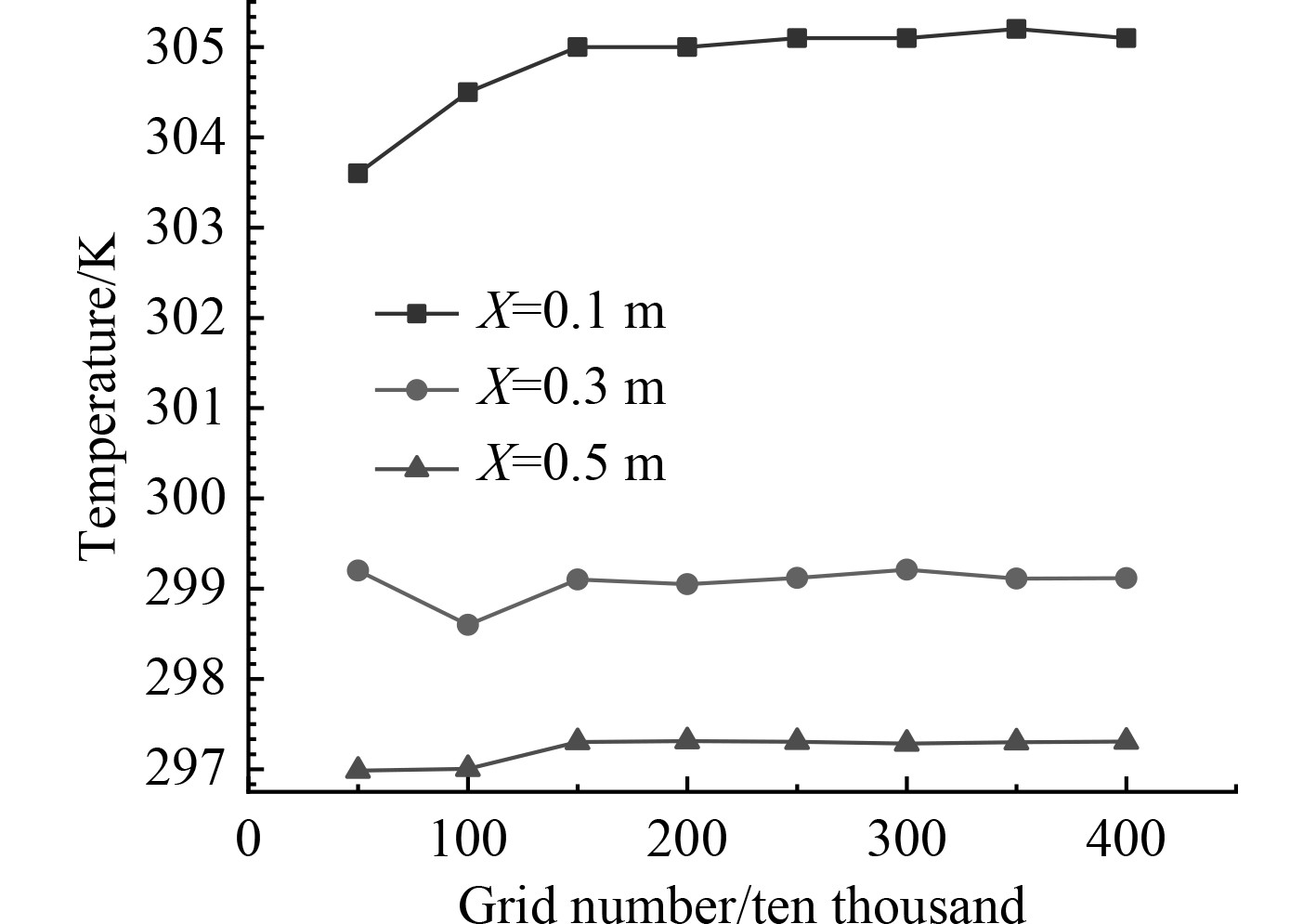
为消除网格数量对计算结果的影响,选取热射流距排放口中心水平距离0.1 m,0.3 m,0.5 m处中心最高温度值作为验证数据,对比验证相同位置、不同网格数量条件下,水下航行器热射流中心最高温度。验证结果如图3所示。图中数据表明,当网格数量超过100万时,热射流在距离排放口中心不同距离处中心最高温度值较为一致,误差值较小,在0.01 K以内。因此在设置网格尺寸时,将网格数量控制在150万左右较为合适。
|
图 3 网格无关性验证 Fig. 3 Grid independence test |
在空间维度中,以排放口中心为坐标原点,环境流体流动方向为X轴负方向,热射流排出方向为Y轴正方向,重力方向为Z
在单孔、横式双孔、横式三孔排放口作用下,水下航行器热射流在来流方向上温度衰减水平距离以及在重力方向上温度衰减浮升高度如图4所示。

|
图 4 横式排列排放口热射流温度衰减特征曲线 Fig. 4 Temperature attenuation indicatrix of thermal jet from heng discharge ports |
从图中数据分析可知,单孔、横式双孔、横式三孔排放口作用下热射流在来流方向上最大温度衰减水平距离分别为2.910 m,2.958 m,2.683 m,在重力方向上最大温度衰减浮升高度均为0.164 m。与单孔排放口作用相比,横式双孔、三孔排放口作用下热射流最大温度衰减水平距离分布增加1.65%,减少7.80%;3种排放口作用下热射流最大温度衰减浮升高度相同。由于排放口本身具有一定的宽度,所以不同结构排放口排出热射流在初始高度上有所不同,单孔、横式双孔、横式三孔排放口半宽分别为4 mm,6.16 mm,7.93 mm,但最大浮升高度均为0.164 m,体现出分孔热射流之间相互吸附作用抑制了热射流向上浮升的趋势。
在水下航行器排放口附近壳体表面绘制速度矢量图,以温度为区分条件的横式排列排放口局部速度特征如图5所示。

|
图 5 横式排列排放口热射流局部速度矢量图 Fig. 5 Local velocity vector diagram of thermal jet from heng discharge ports |
可以看出,分孔热射流之间相互吸附作用导致环境流体无法很好地在排放口间隙与热射流掺混换热。在单孔、横式双孔、横式三孔排放口作用下,热射流与环境流体掺混换热接触面周长分别为241.080 mm,188.268 mm,168.278 mm,掺混换热效果逐渐下降。
横式排列排放口作用下水下航行器热射流水面红外特征如图6所示。

|
图 6 横式排列排放口热射流水面红外特征 Fig. 6 Surface temperature contour of thermal jet from heng discharge ports |
可以看出,单孔、横式双孔、横式三孔排放口作用下热射流在自由液面上水面最高峰值温度分别为293.071 K,293.128 K,293.126 K,热射流温度在自由液面上横向扩散最大距离分别为2.152 m,2.162 m,1.750 m,纵向扩散最大距离分别为0.521 m,0.663 m,0.614 m。与单孔排放口作用下热射流水面红外特征相比,横式双孔、三孔排放口作用下热射流在自由液面上水面最高峰值温度分别提高了80.28%,77.46%;热射流温度在自由液面上横向扩散最大距离分别增加了6.58%、减少了18.68%,纵向扩散最大距离分别增加了27.26%,17.85%。分析可知,横式排列排放口不利于抑制热射流水面红外特征。
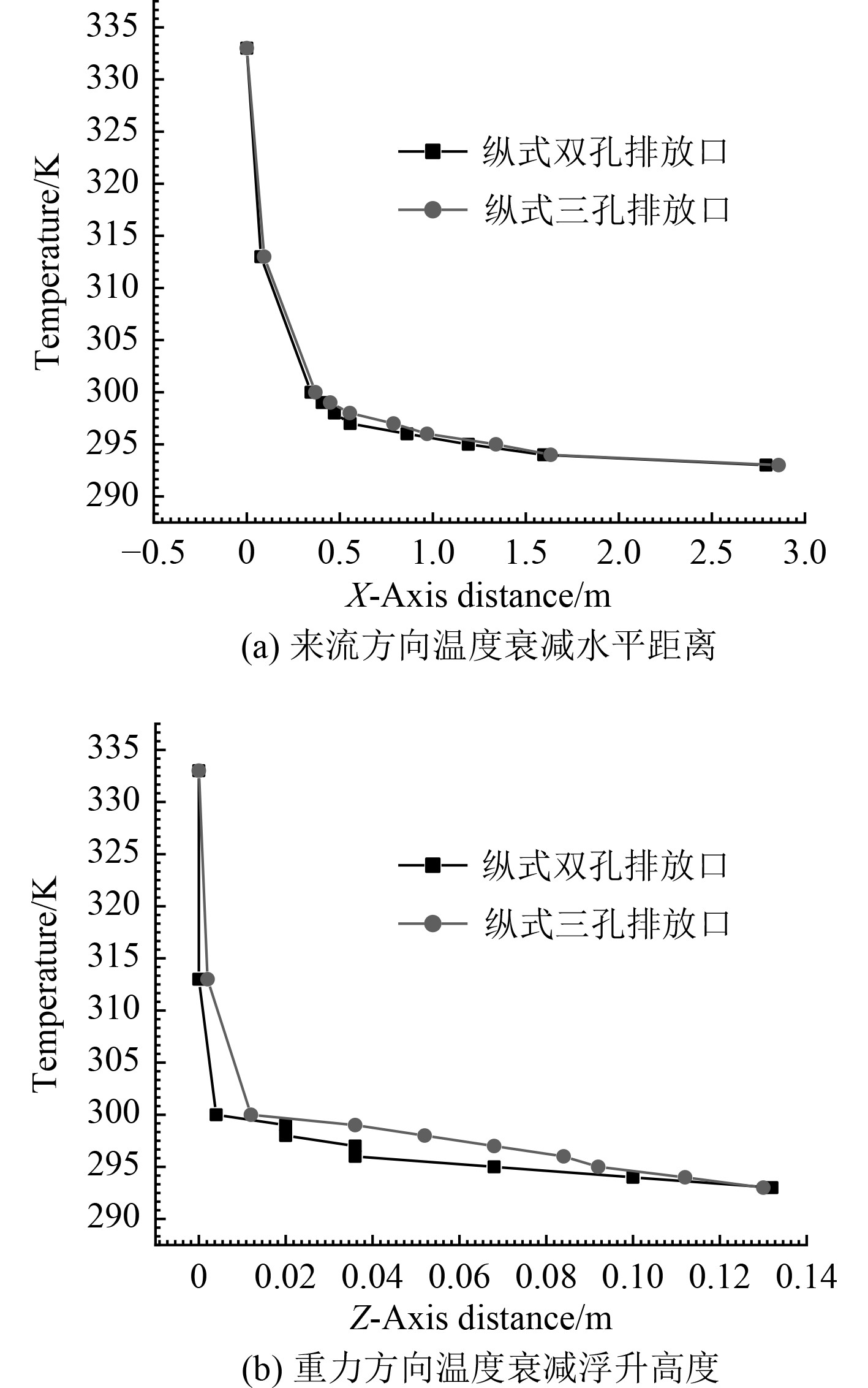
3.2 纵式排列排放口在纵式双孔、三孔排放口作用下,水下航行器热射流在来流方向上温度衰减水平距离以及在重力方向上温度衰减浮升高度如图7所示。
|
图 7 纵式排列排放口热射流温度衰减特征曲线 Fig. 7 Temperature attenuation indicatrix of thermal jet from zong discharge ports |
从图中数据分析可知,纵式双孔、三孔排放口作用下热射流在来流方向上最大温度衰减水平距离分别为2.791 m,2.859 m,在重力方向上最大温度衰减浮升高度分别为0.132 m,0.130 m。与单孔排放口作用相比,纵式双孔、三孔排放口作用下热射流最大温度衰减水平距离分别减少4.09%,1.75%;最大浮升高度分别降低19.51%,20.73%。纵式排列排放口作用下,水下航行器热射流温度衰减过程加快。
在水下航行器排放口附近壳体表面绘制速度矢量图,以温度为区分条件的纵式排列排放口局部速度特征如图8所示。

|
图 8 纵式排列排放口热射流局部速度矢量图 Fig. 8 Local velocity vector diagram of thermal jet from zong discharge ports |
纵式排列排放口分孔间隙处接触面较小,分孔热射流之间相互吸附作用受到限制,与横式排列排放口相比,热射流与环境流体在排放口分孔间隙处掺混换热效果大大增强。纵式双孔、三孔排放口作用下热射流与环境流体掺混换热接触面周长分别为340.973 mm,417.748 mm,均大于单孔排放口作用下241.080 mm的接触面周长,掺混换热效果明显提升。
纵式排列排放口作用下水下航行器热射流水面红外特征如图9所示。

|
图 9 纵式排列排放口热射流水面红外特征 Fig. 9 Surface temperature contour of thermal jet from zong discharge ports |
可以看出,纵式双孔、三孔排放口作用下热射流在自由液面上水面最高峰值温度分别为293.050 K,293.046 K,热射流温度在自由液面上横向扩散最大距离分别为1.733 m,1.872 m,纵向扩散最大距离分别为0.459 m,0.533 m。与单孔排放口作用下热射流水面红外特征相比,纵式双孔、三孔排放口作用下热射流在自由液面上水面最高峰值温度分别降低了29.58%,35.21%;热射流温度在自由液面上横向扩散最大距离分别减少了19.47%,13.01%,纵向扩散最大距离分别减少了11.90%、增加了2.30%。由此可知,纵式排列排放口有效抑制了热射流水面红外特征。
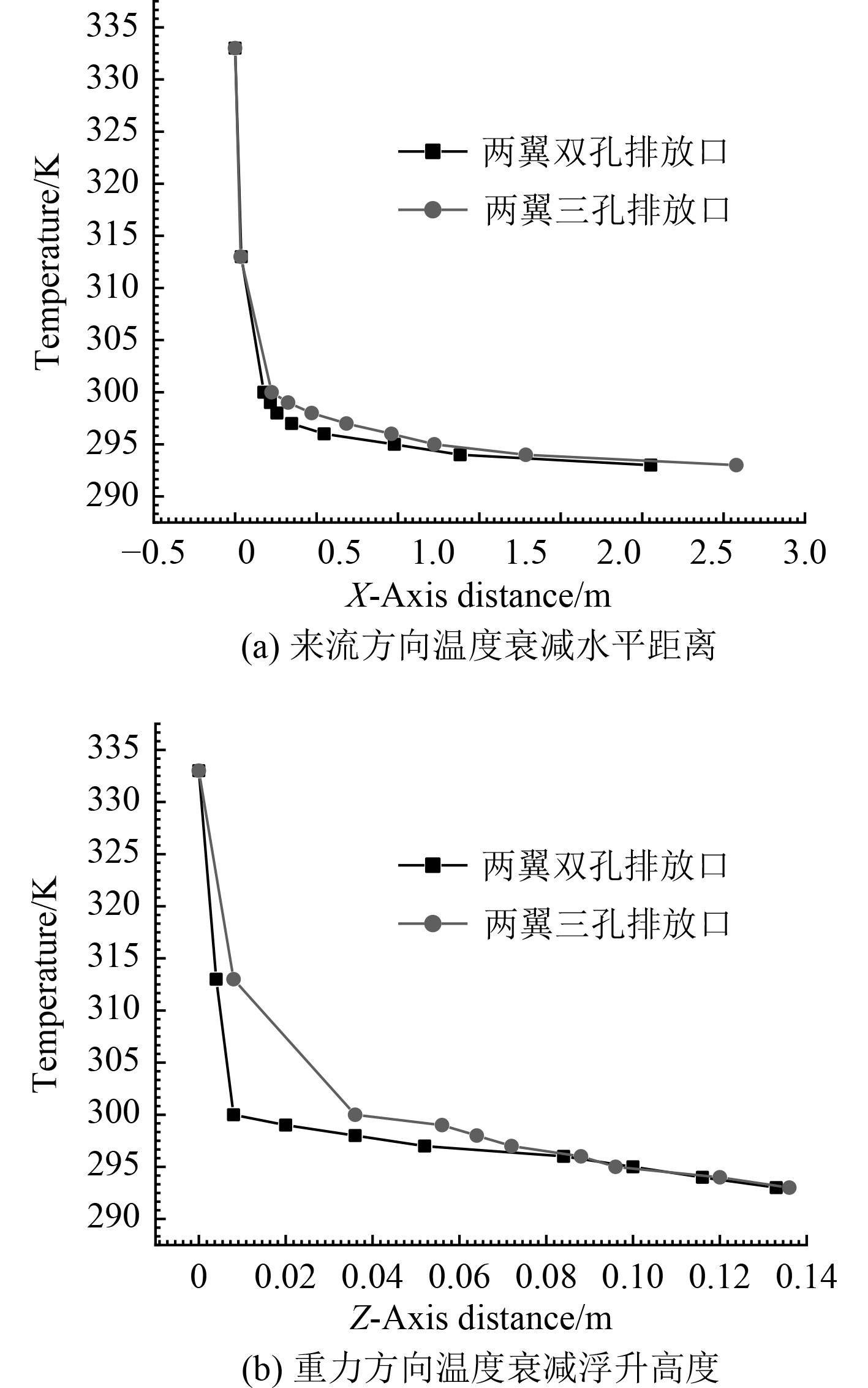
3.3 两翼排列排放口在两翼双孔、三孔排放口作用下,水下航行器热射流在来流方向上的温度衰减水平距离以及在重力方向上的温度衰减浮升高度如图10所示。
|
图 10 两翼排列排放口热射流温度衰减特征曲线 Fig. 10 Temperature attenuation indicatrix of thermal jet from symmetrical discharge ports |
从图中数据分析可知,两翼双孔、三孔排放口作用下热射流在来流方向上最大温度衰减水平距离分别为2.533 m,3.079 m,在重力方向上最大温度衰减浮升高度分别为0.133 m,0.136 m。与单孔排放口作用相比,两翼双孔、三孔排放口作用下最大温度衰减水平距离分别减少了12.27%、增加了5.81%;最大浮升高度分别降低了18.90%,17.07%。
在水下航行器排放口附近壳体表面绘制速度矢量图,以温度为区分条件的两翼排列排放口局部速度特征如图11所示。

|
图 11 两翼排列排放口热射流局部速度矢量图 Fig. 11 Local velocity vector diagram of thermal jet from symmetrical discharge ports |
可以看出,两翼排列排放口与横式、纵式排列排放口在结构上的差异主要体现在分孔之间相互吸附作用消失。在热射流与环境流体掺混换热接触面上则与纵式排列排放口保持一致,均为分孔结构下掺混换热接触面周长最大的排放口结构。在掺混换热效果上,两翼排列排放口作用与纵式排列排放口作用较为一致。
两翼排列排放口作用下水下航行器热射流水面红外特征如图12所示。

|
图 12 两翼排列排放口热射流水面红外特征 Fig. 12 Surface temperature contour of thermal jet from symmetrical discharge ports |
可以看出,两翼双孔、三孔排放口作用下热射流在自由液面上水面最高峰值温度分别为293.052 K,293.045 K,热射流温度在自由液面上横向扩散最大距离分别为1.113 m,1.469 m,纵向扩散最大距离分别为0.579 m,0.660 m。与单孔排放口作用下热射流水面红外特征相比,两翼双孔、三孔排放口作用下热射流在自由液面上水面最高峰值温度分别降低26.76%,36.62%;热射流温度在自由液面上横向扩散最大距离分别减少19.47%,31.74%,纵向扩散最大距离分别增加11.13%,26.68%。
4 结 语通过对多孔排放口作用下水下航行器热射流排出过程进行相关仿真模拟计算,并对计算结果进行分析得到如下结论:
1) 与单孔排放口作用相比,多孔排放口作用增大了热射流与环境流体掺混换热接触面,提升了热射流与环境流体掺混换热效果;
2) 多孔结构下纵式排列及两翼排列排放口有利于抑制热射流红外特征,提升水下航行器热隐身性能;
3)多孔结构下相邻分孔热射流之间出现相互吸附现象,在一定程度上抑制热射流温度衰减过程。同时,分孔之间相互吸附作用也在一定程度上阻碍热射流向上浮升过程。
通过本文研究发现,多孔排放口结构作用对提升热射流与环境流体掺混换热效果,减弱热射流红外特征,降低水下航行器暴露风险有明显作用,为工业设计制造提供新思路。
| [1] |
VOROPAYEV S I, FERNANDO H J S, SMIRNOV S A, et al. On surface signatures generated by submerged momentum sources[J]. Physics of Fluids, 2007, 19(7): 076603. DOI:10.1063/1.2749713 |
| [2] |
VOROPAYEV S I, FERNANDO H J S, NATH C. Thermal and dynamic surface signatures of the wake of a submerged sphere[J]. Journal of Visualization, 2009, 12(4): 285-285. DOI:10.1007/BF03181868 |
| [3] |
VOROPAYEV S I, NATH C, FERNANDO H J S. Thermal surface signatures of ship propeller wakes in stratified waters[J]. Physics of Fluids, 2012, 24(11): 469-266. |
| [4] |
VOROPAYEV S I, NATH C, FERNANDO H J S. Surface signatures of submerged heated jet[J]. Environ Fluid Mech, 2014, 14(5): 1105-1121. DOI:10.1007/s10652-013-9301-8 |
| [5] |
张旭升, 郭亮, 胡日查, 等. 潜艇热尾流的浮升扩散规律及海表温度特性[J]. 红外技术, 2016, 38(8): 678-682. |
| [6] |
来庆志, 王成安, 谭建宇, 等. 基于三维动网格技术的潜艇热尾流浮升规律及水面温度特征研究[J]. 舰船科学技术, 2018, 40(5): 8-13. |
| [7] |
刘洋, 朱飞定, 谭佩钰, 等. 潜艇水动力尾迹与热尾迹耦合作用的数值模拟[J]. 红外技术, 2018, 40(1): 62-67. |
| [8] |
周哲, 白宗良, 史径丞, 等. 基于温度插值技术的潜艇热尾流浮升规律及海面热特征仿真方法研究[J]. 红外技术, 2019, 41(11): 1039-1046. |
| [9] |
肖洋, 梁嘉斌, 李志伟. 射流孔间距对横流中两孔射流稀释特性的影响[J]. 水利水电科技进展, 2016, 36(3): 20-25. |
| [10] |
高猛, 槐文信, 曾玉红. 横流中垂直出流式多孔射流稀释特性研究[J]. 华中科技大学学报(自然科学版), 2018, 46(6): 94-98. DOI:10.13245/j.hust.180617 |
| [11] |
朱科铃, 李美香, 蔡婷婷, 等. 小间距多孔受限射流流场特性实验研究[J]. 常州大学学报(自然科学版), 2019, 31(1): 35-40. |
| [12] |
郑亚男, 王国玉, 吕亚飞, 等. 平板多孔气-液两相横射流流场特性研究[C]. 第三十二届全国水动力学研讨会文集, 2020.
|
 2023, Vol. 45
2023, Vol. 45
