2. 北京质远恒峰科技有限公司,北京 100010
2. ZYE ver TOP Technology Co. Ltd., Beijing 100010, China
通用质量特性指标是装备寿命周期管理的重要对象,贯穿于装备论证、设计、生产、使用和退役报废的各个阶段。通用质量特性指标研究包括指标论证、分配、验证与评估等多项内容,其管理水平直接影响武器装备的作战效能发挥[1-3]。在装备综合保障的体系中,作战需求牵引着装备的发展和运用、保障系统的设计与运行,而保障系统则会影响装备系统的作战效能发挥。从本质上讲,通用质量特性指标论证与优化,是在把握装备作战任务要求的基础上,对装备各项性能和保障系统设计的论证与优化,通用质量特性指标评估是对保障对象和保障系统及其适用性的度量,是指标论证与优化的重要手段。因此,通用质量特性指标论证的科学性与评估的准确性对于装备发展论证、迭代设计、作战使用等有着重要作用。
舰载机作为航母编队的主要战斗单元,其作战效能的发挥对航母体系的影响至关重要。但影响舰载机作战适用性的因素较多,舰载机在使用过程中受到恶劣的自然环境和苛刻的平台环境影响,存在2项主要矛盾:一是高可靠要求与高故障率之间的矛盾[4-8],二是快速出动能力与强舰基约束之间的矛盾。前者主要指高温、高盐、高湿的海洋环境易导致舰载机机体和机载产品发生故障与舰载机高可靠要求之间的矛盾;后者主要体现在舰面有限空间约束、母舰多自由度运动与舰载机保障作业流程复杂、保障强度高之间的矛盾。为了解决这两项矛盾,就需要在装备设计之初对装备的各项通用质量特性指标进行科学论证,从而以各项指标为依据规划装备全系统全寿命周期的管理工作。
目前通用质量特性指标论证与优化方法主要有解析和建模仿真两类。解析方法主要有经典的概率统计模型、模糊评判、贝叶斯分析等[7];建模仿真方法主要有系统动力学、离散事件、智能体仿真等[8-11]。解析方法主要针对单一指标的设计与分析,如在可靠性指标设计过程中如何将整机级可靠性指标向系统级、分系统级或者关键部件分配等。仿真方法可以实现多指标一体化论证,基于装备的总体效能要求对可靠性、维修性、保障性指标与作战性能等的统一论证,可根据仿真结果进行单项、多项指标的灵敏度分析,从而对指标在阈值范围内进行调整优化,这是以后指标论证与优化的主要趋势。但是目前在工程实践中,指标论证的顶层输入不够明确,即型号作战任务要求向装备作战性能与通用质量特性指标转化的定量分析方法不够完善。虽然近些年来,越来越重视装备的体系贡献率,但还不能将装备体系贡献率与装备通用质量特性论证的映射关系清晰表述[12]。体系贡献率涉及诸多不确定性因素,因为构成装备体系的各系统之间存在涌现性、非线性、随机性等特点,制约到装备体系贡献的度量与评估。
针对上述问题,设计面向作战任务的舰载机通用质量特性指标论证流程,构建论证模型和优化模型,并结合算例,说明设计方法的可行性,从而提高论证科学性与精确性。
1 面向作战任务的舰载机通用质量特性指标论证随着新型舰载机结构一体化、轻质化和隐身化等要求的提升,机载产品集成化、模块化、可测化的水平增强,要求新型舰载机具备可靠性高、故障自诊断能力强、环境适应性好、易于维护保障的特性,保证较高的作战适用性和舰机适配性。但舰载机在使用过程中受到自然环境、平台环境、保障系统等诸多因素的影响,保障作业过程中充斥着不确定性和随机性。为了提高舰载保障作业效率,提高舰载机的出动能力、任务可靠性和任务持续性,必须基于系统工程思想开展舰载机通用质量特性指标论证。
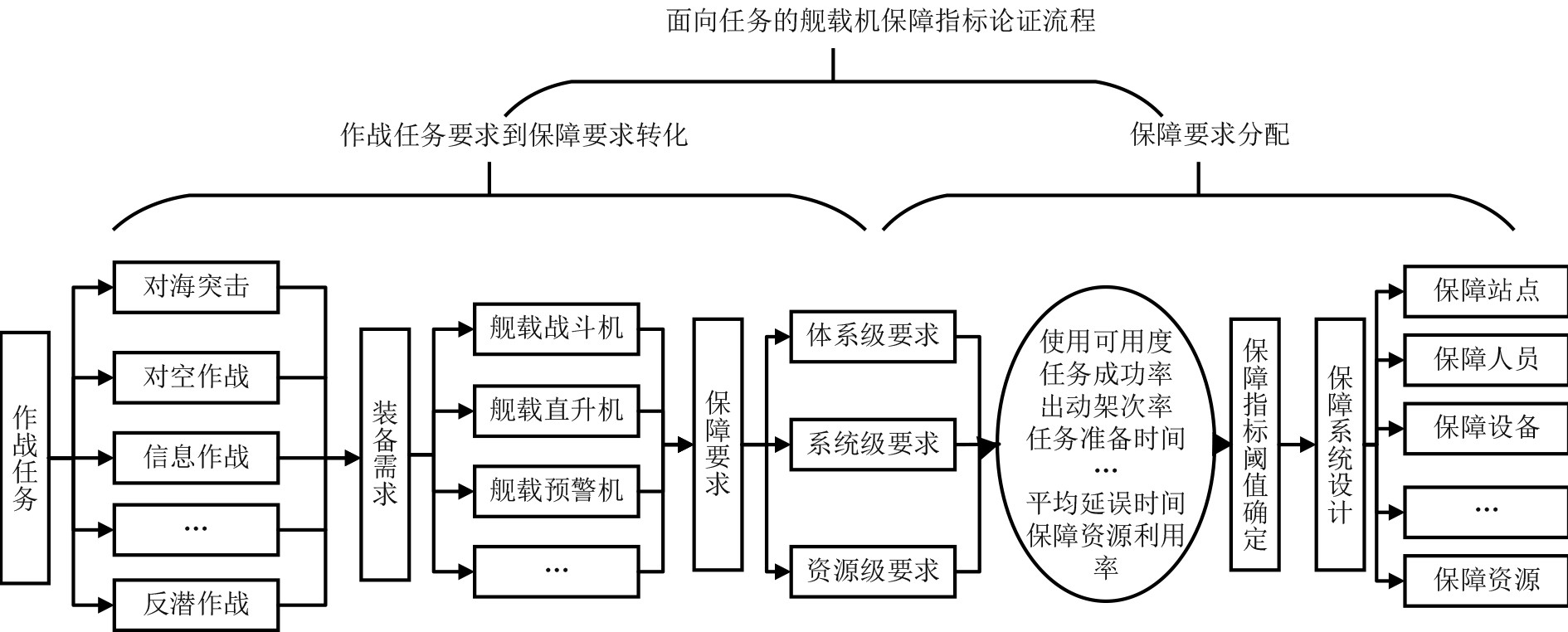
以航母编队和多机种舰载机的作战任务要求为顶层输入,以先进保障理论和技术体系为驱动,深入分析舰基保障平台和舰载机自身的结构与性能特征,明确舰载机的保障需求,论证舰机一体化的保障性指标体系。包括体系级、系统级和资源级指标(如使用可用度、任务成功率、出动架次率、平均延误时间、资源利用率等)以及各指标的性能阈值,根据指标要求进一步明确保障系统各要素的设计要求,如保障设备、信息系统、舰面接口数量、布局等的设计,从而做到舰机保障力量运用一体化、保障资源配置优化、信息资源共享化[1,8]。舰载机保障性指标论证总体流程如图1所示。
|
图 1 舰载机保障指标论证流程 Fig. 1 Demonstration process of carrier-based aircraft support indicators |
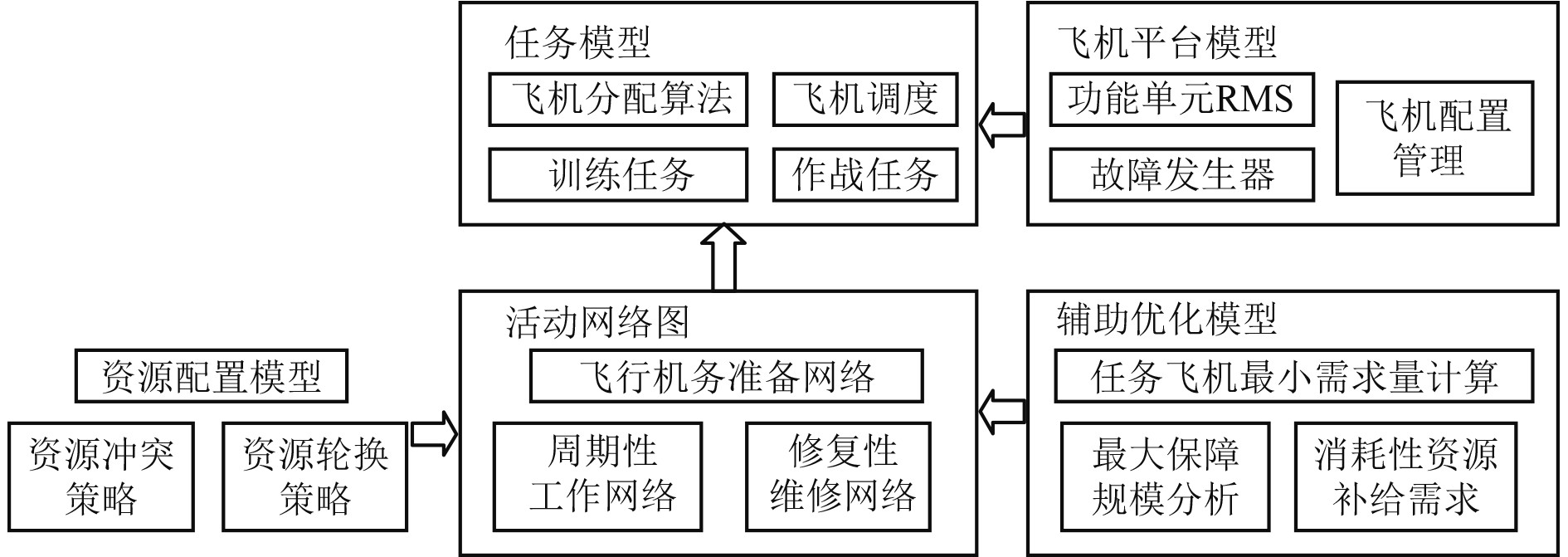
对舰基环境下舰载机使用与维修保障过程进行抽象描述,客观真实地构建由飞行任务和随机故障驱动的保障活动流程以及保障作业模型。舰载机的综合保障工作主要涉及了2类作业[1,8]:1)使用保障作业,如起降、调运、电气液保障、弹药保障等专项作业;2)维修保障作业:包括预防性维修与修复性维修作业。完成以上内容需构建出下列基本模型:不同机型舰载机(舰载战斗机、直升机、固定翼预警机等)的任务模型、飞机平台模型(舰载机的基本构型、RMS要求等)、活动网络图模型、保障资源模型和辅助优化模型等,其概念模型如图2所示。
|
图 2 舰载机保障流程建模的基本内容 Fig. 2 The basic content of carrier-based aircraft support process modeling |
在此基础上,基于离散事件建模的原理,采用ILSBox-Designer软件构建各类子模型。
2.1 任务模型任务模型用于对作战单元中装备所需执行的任务进行建模,其以作战与训练想定、装备使用方案为建模对象,以适当的形式表现任务发生、任务时序、任务之间逻辑关系、任务结构等内容,模型中包括装备数量、任务时间、任务强度等。
2.2 装备模型装备模型用于对装备种类、数量、构型以及各功能单元的通用质量特性数据进行建模,是描述装备及其组成单元特性的模型。
2.3 保障资源模型保障资源模型以表单方式对人员、备件、设备等保障资源进行建模,描述保障资源的种类、数量、库存、供应及使用机制等。
2.4 保障组织模型保障组织包括了基层级,中继级和库房等站点和相互间的保障关系。
2.5 保障活动模型保障过程模型使用活动网络图技术,将装备使用维护过程中的各类工作进行建模,支持装备的使用保障、修复性维修保障、预防性维修保障等保障活动的构建。
3 面向保障效能的保障指标优化在舰面作业空间、保障资源等各类约束下,需要对舰载机进行专项使用保障或维修保障,从而为执行作战任务做好准备。舰载机保障过程是一个确定性与随机性相结合的动态过程,具有动态与不平衡的特征,保障过程中涉及到多架舰载机、多种保障资源在多个作业阶段、多个保障站点之间的有效协调[8,10]。针对保障指标的确定性和保障过程与保障环境的随机性与不确定性,综合运用解析与离散事件仿真方法构建舰载机保障指标论证的技术框架,根据仿真结果对保障要素的灵敏度进行分析,并适当调整保障系统的配置,实现保障资源的精确化与保障作业活动的快速化。
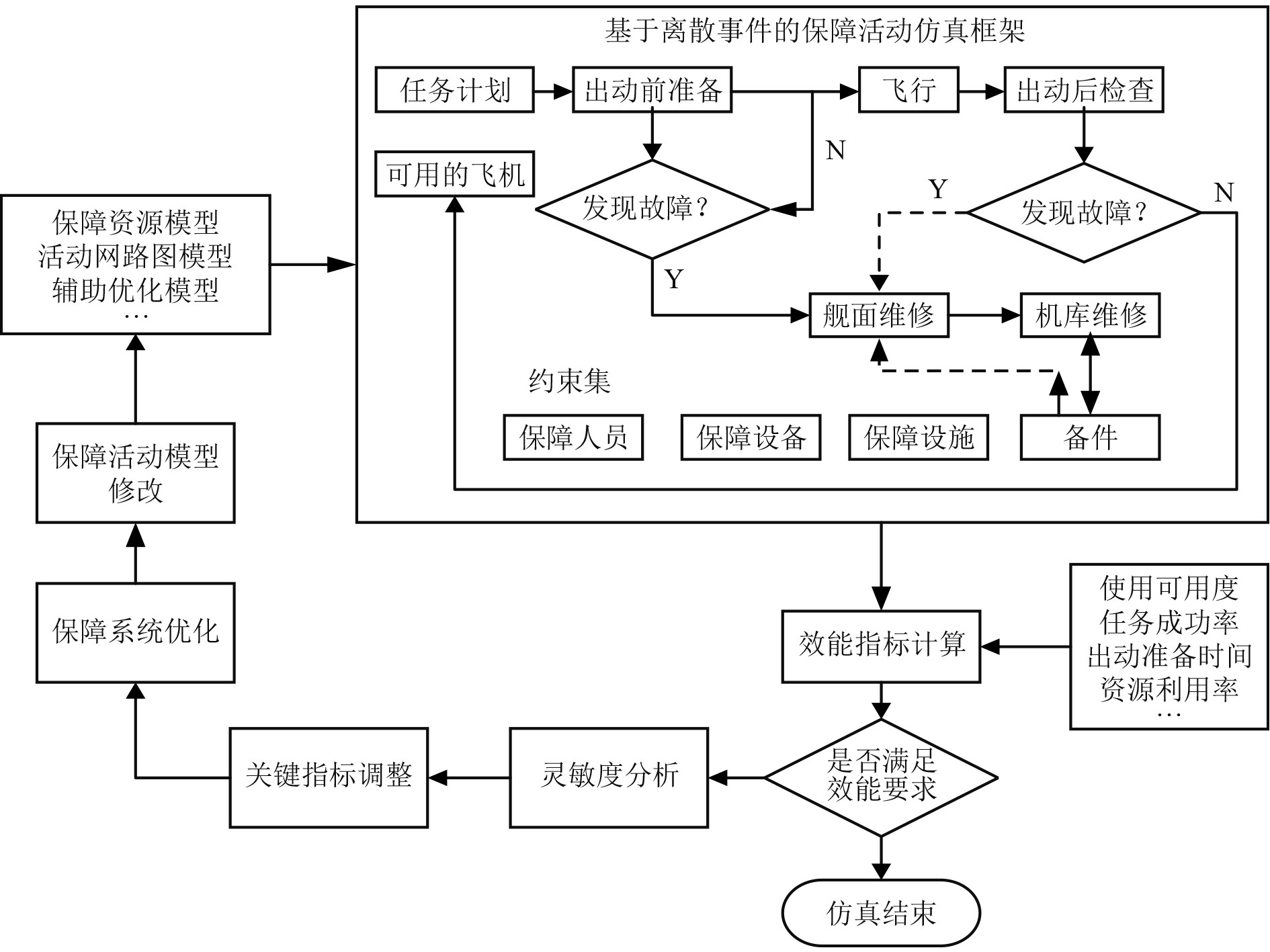
图3给出了通用的优化仿真基本框架,在具体建模过程中,需要根据描述的方法构建出具体的装备模型、保障资源模型、保障活动网络模型等,然后根据具体的任务要求建立相应的优化模型,并结合仿真结果对影响保障效能的因子进行灵敏度分析,进一步合理确定保障指标阈值范围,也就是优化指标的解空间,不同优化模型可以采取不同的优化算法。
|
图 3 基于离散事件舰载机保障指标优化 Fig. 3 Optimization of carrier-based aircraft support indicators based on discrete events |
在作战任务明确的情况下,故障是驱动舰载机维修保障的主要事件。为了充分满足舰载机在恶劣服役环境下的可靠性要求,算例1主要研究任务周期内可靠性指标对机群保障效能的影响,从而给出基于保障效能约束的可靠性指标优化方法。假设某机群有16架舰载机,任务周期持续时间60 d,每架飞机的出动准备时间为60 min,任务取消时间为30 min,每次任务须出动2架飞机,每飞行日固定任务时间为7:00~17:00,间隔2 h出动一次。分析机群在任务周期内的使用可用度、任务成功率等指标,判断是否达到规定要求,若不满足规定要求则进行调整优化。
根据给定的建模方法,基于ILSBox-Designer软件进行仿真,首先构建型号舰载机模型、构型模型以及任务模型。
构建各种基本模型后,设定仿真参数:仿真次数1000次,仿真总时间60 d,置信度水平0.95,装备调度方式为寿命梯次优先。
仿真结束后,相关保障指标的仿真结果如表1所示。
|
|
表 1 仿真结果展示 Tab.1 the simulation result |
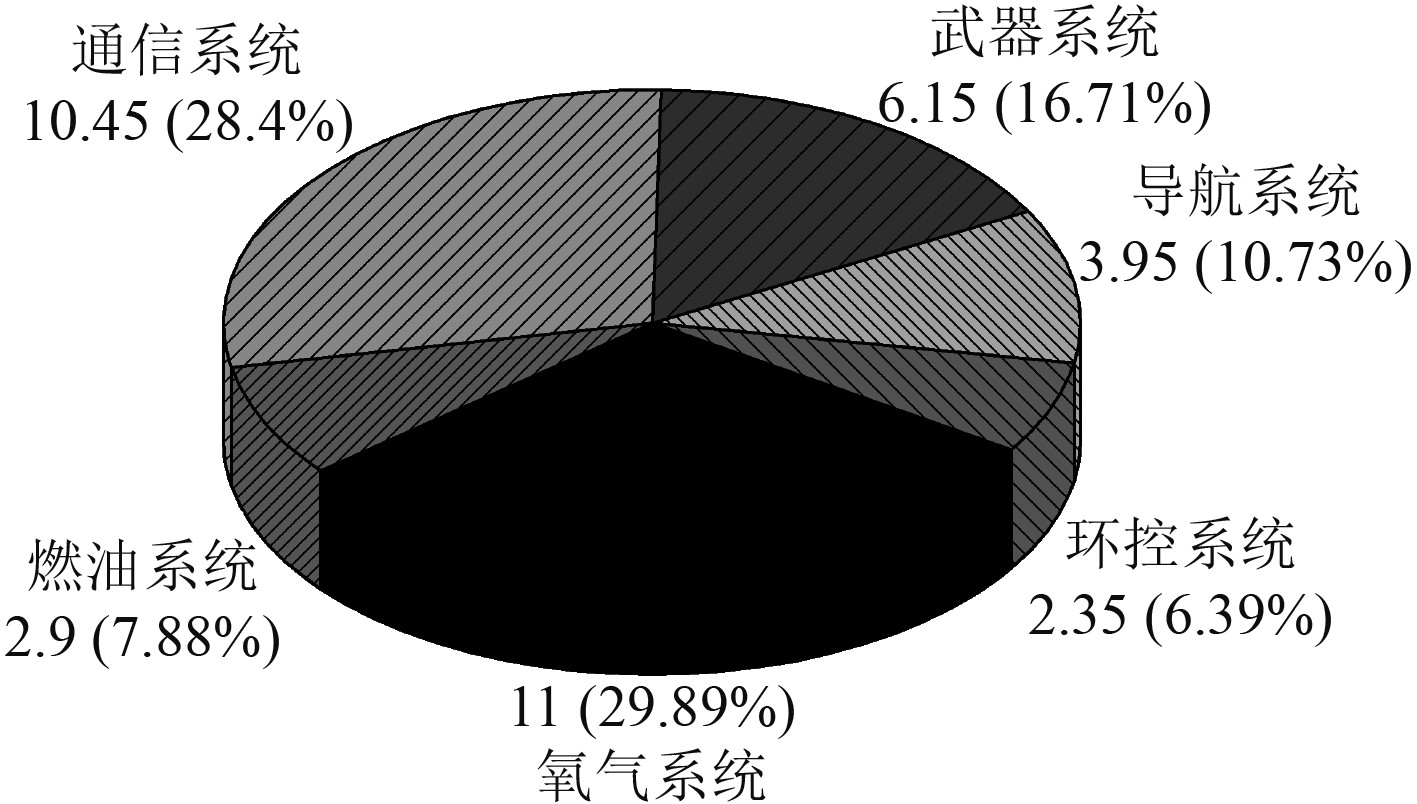
根据仿真结果可知,2项机群保障效能指标均不满足规定要求。在装备保障系统能力满足保障要求的情况下,装备故障是影响使用可用度和任务成功率的主要因素。追溯仿真过程的故障信息,各系统在任务期内的故障次数和占比分别如图4所示。
|
图 4 某型舰载机各系统的故障占比分布 Fig. 4 The distribution of fault proportion of each system of a certain type of carrier-based aircraft |
可知,氧气系统的故障占比最高,为28.89%,总共发生了11次。统计出机群的任务时间,将各项数据代入式(1)可得该系统的平均故障间隔时间为97 h。
| $ MTB{F_L} = \frac{{2T}}{{{\chi ^2}\left( {\alpha ,2r + 2} \right)}} 。$ | (1) |
式中:
针对国军标中定义的使用可用度和任务成功率的有限适用性问题,丁定浩[2]在时域维重新推导了战备完好性参数及其定义,其中使用可用度的定义如下式:
| $ A({t_a} + {t_m}) = R({t_m}) + {\gamma _{FD}}M({t_r})[1 - R({t_m})] 。$ | (2) |
式中:
任务成功率模型如下式:
| $ {P_{SM}} = R({t_s})\frac{{{t_d}}}{{{t_d} + {{\overline t }_m} + {{\overline t }_p}}} 。$ | (3) |
式中:
| $ R({t_{\text{s}}}) = {e^{ - \lambda {t_s}}} ,$ | (4) |
式中,
分析可知,可以根据平均故障间隔时间来调整系统的可靠性设计参数,前提是可靠性参数能够满足式(3)和式(2),即满足以下优化模型:
| $ \left\{ {\begin{array}{*{20}{l}} {\min R({t_s})}, \\ {{\rm{s}}.{\rm{t}}\left\{ {\begin{array}{*{20}{c}} {A({t_a} + {t_s}) = R({t_s}) + {\gamma _{FD}}M({t_r})[1 - R({t_s})] \geqslant 0.9} ,\\ {{P_{SM}} = R({t_s})\dfrac{{{t_d}}}{{{t_d} + {{\overline t }_m} + {{\overline t }_p}}} \geqslant 0.7} 。\end{array}} \right.} \end{array}} \right. $ | (5) |
在满足式(5)约束条件的前提下,可得系统的MTBF为124 h时,满足上述要求,因此可按照该要求对系统进行设计和改型。
4.2 考虑故障预测率的某型机通用质量特性指标评估优化随着先进传感器技术、网络技术和智能算法的不断进步,先进舰载机主要采取自主保障模式,故障诊断与预测能力是其中的一项核心能力[13]。因此,在该算例中重点考虑故障预测率对舰载机保障效能指标的影响。假设任务持续时间60 d,每架飞机的出动准备时60 min,取消时间为30 min,每次出动2架飞机。装备具备故障预测功能,故障预测率指标分别设置为(0, 0.2, 0.4, 0.6. 0.8, 1.0)。试判断任务周期内该产品的使用可用度是否大于0.9,任务成功率是否大于0.8。
仿真次数1000次,仿真总时间60 d,置信度水平0.95,装备调度方式为寿命梯次优先。
在不同的故障预测率下,任务周期内的保障效能指标见表1,2项指标基本满足要求,只有在故障预测率为0时,单机的任务成功率达不到指标要求。根据分析结果可知,当预测率为(0.2,0.4,0.6.0.8,1.0)时,均满足任务成功率要求。
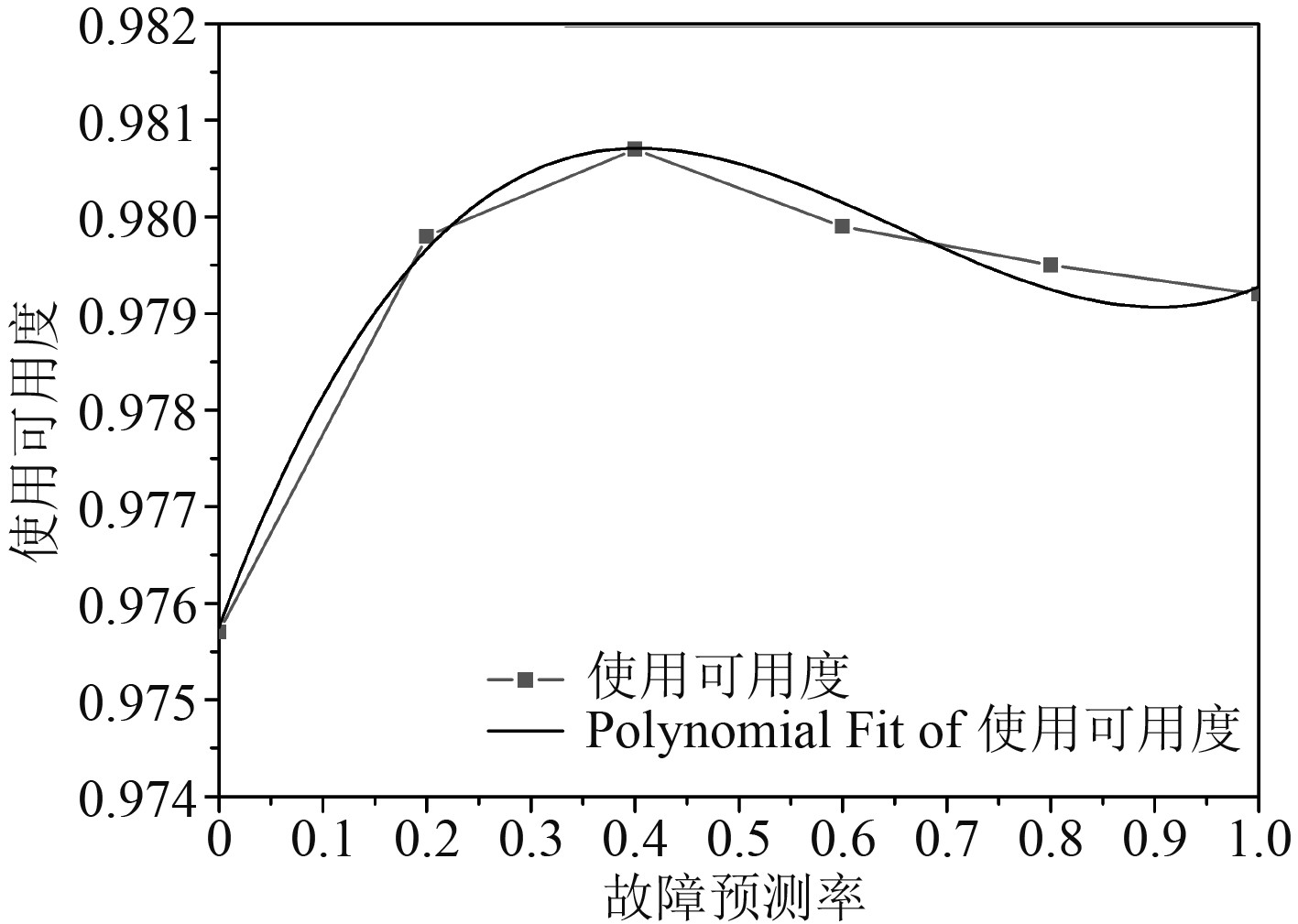
仿真模型仿真过程比较复杂,可以较好的刻画保障过程的不缺性与随机性,但是很难获得系统解析模型,只能得到一些离散点的仿真结果,如图5和图6所示。如果将故障预测率设置为连续变量时,仿真时间将会大幅度增加。在获得复杂系统仿真结果的基础上,使用代理模型是工程中比较常见的技术手段,其可以根据仿真结果得到简单的解析模型进行定量分析和迭代。代理模型有多项式拟合、拟合响应面法、支持向量机、神经网络法等,崔利杰证明了多项式拟合算法在基于离散事件的保障流程仿真中有较好的适用性[11]。在此,设置拟合度大于95%的要求,可得单机在不同故障预测率下的代理模型。
|
图 5 故障预测率对使用可用度的灵敏度仿真 Fig. 5 Sensitivity simulation of failure prediction rate to operation availability |
|
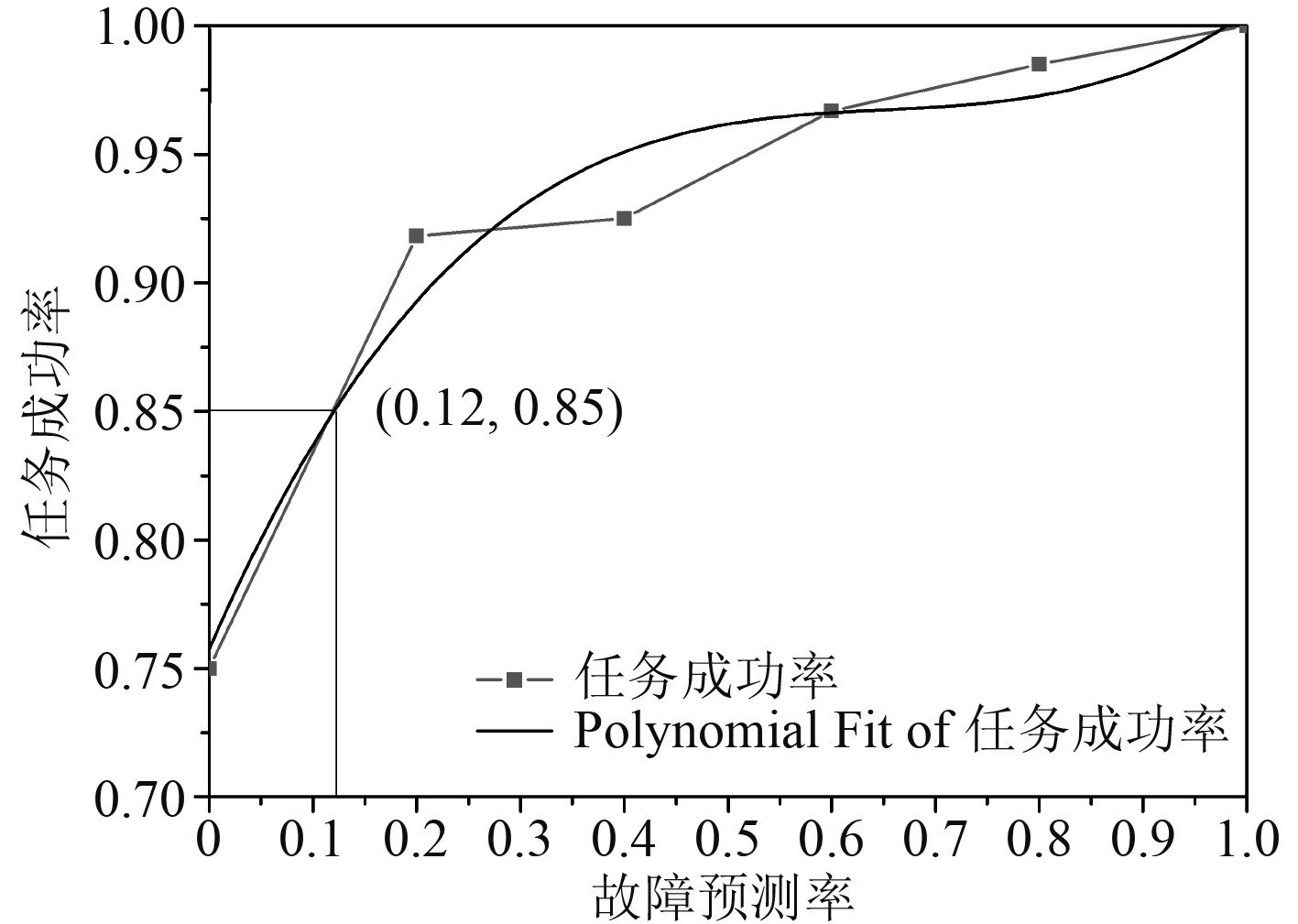
图 6 故障预测率对任务成功率的灵敏度仿真 Fig. 6 Sensitivity simulation of failure prediction rate to mission success rate |
使用基于多项式拟合的代理模型,拟合精度约束为0.95,拟合度为0.97,多项式参数分别为:a0=0.975, a=0.0325, b=−0.0582,c=0.052。
使用基于多项式拟合的代理模型,拟合精度约束为0.95,拟合度为0.9,多项式参数分别为:a0=0.75,a=0.92545,b=−1.39,c=0.71。
分析可知,当预测率达到0.12时可以满足使用可用度和任务成功率要求,比设定的0.2的预测率要求要低。在工程中受到产品设计、制造成本等的影响,不同指标精度对应的经济性必然不同,因此在仿真模型的基础上使用代理模型可以得到更为精确的数值解,进一步优化通用质量特性指标。
5 结 语结合舰载机的使用特性,提出舰载通用质量特性指标论证的一般流程,综合运用解析和离散事件仿真的方法构建了指标论证的基本模型,并基于ILSBox-Designer软件进行了仿真。2个算例分别对故障率和故障预测率的灵敏度进行了评估与优化,结果表明设计方法科学可行,有较好的工程应用性。
虽然研究过程中算例设置比较简单,但可为复杂工程系统的指标论证与评估提供一种思路。对大型复杂系统,则需要嵌入优化算法,提高仿真效率,如强化学习算法等。
在研究过程中对于装备经济性影响没有解析,后续可以考虑引入装备的各种成本模型,更为系统地论证装备的保障指标。
| [1] |
屈也频, 金惠明, 何肇雄. 航母舰载机装备体系及指标论证方法[J]. 航空学报, 2018, 39(5): 113-124. DOI:10.7527/S1000-6893.2017.221675 |
| [2] |
丁定浩. 论证军用装备 RMS 顶层参数指标的意义和建议[J]. 电子产品可靠性与环境试验, 2011, 29(5): 1-5. DOI:10.3969/j.issn.1672-5468.2011.05.001 |
| [3] |
祝华远, 李军亮, 贾向军, 等. 航空装备通用质量特性概论[M]. 航空工业出版社, 北京, 2021, 01
|
| [4] |
李军亮, 滕克难, 夏菲. 一种复杂可修系统的可用度计算方法[J]. 航空学报, 2017, 38(12): 150-158. DOI:10.7527/S1000-6893.2017.221169 |
| [5] |
李军亮, 陈跃良, 张勇, 等. 基于可用度的预防性维修周期优化[J]. 系统工程理论与实践, 2021, 41(6): ;1611-1624. |
| [6] |
LI J L, CHEN Y L, ZHANG Y, et al. Availability modelling for periodically inspected systems under mixed maintenance policies[J]. Journal of Systems Engineering and Electronics, 2021, 32(3): 722-731. DOI:10.23919/JSEE.2021.000062 |
| [7] |
韩维, 李正阳, 苏析超, 等. 航母航空保障效能评估综述[J]. 科学技术与工程, 2021, 21(7): 2586-2594. DOI:10.3969/j.issn.1671-1815.2021.07.004 |
| [8] |
刘东, 吴家仁, 周一舟, 等. 舰载机综合保障技术实践及发展展望[J]. 航空学报, 2021, 42(8): 106−123.
|
| [9] |
丁善婷, 王淼, 董正琼, 等. 基于多智能体的舰船装备健康状态仿真评估方法[J]. 中国机械工程, 2022, 33(10): 1169−1177.
|
| [10] |
张豪, 郑茂, 初秀民, 等. 舰载机高强度作业流程仿真研究[J]. 舰船科学与技术, 2019, 41(6): 147-153. ZHANG H, ZEHNG M, CHU X M, et al. Carrier-based aircraft surge operation simulation based on linear index policies[J]. Ship Science and Technology, 2019, 41(6): 147-153. |
| [11] |
崔利杰, 丛继平, 丁刚, 等. 基于不确定性的航空装备体系保障性评估[J]. 北京航空航天大学学报, 2021, 47(12): 2452-2461. CUI L J, CONG J P, DING G, et al. Supportability evaluation of aviation equipment system based on uncertainty[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(12): 2452-2461. DOI:10.13700/j.bh.1001-5965.2020.0490 |
| [12] |
潘星, 左督军, 张跃东. 基于系统动力学的装备体系贡献率评估方法[J]. 系统工程与电子技术, 2021, 43(1): 112-120. DOI:10.3969/j.issn.1001-506X.2021.01.14 |
| [13] |
杨鹏, 邱静, 刘冠军, 等. 一种基于ROM模型的测试性指标论证方法[J]. 航空学报, 2021, 42(12): 273-286. |
 2023, Vol. 45
2023, Vol. 45
