2. 长春理工大学 化学与环境工程学院,吉林 长春 130000
2. College of Chemical and Environmental Engineering, Changchun University of Science and Tecnology, Changchun 130000, China
船舶在航行过程中,会遇到海面勘探、石油开发等水域作业情况,为使船舶安全航行,规划其航行航线意义重大。杨琪森等[1]提出的船舶路径规划与避障方法,该方法通过构建马尔可夫决策过程抽象模型,通过深度强化学习算法,规划了船舶航行路径。谢新连等[2]提出复杂水域船舶路径规划方法,该方法建立环境模型,分析海浪对船舶速度的影响,利用改进粒子群算法优化船舶航行路径。上述2种方法虽可实现船舶航线优化,但优化结果不够准确。人工智能算法也被称为机器学习算法,其包含寻优算法、识别算法等多种算法[3],是求解目标函数算法,可通过反复迭代输出最优解。面对当前船舶航线优化算法存在的不足,研究人工智能在船舶航行数学建模中的应用,为船舶导航提供技术支持。
1 基于人工智能的船舶航行数学建模 1.1 船舶航线规划数学模型构建海上钻井平台或勘探区域作业通常包含多个水上、水下作业点,船舶在该区域航行时,受其作业点影响,威胁其航行安全[6],因此船舶航行时需规避海上不同作业点。
在建立船舶航线优化模型之前,使用Maklink图论方法描述海上作业点分布,在海上作业水域建立Maklink连接图,利用该图描述船舶在作业水域内可航行网络图,并将其表述为可求解的数学模型。令
|
|
表 1 船舶最小转弯半径参数设计 Tab.1 Parameter design of minimum turning radius of ship |
令
| $ R = 0.5{V_t}L \cdot \frac{1}{{1 - \sin \left( {\dfrac{\theta }{2}} \right)}} 。$ | (1) |
式中:
在综合考虑船舶转向角度和转弯半径后,建立船舶在海上作业区域航线规划数学模型,其表达公式如下:
| $ \min Z = \sum\limits_{i = 1}^{k - 1} {d({q_i},{q_{i + 1}})} + \sum\limits_{i = 1}^{k - 1} {d(S,{q_1})} + \sum\limits_{i = 1}^{k - 1} {d({q_k},T)}。$ | (2) |
式中:
令
| $ \forall l({q_i},{q_{i + 1}}) \cap {S_j} = \emptyset,$ | (3) |
| $ \forall {\theta _{{q_j} \in (1,2, \cdots ,k)}} \leqslant {\varphi_{{\rm{max}}}},$ | (4) |
| $ {R_{{q_j} \in (1,2, \cdots ,k)}} \geqslant \lambda L,$ | (5) |
| $ Z \geqslant {Z_{{\rm{min}}}}。$ | (6) |
式中:
经过上述步骤,完成船舶航线规划模型构建。
1.2 基于Dijkstra算法的船舶航线规划模型求解通过构建船舶在海上作业危险区域航线规划模型,利用Dijkstra算法求解该模型,获得船舶在海上作业区域初始航线,其详细过程如下:
将求解船舶在海上作业危险区域航线规划模型问题转换成有向图最短路基问题[8],利用图论方式描述该模型,令
| $ G = (V,A,W)。$ | (7) |
式中:
利用Dijkstra算法求解船舶在海上作业危险区域航线规划模型步骤为:
步骤1 对航线有向图顶点
步骤2 当
步骤3 求解
步骤4 当
步骤5 当
经过上述步骤,得到船舶在海上作业区域初始航线。
1.3 基于人工智能算法的船舶初始航线优化方法使用Dijkstra算法求解船舶在海上作业危险区域航线规划模型,得到其初始航线时,受航线点数量较多影响,其生成的初始航线无法满足船舶航行时的机动性能,因此以船舶在海上作业危险区域初始航线为基础,使用人工智能算法内的蚁群优化算法对船舶初始航线优化处理。
将船舶航行初始航线上的节点赋予初始值,生成初始信息素矩阵,其中危险区域节点的初始值为0,其他节点初始值为1。当时刻为
| $ {\rho _{kab}} = \left\{ {\begin{array}{*{20}{l}} {\psi _{ab}^\alpha (t)\eta _{ab}^\beta (t) \cdot \dfrac{1}{{\displaystyle\sum {\psi _{ab}^\alpha } (t)\eta _{ab}^\beta (t)}}b \in \varOmega },\\ {0 \in {\varOmega ' }}。\end{array}} \right. $ | (8) |
式中:
蚂蚁依据公式(7)概率搜索,在搜索过程中按照下式全局更新规则更新其行走路径:
| $ \psi (j) = (1 - \vartheta ){\rho _{kab}} \cdot \left[ {\psi (j) + \vartheta \Delta \psi (j)} \right]。$ | (9) |
式中:
| $ \Delta \psi (j) = \sum\limits_{k = 1}^h {\Delta {\psi _k}(j)},$ | (10) |
| $ \Delta {\psi _k}(j) = \left\{ \begin{gathered} Q/{J_k},\\ 0。\\ \end{gathered} \right. $ | (11) |
式中:
蚁群按照公式(9)更新其路径后,当迭代次数达到阈值次数,则输出当前路径,该路径即为优化后的船舶在海上作业区域航行路径,利用该路径为船舶导航,保障其安全航行。
2 实验分析以某中型货运船舶作为实验对象,其需穿越海上石油钻井平台作业区域,其作业区域分布以及船舶航行起点位置如图1所示。
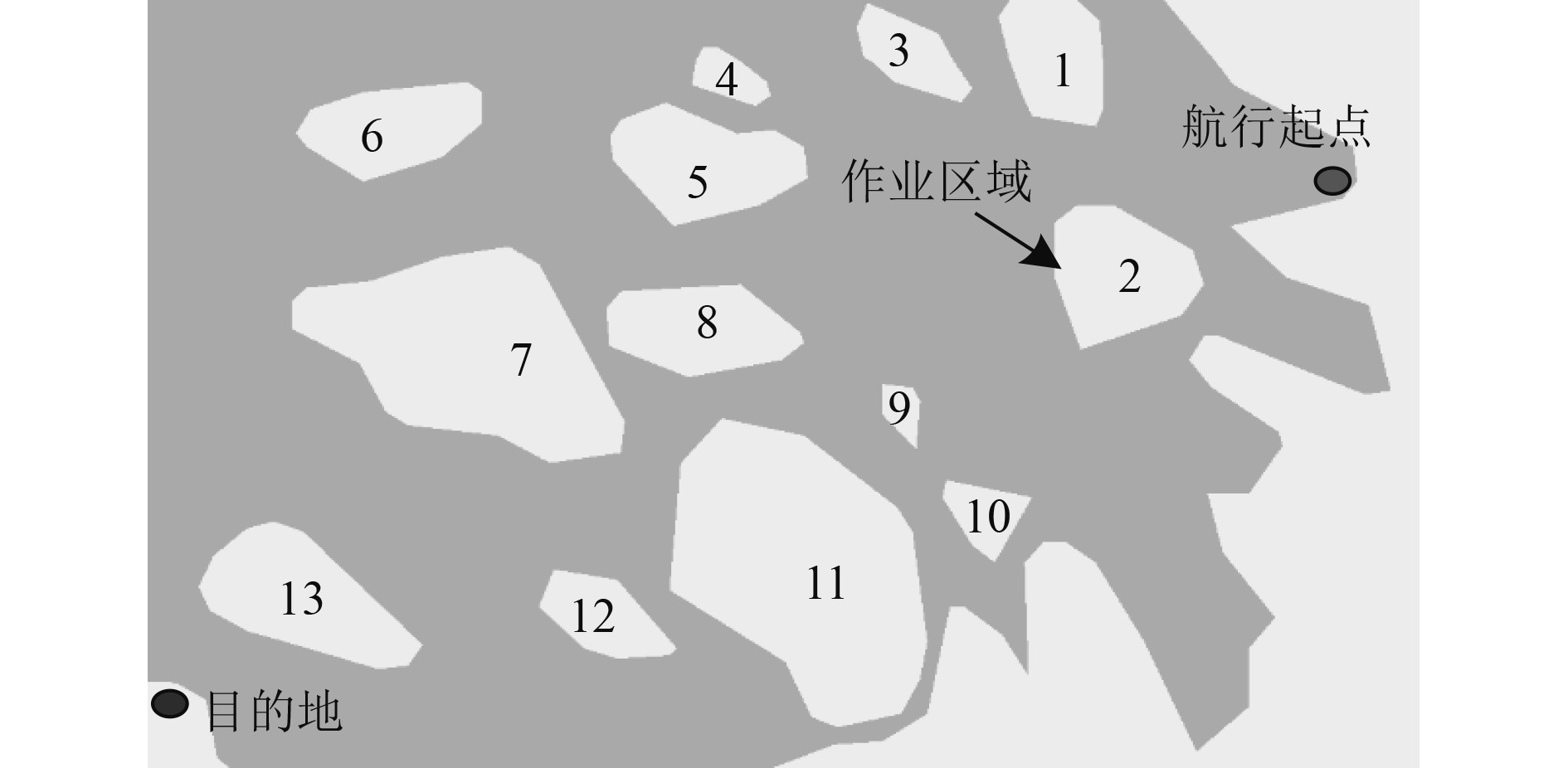
|
图 1 海上作业区域与船舶航行起点 Fig. 1 Offshore construction area and ship navigation starting point |
生成海上作业区域可航行网络图是获得船舶初始航线和航线优化的基础,使用本文方法获取海上作业区域,作业水域可航行网络如图2所示。
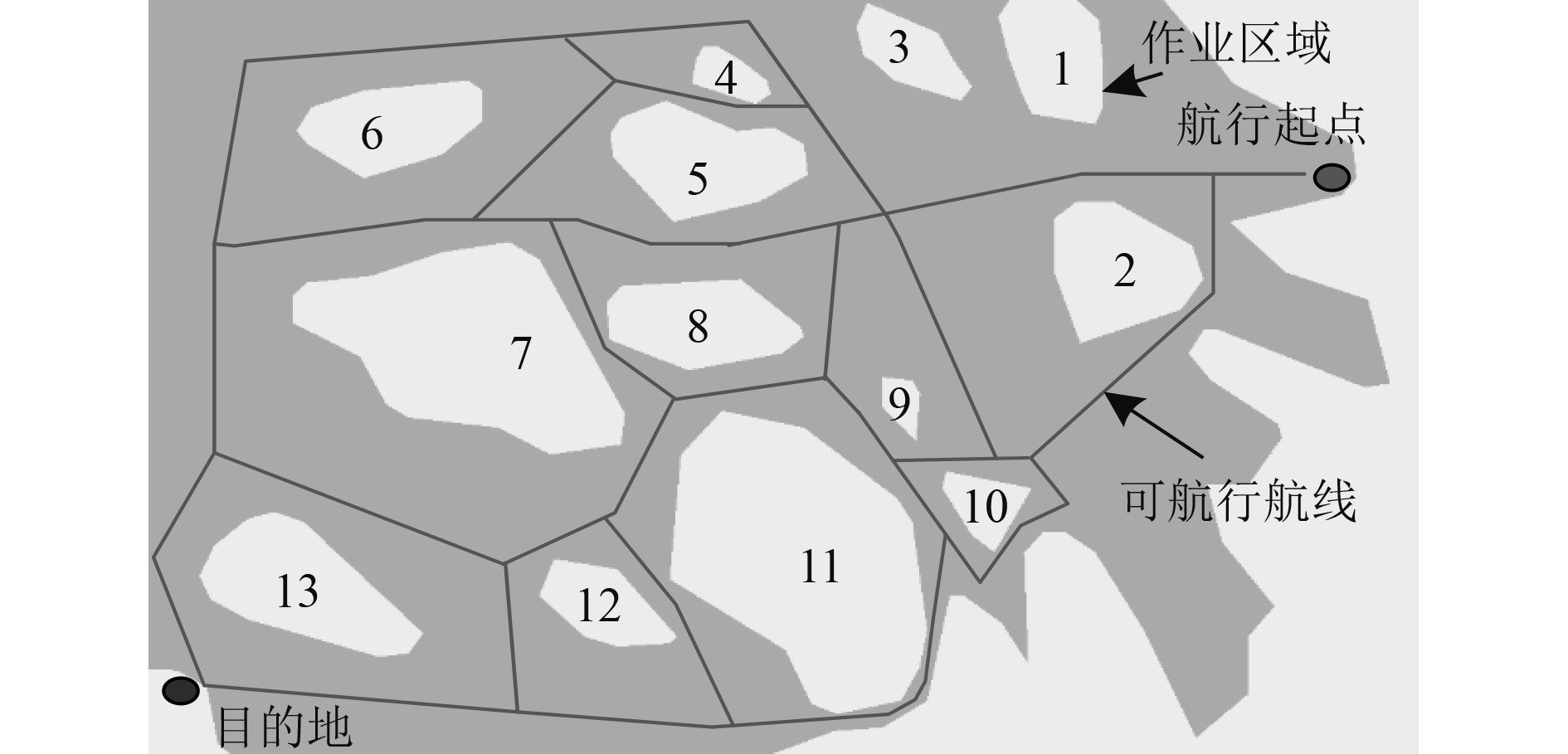
|
图 2 作业水域可航行网络 Fig. 2 Navigable network of construction waters |
可知,本文方法可有效依据海上石油钻井平台作业区域得到船舶可航行线路,生成船舶可航行线路网络图,为后续得到船舶初始航线与初始航线优化打下良好基础。
2.2 船舶初始航线生成与航线优化使用本文方法生成该船舶从起点到目的地航线,并对该航线优化处理,初始航线生成与航线优化结果如图3所示。
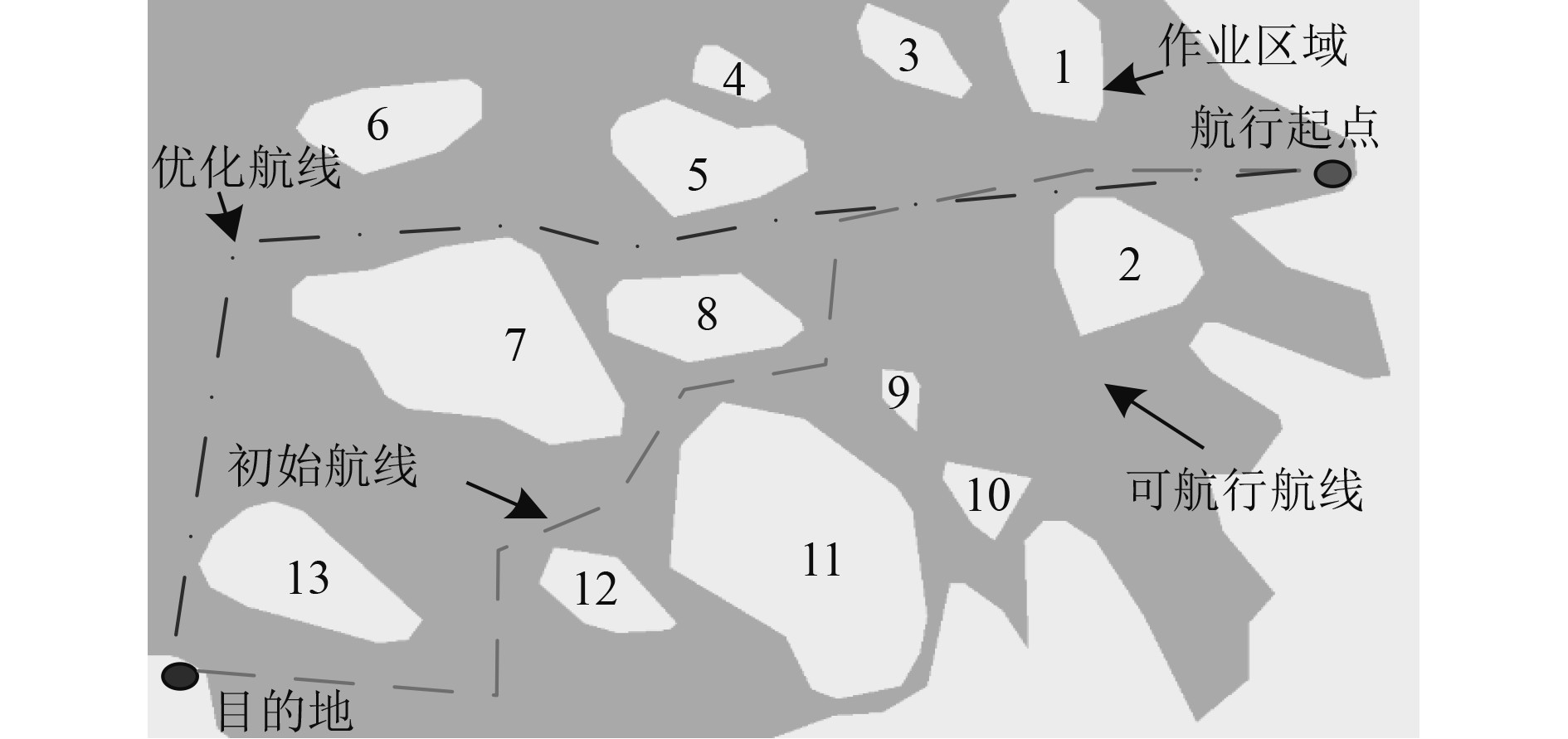
|
图 3 初始航线生成与航线优化结果 Fig. 3 Initial route generation and route optimization results |
可知,使用本文方法可有效生成该船舶航行的初始航线,但该初始航线需要多次变更航向才可到达目的地,且生成的初始航线穿过7号、8号作业区域与11号作业区域,该3个作业区域呈三角形分布,中间航道较为狭窄,影响船舶航行航速。而使用本文方法对该初始航线优化后,优化后的航线仅需变更一次航向即可到达目的地,同时航行穿越作业区域时,其航道较宽,船舶可安全航行。综上结果,本文方法可有效生成船舶航行初始航线,并使用人工智能算法对其优化处理,具有较好的应用效果。
3 结 语为了保证船舶的安全航行,研究人工智能在船舶航行数学建模中的应用方法。通过建立船舶航行数学模型并求解后,得到船舶航行初始航迹,通过人工智能算法中的蚁群算法,对其初始航迹优化,使船舶航行更加安全。通过对本文方法实际验证,其在生成船舶航线网络图,得到初始航线并优化方面均具备较好的能力,可用于船舶穿越海上作业区域导航,为船舶安全航行提供保障。
| [1] |
杨琪森, 王慎执, 桑金楠, 等. 复杂开放水域下智能船舶路径规划与避障方法[J]. 计算机集成制造系统, 2022, 28(7): 2030-2040. YANG Qisen, WANG Shenzhi, SANG Jinnan, et al. Path planning and real-time obstacle avoidance methods of intelligent ships in complex open water environment[J]. Computer Integrated Manufacturing Systems, 2022, 28(7): 2030-2040. DOI:10.13196/j.cims.2022.07.009 |
| [2] |
谢新连, 刘超, 魏照坤. 海洋气象环境影响下的复杂水域船舶路径规划[J]. 重庆交通大学学报(自然科学版), 2021, 40(2): 1-7+20. XIE Xinlian, LIU Chao, WEI Zhaokun. Ship path planning in complex water areas under the influence of marine meteorological environment[J]. Journal of Chongqing Jiaotong University (Natural Science), 2021, 40(2): 1-7+20. |
| [3] |
闫兆进, 杨慧. 基于多源数据和船舶停留轨迹语义建模的港口目标识别[J]. 地球信息科学学报, 2022, 24(9): 1662-1675. YAN Zhaojin, YANG Hui. Harbor detection based on multi-source data and semantic modeling of ship stop trajectory[J]. Journal of Geo-Information Science, 2022, 24(9): 1662-1675. |
| [4] |
陈影玉, 索永峰, 杨神化. 基于灰狼优化支持向量回归的船舶航迹预测[J]. 上海海事大学学报, 2021, 42(4): 20–25, 46. CHEN Yingyu, SUO Yongfeng, YANG Shenhua. Ship trajectory prediction based on grey wolf optimization support vector regression[J]. Journal of Shanghai Maritime University, 2021, 42(4): 20–25, 46. |
| [5] |
陈新, 袁宇浩, 饶丹. 一种改进A~*算法在无人船路径规划中的应用[J]. 计算机仿真, 2021, 38(3): 277-281. CHEN Xin, YUAN Yuhao, RAO Dan. Improved A* algorithm and its application in path planning of unmanned surface vehicle[J]. Computer Simulation, 2021, 38(3): 277-281. DOI:10.3969/j.issn.1006-9348.2021.03.057 |
| [6] |
牟红梅, 胡青. 基于神经网络的异常船舶航迹特征因子模型[J]. 科学技术与工程, 2021, 21(34): 14610-14617. MO Hongmei, HU Qing. Characteristic factor model of abnormal ship track based on neural network[J]. Science Technology and Engineering, 2021, 21(34): 14610-14617. |
 2023, Vol. 45
2023, Vol. 45
