2. 河南科技职业大学,河南 周口 466000
2. Henan Vocational University of Science and Technology, Zhoukou 466000, China
长久以来,通信系统均采用合作通信的模式,即信号发射端和接收端采用一致的信号调制方法,用户接收到来自其他终端的信号后,无需对信号进行特殊解调就可以实现信号的识别和后处理,这种通信模式尽管节省了信号解调环节,但通信系统的信号传输方式和信道单一,存在着一定的局限性。随着无线通信技术的日益成熟,通信模式越来越多元化,信号的调制方式和模式识别技术越来越得到重视。海上船舶通信主要是无线通信模式,由于通信环境复杂、干扰噪声较多,因此海上无线通信的信号调制与模式识别对于通信系统稳定性有重要作用。
船舶通信系统的信号调制与模式识别技术在军事领域和民用领域均有重要作用。
1)民用领域
船舶无线通信系统的信号监控、通信频谱检测等均离不开信号的调制和模式识别,尤其是大型船舶货运公司在进行船舶远程管理和监控时,提高通信系统信号识别精度非常重要。
2)军事领域
在海上军事领域,信号调制和模式识别技术被广泛的应用在敌船侦察、海上救援、通信信号的干扰和防干扰等。
本文针对船舶通信系统的模拟调制和数字信号调制技术进行详细研究,并对通信系统的模式识别从时域和频域2个方面进行优化,取得了较好的效果。
1 船舶通信系统的信号模拟调制技术船舶通信系统的信号模拟调制包括幅度调制和频率调制2种。
1)幅度调制(AM调制)
幅度调制是一种典型的线性调制,利用调制信号的幅度参数改善通信信号的特性,幅度调制又可以分为双边带调幅 ( DSB-AM )、单边带调幅[1]等。
AM调制信号的表达式可写为:
| $ {s_{AM}}(f) = \frac{{{A_c}}}{2}\left( {1 + m\left( t \right)} \right)\cos 2{\text{π}} {f_c}t。$ |
式中:
船舶通信系统的信号AM调制示意图如图1所示。
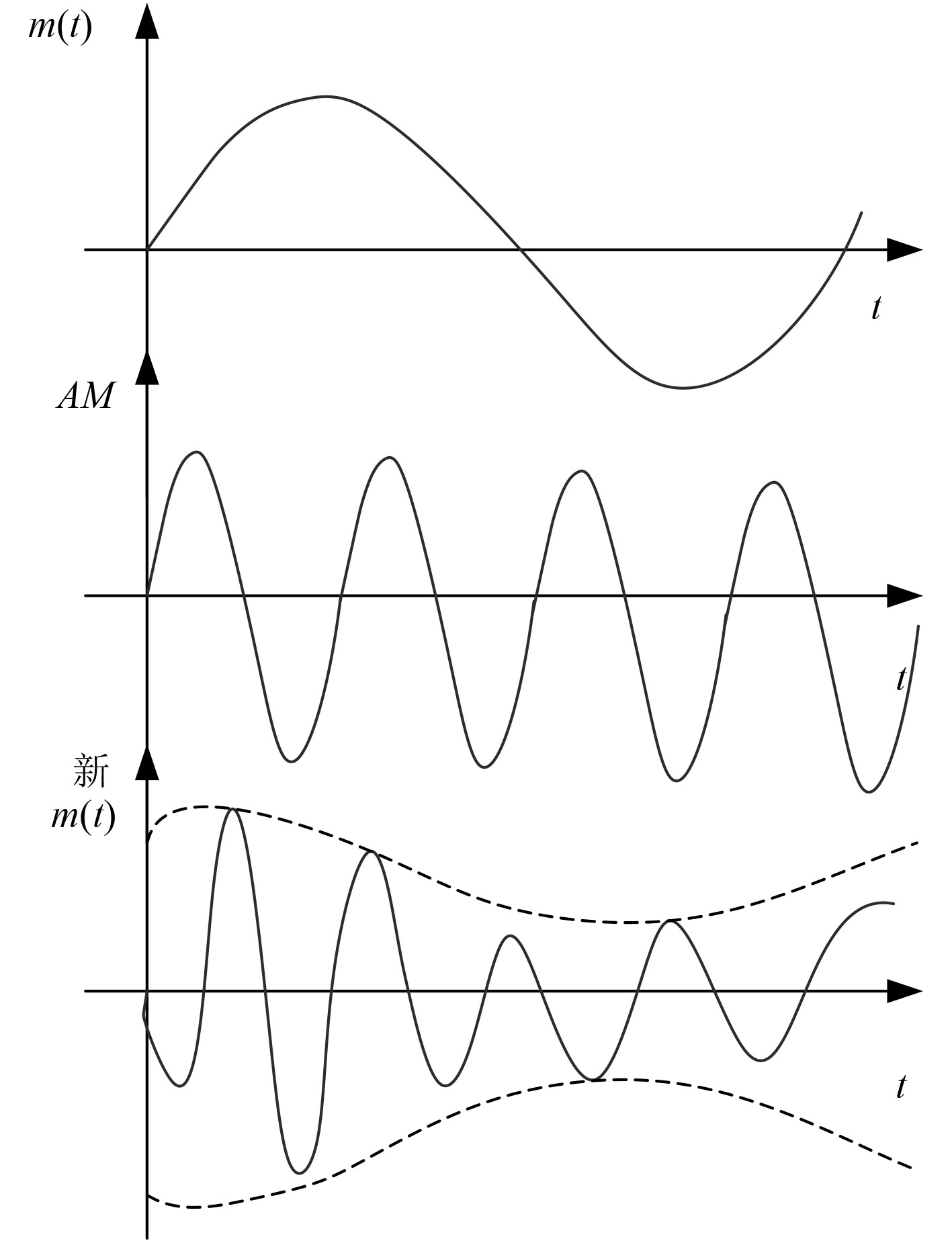
|
图 1 船舶通信系统的信号AM调制示意图 Fig. 1 Signal AM modulation diagram of ship communication system |
当
| $ {s_{AM}}(f) = \frac{{{A_c}}}{2}\left[ {M\left( {f - {f_c}} \right) + \delta \left( {f - {f_c}} \right)} \right] 。$ |
2)频率调制
频率调制也是信号模拟调制的一种重要方式,这种调制方式是一种非线性调制,频率调制信号可写为:
| $ s(t) = \frac{{{A_c}}}{2}\cos \left[ {2{\text{π}} {f_c}t + \varphi \left( t \right)} \right] \text{,} $ |
式中,
频率调制信号的频率偏移与基带信号
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\varphi (t) = 2{\text{π}} {K_f}m(t) \text{,} $ |
式中:
频率调制信号在时域的模型:
| $ {s_f}(t) = {A_c}\cos \left[ {2{\text{π}} {f_t}t + 2{\text{π}} {K_f}\int_{ - \infty }^t m (t){\rm{d}}t} \right] 。$ |
定义频率调制的指数
| $ {\beta _f} = \frac{{\Delta {f_{{\text{max }}}}}}{W} = {K_f}\frac{{\max |m(t)|}}{W} \text{,} $ |
式中:
| $ {S_F}(f) = \frac{{{A_c}}}{2}\sum\limits_{n = - \infty }^\infty {{J_n}(v)} \left[ {\delta \left( {f - {f_c} - n{f_m}} \right)} \right]。$ |
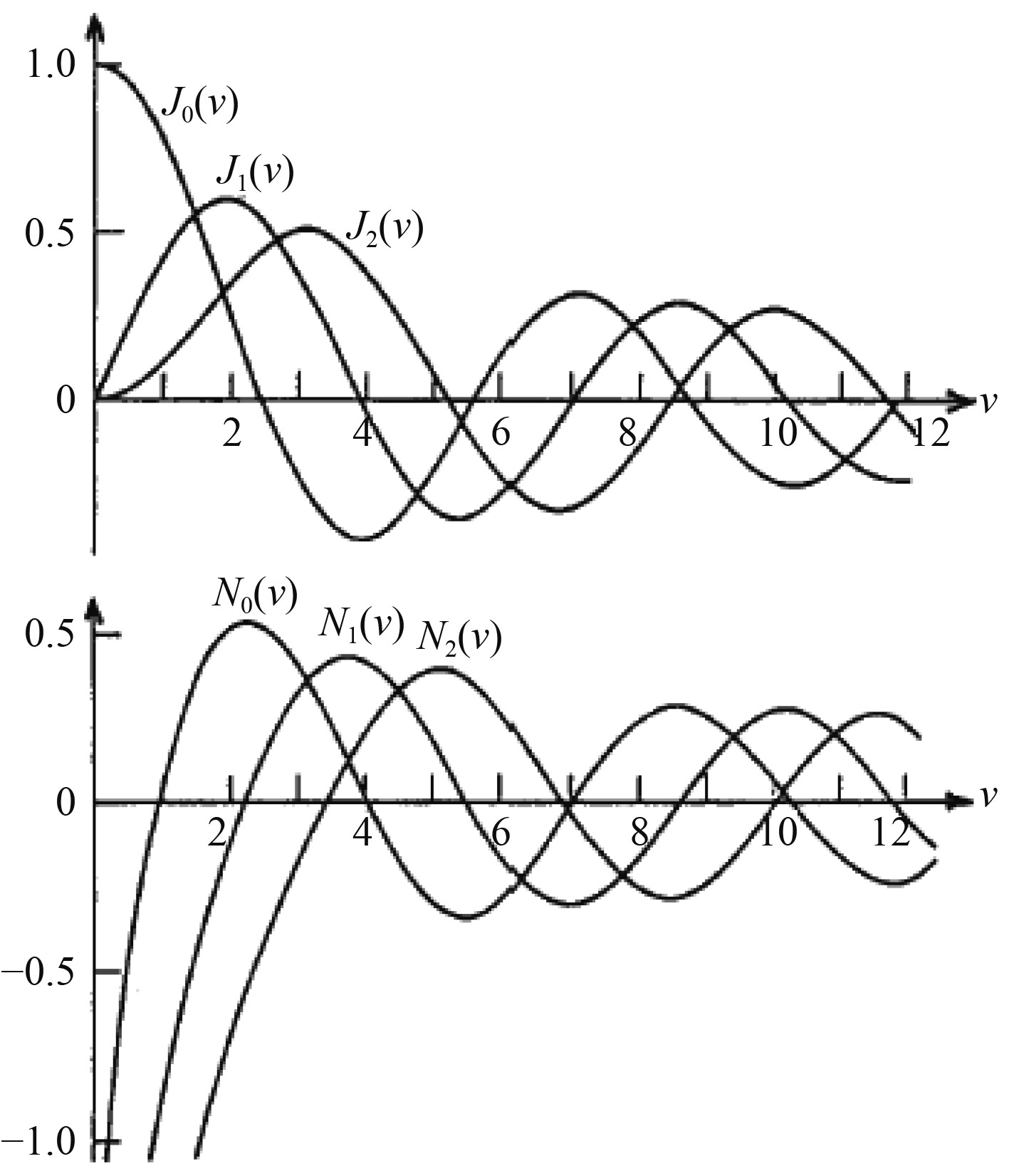
|
图 2 n阶贝塞尔函数的波形图 Fig. 2 Waveform diagram of n order Bessel function |
随着船舶通信系统的发展,数字信号调制技术已经成为主流的调制方式,相对于模拟信号调制技术,数字信号调制的安全性、信号精度更高。此外,数字信号调制技术是利用时间和幅度上离散的信号进行调制,结合现代计算机技术,具有更高的调制效率。
数字调制技术在原理上是利用基带数字信号去改变载波的信号参量,比如ASK振幅调制、FSK频率调制方法。
1)ASK振幅数字调制技术
ASK振幅键控信号离散函数表示为:
| $ {f_{ask - 1}} = \sum\limits_{n = 0}^\infty {{a_n}\delta \left( {t - n{T_b}} \right)} 。$ |
信号经过滤波调制函数[3]
| $ {f_{ask}} = A\cos 2{\text{π}} {f_{ask}}t\sum\limits_{n = 0}^\infty {{a_n}{g_t}\left( t \right)\delta \left( {t - n{T_b}} \right)}。$ |
式中:
ASK振幅键控信号的功率谱密度函数为:
| $ {P_{ask}} = \frac{A}{4}{P_n}\left[ {\left( {f - {f_{ask}}} \right) + \left( {f + {f_{ask}}} \right)} \right] 。$ |
基于ASK振幅键控信号的信号振幅数字调制原理图如图3所示。
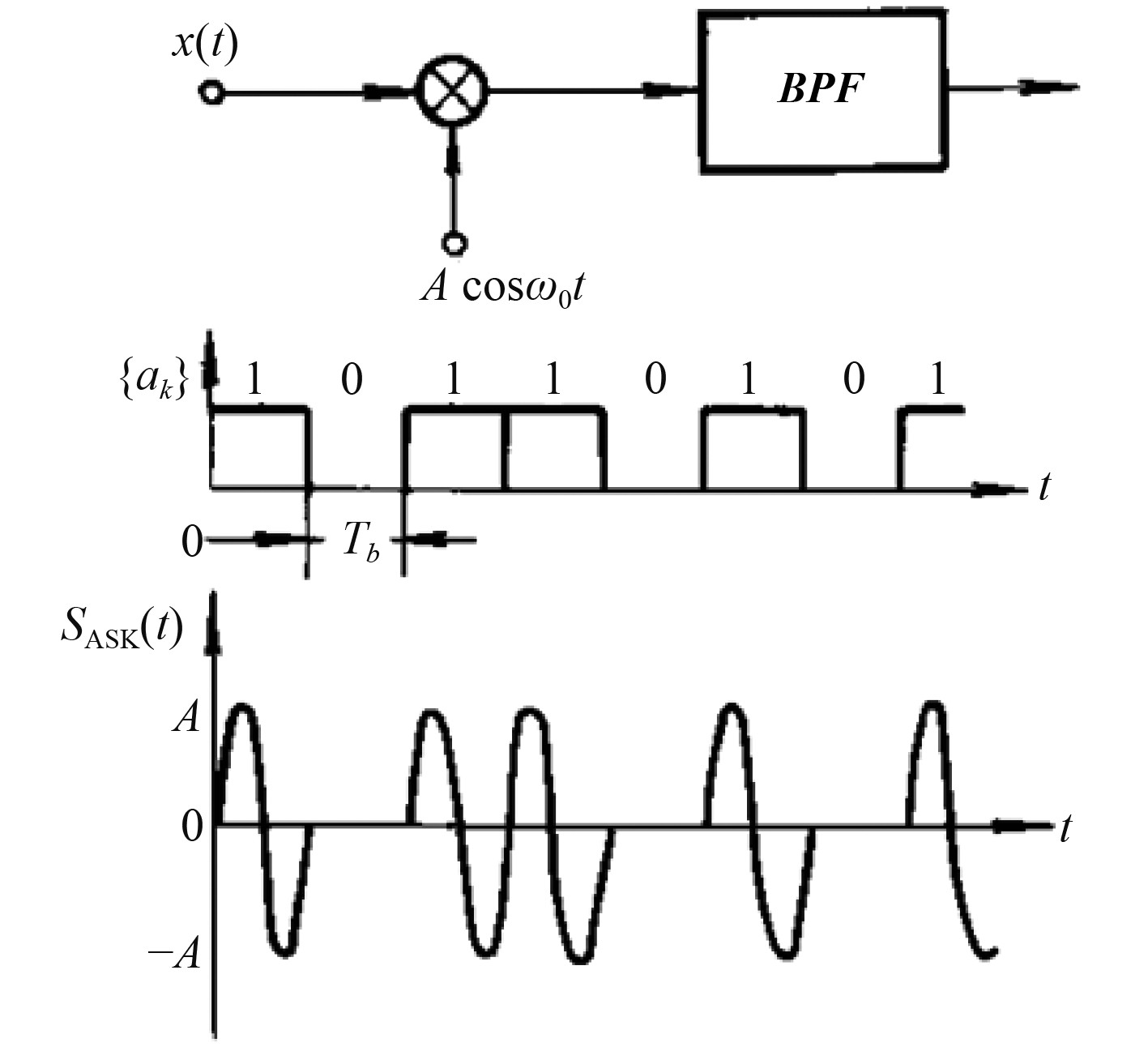
|
图 3 ASK振幅键控信号的信号振幅数字调制原理图 Fig. 3 Schematic diagram of signal amplitude digital modulation of ASK amplitude keying signal |
ASK振幅键控信号调制技术目前被广泛应用在光纤等通信场景中,但仍存在一些问题,比如噪声信号干扰较大等。M进制振幅键控信号MASK调制是在ASK基础上的一种优化方法[4],它的载波幅度取值范围为
| $ {f_{mask}} = A\sum\limits_{n = 0}^\infty {{a_n}{g_t}\left( {t - n{T_i}} \right)\cos {w_c}t} \text{,} $ |
式中,
2)FSK频率调制技术
频率数字调制常用的方法为二进制移频键控(2FSK)方法,数学表达式为:
| $ {s}_{FSK}(t)=\left\{\begin{array}{ll}{s}_{1}(t)=A{\cos}2\text{π} {f}_{1}t & 序列值为1 \\ {s}_{2}(t)=A{\cos}2\text{π} {f}_{2}t & {\rm{else}} \end{array}\right.\quad 0\leqslant t\leqslant {T}_{b} \text{,} $ |
频率数字调制信号的时域表达式为:
| $ {s_{FSK}}(t) = A\cos \left[ {{\omega _c}t + 2{\text{π}}{K_f}\int_{ - \infty }^t b (t){\rm{d}}t} \right] 。$ |
图4为频率数字调制技术的示意图。

|
图 4 频率数字调制技术的示意图 Fig. 4 Schematic diagram of frequency digital modulation technique |
由于船舶通信领域的信号调制技术有多种,每种调制方法在信号强度、解调方式、信号精度等方面均存在不同,因此,为了保障通信系统的信号稳定性特性,必须要提高模式识别技术[5]。
常用的通信系统模式识别方法包括基于时域特征参数的识别方法、基于频域的特征参数识别方法,其中基于频域的识别方法又包括谱分析法等,是本文介绍的重点。
基于频域的相关特征参数识别方法更加灵活,模式识别的精度也更高,本文采用的频域谱分析模式识别方法基本原理如图5所示。
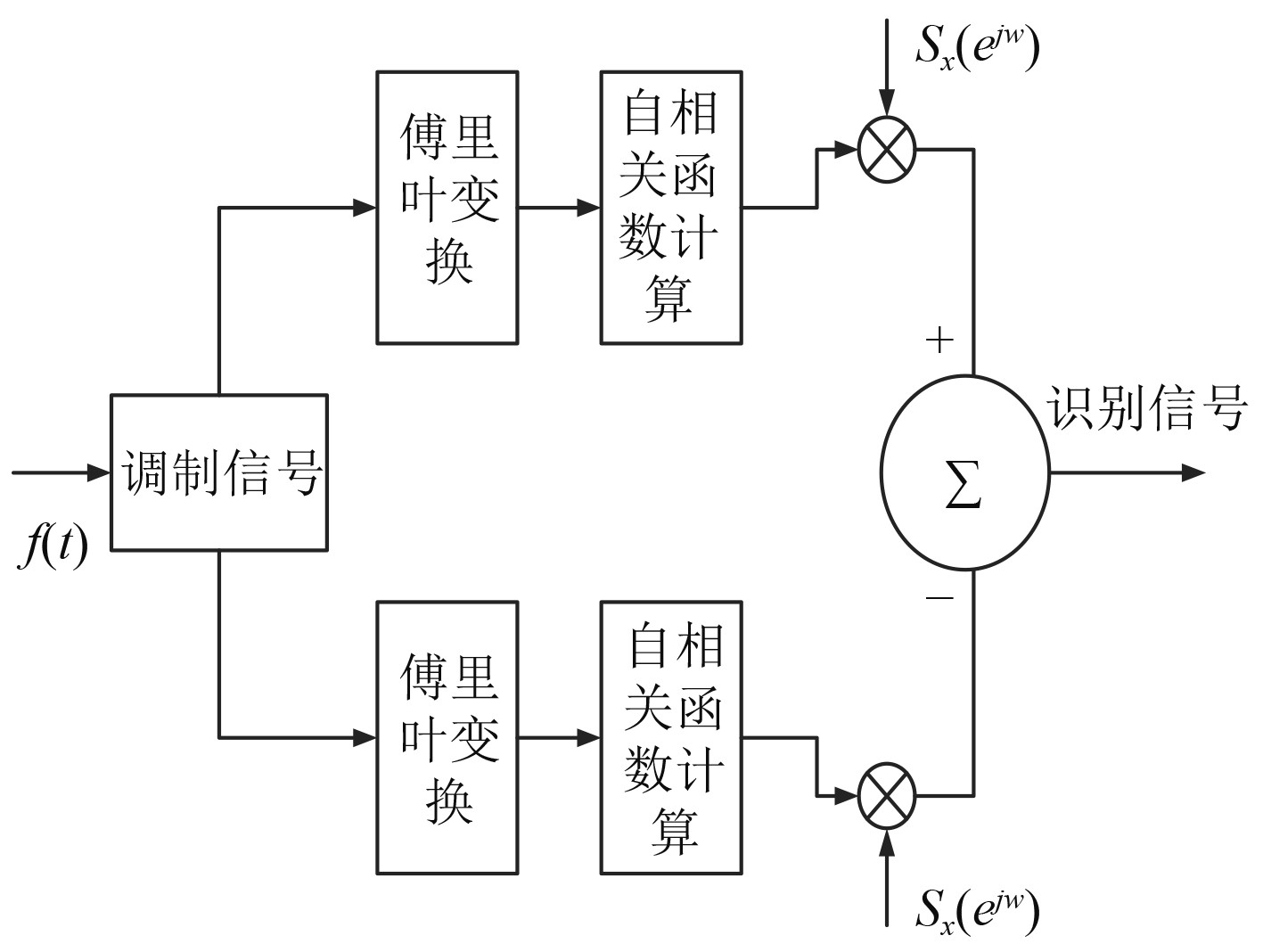
|
图 5 频域谱分析模式识别方法基本原理 Fig. 5 Basic principle of pattern recognition method in frequency domain spectral analysis |
谱分析法的自相关函数计算公式为:
| $ {S_x}\left( {{e^{jw}}} \right) = \sum\limits_{m = - \infty }^\infty {{R_x}} (m){e^{ - j\omega t}} \text{,} $ |
信号的功率谱密度为:
| $ {p_x}(w) = \frac{1}{{2{\text{π}} }}\int_{ -{\text{π}} }^{\text{π}} {{S_x}} \left( {{e^{jw}}} \right){e^{j\omega }}{\rm{d}}\omega 。$ |
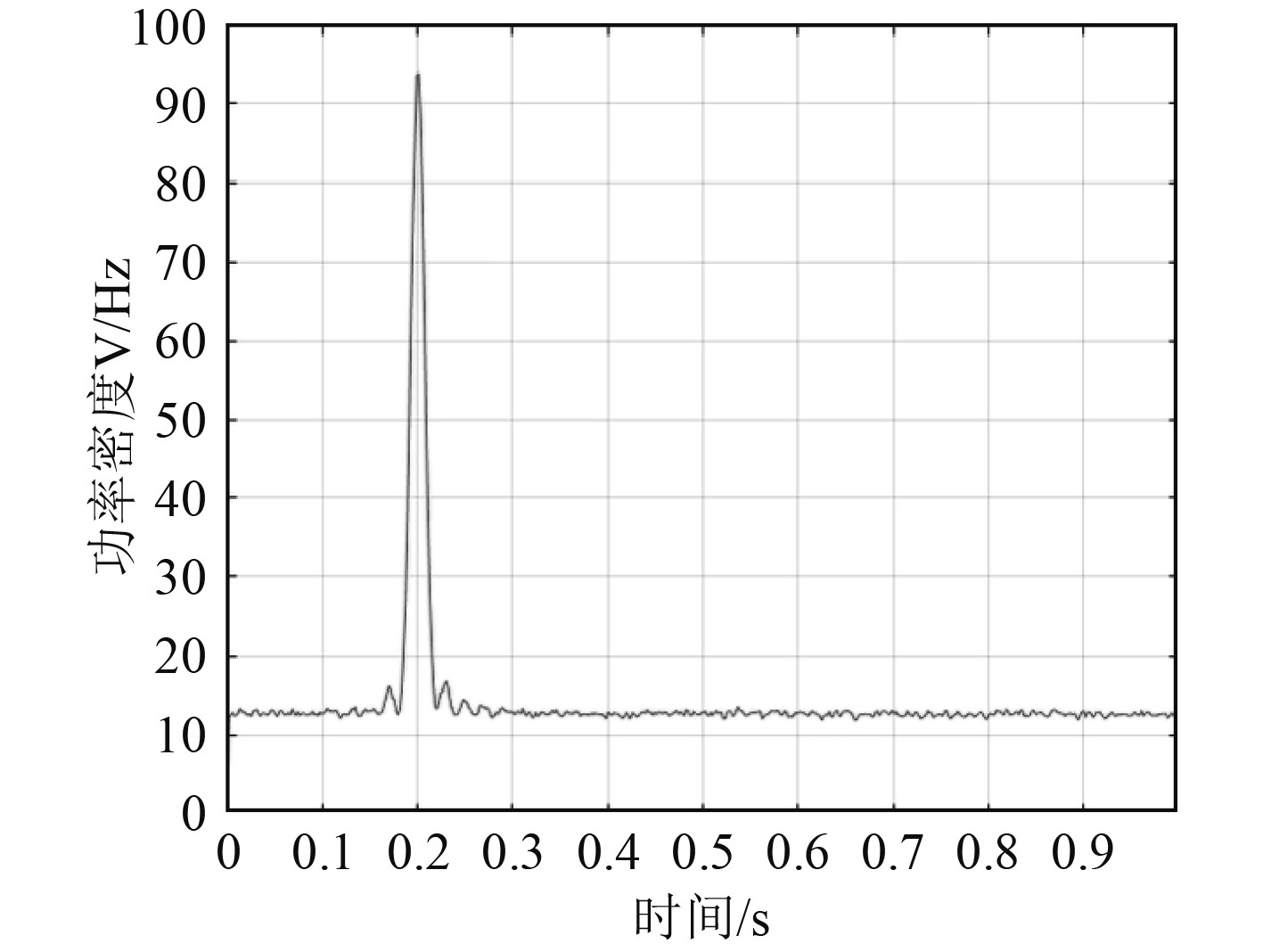
本文采用Matlab对输入调制信号的模式识别效果进行测试,输入信号为ASK振幅键控信号[6],在Matlab中得到的功率谱密度仿真曲线如图6所示。
|
图 6 Matlab中得到的功率谱密度仿真曲线 Fig. 6 The power spectral density simulation curve obtained in Matlab |
| [1] |
李鹏程, 程俊平, 叶畅, 等. 基于深度学习的电磁信号调制识别方法[J]. 安全与电磁兼容, 2023(1): 34–40. LI Peng-cheng, CHENG Jun-ping, YE Chang, et al. Modulation and identification method of electromagnetic signal based on deep learning[J]. Safety and Electromagnetic Compatibility, 2023(1): 34–40. |
| [2] |
冯忠明, 王景岩, 李奎贤. 基于多模态深度学习的信号调制识别[J]. 太赫兹科学与电子信息学报, 2022, 20(12): 1326-1334. FENG Zhong-ming, WANG Jing-yan, LI Kui-xian. Signal modulation recognition based on multimodal deep learning[J]. Journal of Terahertz Science and Electronics Information Technology, 2022, 20(12): 1326-1334. |
| [3] |
李振星, 赵晓蕾, 刘伟承, 等. 基于Transformer的通信信号调制识别方法[J]. 太赫兹科学与电子信息学报, 2022, 20(12): 1311-1317. LI Zhen-xing, ZHAO Xiao-lei, LIU Wei-cheng, et al. Communication signal modulation recognition method based on Transformer[J]. Journal of Terahertz Science and Electronics Information Technology, 2022, 20(12): 1311-1317. |
| [4] |
杜宇, 杨新权, 张建华, 等. 基于循环谱截面智能分析的混合信号调制识别方法[J]. 系统仿真学报, 2023, 35(1): 146-157. DU Yu, YANG Xin-quan, ZHANG Jian-hua, et al. Mixed-signal modulation and identification method based on intelligent analysis of cyclic spectrum cross-section[J]. Journal of System Simulation, 2023, 35(1): 146-157. |
| [5] |
薛德鑫, 单涛, 董士军, 等. 一种非协作通信信号调制方式识别方法[J]. 现代防御技术, 2022, 50(5): 152-159. XUE De-xin, SHAN Tao, DONG Shi-jun, et al. A method for identifying the modulation mode of non-cooperative communication signal[J]. Modern Defense Technology, 2022, 50(5): 152-159. |
| [6] |
张静, 于蕾, 侯长波, 等. 基于时频特征的跳频信号调制识别[J]. 太赫兹科学与电子信息学报, 2022, 20(1): 40-46. ZHANG Jing, YU Lei, HOU Chang-bo, et al. Frequency hopping signal modulation recognition based on time-frequency characteristics[J]. Journal of Terahertz Science and Electronics Information Technology, 2022, 20(1): 40-46. |
 2023, Vol. 45
2023, Vol. 45
