2. 武汉理工大学 船海与能源动力工程学院,湖北 武汉 430063;
3. 国家水运安全工程技术研究中心,湖北 武汉 430063
2. School of Marine and Energy Power Engineering, Wuhan University of Technology, Wuhan 430063, China;
3. WTS Center, Wuhan 430063, China
振动常常出现于各种工程应用,其危害不容小觑,尤其在动车[1-2]、船舶[3]、航空[4]、汽车[5]、精密仪器[6]等领域对于振动的控制有很高要求,因此振动控制成为了热点探索问题。以船舶为例,振动不仅会让内部结构变形,缩短各零件的使用寿命,还会影响船体稳定性,降低乘客的舒适感。因此,采取有效的控制策略减少振动带来的危害非常必要。
振动控制分为被动控制和主动控制[7-8],其中被动控制不需要外界的能量,结构简单,经济可靠,稳定性好,多适用于高频的振动,只能满足一般减振的场合。主动控制更倾向于控制低频振动,且可以与被动控制相结合,大大提高振动控制的效果,因此,主动控制技术开始渐渐发展,国内外对于主动控制技术开展探索取得了不少的成果[9-13]。
在主动控制技术中,作动器的研制成为热点和难点,作动器种类繁多[14],其中的电磁作动器因具有效率高、响应速度快、能量密度高、行程范围大等优点[15]得到广泛应用。惯性式电磁作动器更是因为易安装、线性度好、谐波失真小深受青睐。MEMG SHEN等[16]通过建模仿真,进行磁路的优化,研制出了一款微型电磁作动器;WINBERG等[17]将电动式作动器应用在了船用振动主动控制;安峰岩等[18]研制出了一种新型电磁作动器,在相同质量下,相同体积下可以有更大的输出力。
近年来,国内加大了对于电磁作动器的研究,其研究难点在于如何让相同单位质量体积下的作动器输出力更高,可靠性更强。同时电磁作动器建模上,也缺乏成熟的技术,对于作动器磁路优化缺乏可靠的方法。
基于已有研究,本文对一款新型筒形低频大力值惯性式电磁作动器进行优化分析,得出该电磁作动器可在低频时产生高输出力,对于振动较大的大型结构或设备有良好的应用前景。首先根据电磁作动器特征对其进行了理论分析和仿真建模,利用仿真软件验证该电磁作动漏磁少,线圈处磁感应强度大,磁路质量好等特点,在磁路尺寸方面通过优化方法得到其最优尺寸。从电磁力仿真和实测结果可以得出其性能:输出力大,漏磁少,质量较小,可以满足在低频状态下振动的主动控制。
1 筒形大力值惯性电磁作动器结构原理筒形大力值惯性电磁作动器内部结构如图1所示,主要由动子部分和定子部分组成,其中动子部分由永磁体,衔铁组成,定子部分主要包括线圈,线框架,导磁外壳。动子和定子之间留有一定的间隙,供动子上下移动,其工作原理如图2所示。在上、下线圈通入同方向交流电,由于中间线圈反向缠绕,其电流方向与上、下线圈电流方向相反。由左手定则可知,上、中、下线圈受到同一方向的电磁力(安培力),同时中间动子会受到同样大小的反作用力,改变交流电的频率及大小,可改变中间动子往复运动的频率和幅值。该作动器为筒形设计,上下行程较长,且可以布置的线圈长,内部有最佳磁路结构,能产生最大的电磁力,因而能实现大力值输出。
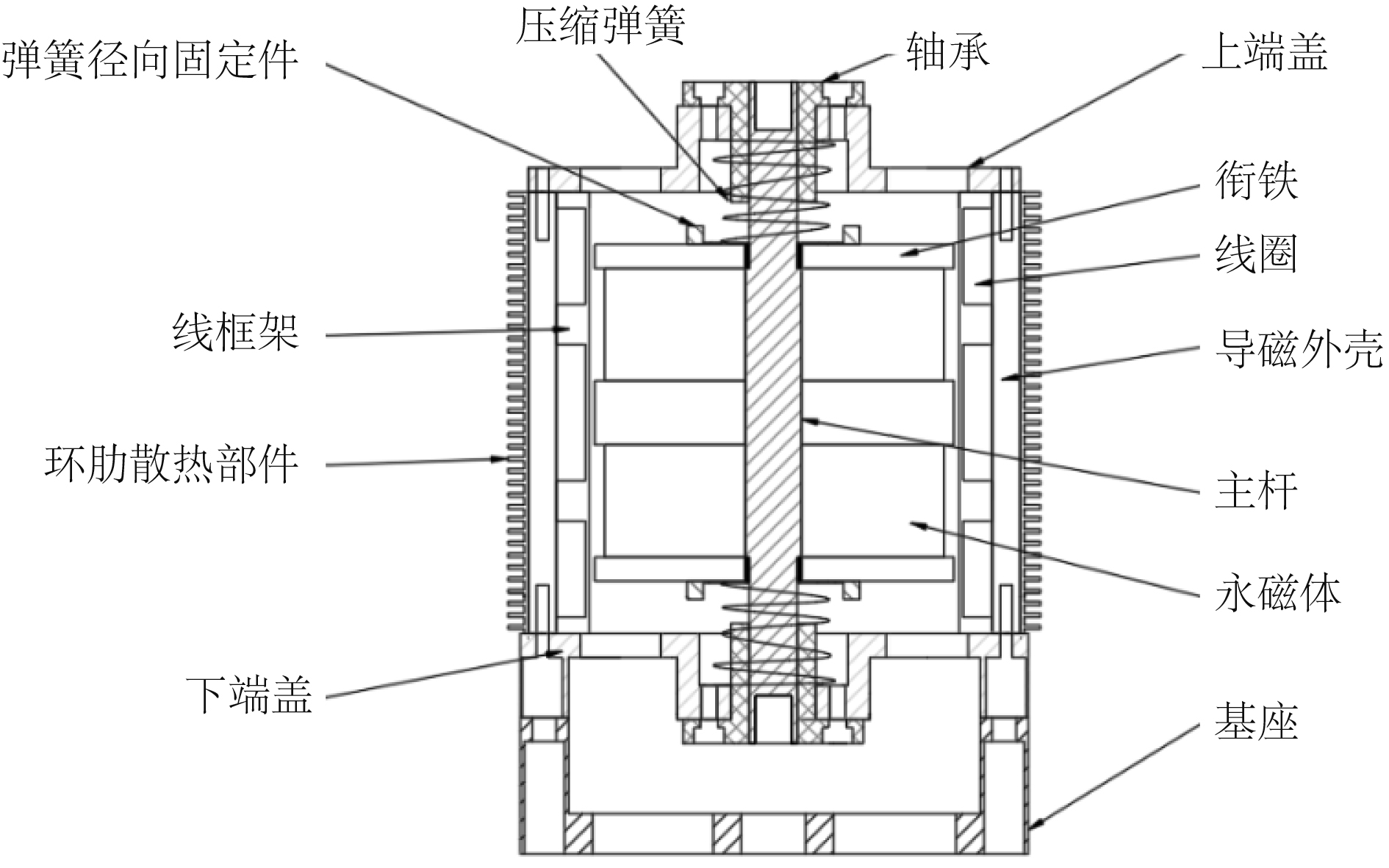
|
图 1 电磁作动器内部结构 Fig. 1 Internal structure of electromagnetic actuator |
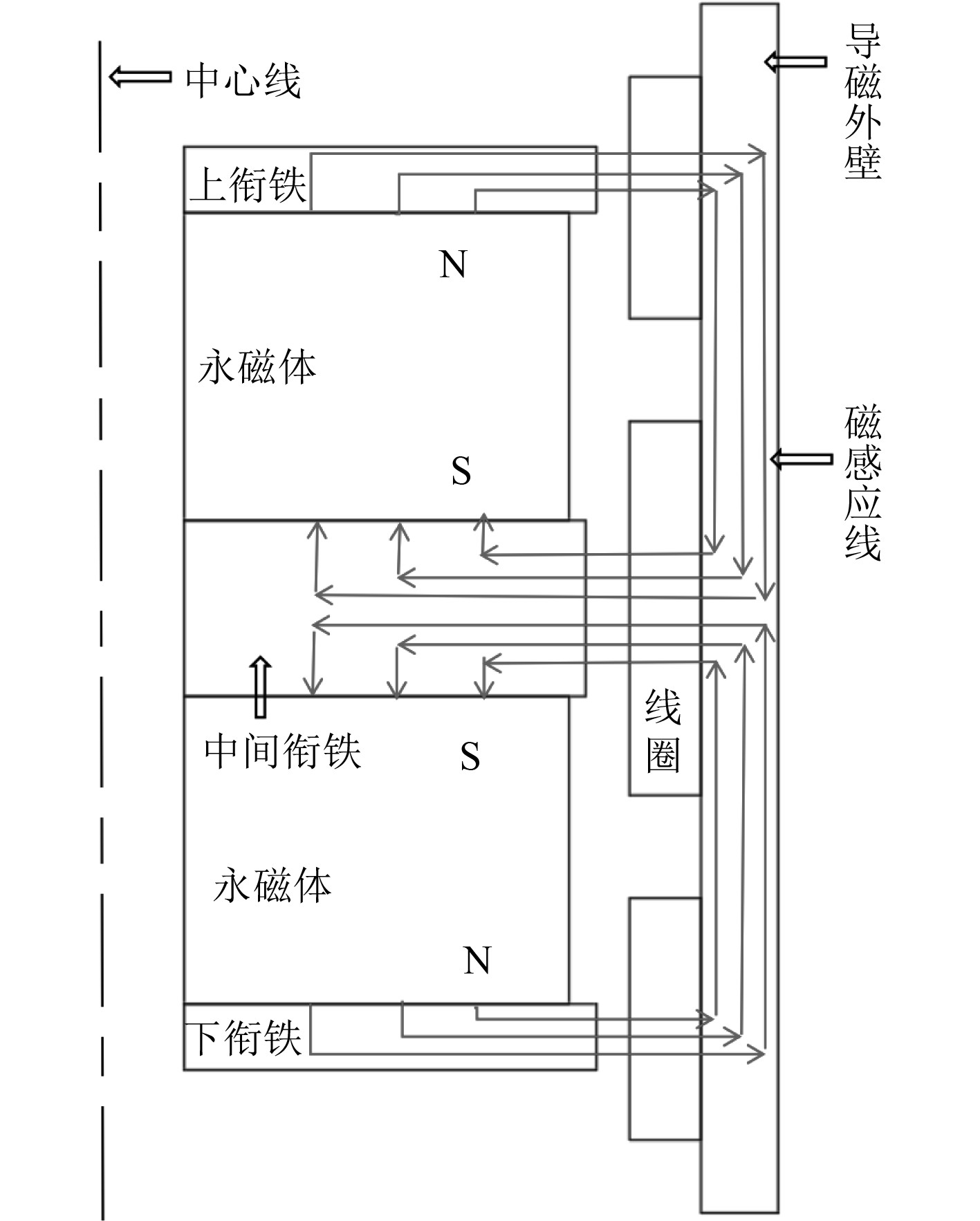
|
图 2 电磁作动器磁路右半部分剖视图 Fig. 2 Sectional view of the right half of the magnetic circuit of the electromagnetic actuator |
该电磁作动器可简化为受电磁激励力作用下的单自由度模型[19],如图3所示。设电磁作动器动子部分的质量为m,动子上下行程y,被控对象质量为M,被控对象的位移为y1,弹簧刚度为k,阻尼系数为c,线圈受到的电磁力为Fa,电磁作动器对外输出力为Fd。
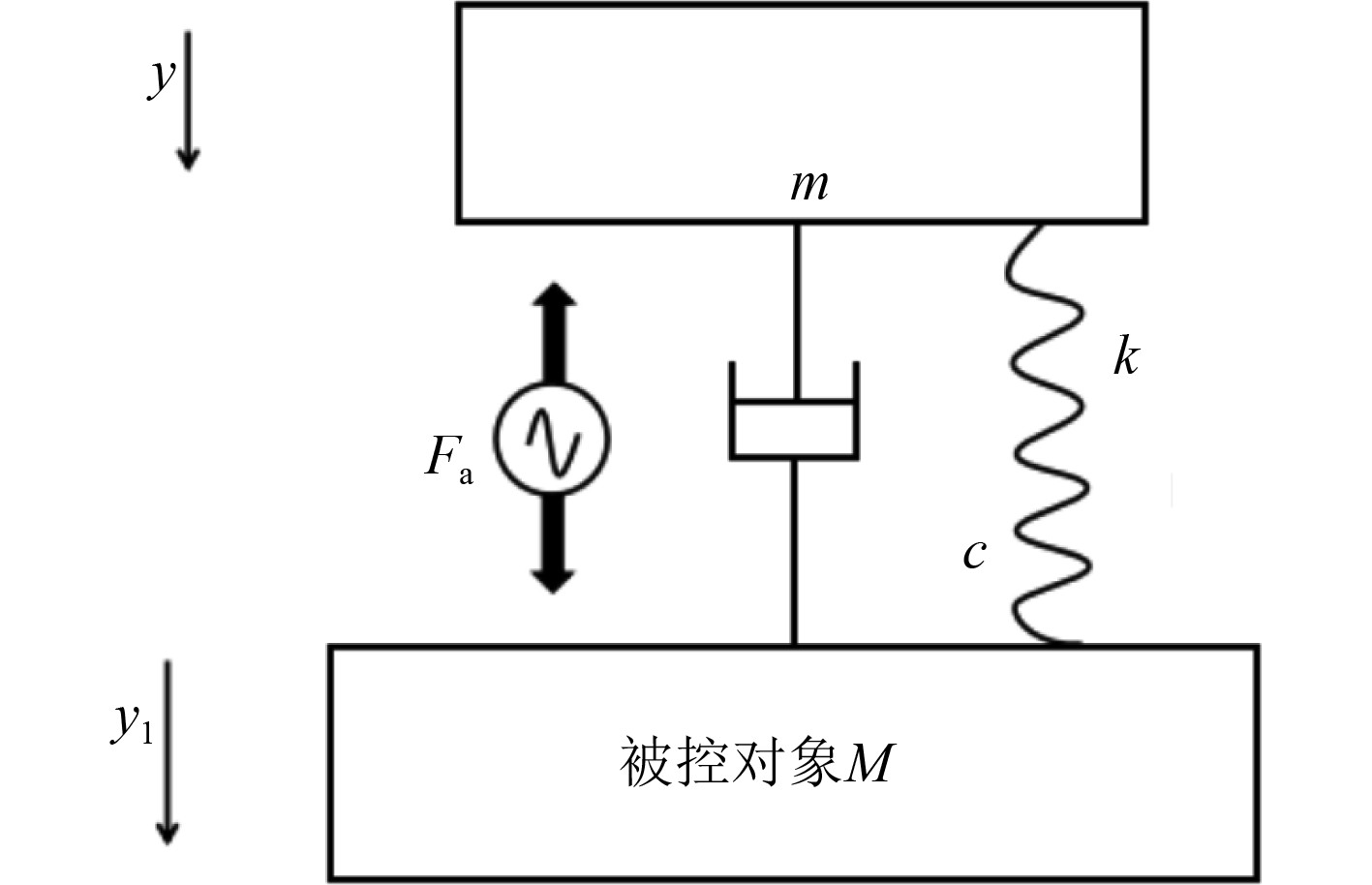
|
图 3 电磁作动器物理模型 Fig. 3 Physical model of electromagnetic actuator |
振动微分方程为:
| $ m\ddot {y} + c(\dot {y}- \dot {{y_1}}) + k(y - {y_1}) = - {F_a} ,$ | (1) |
被控对象M所受合力
| $ {F_{{d}}} = {F_a} + c(\dot y- \dot {{y_1}}) + k(y - {y_1}) ,$ | (2) |
结合式(1)得
| $ {F_d} = - m\ddot y= {F_a} + c(\dot y - \dot {{y_1}}) + k(y - {y_1})。$ | (3) |
从式(3)可以看出,电磁作动器输出力是由质量力提供的,这也是惯性式电磁作动器名称的来源[20]。
一般来说被控对象由基座与地面处于固定状态,因此可以忽略被控对象的位移和加速度。令
| $ {F_d} = \frac{{m{\omega ^2}}}{{m{\omega ^2} - jc\omega - k}}{F_a}。$ | (4) |
令
| $ \frac{{{F_d}}}{{{F_a}}} = \frac{{\omega /\omega _n^2}}{{{\omega ^2}/\omega _n^2 - 2j\zeta \omega /{\omega _n} - 1}} ,$ | (5) |
将频率比
| $ H(\overline \omega ) = \frac{{{F_d}}}{{{F_a}}} = \frac{{\overline \omega }}{{{{\overline \omega }^2} - 1 - 2j\zeta \overline \omega }}。$ | (6) |
从式(6)可知,电磁作动器对外输出力
| $ \left| {H(\overline \omega )} \right| = \left| {\frac{{{F_d}}}{{{F_a}}}} \right| = \frac{{{{\overline \omega }^2}}}{{\sqrt {{{({{\overline \omega }^2} - 1)}^2} + 4{\zeta ^2}{{\overline \omega }^2}} }},$ | (7) |
| $ \angle H(\overline \omega ) = \angle \left| {\frac{{{F_d}}}{{{F_a}}}} \right| = \arctan \left(\frac{{2\zeta \overline \omega }}{{{{\overline \omega }^2} - 1}}\right)。$ | (8) |
根据式(7)和式(8),利用Matlab画出电磁作动器输出力和电磁力比值的幅值特性和相频特性在不同阻尼比下随强迫振动频率比变化规律,如图4所示。

|
图 4 电磁作动器输出力和电磁力比值的幅频特性及相频特性曲线 Fig. 4 Amplitude frequency characteristic and phase frequency characteristic curve of output force and electromagnetic force ratio of electromagnetic actuator |
可知,当阻尼比取值小于0.7,频率比接近1时,输出力均大于电磁力,其相位差为90°,此时的动子部分发生共振。随着频率的增大,输出力与电磁力之比逐渐趋近于1,即在非共振区,电磁力在数值上与输出力大小相等。因此在频率足够大时,可以通过对电磁作动器进行建模仿真,检测该电磁作动器的磁路结构是否有最大电磁力,从而反映其输出力大小,验证该电磁作动器的低频大力值输出的特性[21]。
3 筒形大力值惯性电磁作动器建模及优化分析基于以上特性分析,对设计的电磁作动器进行研究,其磁路尺寸如图5所示。该作动器整机质量为8 kg,动子质量为3.595 kg,动子部分主要由上中下衔铁和上下2块永磁体组成,衔铁采用DT4C电工纯铁,永磁体材料为N52M。定子部分由上中下线圈和导磁外壁组成,材料分别为铜线和DT4C,固有频率在20 Hz左右,线圈可布置匝数为575,设定通过的激励为2.5 A。
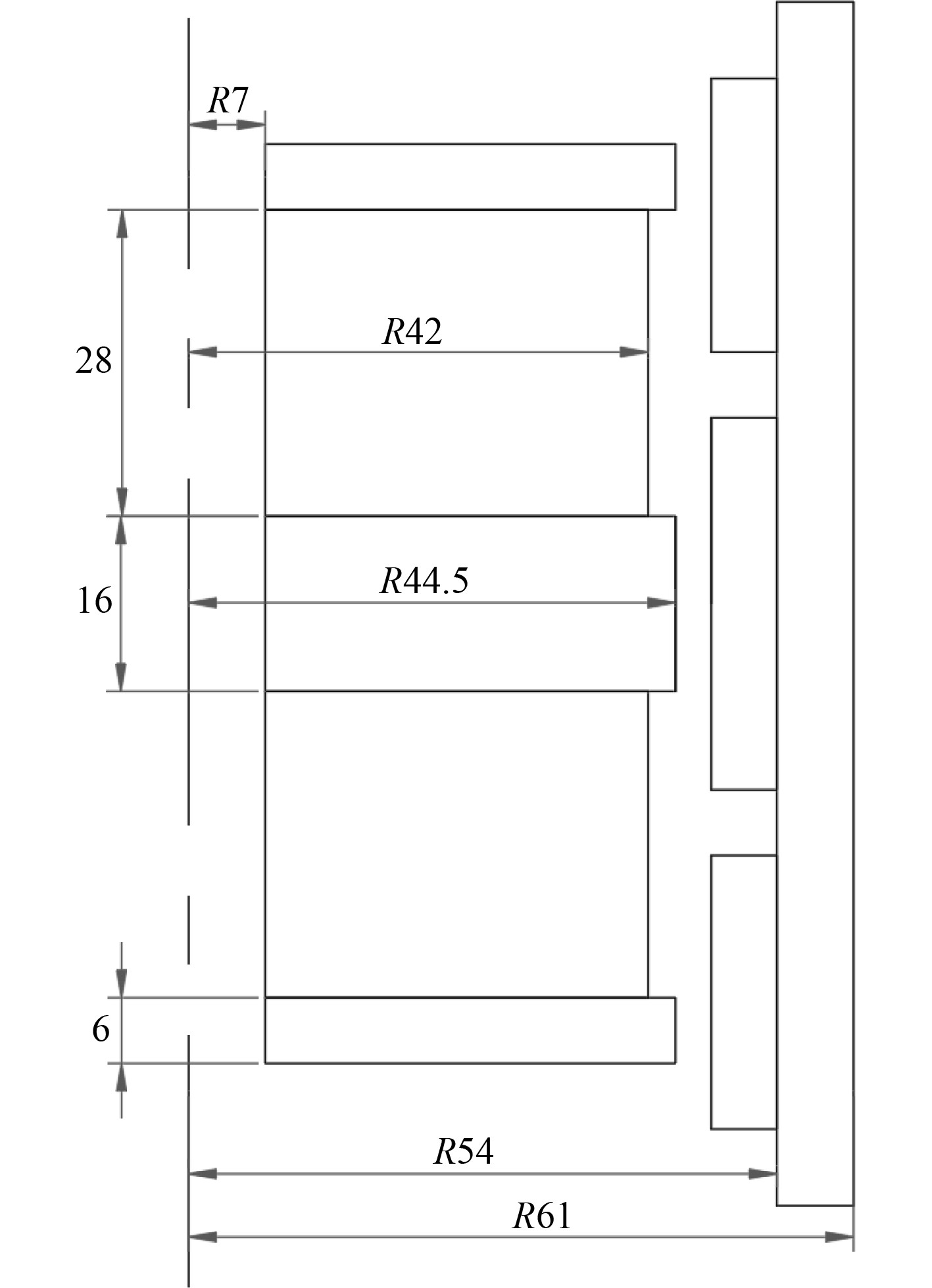
|
图 5 电磁作动器算例模型尺寸 Fig. 5 Model dimensions of electromagnetic actuator |
采用Ansoft Maxwell对电磁作动器动子和定子部分建模及电磁力计算,得出电磁作动器磁场及磁感应强度分布情况,如图6所示。其中,模型为圆柱形且对称的半边结构。
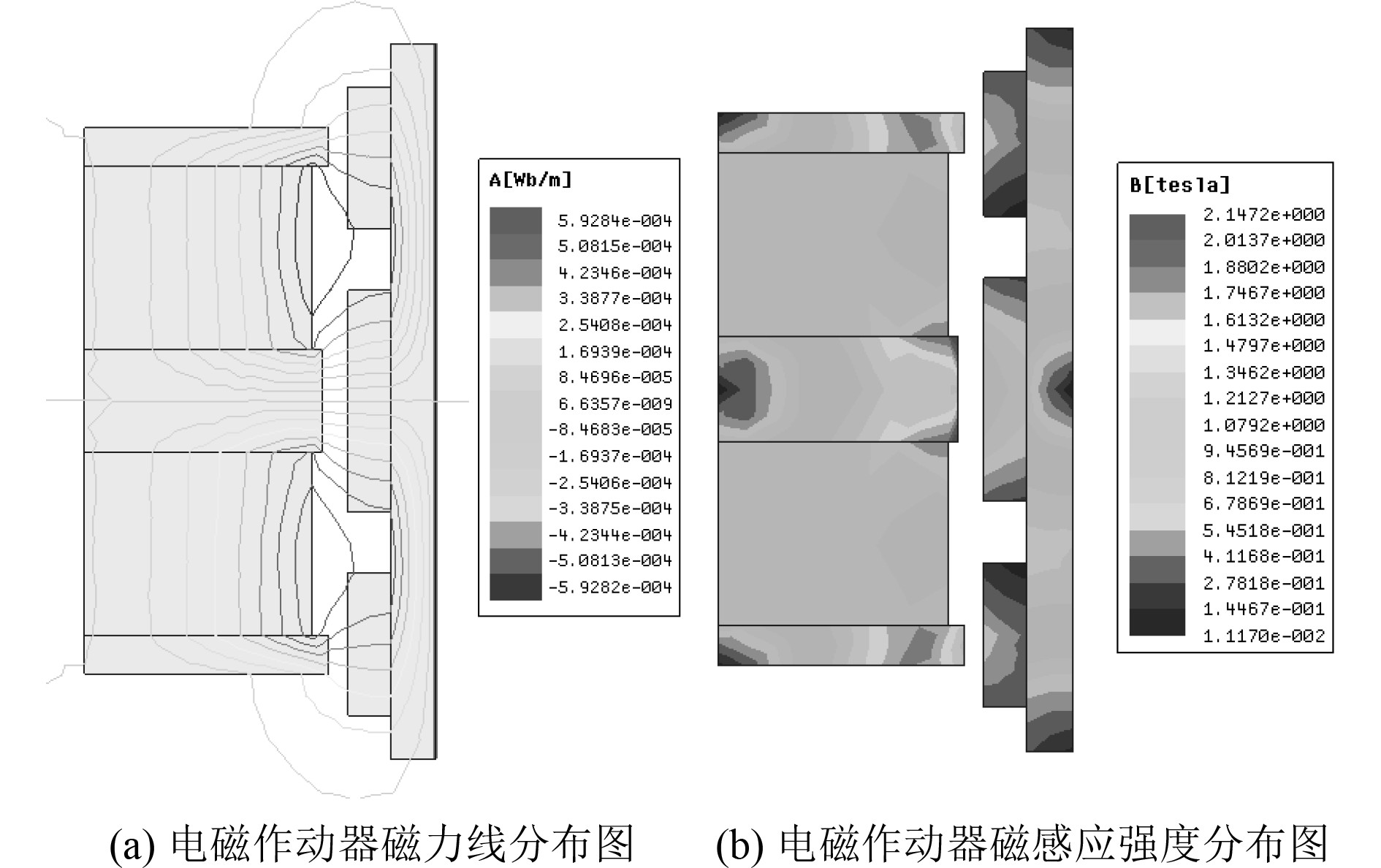
|
图 6 电磁作动器建模仿真计算结果 Fig. 6 Modeling and simulation results of electromagnetic actuator |
从图6 (a)磁路磁力线分布图可看出,除了永磁体内侧存在少量的漏磁外,其余磁力线均从磁源发出,经衔铁和线圈回到永磁体,磁场漏磁少。从图6 (b)的磁感应强度分布云图可看出,最大磁感应强度出现在中间衔铁右端,上下衔铁磁感应强度达到1.8 T左右,接近电工纯铁DT4C的饱和磁感应强度,衔铁的利用率高,磁路得到了较好的利用。
3.1 电磁作动器磁路结构参数对其磁感应强度影响分析通过改变中间衔铁厚度与永磁体厚度以及导磁外壁厚度与永磁体外径的参数,研究主要部件参数对线圈磁感应强度的影响,并确定作动器在该算例质量下输出力最大时主要部件的最优磁路尺寸。
1)中间衔铁厚度与永磁体厚度对磁感应强度的影响
参考该作动器尺寸(中间衔铁厚度16 mm,永磁体厚度28 mm),将电磁作动器的中间衔铁厚度取值为10~20 mm,间隔2 mm,共6组,每组的永磁体厚度分别取26~32 mm,间隔为1 mm,其他尺寸保持不变,共42个数据,通过仿真计算,得到不同中间衔铁厚度和不同永磁体厚度情况下线圈处磁场强度变化,如图7所示。
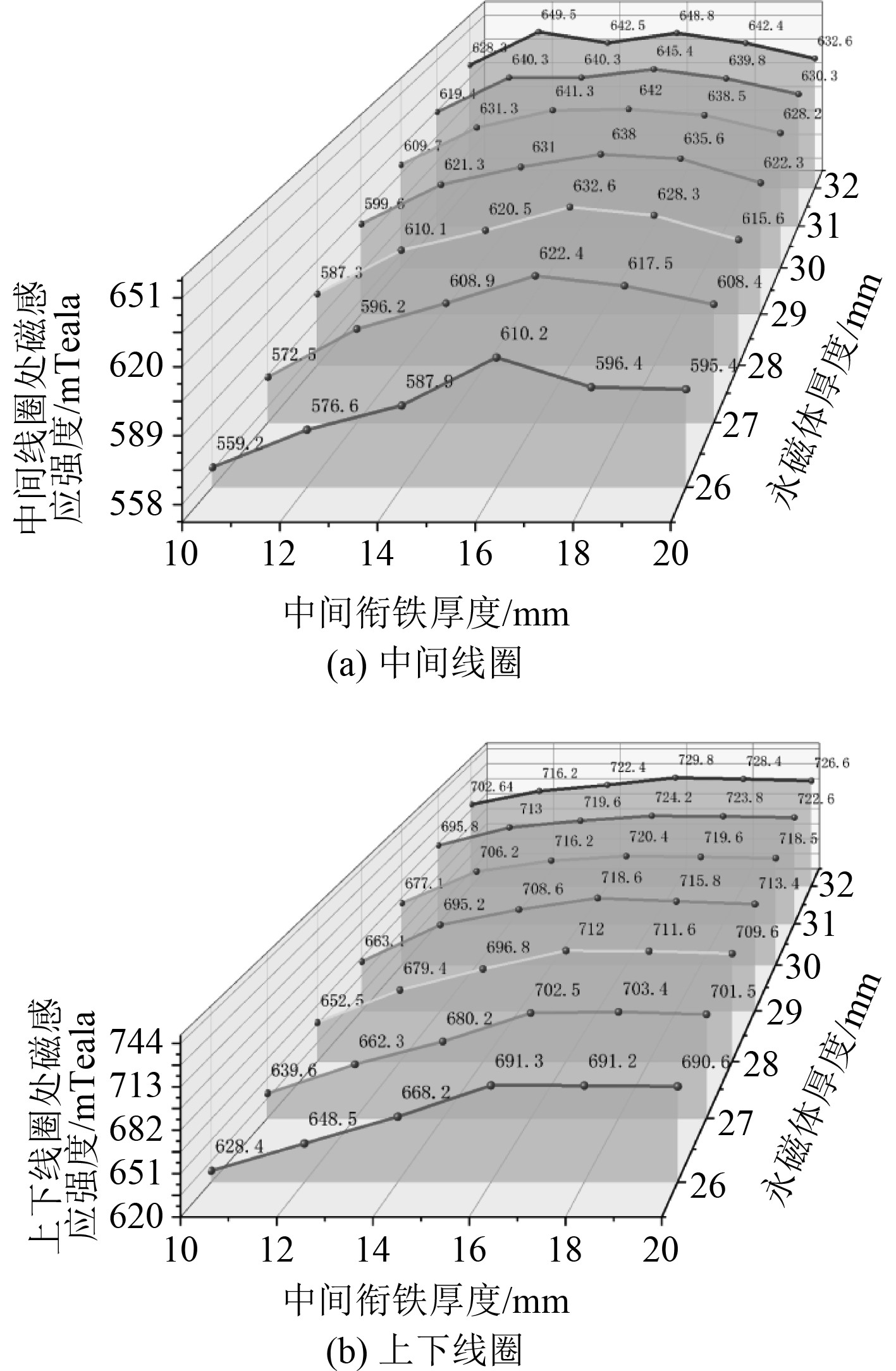
|
图 7 线圈处磁感应强度随中间衔铁厚度与永磁体厚度变化曲线图 Fig. 7 Variation curve of magnetic induction intensity at the coil with the thickness of intermediate armature and permanent magnet |
可以看出,随着中间衔铁厚度的增大,上中下间线圈处磁感应强度先增大,到16 mm时整体最大,然后缓慢减小,原因在于当中间衔铁厚度持续减小时,其磁阻会急剧增大,使得线圈处磁感应强度开始下降。而随着永磁体厚度的增大,各组的磁感应强度都增大,主要原因是磁路磁能会随着永磁体厚度增大而增大,进而导致线圈处磁感应强度增大,取与该电磁作动器动子厚度相同的几组尺寸,算出其磁感应强度及在该尺寸下动子的质量,如表1所示。
|
|
表 1 相同动子厚度下的磁感应强度及质量 Tab.1 Magnetic induction intensity and mass under the same thickness |
可以看出,当中间衔铁厚度为16 mm,永磁体厚度为28 mm时,上中下线圈处的磁感应强度总值最大,且质量相对较轻,说明该作动器在永磁体厚度及中间衔铁厚度上为最优尺寸。
2)导磁外壁厚度与永磁体外径对磁感应强度的影响
参考该作动器尺寸(导磁外壁厚度7 mm,永磁体外径42 mm),将电磁作动器的永磁体外径取为40~44 mm,间隔1 mm,共5组,每组的导磁外壁厚度分别取为5~9 mm,间隔1 mm,共25个数据,通过仿真计算,得出结果如图8所示。
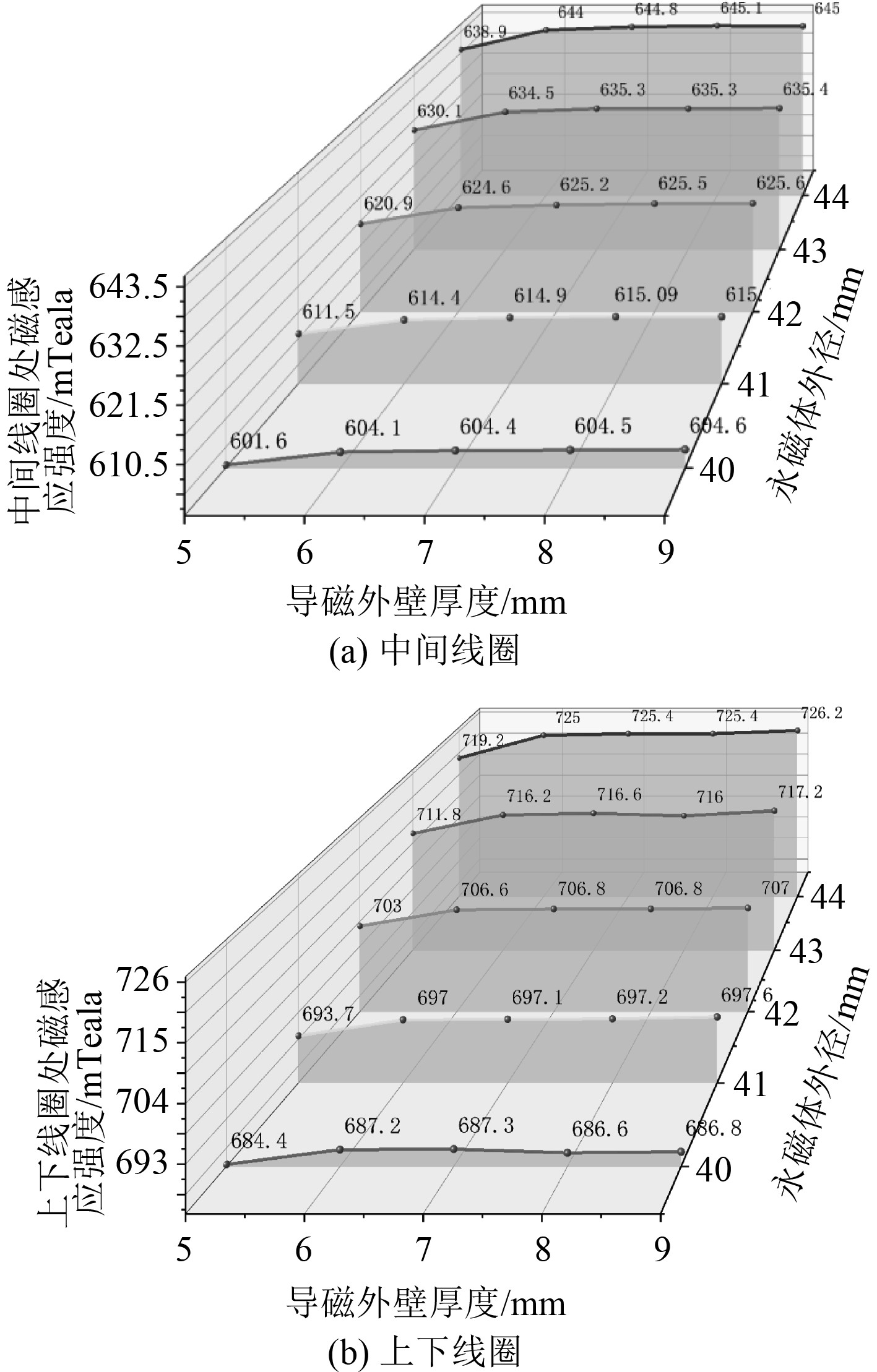
|
图 8 线圈处磁感应强度随永磁体外径与导磁外壁厚度变化曲线图 Fig. 8 Variation curve of magnetic induction intensity at coil with outer diameter of permanent magnet and outer wall thickness of magnetic conduction |
可以看出,导磁外壁厚度在6~9 mm之间变化时,中间线圈处磁感应强度变化很小,上下线圈处磁感应强度有小幅度减小后增大,但在导磁外壁小于6 mm时,其磁阻进入快速增长区间,磁感应强度快速减小。而随着永磁体外径的不断增大,磁感应强度明显增大。
考虑到稳定性及质量问题,选取导磁外壁为7 mm时,各永磁体外径下对应的磁感应强度和动子及外壁质量参数如表2所示。
|
|
表 2 导磁外壁为7 mm时磁感应强度及质量参数 Tab.2 Magnetic induction intensity and quality parameters when the outer wall of magnetic conduction is 7 mm |
可以看出,随着永磁体外径的增加,线圈处的磁感应强度线性增大,但随之牺牲的便是质量和尺寸的不断增加,因此,如果设计的电磁作动器对质量尺寸有要求,便可以取最小永磁体外径.反之,可以选择增大永磁体外径增大输出力,该作动器考虑到输出力要求,在导磁外壁和永磁体外径的选取上符合最优尺寸。
3)永磁体内径与气隙宽度对磁感应强度的影响
同样参考该作动器尺寸(永磁体内径7 mm,气隙宽度3.0 mm),将电磁作动器的永磁体内径取为5~9 mm,间隔为1 mm,共5组,每组的气隙宽度分别取2~4 mm,间隔为0.5 mm,共25个数据,通过仿真计算,得出结果如图9所示。
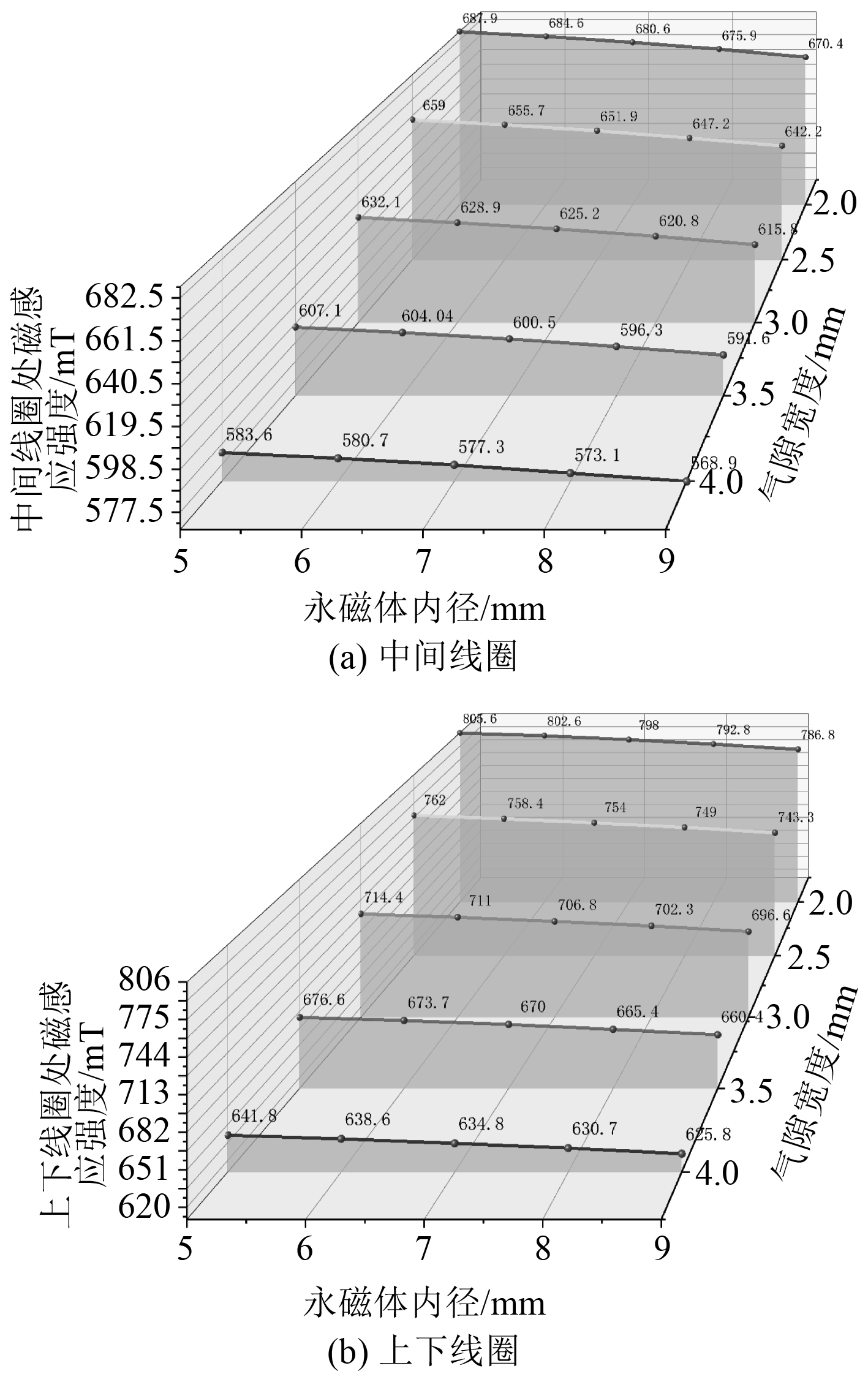
|
图 9 线圈处磁感应强度随永磁体外径与导磁外壁厚度变化曲线图 Fig. 9 Variation curve of magnetic induction intensity at coil with outer diameter of permanent magnet and outer wall thickness of magnetic conduction |
可以看出,随着永磁体内径的不断增大,线圈处的磁感应强度呈线性下降,原因是永磁体面积减小,磁路磁能减小。而随着气隙宽度的不断减小,磁感应强度大幅增长,因此,在能保证装配精度的情况下,气隙宽度越小越好,但也需要留有一定间隙来保证动子的上下运动。永磁体内径的增大,可以减小动子的质量,在一定范围内对磁感应强度的影响不是很大,可以考虑适当增大永磁体内径,该电磁作动器考虑到装配精度的问题,选取气隙宽度3.0 mm,永磁体内径7 mm,符合最优尺寸的选取。
通过以上分析可以看出,该电磁作动器算例模型尺寸为最佳磁路尺寸,同时增大永磁体厚度、永磁体外径或气隙宽度有利于增大磁感应强度。导磁体外壁厚度对磁感应强度的影响不大,但却会增大质量;永磁体内径的增大会减小磁感应强度,但能减小质量。因此,对于这两者的选择可以根据需求考虑。
3.2 筒形大力值惯性电磁作动器电磁力仿真分析根据该电磁作动器算例模型尺寸,利用Ansoft Maxwell仿真软件,设定线圈通过最大电流为2.5 A,频率为20 Hz,上中下线圈匝数分别为162匝,251匝,162匝,总安匝数为1437.5 A。计算该电磁作动器输出力值大小,结果分析得到导磁外壁所受电磁力如图10所示。
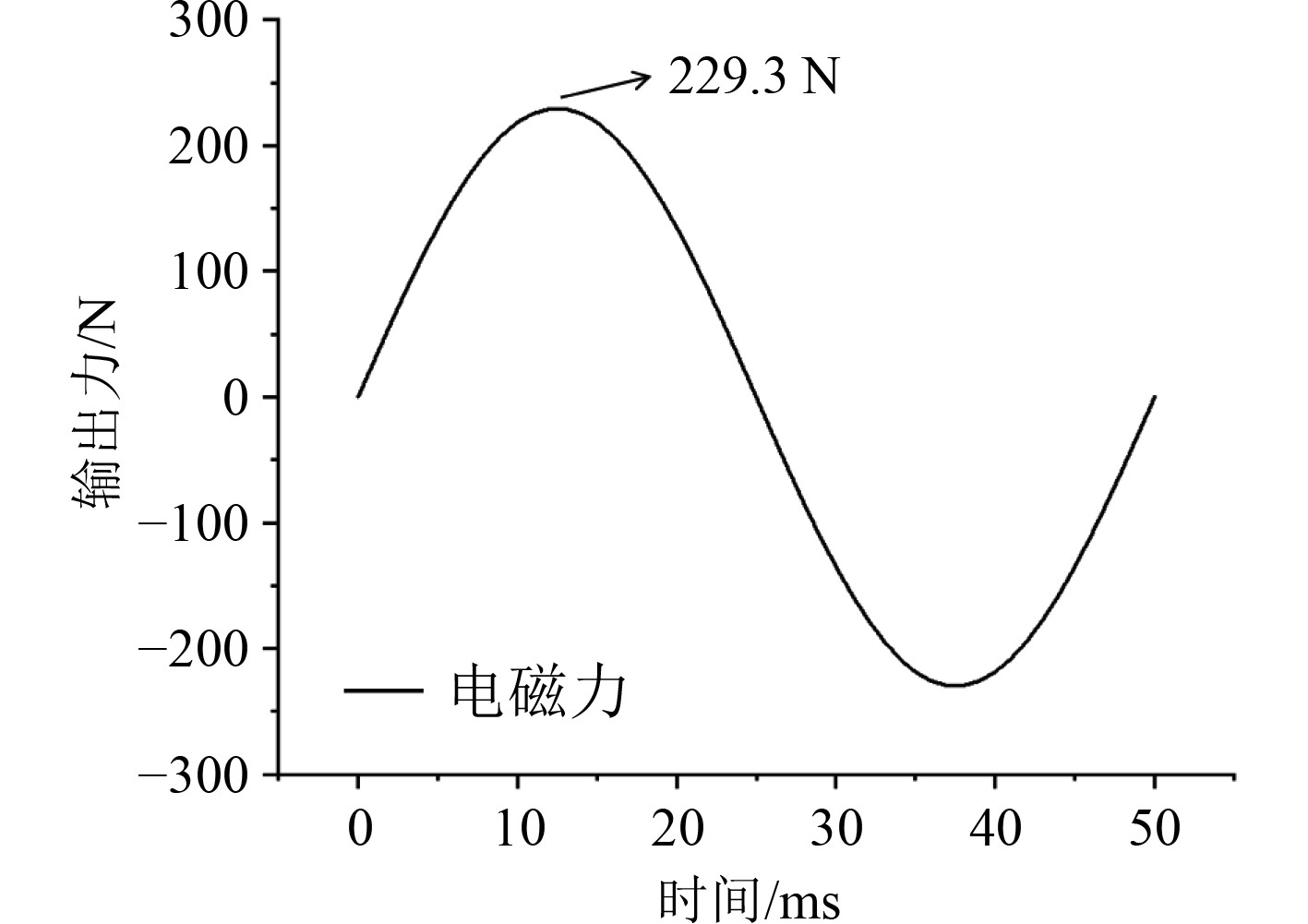
|
图 10 导磁外壁所受电磁力 Fig. 10 Electromagnetic force on magnetic conducting outer wall |
可以看出,电磁作动器电磁力大小随时间变化呈正弦函数,在峰值处产生的最大电磁力为229.3 N。
4 筒形大力值惯性电磁作动器电磁力测试结果 4.1 输出力幅频特性测试通过测试电磁作动器输出力随电流频率的变化关系,并结合理论分析可以得出动子的共振频率。电流幅值分别在1 A,1.5 A,2 A,2.5 A和3 A时,电磁作动器惯性质量部分的最大输出力随电流频率变化的规律如图11所示。
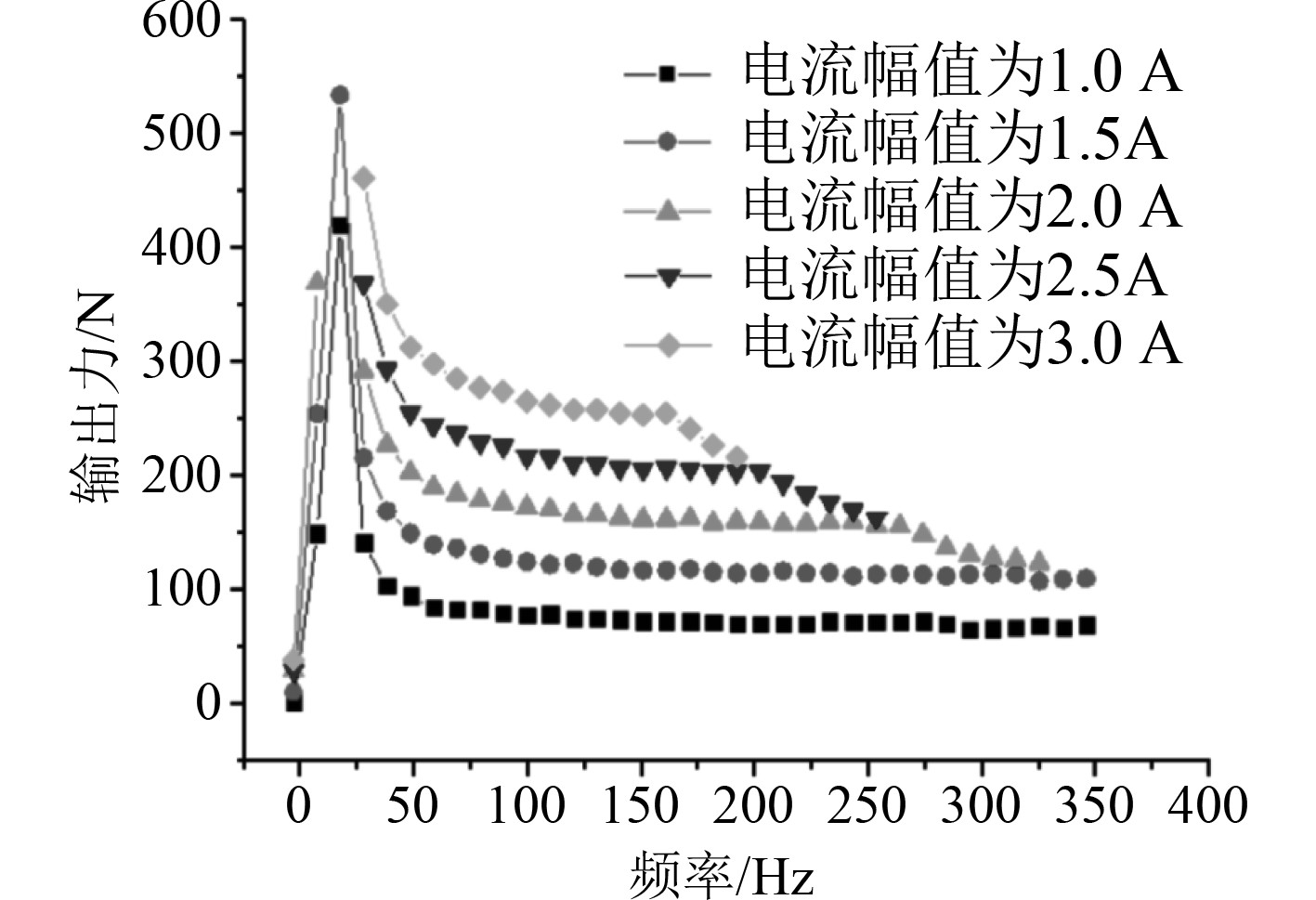
|
图 11 电磁作动器最大输出力的幅频特性曲线图 Fig. 11 Amplitude frequency characteristic curve of maximum output force of electromagnetic actuator |
可以看出,当电流频率在20 Hz左右时,输出力振动响应最大,表明此频率附近是中间动子的共振频率。在实际测试时,共振频率附近的输出力虽然很大,但是产生的噪声和振动也特别大,可能对作动器产生较大的损耗,因此其最佳工作范围需高于固有频率。电磁作动器20~300 Hz之间都具有很大的输出力,表明该电磁作动器低频大力值输出的特点。
4.2 输出力线性度测试输出力特性作为电磁作动器重要的性能参数,其线性度影响着实际的控制效果。在电磁作动器运行的稳定区间下(以100 Hz,150 Hz ,200 Hz电流为例),其输出力随电流大小的响应规律如图12所示。

|
图 12 定频下电磁作动器输出力随电流的响应曲线 Fig. 12 Response curve of output force of electromagnetic actuator with current under constant frequency |
可知,动子输出力与电流具有良好的线性,有利于对电磁作动器输出力的可控性。
根据幅频特性的理论分析,将电流频率调整为电磁作动器固有频率的10倍以上,得到与电磁力相等的实际输出力。因此,将频率定为200 Hz的正弦交流电,其幅值为2.5 A,实测电磁作动器最大输出力即电磁力为223.5 N(见图12),与仿真计算得出的电磁力大小略有误差。考虑到电磁力仿真计算与实际测试环境不同,永磁体性能参数是在20 ℃环境下设定的,永磁体性能会受到温度的影响,而实际运行中电磁作动器会产生温升,所以电磁力仿真计算和实测的误差在可接受范围内,基本验证了仿真的正确性。
5 结 语本文研究一种筒形大力值惯性式作动器,通过仿真建模,改变磁路结构等优化方法以及测试实验,得出了以下结论:
1)在该电磁作动器的磁路结构中,产生的漏磁少,线圈中磁感应强度高,磁路质量好,衔铁的利用率高。
2)该电磁作动器在中间衔铁厚度及永磁体厚度的选取上为最优尺寸,达到了质量最小、磁感应强度最高的要求。而在导磁外壁厚度及永磁体外径、气隙宽度和永磁体内径的选取上,满足了该作动器在相同质量下拥有最大输出力的要求。
3)该电磁作动器在电流为20 Hz左右产生共振,其输出力最大,但是噪声和振动也很大,因此其最佳输出频率范围在20~300 Hz之间,具有低频大力值输出的特点。同时动子的输出力与电流具有良好的线性,可控性较好。该测试结果证明了仿真的正确性。
| [1] |
黄彩虹, 曾 京, 魏 来. 铁道车辆蛇行稳定性主动控制综述[J]. 交通运输工程学报, 2021, 21(1): 267-284. |
| [2] |
曹辉, 张卫华, 缪炳荣. 基于二系垂向作动器与压电作动器的动车组车体振动控制[J]. 交通运输工程学报, 2018, 18(3): 105-113. DOI:10.3969/j.issn.1671-1637.2018.03.012 |
| [3] |
尚国清, 郭有松. 舰船振动隔离技术理论与应用研究进展[J]. 舰船科学技术, 2006, 28(1): 15-18. SHANG G Q, GUO Y S. Research progress on theory and application of ship vibration isolation technology[J]. Ship Science and Technology, 2006, 28(1): 15-18. |
| [4] |
康建云. 压电智能柔性结构振动主动控制研究[D]. 厦门: 厦门大学, 2019.
|
| [5] |
METERED H, KOZEK M, ŠIKA Z. Vibration control of active vehicle suspension using fuzzy based sliding surface[J]. International Journal of Fuzzy Systems and Advanced Applications, 2015, 2: 41-48. |
| [6] |
ULGEN D, ERTUGRUL O L, OZKAN M Y, Measurement of ground borne vibrations for foundation design and vibration isolation of a high-precision instrument[J]. Measurement, 2016, 93(1): 385–396.
|
| [7] |
徐鉴. 振动控制研究进展综述[J]. 力学季刊, 2015, 36(4): 547-564. XU J. Review on research progress of vibration control[J]. Quarterly Journal of Mechanics, 2015, 36(4): 547-564. DOI:10.15959/j.cnki.0254-0053.2015.04.001 |
| [8] |
MOMENI M, FALLAH N, Meshfree finite volume method for active vibration control of temperature-dependent piezoelectric laminated composite plates[J]. Engineering Analysis with Boundary Elements, 2021, 130(1): 364–378.
|
| [9] |
张春良, 梅德庆, 陈子辰著. 振动主动控制及其应用(第一版)[M]. 哈尔滨: 哈尔滨工业大学出版社, 2011.
|
| [10] |
XI L X, MING K R, HONG B Z, ZHI Y Z. Active vibration control of a time-varying shafting system using an adaptive algorithm with online auxiliary filter estimation[J]. Sound and Vibration, 2021, 513(1): 116430-1-13. |
| [11] |
SURESH T, YU W. Stability analysis of active vibration of building structures using PD/PID control [J]. Engineering Structures. 2014, 81(1) : 208-218.
|
| [12] |
BENASS L, ELLIOTT SJ, GARDONIO P. Active vibration isolation using an inertial actuator with local force feedback control[J]. Journal of Sound and Vibration. 2004, 276(1-2): 157-179.
|
| [13] |
王震, 孙玉东. 基于惯性作动器的管路系统振动主动控制研究[D]. 北京: 中国舰船研究院, 2014.
|
| [14] |
朱明刚, 刘志刚. 船用柴油发电机组振动主动控制研究[D]. 哈尔滨: 哈尔滨工程大学. 2012.
|
| [15] |
马建国, 帅长庚, 李彦. 主动控制用大输出力电磁作动器优化设计[J]. 应用力学学报, 2018, 35(1): 106-110. |
| [16] |
MENG S, CHRISTOPHE Y, MARTIN A. M. G. Miniaturized PMMA ball valve micropump with cylindrical electromagnetic actuator[J]. Journal of Microelectronic Engineering, 2008, 85(5-6): 1104-1107. DOI:10.1016/j.mee.2007.12.013 |
| [17] |
WINBERG M, JOHANSSON S. Active vibration isolation in ships: a pre-analysis of sound and vibration problem[J]. International Journal of Acoustic and Vibration, 2005, 10(4): 175-196. |
| [18] |
孙红灵, 安峰岩. 一种基于双线圈单动磁体结构的惯性式激振器[P]. CN 204933923U, 2016.
|
| [19] |
STANISLAS L G, MARCO A. Identification by means of a genetic algorithm of nonlinear damping and stiffness of continuous structures subjected to large-amplitude vibrations. Part I: single-degree-of-freedom responses[J]. Mechanical Systems and Signal Processing, 2021, 153(1): 107470-1-28. |
| [20] |
KAI Y, WEI H T, LI Q L, DANIIL Y, JUN lei Wang. Active vibration isolation performance of the bistable nonlinear electromagnetic actuator with the elastic boundary[J]. Sound and Vibration, 2021, 31(1): 116588-1-15. |
| [21] |
LI X H, WAN S K, YUAN J P, YIN Y J, HONG J. Active suppression of milling chatter with LMI-based robust controller and electromagnetic actuator[J]. Journal of Materials Processing Technology, 2021, 297(1): 117238-1-13. |
 2023, Vol. 45
2023, Vol. 45
