0 引　言

在船舶电力驱动系统、船舵、甲板起吊装置中，永磁同步电机被广泛应用。一方面，永磁同步电机因其高可靠性和成本优势，在船舶实际运行过程中发挥着重要作用；另一方面，永磁同步电机的控制技术也决定了电机的能耗、功率曲线等指标，提高船舶电气设备永磁同步电机的控制水平具有十分重要的意义。

在电机控制领域，PID控制技术是一种常用的技术，利用PID比例系数、微分系数、积分系数3个参数的不断优化，永磁同步电机的控制水平能够达到较好的效果。但是随着船载电气设备数量的增加，对电机效率、驱动特性的要求也在不断提高，仅仅依靠PID控制算法进行电机控制已经无法满足要求。目前行业内常用的控制策略优化方式是基于数据库和专家库进行参数修正，但始终无法解决PID控制算法的灵活性较差、控制参数寻优时间长的缺点^[1-2]。

本文提出一种基于粒子群算法和PID算法相结合的永磁同步电机控制算法，与传统的PID控制算法不同，粒子群优化PID算法结合了粒子群算法在参数寻优方面的优势，能够弥补PID算法的一些短板。建立船舶电气设备永磁同步电动机的数学模型，基于粒子群优化PID算法设计了电气设备永磁同步电机的控制器，并结合Simulink软件平台进行了控制器的仿真。

1 永磁同步电动机的数学建模

建立船舶电气设备永磁同步电动机数学模型时，需做以下假设^[3-4]：

1）电动机的转子绕组无阻尼，分布为对称分布；

2）电机的气隙分布均匀；

3）电动机的磁耗忽略不计。

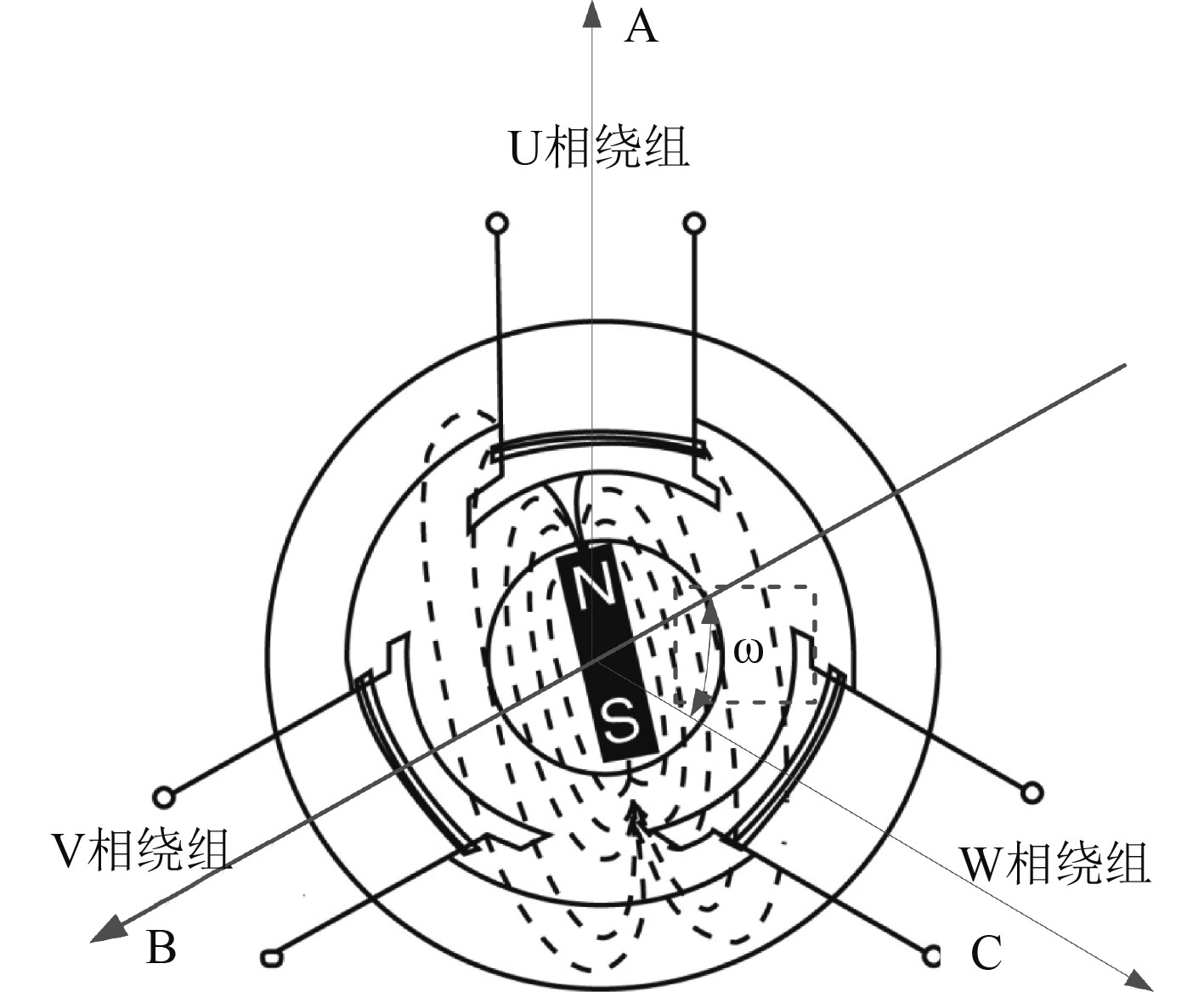
建立永磁同步电动机数学模型如图1所示。

可知，永磁同步电机分为三相绕组，建立永磁同步电机数学模型为：

$\begin{split}\left[ {\begin{array}{*{20}{l}} {{u_{{sA}}}} \\ {{u_{{sB}}}} \\ {{u_{{sC}}}} \end{array}} \right] = &\left[ {\begin{array}{*{20}{c}} {{R_{s}} + p{L_{a}}}&{ - \dfrac{1}{2}p{M_{a}}}&{ - \dfrac{1}{2}p{M_{a}}} \\ { - \dfrac{1}{2}p{M_{a}}}&{{R_{s}} + p{L_{a}}}&{ - \dfrac{1}{2}p{M_{a}}} \\ { - \dfrac{1}{2}p{M_{a}}}&{ - \dfrac{1}{2}p{M_{a}}}&{{R_{s}} + p{L_{a}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{i_{{sA}}}} \\ {{i_{{sB}}}} \\ {{i_{{sC}}}} \end{array}} \right] + \\ &\left[ {\begin{array}{*{20}{l}} {{e_{{sA}}}} \\ {{e_{{sB}}}} \\ {{e_{{sC}}}} \end{array}} \right] \text{。}\end{split}$

其中， $\left[ {\begin{array}{*{20}{l}} {{u_{{sA}}}} \\ {{u_{{sB}}}} \\ {{u_{{sC}}}} \end{array}} \right]$ 为永磁同步电机的三相电压， $\left[ {\begin{array}{*{20}{l}} {{i_{{sA}}}} \\ {{i_{{sB}}}} \\ {{i_{{sC}}}} \end{array}} \right]$ 为永磁同步电机的三相电流， $\left[ {\begin{array}{*{20}{l}} {{e_{{sA}}}} \\ {{e_{{sB}}}} \\ {{e_{{sC}}}} \end{array}} \right]$ 为永磁同步电机的三相感应电动势， ${R_{s}}$ 为电机绕组的电阻， ${L_{a}}$ 为电机绕组的电感， ${M_{a}}$ 为定子的电感， $p$ 为分项系数。

已知电机转动的角速度为 $\omega$ ，可由下式计算出电机的三相感应电动为：

$\left[ {\begin{array}{*{20}{l}} {{e_{{sA}}}} \\ {{e_{{sB}}}} \\ {{e_{{sC}}}} \end{array}} \right] = - {\omega _{}}\psi \left[ {\begin{array}{*{20}{c}} {\sin {\theta _{c}}} \\ {\sin \left( {{\theta _{c}} - \dfrac{{2\text{π} }}{3}} \right)} \\ {\sin \left( {{\theta _{c}} + \dfrac{{2\text{π} }}{3}} \right)} \end{array}} \right] \text{。}$

式中： $\psi$ 为永磁电机的磁链， ${\theta _{\text{c}}}$ 为转子的旋转角度。

2 基于粒子群优化PID算法的舰船电气设备自动控制研究 2.1 粒子群优化PID算法原理

粒子群优化PID控制是在PID控制器的基础上，将控制参数寻优算法引入粒子群优化，这种优化算法的优势在于提高PID控制器控制水平的同时，缩短PID控制参数的寻优周期^[5]。

首先介绍PID控制器的基本原理，它是一种基础的负反馈控制器，控制模型为：

$F\left( t \right) = {K_p}\left[ {f\left( t \right) + \frac{1}{{{T_i}}} \int {\begin{array}{*{20}{c}} i\\ 0 \end{array}} {f\left( t \right){\rm{d}}t + {T_d}\frac{{{\rm{d}}f\left( t \right)}}{{{\rm{d}}t}}} } \right] + u\left( t \right) \text{。}$

式中： ${T_i}$ 为积分常数， ${K_p}$ 为比例系数， ${T_d}$ 为微分系数， $u\left( t \right)$ 为噪声信号， $f\left( t \right)$ 为输入信号。

粒子群优化算法是基于鸟群中个体与种群觅食行为演变而来的智能算法，粒子群优化算法的基本方程为：

${v_{iD}}^{k + 1} = \omega {v_{iD}}^k + {c_1}\xi \left( {{p_{iD}}^k - {x_{iD}}^k} \right) + {c_2}\eta \left( {{p_{gD}}^k - {x_{iD}}^k} \right) \text{，}$

式中：k为迭代次数， ${c}_{1}$ 和 ${c}_{2}$ 为学习因子， $\xi$ 和 $\eta$ 分别为粒子更新的速度指数和位移指数。

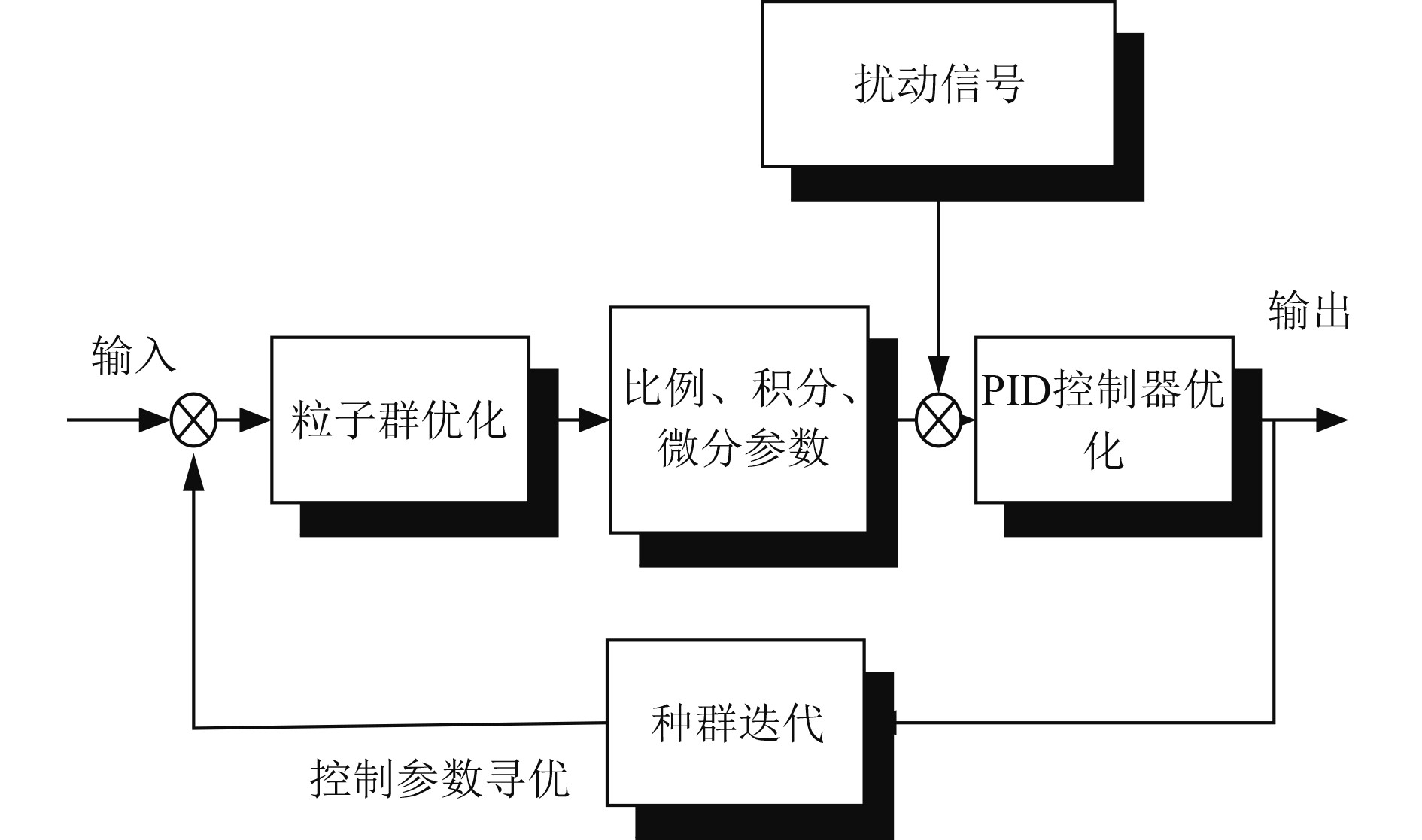
粒子群优化PID控制算法的原理图如图2所示。

粒子群优化PID算法的基本流程如下：

步骤1　参数初始化

包括PID控制器积分常数、比例系数、微分系数的初始化、学习因子和粒子群寻优方程的惯性权值初始化，惯性权值初始化方程为：

$\omega = \frac{{\left( {\mu - 0.5} \right) \cdot \left( {{k_{\max }} - k} \right)}}{{{k_{\max }} + 0.5}} 。$

学习因子 ${c}_{1}，{c}_{2}$ 是粒子群算法的重要参数，该参数决定了种群的位置信息特性，学习因子越大，局部寻优时间越短。

步骤2　控制参数的寻优

PID控制参数寻优是本控制算法的关键，将PID控制算法的参数总数设定为k的种群， ${v_{iD}}^k$ 是指初始参数， ${c_1}\xi \left( {{p_{iD}}^k - {x_{iD}}^k} \right)$ 是参数寻优方程。

步骤3　适应度判断

适应度判断是确定PID控制参数的重要步骤，适应度值 $\varepsilon$ 定义为：

$\varepsilon = \left\{ \begin{array}{*{20}{l}} \dfrac{1}{{1 + {e^{ - 12(8{\delta _i} - 0.6)}}}},& c \leqslant {c_{BEST}}\text{，} \\ \dfrac{1}{{1 + {e^{ - 12(8{\delta _i} - 0.6)}}}},& c > {c_{BEST}}\text{。} \end{array} \right.$

以此进行参数确定和电机控制。

2.2 基于改进粒子群优化PID算法的永磁同步电动机控制器开发

在船舶永磁同步电机的控制时，本文结合SVPWM空间矢量控制和PID控制器，建立一种电机的矢量控制器。

永磁同步电机的矢量控制器原理图如图3所示。

永磁同步电机控制器的控制矢量包括电压、电机转矩、电机角速度3种。

1）永磁同步电机的电压

在该矢量控制器中，将船舶永磁同步电机的三相电压 $\left[ {\begin{array}{*{20}{l}} {{u_{{\text{sA}}}}} \\ {{u_{{\text{sB}}}}} \\ {{u_{{\text{sC}}}}} \end{array}} \right]$ 进行矢量合成可得：

$\vec U = \sqrt {\frac{2}{3}} \left( {{u_{{sA}}} + {u_{{sB}}} \cdot {{e}^{^{2\text{π} j}}} + {u_{{s}C}} \cdot {{e}^{{j}\frac{{4\text{π} }}{3}}}} \right) \text{。}$

2）永磁同步电机的输出转矩

建立转矩方程为：

${T_c} = \frac{3}{2}{p_n}\left[ {\psi {i_q} - 1} \right] \text{，}$

式中： ${p_n}$ 为永磁电机的磁极个数， ${i_q}$ 为电机的定子电流矢量， $\psi$ 为永磁电机的磁链。

3）永磁同步电机角速度

将矢量控制器的角速度状态变量设置为：

$\left\{\begin{array}{l}{x}_{1}={\omega }_{f}-{\omega }_{\text{c}} \text{，} \\ {x}_{2}={\displaystyle {\int }_{0}^{t}{x}_{1}} \text{d}t \text{。} \end{array} \right.$

式中： ${\omega _f}$ 为输入角速度， ${\omega _{\text{c}}}$ 为实际旋转的角速度。

角加速度表示为：

$\left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1} = - \dfrac{{3p_{n}^2\psi }}{{2J}}{i_{q}} + \dfrac{{B{p_{n}}}}{J}}\text{，} \\ {{{\dot x}_2} = {x_1}}。\end{array}} \right.$

式中， $J$ 为电机转动惯量。

2.3 基于粒子群优化PID的电机控制仿真

结合船舶永磁同步电机的工作场景，利用Simulink软件进行粒子群优化PID控制器的仿真，主要步骤包括：

步骤1　参数选择

将粒子群算法的种群大小设置为100，最大迭代次数设置为150，学习因子 ${c}_{1}$ 和 ${c}_{2}$ 设置为0.35，积分常数设置为10，比例系数设置为0.8，微分系数设置为0.8。

步骤2　适应度函数选择

适应度函数对于参数寻优非常关键，适应度函数的选择需要满足：1）能够准确判断PID控制参数的优劣；2）能够反映系统的响应。

选用的适应度函数为：

$F = \int {\begin{array}{*{20}{c}} \infty \\ 0 \end{array}} \lambda {t\left| {e\left( t \right)} \right|} {\rm{d}}t 。$

步骤3　仿真程序搭建

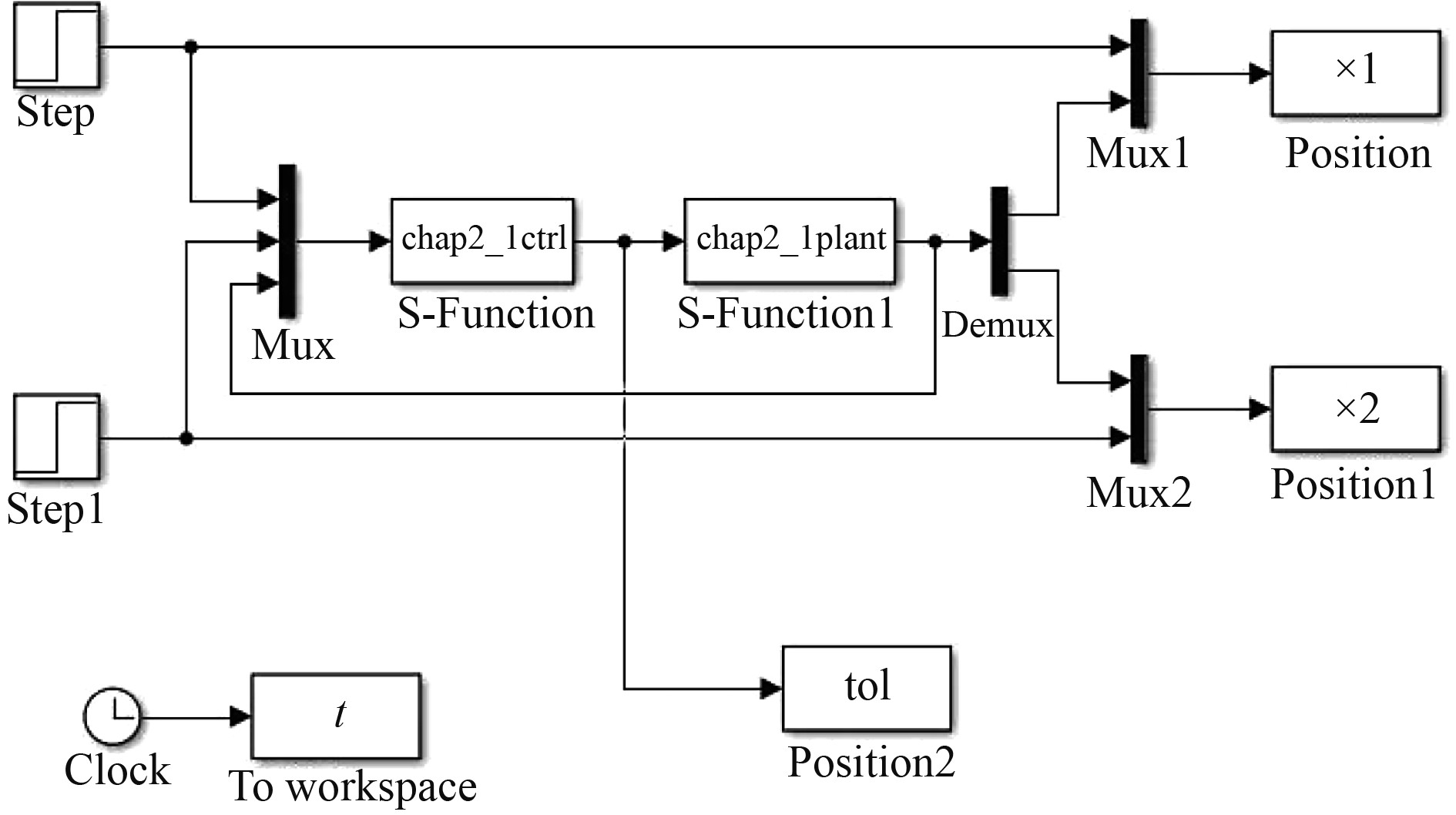
在Simulink软件中搭建船舶永磁同步电机的控制程序，图4为永磁同步电机位置量参数采集的Simulink程序。

步骤4　仿真边界条件

为了验证粒子群理论检测永磁同步电机运行特性，在Smulink中进行仿真，首先设置仿真参数如表1所示。

定义电机的转速为1500 r/min，电机的负载N=2 kN·m。

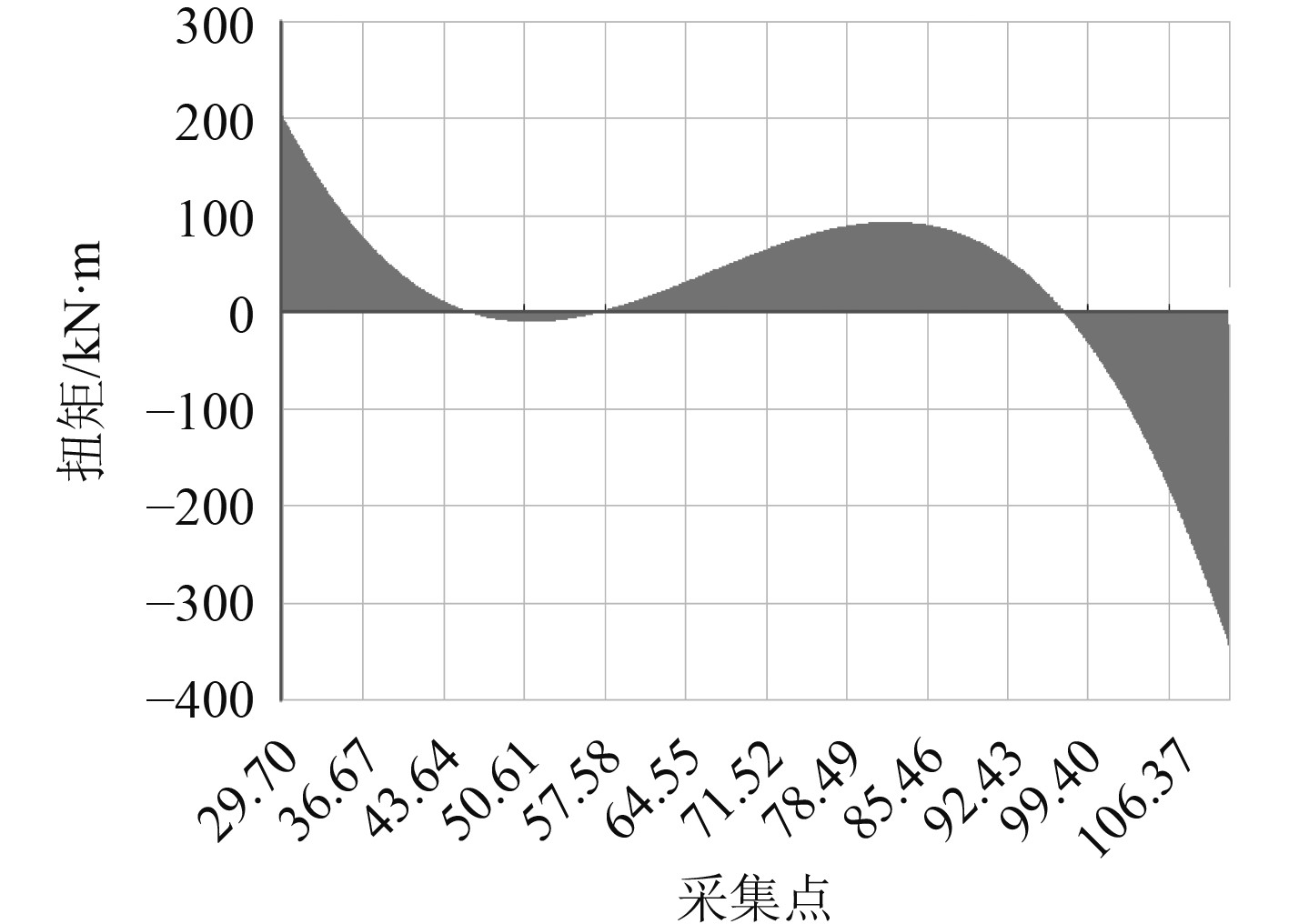
图5为永磁同步电机的扭矩参数控制仿真曲线。

3 结　语

本文针对永磁同步电机的优化控制问题进行研究，在传统PID控制器的基础上，提出了一种粒子群优化PID算法。该算法利用粒子群算法在参数寻优上的优势，在Simulink软件的仿真结果表明，该控制器能够实现永磁同步电机的快速、准确控制。