2. 国家管网集团联合管道有限责任公司西部分公司,新疆 乌鲁木齐 830000;
3. 中国科学院 工程热物理研究所,北京 100190
2. Western Branch of National Pipe Network Group United Pipeline Co., Ltd., Wulumuqi 830000, China;
3. Institute of Engineering Thermophysics, Chinese Academy of Sciences, Beijing 100190, China
随着我国碳达峰碳中和战略的实施,燃气轮机将在我国工业系统中发挥重要的作用[1]。由于燃气轮机监测设备长期需要在高温、高压的恶劣环境下工作,监测信号的失真不可避免[2],进而会造成燃气轮机控制偏离预期,从而对燃气轮机整体运行稳定性和安全性造成严重的影响[3]。
燃气轮机监测设备常见问题主要包括监测信号丢失、测量值超限、信号干扰波动,以及监测信号迟滞等。其中,监测信号丢失及测量值超限主要由传感器内部元器件或接线电缆故障造成[4-6],尽管这类信号问题会导致燃气轮机机组跳闸停机等事故[7-9],但在燃气轮机控制系统中这类监测故障易于辨识并可实现精确定位和保护。监测设备信号干扰主要由运行环境电磁干扰引发,会造成监测数据的非正常尖峰、脉动[10],从而造成燃气轮机工作不稳定,可以通过加强线缆屏蔽及滤波等方法来抑制这一问题。监测信号迟滞问题可能由传感器测量元器件感应速率慢、监测信号传输速率、传感器精度误差等多方面因素引发,在所有监测设备问题中最不易快速辨识和调控。存在监测信号迟滞时,对于基于多监测信号进行综合判断的燃气轮机燃料量及转速目标量,往往与燃气轮机实际控制需求产生偏差,造成燃气轮机性能达不到预期甚至会在起动过程中造成冷热悬挂问题。
本文通过Matlab/Simulink仿真平台搭建工业燃气轮机仿真模型、监测信号迟滞模型和燃料量控制算法,主要研究监测信号迟滞对燃气轮机转速控制的影响规律及监测信号在不同迟滞程度时PID控制参数对燃气轮机转速控制性能的影响规律。
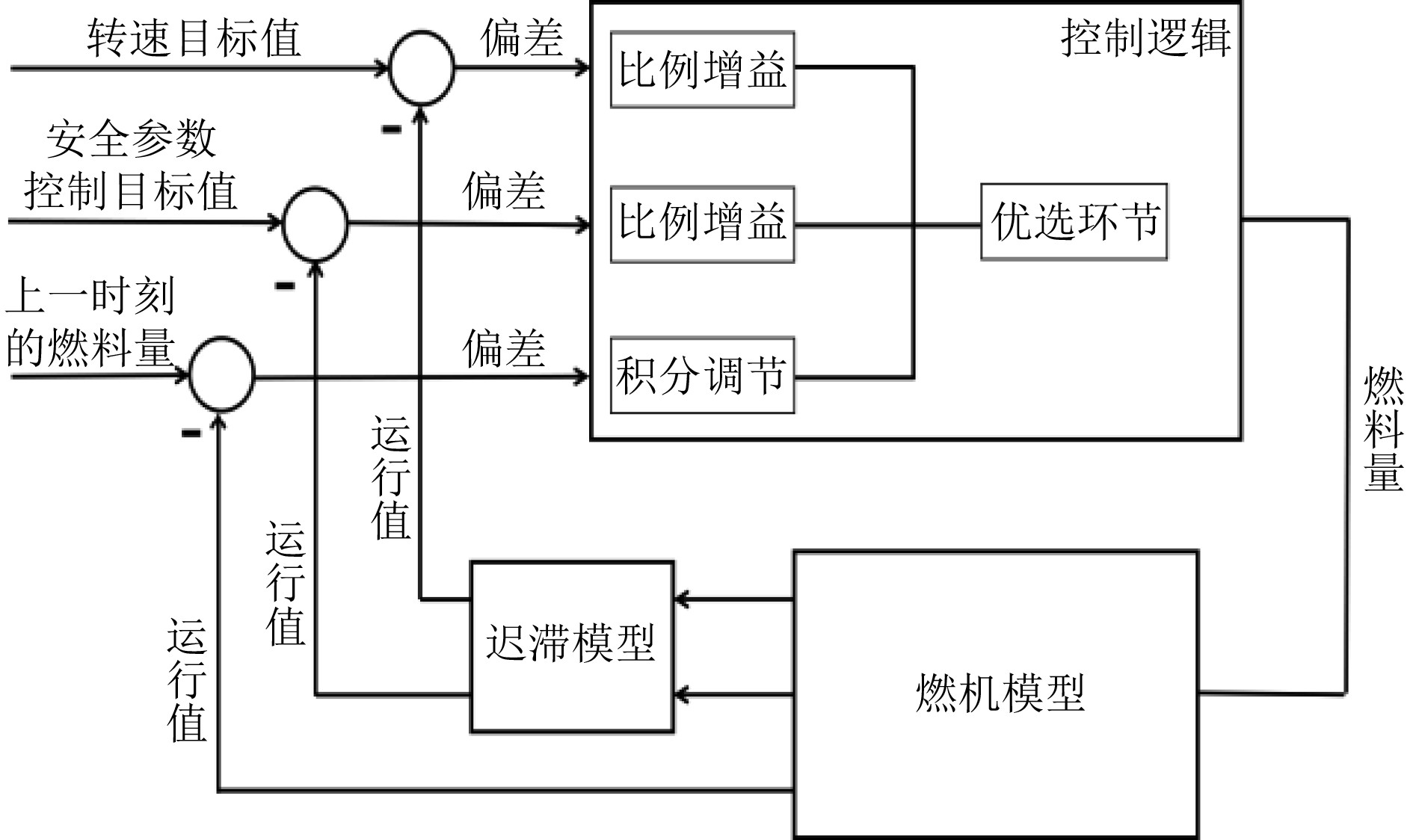
1 仿真模型的构建为复现燃气轮机监测信号迟滞现象,基于Matlab/Simulink建立监测信号迟滞模型、燃气轮机模型和转速控制逻辑,并将三者进行了耦合,构成具有监测信号迟滞功能的数字仿真系统[11]。建立的具有监测信号迟滞功能的数字仿真系统基本结构如图1所示。
|
图 1 具有监测信号迟滞功能的数字仿真系统 Fig. 1 Digital simulation system with monitoring signal hysteresis function |
燃气轮机模型采用机理建模法[11-13]进行建模,包含压气机、燃烧室、动力透平等部件,主要用于模拟提供燃气轮机在控制系统控制下的监测反馈信号。
1.2 转速控制逻辑燃料量是改变燃气轮机运行状态的最主要控制变量,通过改变燃料量可以控制燃气轮机完成加速或减速动作。
控制逻辑模块主要包含燃料量控制算法和优选环节,用于接收燃气轮机模型提供的监测信号,计算出燃料量,并经优选环节将燃料量反馈给燃气轮机模型。为消除燃料量初始值对数字仿真模型迭代结果的影响,对燃料量进行最小值限制,保证数字仿真模型迭代计算的准确性。
1.2.1 燃料量控制算法由于PID控制是最早实用化的控制算法,现在仍然是控制系统中应用最为普遍的一种控制规律。它所涉及的算法和控制结构简单,实际经验以及理论分析都表明,这种控制规律对许多工业过程进行控制时,一般都能得到较为满意的控制效果[14]。因此本文采用PID控制调控燃料量实现燃气轮机的转速控制。
燃料量控制采用比例积分运算(PI控制),与传统的积分环节不同,本文采用可变积分增益系数进行积分环节的构建。
| $ {W_{fx}} = {K_P}\Delta - \int_0^\tau {K_I^{\tau - t}} {W_f}\left( {t - 1} \right){\rm{d}}t\quad {t} = {\text{1,2,3}}\cdots ,\tau 。$ | (1) |
式中:Wfx为燃料量差值,x为代入的不同控制变量;KP为比例增益系数;KI为积分增益系数;∆为限制条件值或控制变量的目标值与当前状态值的偏差;Wf为经优选环节后反馈的燃料增量;τ为已运行的控制逻辑运算次数。
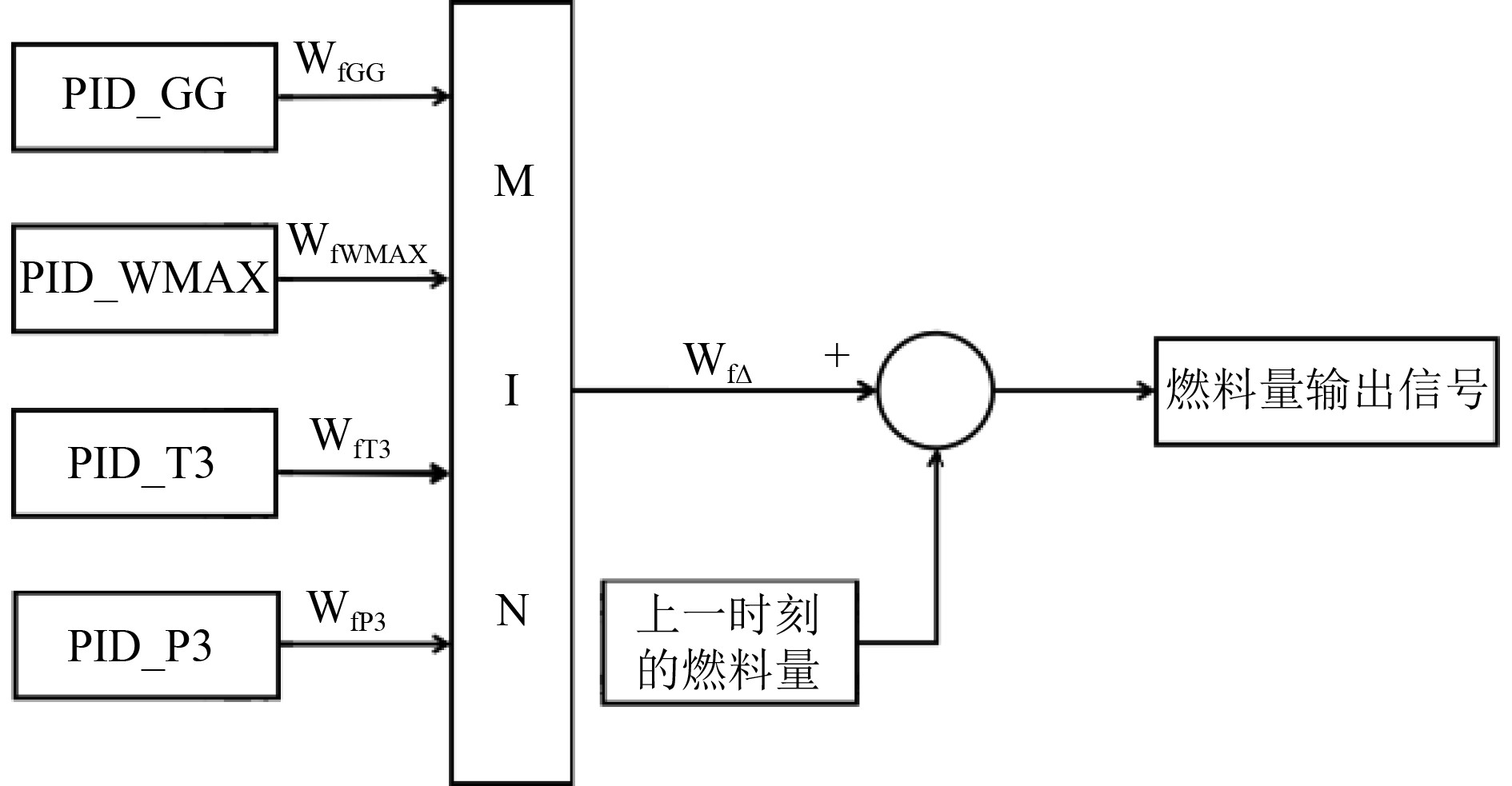
1.2.2 优选环节如图2所示,燃料量调节输出的优选环节采用最小值选取原则,具体包含4个控制变量,分别为燃气发生器转速调节(PID_GG)、压气机出口压力安全控制燃料量限制(PID_P3)、压气机出口温度安全控制燃料量限制(PID_T3)、最大燃料量限制(PID_WMAX),其中燃气发生器转速为主控制变量,其余3路为限制条件,保证所选取的燃料量满足燃气轮机运行需求。
|
图 2 燃料量优选逻辑 Fig. 2 Fuel quantity optimization logic |
为达到监测信号每隔一定时间传输一次真实数据的迟滞效果,在监测信号输出模块之后增加零阶保持模块,并补充速率转换模块,保证采样时间一致。零阶保持模块的采样时间为迟滞时间,可根据需求设置为0.1 s和0.2 s等。
零阶保持模块是一种按照恒指规律外推的保持模块,具有将当前采样时刻的信号值保持到下一个采样时刻的功能。其原理如下式:
| $ \begin{split} & nT \leqslant t \leqslant \left( {n + 1} \right)T,n = 0,1,2,3\cdots,\\ & {U_{\left( t \right)}} = {U_{\left( {nT} \right)}},n = 0,1,2,3\cdots。\end{split} $ | (2) |
式中:T为迟滞时间;t为采样时刻;U(t)为当前采样时刻的信号值;U(nT)为上一采样时刻的信号值。
2 监测信号迟滞的影响分析 2.1 调节时间调节时间是反映控制系统响应速度的指标。其定义为控制系统受到外界扰动作用后,被控变量由之前的稳定状态转变到新的稳定状态所经历的最短时间。理论上调节时间为无限长,在实际应用中,只要被控变量进入新的稳态值±5%或±2%范围内,且不在超出该范围时所需的最短时间作为该控制系统的调节时间。
调节时间的计算方式如下式:
| $ {t_S} = {t_2} - {t_{1}}。$ | (3) |
式中:tS为调节时间;t2为被控变量由初始平衡态到达新的平衡态的时刻;t1为被控变量初始平衡态向新的平衡态转变的时刻。
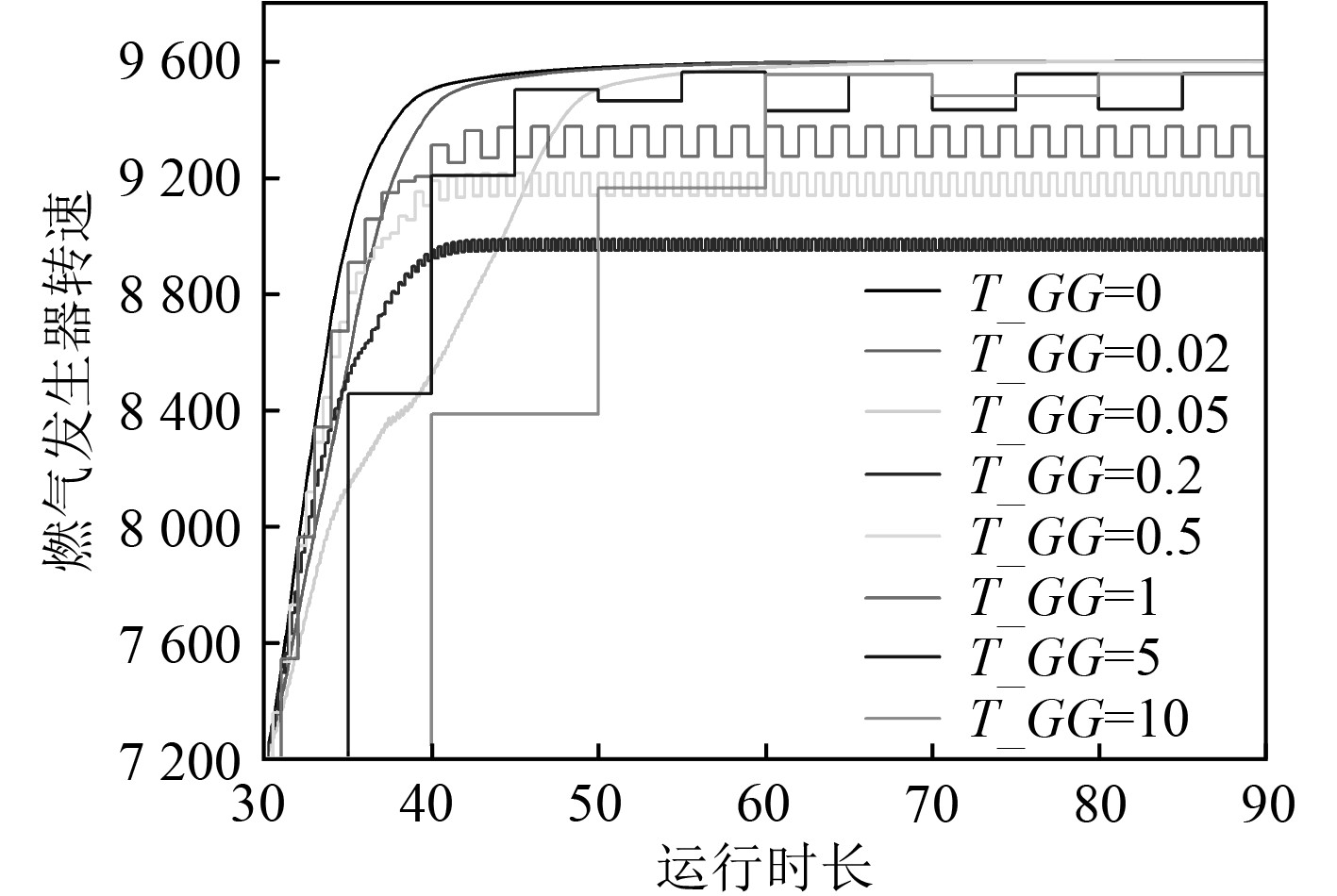
2.2 转速迟滞的影响为获得转速迟滞对燃气轮机转速控制的影响,以转速迟滞时间T_GG为变量进行计算,计算结果如图3所示。可知,随着T_GG的增大转速控制呈现2种特性。转速曲线的阶梯式变化趋势更为明显,到达目标转速的调节时间逐渐增长。另一方面,转速曲线随T_GG增大时所呈现的阶梯式变化趋势,表明监测信号迟滞模型具有良好的监测信号迟滞的复现能力,为研究监测信号迟滞对转速控制的影响提供了必要保证。
|
图 3 存在转速迟滞的转速曲线 Fig. 3 Speed curve with speed hysteresis |
由于存在转速迟滞时,转速控制所呈现的特性均会严重影响燃气轮机正常运行。如图4所示,与无迟滞的燃料量曲线相比,存在转速迟滞时燃料量曲线产生了不同程度的振荡,且T_GG越小振荡越明显。这种燃料量剧烈波动的情况在实际运行过程中所引起的转速波动远大于数字仿真所展示的现象。

|
图 4 存在转速迟滞的燃料量曲线 Fig. 4 Fuel quantity curve with speed hysteresis |
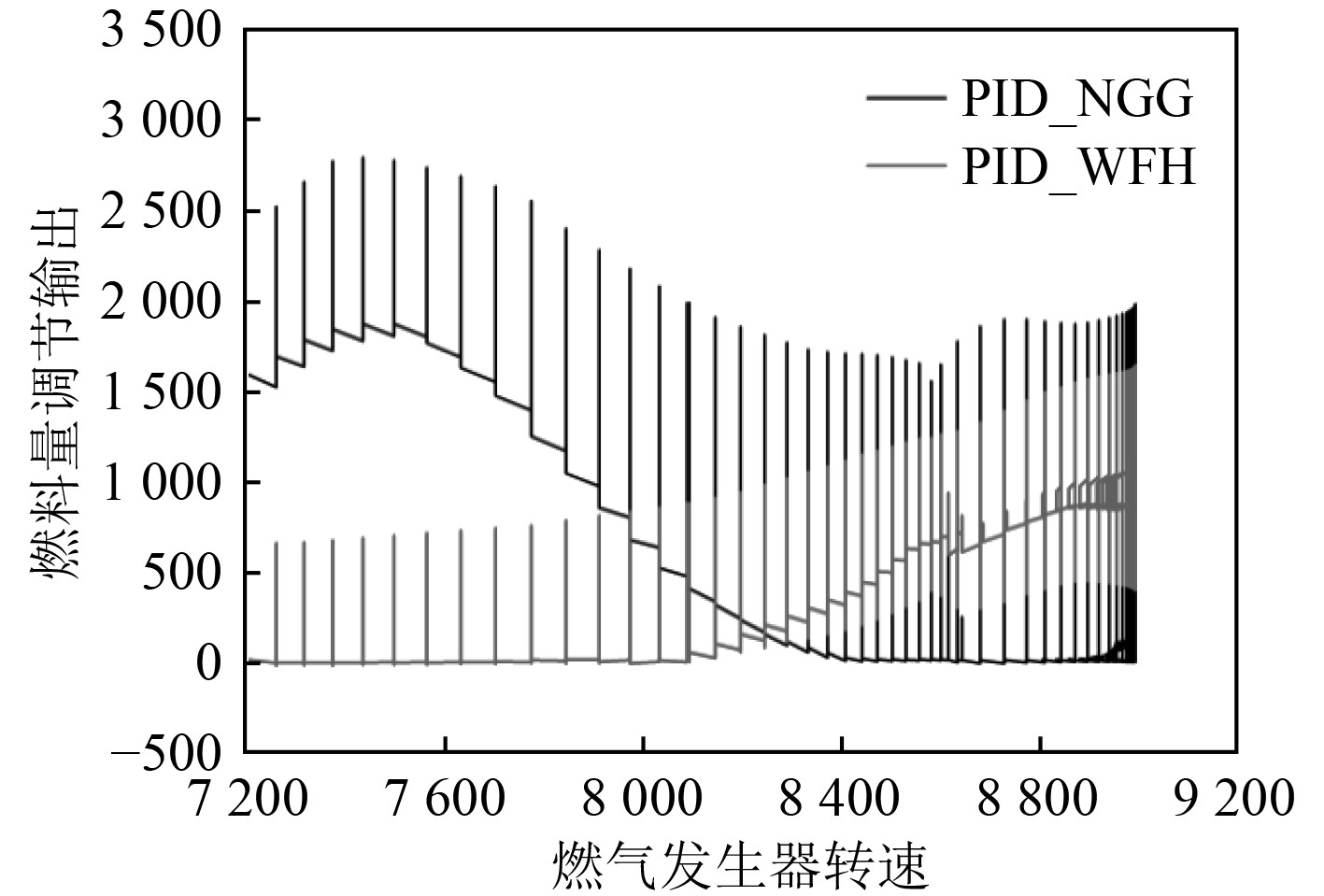
当转速存在迟滞时,每个迟滞周期的转速为恒定值,此时转速调节可以看成存在多次阶跃的转速调节。每次阶跃均需要进行燃料量调节,以保证所供应的燃料量满足转速需求。如图5所示,当T_GG较小时,转速控制阶跃次数多、间隔时间短、且由于积分项的耦合作用,导致燃料量调节输出振荡,燃料量优选环节混乱,燃料量波动大且供应不足,使得燃气发生器转速未能到达调节目标。
|
图 5 T_GG=0.2 s的燃料量调节输出 Fig. 5 Fuel quantity regulation output with T_GG=0.2 s |
随着T_GG的增大,转速阶跃次数减少,间隔时间增大,燃料量优选环节趋于正常,燃料量趋于稳定,使得燃气发生器转速趋于调节目标。因此对转速信号的采集上传时间应该严格要求,且应严格控制在100 ms以内。
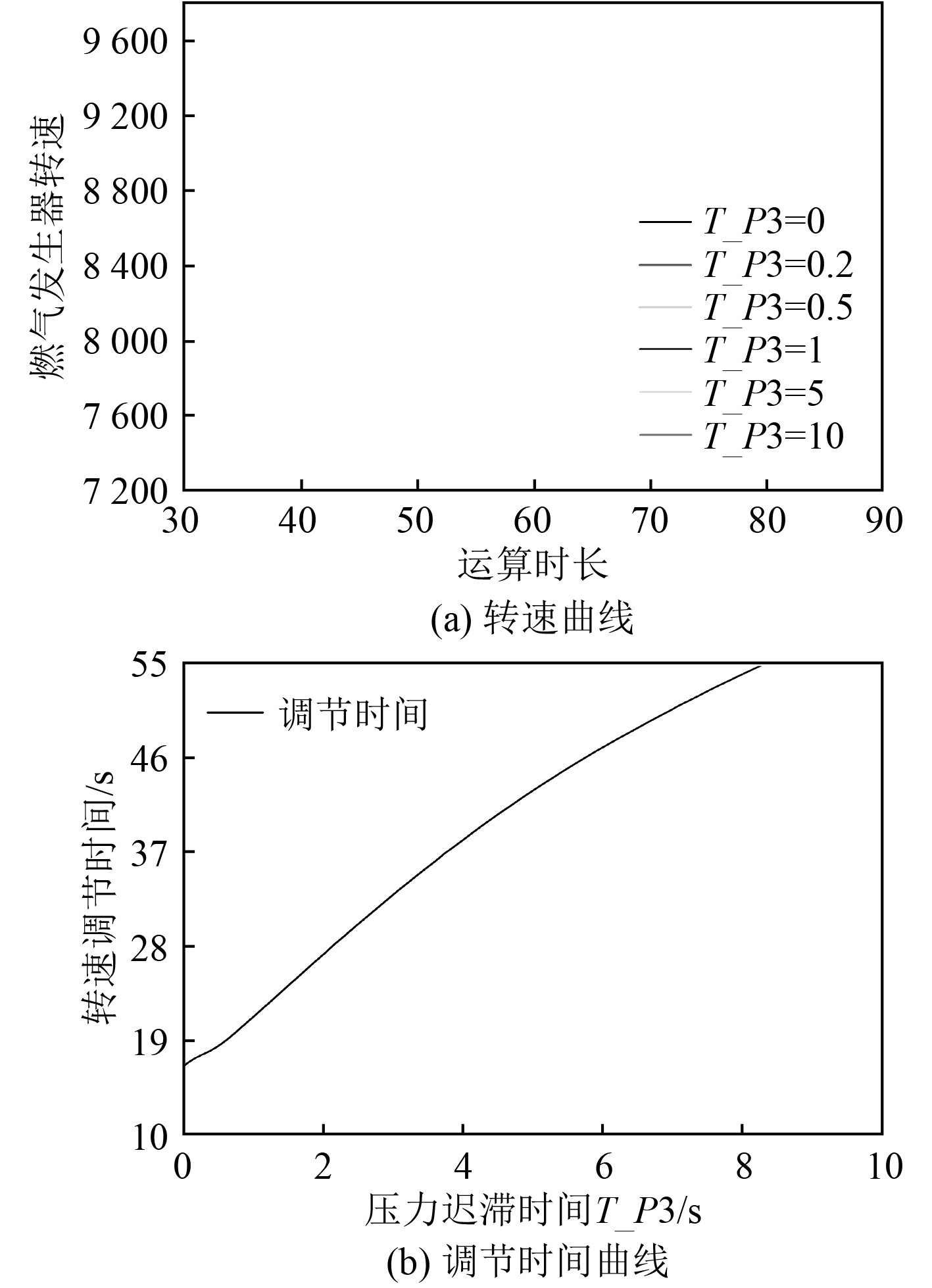
2.3 压力迟滞的影响为获得压力迟滞对转速控制的影响,以压力迟滞时间T_P3为变量进行计算,计算结果如图6所示。由图6(a)可知,随着T_P3的增大,燃气发生器转速的稳态值逐渐减小;由图6(b)可知,调节时间与T_P3成正比例关系,且T_P3小于0.2 s时,调节时间与无迟滞时的调节时间接近,因此压力迟滞应严格控制在200 ms以内。
|
图 6 存在压力迟滞的转速曲线和调节时间曲线 Fig. 6 Speed curve and regulation time curve with pressure hysteresis |
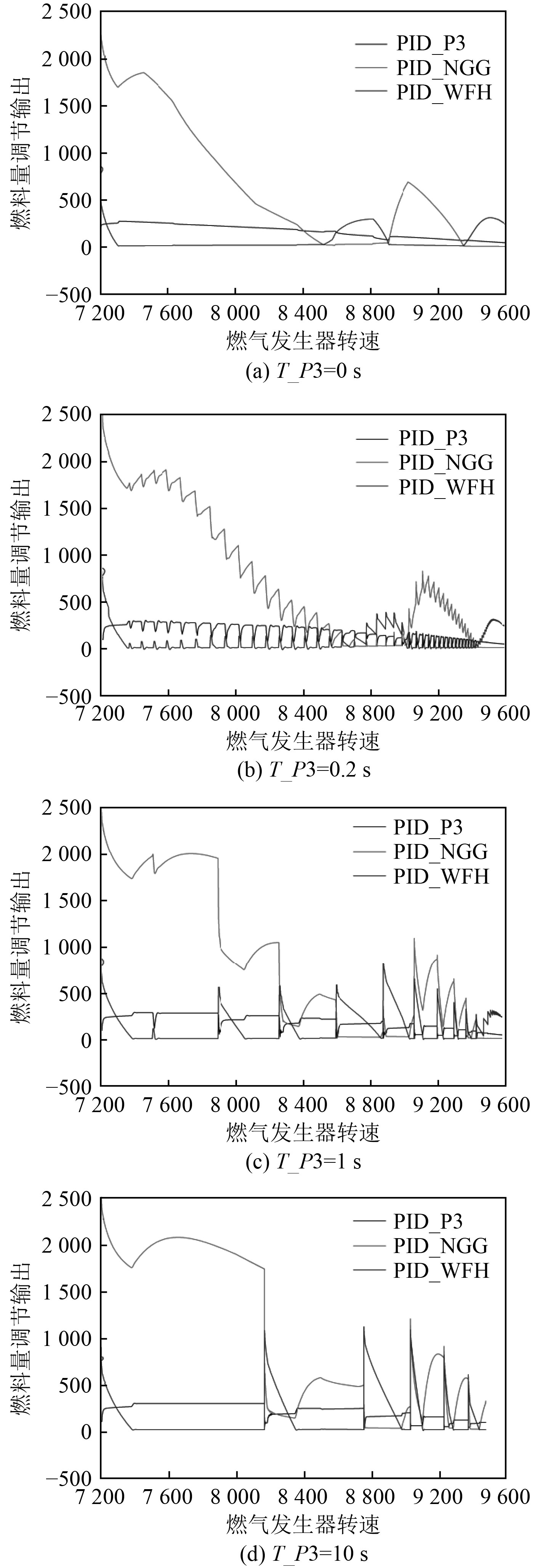
如图7所示,与无迟滞的燃料量调节输出曲线相比,存在迟滞的燃料量调节输出曲线呈现出阶梯式变化趋势。产生阶梯式变化趋势的原因在于,燃料量优选结果在PID_P3和PID_WMAX之间交替变换,导致燃料量计算值偏小,燃气发生器转速升速减缓,调节时间增长。
|
图 7 存在压力迟滞的燃料量调节输出 Fig. 7 Fuel quantity regulation output with pressure hysteresis |
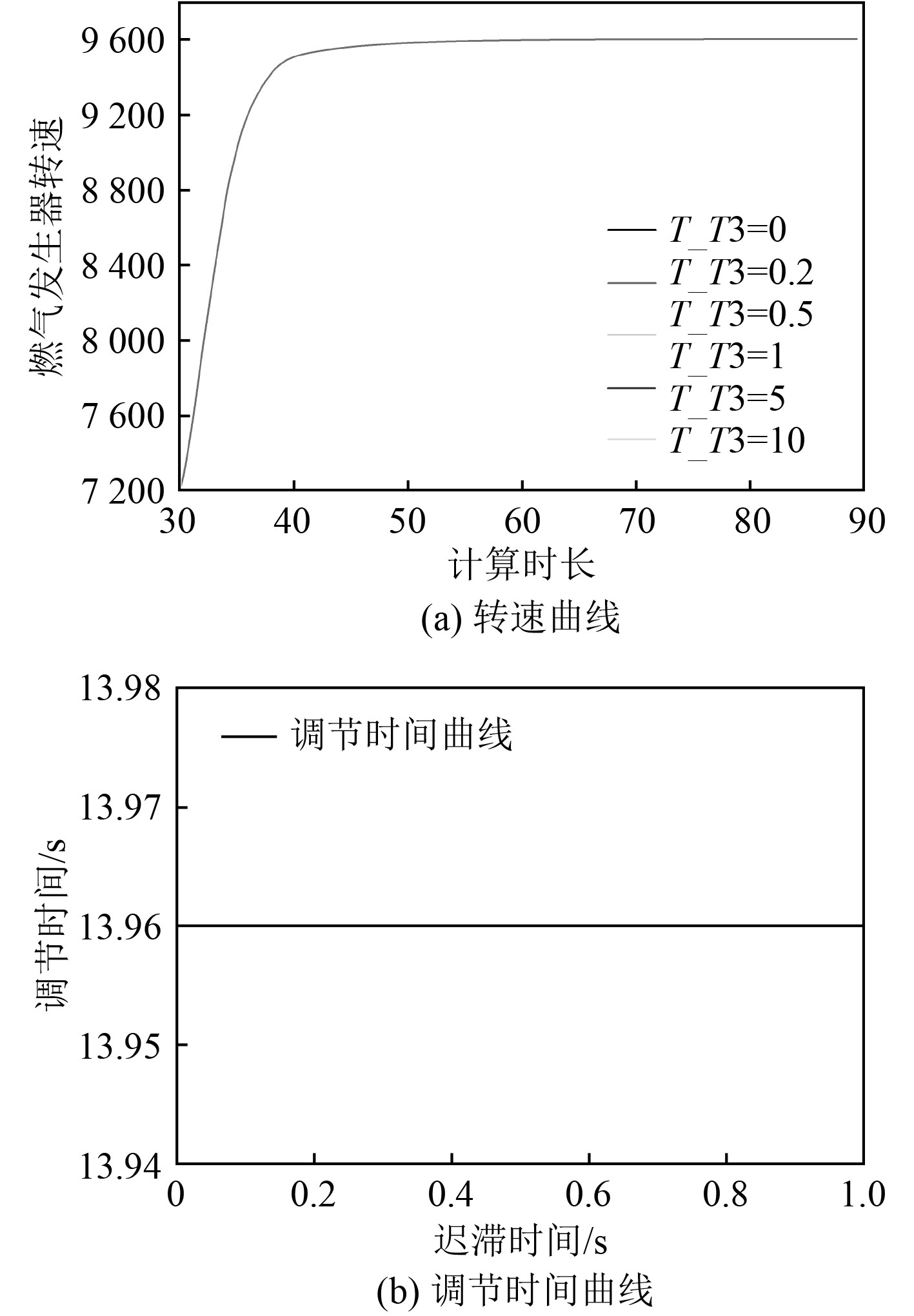
为获得温度迟滞对转速控制的影响,以温度迟滞时间T_T3为变量进行计算,计算结果如图8所示。由图8(a)可知,随着T_T3的增大,转速曲线基本重合;由图8(b)可知,无论T_T3如何变化,调节时间无明显改变,因此温度迟滞对转速控制的影响较小。
|
图 8 存在温度迟滞的转速曲线和调节时间曲线 Fig. 8 Speed curve and regulation time curve with temperature hysteresis |
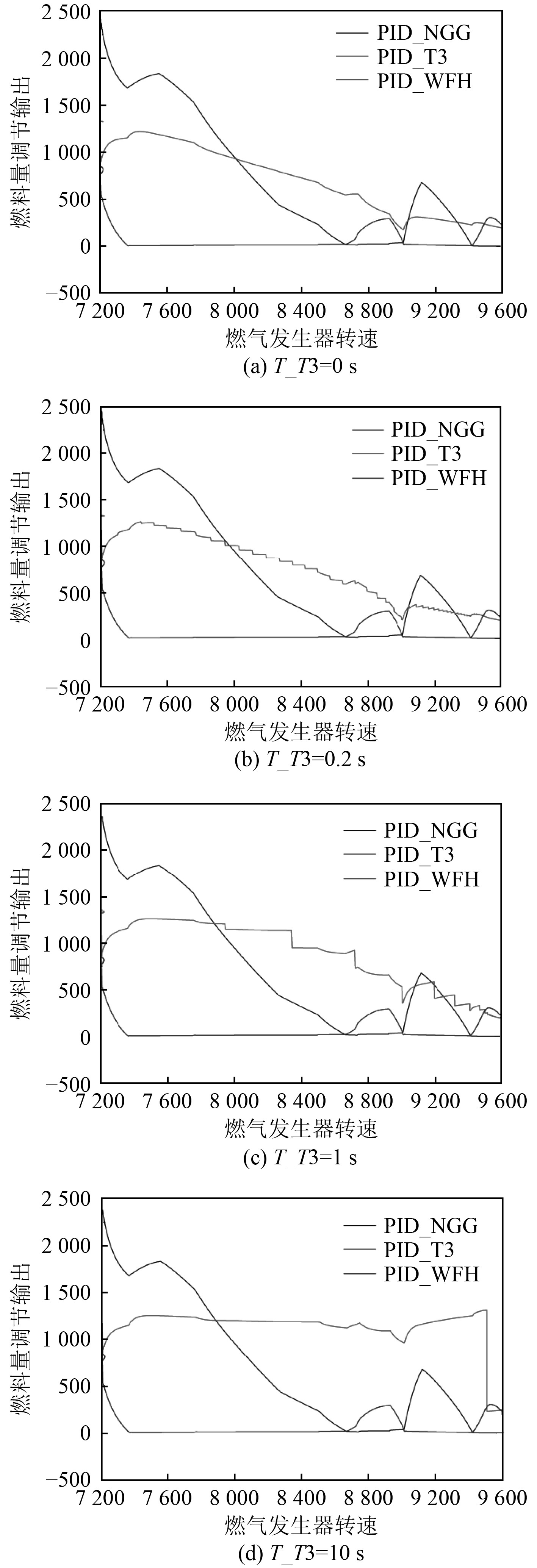
如图9所示,与无迟滞的燃料量调节输出曲线相比,存在温度迟滞时,仅有PID_T3呈现阶梯式变化趋势,且并未改变燃料量优选结果,由此可见,温度迟滞对转速控制的影响极小。
|
图 9 存在温度迟滞的燃料量调节输出 Fig. 9 fuel quantity regulation output with temperature hysteresis |
为获得压力迟滞与比例增益系数KP耦合对转速控制的影响,选取变量为T_P3和KP,计算结果如图10所示。可知,转速控制存在2个特性。调节时间与KP成反比例关系,且KP大于0.5时,调节时间趋于恒定值;随着T_P3的增大,增大KP对调节时间的影响减弱。

|
图 10 T_P3和KP耦合时的调节时间曲线 Fig. 10 Adjustment time curve when T_P3 and KP are coupled |
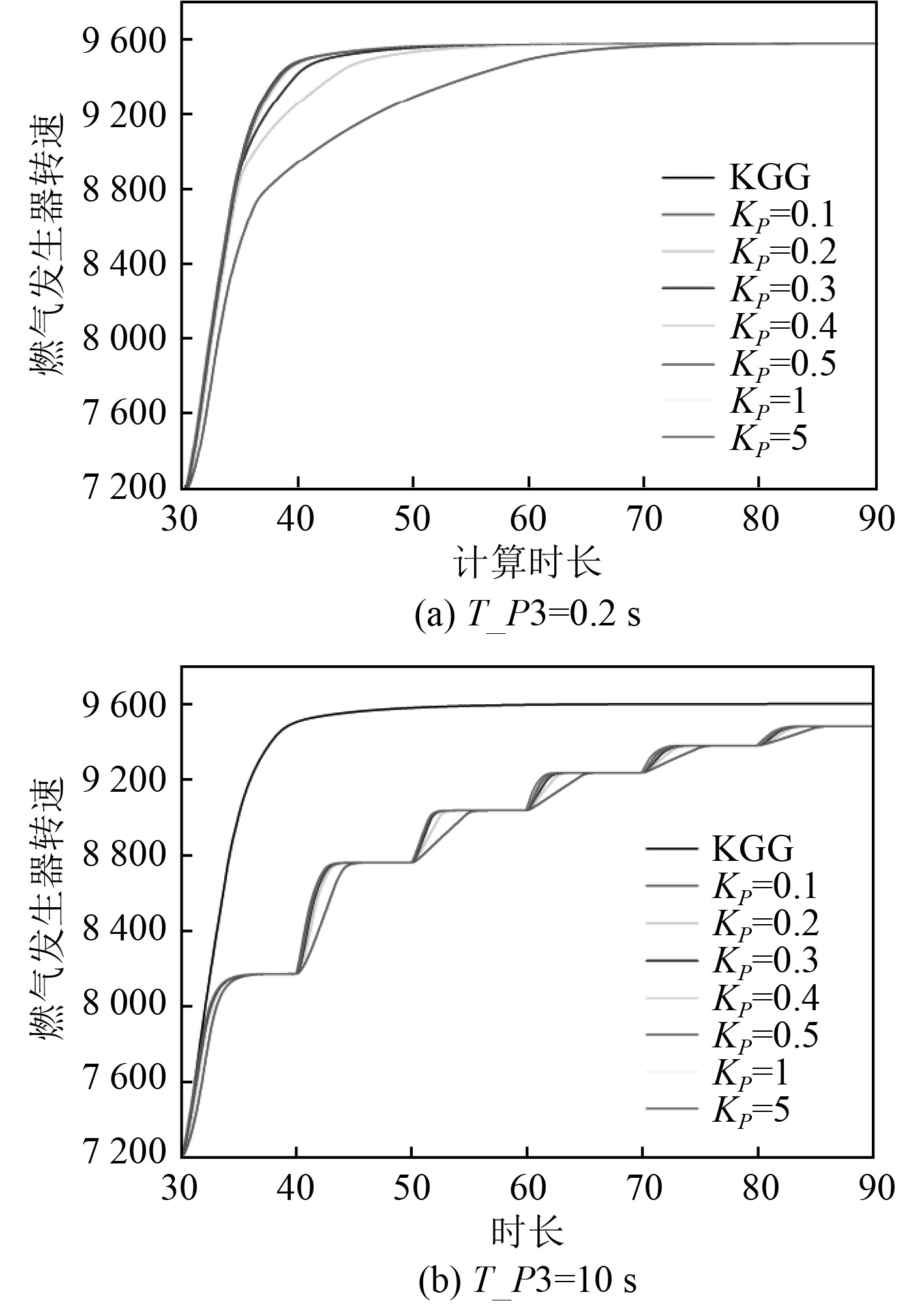
为探究T_P3和KP耦合时对转速控制产生前述影响的原因,从燃气发生器转速和燃料量调节输出的角度进行分析,如图11和图12所示。
|
图 11 固定T_P3且改变KP时的转速曲线 Fig. 11 Speed curve when fixing T_P3 and changing KP |

|
图 12 T_P3和KP耦合时的燃料量调节输出 Fig. 12 Fuel quantity regulation output when T_P3 and KP are coupled |
1)首先从保持T_P3恒定,改变KP的角度进行分析:由图11可知,随着KP的增大,燃气发生器转速趋近于无迟滞时的转速;由图12可知,随着KP的增大,燃料量调节输出增大,燃料量优选结果由PID_P3逐渐转变为PID_GG和PID_WMAX之间交替选择,使得转速控制效果更佳,燃气发生器转速趋于调节目标,调节时间减小。
2)结合压力迟滞对转速控制的影响规律,对T_P3和KP耦合时转速控制的变化趋势展开分析。当T_P3较小时,燃料量调节输出虽然存在波动,但其对燃料量优选结果的干扰较小,KP大于0.4时转速曲线与无迟滞的转速曲线基本重合,与图6(a)中T_P3=0.2 s时的转速曲线相比,增大KP可以提升转速控制性能;当T_P3较大时,受压力迟滞的影响,燃料量调节输出的阶梯式变化极为明显,对燃料量优选结果的干扰较大,燃料供应不足,调节时间增大,且增大KP基本无变化。
综上所述,当燃气轮机存在压力迟滞现象时,可通过增大KP的途径提升转速控制性能;当T_P3较小时,增大KP对转速控制性能的提升较为明显;当T_P3较大时,增大KP对转速控制性能无明显提升。
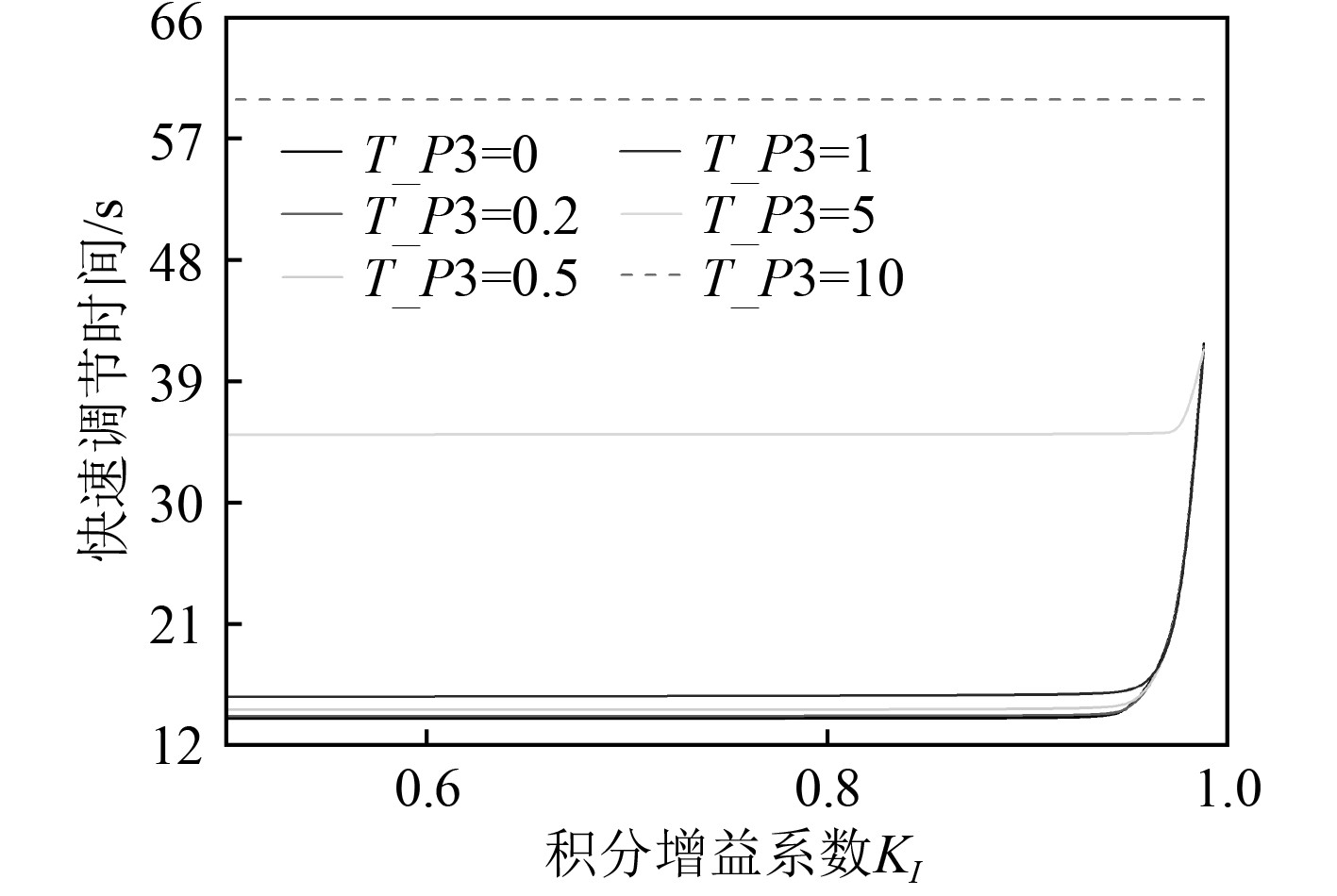
3.2 压力迟滞与积分增益系数耦合的影响为获得压力迟滞与积分增益系数KI耦合对转速控制的影响,所选取变量为T_P3和KI,计算结果如图13所示。可知,转速控制存在2个特性:调节时间与KI成正比关系,且KI小于0.95时,调节时间趋于恒定值;随着T_P3的增大,改变KI对调节时间影响减弱。
|
图 13 T_P3与KI耦合时的调节时间曲线 Fig. 13 Adjustment time curve when T_P3 and KI are coupled |
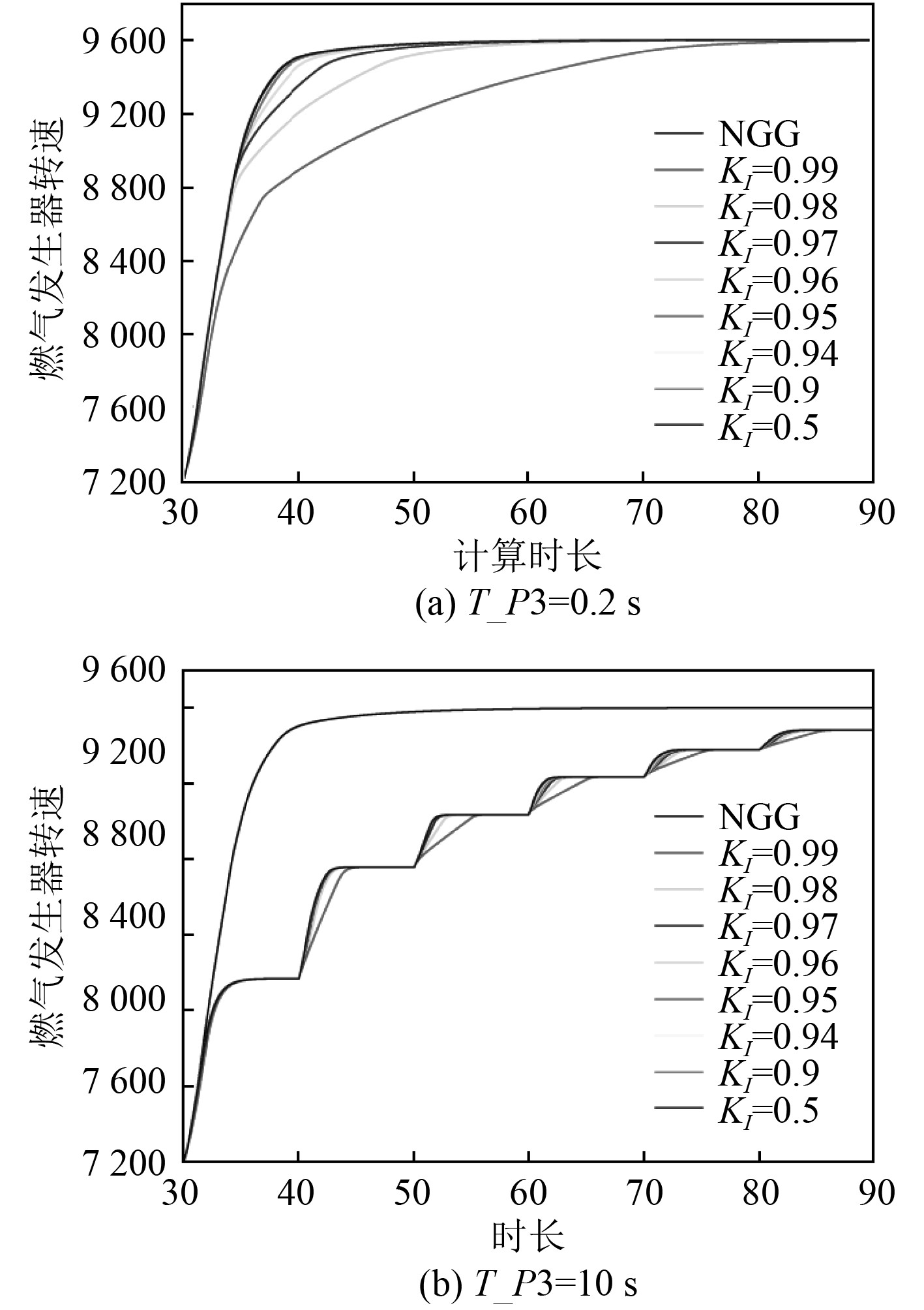
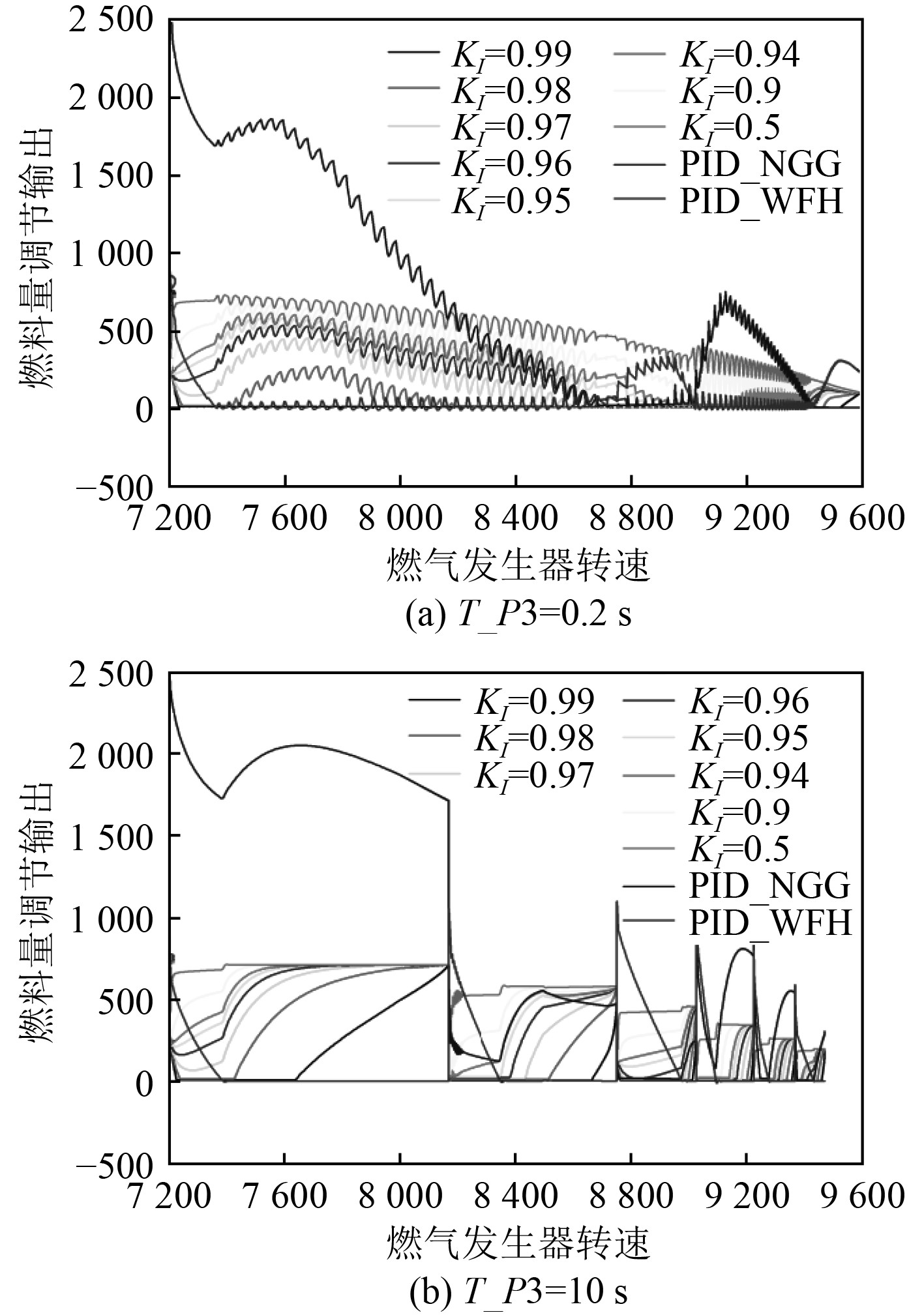
为探究T_P3和KI耦合时对转速控制产生前述影响的原因,采用与T_P3和KP耦合影响相同的分析方法进行分析,如图14和图15所示。分析结果如下:
|
图 14 固定T_P3且改变KI时的转速曲线 Fig. 14 Speed curve when fixing T_P3 and changing KI |
|
图 15 T_P3和KI耦合时的燃料量调节输出 Fig. 15 Fuel quantity regulation output when T_P3 and KI are coupled |
与KP对转速控制的影响原因基本一致,主要表现为:随着KI的减小燃料量调节输出增大,燃料量优选结果由PID_P3逐渐转变为PID_GG和PID_WMAX之间交替选择,且更加接近无迟滞时的优选结果,使得燃气轮机转速控制效果更佳,转速升速率增大,调节时间减小;当T_P3较小时,减小KI有利于提升转速控制性能;当T_P3较大时,减小KI的对转速控制基本无影响。
4 结 语通过Matlab/Simulink建立具有监测信号迟滞功能的数字仿真系统,进行转速迟滞、压力迟滞和温度迟滞对燃气轮机转速控制效果的影响及PID控制参数与监测信号迟滞耦合对燃气轮机转速控制的影响研究。所得结论如下:
1) 转速迟滞和压力迟滞是燃气轮机转速控制的主要影响因素,且转速迟滞的影响大于压力迟滞,温度迟滞对燃气轮机转速控制无影响;
2) 为提升燃气轮机转速控制的可靠性和稳定性,转速迟滞时间应控制在100毫秒级以内,压力迟滞时间应控制在200毫秒级以内;
3) 在监测信号迟滞较小时,增大比例增益系数KP和减小积分增益系数KI有利于提升燃气轮机转速控制性能,但随着监测信号迟滞时间的增大,改变PID控制参数对燃气轮机转速控制性能的提升效果逐渐减弱,甚至消失。
| [1] |
秦锋, 秦亚迪, 单彤文. 碳中和背景下氢燃料燃气轮机技术现状及发展前景[J]. 广东电力, 2021, 34(10): 10-17. |
| [2] |
曲文浩. 燃气轮机转速传感器断路故障分析[J]. 机械研究与应用, 2015, 28(2): 150-151. |
| [3] |
徐含灵. 燃气轮机控制系统传感器故障诊断与信号重构方法研究[D]. 北京: 中国科学院大学(中国科学院工程热物理研究所), 2019.
|
| [4] |
罗旭, 苏海峰, 耿红卫. 电控系统传感器信号失真原因分析与研究[J]. 制造业自动化, 2009(2): 175-178. DOI:10.3969/j.issn.1009-0134.2009.12.055 |
| [5] |
王靖, 高贵军, 寇子明, 等. 电阻应变式称重传感器迟滞性建模及实验研究[J]. 机电工程, 2021, 38(2): 191-197. |
| [6] |
陈高华, 闫献国, 郭宏, 等. 压电陶瓷振动传感器的迟滞非线性误差补偿研究[J]. 振动与冲击, 2018, 37(23): 278-285. |
| [7] |
宋飞翔. M701F3型燃气轮机燃烧室压力波动大跳闸原因分析及处理方法[J]. 智能城市, 2019, 5(13): 212-213. |
| [8] |
周登极, 张会生, 翁史烈. 变控制线的燃气轮机传感器故障诊断方法[J]. 燃气轮机技术, 2017, 30(1): 1-6. |
| [9] |
刘子英, 张靖, 付智辉, 等. 基于光纤角度传感器的高压隔离开关角度测量技术研究[J]. 高压电器, 2021, 57(10): 9-17. |
| [10] |
陈婷, 赵祥模, 高涛, 等. 传感器特性自动化测试系统研究与实现[J]. 科学技术与工程, 2016, 16(14): 36-40. |
| [11] |
林向雨. SGT5-4000F燃气轮机本体建模与仿真[D]. 北京: 华北电力大学, 2015.
|
| [12] |
刘尚明, 李忠义. 基于SIMULNK 的单轴重型燃气轮机建模与仿真研究[J]. 燃气轮机技术, 2009, 22(3): 33-39,45. |
| [13] |
郭磊. 燃气轮机系统建模与性能分析[D]. 北京: 中国科学院研究生院, 2009.
|
| [14] |
郑英杰, 牛兴华, 高卫国, 等. 温度控制系统时滞对象的先进PID控制方法研究[J]. 天津理工大学学报, 2018, 34(4): 20-25. |
 2023, Vol. 45
2023, Vol. 45

