2. 上海振华重工(集团)股份有限公司,上海 200125
2. Shanghai Zhenhua Heavy Industry Co., Ltd., Shanghai 200125, China
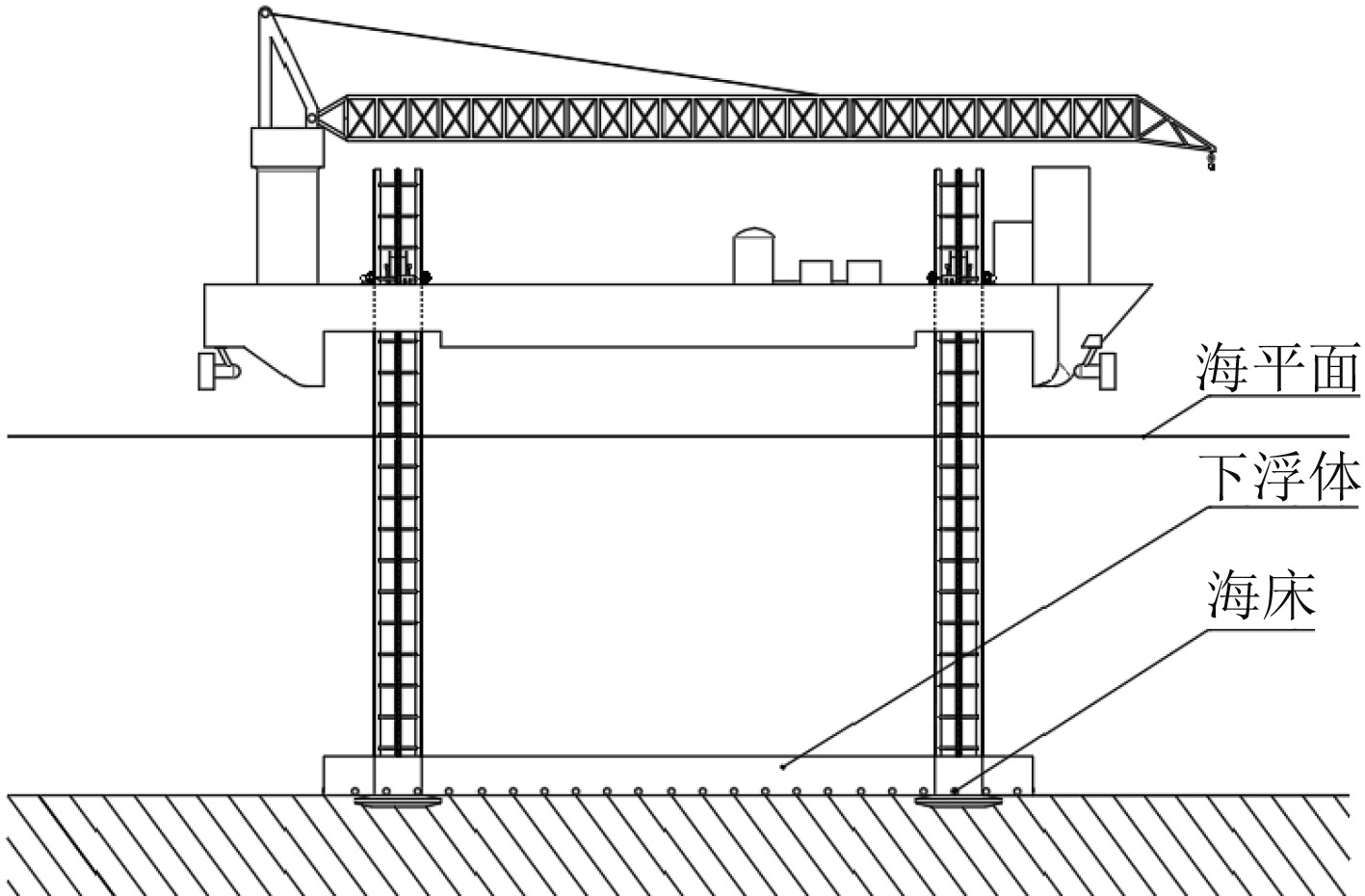
风能作为一种可再生能源,近年来得到快速的发展,其中海上风电的发展也取得了巨大的进步[1]。目前世界各国对沿海风电,尤其是深远海风能资源开发都尤为重视[2],虽然深海区域的风能资源充沛,但近年来海上风电的发展多在近海和浅海(水深不超过50 m),其主要原因是深海情况下风机组施工难度大,设备运行环境恶劣,现有的一些风电安装平台不能适应深水作业,为此创新设计一种基于正压型下浮体的3500型深水高效海上风电安装平台,如图1所示。
|
图 1 3500型风电安装平台结构原理图 Fig. 1 Structure schematic diagram of type 3500 wind power installation platform |
3500型海上风电安装平台通过底部中空的正压型下浮体冲排水获得浮力顶升平台实现作业,作业期间,承受浮体内超压和外界水压。下浮体是一个体积超20 000 m3的密闭区域,且表面连接有输气管线等部件,而在实际工程中容器气密性越高,则建造难度和成本越高,为此下浮体允许制造过程有微量的泄漏,但泄漏过程要满足下浮体建立保压控制系统的要求[3]。要想实现下浮体加压及保压控制系统的设计,对下浮体泄漏过程进行研究,即控制下浮体的气密性非常有必要。
目前,对于气密性的研究多为气密性检测方法,如气泡法和涂抹法等[4],且对气密性泄漏过程压降规律的研究更多是对泄漏量和泄漏压力的理论计算,而对泄漏过程影响因素的探究相对较少。黄震等[5]通过理论计算方法研究了航天领域中密封舱再入过程中的泄漏压降规律。王兆芹[6]分析了高压输气管道泄漏孔径与管径之比对泄漏速率的影响。Schatzel等[7]通过实验研究了煤矿井封件的泄漏速率。本文建立下浮体容器泄漏过程的数学模型,结合Fluent对下浮体理论计算结果进行仿真分析验证,并探究下浮体泄漏口位置和数量以及下浮体内部结构对压降过程的影响。
1 理论计算 1.1 数学模型建立下浮体计算时不考虑箱体变形所带来的容积变化,即下浮体静态泄漏模型可简化为图2所示的结构,模型容积为V,内压力为Pi,气体密度为ρi,外界环境压力为Pe,密度为ρe,假设所有泄漏口都由一个面积为A的等效泄漏孔来代替,开口处压力和密度分别为P2和ρ2,流出速度为u2。

|
图 2 泄漏模型图 Fig. 2 Leakage model diagram |
下浮体在发生泄漏时,可以将泄漏过程看成许多微小时间段dt组合而成,而每个时间段dt都处于稳态过程,并且由于泄漏口尺寸相对下浮体的尺寸较小,整个过程可以看成可逆绝热过程,为此通过以下流体运动基本方程推导下浮体泄漏过程的压降参数。
| $连续性方程:\dfrac{{\rm{d}} \rho}{\rho}+\dfrac{{\rm{d}} u}{u}+\dfrac{{\rm{d}} A}{A}=0 ,$ | (1) |
| $动量方程:\dfrac{{\rm{d}} P}{\rho}+w {\rm{d}} u+\dfrac{\tau L}{\rho A} {\rm{d}} x=0 ,$ | (2) |
| $能量方程:\delta q = {\rm{d}}h + \dfrac{1}{2}{\rm{d}}{u^2} + g{\rm{d}}z + \delta {w_{net}}, $ | (3) |
| $状态方程:\dfrac{{{\rm{d}}P}}{P} = \dfrac{{{\rm{d}}\rho }}{\rho } + \dfrac{{{\rm{d}}T}}{T} 。$ | (4) |
式中:
基于等熵可压缩流动理论的压降参数模型为[8]:
| $\begin{aligned} & \dfrac{{\rm{d}}{P}_{i}}{{\rm{d}}t}=\\ & \left\{\begin{array}{cc}-{C}_{p}{P}_{i}\dfrac{A}{V}\sqrt{\dfrac{2K}{K-1}RT\left[{\left(\dfrac{{P}_{2}}{{P}_{i}}\right)}^{\frac{2}{K}} - {\left(\dfrac{{P}_{2}}{{P}_{i}}\right)}^{\frac{K+1}{K}}\right]} ,&{亚音速},\\ -{C}_{p}{P}_{i}\dfrac{A}{V}\sqrt{\dfrac{RT}{{\left(\dfrac{2}{R+1}\right)}^{\frac{R+1}{R-1}}}},& {音速}。\end{array}\right. \end{aligned}$ | (5) |
基于不可压缩流动理论的压降参数模型为:
| $ \dfrac{{{\rm{d}}{P_i}}}{{{\rm{d}}t}} = - R{T_i}\dfrac{{{C_p}A}}{V}\sqrt {2{\rho _e}\left( {{P_i} - {P_e}} \right)}。$ | (6) |
式中,Cp为形状系数。
1.2 泄漏计算本文研究的3500型风电安装平台主要在我国南海沿岸区域工作,以往风电安装设备多是针对浅海区域,业内常把水深60 m以内作为浅海区域,而此平台可适应深水60 m及以上区域。下浮体工作时要求内部保持正压,即保证内压Pi大于外压Pe,压差不超过一个大气压,研究时下浮体泄漏口取光滑圆孔,此时可以得到下浮体初始状态时的相关参数,如表1所示。
|
|
表 1 初始泄漏参数 Tab.1 Initial leak parameter |
结合表1数据,可以计算泄漏开始时的流速和马赫数值:
| $ {u_2} = \sqrt {\dfrac{{2K}}{{K - 1}}R{T_i}\left[ {1 - {{\left( {\dfrac{{{P_2}}}{{{P_i}}}} \right)}^{\frac{{K - 1}}{K}}}} \right]} = 132.6\sim 159.8\;{\rm{m/s}} ,$ |
| $ Ma = \dfrac{{{u_2}}}{c} = 0.088\sim 0.107。$ |
式中:Ma为马赫数;
一般来说没有不可压缩的流体,经相关计算表明,当0<Ma≤0.3时,忽略流体压缩性造成的最大误差约2%,所以在实际工程中可以忽略其压缩性;当Ma>0.3时,一般工程计算就应考虑流体的压缩性[9]。
通过计算可以知道下浮体泄漏过程中马赫数小于0.3,故可忽略其压缩性,计算采用不可压缩流动理论,对式(6)解微分方程并代入
| $ \Delta P = {\left( { - \dfrac{1}{2}\dfrac{{{C_p}A}}{V}\sqrt {2{P_e}R{T_i}} t + \sqrt {\Delta {P_{\max }}} } \right)^2} ,$ | (7) |
式中,
为研究下浮体装置的不同泄漏口面积和水深的压降情况,计算下浮体达到平衡状态所需时间,平衡状态即压差时
| $ t = \dfrac{{2V\sqrt {\Delta {P_{\max }}} }}{{{C_p}A\sqrt {2\left( {{P_0} + \rho gh} \right)R{T_i}} }} 。$ | (8) |
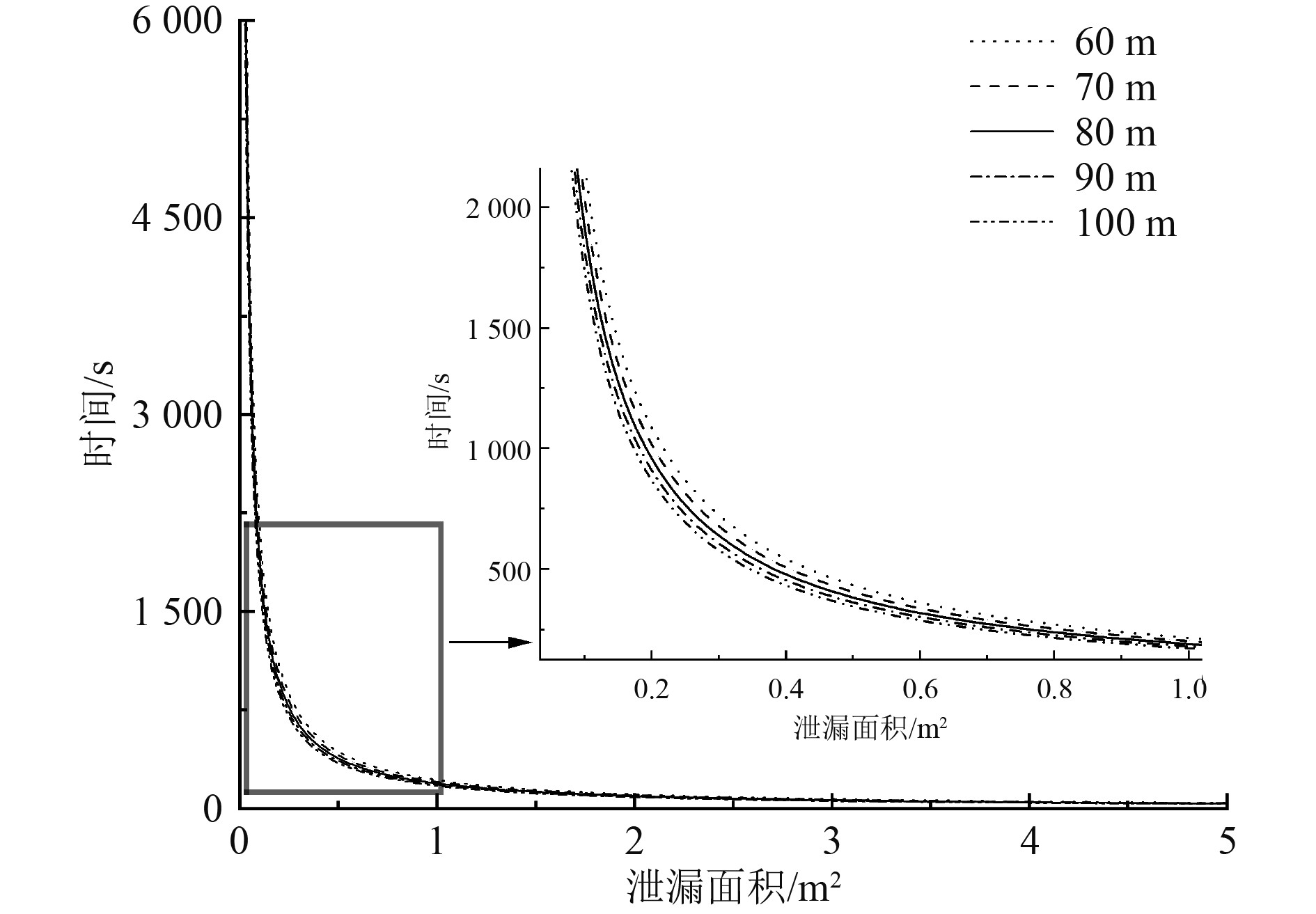
为更好地分析下浮体泄漏过程压降规律,根据下浮体的水深作业范围,探究下浮体在60 m,70 m,80 m,90 m和100 m等5类水深下平衡时间与泄漏面积的关系,如图3所示。
|
图 3 平衡时间与泄漏面积关系 Fig. 3 Relationship between equilibrium time and leakage area |
可以看出,在相同水深情况下随着泄漏面积的增加,下浮体内压到达平衡状体的时间逐渐增大,而时间增大的速度却随着泄漏面积的增多而逐渐减少。此外,下浮体泄漏面积小于0.1 m2时,所需平衡时间趋于无穷大,而泄漏面积大于1 m2时,所需平衡时间基本不再受泄漏面积影响,趋于一个稳定值。为此对下浮体气密性泄漏面积的研究主要集中在0.1~1 m2,即研究0.1 m2,0.25 m2,0.5 m2,0.75 m2和1 m2等5五种泄漏面积下的压降规律,表2为不同状态下下浮体到达平衡状态所需时间。
|
|
表 2 不同状态下达到平衡所需时间 Tab.2 Time required to reach equilibrium in different states |
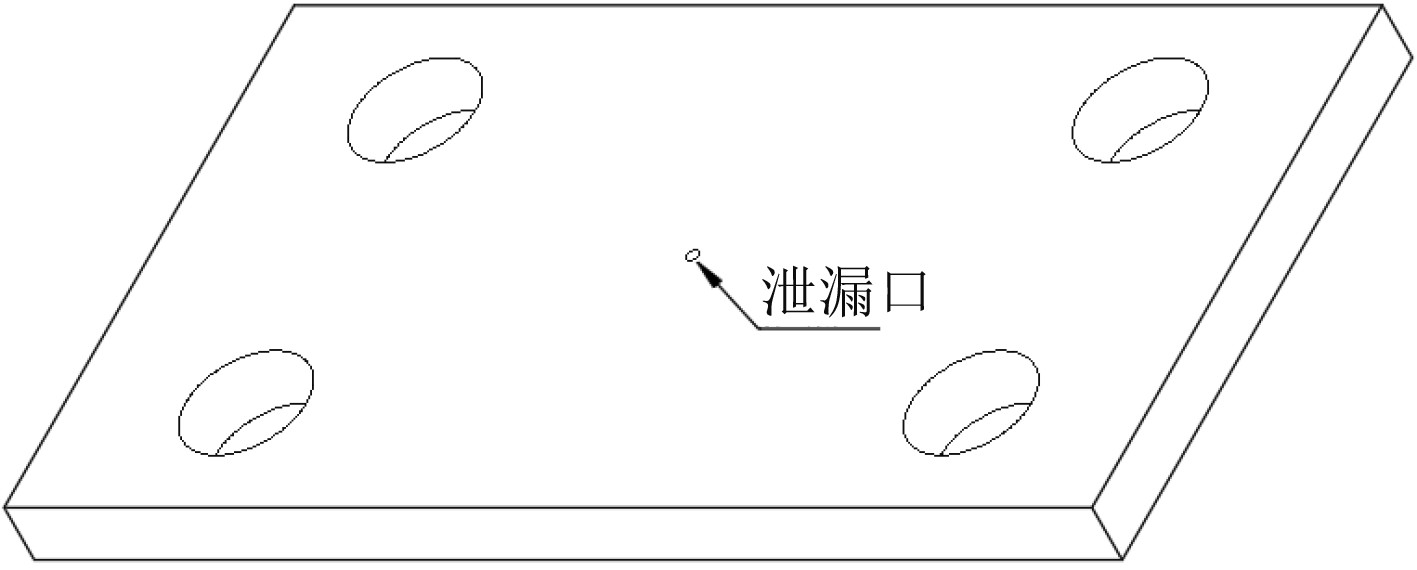
采用仿真模拟方法进行数学模型的验证,试验条件基于工况和正压型下浮体的特性而定,而下浮体泄漏面积需要制作等尺寸模型进行试验测得,本次验证以0.5 m2的圆形泄漏口和作业水深60 m为试验条件,下浮体仿真模型长宽高分别为90 m,48 m和5 m,并开有4个半径5 m的圆柱桩腿孔,如图4所示。
|
图 4 仿真模型结构图 Fig. 4 Structure diagram of simulation model |
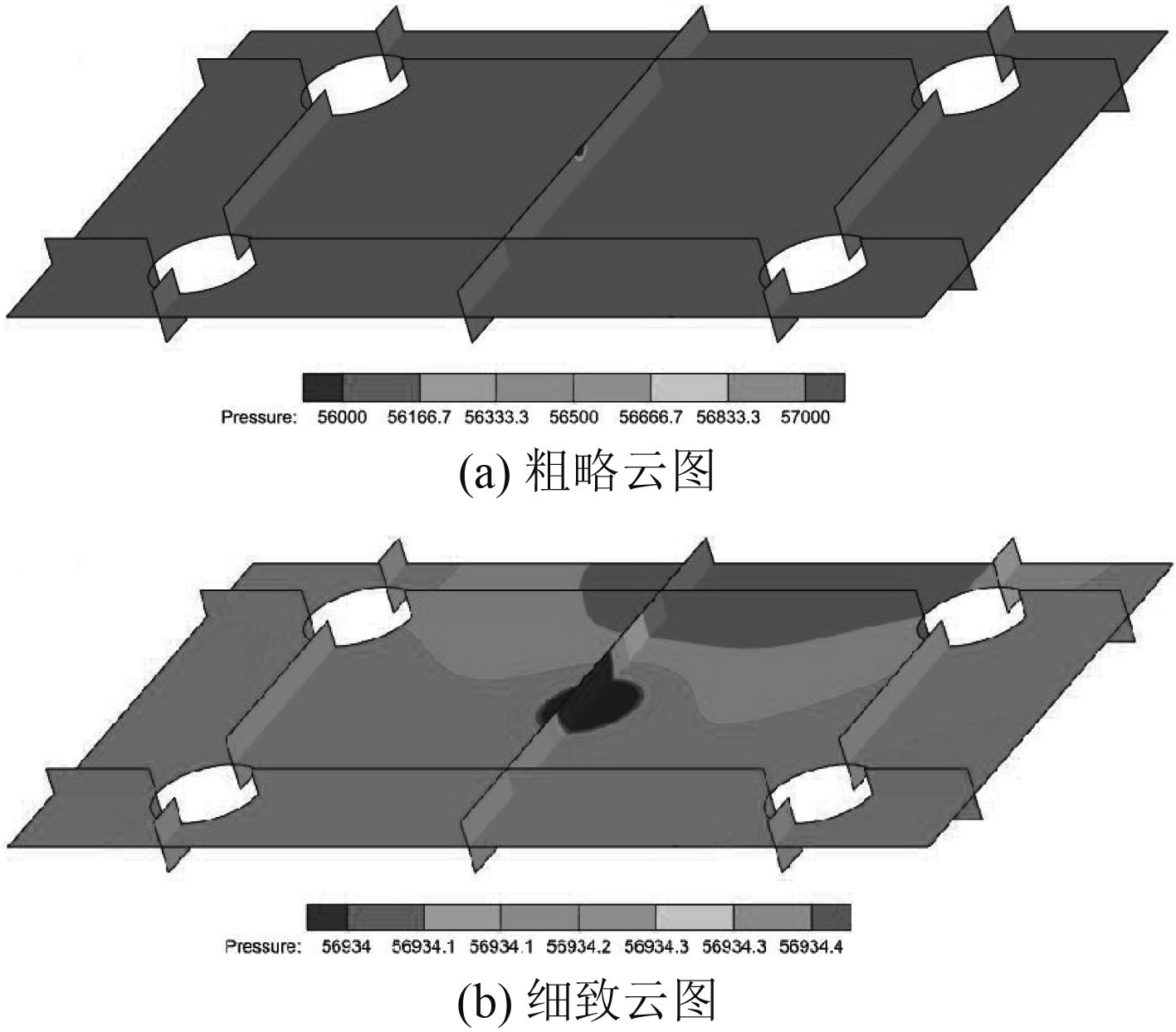
计算采用Ansys Fluent模块进行数值模拟计算,仿真过程中,为保证下浮体泄漏口处的压力在泄漏过程中保持不变,设置泄漏口出口压力为0 Pa,操作压力取工作水深的外压,初始化后通过patch给内部计算区域施加初始压力101325 Pa。为直观显示下浮体内部计算区域的压力分布情况,在下浮体内部沿3个方向建立观测截面,图5为各观察截面的压力云图。
|
图 5 各截面压力云图 Fig. 5 Pressure cloud of each section |
可以看出,靠近泄漏口区域处压力变化较大,与周边区域压力差超过1000 Pa,此时应避免在泄漏口附近建立监测点,转而在其周围区域建立监测点。图5(b)可以清楚表现出其他区域处压力具体范围,可以看出除泄漏口区域,各单元之间压力变化小,压差不超过1Pa,为此可以在下浮体泄漏口区域外的任意区域取一点作为压力监测点,通过监测点的压力变化来反映下浮体泄漏过程中的整体压力变化。
为了减小网格尺寸引起的计算误差并选取合理的网格尺寸,对计算模型进行网格独立性检验[10],整个计算区域采用四面体进行网格划分并添加膨胀层,在泄漏口部分区域进行网格加密,如图6所示。

|
图 6 泄漏口处网格划分 Fig. 6 Mesh division at leakage outlet |
表3给出了用于计算模型内部压力变化情况的4种不同网格参数,编号从Mesh1~Mesh4,4种网格均划分了膨胀层,最大网格尺寸取0.4 m,0.5 m和0.6 m,膨胀层分为4层和5层进行网格的验证,网格数量从107万增加到292万,网格质量以Skewness值衡量,高Skewness的单元极易造成计算的发散,而其值越接近0,则说明网格质量越好。
|
|
表 3 网格尺寸 Tab.3 Size of mesh opening |
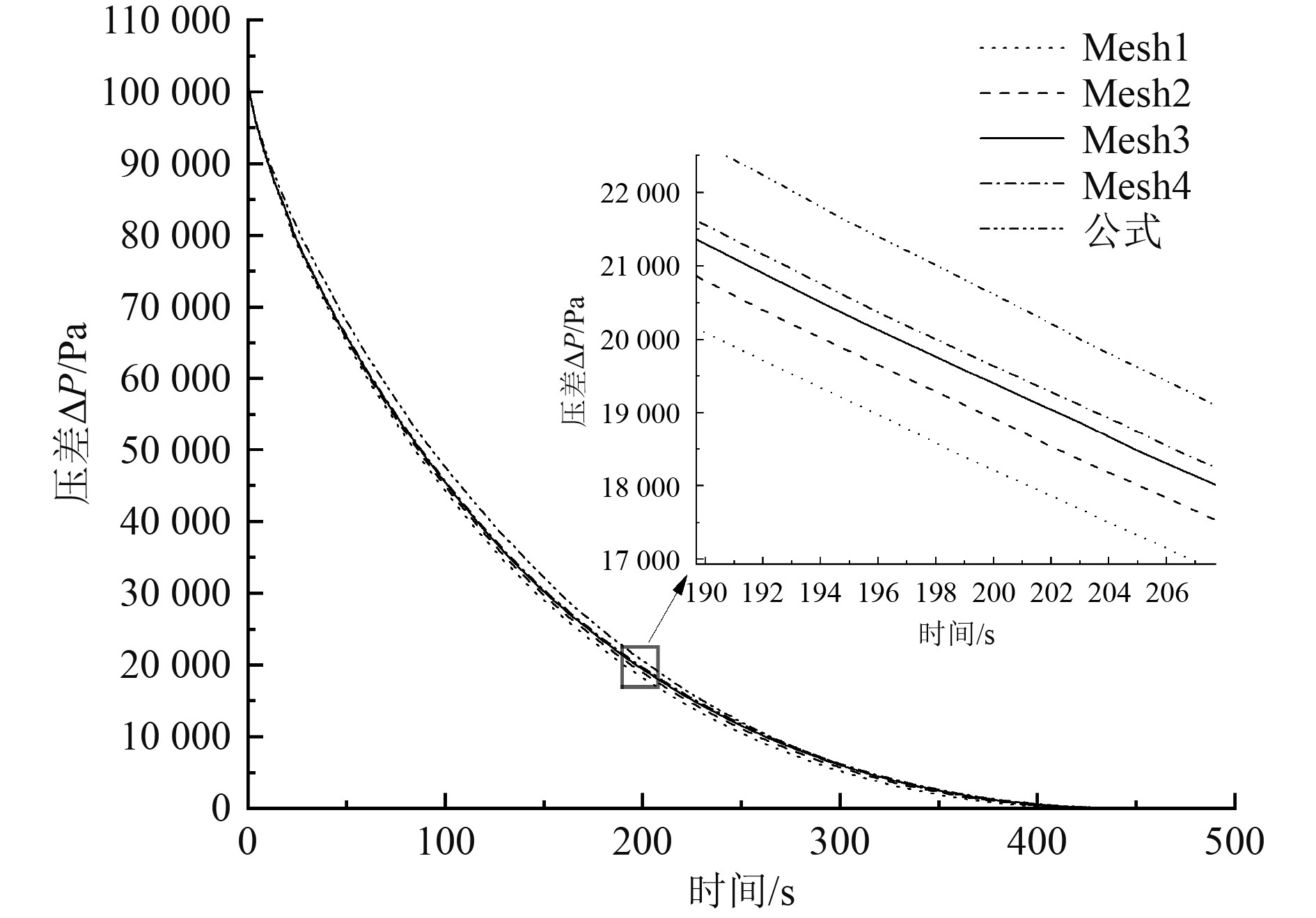
图7表示4种不同网格尺寸下,下浮体经Fluent仿真模拟后内部压力变化曲线。可以看出,下浮体达到平衡状态的时间从Mesh1~Mesh4呈增大趋势,Mesh1到达平衡时间为430.5 s,Mesh2为438.0 s,Mesh3为444.0 s,Mesh4为446.5 s,而理论公式计算平衡时间为434.1 s。
|
图 7 不同网格尺寸下的压降曲线 Fig. 7 Pressure drop curves under different mesh sizes |
为更直观地反映各曲线与理论公式的相似性,通过Spss软件进行数据分析计算数据间相关性,相关性计算值为Pearson,Spearman和Kendall系数,如表4所示。3个系数反映的都是2个变量之间变化趋势的方向以及程度,其绝对值越接近1,相关性就越强,越接近0,则相关性越弱[11]。
|
|
表 4 各曲线间相关性系数 Tab.4 Correlation Coefficient between curves |
在仿真分析过程中Mesh1平衡时间与Mesh2平衡时间的增量为1.86%,Mesh2与Mesh3增量为1.37%,而Mesh3加密至Mesh4时增量仅变化了0.4%。可以看出,Mesh3和Mesh4的相关系数基本一致。仿真计算结果和理论公式计算结果较为吻合,验证了理论公式与仿真分析的正确性,同时也可以确定Mesh3为网格尺寸的基准进行后续分析。
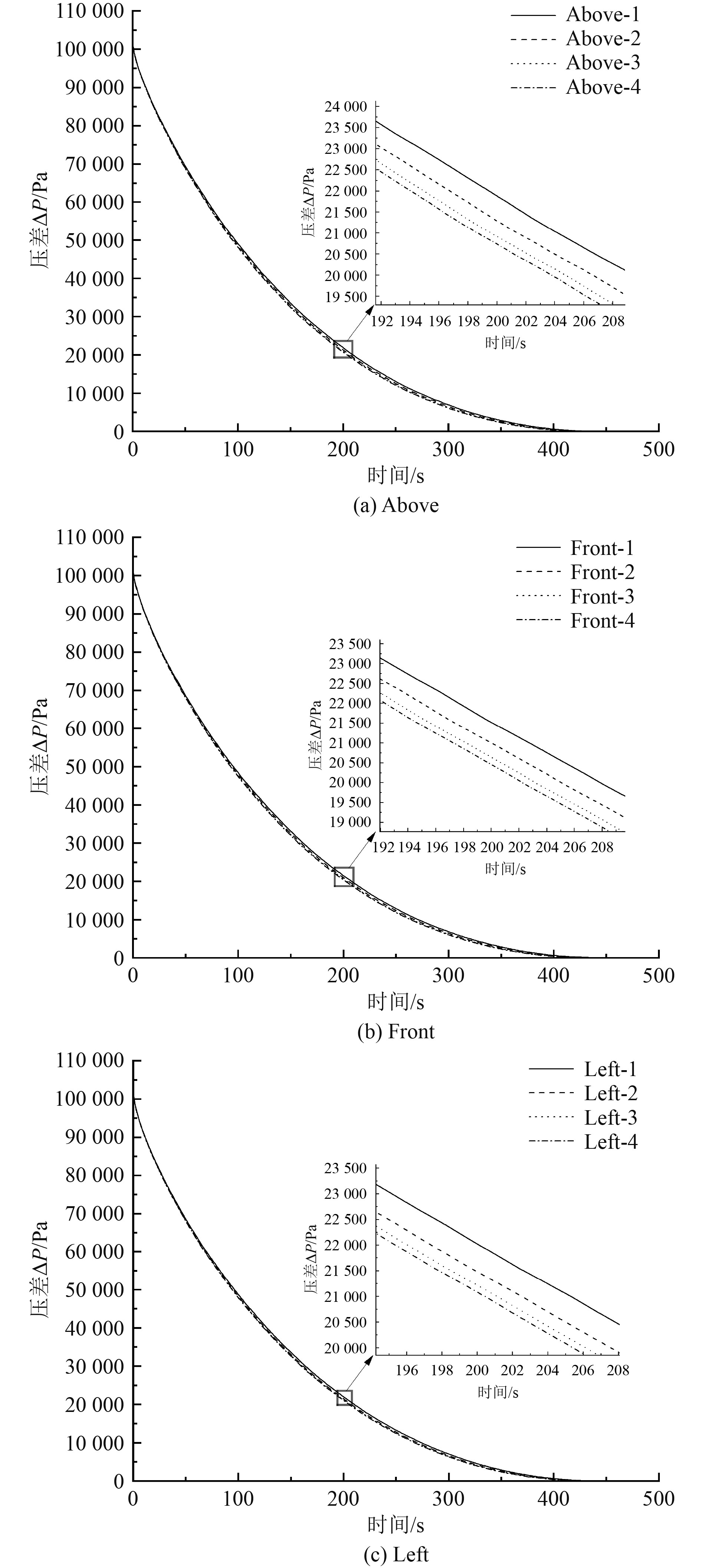
3 影响因素分析 3.1 泄漏口数量影响对泄漏口数量进行计算时,模型泄漏口包含1~4个的情况,面积关系为S1=2S2=3S3=4S4=0.5 m2;泄漏口位置分析时分别在上表面(above)、前表面(front)及左表面(left)进行开口,同时为了便于观察和记录,对泄漏口数量和位置进行编号,如上表面开1个泄漏口表示为above-1。图8为下浮体仿真模型各表面不同泄漏口数量下的压降曲线。
|
图 8 各表面不同泄漏口数压降曲线 Fig. 8 Pressure drop curves of different leakage ports on the same plane |
可以判断,随着泄漏口数的增多,下浮体内部到达平衡的时间逐渐减少,为探究这一现象取y=0这一截面分析其流速图,如图9所示。可以看出,不同数量泄漏口时下浮体内分为不同的气体区域,泄漏口数越多气体区域也越多,相校于泄漏口数少的模型,气体分子流经的区域也就越小,所以流出的时间也会稍微减少。

|
图 9 不同泄漏口数流速图 Fig. 9 Flow rate diagram of different leakage ports |
为更好分析不同压降曲线的差异程度,引入均方根误差(RMSE)指标,计算时以上一曲线为基准,计算公式为:
| $RMSE = \sqrt {\dfrac{1}{n} \displaystyle\sum\limits_{i = 1}^n {{{\left( {{P_{2i}} - {P_{1i}}} \right)}^2}} }。$ | (9) |
通过计算可以知道各表面不同泄漏口数下平衡时间的时差及数据间的RMSE值,如表5所示。表中平衡时间为整个泄漏过程结束时刻,如果把平衡时间取为433.5s,那么1个和2个泄漏口之间时差占总时间的1.2%~1.3%,此时RMSE值为450左右;2和3个泄漏口之间时差占0.90%~0.97%,此时RMSE值为230左右;3和4个泄漏口之间时差仅占0.39%~0.43%,此时RMSE值不超过100。
|
|
表 5 各表面不同泄漏口数下时差和RMSE Tab.5 The time difference and rmse of different leakage ports on each surface |
即在同一表面内随着泄漏口数的增多,平衡时差和RMSE值都逐渐减小且减小幅度变缓,而3个和4个泄漏口时的压降情况基本一致。可以认为当泄漏口数大于一定量时,压力变化曲线与泄漏口数量无关,同时可以把RMSE值作为压降过程差异大小的标准,当2个过程RMSE小于100时,压降情况可以视为一致。
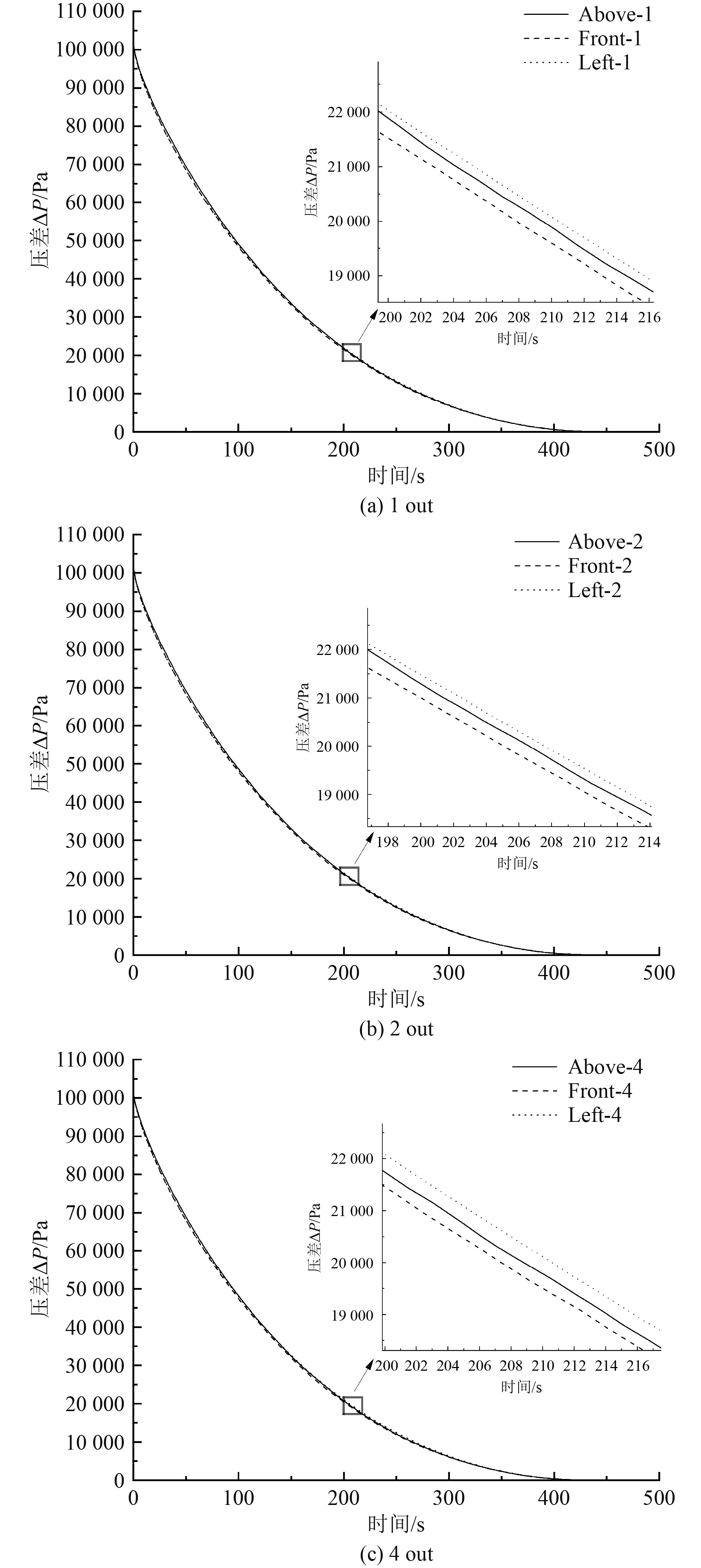
3.2 泄漏口位置影响对不同表面与不同泄漏口数情况下的压降规律进行差异分析,从图10可以看出,泄漏口数相同情况下不同表面间的曲线存在些许差异。
|
图 10 各泄漏口数不同表面压降曲线 Fig. 10 Different surface pressure drop curves for each leakage port number |
为进一步验证差异,计算各表面在泄漏口数相同时压降数据的RMSE值,如表6所示。其中不同表面间相同泄漏口数下的时差最大为1.8 s,占平衡时间的0.41%。同时各泄漏过程间RMSE均小于100,此时就可以把各压降情况视为一致,即泄漏口位置对泄漏过程的影响几乎可以忽略不计。
|
|
表 6 各状态间的平衡时差和RSME值 Tab.6 Equilibrium time difference and rsme value between states |
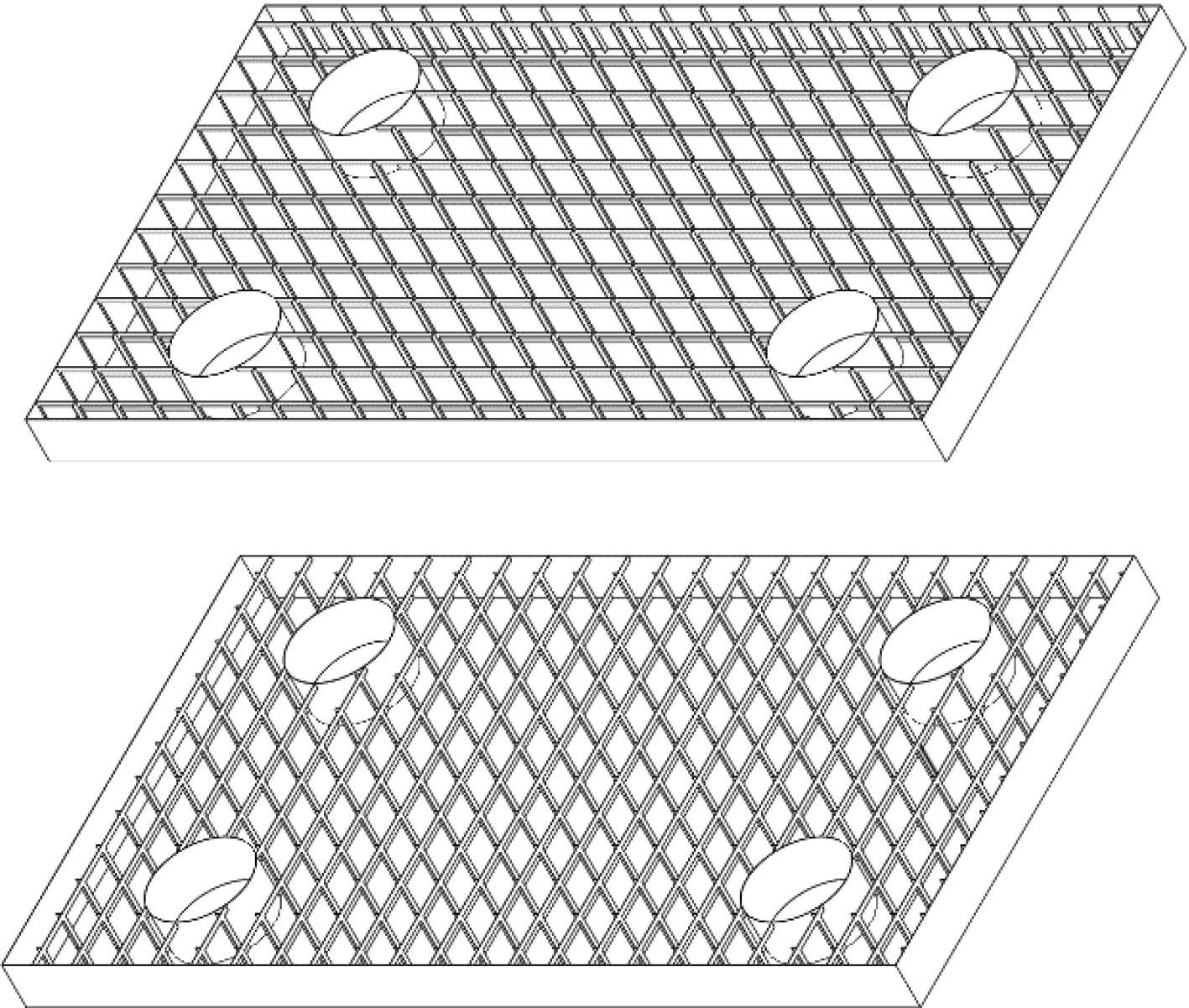
下浮体上下箱体中间有横向或纵向加强筋板支撑结构,图11为下浮体内部筋板结构。为探讨下浮体内部结构对泄漏过程的影响,对比下浮体内部无筋板,横向筋板和纵向筋板3种情况,其中在不同下浮体内部结构中横向筋板和纵向筋板数量一致,筋板体积占下浮体总体积的0.3%,可以忽略不计。
|
图 11 内部筋板结构 Fig. 11 Internal stiffened plate construction |
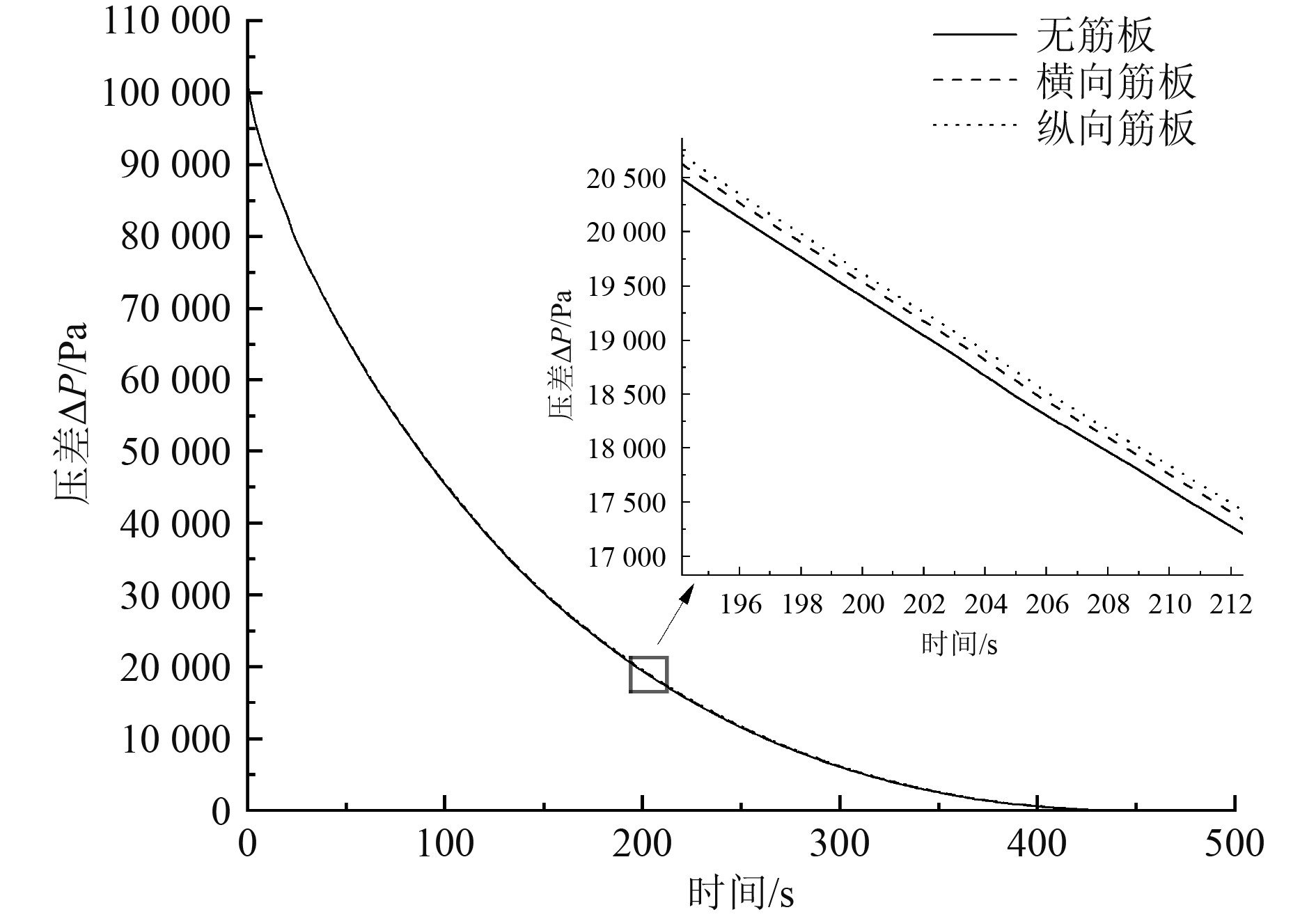
下浮体内部无筋板,有横向筋板和纵向筋板的压降曲线如图12所示。可以看出在有筋板的情况下横向筋板压降和纵向筋板压降情况相差较小,无筋板和有筋板情况相差也不大。
|
图 12 不同内部结构下的影响曲线 Fig. 12 Influence curves of different internal structures |
表7为3种内部结构压降平衡时间的时差和压降过程的RMSE值。可以看出无筋板的情况下与横向筋板和纵向筋板的时差占比0.39%和0.48%,横向筋板与纵向筋板的时差占比仅为0.14%,并且RMSE值均小于100。即在筋板体积占比下浮体总体积较小的情况下,无筋板泄漏,横向筋板泄漏和纵向筋板泄漏的泄漏状态基本保持一致。
|
|
表 7 不同内部结构的平衡时差和RMSE值 Tab.7 Balance time difference and rmse values for different internal structures |
基于Fluent仿真模拟,将有限元仿真结果与数学模型理论计算结果对比可知结果较为吻合。对下浮体泄漏过程中不同影响因素进行研究,结果表明:随着泄漏口数量的增多,下浮体平衡时间逐渐减少,并且3个和4个泄漏口的压降过程基本保持一致,即泄漏口数量超过一定量时压降过程不会发生变化;泄漏口所在的表面位置不影响泄漏过程,且在下浮体内部结构体积占比较小情况下,内部筋板结构对压降过程影响可以忽略不计。
本文研究为下浮体密封和加压及保压控制系统设计提供了理论基础,同时也为相关领域探究容器泄漏过程提供了参考依据。
| [1] |
崔东岭, 摆念宗. 海上风电与陆上风电差异性分析(上)[J]. 风能, 2019(5): 74-76. DOI:10.3969/j.issn.1674-9219.2019.05.017 |
| [2] |
苏峰. 浅谈海上深水风电难点及方向[J]. 电力系统装备, 2020(6): 2. |
| [3] |
李光. 舰船密闭区域气密特性研究[J]. 中国舰船研究, 2015, 10(4): 125-131. DOI:10.3969/j.issn.1673-3185.2015.04.019 |
| [4] |
易姣. 差压气密性检测仪的研制及其优化补偿方法研究 [D]. 杭州: 中国计量学院, 2014.
|
| [5] |
黄震, 赵建贺, 李志杰. 返回舱再入过程密封舱气体泄漏计算研究[J]. 航天器环境工程, 2017, 34(4): 415-418. DOI:10.3969/j.issn.1673-1379.2017.04.013 |
| [6] |
王兆芹, 冯文兴, 李在蓉, 等. 高压输气管道泄漏模型[J]. 油气储运, 2009, 28(12): 28-30+79+3. |
| [7] |
SCHATZEL S J, KROG R B, MAZZELLA A, et al. A study of leakage rates through mine seals in underground coal mines[J]. International Journal of Surface Mining Reclamation & Environment, 2016, 30(2): 165-179. |
| [8] |
EcosimPro ECLSS Library Reference Manual: Professional dynamic modeling and simulation tool for industrial applications[G]. Version 3.0. EA International, 2008: 317-319.
|
| [9] |
林建忠, 阮晓东, 陈邦国, 等.流体力学[M]. 北京: 清华大学出版社, 2013.
|
| [10] |
孟添. 列车气密性及车内热舒适性研究 [D]. 成都: 西南交通大学, 2017.
|
| [11] |
BONETT D, WRIGHT T. Sample size requirements for estimating pearson, kendall and spearman correlations[J]. Psychometrika, 2000, 65(1): 23-28. DOI:10.1007/BF02294183 |
 2023, Vol. 45
2023, Vol. 45

