随着科学技术的发展,海洋在政治、军事、经济等领域的战略地位日益提高,自主水下航行器(autonomous underwater vehicle,AUV)具有控制智能化、活动范围大等优点,其运动姿态控制问题成为近些年的研究热点。AUV在近水面完成规定任务的先决条件是能否对艇体的运动和位姿进行有效控制[1],众多学者就航向控制、运动轨迹跟踪、路径规划、深度控制、编队控制和姿态控制等方向展开研究。杨清等[2]针对非线性AUV运动模型,利用局部微分同胚原理对模型线性化,针对海浪扰动设计AUV的最优控制律。Wrzos-kaminska等[3]提出了一种用于铰接式干预式自主水下航行器(articulated intervention autonomous underwater vehicle, AIAUV)在3D中移动的路径跟踪控制方法,用于减少AIAUV推进器的使用,并且与视线引导法(line-of-sight, LOS)相结合,使AIAUV的运动轨迹收敛到预定路径。YUE等[4]提出了一种基于平滑函数(fuzzy controller used smoothing function, SFFC)的AUV深度控制模糊控制器,并和VSC(variable structure control)、PID方法进行对比仿真,验证了SFFC控制精度高、收敛速度快以及鲁棒性强的优点。
本文将重点放在AUV近水面低速下潜过程,分析此时AUV受到的随机海浪干扰以及相应的运动姿态变化情况,为了使AUV能够以较快速度平稳下潜,利用AUV耦合性的特点提出了直接控制和间接控制方法。考虑到AUV运动模型的非线性,利用滑模控制设计AUV的运动姿态控制器。并从快速性和稳定性2个角度分析不同控制方法的控制特点和适用范围。
1 随机海浪干扰模型 1.1 海浪频谱AUV在近水面航行过程中不可避免会受到随机海浪的影响,导致AUV产生六自由度的摇荡运动。海浪具备形状多样、运动不规则、随机变化、相互作用和边界无线等特性[5],因此通常将海浪视为随机过程。专家学者根据对海浪长期观测和统计,提出不同的频谱函数近似模拟海浪,如P-M谱、ITTC谱、Jonswap谱、文氏谱等。其中ITTC双参数海浪谱较为准确地描述成长期和成熟期海浪,其表达式如下:
| $ {S_\zeta }({\omega _w}) = \frac{A}{{\omega _w^5}}\exp \left( { - \frac{B}{{\omega _w^4}}} \right)。$ | (1) |
式中:
然而实际上AUV遇到海浪的遭遇周期与观测的海浪周期并不相等,AUV的遭遇周期实际上会随遭遇角改变而改变。遭遇角频率
| $ {\omega _e} = {\omega _w}\left( {1 - \frac{{{\omega _w}U}}{g}\cos ({\beta _w})} \right)。$ | (2) |
式中:
将式(2)引入海浪频谱并考虑波倾角的作用,则遭遇角频率对应的海浪频谱为
| $ {S}_{\alpha \omega }({\omega }_{e})=\frac{{\omega }^{4}}{{g}^{2}}\cdot \frac{{S}_{\xi }({\omega }_{w})}{1-(2{\omega }_{w}/g)U\mathrm{cos}{\beta }_{w}} 。$ | (3) |
随机海浪可由多个(理论上无穷多个)不同周期、波幅和随机初始相位的余弦波叠加而成[6],将频率区间等分为N段,则海面上定点波的波面高度可以表示为:
| $ \eta (x,y,t) = \sum\limits_{j = 1}^N {{a_j}\cos ({\omega _{wj}} - {k_{xj}}x - {k_{yj}}y + {\varepsilon _j}){\text{ }}} j = 1,2,...,N。$ | (4) |
式中:波高
水下机器人受到的海浪干扰力主要来自海浪流动分离作用的影响而不是波浪绕射力的作用[7],将AUV看做一细长刚体,利用莫里森(Morison)方程可得近水面随机海浪对AUV产生的一阶波浪力/力矩,Morison方程表达式为:
| $ f = \frac{{{C_d}}}{2}\rho DU_n^{}|{U_n}| + {C_m}\rho \frac{{\text{π} {D^2}}}{4}{\dot U_n}。$ | (5) |
式中:
AUV在近水面运动时,由于低频吸力的作用AUV将会被周期性地抛起,这种现象称为空吸现象[8]。而这种指向水表面的均值不为0、垂直向上的力就是二阶波浪力,也叫波吸力。和一阶波浪力的大小相比,二阶波浪力的幅值很小,但在较长时间内某一固定位置是个定值。随着深度的增加,二阶波浪力将急剧减小[9]。
目前主要利用势流理论和切片法等理论方法确定二阶波浪力。其步骤如下:
步骤1 确定速度势。取不规则的长峰波,则其在波浪流场的速度势在坐标点
| $ {\varPhi _m} = {\int_0^\infty \zeta _a}(\omega )C(\omega ){e^{ - kh}}{e^{k({z_0} - ({x_0}\cos \beta + {y_0}\sin \beta - Ct + \varepsilon (\omega )/k))}}{\rm{d}}\omega。$ | (6) |
式中:
任何一个物体在不可压缩的流体中运动,都会形成一个流场。如果这个流场是理想的无旋流场,则一定存在速度势。速度势可近似表达为:
| $ {\varPhi _m} = v\frac{{{R^2}}}{r}\cos \varphi + (w -{{ qx)\frac{{{R^2}}}{r}\sin \varphi + u\frac{{{\rm{d}}R(x)}}{{{\rm{d}}x}}}}R\ln r 。$ | (7) |
这样,流场的总速度势为:
| $ \varPhi (x,r,\phi ;{x}_{og}(t),{y}_{og}(t),{z}_{og}(t),\theta (t);t)={\varPhi }_{\omega }+{\varPhi }_{b}+{\varPhi }_{m}。$ | (8) |
步骤2 计算二阶波浪力和力矩。
非定常情况下的伯努利方程如下:
| $ \frac{1}{\rho }P = \frac{{{\rm{d}}\varphi }}{{{\rm{d}}t}} - \frac{1}{2}\left[{\left(\frac{1}{r}\frac{{\partial \varphi }}{{\partial \phi }}\right)^2} + {\left(\frac{{\partial \varphi }}{{\partial r}}\right)^2} + {\left(\frac{{\partial \varphi }}{{\partial x}}\right)^2}\right]。$ | (9) |
联立式(8)和式(9)可得到流场的压力分布,沿着机器人长度的方向积分可得到机器人所受到的二阶波浪力和力矩。水下机器人受到的二阶波浪干扰力如下式:
| $ {Z_{wave}} = - \int_{ - L/2}^{L/2} {R{\rm{d}}x\int_0^{2\text{π}} {P\sin \phi {\rm{d}}\phi } },$ | (10) |
二阶波浪干扰力矩如下式:
| $ {M_{wave}} = \int_{ - L/2}^{L/2} {R\int_0^{2\text{π}} {xP\sin \phi {\rm{d}}\phi } } {\rm{d}}x。$ | (11) |
美国海军研究生院(naval postgraduate school,NPS)在AUV Ⅰ的基础之上研发的AUV Ⅱ,尺寸上有所增大,用于近水面搜索、调查、区域卫生、目标成像和定位、监视和测绘等任务以及任务后的高级控制分析。NPS AUV Ⅱ 作为一种研究中常见的AUV,在非线性、非仿射建模研究中经常出现,其扁平状的外形对横摇运动的反应更敏感。
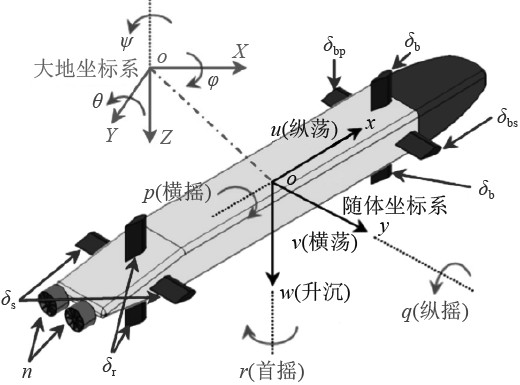
NPS AUV Ⅱ有6个控制输入,航行器的姿态由3组水平舵(左舷首翼、右舷首翼和左右舷尾翼)、2组垂直舵(上下首舵和上下尾舵)以及螺旋桨的转速控制。通过控制这些装置能够实现对AUV六自由度运动的调节。NPS AUV Ⅱ各控制面及符号如图1所示。
非线性AUV的运动问题可以分成运动学和动力学两部分[10]。AUV在近水面的运动根据图1定义的坐标系进行分解,就可以得到AUV的六自由度运动。目前通用的AUV六自由度运动符号是由海军建筑师和海洋工程师学会(SNAME)于1950年定义的,如表1所示。
AUV的运动姿态在图1所示的坐标系中能够进行转换,旋转矩阵为:
| $\begin{split} {\boldsymbol{R}} =& \left[ {\begin{array}{*{20}{c}} {\cos \psi }&{\sin \psi }&0 \\ { - \sin \psi }&{\cos \psi }&0 \\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\cos \theta }&0&{ - \sin \theta } \\ 0&1&0 \\ {\sin \theta }&0&{\cos \theta } \end{array}} \right]\times\\ & \left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos \varphi }&{ - \sin \varphi } \\ 0&{\sin \varphi }&{\cos \varphi } \end{array}} \right] ,\end{split}$ | (12) |
最终得到两坐标系速度的转换关系为:
| $ \begin{split} \left[ {\begin{array}{*{20}{c}} {\dot X}\\ {\dot Y}\\ {\dot Z} \end{array}} \right] =& \left[ {\begin{array}{*{20}{c}} {\cos \theta \cos \psi }&{\sin \varphi \sin \theta \cos \psi - \cos \varphi \sin \psi }\\ {\cos \theta \sin \psi }&{\sin \varphi \sin \theta \sin \psi + \cos \varphi \cos \psi }\\ { - \sin \theta }&{\sin \varphi \cos \theta } \end{array}} \right.\\ &\left. {\begin{array}{*{20}{c}} {\sin \varphi \sin \psi + \cos \varphi \sin \theta \cos \psi }\\ {\cos \varphi \sin \theta \sin \psi - \sin \varphi \cos \psi }\\ {\cos \varphi \cos \theta } \end{array}} \right]。\end{split} $ | (13) |
|
图 1 NPS AUV Ⅱ各控制面及符号示意图 Fig. 1 Schematic diagram of NPS AUV Ⅱ control surfaces and symbols |
|
|
表 1 ITTC推荐的符号 Tab.1 ITTC recommended symbol |
NPS AUV Ⅱ除了使用六自由度运动方程描述之外,Fossen还使用了更通用的描述方法:
| $ \left\{ {\begin{array}{*{20}{l}} {{\boldsymbol{M}}\dot v + {\boldsymbol{C}}(v)v + {\boldsymbol{D}}(v)v + {\boldsymbol{G}}(\eta ) = {\boldsymbol{\tau}} + {{\boldsymbol{\tau}} _{wave}}} ,\\ {\dot \eta = {\boldsymbol{J}}(\eta ){\boldsymbol{v}}}。\end{array}} \right. $ | (14) |
式中:
利用欧拉角定义AUV模型运动学方程为:
| $ \dot \eta = J(\eta ){\boldsymbol{v}} = \left[ {\begin{array}{*{20}{c}} {R(\eta )}&{{0_{3 \times 3}}} \\ {{0_{3 \times 3}}}&{T(\eta )} \end{array}} \right]{\boldsymbol{v}},$ | (15) |
控制力和力矩
| $ {\boldsymbol{u}} = {[\begin{array}{*{20}{c}} {{\delta _r}}&{{\delta _s}}&{{\delta _b}}&{{\delta _{bp}}}&{{\delta _{bs}}}&n \end{array}]^{\rm{T}}} 。$ | (16) |
AUV近水面下潜过程中,受随机海浪影响产生垂荡、横摇等一系列摇荡运动。其中,为了使AUV能够顺利下潜,需要设计控制器控制AUV的运动姿态。
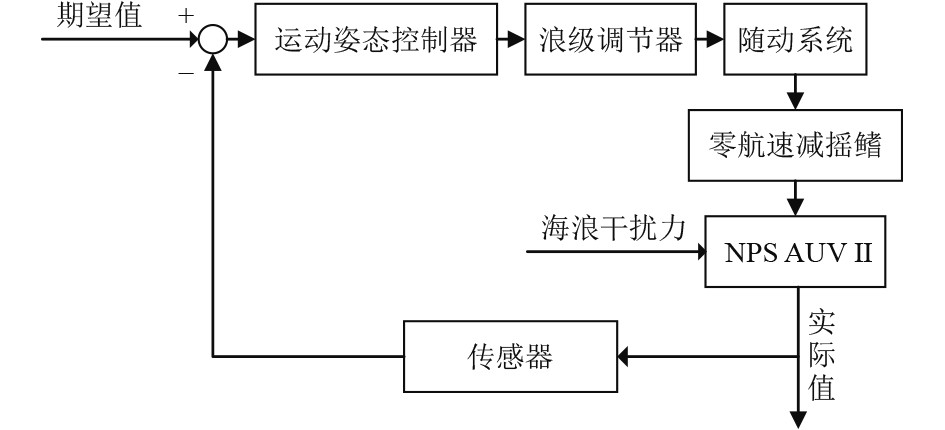
3.1 AUV运动姿态控制原理随机海浪对AUV的干扰可以以力或力矩的方式计算,在AUV运动姿态控制问题中,这种控制方法也称为“对抗控制”,根据“对抗控制”方法,能够得到AUV运动姿态控制原理,如图2所示。
|
图 2 AUV运动姿态控制原理图 Fig. 2 Principle diagram of AUV motion attitude control |
零航速减摇鳍在高速拍动的过程当中,受到的流体作用力主要分为三部分:减摇鳍的形状阻力、零航速减摇鳍的附加质量力和漩涡作用力[11]。
零航速减摇鳍纵向以角速度
| $\begin{split} F\left( t \right) =& {F_1}\left( t \right) + {F_2}\left( t \right) + {F_3}\left( t \right) = e\rho \left( {k + \frac{{{C_d}}}{3}} \right)\times \\ & \left( {3{a^2}c + {c^3}} \right)\omega (t)|\omega (t)| + \frac{J}{d}\dot \omega \left( t \right)。\end{split}$ | (17) |
式中:
同时考虑零航速减摇鳍与水平方向的夹角,则零航速减摇鳍拍动产生的横摇扶正力矩的表达式为:
| $ {M_{fin}} = 2{L_1}{l_f} = 2{L_f}\left( {{a_1}{\omega _{}}^2 + {a_2}{{\dot \omega }_{}}} \right)\cos \left( {{\omega _{}}t} \right),$ | (18) |
式中,
AUV是一个紧密耦合的系统,必须处理高度非线性、不确定运动和严重干扰[12]问题。滑模变结构控制(sliding mode control, SMC)相比传统PID控制器鲁棒性更强,被广泛用于控制受不可预测外部干扰影响的非线性和不确定系统,如机器人控制、飞行器控制、永磁同步电机控制等领域。

|
图 3 零航速减摇鳍工作原理 Fig. 3 Working principle of fin stabilizer at zero speed |
|
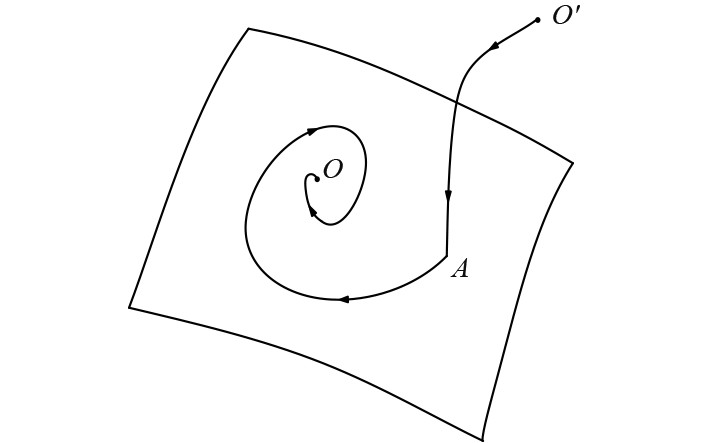
图 4 滑模变结构基本原理 Fig. 4 Basic principle of sliding mode variable structure |
考虑一般情况下的单输入非线性系统为:
| $ x = f(x,u,t),x \in {R^n},u,t \in R,$ | (19) |
设计滑模控制律为:
| $ u(x) = \left\{ {\begin{array}{*{20}{c}} {{u^ + }(x),s(x) > 0},\\ {{u^ - }(x),s(x) < 0} 。\end{array}} \right. $ | (20) |
式中:
| $ s(x)\dot s(x) < 0,$ | (21) |
而当
在实际工程应用中,滑模控制系统的抖振现象是不可能被消除的,消除抖振现象实际上也会使滑模控制系统失去抗扰动的特性
为削弱抖振现象对滑模控制系统的不利影响,国内外学者从不同角度提出各种方法削弱控制系统的抖振现象和提高系统的收敛速度,如二阶滑模控制、准滑模动态法、趋近率方法等。为削弱AUV控制器的抖振,将AUV系统特点和抖振方法的特点综合考虑。其中系统的二阶导数可能使设备不稳定,进而导致系统参数不确定性和外部干扰增大。相比于其他方法,趋近律法的优点在于改善了系统趋近过程的动态品质。
根据NPS AUV Ⅱ的六自由度运动方程,本文在双幂次组合函数趋近率[13]的基础上进行改进:
| $ \begin{split} & \dot s = - {k_1}fal(s,a,\delta ) - {k_2}|s{|^b}{{\rm{sgn}}} {\rm{h}}(s),\\ & fal(s,a,\delta ) = \left\{ {\begin{array}{*{20}{l}} {|s{|^a}{{\rm{sgn}}} {\rm{h}}(s),|s| > \delta },\\ {s,|s| < \delta } 。\end{array}} \right. \end{split} $ | (22) |
为了进一步减弱系统状态在滑模面切换时的开关特性,将式(22)中的符号函数sgn()替换为双曲函数
| $ \begin{split} & \dot s = - {k_1}fal(s,a,\delta ) - {k_2}|s{|^b}\tanh (s) ,\\ & fal(s,a,\delta ) = \left\{ {\begin{array}{*{20}{l}} {|s{|^a}\tanh (s),|s| > \delta } ,\\ {s,|s| < \delta } 。\end{array}} \right. \end{split} $ | (23) |
式中:
定义Lyapunov函数:
| $ V = \frac{1}{2}{s^2} ,$ | (24) |
对式(24)求导,有
| $ \dot V = s\dot s。$ | (25) |
由LaSalle不变性原理可知,Lyapunov函数非正定,系统渐进稳定,而系统收敛于状态原点的速度取决于
根据式(14)AUV六自由度运动模型以及式(13)中AUV下潜速度的转换关系,能够将控制AUV垂荡运动的方法分为直接控制和间接控制。这些控制方法的共同点是都将零航速减摇鳍视为运动姿态控制的执行机构,不同之处在于选取的状态量不同。
1)直接控制。
描述AUV下潜过程好坏的是垂荡运动,因此直接控制方法是通过设定期望的下潜深度。控制器根据偏差控制减摇鳍拍动频率,从而使AUV的下潜速度尽快达到期望值并且保持稳定,控制AUV垂荡运动。
| $\begin{split} & m\left[ {\dot w - uq + vp + {x_G}\left( {pr - \dot q} \right) + {y_G}\left( {qr + \dot p} \right) - {z_G}\left( {{p^2} + {q^2}} \right)} \right] =\\ & Z + {Z_{wave}} + F(t)\cos (\omega t)。\end{split} $ | (26) |
假设期望AUV在100 s的时间内下潜15 m,即
| $ {e_h} = h(t) - {h_d} ,$ | (27) |
则有误差跟踪函数:
| $ \left\{ {\begin{array}{*{20}{c}} {{S_h} = {{\dot e}_h} + {c_h}{e_h}} ,\\ {{{\dot S}_h} = {{\ddot e}_h} + {c_h}{{\dot e}_h}}。\end{array}} \right. $ | (28) |
将式(17)、式(23)、式(28)代入式(26),即可推导出减摇鳍拍动角加速度的表达式。
2)间接控制
根据式(13)坐标系转换关系,AUV近水面下潜速度的快慢或者是否稳定还与横摇角
① 横摇角控制
由式(13)可知:随体坐标系中AUV沿3个坐标轴的速度一定时,横摇角越小下潜速度越大。AUV横摇减摇时,根据横摇角偏差控制器输出控制信号进入浪级调节器和随动系统。控制信号驱动电机,使零航速减摇鳍的纵向拍动角速度产生横摇扶正力矩,最终实现横摇减摇和控制AUV下潜的目的。
假设AUV是小幅运动[14],此时近似地认为:
| $ {\text{sin}}\phi \approx \phi ,$ | (29) |
选取
| $ {e_{roll}} = \phi \left( t \right) - {\phi _d},$ | (30) |
定义跟踪误差函数为:
| $ \left\{ {\begin{array}{*{20}{c}} {{S_{roll}} = \dot e{}_{roll} + {c_{roll}}{e_{roll}}} ,\\ {{{\dot S}_{roll}} = {{\ddot e}_{roll}} + {c_{roll}}{{\dot e}_{roll}}} 。\end{array}} \right. $ | (31) |
整理得到NPS AUV Ⅱ基于零航速减摇鳍理论的水平舵纵向拍动的角加速度表达式:
| $\begin{split} {{\dot \omega }_k} = &\frac{1}{{2{l_f}{a_2}\cos {\alpha _{(k - 1)}}}} \Biggr\{ [{k_1}fal\left( {{S_{roll}},a,\delta } \right) +\\ & {k_2}|{S_{roll}}{|^b}{{\rm{sgn}}} ({S_{roll}}) - {c_{roll}}\dot \varphi (t)]\left( {{I_x} - \frac{\rho }{2}{L^5}K'_{\dot p}} \right) - \\ & [ {I_{xy}}(q - r) - m{z_G}w + \tfrac{\rho }{2}{L^5}{{K'}_{pq}}q + \tfrac{\rho }{2}{L^4}({{K'}_p}u +{{K'}_{wp}}w + \\ & {{K'}_{pn}}u \varepsilon (n))] \cdot \dot \varphi + {z_G}W\cos \theta \cdot \varphi - {I_{xy}}( \dot q + {q^2} - {r^2} + \dot r ) -\\ & m{z_G}(v + \dot ur) - \frac{\rho }{2}{L^5}[ {{{K'}_{\dot r}}\dot r + {{K'}_{qr}}qr} ] - \frac{\rho }{2}{L^4}[ {{K'}_{\dot v}}\dot v + \\ &{{K'}_r}ur + {{K'}_{vq}}vq + {{K'}_{wr}}wr ] - \frac{\rho }{2}{L^3}[ {{K'}_v}uv +\\ & {{K'}_{vw}}vw ] - {M_{wr}} - 2{l_f}{a_1}\omega _{(k - 1)}^2\cos {\alpha _{(k - 1)}}\Biggr\}。\\[-15pt] \end{split} $ | (32) |
式中:
| $ \left\{ {\begin{array}{*{20}{c}} {{\omega _k} = {\omega _{(k - 1)}} + {{\dot \omega }_{(k - 1)}}{{T}}} ,\\ {{\alpha _k} = {\alpha _{(k - 1)}} + {\omega _k}T} 。\end{array}} \right. $ | (33) |
式中:
②纵倾角控制
为保证AUV稳定下潜,纵倾角需要维持在一个角度。控制器根据纵倾角偏差控制减摇鳍的拍动频率以产生纵摇扶正力矩,使AUV的纵倾角稳定在某个角度附近,
假设AUV是小幅运动,此时近似地认为:
| $ \dot \theta = q ,$ | (34) |
设
| $ {e_{pitch}}(t) = \theta (t) - {\theta _d} ,$ | (35) |
纵倾角的误差跟踪函数
| $ \left\{ {\begin{array}{*{20}{c}} {{S_{pitch}} = \dot e{}_{pitch} + {c_{pitch}}{e_{pitch}}} ,\\ {{{\dot S}_{pitch}} = {{\ddot e}_{pitch}} + {c_{pitch}}{{\dot e}_{pitch}}} 。\end{array}} \right. $ | (36) |
减纵摇翼面的转动加速度控制规律。
| $ \begin{split} \ddot \theta (t) =& {k_{12}}/N({s_2})|{s_2}{|^{{a_1}}}\tanh ({s_2}) + {k_{22}}/N({s_2})|{s_2}{|^{{b_1}}}\tanh ({s_2}) +\\ & {k_{32}}/N({s_2}){s_2} - {C_{pitch}}\dot \theta (t) 。\\[-10pt] \end{split}$ | (37) |
对AUV近水面低速下潜过程进行仿真。其中海浪情况有义波高取1.87 m,遭遇角取45°,90°及135°。AUV的初始深度0.5 m,下潜过程中u=0.8 m/s恒速航行。方向舵角保持0 rad,水平尾舵
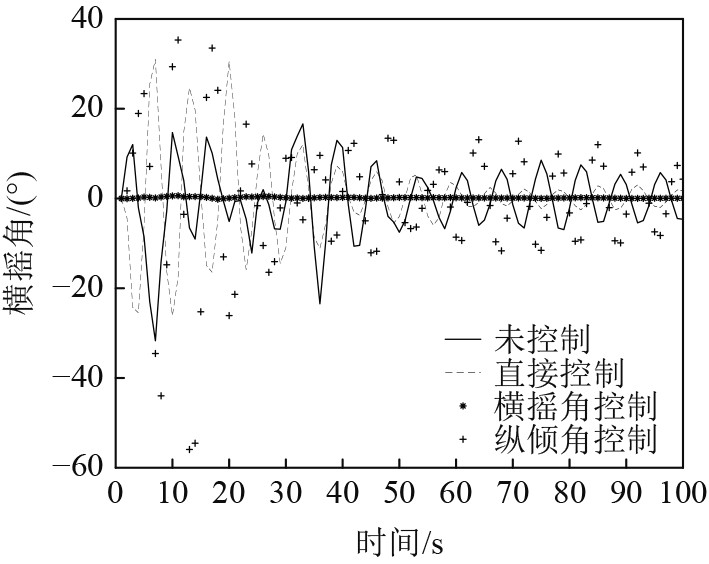
以有义波高1.87 m,遭遇角45°时AUV下潜过程为例,各种控制方法下潜过程中AUV 的下潜深度、下潜速度以及横摇角的变化对比如图5~图7所示。

|
图 5 AUV下潜深度变化对比图 Fig. 5 Comparison diagram of AUV diving depth variation |

|
图 6 AUV下潜速度变化对比图 Fig. 6 Comparison diagram of AUV diving velocity variation |
|
图 7 AUV横摇角变化对比图 Fig. 7 Contrast diagram of AUV roll angle change |
|
|
表 2 AUV下潜深度(m) Tab.2 AUV diving depth (m) |
1)从最大下潜深度和下潜速度的平均值来看,直接控制AUV的垂荡运动能够使AUV以最快速度下潜,其次是横摇角控制,而通过纵倾角间接控制AUV下潜最慢。
|
|
表 3 AUV下潜速度平均值(m/s) Tab.3 Average AUV diving speed (m/s) |
|
|
表 4 AUV下潜速度标准差 Tab.4 Standard deviation of AUV diving speed |
|
|
表 5 AUV横摇角标准差 Tab.5 Standard deviation of AUV roll angle |
2)从下潜速度标准差来看,利用横摇角间接控制AUV的垂荡运动能使AUV速度变化最稳定,其次是纵倾角控制。直接控制与未控制相比差距不大。
3)从横摇角标准差来看,只有横摇角控制方法能够对AUV的横摇运动起到抑制作用,其余2种方法对横摇运动没有作用。这是由于横摇角控制时水平首舵
综上所述,若是需要AUV快速下潜到指定位置且不考虑姿态稳定时,可以选择直接控制方法,此方法能使AUV下潜速度加快。若是需要同时兼顾AUV的下潜速度和下潜过程运动姿态的稳定性时,则可以选择横摇角控制方法。
5 结 语由于AUV在近水面时海浪会对其运动姿态产生影响,使AUV不能平稳快速下潜。针对这种情况,从不同角度分析AUV的控制方法并设计滑模控制器,通过对比仿真,能够比较出各种控制方法的优缺点以及适用情况。其中,通过横摇角间接控制AUV的运动过程总体效果最好,能够同时兼顾AUV的下潜速度和下潜过程中的稳定性。
| [1] |
王永鼎, 王鹏, 孙鹏飞. 自主式水下机器人控制技术研究综述[J]. 世界科技研究与发展, 2021, 43(6): 636-648. DOI:10.16507/j.issn.1006-6055.2021.01.004 |
| [2] |
杨清, 宿浩, 唐功友. 受扰欠驱动自主水下航行器的最优扰动抑制控制[J]. 中国海洋大学学报(自然科学版), 2017, 47(6): 139-145. DOI:10.16441/j.cnki.hdxb.20140390 |
| [3] |
WRZOS-KAMINSKA M, PETTERSEN K Y, GRAVDAHL J T. Path following control for articulated intervention-AUVs using geometric control of reduced attitude - ScienceDirect[J]. IFAC-PapersOnLine, 2019, 52(16): 192-197. DOI:10.1016/j.ifacol.2019.11.777 |
| [4] |
YUE W, YUE S, WANG K, et al. Fuzzy controller used smoothing function for depth control of autonomous underwater vehicle[J]. Oceans. IEEE, 2016: 1–5.
|
| [5] |
DAN L, WU H, LUO G. Simulation of 3D dynamic seas based on OpenGL[C]// 2016 7th IEEE International Conference on Software Engineering and Service Science (ICSESS), IEEE, 2016: 144–147.
|
| [6] |
沈祉怡, 赵冰化, 张晓蕾. 基于OpenGL的实时三维海浪可视化仿真[J]. 舰船电子工程, 2015, 35(7): 124-126. |
| [7] |
徐强, 章家岩, 杜翠翠. 基于遗传算法的水下机器人滑模变结构控制策略[J]. 安徽工业大学学报, 2016, 33(3): 261-265. |
| [8] |
HANGIL J, MINSUNG K, SON-CHEOL Y. Second-order sliding-mode controller for autonomous underwater vehicle in the presence of unknown disturbances[J]. Nonlinear Dynamics, 2014(78): 183-196. |
| [9] |
THOR I FOSSEN. Guidance and control of ocean vehicles[M]. Chichester: John Wiley & Sons, 1994.
|
| [10] |
GERANMEHR B, NEKOO S R. Nonlinear suboptimal control of fully coupled non-affine six-DOF autonomous underwater [11]vehicle using the state-dependent Riccati equation[J]. Ocean Engineering, 2015, 96(1): 248-257. |
| [11] |
金鸿章, 张晓飞, 罗延明, 等. 零航速减摇鳍升力模型研究[J]. 海洋工程, 2007, 25(3): 83-87+114. DOI:10.3969/j.issn.1005-9865.2007.03.013 |
| [12] |
WANG M, ZENG B, WANG Q. Study of motion control and a virtual reality system for autonomous underwater vehicles[J]. Algorithms, 2021, 14(3): 93-113. DOI:10.3390/a14030093 |
| [13] |
廖瑛, 杨雅君, 王勇. 滑模控制的新型双幂次组合函数趋近律[J]. 国防科技大学学报, 2017, 39(3): 105-110. DOI:10.11887/j.cn.201703017 |
| [14] |
HASSAN S M, ABOZIED M, KHAMIS A, et al. Non-linear modeling and simulation with 3-D animation for 6-DOF autonomous underwater vehicle[C]// 2018 26th International Conference on Systems Engineering (ICSE), IEEE, 2018: 1–7.
|
 2023, Vol. 45
2023, Vol. 45
