无人水下航行器(unmanned underwater vehicle,UUV)凭借操纵灵活、可控性好、航行时间长等优势,被广泛应用于执行各种任务,如海洋环境数据采集、海洋资源勘探、通信中继、反潜警戒、水下侦察与监视、海洋工程和海底电缆检测等[1-3]。具有智能化、程度高和成本低的优点,可以代替人类执行水下危险任务。
UUV因自身结构的限制,其大多采用“人在回路中”的控制方式[4],但是UUV在水下航行中易受到风、浪和流等外界因素的影响,特别是在恶劣的海洋环境下,通信环境受到干扰,通信可靠性降低[5],造成通信中断。因此在复杂海洋环境下工作的UUV必须要求具备一定的自主航行控制能力和自主校正能力,以适应航行过程中复杂变化的海洋环境[6]。另一方面精确的导航与定位技术是UUV完成水下航行任务的关键因素,目前,UUV的导航定位主要采用惯性导航系统[7],其在航行的过程中会产生位置误差,定位系统无法对自身进行准确定位,误差会随着时间累积,当误差积累到一定值时,将导致航行任务失败[8]。航迹规划技术是实现UUV自主航行并完成水下任务的关键,其主要思想是在特定的环境中,规划出一条满足约束条件、目标最优的航迹。
随着控制技术的发展,多约束条件航迹快速规划越来越重要,国内外学者对航迹规划问题进行了大量研究,并取得了一定成果。其中常用的方法有Dijkstra 算法[9]、人工势场法[10]、模拟退火算法[11]、A*算法[12]等,本文主要从航迹规划、转向角、校正定位3个方面建立模型,提出一种基于最小转向角搜索算法,并对算法的有效性对比讨论。
1 问题描述及模型的构建 1.1 问题描述UUV在水下执行任务时,可能会遇到恶劣的海洋环境,其通信受到影响,无法定位自身位置,定位误差累积增加,将会造成航行任务失败。航行区域中存在水平和垂直校正点,即用于校正定位误差的安全位置,且UUV航迹转向点都在所给的校正点上,每次校正只能选取一个方向,需要在复杂海洋环境条件下找出一条满足以下条件的最优航迹:
1)UUV的航迹长度尽可能的短;
2)经过校正点的次数尽可能的少;
3)UUV在转弯时受到自身机动性能的限制,无法突然改变前进方向,其转向角应在一定的限制范围内,考虑到航迹的光滑度,要求转向角尽可能的小,UUV 允许的最大转向角为
UUV自起点
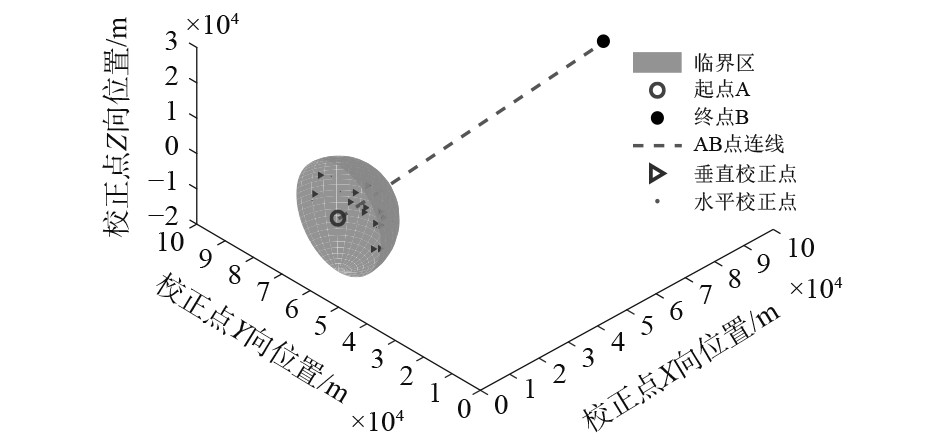
|
图 1 校正点选取示意图 Fig. 1 Correction point selection schematic |
已知UUV的起点和终点,要使航迹长度尽可能短,满足约束条件下构建数学模型。本文设计一条经过若干校正点航迹长度最短的轨迹,使得在航经校正点处误差不断校正,从而能顺利达到终点。
| $ \mu ({x}_{i},{y}_{i},{z}_{i})=\left\{\begin{array}{l}1,{垂直校正},\\ 0,{水平校正}。\end{array} \right.$ | (1) |
|
|
表 1 符号变量说明 Tab.1 Symbolic variable description |
1)目标函数
要使航迹长度尽可能短,即目标函数为:
| $ \mathrm{min}L=\left[{{d}}_{(0,1)}+\left({\displaystyle \sum _{i=1}^{n-1}{d}_{(i,i+1)}}\right){{+d}}_{(\text{n},n+1)}\right]。$ | (2) |
式中:
| $ {d_{(i,i + 1)}} = \sqrt {{{({x_i} - {x_{i + 1}})}^2} + {{({y_{_i}} - {y_{i + 1}})}^2} + {{({z_{_i}} - {z_{i + 1}})}^2}}。$ | (3) |
2)校正条件约束
第1个约束条件是校正次数尽可能少:在起点
因此,校正前该点的垂直误差
| $ \left\{ \begin{gathered} {r_i} = {r_{i - 1}} + \delta {d_{i - 1,i}},\\ {s_i} = {s_{i - 1}} + \delta {d_{i - 1,i}}。\\ \end{gathered} \right. $ | (4) |
当
| $ \left\{ \begin{gathered} {r_{i - 1}} + \delta {d_{i - 1,i}} \leqslant {\alpha _1} ,\\ {s_{i - 1}} + \delta {d_{i - 1,i}} \leqslant {\alpha _2} 。\\ \end{gathered} \right. $ | (5) |
校正后:
| $ \left\{ \begin{gathered} {r_i} = 0,\\ {s_i} = {s_{i - 1}} + \delta {d_{i - 1,i}}。\\ \end{gathered} \right. $ | (6) |
当
| $ \left\{ \begin{gathered} {r_{i - 1}} + \delta {d_{i - 1,i}} \leqslant {\beta _1},\\ {s_{i - 1}} + \delta {d_{i - 1,i}} \leqslant {\beta _2}。\\ \end{gathered} \right. $ | (7) |
校正后:
| $ \left\{ \begin{gathered} {r_i} = {r_{i - 1}} + \delta {d_{i - 1,i}},\\ {s_i} = 0。\\ \end{gathered} \right. $ | (8) |
到达终点时垂直和水平误差均满足以下条件:
| $ \left\{ \begin{gathered} {r_n} + \delta {d_{n,n + 1}} \leqslant \theta ,\\ {s_n} + \delta {d_{n,n + 1}} \leqslant \theta 。\\ \end{gathered} \right. $ | (9) |
由式(4)~ 式(9)可知校正误差随着航行距离增加,因此,可以把误差校正约束转化为待选点间距离约束。
3)转向角条件约束
第2个约束条件是UUV控制过弯的转向角尽可能的小:UUV在航行的过程中需要依靠辅助推进器实现及时转向,当航迹规划转向角过大时,由于UUV自身推进器及其结构的限制,无法及时控制过弯,而且转向角增大会增加UUV能耗,影响UUV实际航程[13-14],基于此提出转向角约束。图2为转向角示意图,从当前点
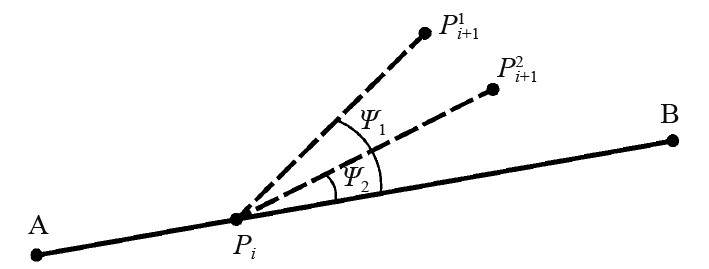
|
图 2 转向角约束示意图 Fig. 2 Diagram of steering angle constraint |
UUV航行校正误差的同时,每次节点的选择都在减少到目标点的航迹长度,在此引入相邻校正点构成的方向向量
| $ {\psi _{\text{i}}}_{(x,y,z)} = \arccos \frac{{\overrightarrow {({p_i},{p_{i + 1}})} \cdot \overrightarrow {(A,B)} }}{{\left| {\overrightarrow {({p_i},{p_{i + 1}})} } \right| \cdot \left| {\overrightarrow {(A,B)} } \right|}}。$ | (10) |
考虑到UUV的操纵性能,当转向角大于90°时,操纵及为困难,且在海底存在暗流的复杂情况下,控制过弯的失误率明显增加,航行过程中还要减少航迹折返的情况,因此在航迹规划时各校正点处转向角越小的点应该优先考虑,在满足校正条件和偏转角约束下建立目标函数。
1.4 算法步骤及流程步骤1 以A为起点,求待选点到A点的距离
条件1:判断待选点是否定在以
条件2:
步骤2 求当前点到待选点偏向夹角
步骤3 从当前点出发到终点B的航迹距离是否满足条件3,如果满足,则输出最终航迹,停止迭代,如若不能到达B点,迭代次数加 1,返回步骤 1。
条件3:
具体算法流程如图3所示。

|
图 3 航迹规划算法流程 Fig. 3 Route planning algorithm flow |
根据上述模型和算法,其参数分别设置为
|
|
表 2 部分校正点坐标 Tab.2 Correction point coordinates |
基于表2数据,针对上述2种约束条件,调整半径10000~20000 m,利用 Matlab数值模拟仿真,可以得出不同调整半径
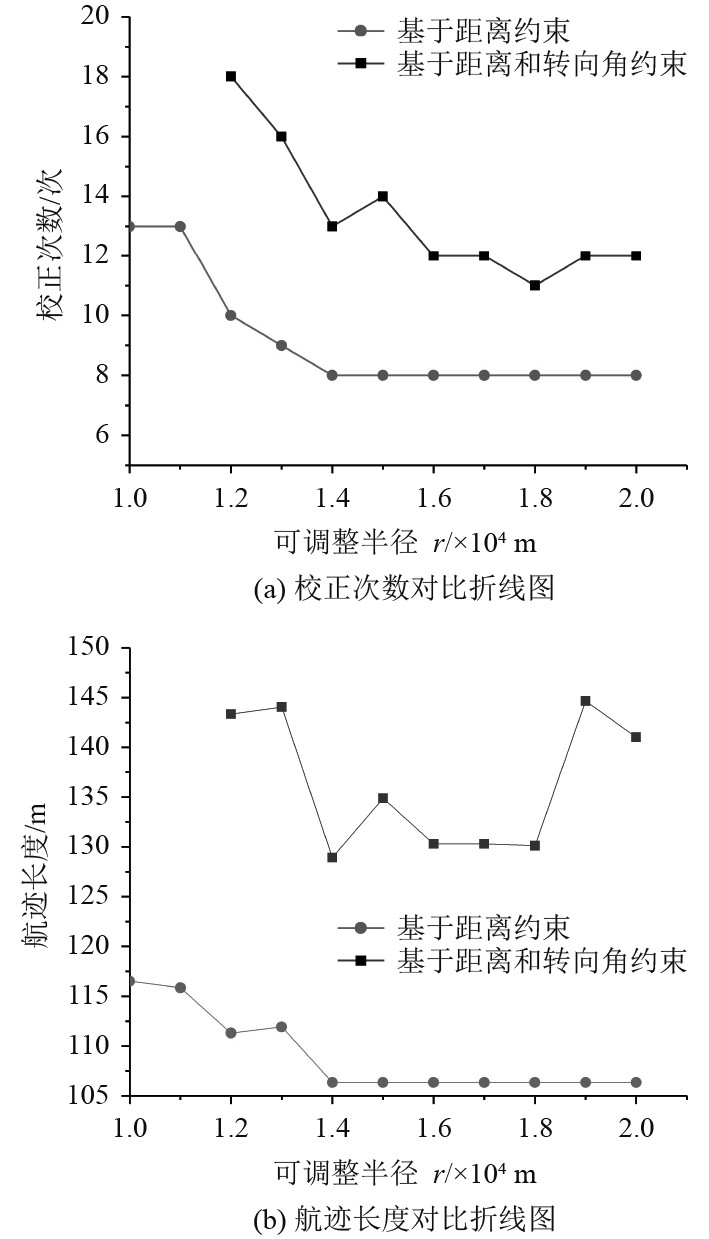
|
图 4 不同调整半径对比图 Fig. 4 Comparison of different adjusting radius |
基于航迹长度约束条件仿真实验数据对比,结果见表3。可知,当调整半径
|
|
表 3 不同调整半径对比结果 Tab.3 Comparison results of different adjustment radius |
如图5所示,在只考虑航迹长度约束的算法下,航迹路径上的校正点会出现从起点到终点方向的折回、相邻、平行的现象。当r=12000 m 时,航迹平面图出现6次折回和 1次相邻的现象,校正点次数多达18次,航迹长度为143331 m,第5个校正点偏向角最大为121.80°;当r=13000 m时,航迹平面图出现3次折回、1次平行和1次相邻的现象,校正点次数为16次,航迹长度为144041 m,第13个校正点偏向角最小为4.52°;当r=14000 m时,航迹平面图出现1次折回和1次相邻现象;当r=18000 m时,航迹平面图出现2次折回现象,航迹最靠近AB直线方向,该算法达到最优,此后再增加调整半径

|
图 5 不同调整半径的航迹规划平面图 Fig. 5 Plane diagram of route planning with different adjustment radius |
在航迹长度约束的基础上增加转向角约束条件对比数据分析,其具体结果见表4。
|
|
表 4 不同调整半径对比结果 Tab.4 Comparison results of different adjustment radius |
由表4可知,调整半径
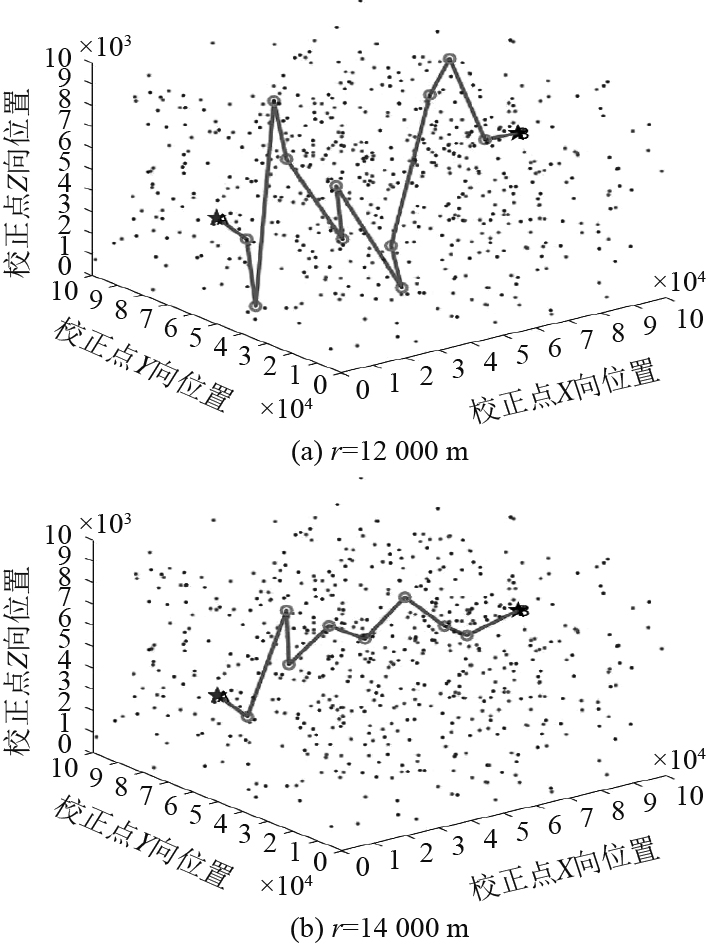
如图6所示,当r=11000 m时,校正点次数多达13次,所得的航迹长度为115848 m,总转向角度为349.24°,第10个校正点转向角最大,最大值为64.34°;当r=12000 m时,校正点次数为10次,所得的航迹长度为111306 m, 总转向角度为202.87°,与 r=11000 m相比,校正点减少3次,总转向角减少146.37°,当r=13000 m时 ,经过9个校正点,所得的航迹长度为111926 m,与r=12000 m时的航迹对比,虽然校正次数减少1次,但航迹距离增加620 m,当r=14000 m时,经过的校正点8个,所得的航迹长度为106350 m,第7个校正点转向角最小,最小值为5.22°,总转向角度变小为120.66°,UUV航行轨迹为A-521-64-80-170-278-369-214-397-B,航迹方向最接近直线AB,得到最优解。
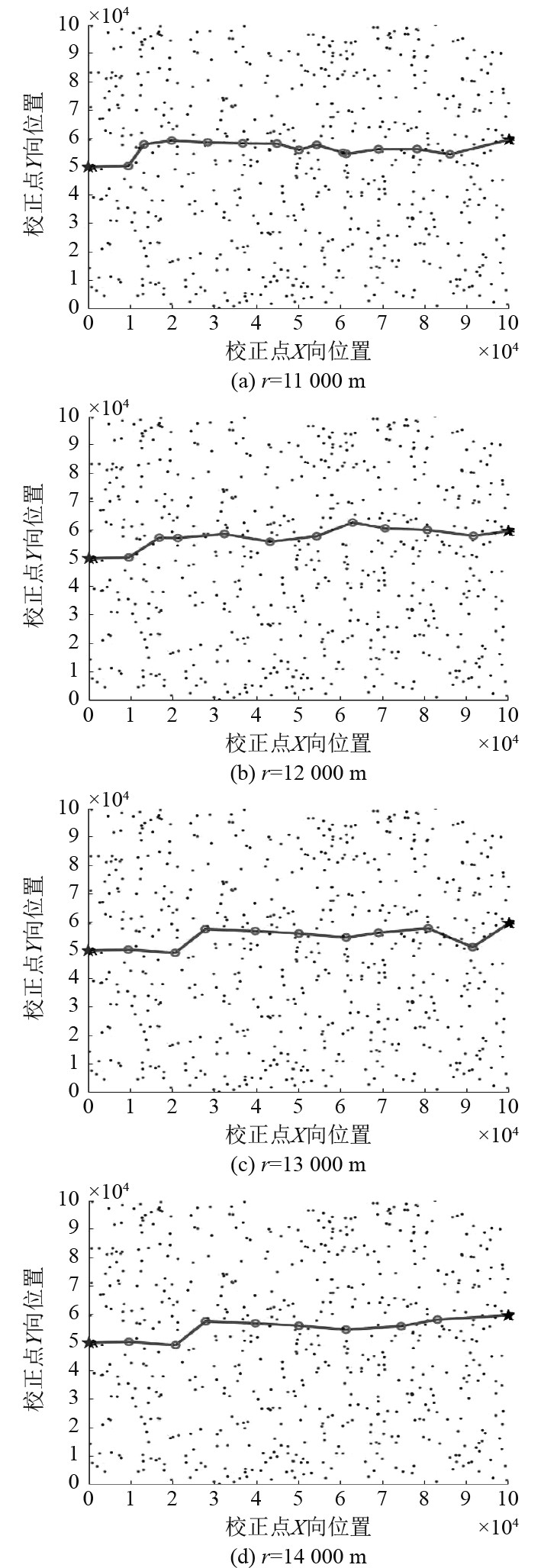
|
图 6 不同调整半径的航迹规划图 Fig. 6 Path planning with different adjustment radius |
结果表明,在合理范围调整半径r,能够有效缩短航迹长度,减少校正次数和总转向角度。如表5所示,对比2种方法,当考虑转向角约束条件时,校正次数为8次,优于单一路径最短规划方法的11次,路径长为106350 m,相较于单一路径最短规划方法的130115 m,其规划航迹长度减少了23765 m,航迹平滑没有折回、比邻、平行的情况,满足UUV在水下复杂环境中的航迹规划,图7 为2种约束条件下对应的最优三维航迹图。
|
|
表 5 两种方法对比 Tab.5 Comparison of two methods |
|
图 7 不同约束下最优三维空间航迹图 Fig. 7 Optimal three-dimensional space trajectory under different constraints |
本文围绕UUV在复杂海洋环境中航行时误差校正问题,建立单目标函数,根据约束条件的不同,在基于单一航迹长度最短规划基础上,提出考虑转向角约束的最小转向角航迹规划算法,通过对比可以发现,考虑转向角约束条件时,航迹长度明显缩短,校正次数减少,路径光滑,满足航行要求。
| [1] |
郝拥军, 程玲, 鲍轩. 多任务UUV的路径规划算法及其应用[J]. 舰船科学技术, 2021, 43(S1): 48-51. |
| [2] |
肖玉杰, 邱志明, 石章松. UUV国内外研究现状及若干关键问题综述[J]. 电光与控制, 2014, 21(2): 46-49+89. |
| [3] |
冯炜, 张静远, 王众, 等. 海洋环境下基于量子行为粒子群优化的时间最短路径规划方法[J]. 海军工程大学学报, 2017, 29(6): 72-77. |
| [4] |
马元. 自主式水下航行器运动控制系统的设计[D]. 青岛: 中国海洋大学, 2014.
|
| [5] |
付俞鑫. 基于模糊神经网络的无人水下航行器航迹跟踪控制[D]. 大连: 大连海事大学, 2017
|
| [6] |
杨雪, 王端民, 查翔. 无人机自主飞行航迹规划研究[J]. 计算机工程, 2012, 38(5): 192-195. |
| [7] |
王英志, 范文涛. 水下导航定位技术研究进展[J]. 数字海洋与水下攻防, 2020, 3(5): 372-381. |
| [8] |
高钟毓. 惯性导航系统技术[M]. 北京: 清华大学出版社, 2012.
|
| [9] |
程凝怡, 刘志乾, 李昱奇. 一种基于Dijkstra的多约束条件下智能飞行器航迹规划算法[J]. 西北工业大学学报, 2020, 38(6): 1284-1290.
|
| [10] |
王伟, 王华. 基于约束人工势场法的弹载飞行器实时避障航迹规划[J]. 航空动力学报, 2014, 29(7): 1738-1743. |
| [11] |
陶重犇, 雷祝兵, 李春光, 等. 基于改进模拟退火算法的搬运机器人路径规划[J]. 计算机测量与控制, 2018, 26(7): 182-185. |
| [12] |
岳秀, 张超峰, 张伟, 等. 基于A-Star和改进模拟退火算法的航迹规划[J]. 控制工程, 2020, 27(8): 1365-1371. |
| [13] |
张楠楠, 姜文刚, 窦刚. 改进蚁群算法在AUV三维路径规划中的研究[J]. 计算机工程与应用, 2019, 55(11): 265-270. |
| [14] |
陈洋, 赵新刚, 韩建达. 移动机器人3维路径规划方法综述[J]. 机器人, 2010, 32(4): 568-576. DOI:10.3724/SP.J.1218.2010.00568 |
 2023, Vol. 45
2023, Vol. 45
