0 引　言

任务决策作为无人系统技术的核心，目前面临着场景复杂多样、事件不确定性难以描述、模型自适应能力差等难题，因此任务决策的理论研究具有重要价值。

任务决策的方法分为基于学习的决策方法和基于规则的决策方法。基于学习算法方面，在无人艇避碰决策方向，使用强化学习^[1]，双向长短记忆网络学习^[2]算法获得避碰策略，验证其在多障碍物复杂模糊场景下的有效性。在无人机空战决策方向，使用深度神经网络算法^[3]训练预测系统，将其输出的机动策略应用于一对一仿真场景，提升了空中作战能力。在无人驾驶决策系统方向，使用卷积神经网络算法^[4]进行端到端学习，实现了无人车转向和油门的输出。基于规则方面，在概率逻辑下的决策规则，文献[5]利用条件随机场评估周围车辆的风险，生成连续时间避碰策略。在不确定性条件下的决策规则，文献[6]使用部分可观察马尔可夫决策过程算法，推理无人机应用中的不确定性，包括观测模型中出现的遮挡、噪声等因素；文献[7]构建多实体贝叶斯网络模型，对水下机器人交换信息过程中的不确定因素进行推理；文献[8]构建模糊逻辑和贝叶斯推理的空战机动决策模型，通过引入模糊逻辑构造决策因子的函数，适用于不确定性的空战博弈，提升了决策结果的鲁棒性。在时序因素作用下的决策规则，文献[9]构建了变结构离散动态贝叶斯网络模型，完成突发威胁下的任务决策，融合威胁评估、目标价值评估和态势评估因素，通过转移概率反映动态环境对决策的影响。总体来说，无人机、无人驾驶等领域能够较好地解决特定场景中的任务决策问题，但无人艇领域中基于规则推理的方法研究还相对不足，仍存在一些局限性：1）决策问题受时序因素影响需进行动态建模；2）决策过程中不确定性因素推理困难；3）决策结果可解释性差且模型修正困难。

为此，本文提出一种动态多实体贝叶斯网络(dynamic multi-entity Bayesian network, DMEBN)模型，该模型采用概率本体语言描述本体属性的不确定性，同时考虑时序因素对变量的作用，将相邻时间步骤的变量关联起来，推理不同时刻的任务决策方案，并依据策略概率结果自适应调整决策因素所占权重，以提高决策的准确性。在设计的场景想定中，该模型能够得到离散时间内不同策略的概率分布，验证了模型的有效性和可靠性。

1 DMEBN模型总体设计方案

综合多实体贝叶斯网络和动态贝叶斯网络模型的优点为DMEBN模型的设计提供思路。多实体贝叶斯网络(multi-entity Bayesian network, MEBN)的优势在于同时具备一阶逻辑的知识表示能力和贝叶斯网络(Bayesian network, BN)的概率推理能力，用于复杂不确定性逻辑关系推理，并且能够通过扩展BN来表示具有重复子结构的图形模型^[10]。动态贝叶斯网络(dynamic Bayesian network, DBN)是以概率网络为基础，将事件信息与BN相结合的逻辑系统，具有处理时序数据的能力^[11]。在不同时间片段下DBN节点概率状态反映了变量的发展变化规律，因此能够对动态事件进行分析处理。

设计面向无人艇本体的语义推理框架，表示无人艇、环境和目标等信息，采用MEBN的概率图模型对其进行知识表达。根据节点和决策结果的动态变化，在概率本体语言描述不确定知识基础上，结合DBN的概率网络对MEBN模型进行改进，考虑时序因素对变量的影响，构建动态多实体贝叶斯网络模型。概率图模型描述了实体和实体间的因果关系，能够考虑到决策问题的逻辑结构，使推理过程具有良好的可解释性；使用概率本体语言描述不确定知识，能够减少不确定因素信息带来的影响；考虑时序因素对变量的影响，综合上一时刻的策略，则能够自适应调整决策因素权重。

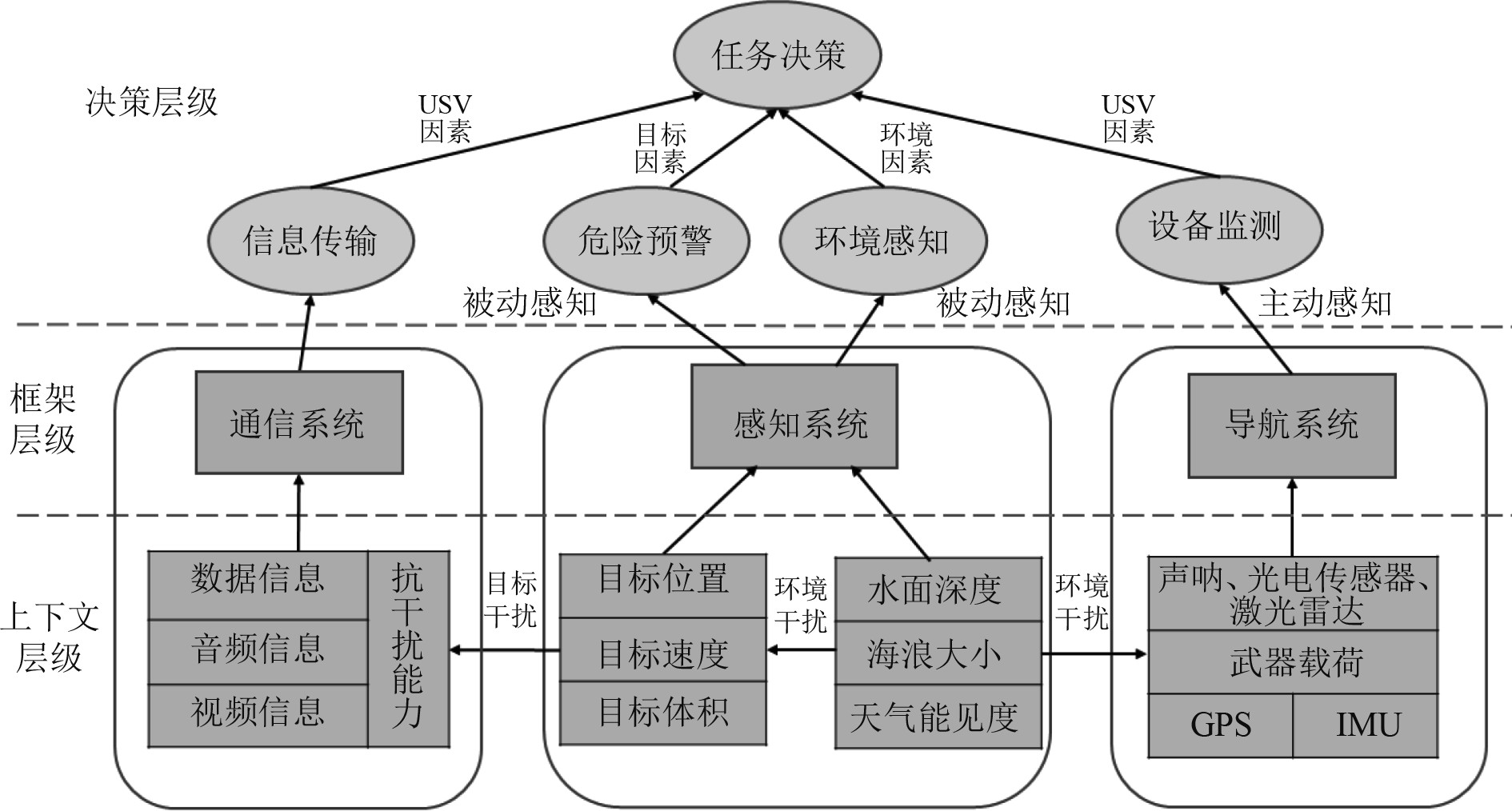
2 动态多实体贝叶斯网络模型构建 2.1 无人艇本体推理框架

本文结合无人艇的特定功能^[12]，并参考水面舰船的总体系统^[13]，将无人艇划分为多个子系统，这些子系统是无人艇本体推理框架的重要组成结构。无人艇本体推理框架如图1所示，它是一种层级式混联结构，决策层级和框架层级的设计采用并联式，上下文层级为串联式。依据无人艇的功能进行划分，决策层级包含设备监测、危险预警、环境感知、信息传输及任务决策；参考水面舰船的设计，框架层级包含通信系统、导航系统和感知系统。建立功能与系统的组成关系，使用上下文层级细化描述类、关系及实体。

上下文层级包含了影响决策的重要因素，能够描述决策层级和框架层级中本体的信息。上下文结构对应实体间的因果关系，同时根据决策场景的变化可灵活调整上下文的实体和关系，因此该推理框架具有可解释性和扩展性。本文从环境、无人艇和目标三方面考虑对决策的影响。环境本体方面，海域环境状况复杂多变，重点研究水面深度对无人艇与目标移动速度的影响，海浪大小和天气能见度对设备与通信有效性的影响等；无人艇本体方面，考虑无人艇搭载的载荷类型以及设备的不同，包括导航设备、传感器设备和武器载荷，其中导航设备由定位系统和惯性导航系统两部分组成，传感器设备主要包含声呐、光电传感器和激光雷达，武器载荷使无人艇可具备攻击能力；目标本体方面，针对突发事件的态势，框架中的目标意图由目标航向、速度和位置等信息推理得到。

2.2 本体概率扩展

本体的概率扩展是在贝叶斯网络概率扩展的基础上，通过定义新的概念类和转换规则，将本体与贝叶斯网络相结合，可以支持不确定知识的表示和推理。常见的方法有BayesOWL^[14]，OntoBayes^[15]等，其中MEBN的逻辑扩展采用概率本体语言的方法。

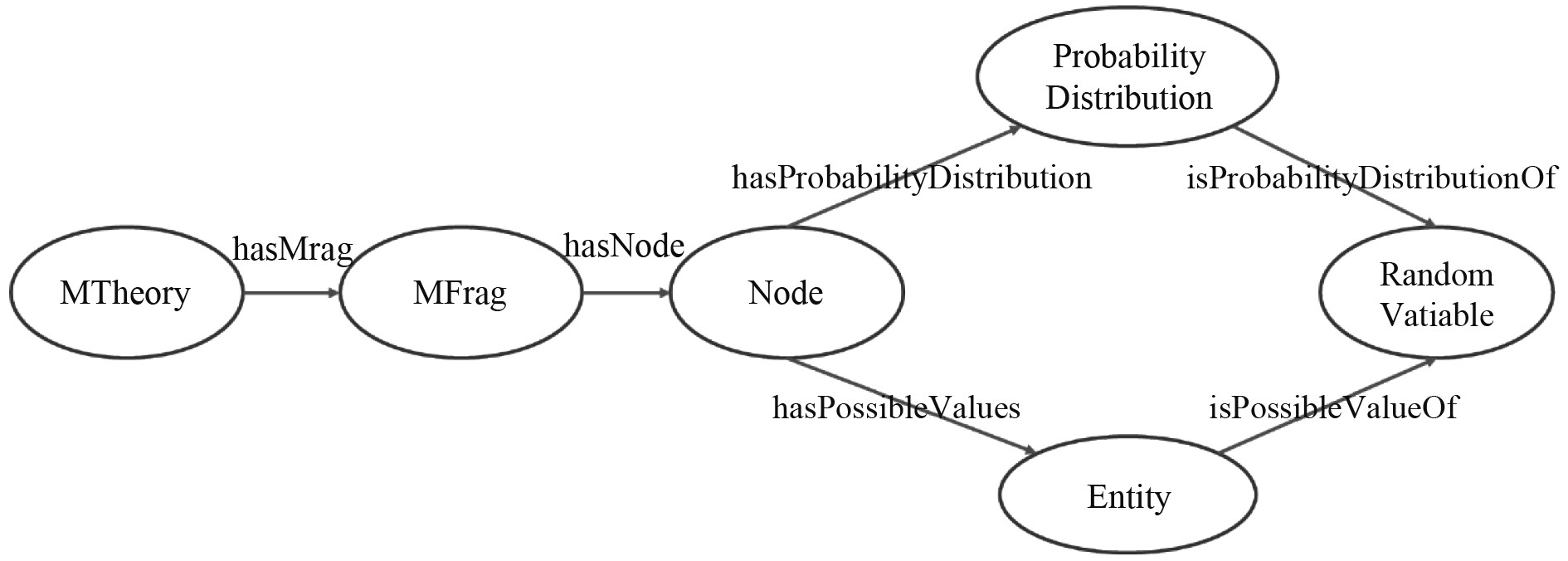
概率本体语言是通过带参数的随机变量表示本体属性的不确定性。定义网络本体语言的类，如MTheory，MFrag，Node等，同时定义类之间的关联属性，如hasMFrag，hasPossibleValues等，完成对MEBN理论的上层本体的扩展，如图2所示。其中类RandomVariable表示本体属性的不确定性，随机变量的参数对应领域本体的实例，作用是推理网络本体语言中不确定部分，类ProbabilityDistribution表示随机变量的概率分布，一般通过UnBBayes工具中的本体概率表定量描述。局部概率分布作为先验条件，概率图模型节点间的因果依赖关系与简单逻辑规则语句对应，编译运行能够获得特定场景贝叶斯网络的推理概率值。

2.3 考虑时序因素的动态建模

与MEBN模型相比，系统动态建模是在其基础上考虑了相邻时间片段的转移网络，体现时序因素对节点的影响。基于DBN模型结构，通过对无人艇的实际应用设计不同的转移网络结构，并计算相应的概率，以此构建DMEBN模型。

2.3.1 局部动态贝叶斯网络结构

局部动态贝叶斯网络是指当前时刻的节点状态受到上一时刻节点的影响，从无人艇的领域本体中选择具有动态特征的节点，节点包含目标属性与无人艇传感器设备等，对应图3两种基本图结构。

如图3(a)所示，同一节点网络结构表示节点A在相邻时刻的状态共同作用于节点B在当前时刻的状态，应用于目标的速度变化、位置变化以及意图分析等方面，例如基于目标在相邻2个时刻的位置来获取目标运动趋势的概率。节点B在 $t + 1$ 时刻的转移概率，计算公式为：

$ P({B^{(t + 1)}}) = \displaystyle\sum\limits_{j = 1}^n {\displaystyle\sum\limits_{i = 1}^n {P(A_j^{(t + 1)})P(A_i^{(t)})P({B^{(t + 1)}}|A_j^{(t + 1)},A_i^{(t)})} }。$

(1)

其中 $A_i^{(t)}$ 表示节点A在 $t$ 时刻下的状态 $i$ ， $P({B^{(t + 1)}}| A_j^{(t + 1)}, A_i^{(t)})$ 表示在节点 $A_j^{(t + 1)}$ 和 $A_i^{(t)}$ 的条件下节点 ${B^{(t + 1)}}$ 发生的概率， $\Sigma $ 表示节点A的状态集合求和。

系统内的各个组件之间相互独立，组件一般有正常和故障2种状态。图3(b)表示上一时刻节点A和B的状态会影响当前时刻节点A和B，同一时刻内的A和B分别为C的父节点并共同作用于节点C。转移概率计算公式为：

$ \left\{ \begin{aligned} &P\left( {{A^{\left( {t + 1} \right)}} = 1|{A^{\left( t \right)}} = 1} \right) = 1 ，\\ &P\left( {{A^{\left( {t + 1} \right)}} = 1|{A^{\left( t \right)}} = 0} \right) = \displaystyle\int_0^{\Delta t} {f_A}\left( t \right){\rm{d}}t= \\&\qquad\qquad \displaystyle\int_0^{\Delta t} {{\lambda _A}{e^{ - {\lambda _A}t}}{\rm{d}}t = 1{\text{ }} - {\text{ }}} {e^{ - {\lambda _A}t}}。\end{aligned} \right. $

(2)

其中 ${A^{\left( t \right)}}$ 表示设备A在 $t$ 时刻的状态，正常和故障分别对应着1和0。若上一时刻状态正常，则下一时刻正常的转移概率为1。若上一时刻状态故障，通过对概率密度函数积分计算其不可靠度的转移概率， ${f_A}\left( t \right)$ 表示设备失效时间的概率密度函数，呈指数函数分布， ${\lambda _A}$ 表示设备失效率。

无人艇常用设备有全球定位系统(global positioning systems, GPS)、惯性导航元件(inertial measurement units, IMU)、声呐、光电传感器和雷达。表1为查询设备故障率的结果^[16]。

$ \Delta t $ 表示传感器已工作时长，设置为1000 h，相对于使用总时长而言，设备在工作过程中的时长误差可以忽略不计，从而计算出传感器可靠性在不同时刻发生转移概率。

2.3.2 全局动态贝叶斯网络结构

无人艇的任务决策是由上一时刻策略的影响和当前时刻领域本体的推理结果共同作用。全局动态贝叶斯网络解决上一时刻策略的定量描述问题，设置相邻时刻的策略转移概率，并引入概率系数表示上一时刻策略权重大小。计算所有的策略概率后，进行归一化，得到新的策略概率分布，计算公式为：

$ {P_i}\left( t \right) = \displaystyle\sum\limits_j^n {P\left( {{X_j}\left( t \right)} \right){\lambda _{ij}}} ,X\left( t \right) = \left\{ {{X_1}\left( t \right), \cdots ,{X_n}\left( t \right)} \right\}，$

(3)

$ U\left( {{P_i}\left( t \right)} \right) = \frac{{{P_i}\left( t \right)}}{{\displaystyle\sum\limits_i^n {{P_i}\left( t \right)} }}。$

(4)

其中转移概率矩阵中元素 ${\lambda _{ij}}$ 表示策略 $j$ 转移到策略 $i$ 的概率， $X\left( t \right)$ 为 $t$ 时刻下的策略集合， $n$ 为设置的策略个数， ${P_i}\left( t \right)$ 表示 $t$ 时刻下策略 $i$ $ \mathrm{i} $ 的概率。

下一时刻策略 $i$ 的概率是通过当前时刻策略 $i$ 的概率与下一时刻策略 $i$ 的推理结果按比例相加求和得到，计算公式为：

$ {P_i}\left( {t + 1} \right) = \beta \cdot U\left( {{P_i}\left( t \right)} \right) + (1 - \beta ) \cdot P^{\prime}_i\left( {t + 1} \right)，$

(5)

$ \beta = \left\{ \begin{gathered} 0.5\;\;，{P_i}\left( t \right) \leqslant \alpha ，\\ 0.7\;\;，{P_i}\left( t \right) > \alpha 。\\ \end{gathered} \right. $

(6)

其中 $P^{\prime} _i\left( {t + 1} \right)$ 表示策略 $i$ 在 $t + 1$ 时刻下MEBN模型的推理概率， $\beta $ 表示自适应概率系数，用于提高场景推理的准确性， $\alpha $ 表示决策阈值，作为不同场景下的决策标准。若某一策略概率与 $\alpha $ 比较，能够动态调整概率系数。当攻击概率未达到策略阈值时，概率系数默认为0.5，表示上一时刻和当前时刻的影响程度相同；当攻击概率超过策略阈值时，概率系数为0.7，表示提高上一时刻影响程度。

3 实验验证 3.1 实验场景设计

基于无人艇集群的安全巡逻背景，设计一个岛礁区域防守的场景想定，目的是阻止敌方目标接触岛礁。无人艇集群在岛礁防守范围内进行巡逻，若目标在某一时刻进入集群覆盖的防守区域，无人艇搭载的传感器就会探测到目标位置等信息，然后结合探测数据和环境信息等因素推理目标意图，进而推理出无人艇在当前时刻下的任务决策，阻止目标进入防守区域。

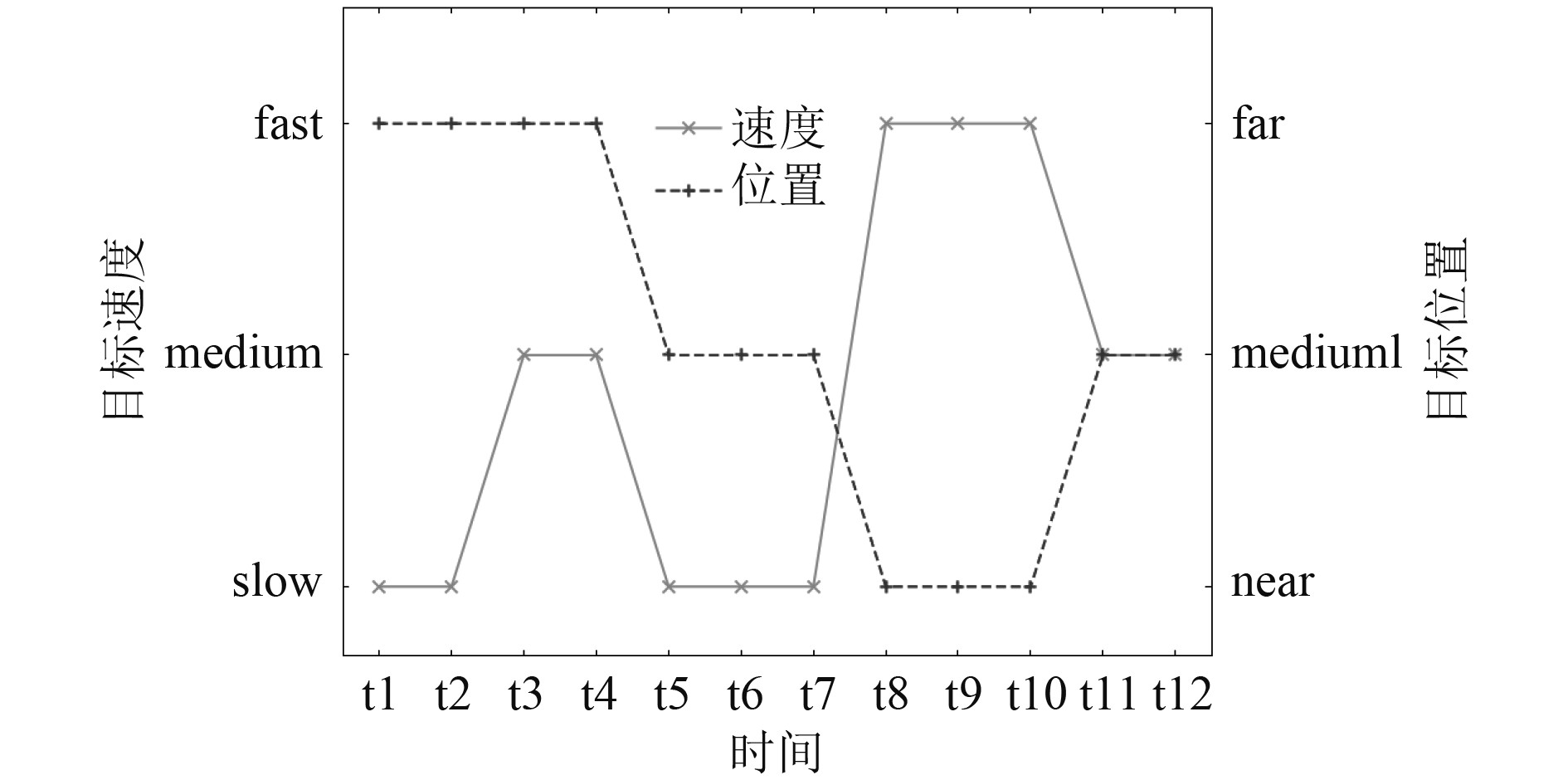
假设环境信息为晴朗、水深中等和无浪，在无人艇巡逻过程中，探测到某一目标出现在岛礁附近，其速度及目标变化如图4所示。离散时间下目标在t₁～t₄时刻远离岛礁位置，由低速到中速。t₅～t₇时刻距离岛礁位置中等，速度降低，同时在t₆～t₈时刻主动干扰信号，引发无人艇GPS和雷达设备的失灵。t₈～t₁₀时刻高速靠近岛礁位置，准备发动攻击。t₁₁～t₁₂时刻目标降速远离岛礁。

3.2 模型推理流程

将无人艇本体推理框架中定义的本体实例化，确定实体状态，任务策略分为4种，包括攻击、跟踪干扰、侦察和巡逻。无人艇在目标威胁程度快速提高或攻击我方重要区域时采用攻击策略，在目标有进攻意图时采用跟踪干扰策略，在敌方意图判断不清且目标威胁程度逐渐提高时采用侦察策略，在目标威胁程度较低且远离我方区域时采用巡逻策略。每一实体状态如表2所示。

基于概率本体语言方法构建无人艇领域推理网络，对场景中的不确定性进行建模和推理。MEBN理论定义了8个实体片段，分别为通信系统、环境感知、任务载荷、控制系统、信息传输、设备监测、任务决策及目标意图。

计算目标属性和无人艇的传感器设备等受时序因素影响的节点的转移概率。DMEBN模型中策略间的转移概率根据专家经验预设。此实验场景下无人艇通常保持巡逻或侦察状态，任务策略频繁切换会导致无人艇执行效率的降低，为增加策略的连续性，需提高这2种状态的转移概率。由侦察或跟踪干扰的状态切换到攻击状态，为综合考虑攻击和跟踪干扰策略的影响因素，需提高其他状态到当前状态下的转移概率。

攻击策略阈值设为20%，其他3种策略不设置。由于攻击策略的约束条件较多，攻击概率最高时再发动攻击会延误时机，因此在其超过阈值时无人艇优先选择攻击策略。

在模型推理开始前，设置局部概率分布作为先验条件。综合目标速度变化、位置变化、上一时刻位置和体积等信息，推理当前时刻下目标意图为佯动，其概率值为49.2%。假设无人艇的数据和视频信号传输正常，声音信号传输异常，抗电磁干扰能力为80%，推理传输正确信息的概率为86%。无人艇配备并安装武器，得到任务载荷的推理结果。无人艇配备雷达、光电传感器和声呐，其中雷达及光电传感器的状态正常，声呐状态未知，推理现有设备完成任务的概率为69.55%。综合无人艇的传输能力、武器配置和设备能力等信息，推理其具备攻击能力的概率为51.02%。无人艇在当前时刻具备攻击、跟踪干扰、巡逻和侦察能力的概率分别为51.02%，57.95%，58.53%及49.72%。最后综合水面目标意图和无人艇的能力推理得到任务决策概率，推理无人艇侦察策略的概率最高，概率值为38.44%。

依次按照上述过程推理12个时刻下的状态概率，分析目标意图，得到无人艇的任务策略。

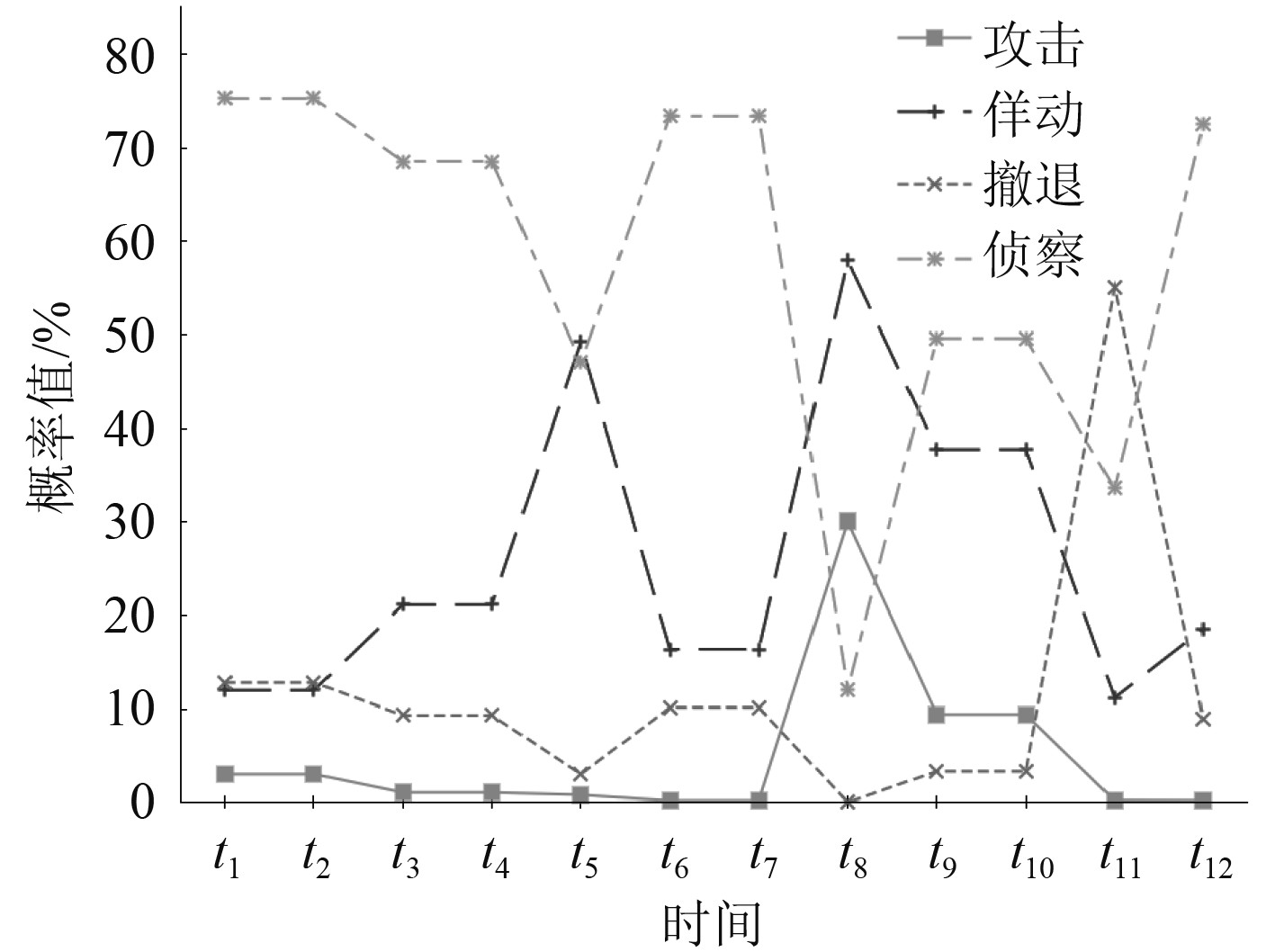
3.3 实验结果分析

在目标进入岛礁安全区域范围后，无人艇的侦察策略概率最高，但在t₅和t₈～t₉时刻概率明显下降，是因为目标意图发生变化，威胁程度提升。在t₅时刻根据目标快速接近岛礁等因素推理出目标佯动的概率最高，在t₈～t₉时刻目标攻击的概率迅速增加，因此无人艇的跟踪干扰和攻击在这2个阶段下概率超过侦察和巡逻，也符合预设场景下目标的真实情况，如图5所示。

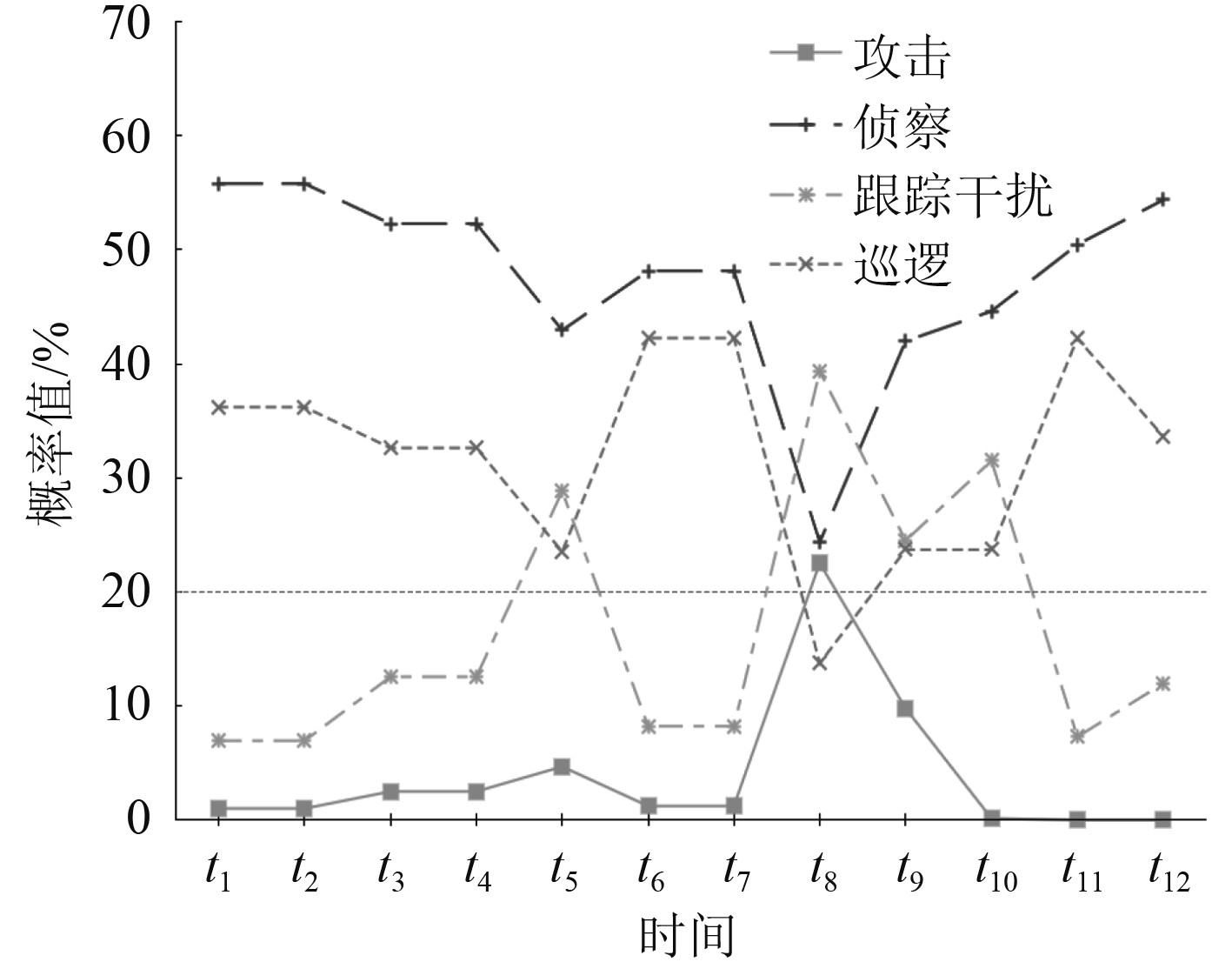
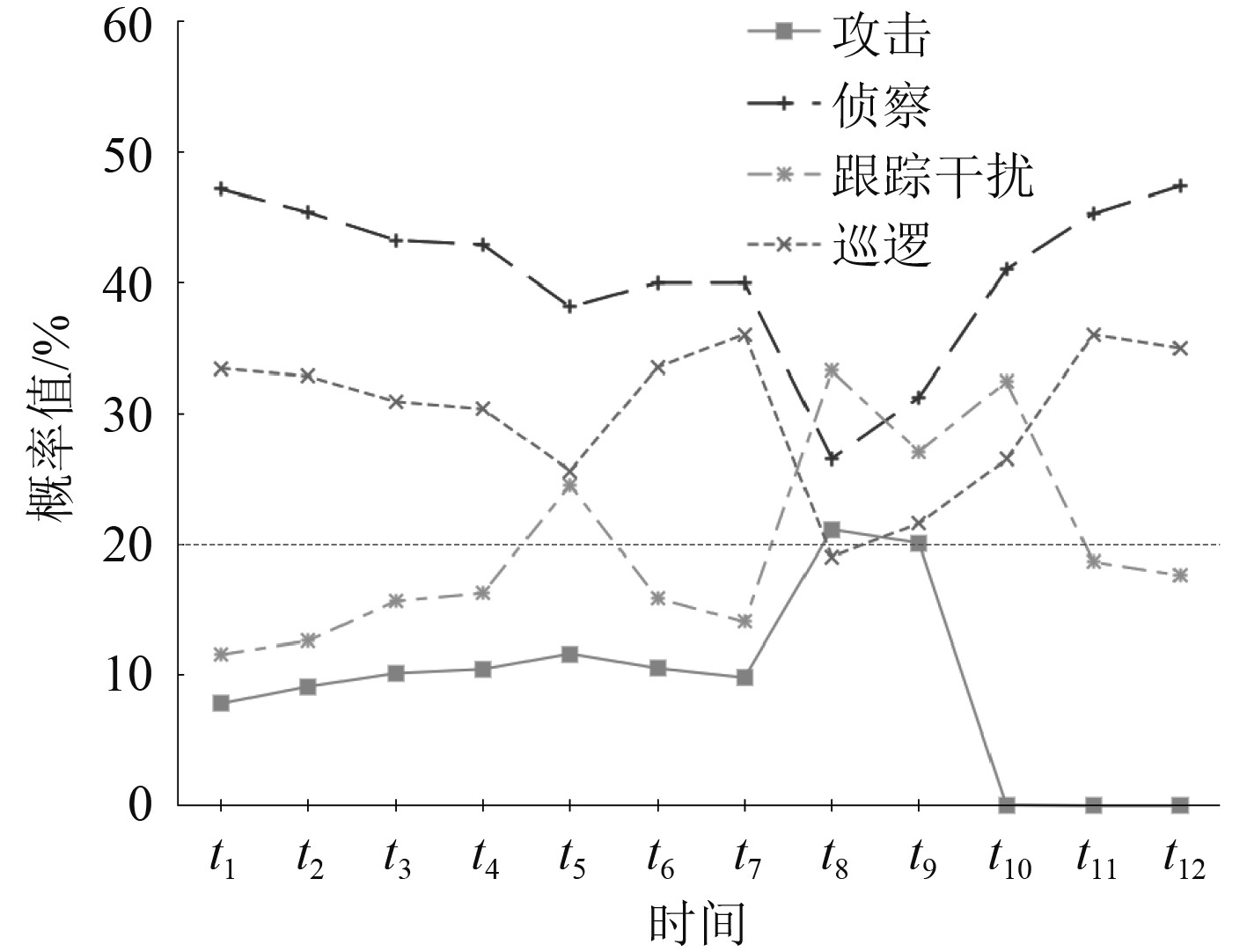
为了判断观测时序对最终任务决策的影响，将DMEBN模型推理任务决策的概率与仅使用MEBN模型得到的结果进行比较。图6和图7显示2种模型在12个时刻下4种任务决策的概率折线图。在t₁～t₄时刻2种模型的无人艇4种任务策略变化趋势相同，DMEBN模型推理结果中执行攻击的概率小幅度增加，是因为攻击策略综合在上一时刻其他状态概率影响。在t₅～t₇时刻DMEBN模型侦察和巡逻的概率波动变化较小，是因为综合相邻时间片段的信息保证推理结果的连续性。在t₈～t₉时刻2种模型任务策略均发生变化，说明获取的本体具有普遍性，能随态势变化推理出正确的任务决策，但在t₉时刻DMEBN模型的攻击策略不会陡然下降，更符合真实战场下攻击的决策，而仅使用MEBN模型未充分完成任务策略就迅速改变。最后t₁₀～t₁₂时刻由于模拟武器载荷被完全使用，攻击策略概率为0，其余策略概率变化趋势相同。

DMEBN模型的在该场景下推理结果与目标意图相符，并得到了合适的任务策略，验证了模型的可行性和有效性。MEBN中没有考虑时序对变量的影响，策略仅由当前时刻的态势决定，策略的概率波动很大，而DMEBN模型的推理可综合上一时刻概率，增加策略执行的连续性，在真实战场中，这种策略变换能够提高决策的准确性。

4 结　语

本文提出基于DMEBN模型的无人艇任务决策方法，确定无人艇的基本功能，综合考虑影响任务决策的因素，用概率本体语言描述领域内实体状态的不确定性，通过模型相邻时刻的转移概率反映动态环境对决策结果的影响，能够自适应地调整决策因素所占权重，并根据定义阈值选择不同场景下的执行策略。设计实验模拟区域安全巡逻的场景，完成水面目标意图推理以及无人艇的决策方案选择，得到离散时间下不同策略的概率分布情况，与MEBN输出结果对比，表明生成策略的连续性，验证了模型的有效性。

本体框架采用自顶向下的方式构建，不能完全覆盖无人艇及环境信息，下一步采用自底向上的方法获取更多的实体及关系，用于构建领域知识图谱，再结合实际场景下先验信息，提高推理能力和准确性。实际应用中无法直接使用基于DMEBN模型得到的推理结果，需要转化为无人艇识别语言，对无人艇的任务问题采用规划领域定义语言表示，进一步在真实场景下验证模型。