2. 沪东中华造船(集团)有限公司,上海 200129
2. Hudong Zhonghua Shipbuilding Group Co., Ltd., Shanghai 200129, China
浮式液化天然气生产储卸装置(floating liquefied natural gas,FLNG)是一种集生产、储存和装卸于一身的船型浮式生产储存和卸载装置[1-2]。我国海洋天然气资源十分丰富,但以深海气田、边际小气田和低品位天然气资源为主[3]。将FLNG装置运用于上述气田的开采之中,是一种对环境友好且具有商业吸引力的发掘大量滞留天然气的方法[4-5]。
FLNG作为储存有大量天然气(liquefied natural gas,LNG)的船型装置,一旦发生事故,会带来极其严重的后果。独立B型舱是考虑质量管理和疲劳强度的周密设计,通常只设置滴水盘式二级屏障,一般没有较为完整的用于收集泄漏LNG的二次屏障[6]。因此,独立B型舱的疲劳强度要求很高,有必要对其进行准确的疲劳损伤评估。FLNG作业时通过单点系泊系统长期系泊于指定服役区域,其转塔系统可使船体在波浪环境载荷的作用下自由转动,以规避恶劣环境带来的负面影响[7-8]。目前各国船级社均未明确给出用于FLNG强度评估的计算指南,因此部分相关工程项目仍会参考 LNG 船的规范标准值进行相关计算[9-12],但LNG船仅校核0%~10%和70%~98%的装载率工况,而FLNG液舱可能存在任何一种装载水平,所受载荷及各工况的营运时间占比也不尽相同,且液舱的主要疲劳外载荷是三向加速度载荷,故合理组合三向加速度载荷,拟定适合FLNG的计算工况校核结构的疲劳损伤是目前所需解决的问题。
本文引入正交试验法进行载荷工况设计,参照LNG船的载荷工况和FLNG的特点设计了3种载荷组合工况讨论不同浪向时间占比对节点疲劳损伤的影响。以满载情况为例,对三舱段模型在设定的载荷作用下进行有限元计算,并进行相应的疲劳损伤计算。最后进行参数影响分析,探究加速度载荷系数对液舱疲劳损伤的影响程度。
1 FLNG载荷组合工况设计正交试验设计的方法起源于上世纪20年代的日本,是建立在多因素试验设计基础上的优化方法。通常3因素3水平的全因素试验需要进行33次试验,而正交试验方法仅需9次试验,是一种具有典型性的优化设计方法[13]。
要直接分析多种液舱装载率下三向加速度载荷对疲劳损伤的影响较为困难,可对不同装载率情况分别进行考虑。美国船级社(ABS)对满载条件下LNG运输船的疲劳强度评估工况有着明确规定,这可以作为本文分析三向加速度载荷对液舱疲劳损伤影响的参考,如表1所示[12]。本文仅对满载状态下三向加速度载荷对液舱疲劳损伤影响进行分析。
|
|
表 1 LNG船疲劳强度评估的标准设计工况 Tab.1 Standard loading conditions for fatigue strength assessment of LNG carriers |
施加加速度载荷时,会根据计算工况的变化赋予不同的垂向加速度系数(
|
|
表 2 载荷系数组合表 Tab.2 Table of load coefficient combinations |
|
|
表 3 不同营运时间占比的计算工况 Tab.3 Loading conditions of different fractions of life time |
本文分析对象为某FLNG的三舱段模型,模型中包含船体结构、独立舱结构以及独立舱的限位装置及其支撑结构。有限元分析时,载荷方面按照中国船级社(CCS)相关规范进行静载荷与动载荷的计算与施加[11]。按照规范要求在PATRAN中建立2种模型分组,分别按照局部载荷边界条件和总体载荷边界条件进行加载。三舱段模型及目标舱段剖面结构如图1所示。
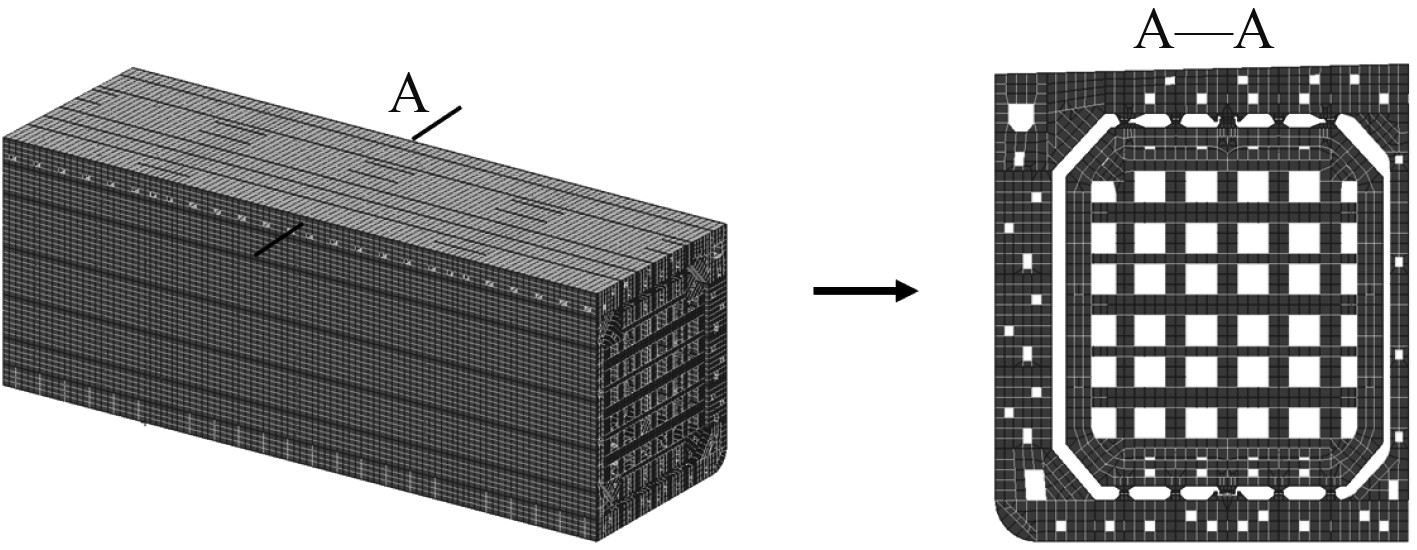
|
图 1 三舱段模型及其剖面结构 Fig. 1 Three-cargo-FEM model and profile structure |
FLNG独立B型舱的限位装置和支撑结构为承压装置,主要为舱底垂向层压木和舱顶止浮层压木,在有限元软件中均使用ROD单元模拟其刚度。由于层压木不能承受拉力,而ROD单元既能受拉也能受压,因此分析时需删除承受拉应力的单元,并通过迭代分析得到最终结果。
2.3 典型节点选取分析结构的疲劳寿命时,首要任务是确定结构的疲劳热点。为使所选热点位置具有代表性,综合考量各工况的粗网格模型应力结果,在舱壁的不同部位各选定一个热点位置进行网格细化工作,细化区域的单元尺寸为t×t,t为热点所在位置板的厚度[14]。所选定的3处热点位置如表4所示,示意图如图2所示。
|
|
表 4 三处热点位置 Tab.4 Positions of three hot spots |
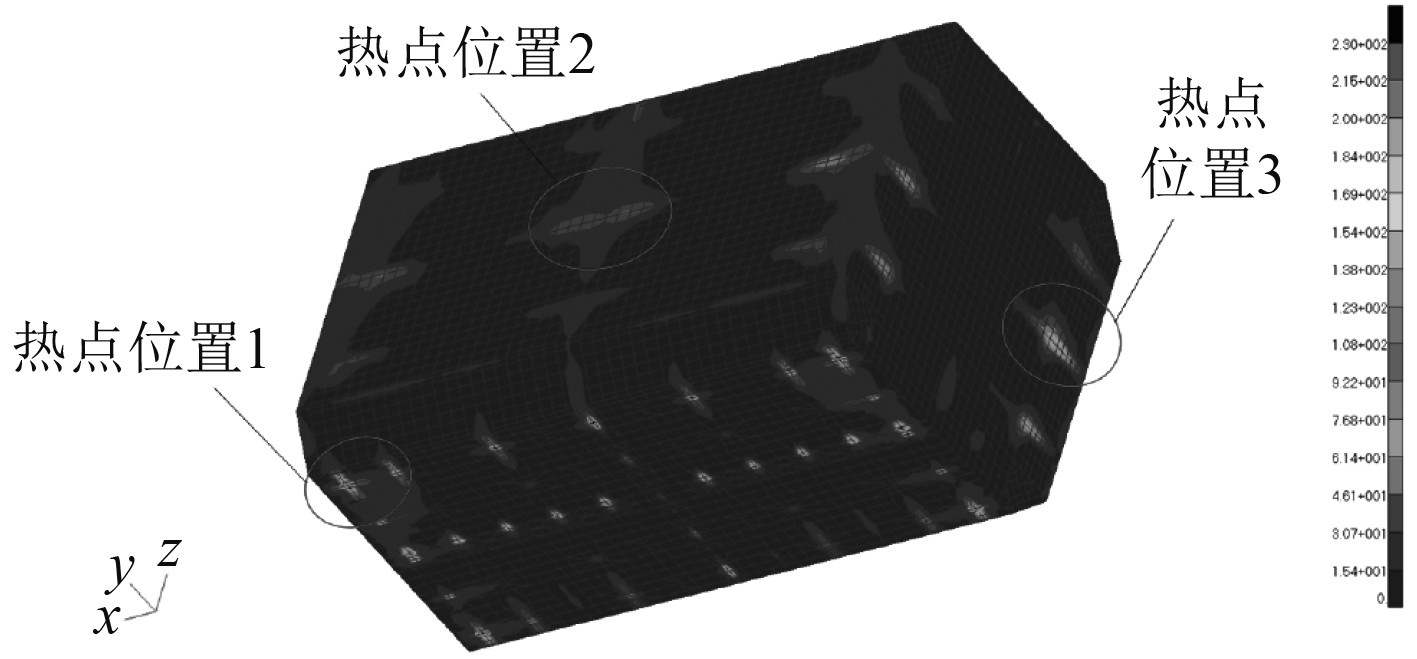
|
图 2 三处热点位置示意图 Fig. 2 Diagram of the positions of three hot spots |
根据CCS规范要求细化热点区域的有限元网格并计算热点应力[15]。疲劳热点多位于高应力梯度区域,该区域的应力通常较为复杂,并不呈线性分布。热点应力通常视为由弯曲应力与薄膜应力两部分组成,为方便对热点应力进行插值计算,可近似认为热点区域的应力呈线性分布。因此,可将结构表面上离开热点0.5t和1.5t的2个点的应力分量外插到热点,从而获取热点应力值,且此两点的应力分量应取相邻2个单元应力分量的平均值。两点线性外推法图如图3所示,其插值公式如式(1):

|
图 3 热点应力外插示意图 Fig. 3 Diagram of hot spot stress extrapolation |
| $\begin{aligned} &{\sigma }_{D}=\frac{3{\sigma }_{D0.5t}}{2}-\frac{{\sigma }_{D1.5t}}{2}=\frac{3}{2}\times \\ &\frac{{\sigma }_{E0.5t}+{\sigma }_{F0.5t}}{2}-\frac{1}{2}\times \frac{{\sigma }_{E1.5t}+{\sigma }_{F1.5t}}{2}。\end{aligned} $ | (1) |
式中,
结构在交变应力的作用下会产生疲劳损伤,拉应力作为疲劳裂纹扩展的主要驱动力,确定以拉应力为主的第一主应力的应力范围是评估疲劳损伤的重要前提。运用PATRAN后处理模块的Combine功能对施加正向加速度载荷与反向加速度载荷相应工况的计算结果求矢量和,从而获得相应的应力范围值。
对非对称循环的交变应力需进行平均应力修正,采用CCS的热点平均应力修正系数将平均应力对疲劳寿命的影响考虑在内[15]。焊接节点的平均应力修正系数公式如下:
| $\left\{ \begin{aligned} &{f}_{m,i\left(k\right)}=\mathrm{m}\mathrm{i}\mathrm{n}\left[\mathrm{1.0,0.85}+0.3\frac{{\sigma }_{m,i\left(k\right)}}{{C}_{S}{S}_{h,i\left(k\right)}}\right],{\sigma }_{m,i\left(k\right)}\geqslant 0,\\ &{f}_{m,i\left(k\right)}=\mathrm{m}\mathrm{a}\mathrm{x}\left[\mathrm{0.7,0.85}+0.3\frac{{\sigma }_{m,i\left(k\right)}}{{C}_{S}{S}_{h,i\left(k\right)}}\right],{\sigma }_{m,i\left(k\right)} < 0。\end{aligned}\right. $ | (2) |
式中:
采用双参数的韦布尔分布(Weibull distribution)模拟应力范围的长期分布,其应力范围的韦布尔分布概率密度函数为:
| $ {f}_{s}\left(S\right)=\frac{k}{\lambda }{\left(\frac{S}{\lambda }\right)}^{k-1}\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\left(\frac{S}{\lambda }\right)}^{k}\right],S > 0 。$ | (3) |
式中:
上述应力范围的超越概率为:
| $ {P}_{s}\left(S\right)=1-\ \int_{0}^{S} {} \ {f}_{s}\left(S\right){\rm{d}}S=\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\left(\frac{S}{\lambda }\right)}^{k}\right],S > 0 。$ | (4) |
通过假定超越概率
| $ \lambda ={S}_{{\rm{MAX}}}/{\left[\mathrm{ln}{P}_{s}\left(S\right)\right]}^{\frac{1}{k}} ,$ | (5) |
当应力以连续概率密度函数的形式表达时,疲劳累积损伤度的表达式为:
| $ D=\int_{L}^{} {} \frac{{\rm{d}}n}{N\left(S\right)}={N}_{T}\int_{0}^{\infty} {} \frac{{f}_{s}\left(S\right)}{N\left(S\right)}{\rm{d}}S 。$ | (6) |
式中:
将式(3)~式(5)代入式(6),可得单一斜率S-N曲线的疲劳累积损伤公式:
| $ D=\frac{{N}_{T}}{K}·{\lambda }^{m}·\mathrm{\Gamma }\left(\frac{m}{k}+1\right) ,$ | (7) |
式中:
| $ \mathrm{\Gamma }\left(x\right)=\int_{0}^{\infty} {} \ {t}^{x-1}{e}^{-t}{\rm{d}}t 。$ | (8) |
液舱疲劳损伤计算的流程图如图4所示。
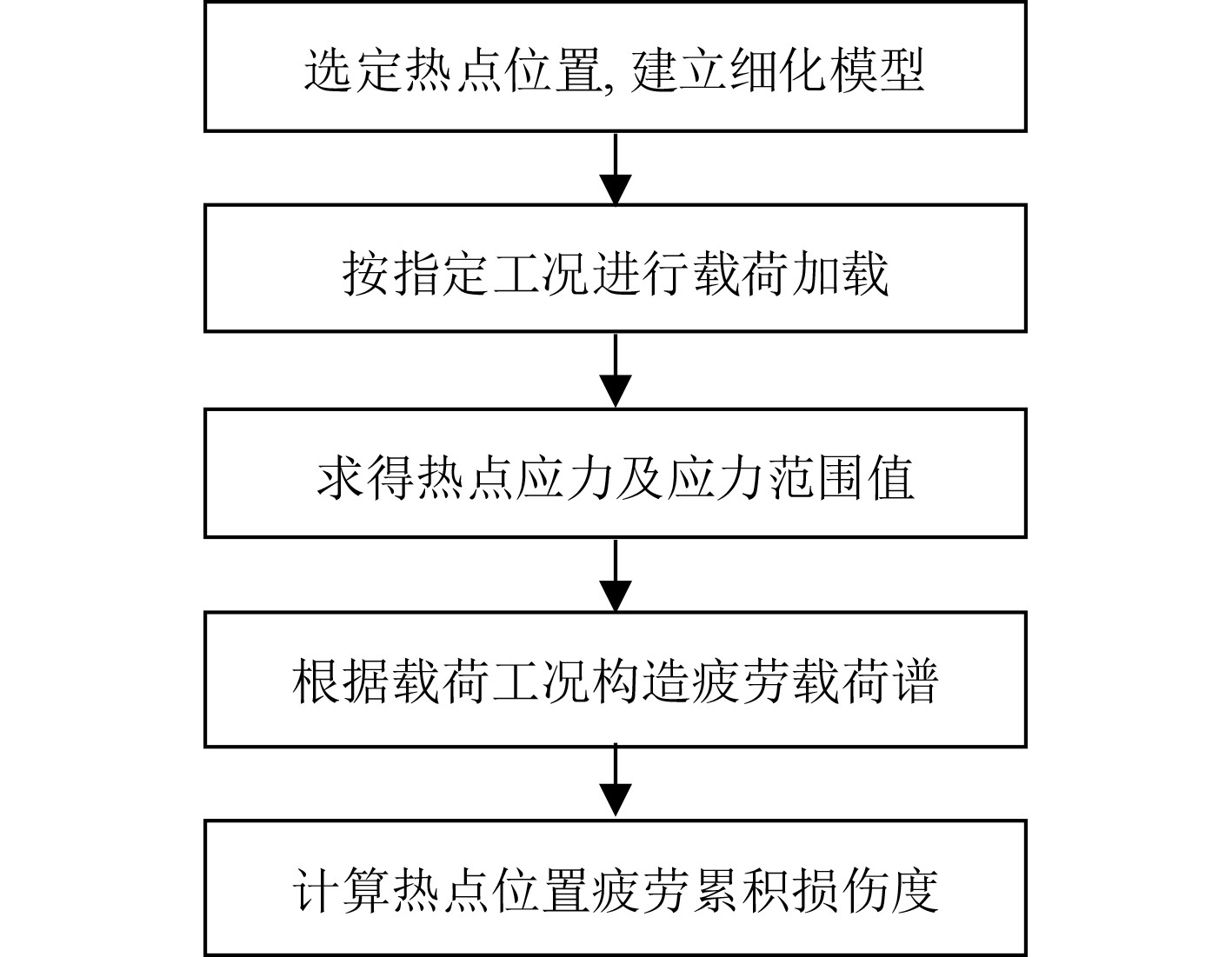
|
图 4 疲劳损伤计算流程图 Fig. 4 Flow chart of fatigue damage calculation |
本文目标舱段的舱壁材料为9%Ni钢及其焊接熔覆金属,杨氏模量E=2.1×105 MPa,泊松比为0.3。所选取的3处热点位置均为焊接部位,根据ABS规范规定[12],选取N1对应的9%Ni钢单一斜率S-N曲线进行疲劳损伤计算,该曲线对应参数为m=3.0,logK=12.37。
对三舱段模型的有限元计算结果进行分析,得到的最大应力范围
|
|
表 5 应力范围及累计损伤计算结果 Tab.5 Results of stress range and cumulative damage |
需要注意的是,规范指出液货舱的许用最大累积损伤度
| $ D\leqslant {C}_{W} 。$ | (9) |
由表5正交设计工况Case1~Case9的计算结果可知,热点位置1和热点位置2处的所有载荷组合工况累积损伤度均在安全限度之内,而热点位置3在组合工况Case7~Case9的累积损伤度大于0.5,不符合疲劳损伤评估要求。实际上液舱完全由单一的Case7,Case8 或Case9组成的疲劳载荷不太可能出现,这3种工况过于严格。实际载荷是上述载荷的某种加权组合,这种组合情况将在后续的研究中讨论。
由不同营运时间占比的Case10~Case12的累积损伤结果可知,随着迎浪工况时间占比从50%增至80%,3处热点位置的累积损伤度都有较为显著的增加,分别为54.3%,57.9%和38.3%。
4 加速度载荷系数对疲劳损伤影响分析分析各向加速度载荷对疲劳损伤影响时,应力范围值和疲劳累积损伤度都有重要的参考价值。因此,将对3处热点位置的应力范围值及疲劳累积损伤结果进行极差分析。
极差分析需要引入三因素指标和
| $ {T}_{i}=\sum _{i=1}^{3}{y}_{i} ,$ | (10) |
| $ {t}_{i}=\frac{{T}_{i}}{3} ,$ | (11) |
| $ {R}_{i}=\mathrm{M}\mathrm{A}\mathrm{X}\left({t}_{i}\right)-\mathrm{M}\mathrm{I}\mathrm{N}\left({t}_{i}\right) 。$ | (12) |
式中,
试验极差分析结果见表6。表中只展示热点位置1的各项指标计算值,热点位置2及热点位置3只给出极差和因素主次顺序结果。
|
|
表 6 极差分析结果 Tab.6 Results of range analysis |
由表6结果可知,对本文模型而言,无论是舱体底部,左侧舱壁或者舱壁尾端,垂向加速度系数
如图5所示,

|
图 5 三系数参数对应力范围结果及疲劳累积损伤结果的影响 Fig. 5 Influence of three type parameters on stress range and cumulative damage |
本文以满载工况下某FLNG的独立B型舱为研究对象,引入正交试验设计,设计了加速度系数的9种载荷组合工况以及3种不同浪向占比的组合工况。利用三舱段模型计算3处热点位置的热点应力结果,计算得相应的应力范围值和疲劳累积损伤度,在计算的结果上进行参数影响分析,得出以下结论:
1)疲劳损伤的参数分析结果显示,无论位于舱体底部,左侧舱壁还是舱壁尾端,
2)运输船标准设计工况的应力范围结果显示,取用的
3)迎浪工况时间占比的增加会使热点位置处的疲劳损伤度有较为显著的增长,但即便是满载状态下的作业工况Case10~Case12,3处热点位置的疲劳累积损伤度仍较小。由此可推测,将LNG船的标准计算工况用于FLNG可能不够保守,应考虑适当提升各工况组合中
| [1] |
薄玉宝. 浮式液化天然气(FLNG)技术在中国海上开发应用探讨[J]. 中国海洋平台, 2013, 28(3): 1-5. BO Y B. Floating liquefied natural gas(FLNG) technology in China offshore development application to discussion[J]. China Offshore Platform, 2013, 28(3): 1-5. |
| [2] |
ZHAO W H, YANG J M, HU Z Q, et al. Numerical investigation on the hydrodynamic difference between internal and external turret-moored FLNG[J]. Journal of Shanghai Jiaotong University (Science), 2013, 18(5): 590-597. |
| [3] |
刘婷婷, 阮诗伦, 尹江洲, 等. 浮式液化天然气液货围护系统的失效模式分析[J]. 海洋工程装备与技术, 2014, 1(1): 50-54. LIU T T, RUAN S L, YIN J Z, et al. Failure modes analysis of box structure of the containment system in FLNG[J]. Ocean Engineering Equipment and Technology, 2014, 1(1): 50-54. |
| [4] |
JOHN W, LONGLEY H. FLNG technology shows promise for stranded gas fields[J]. Offshore, 2009, 69(11). |
| [5] |
叶冬青, 陆文俊, 季腾. FLNG船关键系统技术研究[J]. 中国水运(下半月), 2021, 21(11): 1-2. YE D Q, LU W J, JI T. Research on key system technology of FLNG[J]. China Water Transport, 2021, 21(11): 1-2. |
| [6] |
董问, 袁奕, 张正艺, 等. 晃荡载荷作用下LNG船B型独立液货舱支撑结构受力分析[J]. 舰船科学技术, 2019, 41(15): 17-22. DONG W, YUAN Y, ZHANG Z Y, et al. Force analysis of support structure of LNG independent Type B tank under sloshing loads[J]. Ship Science and Technology, 2019, 41(15): 17-22. |
| [7] |
刘志刚, 何炎平. FPSO转塔系泊系统的技术特征及发展趋势[J]. 中国海洋平台, 2006(5): 1-6. LIU Z G, HE Y P. The technical characteristics and development trend of FPSO turret mooring systems[J]. China Offshore Platform, 2006(5): 1-6. |
| [8] |
张玉奎, 钱笠君, 郑文青, 等. FLNG薄膜型液货舱结构强度分析[J]. 船舶工程, 2019, 41(9): 31-35. ZHANG Y K, QIAN L J, ZHENG W Q, et al. Strength analysis of FLNG membrane cargo hold structure[J]. Ship Engineering, 2019, 41(9): 31-35. |
| [9] |
刘奕谦, 张玉奎, 陈哲超, 等. FLNG结构设计若干关键技术问题分析[J]. 船舶工程, 2019, 41(S2): 167-170. LIU Y Q, ZHANG Y K, CHEN Z C, et al. Analysis of key technology in FLNG structural design[J]. Ship Engineering, 2019, 41(S2): 167-170. |
| [10] |
向琳玲, 刘加一, 阚涛, 等. FLNG热应力分析及其对结构强度的影响[J]. 舰船科学技术, 2017, 39(9): 71-76. XIANG L L, LIU J Y, KAN T, et al. Thermal stress and strength analysis of FLNG's structure[J]. Ship Science and Technology, 2017, 39(9): 71-76. |
| [11] |
中国船级社. 散装运输液化气体船舶构造与设备规范[S]. 北京: 人民交通出版社, 2018. China Classification Society. Rules for construction and equipment of ships carrying liquefied gases in bulk[M]. Beijing: China Communications Press, 2018. |
| [12] |
ABS. GUIDE FOR BUILDING AND CLASSING LIQUEFIED GAS CARRIERS WITH INDEPENDENT TANKS[S]. Houston: American Bureau of Shipping, 2018.
|
| [13] |
丁乐声, 陈金龙, 张聪, 等. 柔性管缆限弯器等效弯曲刚度研究[J]. 船舶力学, 2021, 25(11): 1515-1522. DING L S, CHEN J L, ZHANG C, et al. Study on equivalent bending stiffness of flexible pipe and cable bend restrictor[J]. Journal of Ship Mechanics, 2021, 25(11): 1515-1522. |
| [14] |
阚涛. FLNG全船结构强度计算及疲劳强度分析[D]. 武汉: 华中科技大学, 2017.
|
| [15] |
中国船级社. 船体结构疲劳强度指南[S]. 北京: 人民交通出版社, 2021.
|
 2023, Vol. 45
2023, Vol. 45

