2. 中国特种飞行器研究所高速水动力航空科学技术重点实验室,湖北 荆门 448035
2. Key Aviation Scientific and Technological Laboratory of High Speed Hydrodynamic, AVIC Special Vehicle Research Institute, Jingmen 448035, China
水陆两栖飞机在波浪中高速滑行时存在着大尺度自由液面变形、喷溅等复杂的流动分离现象,严重影响飞机的海况适应性和安全起降需求[1]。由于国内外对水面飞行器的研究较少,波浪滑水载荷很难通过理论计算方法或经验公式进行载荷估算,模型试验则由于尺度效应和试验周期长等因素的限制,目前主要用于分析飞机纵向运动稳定边界和基本参数的影响。
近年来,随着大容量存储和计算机的快速发展,数值仿真在预报水陆两栖飞机波浪运动响应特性方面扮演着日益重要的角色。马增辉等[2]采用ALE方法求解飞机与水体的耦合作用,研究了飞机在不同波面上起降的运动响应以及机身底部压力的动力学特性。Chen等[3]采用RANS方程结合FVM及VOF方法系统研究了水陆两栖飞机在波浪中着水性能。李新颖等[4]基于滑移网格法对某水陆两栖飞机的船身部分开展耐波性数值仿真研究,并与模型试验结果对比验证了该方法的可靠性。
本文基于STAR-CCM软件,采用整体动网格法解决水陆两栖飞机波浪滑行中出现的网格变形和重构问题。采用雷诺平均N-S方程和 SST k-ω两方程模型求解非定常流场,流体体积分数法(VOF)捕捉自由液面,并与模型试验结果对比验证了该方法的可靠性。基于上述方法,研究了滑行速度、波长、波高等参数对飞机滑水载荷的影响,对水陆两栖飞机的性能评估具有一定的指导作用。
1 研究对象以某水陆两栖飞机为例,该飞机采用单船身式机身,船身悬臂式上单翼带翼下支撑式浮筒、“T”型尾翼的气、水动布局形式,船身采用可以提高滑行效率的断阶设计,为了降低飞机在高速滑行和起降过程中产生的喷溅,前机身舭部开设有抑波槽并安装抑波板,飞机的三维模型如图1所示。

|
图 1 水陆两栖飞机三维图 Fig. 1 Three dimensional figure of amphibious aircraft |
连续性方程和动量方程是粘性流体运动数值求解的普适性方程,其基本形式为:
| $ \frac{\partial \rho}{\partial t}+\frac{\partial}{\partial x_{1}}\left(\rho y_{1}\right)=0,$ | (1) |
| $ \frac{\partial }{{\partial t}}(\rho {u_i}) + \frac{\partial }{{\partial {x_j}}}(\rho {u_i}{u_j}) = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left(\mu \frac{{\partial {u_i}}}{{{x_j}}} - \rho \overline {u_i'u_j'} \right) + {S_i}。$ | (2) |
式中:
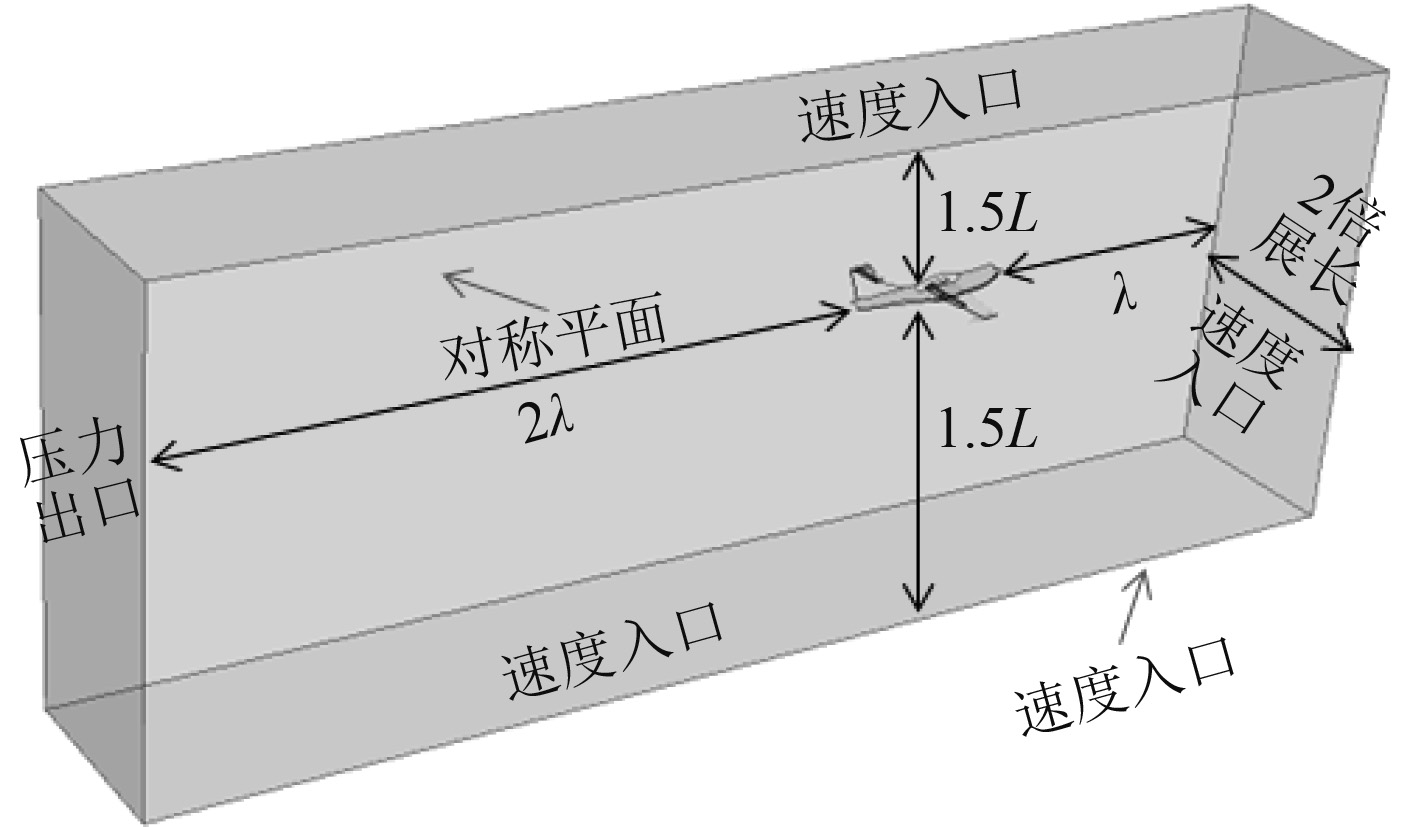
由于飞机在结构上左右对称,采用半模计算。计算域的划分为:机头前方为1倍波长,机身后部为2倍波长,宽度方向为2倍机翼展长,自由液面距离顶部、底部均为1.5倍机身长度。边界条件的设置为:计算域前方、顶部、底部、右侧为速度入口,后方为压力出口,中纵剖面为对称平面。
|
图 2 计算域及边界条件 Fig. 2 Computational domain and boundary condition |
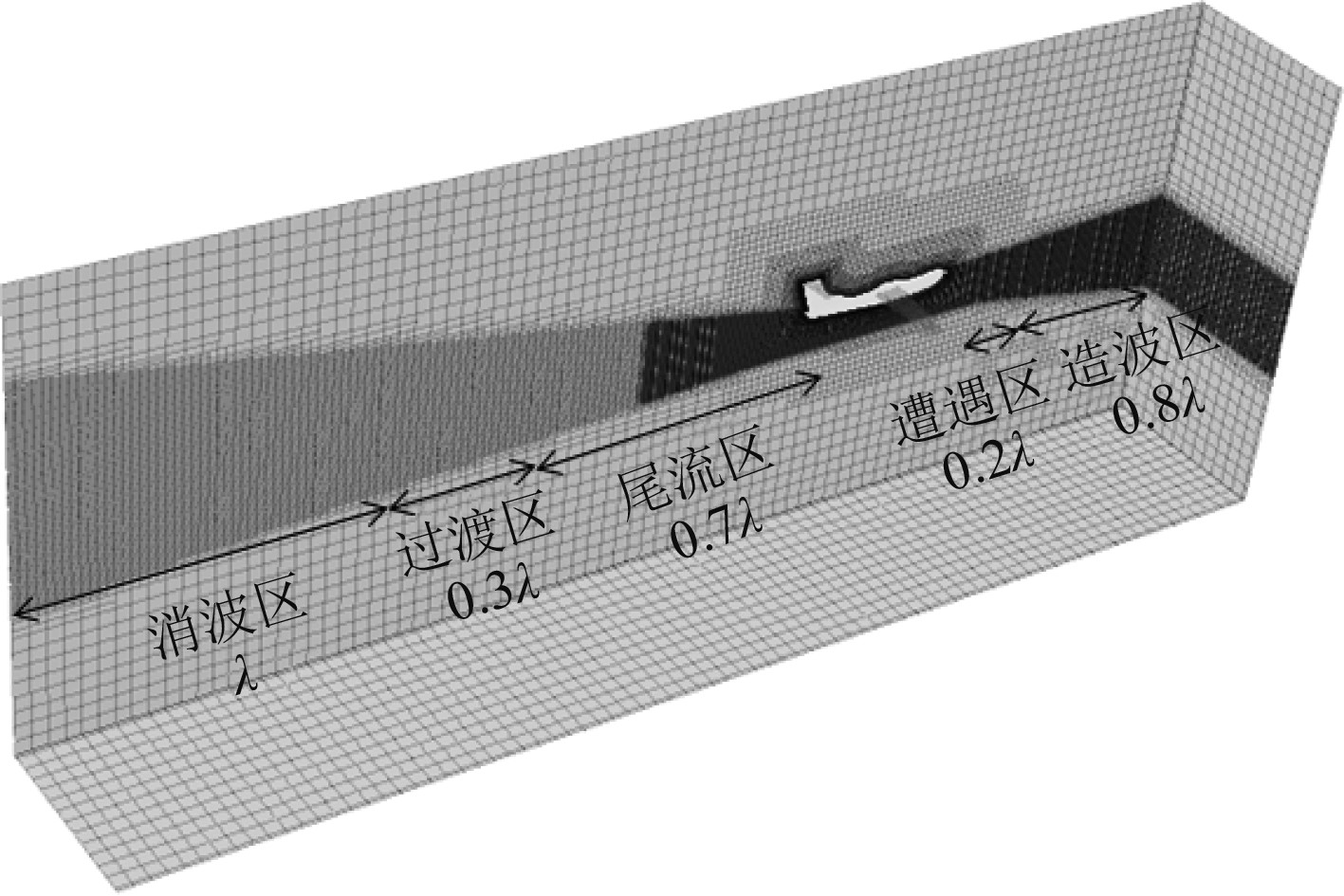
网格划分策略为:考虑到气动力的影响,对飞机升降舵、襟翼、翼尖位置进行加密;考虑水动力的影响,对机身断阶、抑波板及水线附近的区域进行加密。由于采用整体网格法,不涉及到网格变形及重构,因此,在计算前需要根据经验对飞机的运动姿态进行预估[6]。为了降低计算成本,采用梯形网格布局对计算域进行不同程度的过渡加密处理,机头前方分为0.8λ造波区、0.2λ遭遇区,机身尾部为0.7λ尾流区、0.3λ过渡区和λ消波区,计算域网格生成情况如图3所示。
|
图 3 计算域网格生成情况 Fig. 3 Mesh generation of computational domain |
湍流模型采用SST
模型通过拖曳装置、导航装置与拖车连接,套筒与拖车固接,升沉杆穿过套筒,下端与试验模型在重心位置铰接、上端与升力卸载装置连接。导航装置由导航杆和导航片组成,导航杆穿过导航片的通孔,保证模型的中纵剖面与拖车前进方向一致。由于模型试验依据傅汝德数相似开展,模型与实机的傅汝德数满足关系:
| $ {V_m}/\sqrt {g{L_m}} = {V_s}/\sqrt {g{L_s}} 。$ | (3) |
式中:V为速度,下标m代表模型,下标s代表实机。
根据雷诺数的计算公式
| $ {{Re} _m} = {{Re} _s} \times {\lambda ^{1.5}}。$ | (4) |
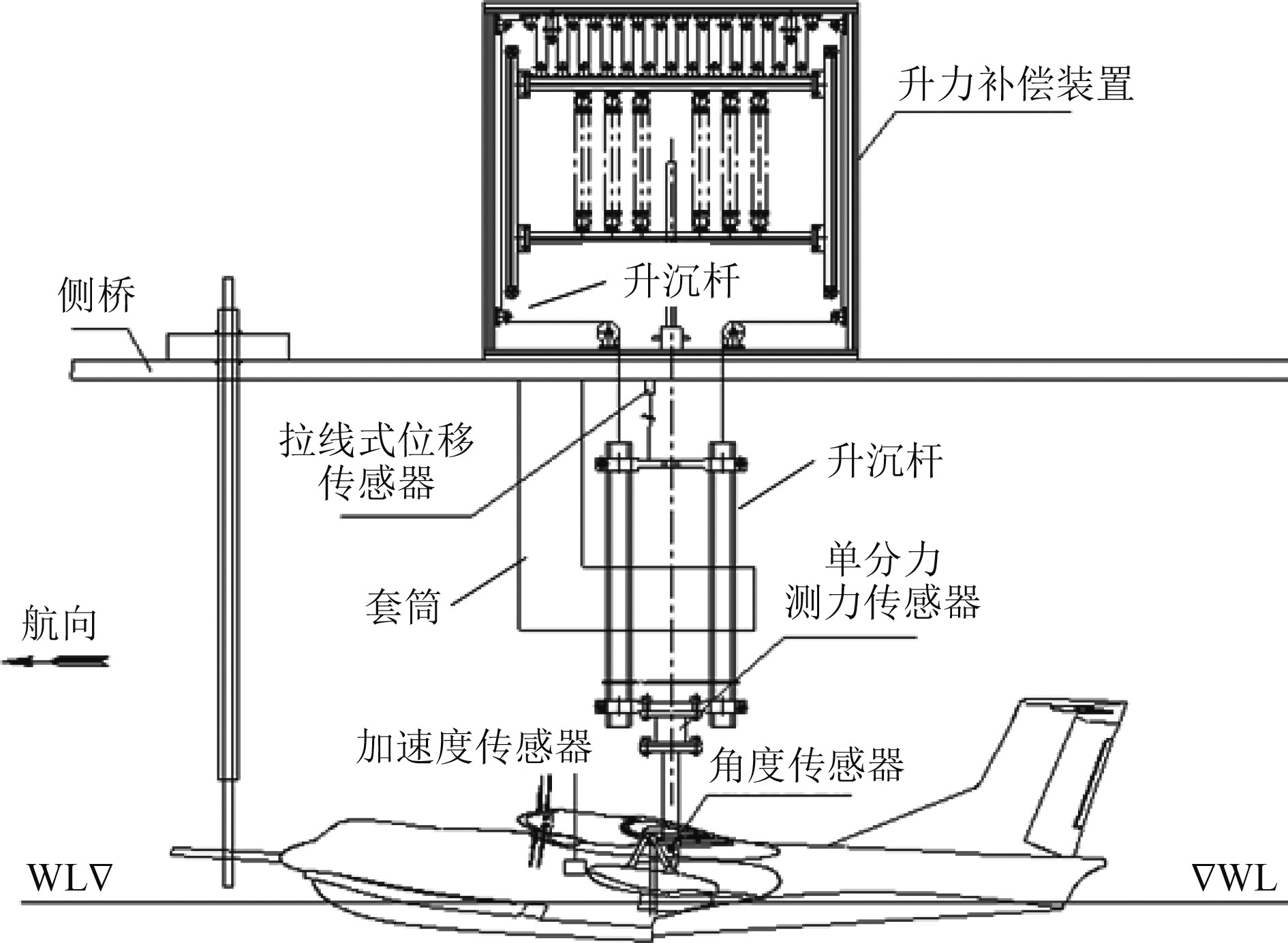
由于模型的缩尺比为1/10,根据式(4),模型的雷诺数为实机雷诺数的1/32,考虑到拖曳水池环境、拖车尺寸对气流的影响,模型与实机的气动升力、气动俯仰力矩有一定差异[5],因此,需要依据模型气动试验结果,采用图4中的升力补偿装置进行修正,俯仰力矩的修正通过调整升降舵舵偏。
|
图 4 试验模型安装示意图 Fig. 4 Installation schematic of the test model |
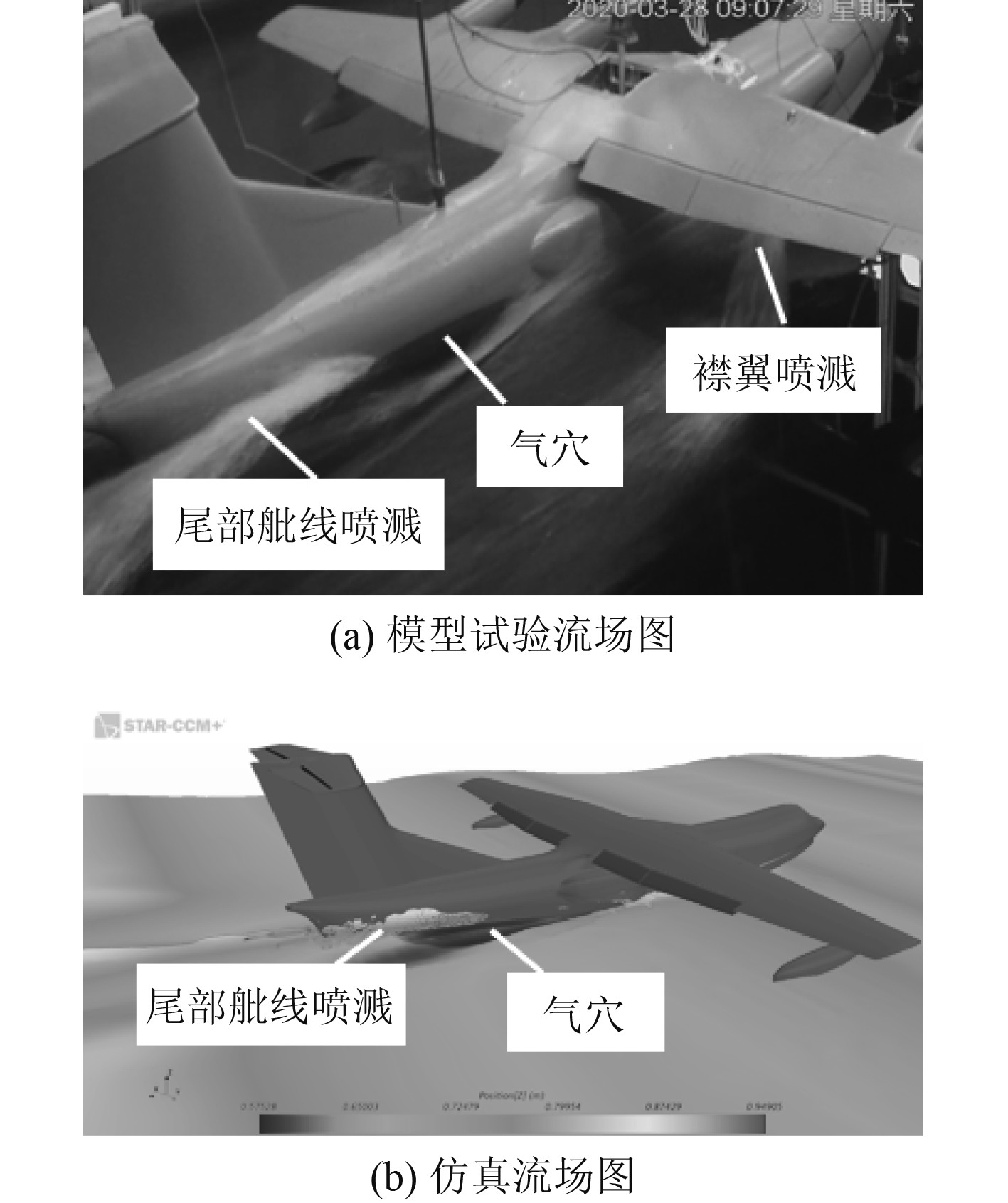
如图5所示,可以发现,数值模拟可以很好地捕捉高速滑行时机身断阶附近和波面之间的气穴以及尾部舭线处的喷溅,但对于襟翼喷溅打水这种自由液面的大变形很难捕捉。这是由于CFD是基于网格技术实现的。在计算域的网格中,每一个点有一个固定数量的预定义相邻的点,与相邻点的连接关系用于网格控制方程的求解并将求解信息传递到整个计算域[6-7],当网格变形较大时,如果不引入误差,网格之间的连接关系很难保持,尽管仿真中可以重新划分网格,但最终还会导致误差的积累增加,进而无法捕捉到这种大尺度的变形[8]。
|
图 5 流场图对比 Fig. 5 Comparison of flow field |
图6为某状态下飞机姿态角和载荷的试验结果和仿真结果的对比曲线。可以看出,数值模拟的时历曲线与试验结果在趋势上基本一致。飞机在波浪中运动时,纵摇角呈规律性的变化,最大角度发生在与波面脱离后上行的最高点,此时,由于飞机与水面之间不存在水动升力,仅受自身重力和气动升力,飞机的载荷最小;最小角度发生在与波面撞击后下行的最低点,此时飞机与波浪的作用最剧烈,载荷最大。仿真精度上,纵摇双幅值的计算值为5.78°,试验值为5.86°,误差为−1.4%,载荷峰值的计算值为1.76g,试验值为1.98g,误差为−12.5%,均在工程应用可接受的范围内。
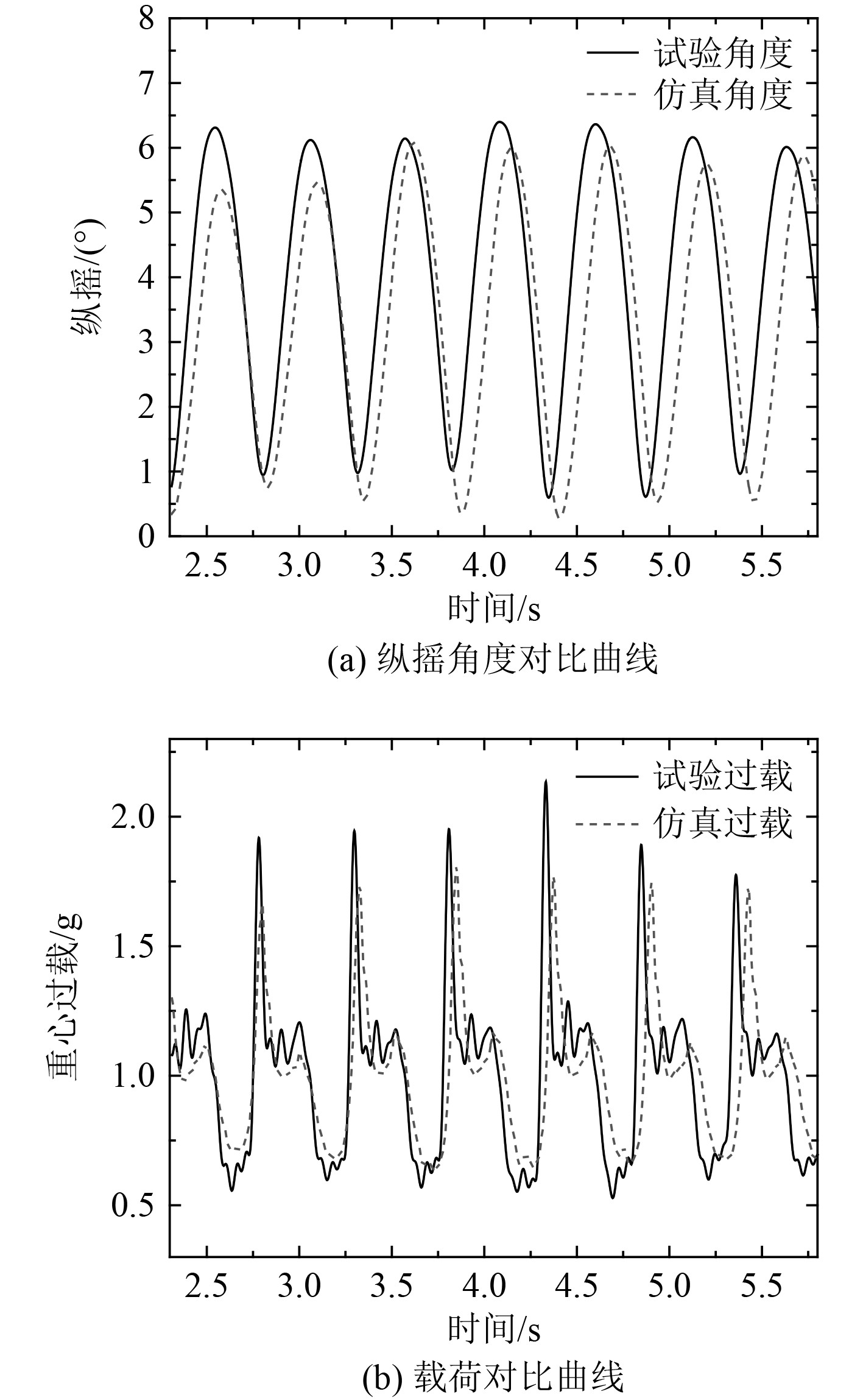
|
图 6 数值模拟与试验对比曲线 Fig. 6 Curve comparison between simulation and experimental result |
图7为不同状态下飞机的滑水载荷计算结果。可以发现,波高、波长及滑行速度对滑水载荷的影响有如下规律:
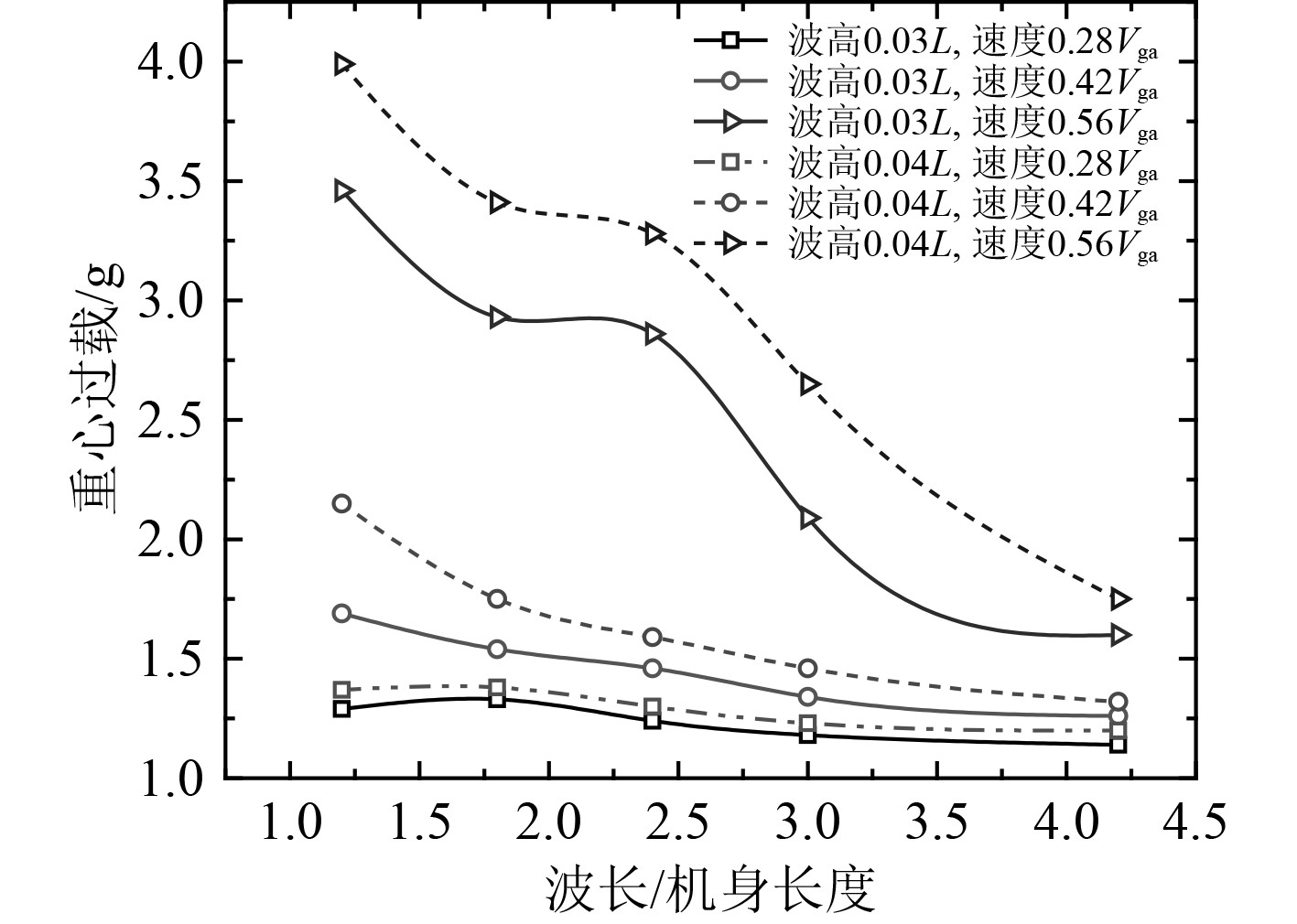
|
图 7 不同波高、速度下飞机载荷随波长变化曲线 Fig. 7 Variation curve of wave load with wavelength under different wave heights and velocities |
1)在同一波高和速度下,飞机的载荷随波长的增加整体上表现出逐渐减小的趋势,重心处的载荷峰值出现在波长为1.2~1.8倍机身长的短波状态,当飞机的遭遇波长大于4倍机身长后,不同波高和速度下飞机的载荷变化幅度值逐渐趋于收敛。
2)在同一波高和波长状态下,滑水载荷随速度的增加而增加,最大载荷一般发生在高速状态。
3)在同一波长和速度状态下,重心位置的载荷随波高的增加而增加,载荷随波高的变化幅度与波长有关,短波状态下不同波高之间的变化幅值要明显大于长波状态。
5 结 语本文采用数值模拟的方法对水陆两栖飞机波浪滑水载荷开展研究,并与模型试验结果对比验证该方法的可行性。在此基础上,研究了波长、波高、滑水速度对载荷的影响,得出的结论有:
1)CFD方法可以很好地捕捉飞机波面滑行时机身断阶附近和水面之间的气穴以及尾部舭线处的喷溅,但对于襟翼喷溅打水这种自由液面的大变形很难捕捉,在数值模拟精度方面,纵摇和载荷的时历曲线和试验结果在趋势和变化规律上基本一致,仿真精度在工程应用允许的范围内。
2)滑水载荷随波高和滑行速度的增加而增加,高海况和较高的速度会使飞机承受较大的载荷。
3)滑水载荷随波长的增加基本上逐渐减小,载荷峰值出现在波长为1.2~1.8倍机身长的短波,当飞机的遭遇波长大于4倍机身长后,因波高和滑行速度造成的载荷变化梯度逐渐减小。
| [1] |
褚林塘. 水上飞机水动力设计[M]. 北京: 航空工业出版社, 2014: 84-93.
|
| [2] |
马增辉, 刘立胜, 岳珍, 等. 水陆两栖飞机波浪水面上降落耐波性数值分析[J]. 计算力学学报, 2018, 35(3): 380-386. MA Z H, LIU L S, YUE Z, et al. Numerical investigation on seakeeping performance of amphibious aircraft landing on waves[J]. Chinese Journal of Computational Mechanics, 2018, 35(3): 380-386. |
| [3] |
CHEN J C, XIAO T H, WANG M, et al. Numerical study of wave effect on aircraft water-landing performance[J]. Applied Sciences, 2022, 12: 2561. DOI:10.3390/app1205256137-52 |
| [4] |
李新颖, 吴彬, 蒋荣. 基于滑移网格方法的水陆两栖飞机单船身耐波性数值模拟[J]. 船海工程, 2020, 49(3): 14-18. LI X Y, WU B, JIANG R. Numerical simulation of seakeeping performance of amphibious aircraft hull based on sliding mesh method[J]. Ship & Ocean Engineering, 2020, 49(3): 14-18. DOI:10.3963/j.issn.1671-7953.2020.03.004 |
| [5] |
黄淼, 褚林塘, 李成华, 等. 大型水陆两栖飞机抗浪能力研究[J]. 航空学报, 2019, 40(1): 522-535. HUANG M, CHU L T, LI C H, et al. Seakeeping performance research of large amphibious aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(1): 522-535. |
| [6] |
张浪, 程用胜, 王福新. 水上飞机静水起飞过程水气耦合性能分析[J]. 科学技术与工程, 2018, 18(11): 190-195. ZHANG L, CHENG Y S, WANG F X. Coupled hydrodynamic and aerodynamic performance analysis of seaplane take-off process in calm water[J]. Science Technology and Engineering, 2018, 18(11): 190-195. |
| [7] |
秦绪国, 刘沛清, 屈秋林. 翼型波浪水面巡航地面效应数值模拟[J]. 北京航空航天大学学报, 2011, 37(3): 295-299. QIN X G, LIU P Q, QU Q L. Numerical simulation on aerodynamics of airfoil flying over wavy water surface[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(3): 295-299. |
| [8] |
GENG X L, Boufadel C M, XIA Y Q, et al. Numerical study of wave effects on groundwater flow and solute transport in a laboratory beach[J]. Journal of Contaminant Hydrology, 2014, 165: 37-52. DOI:10.1016/j.jconhyd.2014.07.001 |
 2023, Vol. 45
2023, Vol. 45

