螺旋桨是一种为水下航行器提供稳定高航速的动力推进装置,随着航行器静音化的需求,新型螺旋桨研制多为复合材料。与传统的金属合金螺旋桨相比,复合材料螺旋桨通常由多层具有一定纤维角度织物堆叠而成,具有高比强度、高阻尼等特性,可大幅降低螺旋桨的重量和转动惯量,自适应船尾伴流场变化,提高推进效率和改善桨叶空泡性能以及材料阻尼特性,并减弱螺旋桨与轴系耦合振动,从而达到降低螺旋桨辐射噪声的目的。螺旋桨在大载荷下工作时,所处工况条件会在一定范围内不断发生变化,桨叶会产生多种弯曲扭转变形,对螺旋桨推进及噪声性能产生影响,通过调整复合材料铺层角度,可改善螺旋桨在多种工况下的适应能力。
研究复合材料铺层角度对宏观特性影响规律时,多数采用流固弱耦合数值模拟法,该方法已发展较为充分[1]。胡晓强[2]基于复合材料螺旋桨流固耦合自迭代算法,构建桨叶弯扭刚度数值计算方法,结果表明,复合材料螺旋桨单桨叶推力系数及其推力系数差值与桨叶刚度之间呈现出较为同步的变化规律。洪毅等[3]运用基于RANS方程计算流体力学法与CFD相结合的方法,设计了一个碳纤维复合材料螺旋桨桨叶,对其水动力载荷进行分析计算,根据载荷对其结构和铺层参数进行优化。刘影等[4]基于CFD计算复合材料螺旋桨水动力性能,应用有限元法计算桨叶结构响应,建立了复合材料螺旋桨在均匀来流下的双向流固耦合数值模拟方法。黄政[5]采用面元法结合有限元法的流固耦合算法,利用Abaqus软件研究纤维铺层对复合材料螺旋桨变形规律的影响,得出纤维铺层在标准工况下发生改变时,螺旋桨侧斜、纵倾和螺距的变化规律。杨光[6]通过比较不同材料螺旋桨的流固耦合特性可得,纤维复合材料影响螺旋桨水动力性能和结构特性,通过优选铺层方式以及材料能够有效地提高螺旋桨效率。丁永乐[7]建立了适用于基于粘流的复合材料螺旋桨流固耦合数值方法及设置,分析了该方法的不确定性,并使用工程算例对方法进行了验证。
以上研究多以提高设计工况下的推进性能为主,虽然证明了其他非设计工况下的推进效率有所改善,但是并未对多个工况进行综合优化设计。本文以P4119桨为例[8],针对铺层角度在大载荷下2种工况(进速系数为0.833、进速系数为0.5)下对其变形情况影响规律的问题,采用流固耦合数值模拟方法,计算不同铺层角度时复合材料螺旋桨的力学性能。从弯曲扭转变形、应力分布、推力系数、扭矩系数与效率等方面得到了复合材料铺层角度对螺旋桨受力特性的影响规律。
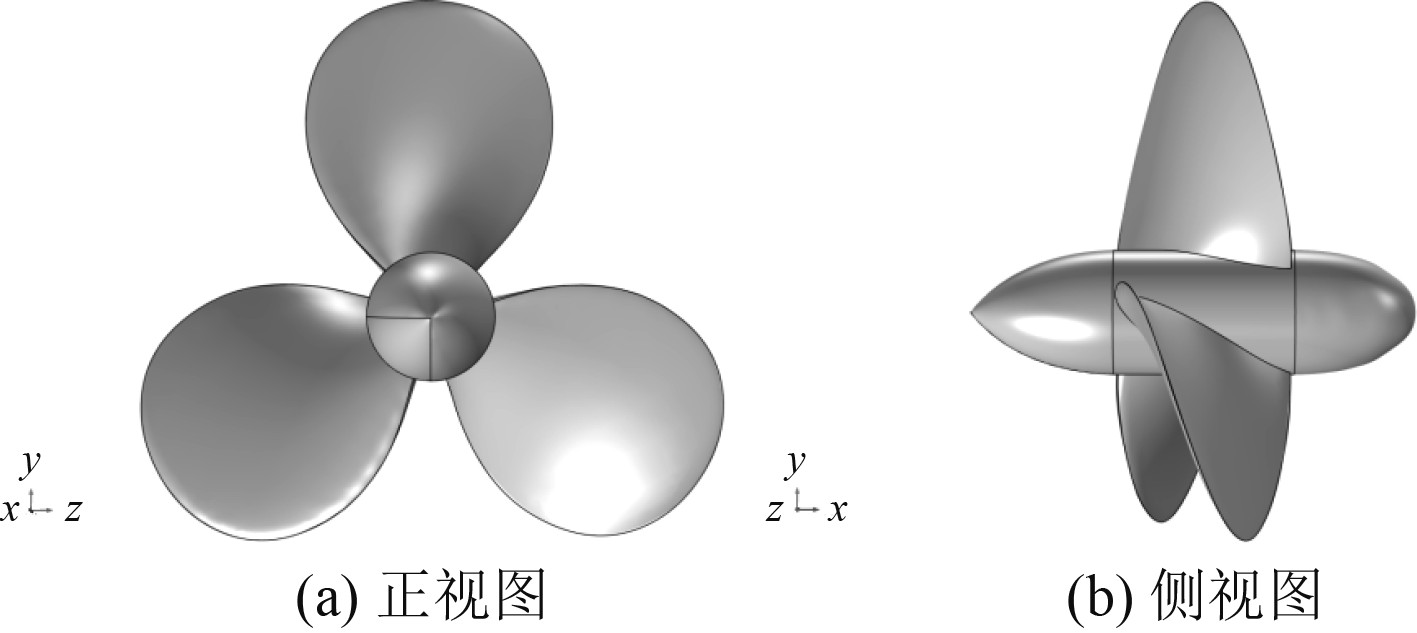
1 复合材料螺旋桨物理模型 1.1 螺旋桨结构针对P4119桨进行复合材料建模,其几何参数如表1所示。首先建立该螺旋桨的三维模型,如图1所示。
|
|
表 1 螺旋桨几何参数 Tab.1 Propeller geometric parameters |
|
图 1 P4119桨几何模型 Fig. 1 The model of P4119 propeller |
复合材料螺旋桨对结构刚度有较高要求,常采用增强纤维制造而成。本文采用环氧碳纤维材料进行复合材料建模,其主要材料参数如表2所示,建模流程如下:
|
|
表 2 复合材料参数 Tab.2 Composite material parameters |
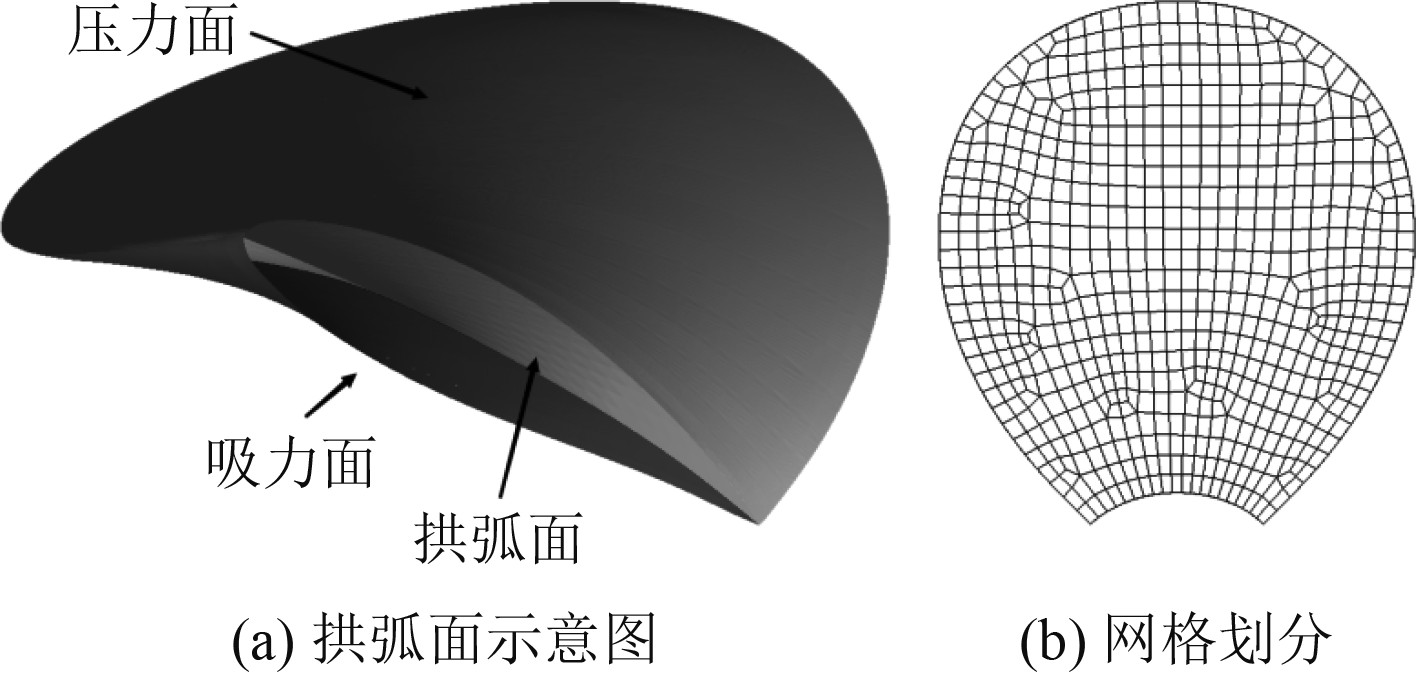
步骤1 生成桨叶拱弧面。将吸力面与压力面各单元坐标取平均得到拱弧面,再对其生成四边形网格,得到铺层基准面,如图2所示。
|
图 2 桨叶拱形面网格划分 Fig. 2 Meshing of blade arch surface |
步骤2 导入推进器外轮廓。将推进器进行面分解处理,再将吸力面与压力面导入,作为切割轮廓。
步骤3 设置铺层基元。基于各项异性材料,纤维布编织厚度设为0.2 mm,纤维角度设置为0°,以铺层单元由6层纤维组成。
步骤4 设置铺层方向。以叶根中心作为参考点,以单元法线为参考,同时向吸力面与压力面2个相反的方向作为铺覆方向进行纤维布堆叠。如图3所示,靠近竖直方向箭头为复合材料厚度的铺敷方向(垂直于中面),水平箭头为铺层角度的参考方向(推进器桨毂正切向方向),斜向右上方箭头即铺层角度方向。为保证各桨叶的结构性能相同,各桨叶的铺层方向和层数均需保持一致。

|
图 3 纤维铺层参考坐标系 Fig. 3 Fiber layering reference frame diagram |
步骤5 生成实体单元。将铺层基元进行堆叠,吸力面与压力面方向各铺设9层,生成产品铺层,如图4(a)所示。铺覆时选择导入轮廓形成的切割规则对分析铺层进行切割,按几何厚度对纤维铺层进行裁剪,长纤维位于内层,铺层层数由所在区域厚度所决定,最终所有铺层形成了中间厚、边缘薄的桨叶形状,如图4(b)所示。再将一层0°纤维布贴附于切割后的桨叶轮廓上,使其表面光滑,即完成复合材料螺旋桨建模工作,如图4(c)所示。

|
图 4 建立复合材料桨叶模型 Fig. 4 A composite blade model was established |
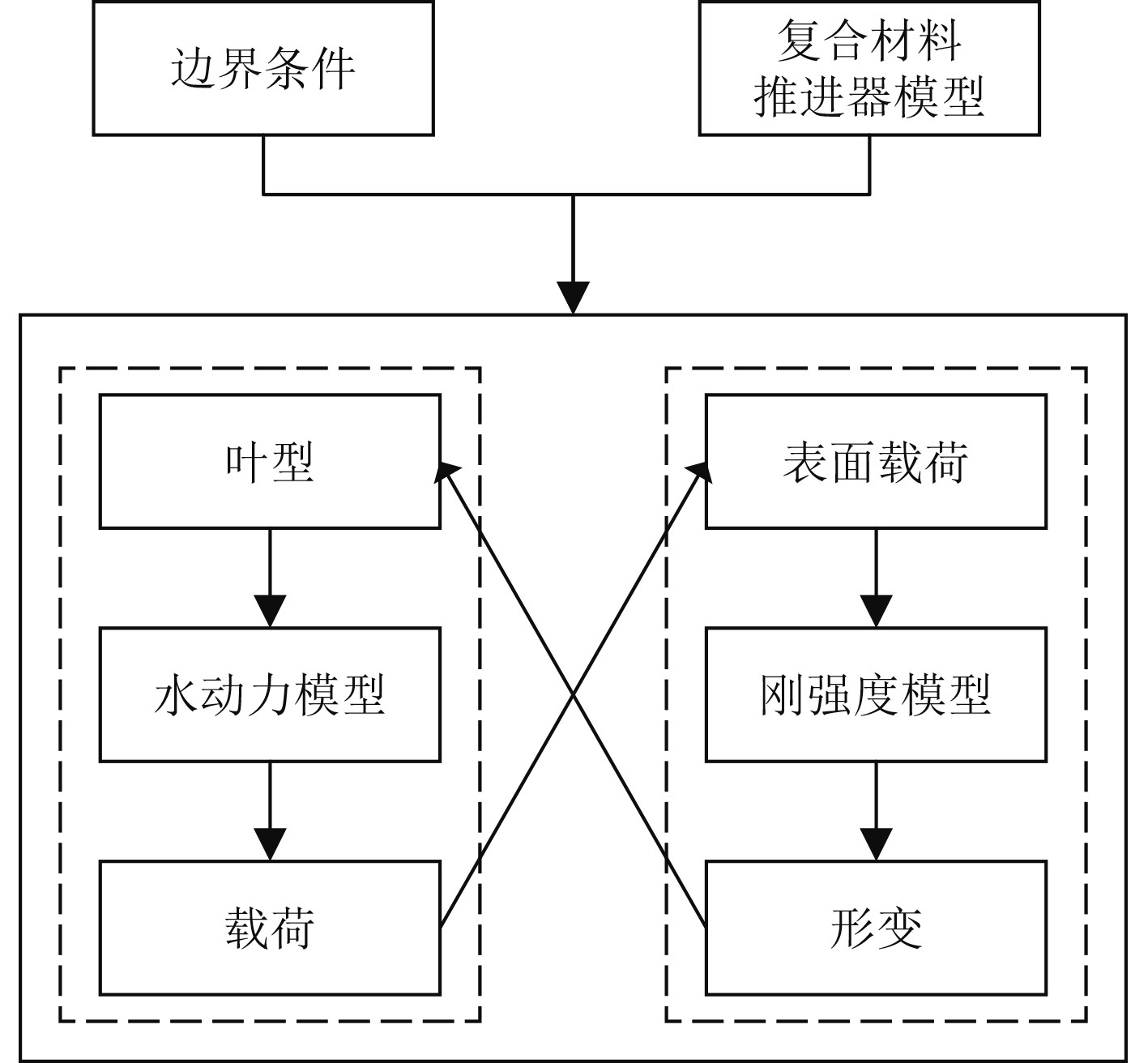
本文用CFD/FEM双向流固耦合方法研究其力学性能与水动力性能。如图5所示,计算时,螺旋桨表面载荷由CFD隐式求解计算得出,作为输入值传递到有限元部分,结构部分将计算得出的桨叶变形数据传递到流体部分并更新流场网格,进行下一个时间步计算。
|
图 5 流固耦合计算过程示意图 Fig. 5 Schematic diagram of fluid-structure interaction calculation process |
其中刚强度模型的动力学平衡方程可以表示为:
| $ \left[{\boldsymbol{M}}_{s}\right]\{\ddot{u}(t)\}+\left[{\boldsymbol{C}}_{s}\right]\{\dot{u}(t)\}+\left[{\boldsymbol{K}}_{s}\right]\{u(t)\}=F_{e z t}(t)。$ | (1) |
式中:
通过求解RANS方程可得到螺旋桨桨叶各处压力分布值,其控制方程为:
| $ \begin{split} &\dfrac{\partial \bar{u}}{\partial x_{i}}=0 ,\\ &\rho \dfrac{\partial \bar{u}_{i}}{\partial t}+\rho \dfrac{\partial \bar{u}_{i} \partial \bar{u}_{f}}{\partial x_{j}}=-\dfrac{\partial \bar{p}}{\partial x_{i}}+\mu \dfrac{\partial^{2} \bar{u}_{i}}{\partial x_{j} \partial x_{j}}+\dfrac{\partial \bar{\tau}_{i v}}{\partial x_{j}}。\end{split} $ | (2) |
式中:
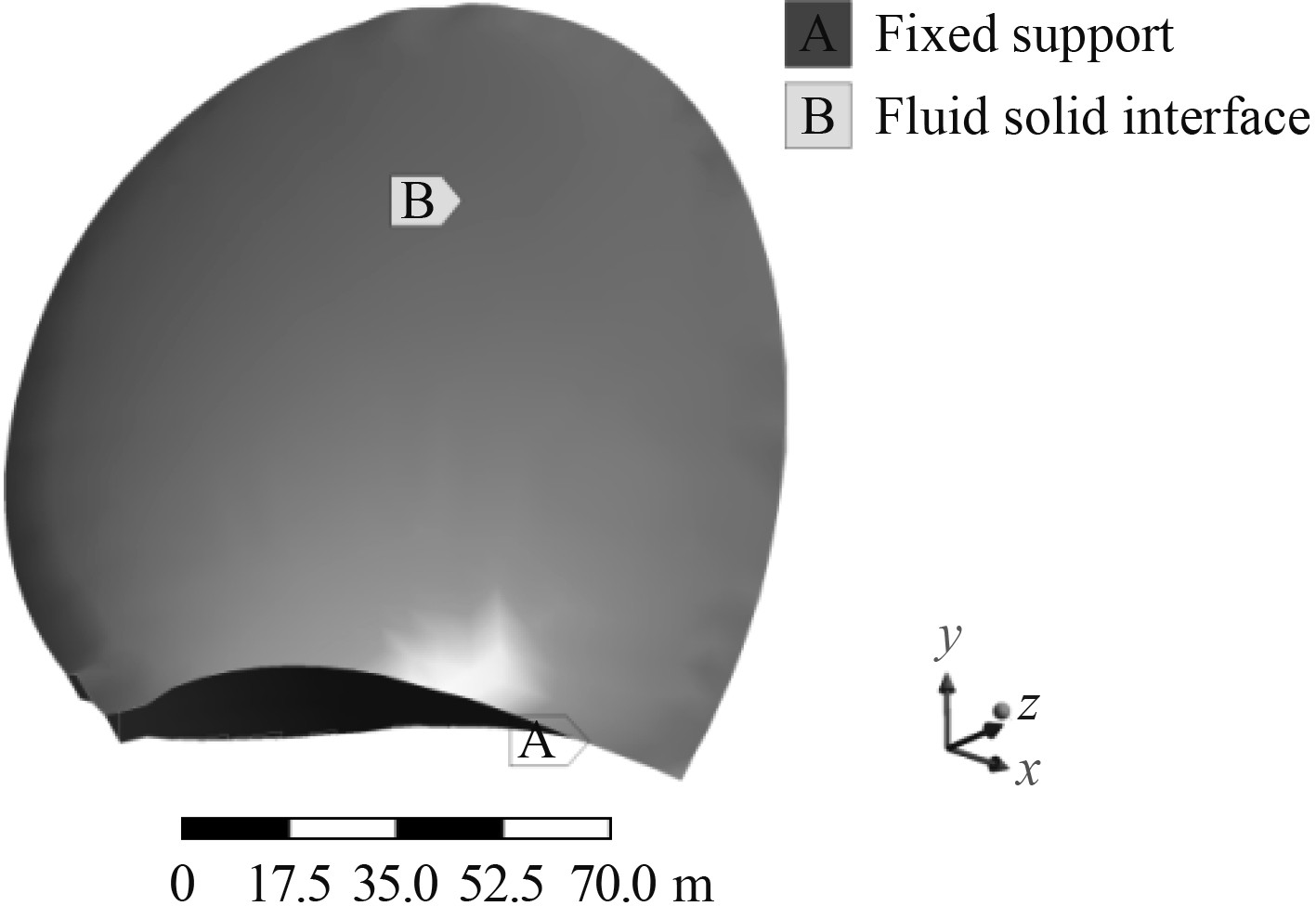
螺旋桨桨叶的吸力面与压力面设置为流固耦合面,螺旋桨桨叶根部设置为固定约束,结构体采用实体单元SOLID185,如图6所示。
|
图 6 桨叶受力约束图 Fig. 6 Diagram of blade force constraints |
假设不考虑水深对推进器性能的影响,流体域整体分为旋转域与静止域。旋转域为包络推进器的圆柱形区域,半径0.25 m,进口距推进器0.2 m,出口距推进器0.2 m,静止域为圆柱形区域,半径1 m,进口距推进器1 m,出口距推进器3 m,最终,计算域划分如图7所示。
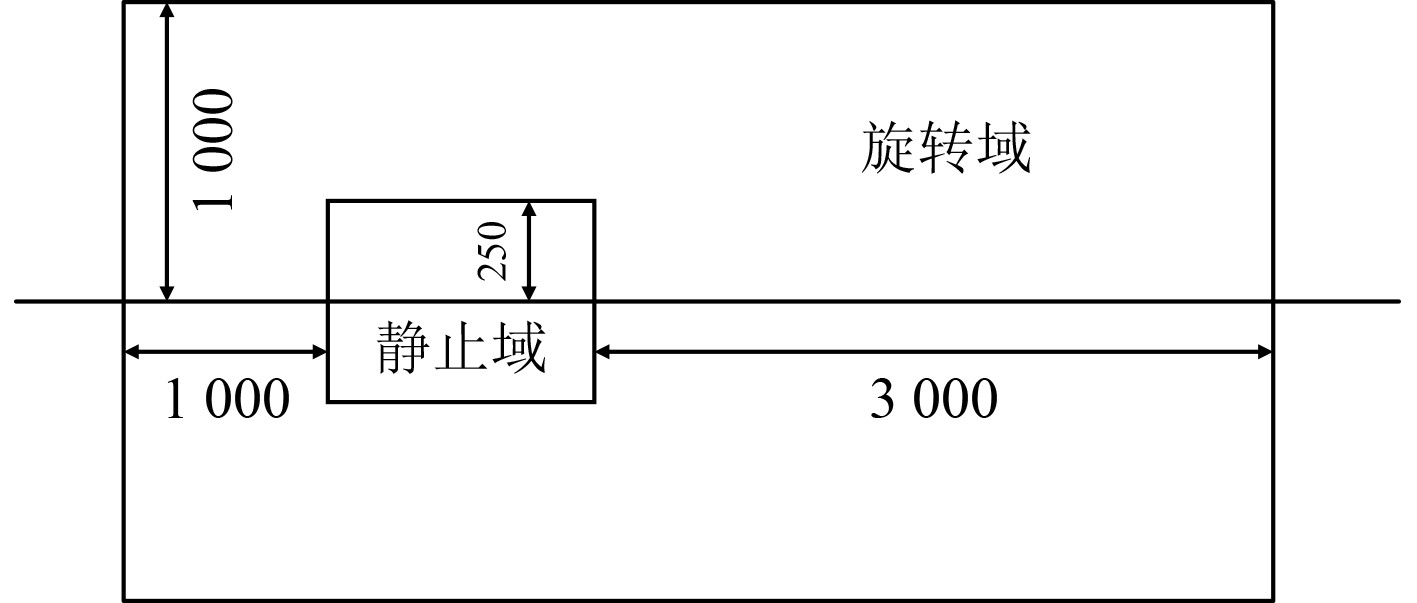
|
图 7 计算域尺寸 Fig. 7 Computing domain size |
复合材料推进器在大载荷条件下工作时易产生较大变形,需要对桨叶梢部周围区域的网格进行重新划分,因此旋转域采用非结构网格,静止域采用结构网格。在流固耦合交界面处,导边与随边进行局部加密处理,增加边界层,提高计算精度。具体参数见文献[9]。
流体部分湍流模型选取SST
|
|
表 3 计算工况设置参数表 Tab.3 Propeller shape and material parameter table |
根据前面的流固耦合模型进行计算,将得到的结果与文献中的试验结果[11]和数值模拟结果[12]进行对比验证,如图8所示。
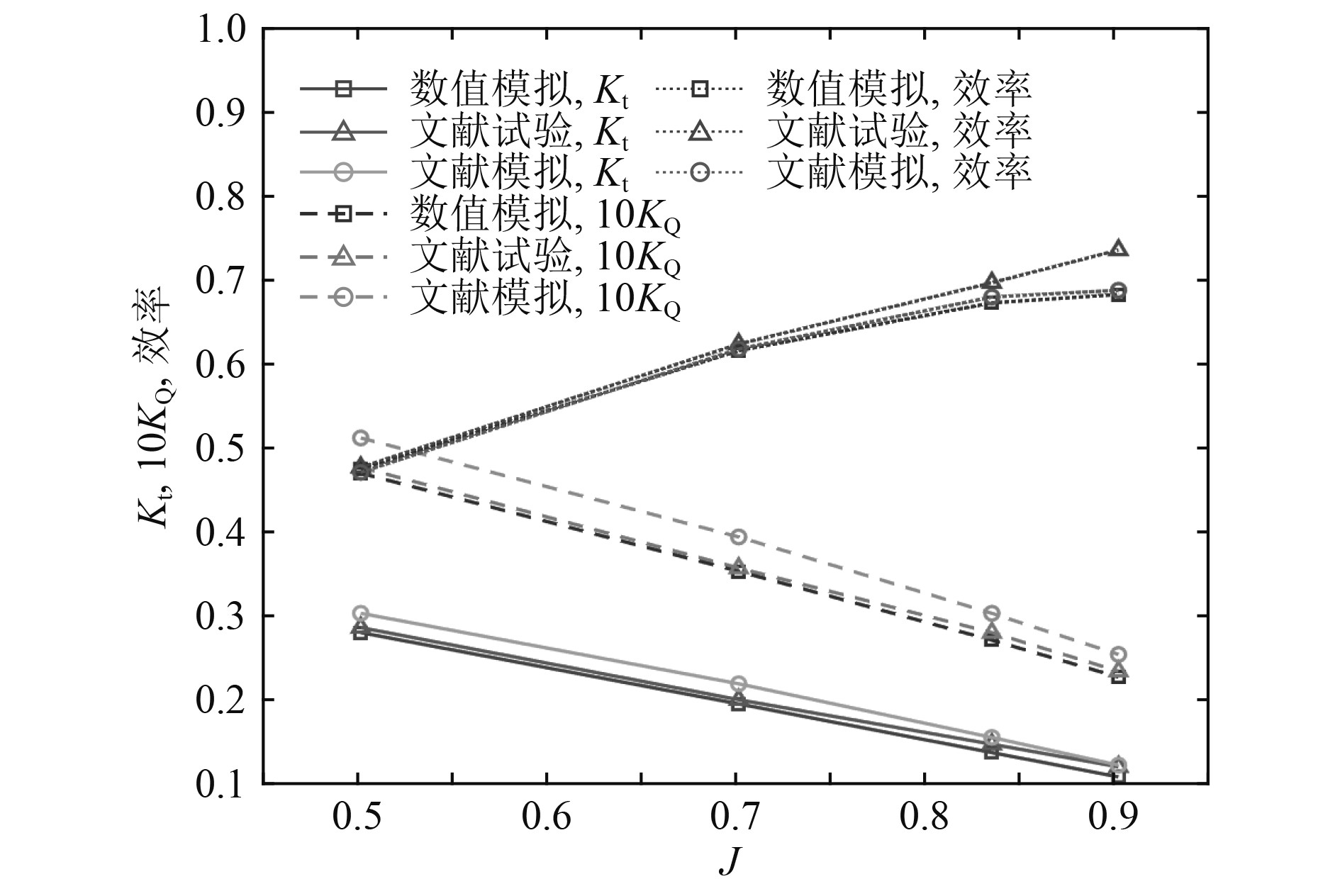
|
图 8 敞水性能对比图 Fig. 8 Open water performance comparison diagram |
可以看出,模拟所得到的敞水性能结果与文献中的试验结果性能曲线趋势相同,在低进速系数时吻合得比较好,在高进速系数下的误差在可接受范围内。说明本文所建立得流固耦合数值模拟方法正确。
3 结果分析及讨论选取大载荷2种工况(进速系数0.5、进速系数0.833)下,采用单一材料,所有铺层采用同一角度。铺层角度选取8种不同的铺层角度(0°,30°,45°,60°,90°,120°,135°,150°)建立复合材料螺旋桨有限元模型进行计算,计算结果从3个方面展现,共同说明复合材料铺层角度对螺旋桨变形情况的影响。
3.1 铺层角度对螺旋桨桨叶变形影响分析复合材料螺旋桨在承受水动力载荷时,桨叶会产生变形。表4给出了不同铺层角度情况下,螺旋桨叶片的总变形情况。2种工况下,当纤维角度为0°~150°时,复合材料桨叶的总变形均先降低后增加,呈现近似“V”形趋势,当铺层角度θ=90°时,总变形量最大,这与铺层角度对推力系数、扭矩系数的影响规律成正相关,与效率的影响规律呈负相关。
|
|
表 4 纤维铺层角度对总变形的影响 Tab.4 Effect of fiber layering angle on total deformation |
图9为2种工况下,半径系数0.5与0.75时的桨叶截面图,由上到下依次为90°铺层、60°铺层、30°铺层和0°铺层时的剖面。可以看出,P4119螺旋桨桨叶均向X轴负方向(轴向)与Z轴正方向(周向)发生弯曲,产生纵倾与侧斜,同铺层角度下,低进速系数变形量大;同工况下,0°铺层角度变形程度最大。当半径系数增大时,螺旋桨桨叶在同一半径处沿着桨轴方向导边变形量要大于随边,使叶片发生扭转,改变了各半径处螺距比分布,其具体变化如图10所示。

|
图 9 桨叶变形图 Fig. 9 Blade deformation diagram |
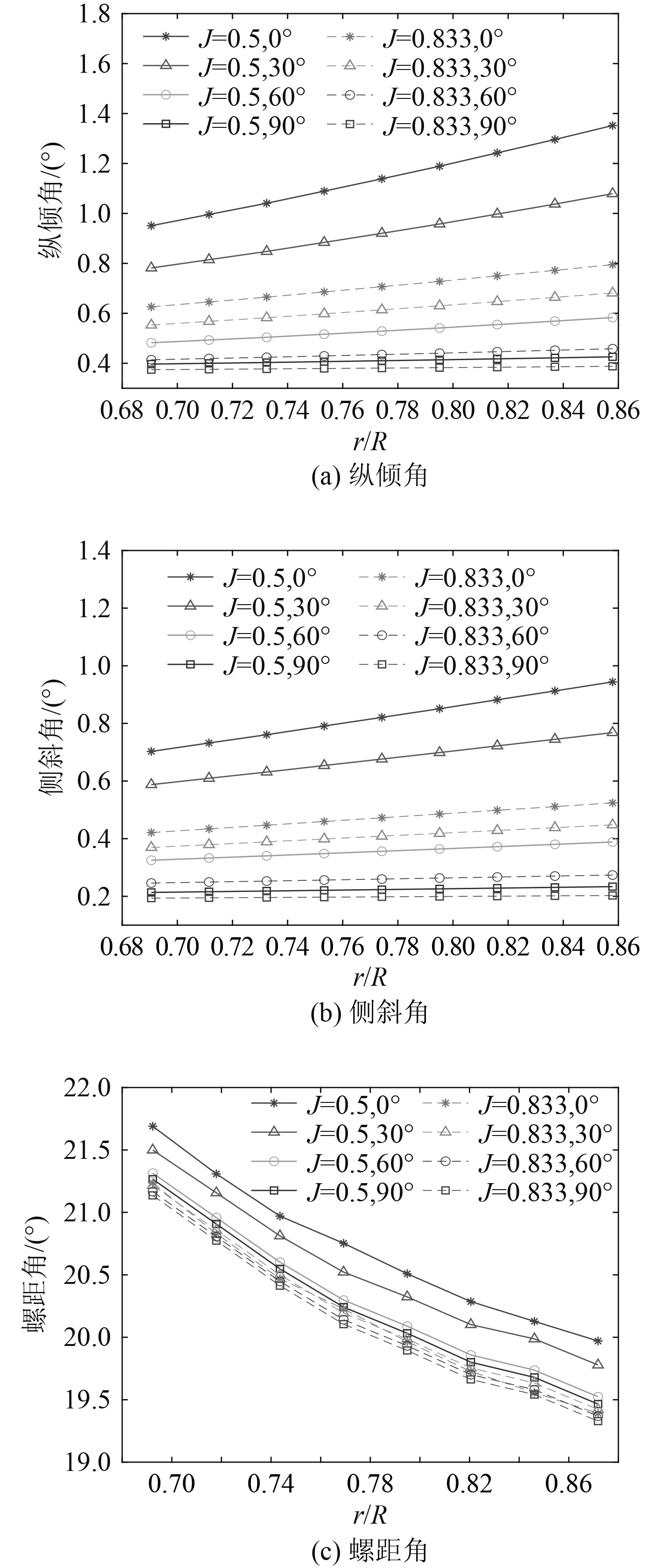
|
图 10 不同铺层角度下侧斜角、纵倾角及螺距角的变化 Fig. 10 Variation of lateral bevel angle, pitch angle and pitch angle under different layering angles |
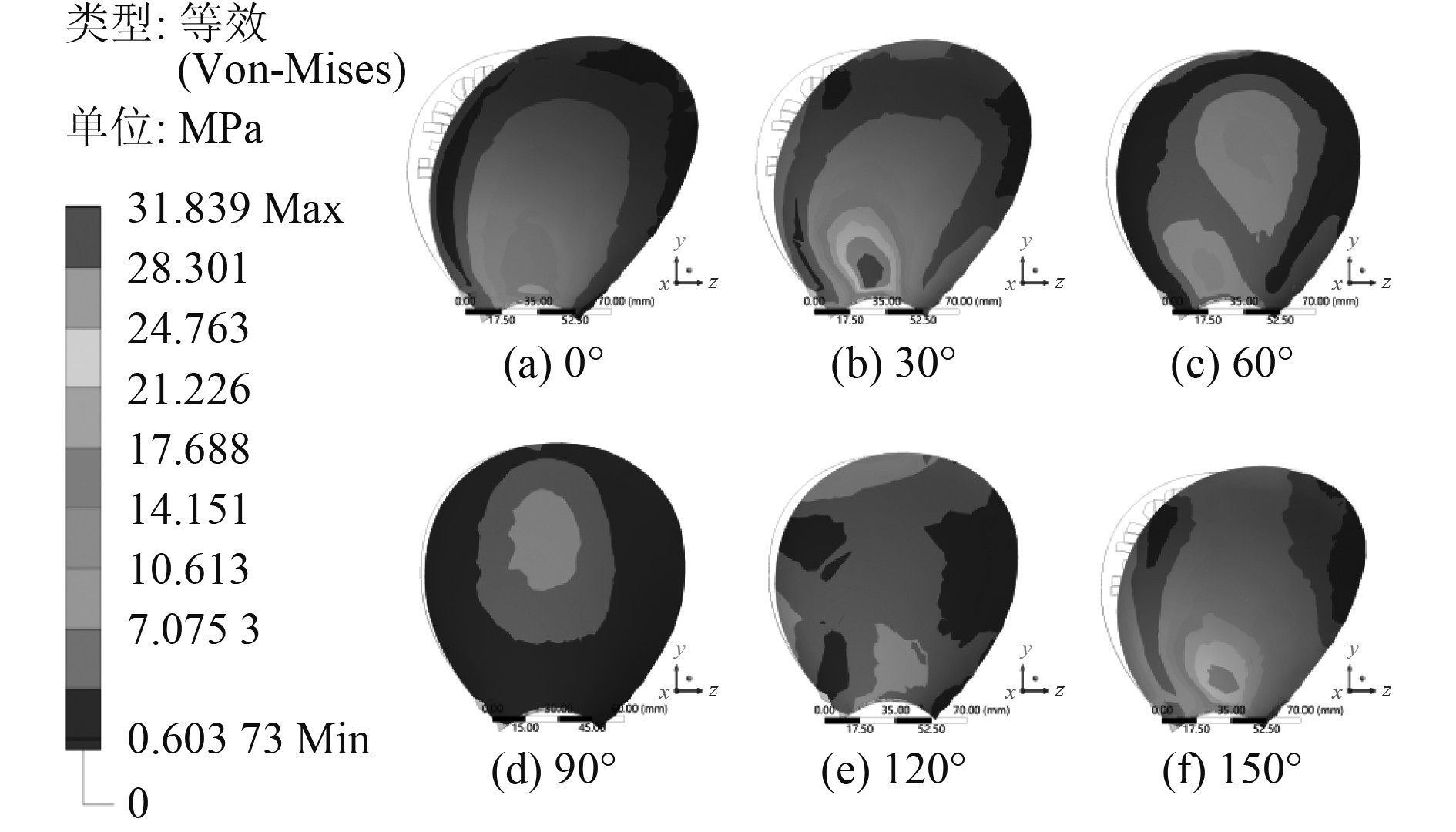
图11和图12给出了不同铺层角度情况下,复合材料螺旋桨桨叶等效应力分布云图。可以看出,应力分布受铺层角度的影响较大。总体上J=0.5时桨叶的等效应力要大于J=0.833时。在铺层角度趋向于水平时,应力沿铺层角度方向向着螺旋桨桨叶根部区域集中;在铺层角度趋于90°时,应力最大值脱离桨叶根部区域,出现在中部区域,且扩大了影响范围,应力集中现象得到显著改善。当纤维角度为0°~150°时,复合材料螺旋桨所受到的最大应力值均先降低后增加,当铺层角度为90°时,最大应力值最小;30°与150°时,最大应力值最大。这是因为螺旋桨所受阻力方向与螺旋桨桨叶根部刚度最大方向接近,拉伸和剪切应力均增大。
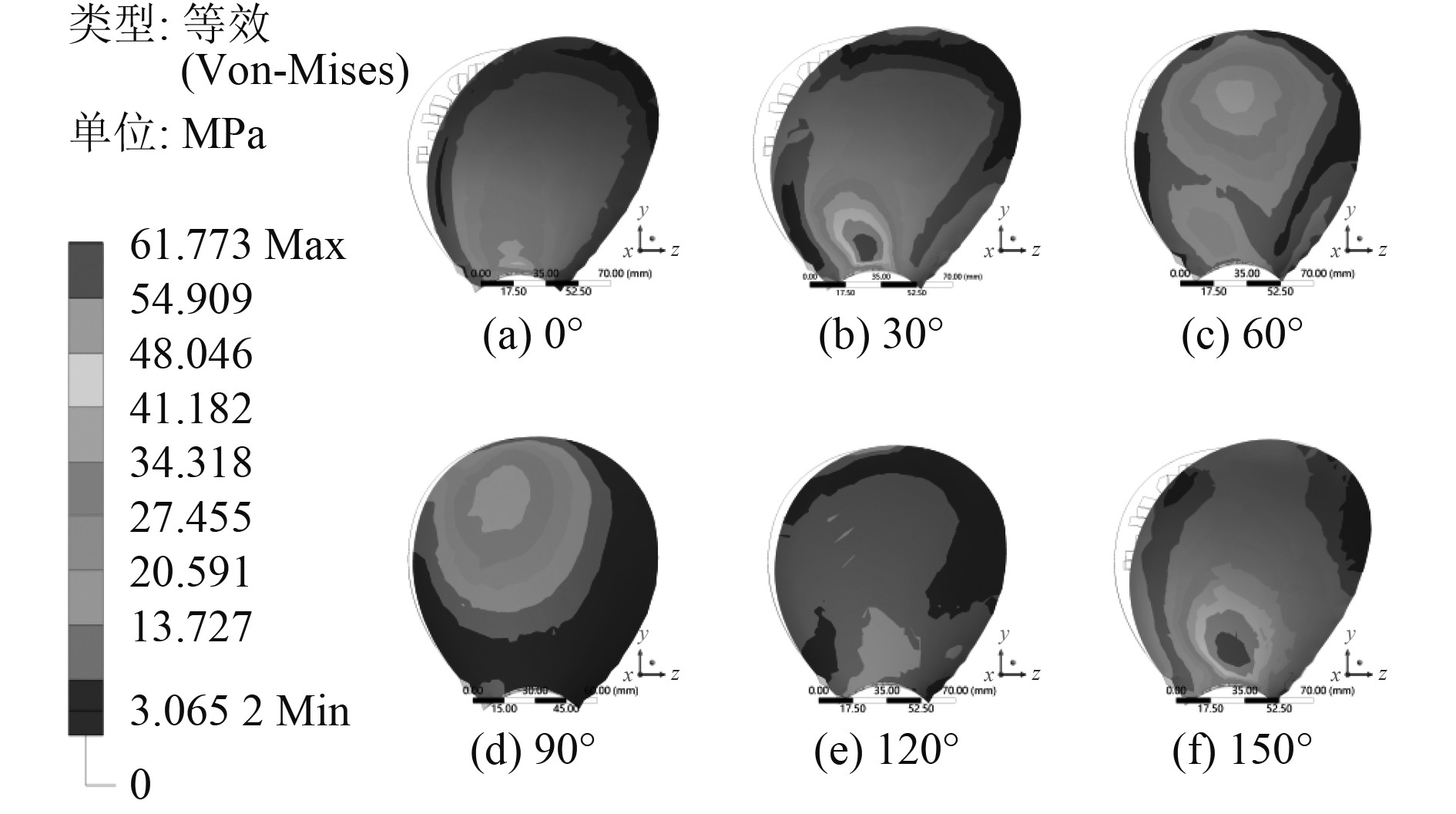
|
图 11 0.5进速系数时桨叶表面应力分布云图 Fig. 11 Von Mises stress distribution on blade surface when advance coefficient is 0.5 |
|
图 12 0.833进速系数时桨叶表面应力分布云图 Fig. 12 Von mises stress distribution on blade surface when advance coefficient is 0.833 |
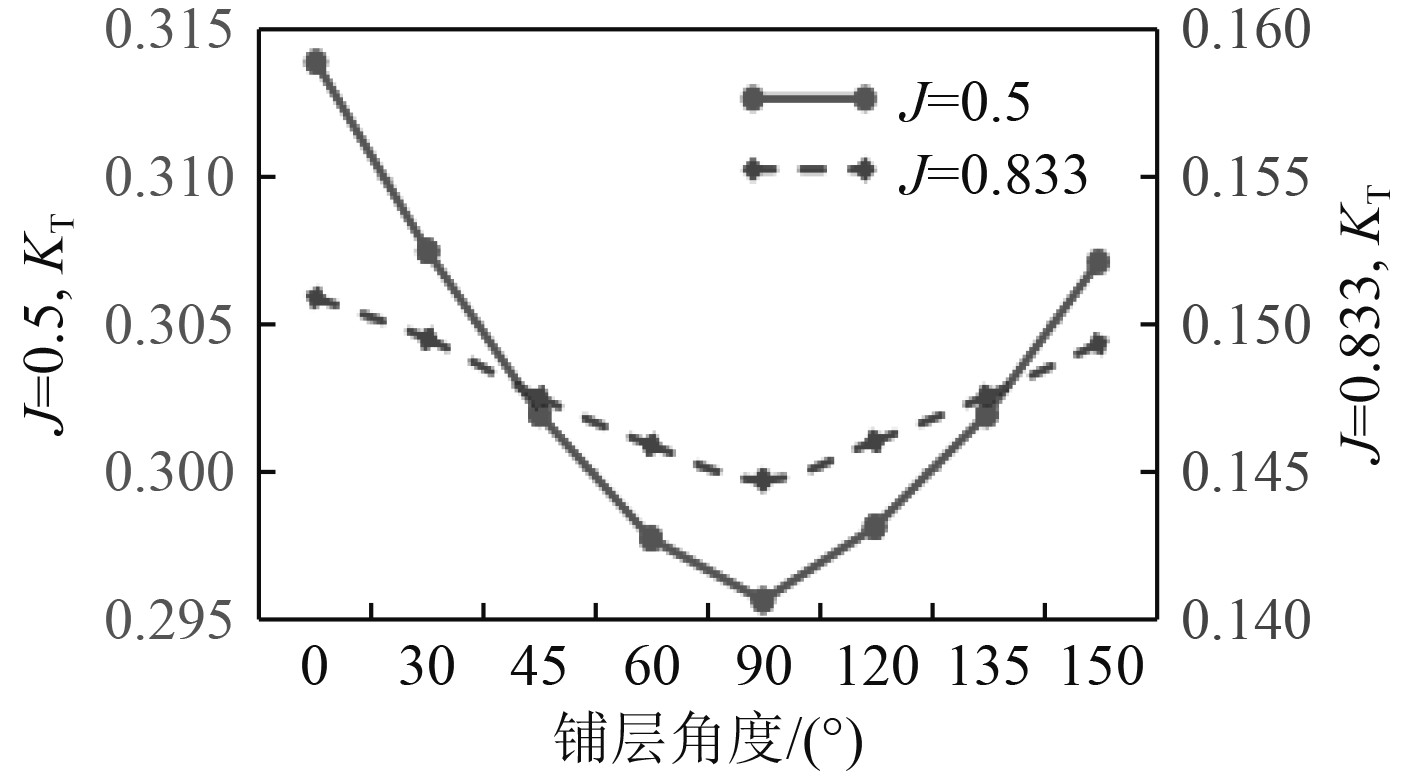
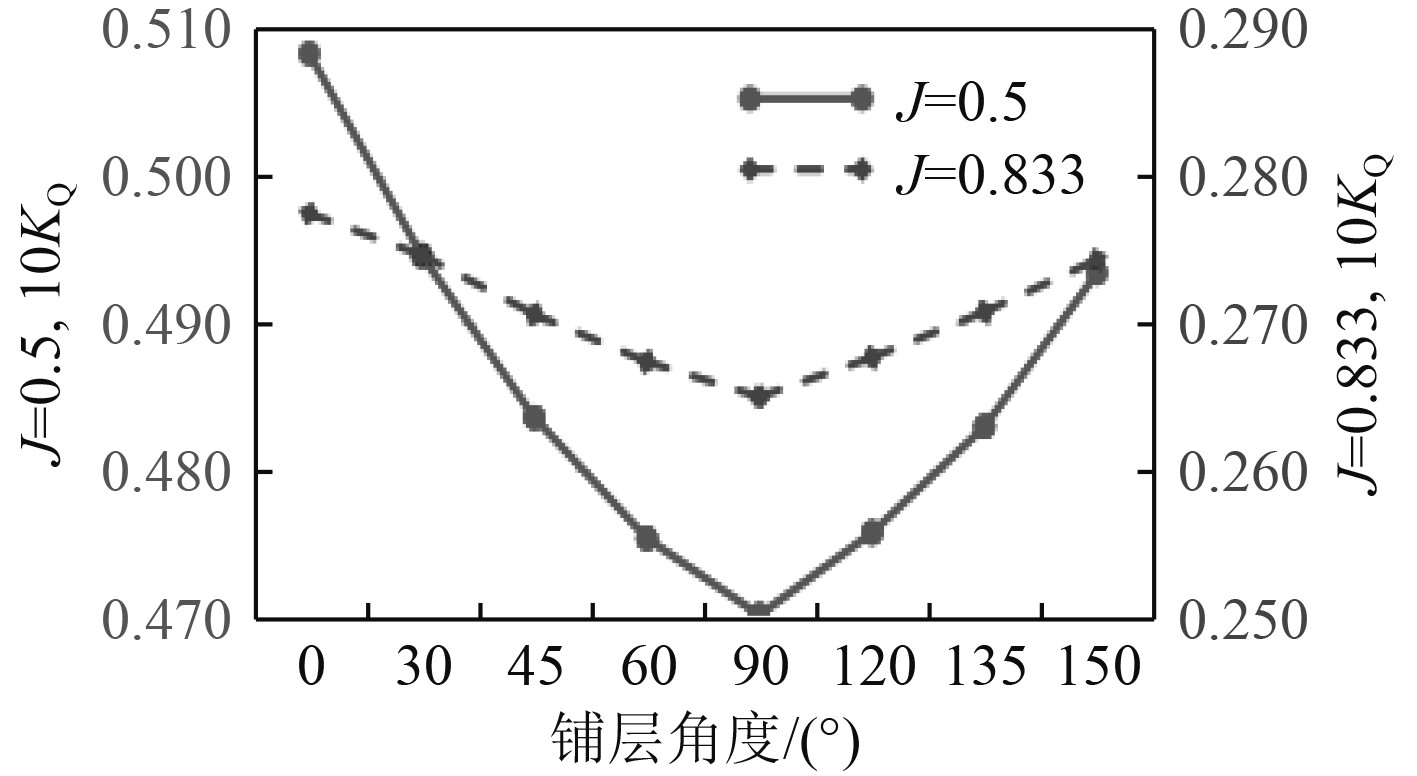
在大载荷2种工况(进速系数0.5、进速系数0.833)下,复合材料螺旋桨推力系数和扭矩系数如图13与图14所示。可以看出,工况对螺旋桨受力情况有较大影响,当铺层角度增大时,螺旋桨推力系数与扭矩系数均呈现近似“V”形趋势,当铺层角度为90°时,复合材料螺旋桨推力系数最小,扭矩系数最小。这是因为90°铺层角度时,螺旋桨桨叶在径向刚度最大,桨叶弯曲变形最小。
|
图 13 纤维铺层角度对推力系数的影响 Fig. 13 Effect of fiber layering Angle on thrust coefficient |
|
图 14 纤维铺层角度对扭矩系数的影响 Fig. 14 Effect of fiber layering angle on torque coefficient |
复合材料螺旋桨效率由推力系数与扭矩系数综合计算得出,公式如下:
| $ \eta=\frac{K_{T}}{K_{q}} \cdot \frac{J}{2 {\text{π}}}。$ |
如图15所示,在2种工况下,当纤维角度为0°~150°时,复合材料螺旋桨的效率均先增加后降低,当铺层角度θ=90°时效率最大。以铺层角度为0°时为基准,铺层角度为90°时,标准工况下,推力系数下降4.12%,扭矩系数下降4.49%,效率提升0.39%;大载荷工况下,推力下降5.85%,扭矩系数下降7.52%,效率提升1.8%。当铺层角度改变时,扭矩系数的变化比推力系数更大,这个现象在低进速系数时,更能体现。这是因为低进速系数时,推力与扭矩较大,螺旋桨所受应力更大,桨叶扭转变形更大,弯扭耦合效应变化更为明显,应力分布更加均匀合理,螺旋桨整体效率提升更多。

|
图 15 纤维铺层角度对效率的影响 Fig. 15 Effect of fiber layering angle on efficiency |
本文针对多工况下螺旋桨桨叶受力变形问题,采用流固耦合数值模拟方法,研究不同铺层角度下复合材料螺旋桨在多工况下的变形、应力分布与效率的变化情况,进而探究复合材料铺层角度对螺旋桨受力特性的影响规律,得出结论如下:
1)复合材料螺旋桨在承受水动力荷载后,由于自身弹性模量各向异性,具有弯扭耦合效应,可自适应产生形变,调节纵倾、侧斜与螺距的分布情况,不同铺层角度整体变形趋势相似,载荷越大,变形程度越高。
2)复合材料螺旋桨应力分布受桨叶铺层角度影响较大,铺层角度的改变可以直接改变复合材料螺旋桨桨叶应力分布情况,当角度为90°时,应力最大值最小,应力集中现象最不明显。
3)单一材料所有铺层采用同一角度时,复合材料螺旋桨在应对不同工况时均可提升推进效率。相较于标准工况而言,大载荷工况下,材料铺层角度对力学性能的影响更为明显,材料铺层角度为90°时,推力与扭矩最低,总体效率最高,螺旋桨的水动力性能最好。
综上所述,本文对不同铺层角度下复合材料螺旋桨桨叶进行研究,铺层角度的改变在不同工况下均对螺旋桨水动力性能与桨叶变形有规律性的影响,在大载荷时,尤为明显。这为后续研究不同工况下最优铺层设计方案提供一定借鉴。
| [1] |
王晓强, 龚正琦. 水下螺旋桨技术发展现状与展望[J]. 中国水运, 2021(4): 74-76. WANG Xiao-qiang, GONG Zheng-qi. Development status and prospect of underwater propeller technology[J]. China Water Transport, 2021(4): 74-76. |
| [2] |
胡晓强, 黄政, 刘志华. 复合材料螺旋桨弯扭耦合刚度特性分析[J]. 中国舰船研究, 2022, 17(1): 25-35. HU Xiao-qiang, HUANG Zhen, LIU Zhi-hua. Numerical analysis on bending-torsional coupling stiffness characteristics ofcomposite propeller[J]. Chinese Journal of Ship Research, 2022, 17(1): 25-35. |
| [3] |
洪毅, 赫晓东. 复合材料船用螺旋桨设计与CFD/FEM计算[J]. 哈尔滨工业大学学报, 2010, 42(3): 404-408. |
| [4] |
刘影, 张晶, 吴钦等. 复合材料螺旋桨水动力性能与结构响应数值研究[J]. 北京理工大学学报, 2021, 41(3): 266-273. |
| [5] |
黄政, 熊鹰, 孙海涛. 纤维铺层对复合材料桨变形规律的影响[J]. 舰船科学技术, 2013, 35(8): 119-122,128. HUANG Zheng, XIONG Ying, SUN Hai-tao. The impact of composite propeller's material stacking sequence on the deformation law[J]. Ship Science and Technology, 2013, 35(8): 119-122,128. |
| [6] |
杨光, 熊鹰, 黄政. 复合材料螺旋桨双向流固耦合计算[J]. 舰船科学技术, 2015, 37(10): 16-20. YANG Guang, XIONG Ying, HUANG Zheng. Computation of composite propeller's two-way fluid-structure coupling[J]. Ship Science and Technology, 2015, 37(10): 16-20. |
| [7] |
丁永乐. 复合材料螺旋桨结构与水弹性一体化优化设计[D]. 西安: 西北工业大学, 2019.
|
| [8] |
郑楠. 桨前射流对螺旋桨水动力噪声影响的研究[D]. 武汉: 华中科技大学, 2020.
|
| [9] |
刘成勇, 罗凯, 郭庆. 水下航行器对转螺旋桨性能预估[J]. 水下无人系统学报, 2017, 25(6): 437-442. LIU Cheng-yong, LUO Kai, GUO Qin. Performance prediction of contra-rotating propellers for undersea vehicle[J]. Journal of Unmanned Undersea Systems, 2017, 25(6): 437-442. |
| [10] |
敖翔. 非均匀来流下螺旋桨的流固耦合特性分析[D]. 哈尔滨: 哈尔滨工业大学, 2021.
|
| [11] |
JESSUP S D. An experimental investigation of viscous aspects of propellerblade flow[D]. Washington: The Catholic University of America, 1989.
|
| [12] |
缪宇跃, 孙江龙. CFD敞水螺旋桨性能计算分析[J]. 中国舰船研究, 2011, 6(5): 63-68. MIAO Yu-yue, SUN Jiang-long. CFD Analysis of Hydrodynamic Performance of Propeller in Open Water[J]. Chinese Journal of Ship Research, 2011, 6(5): 63-68. |
 2023, Vol. 45
2023, Vol. 45
