极地冰区因其丰富资源和极具战略价值的航道,备受关注。冰区船舶是极地开发的重要载体,普遍采用螺旋桨作为推进器。碎冰区航行船舶螺旋桨要克服碎冰对其产生的阻力影响。为了保证螺旋桨在工作时的安全性,有必要对螺旋桨进行冰载荷数值模拟分析。
目前,国内外主要对螺旋桨与块状冰阻塞、铣削问题进行研究,对块状冰作用下的螺旋桨水动力性能研究较多。VEITCH[1]在实验模型的基础上提出了冰桨接触的基础概念。WANG等[2]对冰桨相互作用下产生的混合载荷进行研究。Kim[3]通过冰锥挤压试验,验证了本构模型为弹性断裂失效模型的冰材料。GUO[4]等分析了不同尺寸冰块与螺旋桨相互作用的流场,确定了螺旋桨水动力性能的变化。Xiong[5]研究了前后多桨冰结构和单桨单个桨叶的遮蔽效应。胡志宽[6]对冰桨接触碰撞问题的5种工况进行了数值计算。孙文林[7]研究了单个冰块在非接触、碰撞和铣削3种工况下对螺旋桨性能的影响。常欣等[8]运用数值模拟了冰桨铣削时桨叶的受力及变形情况。
对碎冰区航行船舶螺旋桨在航行时受到的冰载荷影响的研究较少,本文以极地航行船舶螺旋桨为研究对象,运用基于ALE算法的流固耦合分析方法对螺旋桨与碎冰碰撞过程进行冰载荷计算分析,研究不同冰层厚度、冰区密集度以及螺旋桨进速下对冰载荷大小的影响。
1 数值方法本文采用ALE算法研究螺旋桨与碎冰碰撞这一高度非线性瞬态响应问题,ALE算法下的二维不可压粘性流体的连续性方程和动量方程可表达为:
| $ {u_{i,i}} = 0 ,$ | (1) |
| $ \frac{{\partial {u_i}}}{{\partial t}} = - {c_j}{u_{i,j}} - \frac{1}{\rho }{p_{,i}} - v{\left( {{u_{i,j}} + {u_{j,i}}} \right)_{,j}} + {f_i}。$ | (2) |
式中:
离散化的结构动力学方程为:
| $ {\boldsymbol{M}}{a_t} = {P_t} - {F_t} + {H_t} - C \cdot {v_t} 。$ | (3) |
式中:
| $ {a_t} = {{\boldsymbol{M}}^{ - 1}}\left( {F_t^{ext} - F_t^{{int} }} \right)。$ | (4) |
式中:
本文建立刚体挤压冰锥有限元数值模型[3],以验证冰材料数值模型的可靠性和数值模拟计算方法的有效性。刚体固定在升降装置上以恒定速度对冰锥进行碰撞,冰锥底部采用六自由度固定的边界条件,其冲击装置示意图如图1所示。
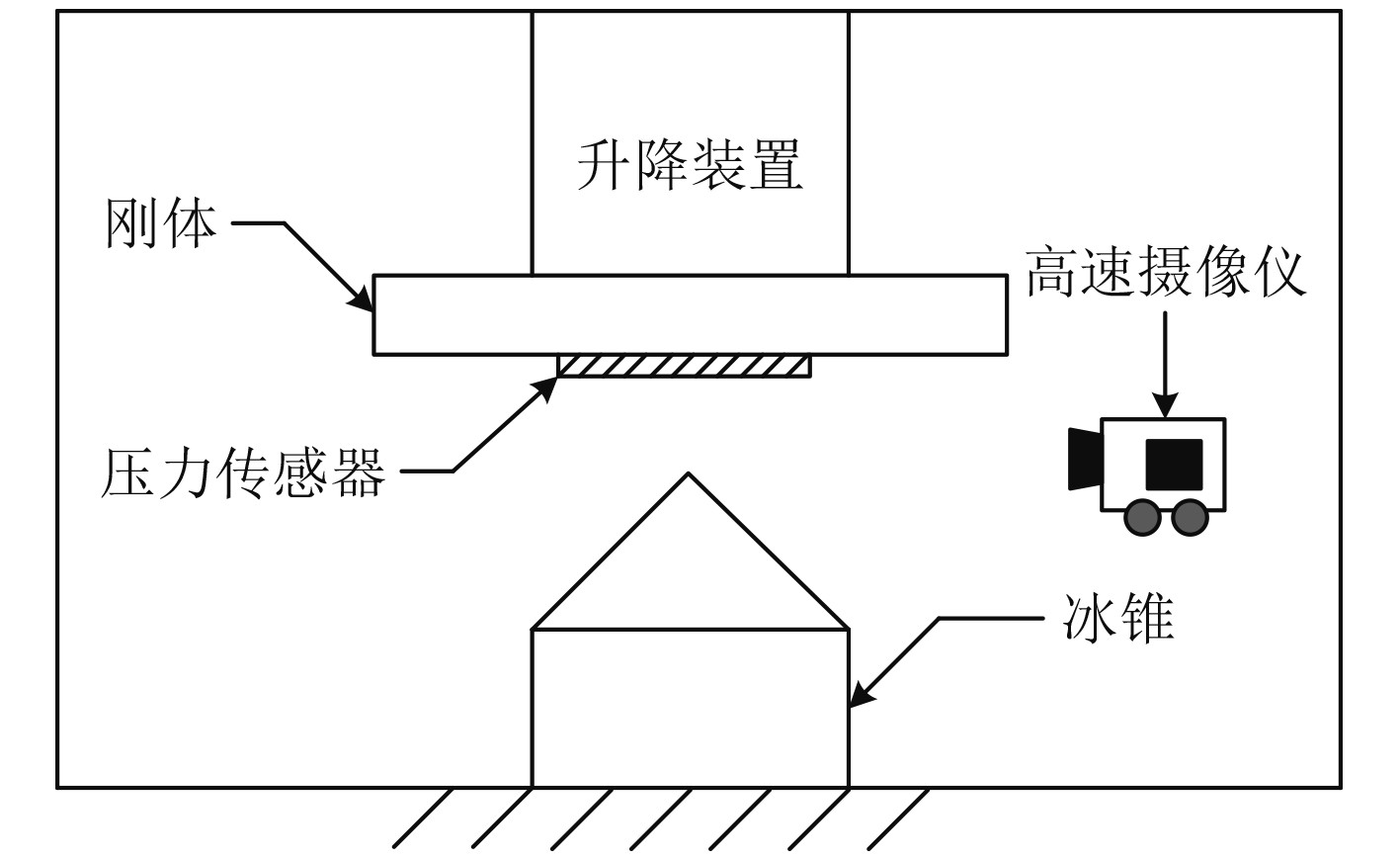
|
图 1 冲击装置示意图 Fig. 1 Schematic diagram of impact device |
在建模过程中,冰锥由2部分组成,上部分为锥角60°、底边半径50 mm的圆锥体,下部分为高10 mm、底边半径50 mm的圆柱体,参考王峰等[9]对网格尺度和时间步长对数值结果影响的收敛性分析,网格单元尺寸为2.5 mm,网格数为10088个。冰锥底部采用完全定位以保证钢板持续作用,材料参数如表1所示。刚体为长200 m,宽200 mm,高10 mm的六面体,网格单元尺寸为5 mm,网格数为3520个,仅允许刚体沿z轴平移运动,材料参数如表2所示。刚体在z方向以100 mm/s的恒定速度撞向冰锥,挤压位移为0.3 mm,计算模型如图2所示。
|
|
表 1 冰材料参数 Tab.1 Ice material parameters |
|
|
表 2 刚体材料参数 Tab.2 Rigid body material parameters |

|
图 2 计算模型 Fig. 2 Computational model |
图3为接触力变化对比曲线。可知,本文计算的数值模拟结果与参考的试验结果基本吻合,表明本文所采用的方法用于冰桨碰撞数值模拟可行有效。
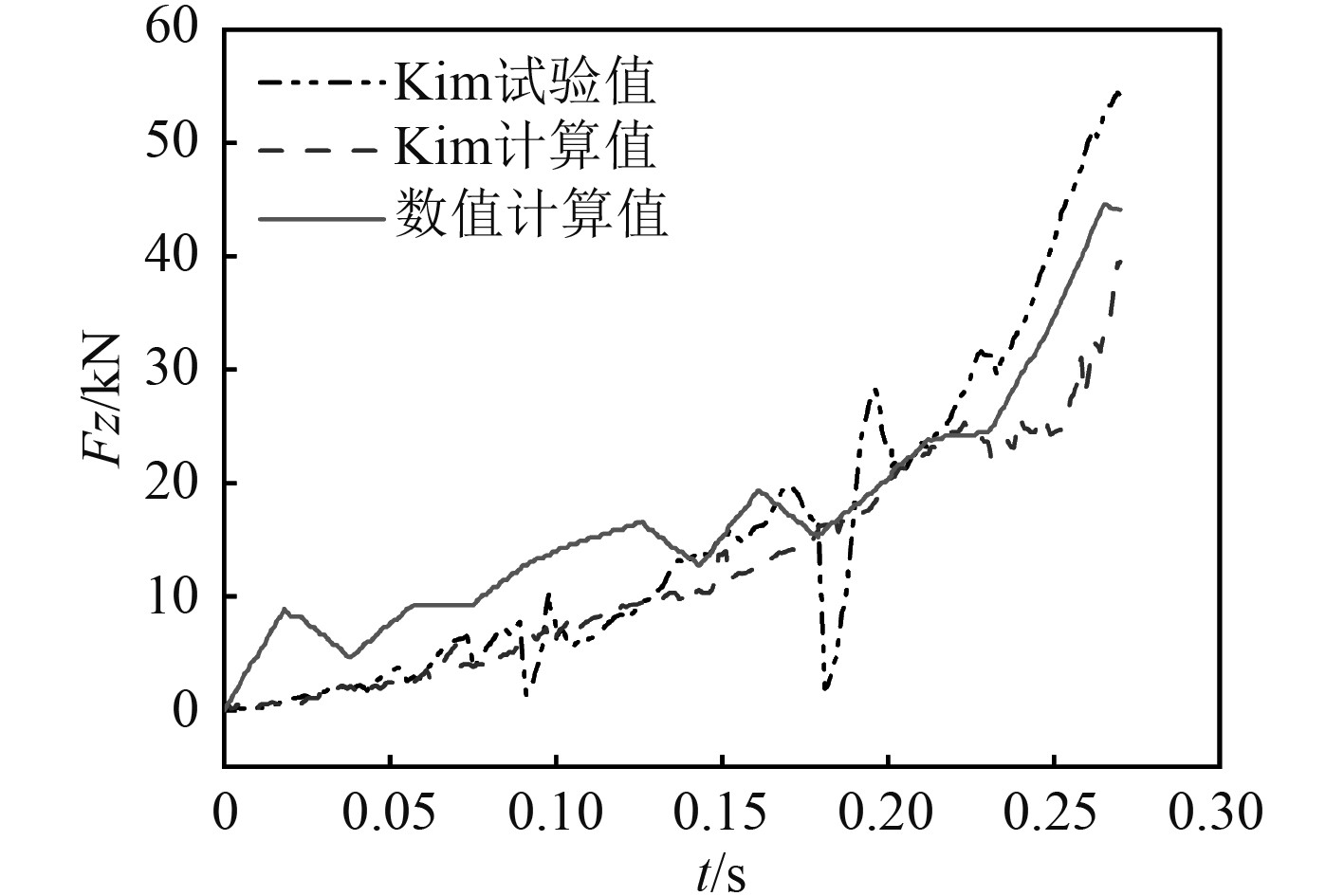
|
图 3 接触力变化对比曲线 Fig. 3 Comparison curve of contact force change |
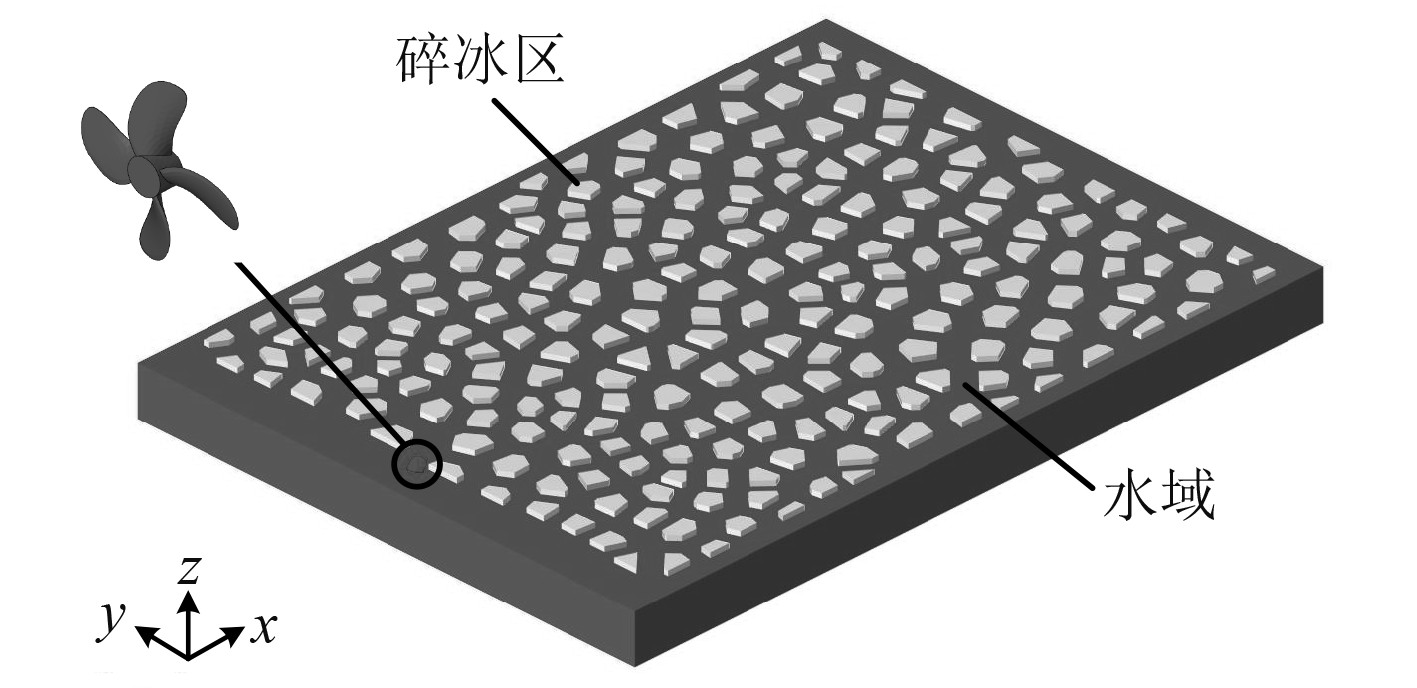
流体域的建模采用长方体结构,包括空气域和水域,两者共面,长宽均为90 m×65 m,水域高6 m,空气域高3 m。划分网格均用尺寸1 m的四面体网格单元,总数共计52650。采用Voronoi细分算法产生随机形状和尺寸的不规则多面体[10],将浮冰区模型导入Hyper-mesh软件进行加厚处理和有限元网格划分,浮冰区由216个非规则的多边形组成,其中浮冰区长宽为60 m×80 m、浮冰位置0.8,后续数值分析中,这4项因素均保持不变。XY平面上网格单元为尺寸0.5 m的六面体网格单元,研究不同密集度和不同厚度的冰对螺旋桨的载荷影响,图4为5/10密集度的碎冰区示意图。

|
图 4 5/10密集度碎冰区 Fig. 4 5/10 dense crushed ice area |
本文的研究对象为整铸式四叶定距桨,主要参数见表3。采用三角形网格单元划分,网格单元尺寸0.1 m,网格数为11464个。螺旋桨位于碎冰区前1 m处,桨毂中心距水平面下2 m,碎冰区X方向距离水域边界为5 m,Y方向距离水域边界2.5 m。图5为螺旋桨-碎冰区有限元模型。
|
|
表 3 螺旋桨参数表 Tab.3 Propeller parameters |
|
图 5 螺旋桨-碎冰区有限元模型(隐去空气域) Fig. 5 Finite element model of propeller ice breaking zone (hidden air domain) |
碎冰区航行船舶螺旋桨会与海冰发生相对作用,其产生的冰载荷与冰的自身性质以及螺旋桨的进速都有较大关系。本文利用控制变量法[11],研究冰层厚度、碎冰区密集度以及螺旋桨进速3个变量与冰载荷的变化关系。通过规律性地修改参数大小,计算不同数值模拟情况下对螺旋桨所受冰载荷的大小影响。
3.1 碎冰区厚度的影响极地海上浮冰的厚度约在0.03 m~1 m之间[12],本文在大量试验结果中,选取冰层厚度为0.30 m,0.45 m,0.60 m,0.75 m和0.90 m五组工况。在保证其他因素不变的情况下,探究不同冰层厚度与冰阻力大小关系。其中碎冰区密集度为5/10,螺旋桨进速1.5 m/s、进速系数0.13、转速1.5 r/s,计算时间为20 s。
设计的数值模型主要考虑螺旋桨在浮冰区前进方向的浮冰阻力,即X方向的冰载荷。不同冰层厚度下冰载荷-时间历程曲线如图6所示,对比5个不同工况的计算结果可以看出,在冰层厚0.30~0.60 m时,冰载荷成离散分布,冰层厚度为0.75~0.90 m时,冰载荷成连续分布,随冰层厚度的增加,冰载荷在螺旋桨上的作用时间增加。
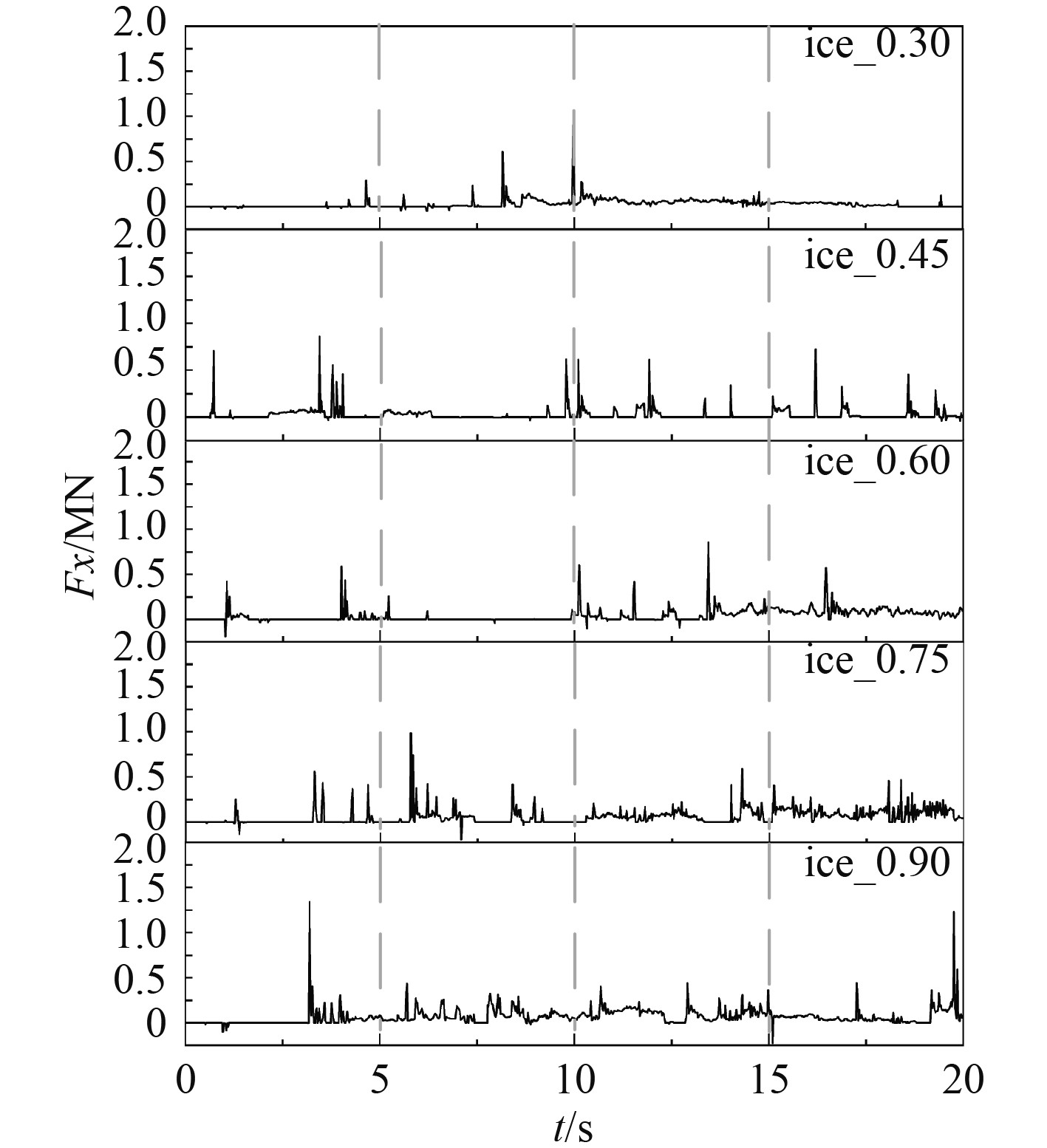
|
图 6 冰载荷-时间历程图(不同冰厚) Fig. 6 Ice load time history diagram (different ice thickness) |
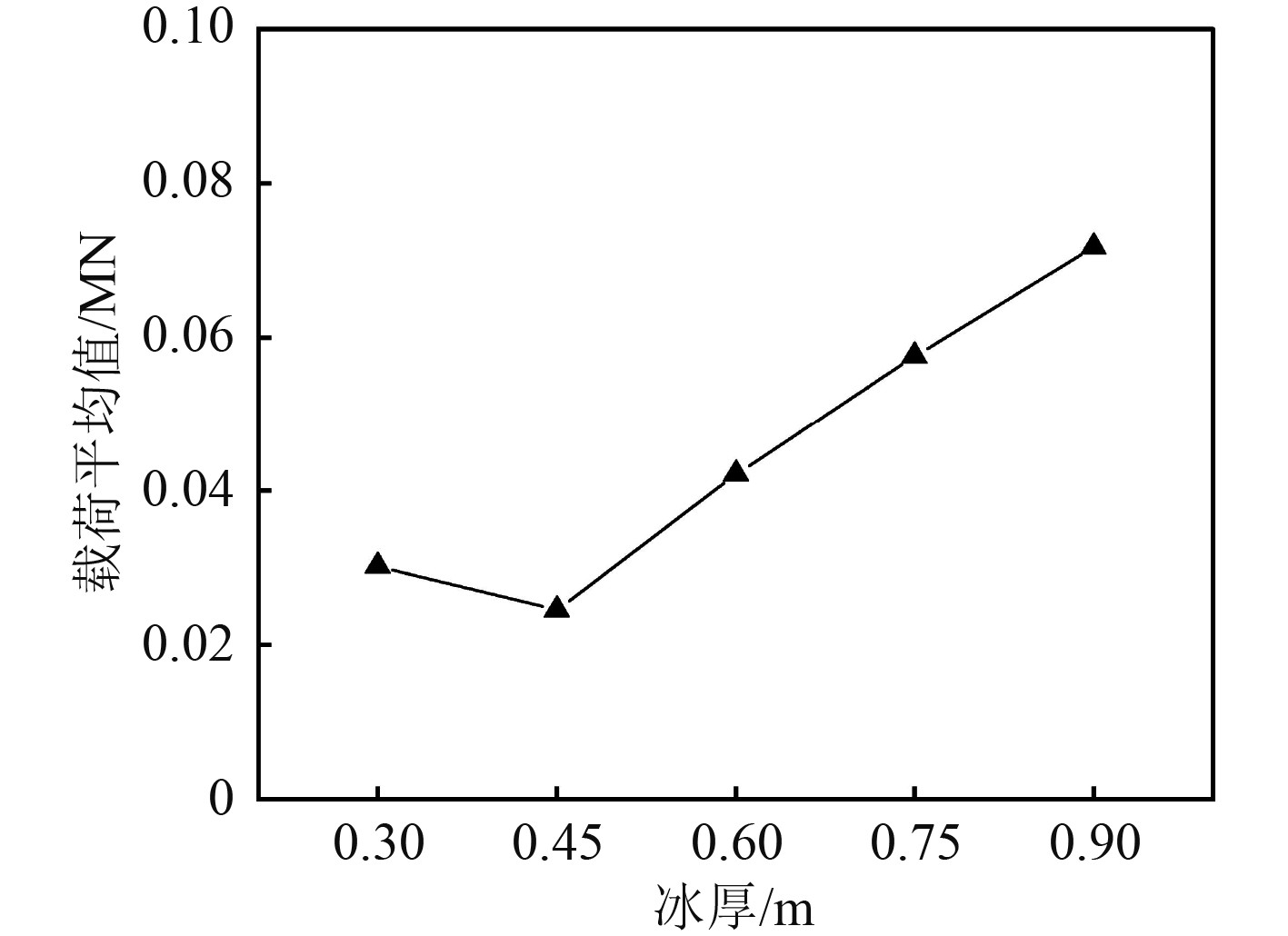
载荷平均值如图7所示。可以看出:冰厚0.30~0.45 m,冰厚越大,平均值越小;当冰厚大于0.45 m,平均值与冰厚呈正相关性;当冰厚为0.90 m时,载荷平均值为0.07MN,比0.30 m冰厚时增加了3倍。载荷最大值如图8所示,冰厚为0.30~0.60 m之间时,最大值变化幅度较小,最大差值仅为0.04 MN;冰厚为0.60~0.90 m时,增长速率较大,最大值增加0.48 MN。
|
图 7 不同冰厚下冰载荷平均值 Fig. 7 Average value of ice load under different ice thickness |

|
图 8 不同冰厚下冰载荷最大值 Fig. 8 Maximum ice load under different ice thickness |
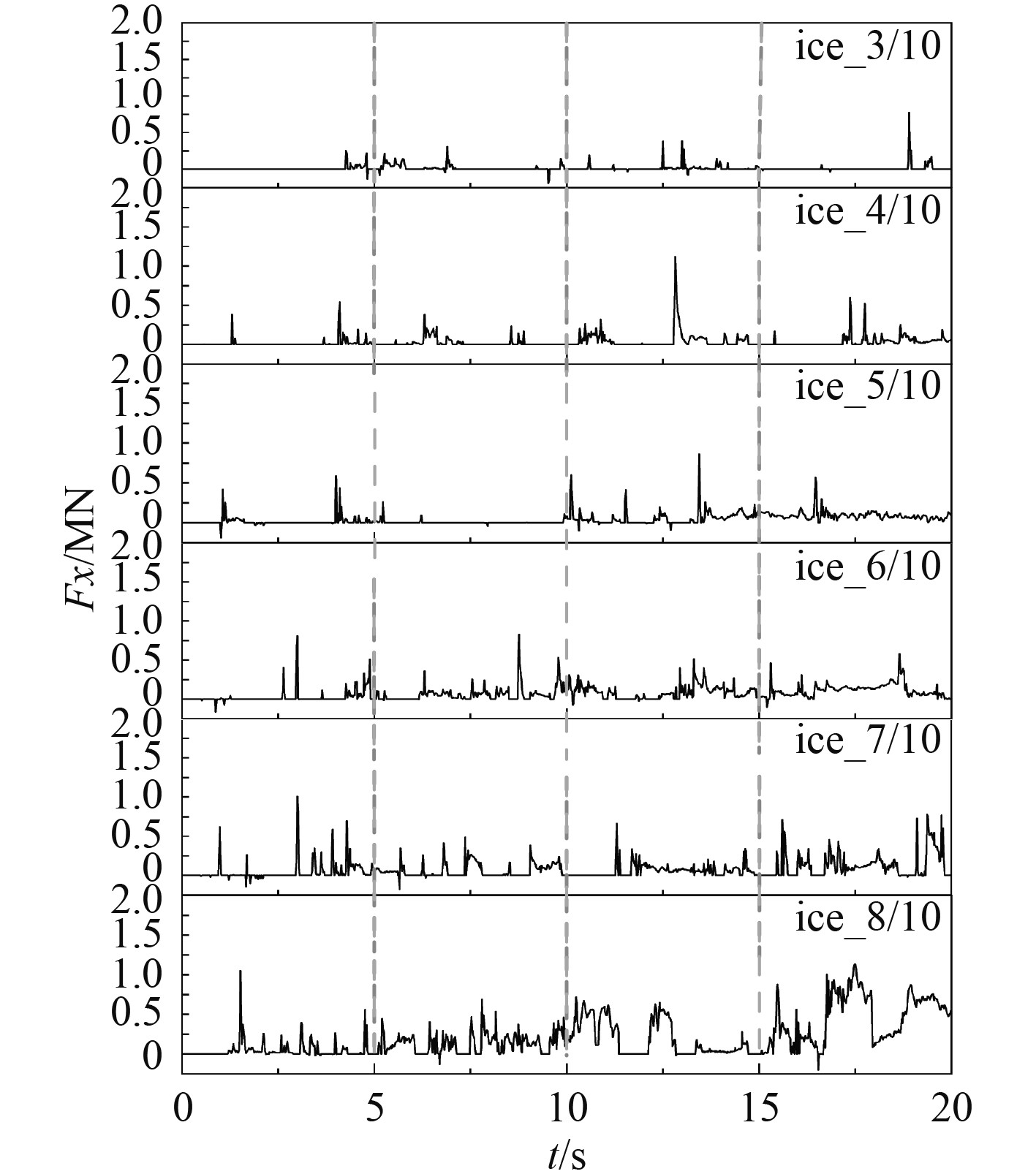
冰的密集度是指在给定区域面积内,冰体面积所占区域总面积的比例。本文将保持螺旋桨在进速1.5 m/s、进速系数0.13、转速1.5 r/s以及冰厚0.6 m不变的条件下,研究冰载荷的密集度敏感性。选取密集度为3/10,4/10,5/10,6/10,7/10,8/10的6组工况,不同密集度下冰载荷-时间历程曲线如图9所示。可知,螺旋桨受冰体的撞击频率随浮冰密集度的增加而增加,当密集度为3/10~5/10时,冰载荷为离散性载荷,当密集度大于7/10时,冰载荷会转变为持续性的载荷。
|
图 9 冰载荷-时间历程图(不同密集度) Fig. 9 Ice load time history diagram (different densities) |
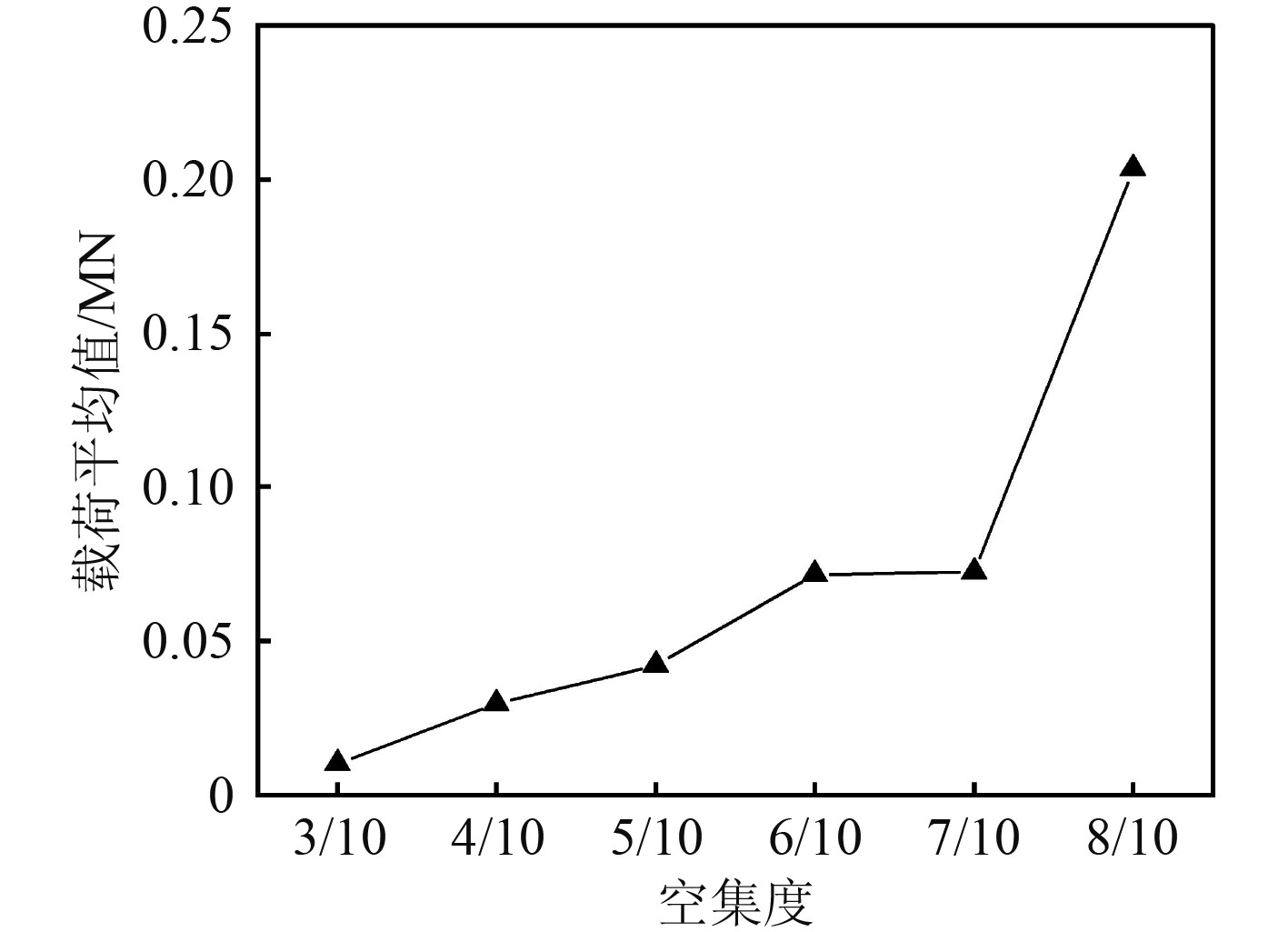
载荷平均值和载荷最大值如图10和图11所示。随着密集度的增加,平均值表现为上升趋势。3/10~7/10密集度时,平均值增长幅度较小,6/10密集度和7/10密集度的平均值近似;当密集度大于7/10时,冰载荷影响剧烈。冰载荷最大值与密集度不呈递增关系,在4/10~6/10密集度范围内,最大值随密集度的增加而减小;密集度为6/10~8/10时,最大值出现了上升趋势,8/10密集度时,最大值增至1.13 MN。
|
图 10 不同密集度下冰载荷平均值 Fig. 10 Average value of ice load under different density |

|
图 11 不同密集度下冰载荷最大值 Fig. 11 Maximum ice load under different density |
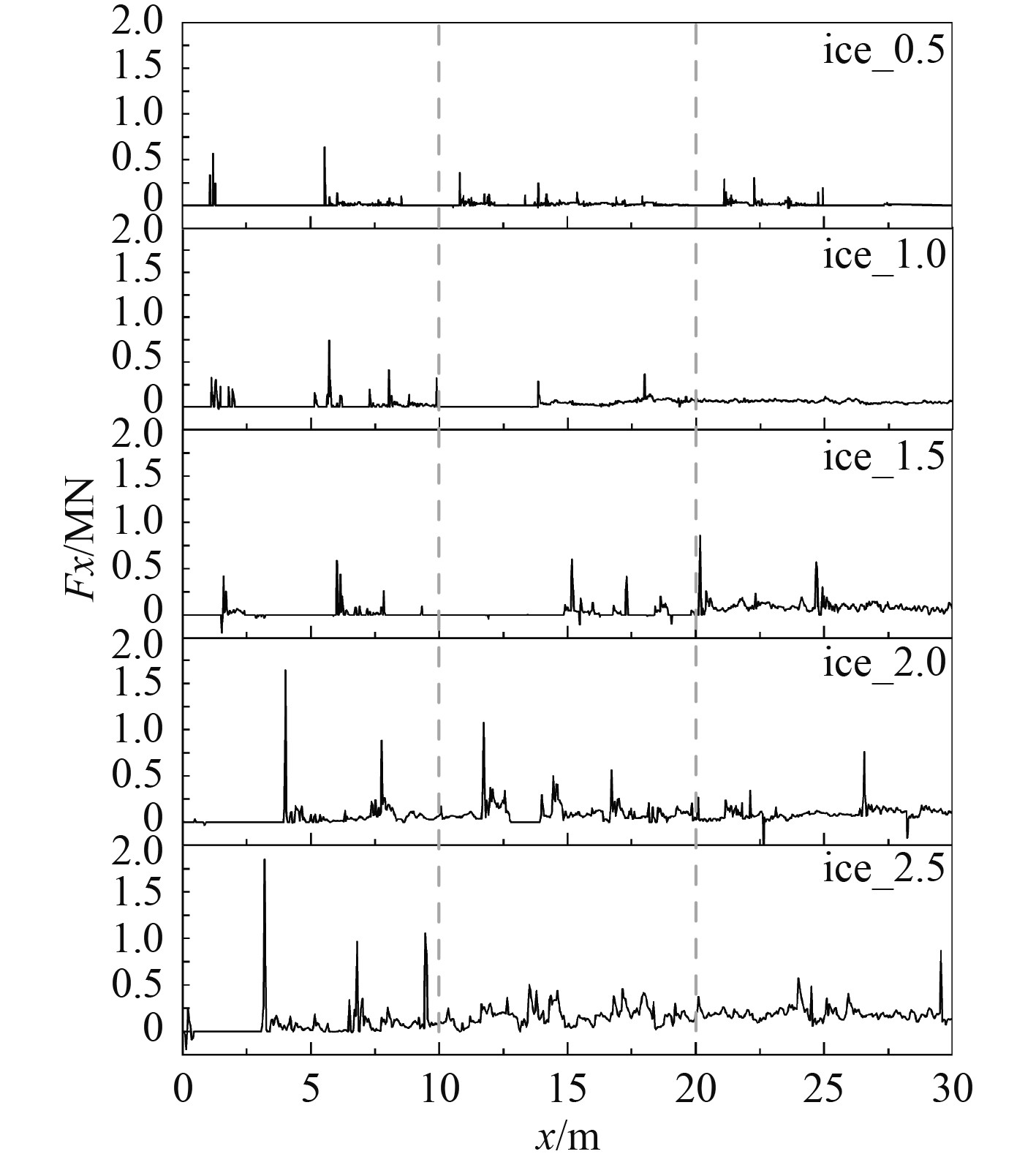
在浮冰区物理参数一定的情况下,螺旋桨与碎冰的碰撞过程除了受到冰的影响外,还与螺旋桨自身的进速有关。保持冰厚0.6 m,碎冰区密集度为5/10,设置0.5 m/s,1.0 m/s,1.5 m/s,2.0 m/s,2.5 m/s五种进速,研究碰撞过程中螺旋桨的进速与冰载荷的关系。其中1.5 m/s为基准工况进速,进速系数0.13,总碰撞位移为30 m,图12为不同进速下冰载荷路程图。可知,冰载荷随着进速的增加而愈加明显,当进速大于1.5 m/s后,冰载荷会转变为持续性的载荷。
|
图 12 冰载荷路程图(不同进速) Fig. 12 Ice load path map (different speeds) |
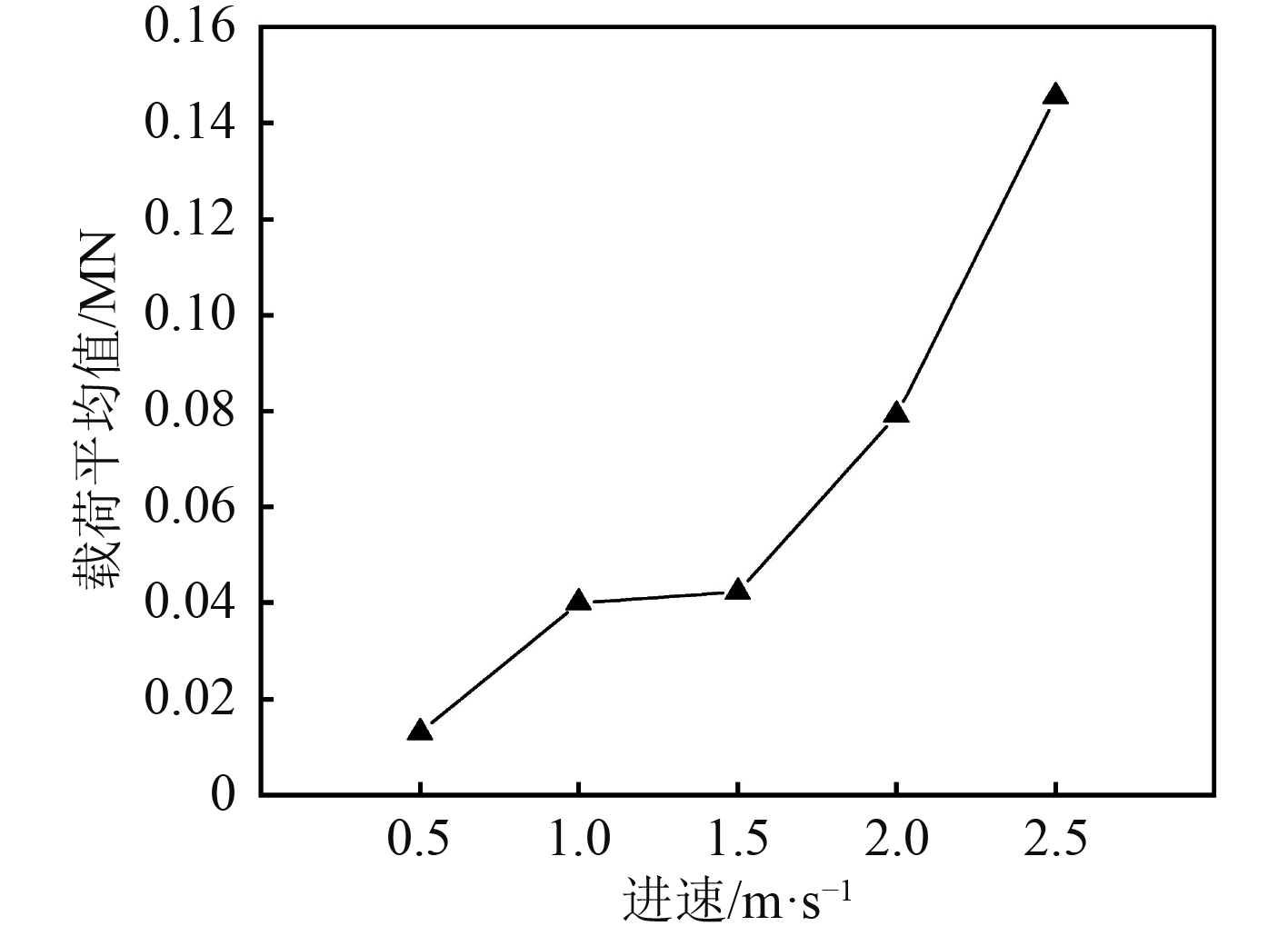
图13和图14为不同进速下碰撞过程中的载荷平均值和载荷最大值。可知,随着进速增加,平均值和最大值均呈现上升趋势。此外,进速1.0~1.5 m/s时,平均值增长速率较缓;进速1.5~2.5 m/s时,平均值增长速率较大,提升了0.10 MN。进速在1.5~2.0 m/s时,最大值增长速率最大,后者约为前者的1.91倍;进速在0.5~1.5 m/s以及2.0~2.5 m/s时,最大值增加速率相对较平缓,但整体呈上升趋势。
|
图 13 不同进速下冰载荷平均值 Fig. 13 Average ice load under different speeds |

|
图 14 不同进速下冰载荷最大值 Fig. 14 Maximum ice load under different speeds |
1)本文基于ALE算法的流固耦合分析方法进行冰桨数值分析是有效的,为实际船舶螺旋桨在碎冰区航行提供一定的参考。
2)螺旋桨-冰碰撞过程中,冰载荷与冰厚基本呈正相关性,冰厚大于0.75 m时,冰载荷成连续分布且最大值增长迅速。
3)随着密集度的增加,平均值表现为上升趋势,最大值与密集度不呈递增关系。当密集度大于7/10时,冰载荷影响剧烈,在该工况下对螺旋桨造成的损伤较大。
4)螺旋桨进速越大,冰载荷越大。进速大于1.5 m/s后,冰载荷会转变为持续性载荷且增长迅速。
5)在实际冰区船舶航行时,选择合适冰层厚度、密集度和螺旋桨进速,能有效避免产生过大冰载荷对螺旋桨的影响。
| [1] |
VEITCH B . Predictions of ice contact forces on a marine screw propeller during the propeller-ice cutting process[J]. Acta Polytechnica Scandinavica Mechanical Engineering, 1995.
|
| [2] |
WANG J, AKINTURK A, BOSE N. Numerical prediction of propeller performance during propeller-ice interaction[J]. Marine technology, 2009, 46(3): 123-139. |
| [3] |
KIM H. Simulation of Compressive ‘Cone-Shaped’ Ice Specimen Experiments using LS-DYNA ®[C]. Proceedings of the International Ls-Dyna Users Conference, 2014.
|
| [4] |
GUO Chun-yu et al. China Ocean Eng. , 2020, Vol. 34, No. 1, P. 30–45.
|
| [5] |
XIONG Wei peng, WANG Chao, WANG Chun hui, et al. Analysis of shadowing effect of propeller-ice milling conditions with dynamics[J]. Ocean Engineering, 2020, 195.
|
| [6] |
胡志宽. 冰载荷下螺旋桨静力分析及冰与桨碰撞动力响应研究[D]. 哈尔滨: 哈尔滨工业大学, 2014.
|
| [7] |
孙文林. 冰区航行船舶螺旋桨强度研究[D]. 哈尔滨: 哈尔滨工程大学, 2016.
|
| [8] |
常欣, 王锡栋, 王超, 孙盛夏. 螺旋桨在冰桨铣削下的强度计算分析[J]. 哈尔滨工程大学学报, 2017, 38(11): 1702-1708. |
| [9] |
王峰. 基于粘聚单元模型的海洋结构物与平整冰相互作用数值研究[D]. 上海: 上海交通大学, 2019.
|
| [10] |
涂勋程. 极地物探船冰阻力预报及参数敏感性研究[D]. 镇江: 江苏科技大学, 2019.
|
| [11] |
孙国威. 冰荷载作用下钻井立管力学性能分析与设计[D]. 杭州: 浙江大学, 2020.
|
| [12] |
HILLIER B. Space is the Machine [M]. Cambridge University Press Cambridge UK, 1996
|
 2023, Vol. 45
2023, Vol. 45
