2. 中国船级社,北京 100010;
3. 武汉理工大学 船海与能源动力工程学院,湖北 武汉 430063
2. China Classification Society, Beijing 100010, China;
3. School of Naval Architecture, Ocean and Energy Power Engineering, Wuhan University of Technology, Wuhan 430063, China
化学品船在货物装卸、换货洗舱、人员保护等方面相比其他船舶危险性更大,一旦化学品船因液货舱爆炸发生化学品货物泄漏造成事故,不仅会威胁船员及周边民众的生命安全,而且破坏海洋环境,这是其他运输方式都不具备的反面特质[1]。因此对化学品船发生液舱爆炸的事故进行过程仿真,研究冲击波载荷传播规律,掌握泄爆参数对泄爆能力的影响,有助于在化学品船设计阶段对结构进行合理优化,加强液货舱的被动泄爆能力,最大程度减小液货舱爆炸造成的损伤。
化学品船爆炸事件,实际上可归结于油气爆炸一类问题。对其过程进行仿真,将油气爆炸的爆炸当量转化为等效TNT下的冲击载荷可以通过经验公式计算出来,剩余的就是舱室内爆下的结构响应问题。Anderson等[6]依据实验提出准静态压力方法,并给出各项参数的计算方法。Kurki T等[7]参考准静态压力方法把初始反射压力累加在准静态压力曲线上,并对舱室内爆炸采用此方法做了数值计算。刘慧泉等[8]通过仿真研究了舱室内爆炸结构响应,主要分析变形、破坏模式、吸能效果等结果。化学品船货舱爆炸时,板架结构除了承受和空爆下相同的初始冲击波外,还会受到反射冲击波和冲击波汇集作用的多重影响,因此破坏性更加强烈。爆炸所产生的高温高压产物无法及时从这种封闭的环境中流出,使舱内存在一个恒定的压力持续作用于结构,迫使结构吸收更多的能量,产生变形或者破坏[9]。所以对封闭舱室中等效爆炸载荷产生的响应进行研究有切实的意义,能够为化学品船爆炸过程下的结构优化设计提供可行的技术方案。
本文参照化学品船液货舱爆炸事故,通过仿真方法分析了液货舱爆炸时冲击波载荷泄爆的传播规律,并掌握了泄爆口大小和距离对泄爆能力的影响,通过实船模型的泄爆计算,评估泄爆效率,并形成了基于基准数法[10]的实船泄爆能力优化方案。
1 化学品船液货舱泄爆参数仿真 1.1 仿真模型建立根据计算需要,建立3个有限元模型,建立与单个液货舱室同等体积的简化带反射面的欧拉空气域模型(L=8400 mm,B=6200 mm,H=6400 mm),根据计算对称性取1/4模型和1/2模型进行计算。空气的密度是1.225 kg/m3,比内能为2.068×105 J/kg,爆点位于整个模型的中心(L=0 mm,B=0 mm,H=3200 mm),货舱口(等效泄爆口)位于模型的上方中心位置(L=0 mm,B=0 mm,H=6400 mm)。空气域采用高阶的欧拉—FCT算法进行计算[2],为了得到载荷所具有的规律,在部分位置布置了测试点。
1.2 货舱口大小对泄爆能力的影响分析在化学品船液货舱爆炸中,冲击波载荷主要通过破坏甲板货舱盖,形成与空气联通的泄爆口进行泄爆[3]。对不同半径的货舱盖的泄爆效率进行仿真分析,使用1/4空气域模型进行计算,模拟装药量100 kg,形成的舱内总能量4.8426E14J,泄爆口位置位于舱室中心正上方h=6400 mm,装药位置位于舱室中心h=3200 mm,根据泄爆口半径从0~1000 mm变化设立8个工况。统计在10 ms中泄出的能量,如表1所示。
|
|
表 1 不同半径泄爆口泄爆能力对比 Tab.1 Energy release efficiency of different explosion vent radius |
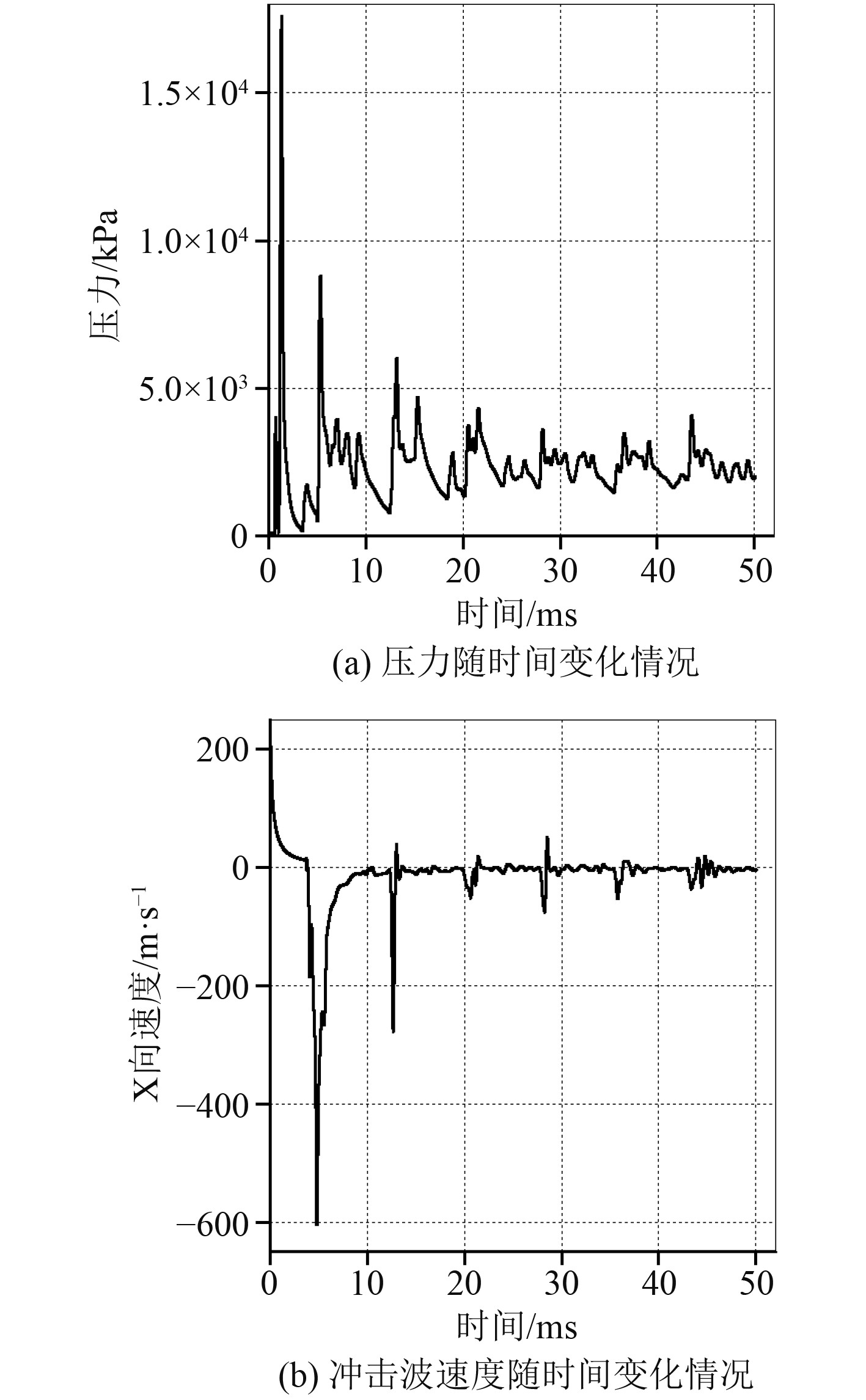
图1(a)为工况5泄爆口中心位置压力随时间变化情况。从图中可知,在初始阶段,泄爆口中心受到初始冲击波、一次、二次以及三次等各种反射波的作用,但是当20 ms之后,该点的压力趋于平稳状态,即表示舱室基本已处于准静态状态。每一次的压力峰值也伴随着冲击波速度下降,都存在对应的关系。图1(b)为工况5爆源中心位置速度随时间变化情况。同样可以看出,泄能速度在20 ms之后基本没有了跳跃式的变化,速度的变化如同运用伯努利方程求解典型的“小孔流水”问题的流水速度变化[4],表示在10 ms之后,舱内处于准静态状态[2]。
|
图 1 工况5中泄爆口中心位置测量曲线 Fig. 1 Explosion vent center curve in condition 5 |
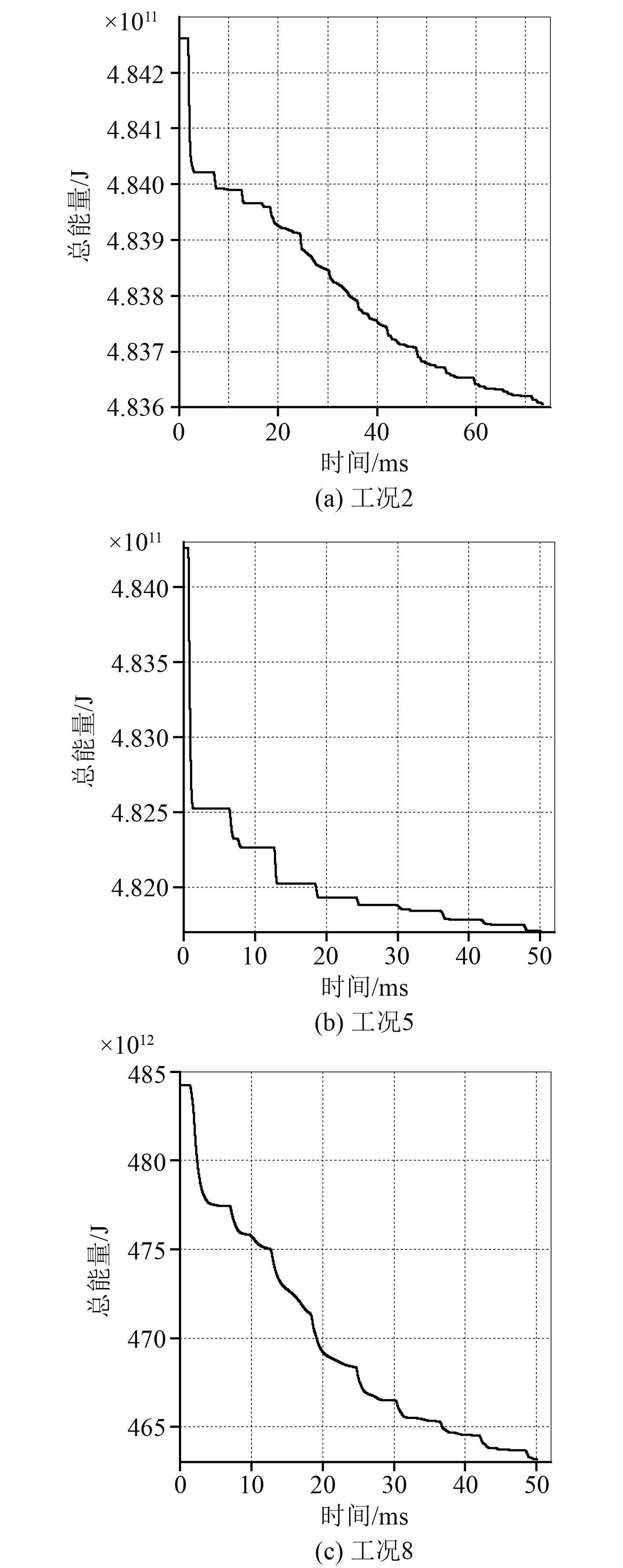
图2为不同工况能量随时间变化情况。在第1次超压峰值产生后泄出了前20 ms能量的70%,第2次超压峰值产生后泄出了前20 ms能量的20%,10~20 ms过程中仅泄出10%的能量,20 ms之后总能量随着时间沿着类似于指数函数的曲线减小,表明在20 ms之后,能量趋于平稳衰减,也表明此时泄爆口以一种准静态的方式与外界发生能量交换。
|
图 2 不同工况中能量随时间变化情况 Fig. 2 Energy-time curve in different conditons |
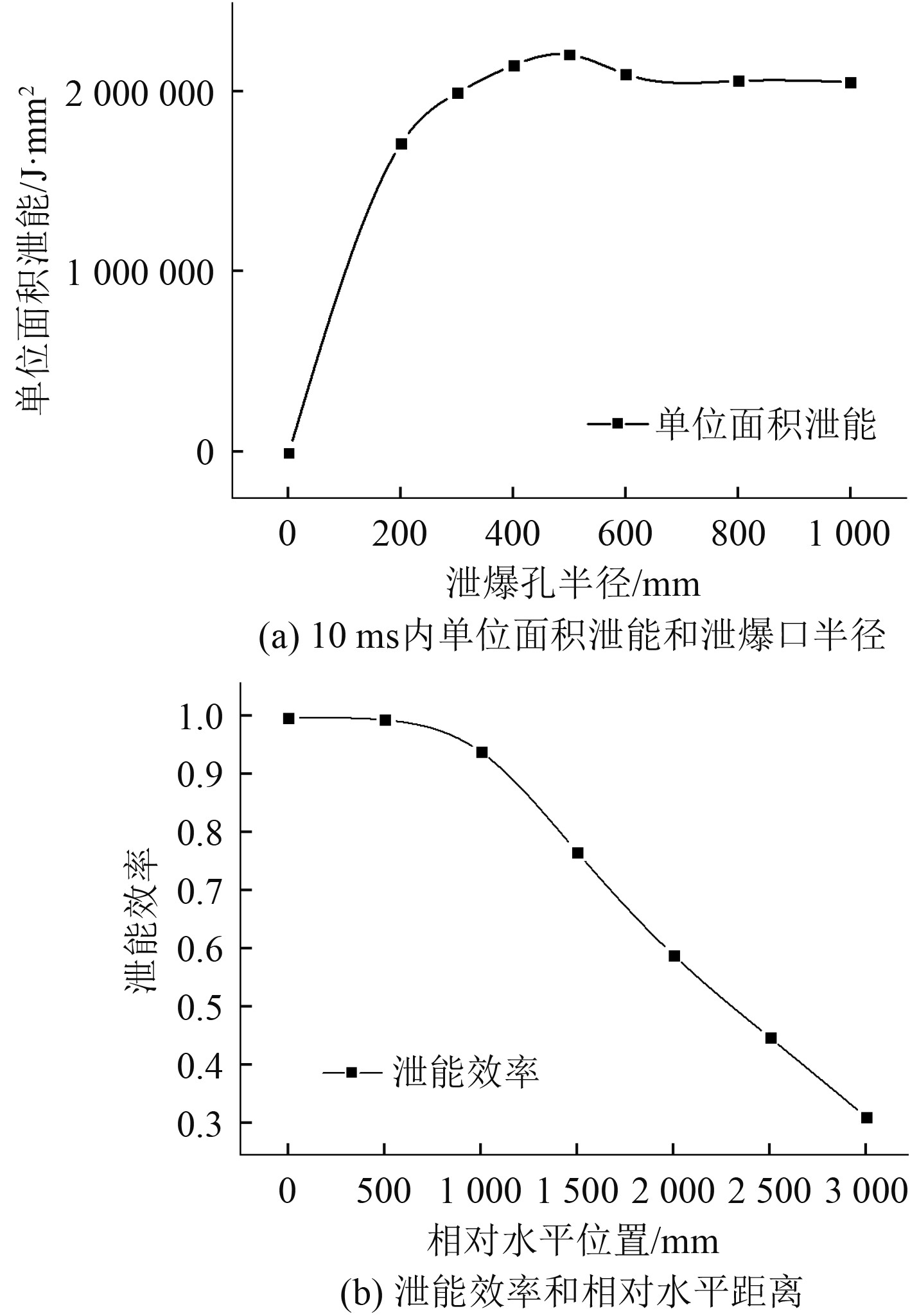
图3(a)为10 ms内单位面积泄能效率与泄爆口半径的插值曲线。可以看出,当泄爆口半径小于500 mm时,随着泄爆口的增大,10 ms内单位面积的泄能越大。当泄爆口半径大于500 mm时,随着泄爆口半径增大,10 ms内单位面积的泄能逐渐减小,并逐步趋向于一个极限。
|
图 3 不同参数的统计规律图表 Fig. 3 Statistical graph of different parameters |
通过在舱室模型沿船长方向不同位置布置爆点,计算货舱口与爆源的相对位置对泄爆能力的影响。根据模型的对称一致性,使用1/2空气域模型进行计算,装药量100 kg,形成的舱内总能量2.2704E14J,泄爆口半径500 mm,泄爆面积7.85E5 mm2,泄爆口位置位于舱室中心正上方h=6400 mm,装药位置位于舱室中心h=3200 mm,沿船长方向布置0~3000 mm位置变化设立7个工况。0代表装药位置在舱室中心,3200 mm代表装药位置在货舱距离最远端,以工况9 15 ms内单位面积泄能为泄能效率(以下简称EV)1,计算其他工况的泄能效率EV计算结果如表2所示。
|
|
表 2 爆源与泄爆孔相对位置的泄能效率对比 Tab.2 Comparison of energy release efficiency between the relative position of the explosion source and explosion vent |
从表2可知,仅考虑相对距离,爆点离泄爆孔越近,泄能效率EV越高;爆点离泄爆孔越远,泄能效率EV越低,泄能效率EV的高低主要体现在第1次超压峰值能量的泄出上。
图3(b)为泄能效率EV和相对水平距离的插值曲线,当两者的相对水平距离小于500 m时,泄能效率EV变化不大;当两者的相对水平距离大于1000 mm后,泄能效率EV与相对水平位置呈线性减小。产生这种情况的原因主要是考虑到含能较大的一次波和二次波没有直接泄出,被舱壁反射所致[5]。
2 实船液舱泄爆的评估及优化 2.1 实船液舱的泄能效率评估上述计算得到的货舱口大小和货舱口与爆源相对水平位置对泄能的分析,解决了相关的规律性问题,但是没有考虑在实船发生液货舱爆炸时的2个基本问题:一是爆点的不确定性;二是实船中单个舱室往往布置2个的货舱口,形成双泄爆口。因此需要设计不同工况对实船中的情况进行具体分析,在货舱中对不同位置的爆炸情况进行危险性评判。
根据对称性取1/2空气域模型,考虑船长、船宽2个维度的特性,通过不同位置布置爆点计算泄爆效率。建立以舱室中心为基准点的坐标系,x轴沿船长方向,y轴沿船宽方向,根据实船货舱口布置,分别位于(0,0)(R=300 mm)和(−2700,0)(R=500 mm)的泄爆口。
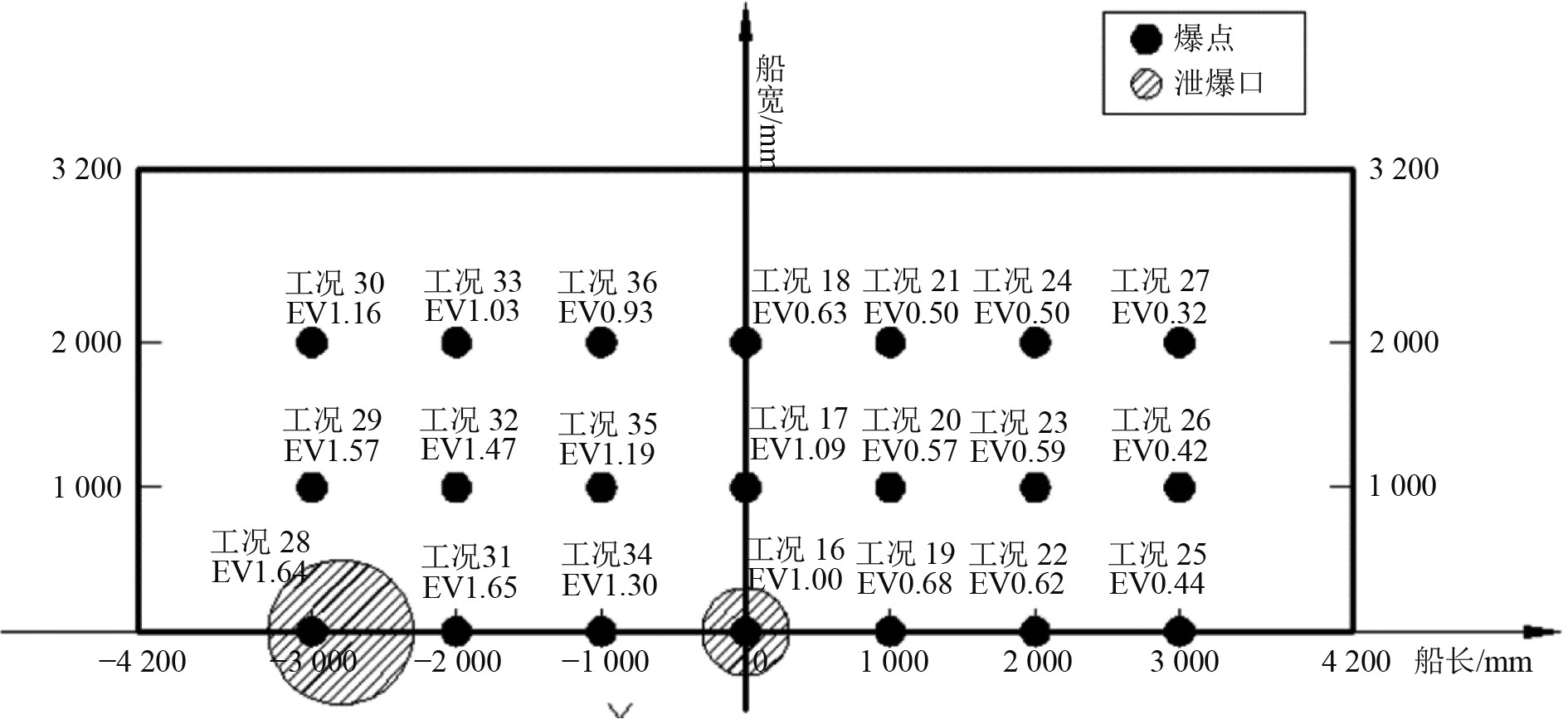
以不同的装药位置设置工况16~工况36,其中工况16装药位置位于舱室正中,作为整个工况计算的基准,设为基准效率1。本文计算只考虑爆点在水平位置不同分布对最终结果的影响,不对高度方向的影响进行考量。装药量100 kg,高度H=3200 mm,舱内总能量4.5408E14 J。在统计泄能时,由于本次工况并非对称布置,采用了1/2空气域模型,因此在能量泄出时,会有较多的反射波成分,能量下降并不会像图2中呈现明显的阶跃状态。取前10 ms的能量泄出量作为判断泄能效率的指标,不同爆点的泄能效率分布如图4所示。可知,相对位置不同时,泄能效率有很大的差异。仅考虑水平方向的距离,爆点离泄爆孔越近,泄能效率越高;爆点离泄爆孔越远,泄能效率越低。
|
图 4 实船液舱的泄爆效率计算 Fig. 4 Cargo hold energy release efficiency result |
根据化学品船液舱爆炸的不确定性,爆点位置根据实船的破坏情况反推才能得知,因此只有掌握了不同位置的泄爆规律,才有可能优化设计,减轻爆炸对结构的破坏。在工况19~工况27的情况下发生爆炸,由于爆点远离泄爆口,整体泄能效率较低,可能加大对结构的破坏。因此,需要考虑改善舱室右侧的泄能情况。在现有条件下,综合考虑船上的布置及结构强度,最直观的方法是增加泄爆口面积。在(2700,0)处增加一个R=300 mm的泄爆口,并对工况16~工况27进行重新计算,命名为工况16'~工况27'。
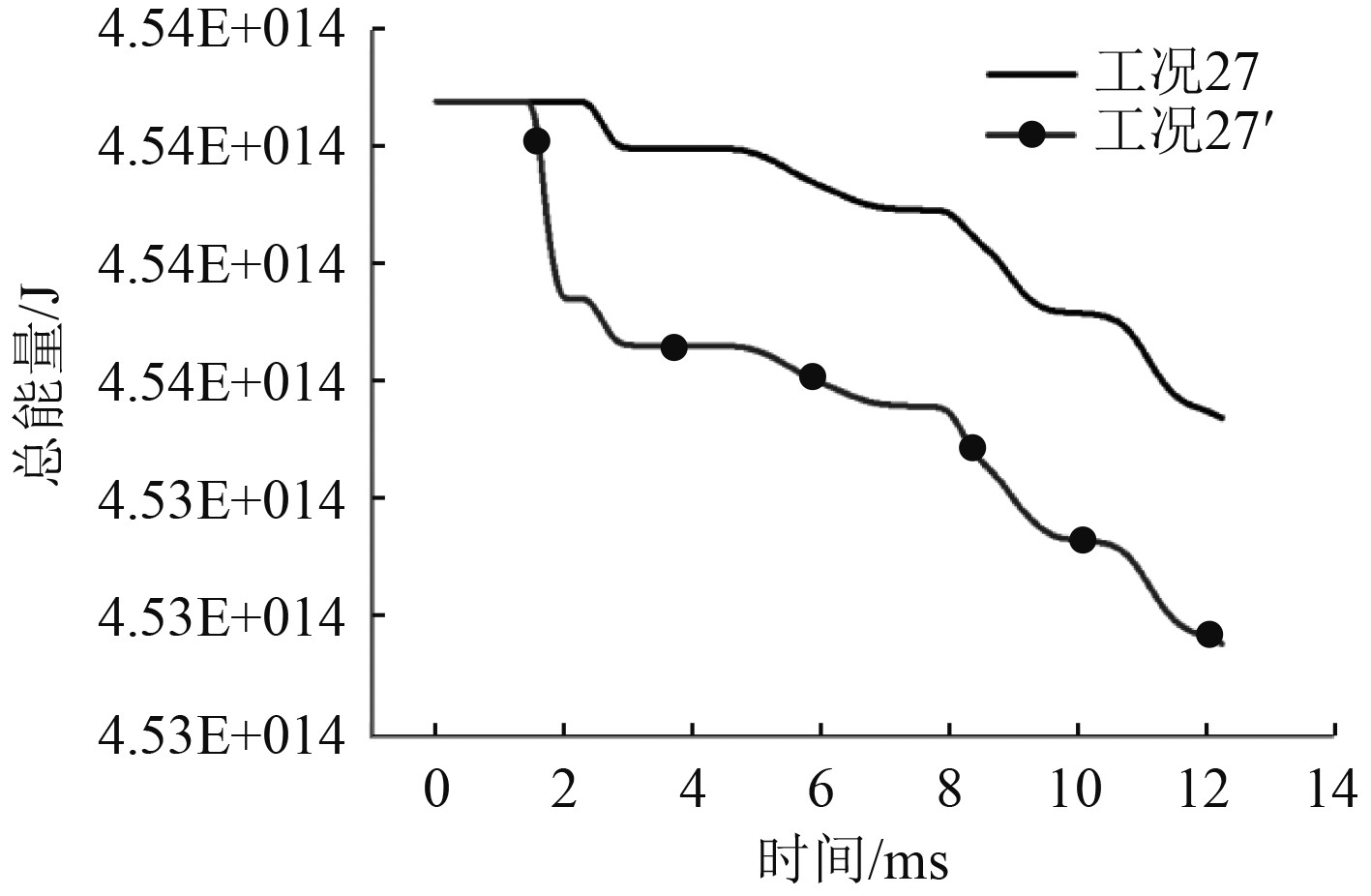
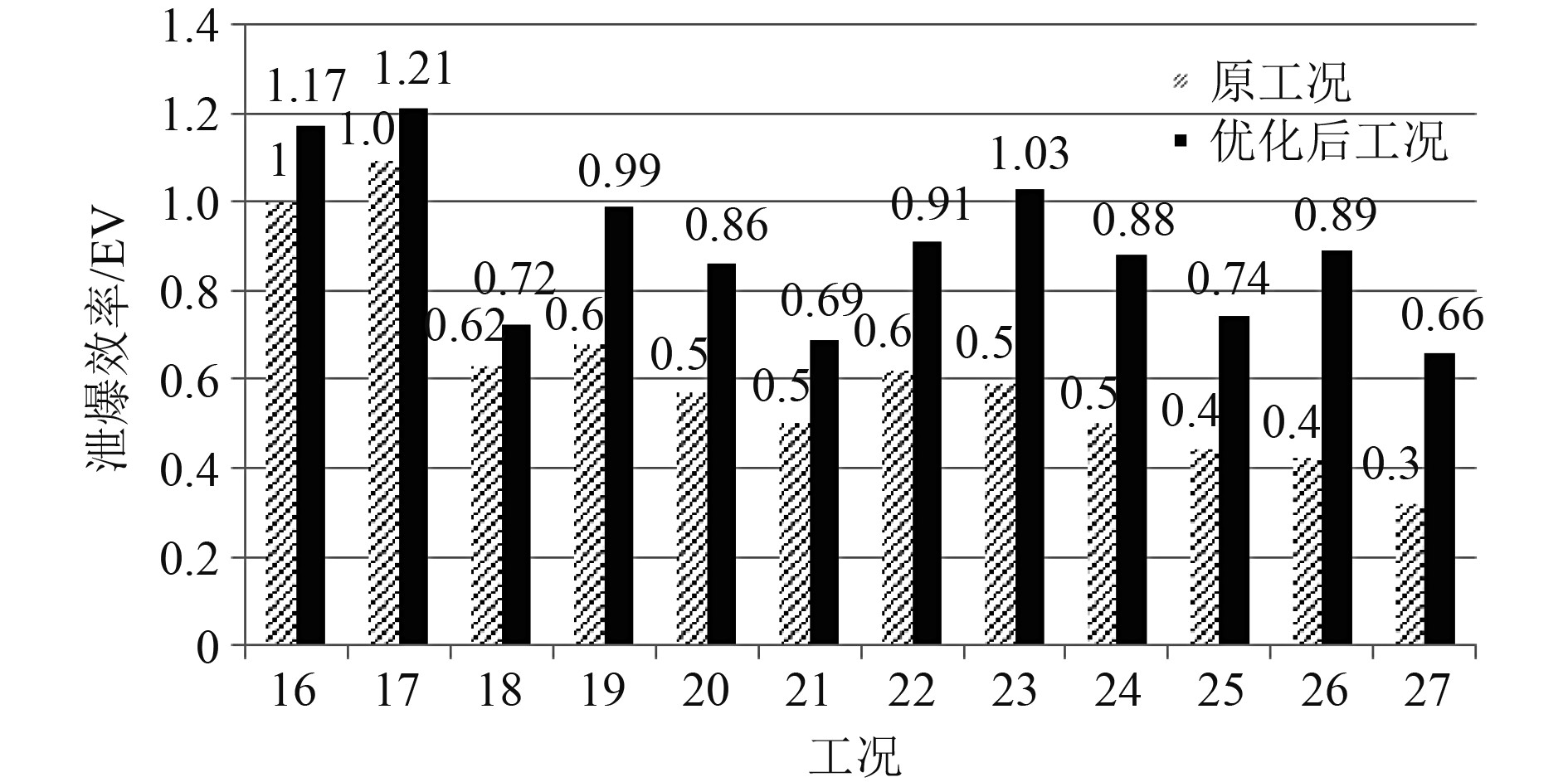
图5为工况27与工况27'的能量随时间变化对比分布。增加了新的泄爆口后,总体的能量泄出速度加快。图6为优化前后的舱室泄爆效率的对比。新增了一个泄爆口,泄爆效率影响较大的区域是新增泄爆口周围的工况。
|
图 5 工况27优化后能量对比 Fig. 5 Comparison of condition 27 after optimizing |
|
图 6 优化前后舱室泄爆效率对比 Fig. 6 Comparison of energy release efficiency result after optimizing |
本文对化学品船液货舱的泄爆过程进行了多工况的计算分析,计算了泄爆口大小和爆源泄爆口间的相对水平位置2个参数对泄爆效率的影响,评估了实船单个液货舱爆炸的泄爆效率,并形成了基于基准数法的实船泄爆能力优化方案,得到以下结论:
1)在液货舱内爆发生的过程中,相同时间内泄出能量随着泄爆口面积增大而增大,当泄爆口面积到达一定值后,单位面积的泄能效率约趋向于一个极限。
2)当爆点离泄爆口越近,在相同时间下泄出能量更多,且这部分能量主要体现在第1次的超压峰值能量泄出的过程中,从第2次超压开始泄能效率趋于一致。
3)在实船的泄爆过程中,爆点距离泄爆口越近,泄能效率最高;距离泄爆口越远,泄能效率最低。
4)在泄爆效率较低的位置开设新的泄爆口,这种泄爆优化方案是有效可行的。
| [1] |
黄东伟, 陆月, 潘甜. 中小型化学品船甲板强横梁端部节点形式[J]. 船海工程, 2021, 50(5): 37-41. DOI:10.3963/j.issn.1671-7953.2021.05.008 |
| [2] |
徐敬博. 舱室内爆载荷作用下结构动态响应相似规律研究[D]. 武汉: 武汉理工大学, 2019.
|
| [3] |
周桂华, 李攀, 陈倩清, 等. 化学品船液货舱泄爆过程的参数仿真[J]. 船舶工程, 2017, 39(S1): 68-72. DOI:10.13788/j.cnki.cbgc.2017.S1.068 |
| [4] |
张玉磊, 陈华, 韩璐, 等. 泄压口面积对温压炸药内爆炸准静态压力的影响[J]. 火炸药学报, 2020, 43(5): 521-525. ZHANG Yulei, CHEN Hua, HAN Lu, et al. Effect of venting area on quasi-static pressure of internal explosion for thermobaric explosive[J]. Chinese Journal of Explosives and Propellants, 2020, 43(5): 521-525. DOI:10.14077/j.issn.1007-7812.201909024 |
| [5] |
孔祥韶, 吴卫国, 李晓彬, 等. 舰船舱室内部爆炸的数值模拟研究[J]. 中国舰船研究, 2009, 4(4): 7-11. KONG Xiangshao, WU Weiguo, LI Xiaobin, et al. Numerical simulation of cabin structure under inner explosion[J]. Chinese Journal of Ship Research, 2009, 4(4): 7-11. DOI:10.3969/j.issn.1673-3185.2009.04.002 |
| [6] |
ANDERSON C E, BAKER W E, WAUTERS D K, et al. Quasi-static pressure, duration, and impulse for explosions (eg HE) in structures[J]. International Journal of Mechanical Sciences, 1983, 25(6): 455-464. DOI:10.1016/0020-7403(83)90059-0 |
| [7] |
KURKI T. Contained explosion inside a naval vessel–evaluation of the structural response[D]. Helsinki University of Technology, 2007.
|
| [8] |
刘慧泉. 箱型梁舱段结构设计及舱内爆炸数值分析[D]. 上海: 上海交通大学, 2012.
|
| [9] |
尹群, 王逸铭, 王珂. 舱室内爆载荷特性研究[J]. 舰船科学技术, 2020, 42(1): 11-16. YIN Qun, WANG Yiming, WANG Ke. Research on explosion load characteristics of cabin[J]. Ship Science and Technology, 2020, 42(1): 11-16. DOI:10.3404/j.issn.1672-7649.2020.01.003 |
| [10] |
郑向文, 郭天文. 烟丝箱式存储烟箱基准数的计算方法[J]. 物流技术与应用, 2013, 18(3): 116-117. DOI:10.3969/j.issn.1007-1059.2013.03.025 |
 2023, Vol. 45
2023, Vol. 45
