绑扎桥是集装箱船上用于绑扎、固定集装箱的主要结构,可防止船体在风浪作用下发生横摇时,甲板上的集装箱倾倒、坠落到海里。随着集装箱船大型化发展,甲板上堆箱不断增加,绑扎桥的高度也随之不断提升,绑扎力产生的力矩相应增大,绑扎桥下加强结构所受载荷也会增加,容易产生结构安全问题。
此前,已有不少学者针对绑扎桥的强度、刚度、振动模态和振动响应,以及轻量化设计等进行了研究[1-3]。然而,针对绑扎桥下加强结构的研究开展较少,对于绑扎桥下加强结构的布置形式、受力情况等还缺少系统性的分析,相关形设计优化工作也有待探究。
拓扑优化设计能够给出指定设计域内材料的最优分布以实现最佳结构性能,是探索新颖结构形式的重要手段。近年来,随着计算机技术的日益发展,变密度法、渐进结构优化方法、水平集法以及群体智能优化法等拓扑优化方法得到了长足发展[4-9]。其中,变密度法和渐进结构优化方法在船舶工程中的应用较为成熟,但这两类方法受限于自身关键参数选取的问题,存在容易得到局部最优解、收敛性较差等问题。基于改进遗传算法的双向渐进结构优化方法(G-BESO)[9]综合了遗传算法全局寻优能力强以及渐进结构优化方法计算效率高的优势,具备更好的工程应用潜力。
本文基于某大型集装箱船,通过有限元分析得到绑扎桥及舱口围结构的应力分布特点,以及大型集装箱船绑扎桥下加强结构的高应力区域。在此基础上,采用G-BESO法对绑扎桥下加强结构进行基于拓扑优化的轻量化设计。
1 绑扎桥及下加强结构布置 1.1 绑扎桥结构本文研究的大型集装箱船采用剪力墙式绑扎桥,主要由立柱、剪力墙、平台板、月牙板、肘板、栏杆等组成。其中,立柱和剪力墙为主要承力构件[10]。立柱沿船宽方向设置在每一列集装箱间隙处,普通立柱选用200 mm×200 mm空心方管,导向立柱(用于舱口盖起吊时定位导向)选用200 mm×300 mm空心方管;剪力墙采用连续片体式布置,在靠近左右舷两侧各设一面,宽度方向跨越3个箱位,高度方向从舱口围延伸至绑扎桥的二平台,主要承受横向载荷。
1.2 下加强结构绑扎桥位于舱口围上,与舱口围的连接结构主要是立柱和剪力墙,在连接结构下方需要有相应的支撑加强结构。
对于立柱而言,在船长方向,方管内侧布置有连续延伸至两舷的横向加强筋,外侧则需要添加短筋进行局部加强;在船宽方向,方管的其中一侧一般踩在垂直桁所在位置,另一侧则需要额外增加板材等下加强构件进行支撑,该面结构为本文研究优化的目标,其初始结构如图1所示。
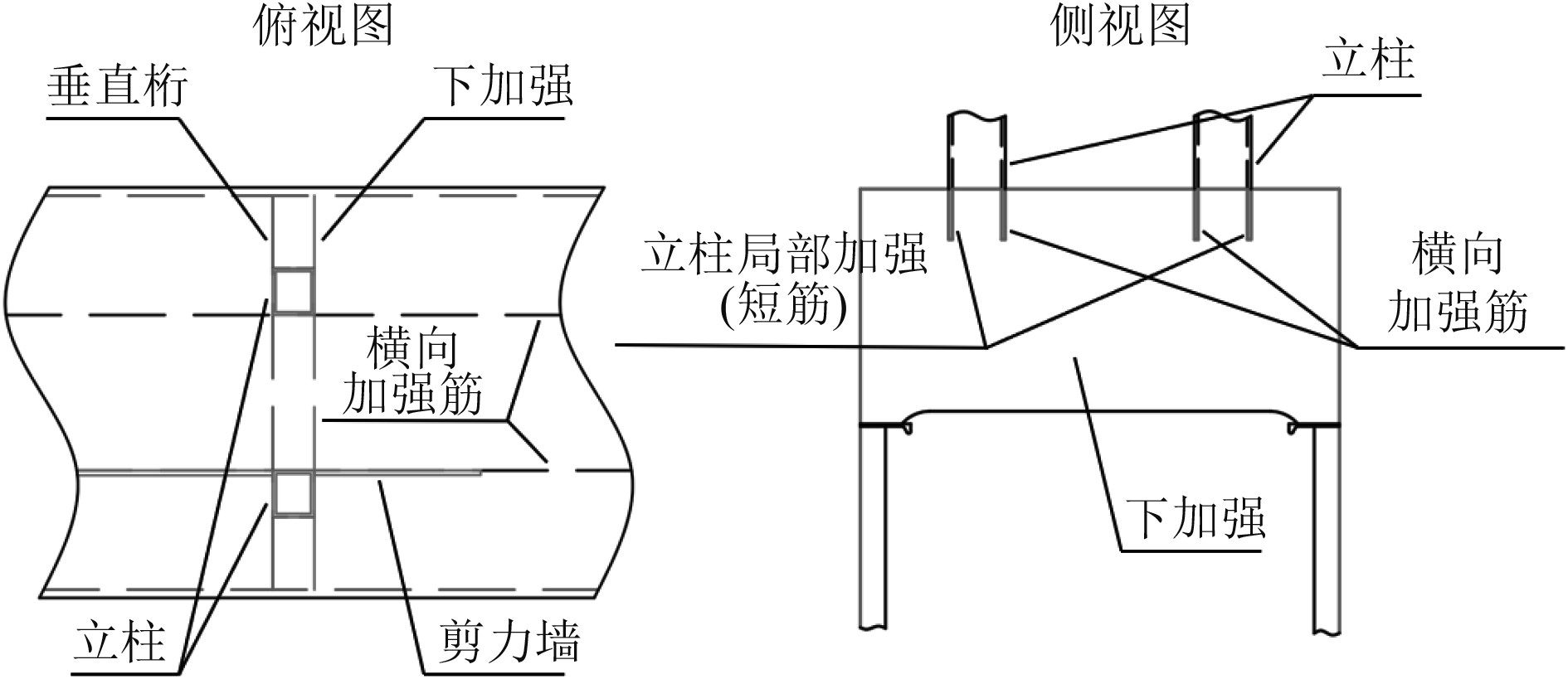
|
图 1 绑扎桥下加强结构布置示意图 Fig. 1 Structural layout of reinforcement under lashing bridge |
对于剪力墙而言,由于其与立柱方管内侧位于同一平面,下方已有连续的横向加强筋进行支撑,故不进行额外加强。
2 绑扎桥及下加强结构布置结构强度计算分析 2.1 有限元模型为了研究绑扎桥下加强结构的受力特征和应力分布,建立包含绑扎桥、箱柱、舱口围的有限元模型,从而更真实反映绑扎桥在实际受载条件下对下加强结构的作用,如图2所示。
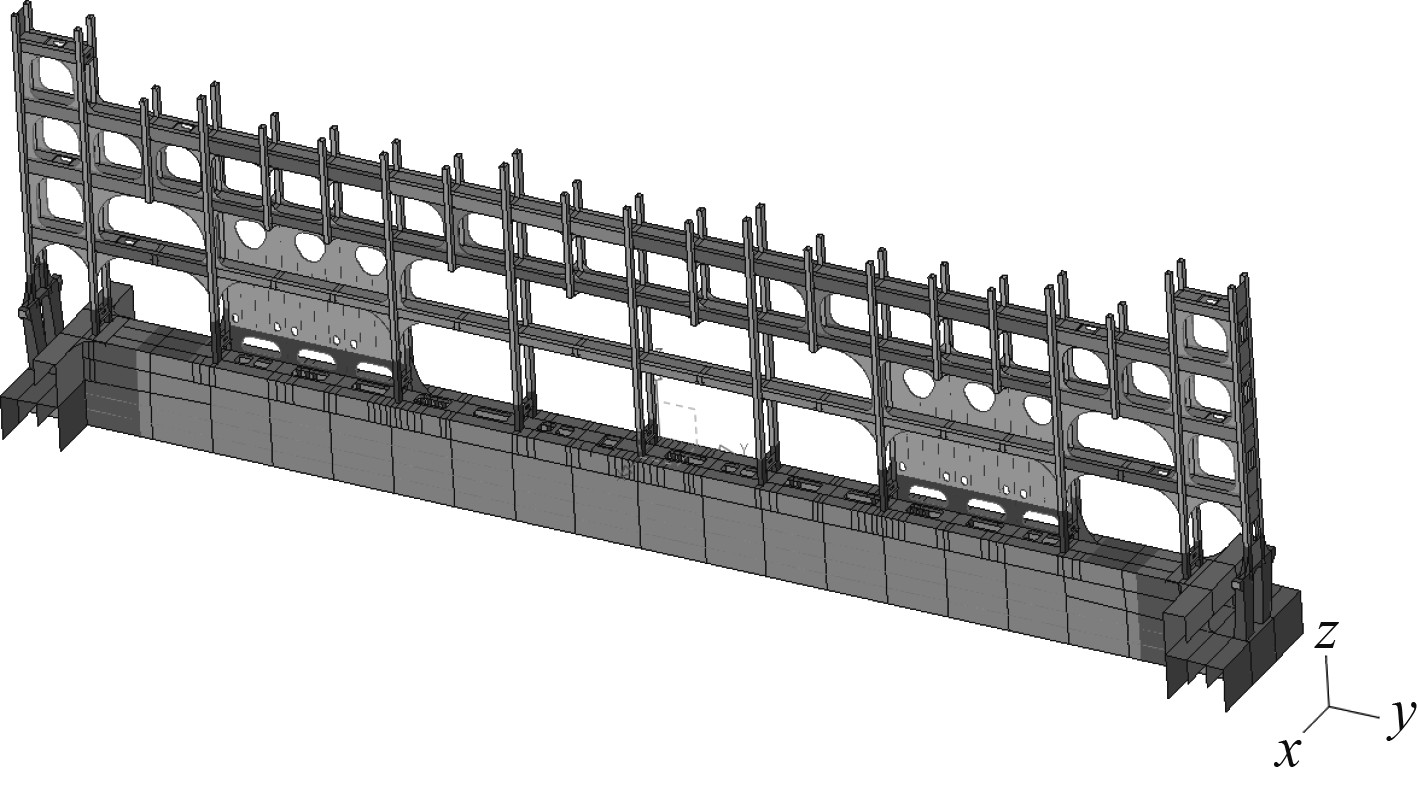
|
图 2 绑扎桥及下加强有限元模型 Fig. 2 Finite element model of lashing bridge and reinforcement |
模型在高度方向上截取至二甲板所在平面,在船长方向上截取至前、后一档强框。边界条件设为各边简支固定。模型采用50 mm的细网格,此时应力衡准可根据规范放宽至原来的1.5倍[11]。
绑扎桥结构在强度分析中一般需校核3个工况,即船首一侧绑扎眼板受拉、船尾一侧绑扎眼板受拉、以及两侧同时受拉。由于绑扎桥下加强的载荷均由绑扎桥主体沿立柱、剪力墙等结构传递而来,故在强度计算中选取同样的工况进行加载。图3为FEMAP中绑扎桥两侧同时受载的有限元模型。
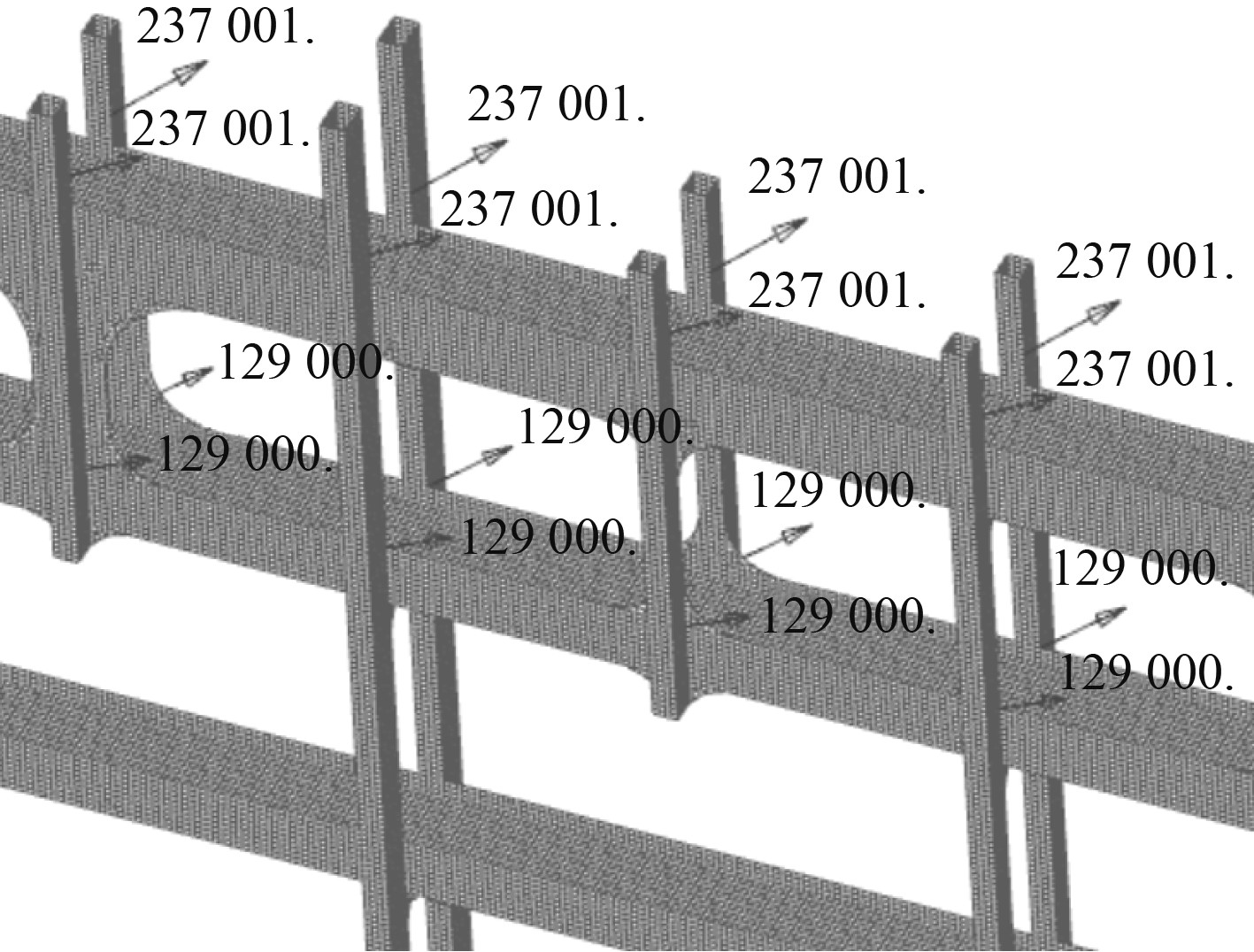
|
图 3 绑扎桥双侧受载示意图 Fig. 3 Loads on both sides of lashing bridge |
采用Nastran计算模型在3个工况下的应力分布,图4为绑扎桥两侧眼板同时受拉时全模型的Von Mises应力云图。该工况下整体应力分布规律与2个单侧受载的工况较为相似,但应力水平明显大于后两者。图中已筛去100 MPa以下的低应力单元,以更直观地展现高应力区域的分布特点。

|
图 4 全模型Von Mises应力云图 Fig. 4 Von Mises stress contour of the entire model |
从图中可见,高应力区域在剪力墙上大致呈“X”形分布,并沿着肘板、立柱等结构向外延伸传递。相应地,位于剪力墙两侧的立柱下方的下加强结构所受应力最大,是结构最危险区域。对于其余非剪力墙两侧的立柱,其所承受的横向载荷较小,对应下加强结构的应力也较小。
图5为位于剪力墙外侧立柱下方的绑扎桥下加强结构的Von Mises应力云图,其中左侧为带剪力墙一侧。由图5可见,绑扎桥下加强结构满足强度要求,且高应力区域集中在带剪力墙一侧的立柱下方,以及该侧靠近横向舱口围板的位置,单元最大应力约为195 MPa,其他区域的单元应力水平均较低。
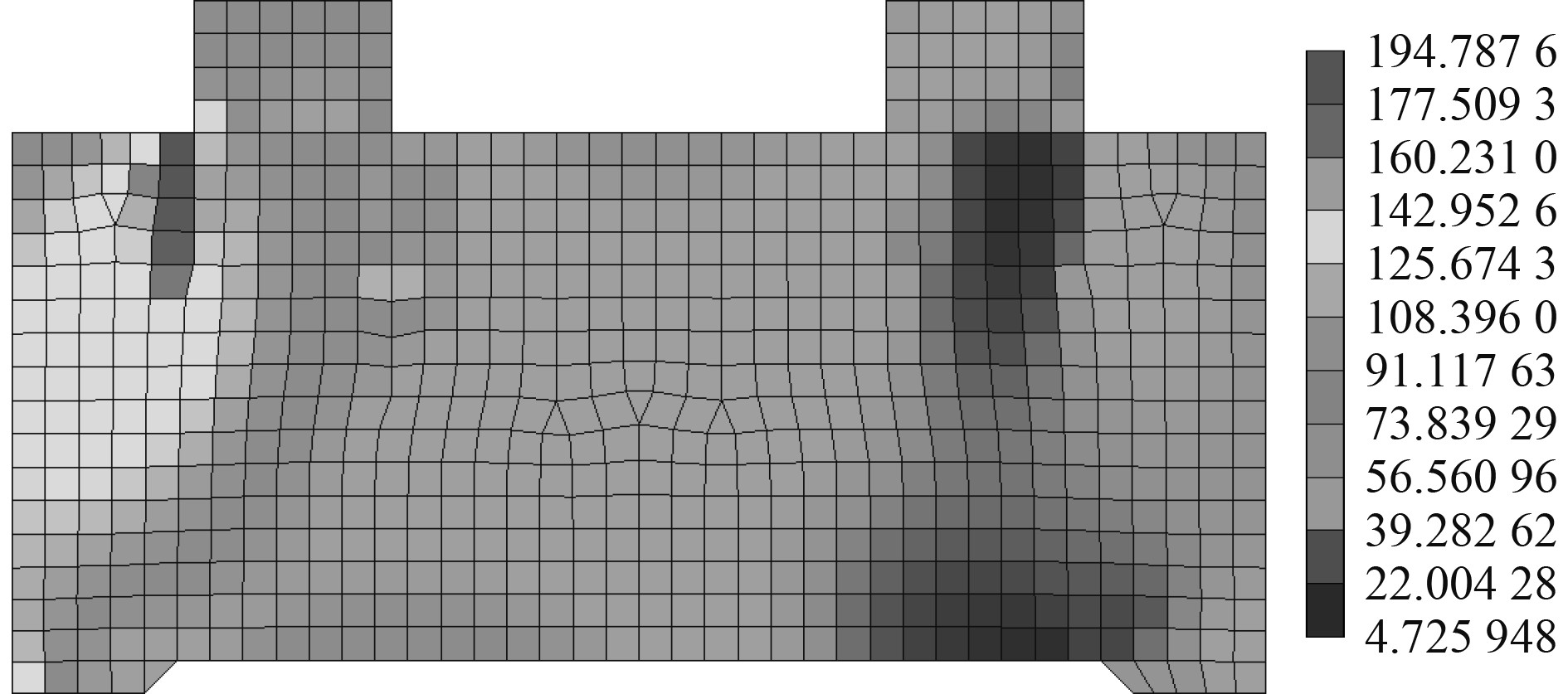
|
图 5 绑扎桥下加强结构Von Mises应力云图 Fig. 5 Von Mises stress contour of reinforcement under lashing bridge |
由于初始设计的绑扎桥下加强结构存在较大面积的低应力区域,考虑对其进行拓扑优化设计,通过删除冗余结构以达到减质量、降成本的目的。
3 拓扑优化方法 3.1 拓扑优化数学模型本文所采用的G−BESO方法中,设计变量取为下加强结构各个单元,约束条件为结构应力水平满足衡准要求,优化目标为结构质量最小化。其拓扑优化数学模型如下:
设计变量
最小化目标函数
约束条件
式中:F和u分别为载荷向量和位移向量;K为刚度矩阵;xi为设计变量,其值为0或1,分别表征空单元和实单元;n为单元数量;σi表示第i个单元的Von Mises应力,σ*表示结构应力约束值。
删除策略增删单元,所采用的材料插值模型如下:
| $ {I^{(k)}} = \delta \times {I^{(k - 1)}} + \left( {1 - \delta } \right) \times {X^{(k)}},{I^{(0)}} = 1,$ | (4) |
| $ {E^{(k)}} = {I^{{{(k)}^p}}}{E^1},$ | (5) |
| $ {K^{(k)}} = {I^{{{(k)}^p}}}{K^1}。$ | (6) |
式中:k为当前迭代步;δ为权重因子;I为单元权重系数矩阵;E1和K1分别为实单元的弹性模量矩阵和刚度矩阵;p为材料惩罚因子。
同时,对单元xi进行编码,即赋予其一定长度的由0和1构成的向量
| $ {x_i}' = \underbrace {[0,0,...,1,1]}_{elen},$ | (7) |
| $ {x_i}^{(k)} = \left\{ {\begin{array}{*{20}{c}} 0&{{\text{if }}{x_i}^{(k - 1)} = 1{\text{ and }}N_1 = 0},\\ 1&{ {\text{if }}{x_i}^{(k - 1)} = 0{\text{ and }}N_1 > \dfrac{{elen}}{2}} 。\end{array}} \right. $ | (8) |
式中:elen是编码长度;N1表示所含1的个数。
3.2 灵敏度分析与收敛准则基于应力全局化思想,将局部应力约束转换为全局的应变能约束,并采用拉格朗日乘子法将应力约束条件并入质量目标函数,构建出新的拉格朗日目标函数为:
| $ L(x) = W(x) + {\lambda _i}(e - \bar e),$ | (9) |
式中,e和ē分别为结构应变能和应变能约束值。
相应地,可得单元灵敏度为:
| $ \begin{gathered} {\alpha _i} = \dfrac{{\partial L({x})}}{{\partial {x_i}}} = \dfrac{{\partial W({x})}}{{\partial {x_i}}} + {\lambda _i}\frac{{\partial e}}{{\partial {x_i}}}= \\ \quad \, {\alpha _i}^{weight} + {\lambda _i}{\alpha _i}^{stiff} 。\\ \end{gathered} $ | (10) |
其中,质量和应变能灵敏度分别为:
| $ {\alpha _i}^{weight} = {\rho _i}{V_i},$ | (11) |
| $ {\alpha _i}^{stiff}={\text{ - }}\dfrac{{\text{1}}}{{\text{2}}}{{u}_i}^{\rm{T}}{{K}_i}{{u}_i}\dfrac{{{\text{1}} - \delta }}{{{I_i}}}{,}\,\,\,{i = 1,2,}...{,n}。$ | (12) |
从而可得整体灵敏度数为:
| $ {\alpha _i} = {\rho _i}{V_i} + \dfrac{{\text{1}}}{{\text{2}}}{\lambda _i}{{u}_{i}}^{\rm T}{{K}_{i}}{{u}_{i}}\dfrac{{{\text{1}}{ - \delta }}}{{{{I}_{i}}}}。$ | (13) |
当某约束不满足时,对应的拉格朗日乘子取值增大,使得后续迭代优化朝着约束条件满足的方向进行。
对于应力约束下的结构质量最小优化问题,需满足应力、质量收敛条件为:
| $ {\sigma _i} \leqslant {\sigma ^*} ,$ | (14) |
| $ error = \tfrac{{|\displaystyle\sum\limits_{i = 1}^N {{W_{k - i + 1}} - {W_{k - N - i + 1}}} |}}{{\displaystyle\sum\limits_{i = 1}^N {{W_{k - i + 1}}} }} \leqslant \tau 。$ | (15) |
至少连续N次迭代中结构重量变化足够小,且满足相应的应力约束,才认为结构稳定。
3.3 方法实现参照文献[9],将设计域视作种群,设计单元视为个体,对单元进行二进制编码,编码中1的个数代表其重要程度,即适应度。根据适应度将设计单元划分为:高等单元、过渡单元和低等单元,不同类别单元有着不同的单元编码更新方式。在迭代优化中,单元之间通过选择、交叉、变异等一系列遗传操作更新编码。随着优化的推进,高效单元的编码中因有更多的1而得到保留,低效单元则会有更多的0而被淘汰,从而实现结构的进化。
当需要考虑多个工况的约束时,综合分析得出各工况的权重因子,通过改变其优化目标为最小化结构合成质量(各工况下结构质量与对应权重因子之积的总和),将其转化为单工况约束问题处理。
本文基于Python编程,集成Hypermesh前处理器和Nastran求解器进行有限元模型的更新和计算分析,实现G−BESO法在绑扎桥下加强结构上的拓扑优化应用。
4 下加强结构优化结果由于绑扎桥双侧受载工况下结构受力明显更严重,故首先尝试针对该工况进行单工况下加强结构质量最小优化设计,约束条件为该工况下模型各单元应力水平满足衡准要求,由此可得图6所示结果。该结果仅保留了剪力墙一侧的少量单元,大幅简化了原有模型。当无剪力墙一侧没有下加强结构时,周围各单元应力水平仍能满足衡准(50 mm网格下普通钢许用应力为352.5 MPa)[11]。

|
图 6 双侧受载单工况拓扑优化结果 Fig. 6 Topology optimization result of two sides loading condition |
然而,当绑扎桥双侧受载时,外载荷在船长方向(x方向)已相互抵消,而在绑扎桥单侧受载时在x方向存在力的分量,此时可能会导致结构应力水平超差。同时,该下加强作为立柱局部加强短筋(见图1)的支撑结构,具有存在的必要性。为此,对该拓扑优化问题进行调整:一方面对绑扎桥下加强结构进行多工况约束下(各工况下结构应力均满足要求)的拓扑优化设计,综合考虑3个工况的作用和影响,并假定各工况同等重要(即权重因子相等);另一方面,要求在减少单元的同时降低立柱周围单元的最大应力值,提高结构的安全性。
调整后程序优化计算结果如图7所示,该结果反映出下加强结构在3种工况综合作用下结构的主要承载路径。可知,无剪力墙一侧的支撑单元略少于带剪力墙一侧,应力水平则明显低于带剪力墙一侧。对比图6可知,周围单元的最高应力从298 MPa降至252 MPa,提高了结构的可靠性。
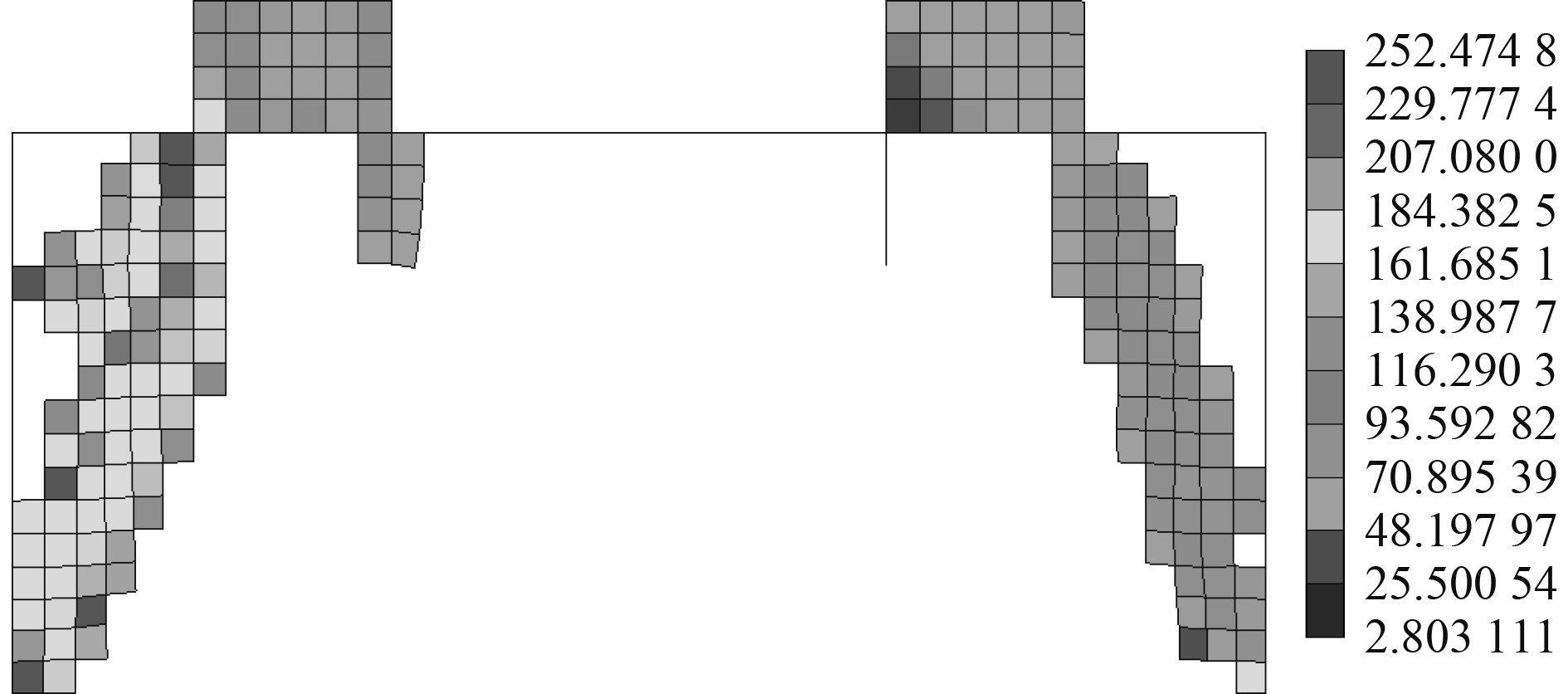
|
图 7 调整后多工况拓扑优化结果 Fig. 7 Topology optimization result of multiple loading conditions after adjustment |
最后,基于拓扑优化结果,结合船舶结构设计知识,对绑扎桥下加强结构进行光顺、修补、删改等,确定最终优化结果如图8所示。对比图7可知,周围单元的最大应力仅有小幅度上升,从252 MPa提高至261 MPa,对比衡准仍有较大裕量。同时,相比最初的完整板(满设计域)大幅节省了材料,减轻了结构质量。
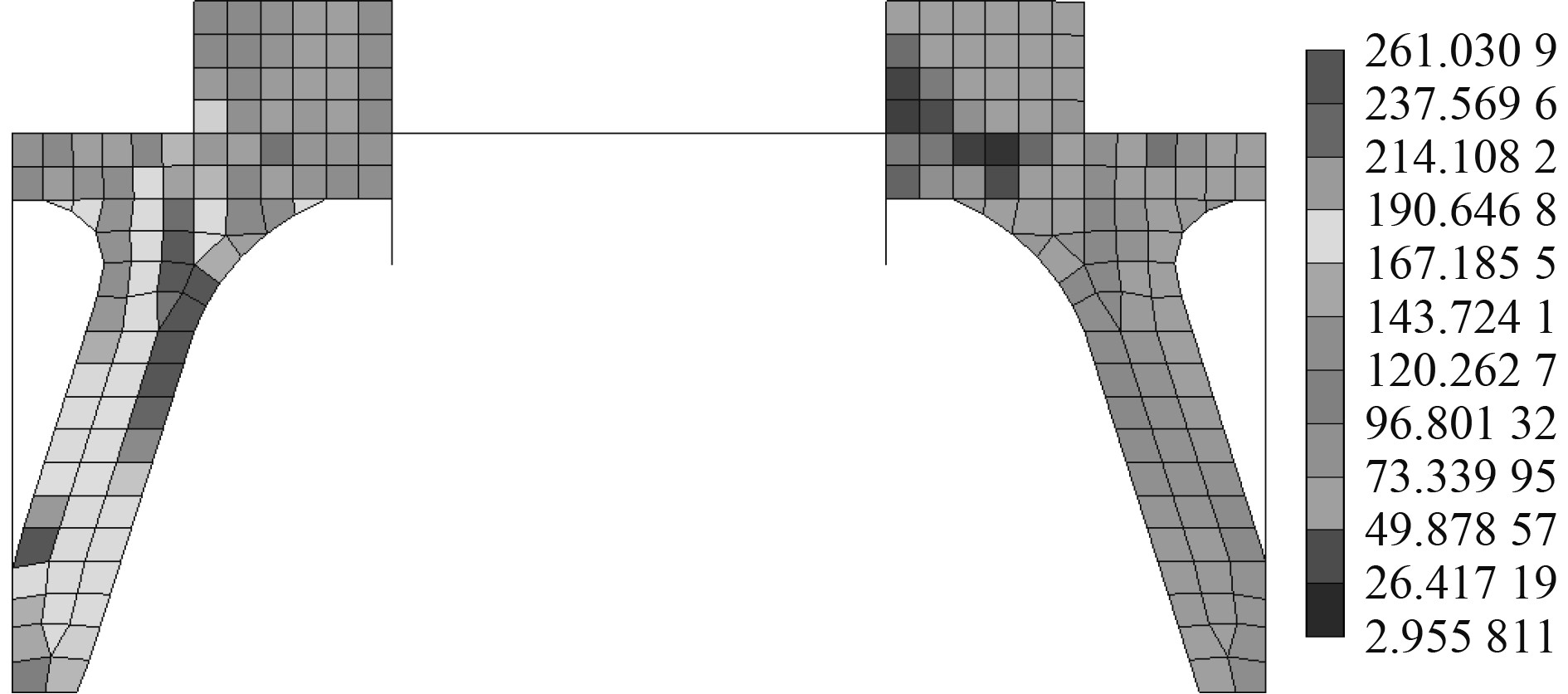
|
图 8 绑扎桥下加强结构最终优化结果 Fig. 8 Final topology optimization result of reinforcement under lashing bridge |
本文通过有限元建模,分析得到绑扎桥及下加强结构的应力分布特点,采用G-BESO法完成了下加强结构的拓扑优化设计,得到的结论有:
1) 高应力区域在剪力墙上大致呈“X”形分布,沿立柱、肘板等向外延伸传递,位于剪力墙两侧立柱下方的下加强结构所受应力相应较大;
2) 对下加强结构进行拓扑优化需综合考虑3个工况的影响,保证结构在不同载荷下所受应力均能满足衡准,同时还要考虑设计中结构的搭接问题;
3)综合减轻结构质量及降低结构应力的考虑,结合船体结构设计知识,完成了绑扎桥下加强结构的拓扑优化,有效降低了下加强结构质量,并保证了结构的安全可靠。
| [1] |
曾骥, 袁博, 周瑞佳, 等. 超大型集装箱船绑扎桥数值模拟及结构优化[J]. 船舶工程, 2019, 41(1): 34-39. |
| [2] |
孙芳胜, 王佳颖. 大型集装箱船绑扎桥振动特性[J]. 船舶与海洋工程, 2020, 36(2): 6-13. |
| [3] |
孔小兵, 张海瑛, 张鼎. 超大型集装箱船剪力墙式绑扎桥结构设计及优化探讨[J]. 船舶, 2020, 31(1): 133-140. |
| [4] |
LI K, YU Y, WANG Y, et al. Research on structural optimization method of FRP fishing vessel based on artificial bee colony algorithm[J]. Advances in Engineering Software, 2018, 121: 250-261. DOI:10.1016/j.advengsoft.2018.03.011 |
| [5] |
QIAO H, WANG S, ZHAO T, et al. Topology optimization for lightweight cellular material and structure simultaneously by combining SIMP with BESO[J]. Journal of Mechanical Science and Technology, 2019, 33(2): 729-739. DOI:10.1007/s12206-019-0127-2 |
| [6] |
NABAKI K, SHEN J, HUANG X. Stress minimization of structures based on bidirectional evolutionary procedure[J]. Journal of Structural Engineering, 2019, 145(2): 1-14. |
| [7] |
杨国威, 梅志远, 郑健. 悬挂舵钢骨架分步拓扑优化方法研究[J]. 舰船科学技术, 2019, 41(21): 64-70. YANG Guowei, MEI Zhiyuan, ZHENG Jian. Study on step-by-step topological optimization of hanging[J]. Ship Science and Technology, 2019, 41(21): 64-70. |
| [8] |
丁卯, 耿达, 周明东, 等. 基于变密度法的结构强度拓扑优化策略[J]. 上海交通大学学报, 2021, 55(6): 764-773. DING Mao, GENG Da, ZHOU Mingdong, et al. Topology optimization strategy of structural strength based on variable density method[J]. Journal of Shanghai Jiaotong University, 2021, 55(6): 764-773. |
| [9] |
吴贝尼, 夏利娟. 基于改进遗传算法的双向渐进结构优化方法研究[J]. 船舶力学, 2021, 25(2): 193-201. WU Beini, XIA Lijuan. Research on bi-directional evolutionary structural optimization method based on improved genetic algorithm[J]. Journal of Ship Mechanics, 2021, 25(2): 193-201. |
| [10] |
张鼎, 黄维, 时永鹏. 两种大型集装箱船绑扎桥结构强度的对比计算浅析[J]. 船舶工程, 2015, 37(S1): 32-34+38. |
| [11] |
DNV. Rules for classification - Ships. Part. 3 - Hull, Chapter. 7 – Finite element analysis[S]. 2021.
|
 2023, Vol. 45
2023, Vol. 45
