2. 遨海科技有限公司,辽宁 大连 116023
2. Aohai Technology Co., Ltd., Dalian 116023, China
GNSS是一个全球性的时间和位置测定系统。其中,全球设施部分是GNSS的核心基础,是系统提供自主导航定位服务必需的组成部分,一般由空间段、空间信号和地面控制系统组成。本文基于多模卫星信号选取其中GPS与北斗的联合GNSS算法,而对于GLONASS和Galileo系统不作介绍与研究[1-3]。
首先需要说明GNSS的时间系统。为了保证导航和定位精度,GNSS的时间系统(简称GNSST)采用的时间基准为原子时1 s时长,但将时间起算点定义在1980年1月6日UTC0时。GNSST启动后,不跳(闰)秒,目的是保持时间的连续性。在利用GNSST进行时间校对时应注意,GNSST与1AT在任意时刻均有一常量偏差,即19 s。此外,部分GNSS系统还包括区域设施,如GPS的外部增强系统EGNOS,本文主要探讨GNSS系统在船载智能定位终端系统的应用[4-5]。
1 GNSS系统误差分析与建模 1.1 系统的误差来源GNSS系统的误差源如表1所示。可大体分为4类,其中部分误差与本文探讨的船载智能定位终端系统解算结果相差不大,且建模解算过于繁琐,对于定位精度影响较小,故在此不予讨论。此外,由于卫星的钟差、对流层延迟误差及电离层延迟误差在定位解算中对结果的影响最大,因此本文关于多模的船载定位系统将重点围绕以上三点展开。
|
|
表 1 GNSS系统误差来源 Tab.1 GNSS system error source |
此外,表1中的多径效应在不同船载系统上存在一定差异,难以模型化,故无法予以消除,可通过改进GNSS接收机硬件(如天线)、软件(各类改进算法),延长观测时间等措施消除部分误差。接收机钟差量级很小,一般可忽略。
在船载智能定位终端系统,由于周围船部件(如钢材、橡胶、集装箱等设备)对信号的遮挡和反射,传统方案的GNSS定位性能会出现大幅度下降,误差会从几米增大到几十米甚至更多。究其原因,主要是散货船中诸如阴影效应、多径效应、多普勒效应、远近效应等常见的影响因素所致。
1.2 系统主要误差的建模与消除1)卫星钟差
卫星对外发送信号的基准是自带的原子钟,但由于存在频率漂移和时间偏差,因此若想校正卫星时间,需要计算卫星钟差。各卫星的钟差可由地表的监控站监测后估算出,将相关参数以导航电文的形式发送至用户接收机。卫星的时钟总差由卫星钟差、相对论效应校正量和群波延时校正量3部分组成。
| $ \delta t = \varDelta t + \varDelta {t_T} - {T_{GD}} 。$ | (1) |
式中:δt为总卫星钟差;Δt为卫星钟差;ΔtT为相对论效应校正量;TGD为群波延时校正量。总卫星钟差可表示为:
| $ \Delta t = {a_{f0}} + {a_{f1}}\left( {t - {t_{oc}}} \right) + {a_{f2}}{\left( {t - {t_{oc}}} \right)^2} 。$ | (2) |
式中:toc为参考时间;af0为卫星的钟差偏差;af1为卫星钟的钟速;af2为卫星钟的钟速变化率。以上4个参数均储存在导航星历电文的第一数据块中。射频信号从天线发出所导致的延时可直接从卫星星历数据中得到。
需要说明的是,此方法修正后的钟差仍然不是准确值,将其用于定位解算依旧会出现一定偏差,这部分偏差将与其他误差一起作为残差用于解算迭代。
2)对流层延时误差
对流层是大气层的底部,平均高度从赤道地区到极地地区,从7~20 km不等。对流层的重量约占大气层总重量的99%。对流层延时由干分量和湿分量两部分构成,其中干分量主要由氮气、氧气等干气体组成,约占总对流层延时的90%,湿分量约占总对流层延时的10%。由于湿分量会随着时间、地点的变化而不断改变,因此很难进行建模分析,而干分量由于其稳定的特性,能够较好建模。目前存在着多种对流层延时修正模型,本文采用其中一种简化模型修正对流层延时误差,公式如下:
| $ T = \frac{{2.47}}{{\sin \theta + 0.0121}} 。$ | (3) |
式中,θ为卫星的高度角。
3)电离层延迟误差
电离层和对流层类似,也是大气层的一部分,高度范围为60~1 000 km,其中的物质在接收到太阳辐射后会发生电离现象,释放出大量带电粒子,这部分带电粒子在作无序运动时产生杂波,从而导致卫星信号在穿越电离层时,这些杂波会叠加在卫星信号中,对卫星信号产生不良影响。由电离层延时造成的误差一般为几米,但是当太阳活动较强时,这部分误差可以达到数十米,因此在解算接收机位置时,须考虑到电离层延迟的影响并加以修正。
本文算法采用Klobuchar近似模型修正电离层延时误差。研究表明,该模型能修正50%左右的电离层误差。公式如下:
| $ I_{z}= F\left( {5 \times {{10}^{ - 9}} + A\cos \left( {2{\text π} \frac{{t - 50400}}{T}} \right)} \right)\left| {t - 50400} \right| < \frac{T}{4} 。$ | (4) |
式中:Iz为电离层延时;A和T为余弦函数的振幅,可由电文中的电离层延迟校正参数求得,F为倾斜率,可由下列公式得到:
| $ F = 1 + 16 \times {\left( {0.53 - \frac{\theta }{{\text π}}} \right)^3} 。$ | (5) |
式中,θ为卫星的高度角。
1.3 最小二乘定位算法的确定利用卫星导航系统进行载体定位的方法有单点定位、差分定位和相对定位。其中单点定位仅用1台接收机即可完成定位,而其余2种需要2台或更多接收机同时工作才能实现,精度较单点定位有明显提升。由于单点定位简易、低成本的特性,符合本文船载智能定位终端系统下定位的需求,故本文采用单点定位原理中的伪距定位原理。
在通过卫星计算用户位置时,需要求得以下2个未知量:卫星在空间位置中的坐标和接收机到卫星的距离。卫星的空间位置坐标可直接通过卫星星历计算获得,但由于卫星钟差,接收机钟差等误差,会使得接收机与卫星的测量距离与二者的实际距离出现偏差,故称该测量值为伪距。伪距的测量值ρ一般通过如下公式得到:
| $ \rho = \Delta tc 。$ | (6) |
式中:Δt为卫星信号从发出到接收的时间;c为信号的传播速度,c=299792.458 m/s。
一般情况下,卫星信号的发射时间与接收时间可由卫星与接收机自带的时钟读出,但GNSS与接收机时钟通常无法同步,二者的差值就是接收机钟差。同理,GNSS与卫星时钟的差值就是卫星钟差。接收机钟差是一个关于GNSS时间的函数,而卫星钟差可以由电文中的卫星钟差修正参数求得。
伪距的测量值ρ与卫星到接收机的真实距离r的关系如下:
| $ \rho = r + \delta {\rho _1} + \delta {\rho _2} + \delta {t_u} - \delta t \text{,} $ | (7) |
式中:δρ1为电离层延时;δρ2为对流层延时;δtu为接收机钟差;δt为卫星钟差。
在实际解算过程中,卫星钟差、电离层延时和对流层延时都可通过导航电文中的相关参数计算得到,故将其统称为伪距测量误差,因此可将式(7)简化为:
| $ \rho = r + \delta {t_u} + {\varepsilon _p}。$ | (8) |
式中,εp为伪距测量误差。
用户接收机到卫星的真实距离r可表示为:
| $ {r^i} = \sqrt {{{\left( {{x^i} - x} \right)}^2} + {{\left( {{y^i} - y} \right)}^2} + {{\left( {{z^i} - z} \right)}^2}} 。$ | (9) |
式中:ri为第i颗卫星到用户的真实距离,(xi,yi,zi)为第i颗卫星的位置坐标,因此(x,y,z)为用户的位置坐标。
由上述基本原理可知,伪距测量误差可以通过计算得到,故可将上述公式简化,简化后的伪距观测方程为:
| $ \sqrt {{{\left( {{x^i} - x} \right)}^2} + {{\left( {{y^i} - y} \right)}^2} + {{\left( {{z^i} - z} \right)}^2}} + \delta {t_u} = \rho _c^i 。$ | (10) |
式中,ρic为第i颗卫星在修正伪距测量误差之后的伪距。
因此至少需要4个方程(组),即最少需要四颗卫星才能实现定位。由上式可知,使用n颗卫星进行定位,则会出现(3+n)个未知数(接收机的三维坐标和n个接收机钟差),故至少需(3+n)个伪距观测方程联立。由于一颗卫星对应一个观测方程,因此至少需要观测(3+n)颗卫星。
普通最小二乘算法流程图如图1所示。

|
图 1 普通最小二乘算法流程图 Fig. 1 Flow chart of ordinary least squares algorithm |
将3种不同加权算法的实验数据进行整合,通过误差的数据特征、分布情况、适用条件等角度对不同算法下的误差进行分析与比较。
由于本次实验所采用的最小二乘算法将接收机的初始位置设置为[0,0,0],故在刚开始的一段时间内,由于迭代次数不够,解算出的接收机近似位置会与真实值出现较大偏差,使这部分的数据不可靠。当一段时间后迭代次数较多时,接收机的近似位置与真实位置已较为接近,此时权重对于定位精度的提升已不明显。如果在迭代开始前已知接收机的近似坐标并将其赋值为接收机坐标的初值,就能很好改善整个定位过程的精度。
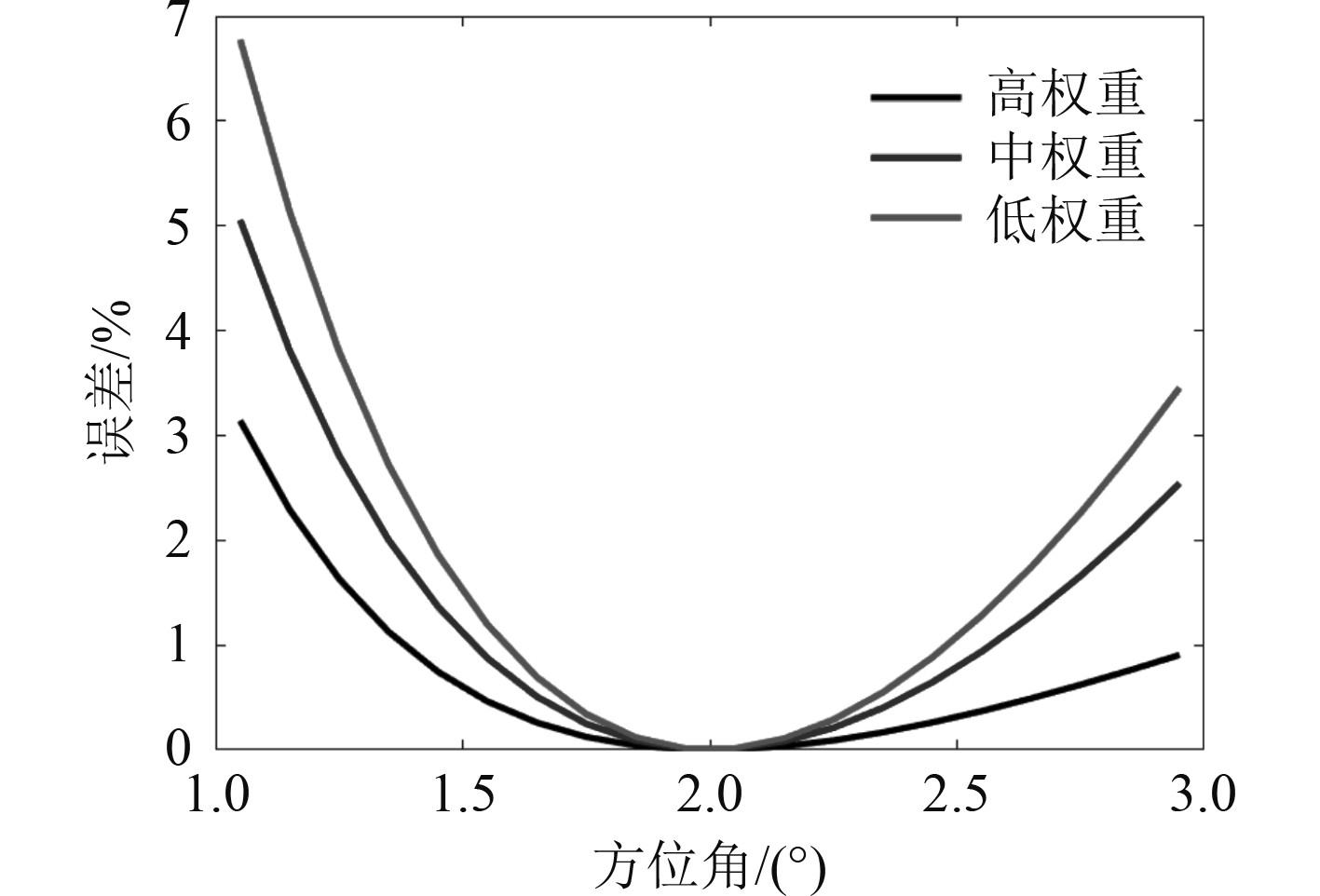
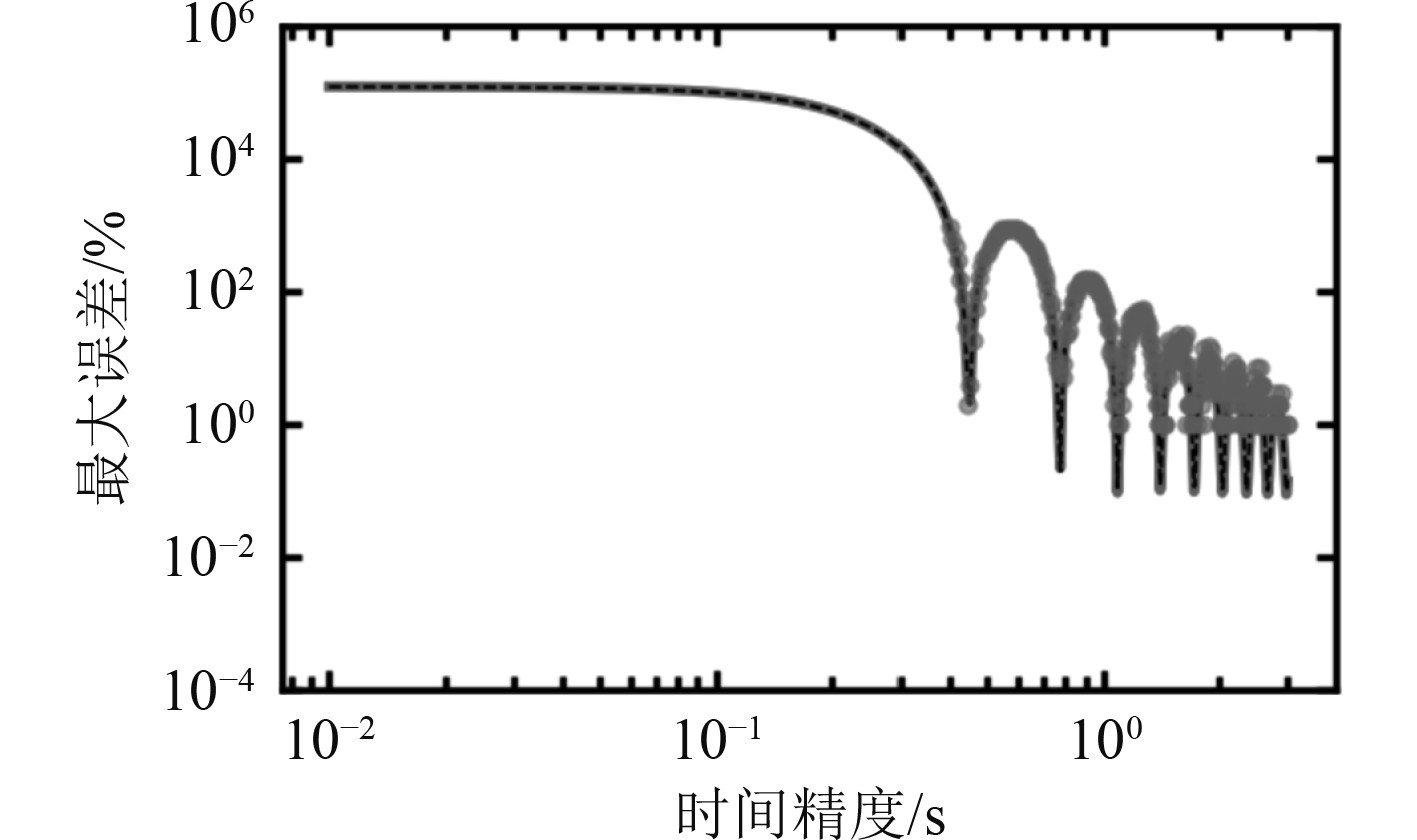
本文讨论的3种加权算法的误差如图2所示,可以发现低权重时比高权重的误差要大,在方位角为2°时,各个权重都能获得最低的误差。经过最小二乘法的定位算法修正后,高维度下最大误差的修正情况如图3所示。可以发现在0.05 s后,最大误差显著降低。其中高维度下95%分位点误差的修正情况如图4所示。
|
图 2 三种加权算法的误差 Fig. 2 Error of three weighting algorithms |
|
图 3 高维度下最大误差的修正情况 Fig. 3 Correction of the maximum error in high dimensions |

|
图 4 高维度下95%分位点误差的修正情况 Fig. 4 Correction of the 95% quantile error in high dimensions |
通过对GNSS卫星的误差来源进行分析,建立消除误差的模型,并研究了不同权重策略下使用GNSS卫星进行定位的误差比较,发现低权重比高权重的误差要大,并对高维度下最大误差的修正情况进行了分析。
| [1] |
牟俊, 李燕茹, 顾万高. 知识产权保护中心专利导航服务模式探索——以南京市知识产权保护中心为例[J]. 河南科技, 2023, 42(1): 116-120. MOU Jun, LI Yan-ru, GU Wan-gao. Exploration of patent navigation service mode of intellectual property protection center——A Case Study of Nanjing Intellectual Property Protection Center[J]. Henan Science and Technology, 2023, 42(1): 116-120. DOI:10.19968/j.cnki.hnkj.1003-5168.2023.01.023 |
| [2] |
黄修炼, 迟瑞娟, 董乃希, 等. 基于Winform的农机导航终端监控系统设计与试验[J]. 农机化研究, 2023, 45(10): 115-120. HUANG Xiu-lian, CHI Rui-juan, DONG Nai-xi, et al. Design and experiment of agricultural machinery navigation terminal monitoring system based on winform[J]. Agricultural Mechanization Research, 2023, 45(10): 115-120. DOI:10.13427/j.cnki.njyi.2023.10.019 |
| [3] |
肖小清. 移动测量系统在导航电子地图质量检测中的应用研究[J]. 测绘技术装备, 2022, 24(4): 125-130. XIAO Xiao-qing. Application research of mobile measurement system in navigation electronic map quality inspection[J]. Surveying and Mapping Technology and Equipment, 2022, 24(4): 125-130. DOI:10.20006/j.cnki.61-1363/P.2022.04.024 |
| [4] |
马祥泰, 胡彦逢, 董绪荣. GNSS技术在GEO、IGSO航天器中的导航精度与适用性分析[J]. 全球定位系统, 2022, 47(6): 1-8. MA Xiang-tai, HU Yan-feng, DONG Xu-rong. Analysis of navigation accuracy and applicability of GNSS technology in GEO and IGSO spacecraft[J]. Global Positioning System, 2022, 47(6): 1-8. DOI:10.12265/j.gnss.2022089 |
| [5] |
汪军民, 胥梓晟, 白刚, 等. 基于BIM的大型场馆室内导航系统设计研究[J]. 土木建筑工程信息技术, 2022, 14(6): 20-26. WANG Jun-min, XU Zi-sheng, BAI Gang, et al. Design and research on bim-based indoor navigation system of large venues[J]. Civil Engineering Information Technology, 2022, 14(6): 20-26. DOI:10.16670/j.cnki.cn11-5823/tu.2022.06.04 |
 2023, Vol. 45
2023, Vol. 45
