0 引　言

浅海水声信道有时—频—空复杂多变的信道特征。随之而来的频率选择性衰落、强多途扩展、可用带宽窄等特性严重影响了水声通信的高可靠、高有效性^[1]。因此，如何有效地抗衰落、抗多途以及合理利用有限带宽是目前也是未来水声通信的难点和挑战。目前，常用的策略有合理的调制解调技术、自适应信道均衡和信道编解码技术等。

在水声调制解调技术研究方面，季赵胜等^[2]将虚拟时间反转（VTR）技术引入分段式线性调频(PLFM)扩频调制系统，有效降低PLFM系统的误码率。岳玲等^[3]研究的FH/MFSK（跳频/非相干频移键控）通信系统在两径瑞利衰落信道下可将误码率降低至 ${10^{ - 3}}$ 级。陈博恒等^[4]研究的MC/FH-DPSK通信系统在与FH/MFSK系统抗多途能力一样的条件下，节约了一半的频带资源。

虽然采用MC-FH/DPSK通信系统可以在一定程度上提升系统的抗多途、抗多普勒能力，提高系统的抗ISI（码间串扰）能力，但是误码率只能降到 ${\text{1}}{0^{ - {\text{3}}}}$ ～ ${\text{1}}{0^{ - 2}}$ 量级，错误平层较高，无法满足水声通信 $ {\text{1}}{0^{ - {\text{5}}}} $ 量级的需求。为了进一步降低错误平层，需要加入合适的信道编解码技术。

早期的水声信道编码采用BCH码、RS码、卷积码等传统编码方式。20世纪90年代，Turbo码的提出^[5]以及LDPC码的重新“发掘”^[6]，使信道编码领域发生了历史变革。近年来，这2种“近香农限”码的编译码方式研究与改进，成为信道编码领域的热门研究方向。尤其是LDPC码，已被写入5G标准协议。

郑权等^[7]在水下通信中使用规则LDPC编码及加权BF译码算法，使信噪比在2 dB时误码率降低至 $ {\text{1}}{0^{ - {\text{4}}}} $ 量级。Sravan 等^[8]在通信距离为1 km、信道带宽为10 kHz的浅海水声环境下仿真了SC-LDPC码的性能，结果表明其比LDPC码（BER为 $ {\text{1}}{0^{ - 3}} $ 时）提高了1dB的信噪比增益。

本文主要对QC-LDPC码的检验矩阵 $ H $ 进行大围长改进，并与Turbo码进行对比，以找出更适合MC/FH-DPSK水声通信系统的编解码方式，使系统误码率降至 $ {\text{1}}{0^{ - {\text{5}}}} $ 量级，保证信息的可靠传输。

1 水声信道模型及实测信道

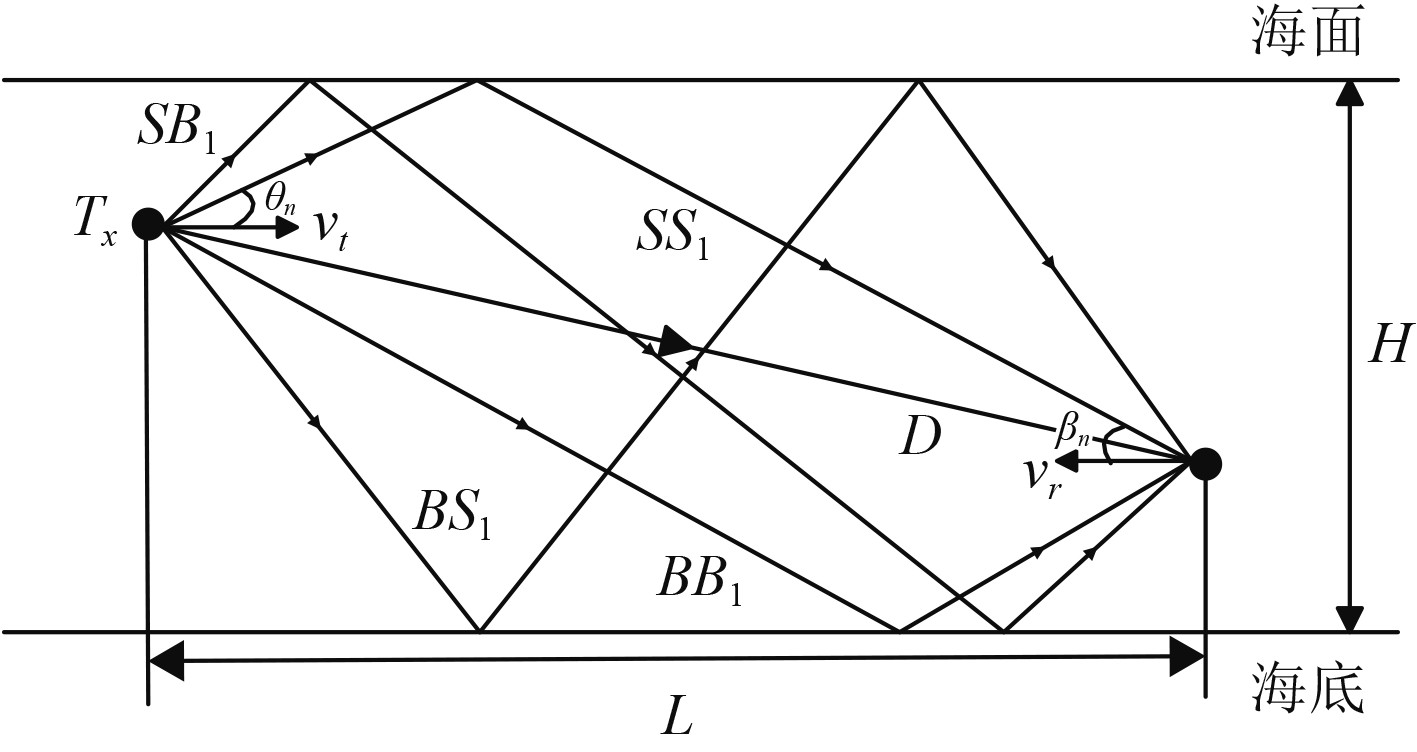
对于浅海移动水声通信信道，除了移动平台运动引起的时变衰落特性外，还会对通信信号产生明显的时间压扩效应，并且由于入射信号的角度弥散，不同路径的多普勒尺度因子也不同，从而严重影响通信同步与解调。因此在对浅海水声通信信道建模时必须考虑到上述因素。

根据BELLHOP射线理论建立的水声信道模型，结构较为简单。一般假设水深 $H$ 为常数，直达声用 $D$ 表示， $S$ 和 $B$ 分别表示海面、海底， $B{S_1}$ 表示海底海面反射声,下角标代表反射次数，其他含义可依此类推。

假设发射信号的复低通等效信号为 $ \tilde x(t) $ ，发射端和接收端的水平移动速度分别为 $ {v_t} $ 和 $ {v_r} $ (向右为正)，则接收信号模型可表示为：

$ \tilde r(t) = \sum\limits_{n = 1}^{N(t)} {{\alpha _n}(t){{\tilde x}_n}({s_n}(t - {\tau _n}(t))} 。$

(1)

式中： $ N(t) $ 为多途分量数量； $ {\tau _n}(t) $ 和 $ {\alpha _n}(t) $ 分别为第 $ n $ 条路径的延时和衰减； $ {s_n} $ 为第 $ n $ 条路径的多普勒尺度因子。

$ {s_n} = {c \mathord{\left/ {\vphantom {c {(c - ({v_t}\cos ({\theta _n}) - {v_r}\cos ({\beta _n})))}}} \right. } {(c - ({v_t}\cos ({\theta _n}) - {v_r}\cos ({\beta _n})))}}。$

(2)

式中： ${\theta _n}$ 和 $ {\beta _n} $ 分别为第 $ n $ 条路径的发射角和入射角； $c$ 为海水中的声速。由此可以建立如图1所示的浅海移动水声信道模型。

浅海移动水声信道能清晰地说明信号产生多途机理以及能获得的最优误码率性能，对实际水声信道条件下系统所能获得的性能提供参考。但是实际水声信道比仿真信道模型更为复杂，如果能预先取得信道的测量数据（如信道的冲击响应以及信道相干时间等），则可以给出更为准确的性能预测。

进行信道参数的实地测量，信道的相干时间大约在1s左右。信道水平距离1800 m左右，发射深度约20 m，接收深度约50 m，信道测量使用的是带宽5 kHz、脉宽40 ms的LFM同步信号。

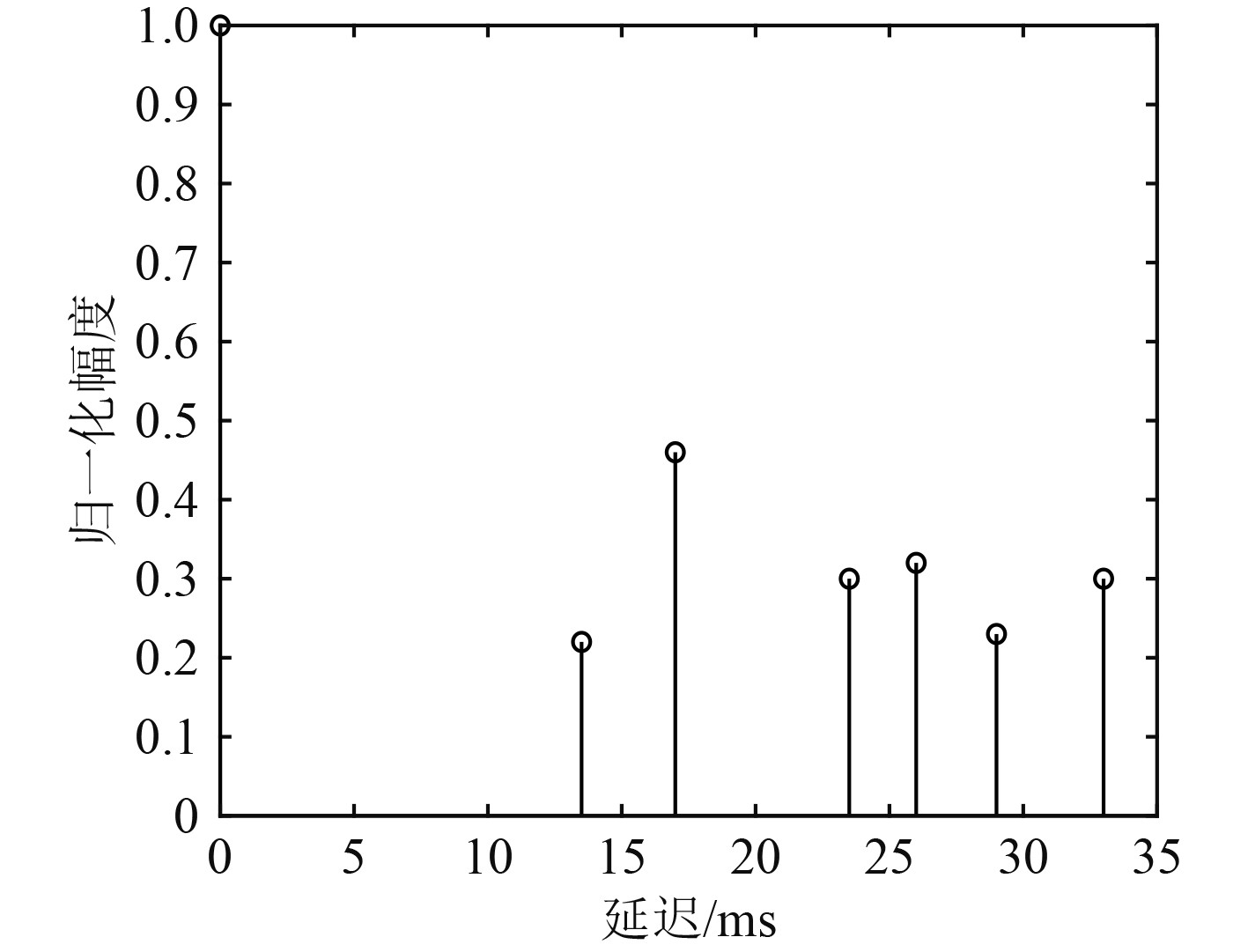
表1为每经相对时延和归一化幅度的计算结果。得到的冲击响应如图2所示。可见共有7条多径路线，其中包含一条直达路径，最大延迟为33 ms。

2 纠错编码方案与系统原理 2.1 Turbo码译码方案

Turbo码常用的译码算法主要有基于最大后验概率的MAP算法和软输出Viterbi译码算法(soft output viterbi algorithm，SOVA)两大类。本文主要对SOVA译码算法进行仿真研究。

SOVA算法是Hagenauer在20世纪80年代末提出的。与log-MAP译码算法相比，SOVA译码算法的运算量较小，更利于工程实现。其是Viterbi算法的改良，它的译码过程是在接收序列控制下，在网格图上寻找一条具有最大“度量”的路径。

SOVA译码算法的执行过程如下：

步骤1　令时刻 $k = 0$ ，初始化其零状态的度量 $ M\left( {S_k^0} \right) = 0 $ ，其他状态度量为 $ - \infty $ ，先验信息 $ \Lambda \left( {{u_k}} \right) = 0 $ ；

步骤2　 $ k = k + 1 $ ，计算网格图中该时刻所有状态的度量为

$ M\left( {S_k^m} \right) = M\left( {S_{k - 1}^{m'}} \right) + \frac{1}{2}{u_k}L\left( {{u_k}} \right) + \frac{{{L_c}}}{2}\left( {y_k^sx_k^s + y_k^px_k^{pi,m}} \right) ，$

(3)

步骤3　对每个状态搜索取 $ \mathop {\max }\limits_m \left\{ {M\left( {S_k^m} \right)} \right\} $ ，保存幸存路径度量值及相应的输入比特和状态路径，并计算出软信息值 $ \Delta _k^m $ ；

步骤4　比较每个状态处的幸存路径和竞争路径，并存储这2条路径上比特判决不同的相对时刻值，从小到大更新所有时刻软信息值的度量值 $ i $ 为

$ \Delta_{k^{{S_k}}} = \mathop {\min }\limits_{\begin{subarray}{l} i = k - \delta \cdots k \\ {u_{k - \delta }} \ne u_{k - \delta }^i \end{subarray} }\Delta _i^{{S_i}} ；$

(4)

步骤5　返回步骤2，直到接收完整个发送序列；

步骤6　获得发送序列的后验概率对数似然比序列 $ L\left( {u|R_1^N} \right) $ 后，由公式

$ L_e^{21}\left( u \right) = L\left( {u|R_1^N} \right) - {L_c}{y^s} - L_e^{12}\left( u \right) $

(5)

计算出RSC1的外信息，并将其作为先验信息 $ {L_a}\left( u \right) $ 用于RSC2的译码；

步骤7　经 $L$ 次迭代后，对RSC2输出的 $ L\left( {u|R_1^N} \right) $ 进行硬判决估计发送序列 $ \left\{ u \right\} $ 。

2.2 LDPC码校验矩阵的改进

LDPC码由校验矩阵 ${\boldsymbol{{H}}}$ 唯一确定，本文使用的 ${\boldsymbol{{H}}}$ 矩阵构造法为QC-LDPC构造法，并对其 ${\boldsymbol{{H}}}$ 矩阵进行结构改进，去除四、六环，提高误码率性能。

QC-LDPC码结构性极强，其校验矩阵 ${\boldsymbol{{H}}}$ 是由维数一致的单位矩阵循环位移得到的。校验矩阵 ${\boldsymbol{{H}}}$ 如下：

$ {{\boldsymbol{{H}}}} = \left[ {\begin{array}{*{20}{c}} {I({p_{1,1}})}&{I({p_{1,2}})}& \cdots &{I({p_{1,L}})} \\ {I({p_{2,1}})}&{I({p_{2,2}})}& \cdots &{I({p_{2,L}})} \\ \vdots & \vdots & \ddots & \vdots \\ {I({p_{J,1}})}&{I({p_{J,2}})}& \cdots &{I({p_{J,L}})} \end{array}} \right]。$

(6)

其中： $1 \leqslant j \leqslant J$ ， $1 \leqslant l \leqslant L$ ； $ I({p_{j,l}}) $ 为一个子循环矩阵； ${p_{i,j}}$ 为单位矩阵的右循环移位值。当 ${p_{i,j}} = 0$ 时， $I(0)$ 即为单位矩阵； ${p_{i,j}} \lt 0$ 时， $ I({p_{j,l}}) $ 为全零矩阵。若 ${\boldsymbol{{H}}}$ 不包含零矩阵，则代表一个 $(J,L)$ 规则QC-LDPC码。

由QC-LDPC码的循环特性可知，其校验矩阵可由指数矩阵 ${{\boldsymbol{{E}}}}$ 唯一确定。

$ {{\boldsymbol{{E}}}} = \left[ {\begin{array}{*{20}{c}} {{p_{1,1}}}&{{p_{1,2}}}& \cdots &{{p_{1,L}}} \\ {{p_{2,1}}}&{{p_{2,2}}}& \cdots &{{p_{2,L}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{p_{J,1}}}&{{p_{J,2}}}& \cdots &{{p_{J,L}}} \end{array}} \right]。$

(7)

因此，QC-LDPC码的构造可转化为对指数矩阵 $E$ 的合理设计。

通过去除四、六环处理设计一种(4,7)非规则QC-LDPC码，其比(5,10)规则QC-LDPC码的非零元素更少，矩阵更稀疏，从而大幅度提升了编解码性能。所构造的指数矩阵 ${\boldsymbol{{E}}}$ 如下：

$\begin{aligned} & {{\boldsymbol{{E}}}} =\\ & \left[ {\begin{array}{*{20}{c}} { - 1}&2&3&4&5&0&0&{ - 1}&{ - 1}&{ - 1} \\ 2&{ - 1}&6&8&{10}&{ - 1}&0&0&{ - 1}&{ - 1} \\ 7&{13}&{ - 1}&{24}&{31}&2&{ - 1}&0&0&{ - 1} \\ {32}&{64}&{96}&{ - 1}&{160}&{ - 1}&{ - 1}&{ - 1}&0&0 \\ {33}&{66}&{99}&{132}&{ - 1}&0&{ - 1}&{ - 1}&{ - 1}&0 \end{array}} \right]。\end{aligned}$

(8)

2.3 LDPC码译码方案

LDPC码的译码方式主要分为软、硬判决两大类。硬判决以BF(bit flipping)译码为基础进行改进，而软判决则是以BP(belief propagation)译码（也称和-积译码）为代表。硬判决译码结构简单，工程实现容易，但误码率性能较差。软判决译码由于内含循环结构，需进行迭代译码，计算量较大，但带来的误码率性能增益很大。

本文采用BP译码方式，其译码的主要步骤如下：

步骤1　初始化外信息。

$ \left\{ \begin{gathered} q_{ji}^0(0) = 1 - {P_j}(1) = \Pr ({x_j} = - 1|{y_j}) = \frac{1}{{1 + {e^{2{y_j}/{\sigma ^2}}}}}，\\ q_{ji}^0(1) = {P_j}(1) = \Pr ({x_j} = + 1|{y_j}) = \frac{1}{{1 + {e^{ - 2{y_j}/{\sigma ^2}}}}}。\\ \end{gathered} \right. $

(9)

步骤2　迭代译码过程。

第 $\zeta $ 次迭代时，校验节点更新：

$ \left\{ \begin{gathered} r_{ij}^\zeta (0) = \frac{1}{2} + \frac{1}{2}\prod\limits_{j' \in {R_{i\backslash j}}} {(1 - 2q_{j'i}^{(\zeta - 1)}(0))} ，\\ r_{ij}^\zeta (1) = \frac{1}{2} + \frac{1}{2}\prod\limits_{j' \in {R_{i\backslash j}}} {(1 - 2q_{j'i}^{(\zeta - 1)}(1))} 。\\ \end{gathered} \right. $

(10)

第 $\zeta $ 次迭代时，变量节点更新：

$ \left\{ \begin{gathered} q_{ij}^\zeta (0) = {K_{ji}}{\alpha _{ji}}{P_j}(0)\prod\limits_{i' \in {C_{j\backslash i}}} {r_{i'j}^{(\zeta - 1)}(0)}，\\ q_{ij}^\zeta (1) = {K_{ji}}{P_j}(1)\prod\limits_{i' \in {C_{j\backslash i}}} {r_{i'j}^{(\zeta - 1)}(1)} 。\\ \end{gathered} \right. $

(11)

为满足 $q_{ji}^\zeta (0) + q_{ji}^\zeta (1) = 1$ ，引入矫正算子 $ {K_{ji}} $ 。

步骤3　译码判决。

完成每次迭代后，计算变量节点信息。

$ \left\{ \begin{gathered} q_j^\zeta (0) = {K_j}{P_j}(0)\prod\limits_{i \in {C_j}} {r_{ij}^\zeta (0)} ，\\ q_j^\zeta (1) = {K_j}{P_j}(1)\prod\limits_{i \in {C_j}} {r_{ij}^\zeta (1)} 。\\ \end{gathered} \right. $

(12)

为满足 $ q_j^\zeta (0) + q_j^\zeta (1) = 1 $ ，引入矫正算子 $ {K_j} $ 。若 $q_j^\zeta (1) \geqslant q_j^\zeta (0)$ ，则判决 $ {\hat c_j} = 1 $ ；反之，则判决 $ {\hat c_j} = 0 $ 。

步骤4　译码完成。

若某次迭代后的输出信息序列 $\hat c$ 满足 $H{\hat c^{\rm{T}}} = 0$ 且 $\hat c \ne 0$ ，标志译码成功，终止迭代。若在给定的最大迭代次数内未成功译码，则立即终止译码，否则重复上述迭代译码过程。

2.4 基于MC-FH/DPSK系统的编码原理

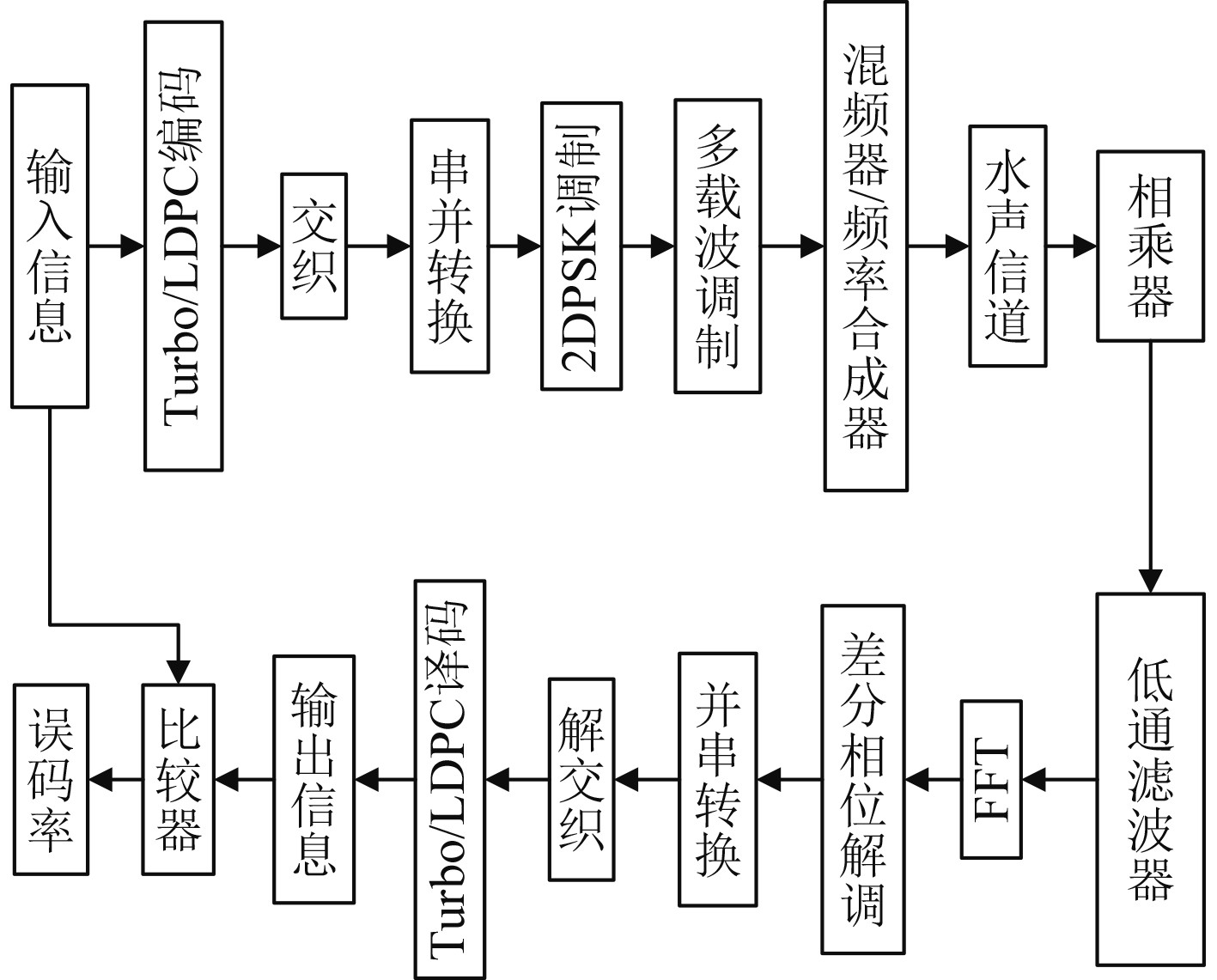
基于MC-FH/DPSK通信系统的编码原理框图如图3所示。

1）对输入的比特流数据 ${\boldsymbol{s}}{\text{ = [}}{s_{\text{1}}}{\text{,}}{s_{\text{2}}}{\text{,}} \cdots {\text{,}}{s_n}{\text{]}}$ 进行信道编码，编码后信息为 ${\boldsymbol{c}}{\text{ = [}}{c_{\text{1}}}{\text{,}}{c_{\text{2}}}{\text{,}} \cdots ,{c_n}{\text{]}}$ 。

2）通过交织重新编排编码后数据流，“打散”突发错误。交织器参数根据码长合理设置，保证所有信息都被充分交织。若编码后长度为1 680 bit，交织器参数可以设置为(56,30)，也可设为(42,40)。

3）通过串并转换将高速串行数据转换为低速并行数据。目的是适配多载波调制，转换依据是多载波的载波数及调频点的设置。若信息长度为1 680 bit，子载波数为6个，跳频点数为10个，则可将数据转换为(60,28)。

4）采用2DPSK调制将比特数据转换为基带相位信息。目的是储存并行的相位信息，为后续相位信息的跳频多载波调制做准备。

5）多载波调制合理地将步骤4中的基带相位信息调制到频带的个子载波上，按照频率合成器生成的跳频序列顺序传输相位信息。子载波中心频率的选取要和跳频点数的设置结合，目的是合理地利用水下有限频带资源，并保证各频点互不干扰。

6）所有子载波通过水声信道进行信息传输。

7）通过水声信道后与本振信号相乘完成解跳，然后经过低通滤波器滤除高频噪声。

8）通过快速傅里叶变换（FFT）估算出子载波中心频率索引值。

9）通过DPSK解调即可恢复码元信息。步骤8中的频率索引值所对应的相位信息是相对相位信息，将相对相位信息进行DPSK解调即可初步恢复信息序列。

10）通过步骤2和步骤3的逆过程，并串转换和解交织，即可获得接收端码元信息 ${{\boldsymbol{{r}}}}{\text{ = [}}{r_{\text{1}}}{\text{,}}{r_{\text{2}}}{\text{,}} \cdots {\text{,}}{r_n}{\text{]}}$ 。

11）将 $ {\boldsymbol{r}}{\text{ = [}}{r_{\text{1}}}{\text{,}}{r_{\text{2}}}{\text{,}} \cdots {\text{,}}{r_n}{\text{]}} $ 通过与步骤1相匹配的译码方式进行信息的译码，获得译码后的信息序列 ${\boldsymbol{d}}{\text{ = [}}{d_{\text{1}}}{\text{,}}{d_{\text{2}}}{\text{,}} \cdots {\text{,}}{d_n}{\text{]}}$ ，与 ${\boldsymbol{s}}{\text{ = [}}{s_{\text{1}}}{\text{,}}{s_{\text{2}}}{\text{,}} \cdots {\text{,}}{s_n}{\text{]}}$ 进行比对计算出系统的误码率。

3 仿真实验验证及性能评估 3.1 QC-LDPC码在实测信道下的仿真

为了控制变量只有编译码方式不同，便于比较2种码的纠错性能，使用如下系统参数设置：

输入信息长度为840 ${\rm{ bit }}$ ，共仿真100个数据帧，总信息长度为84000 ${\rm{bit}}$ 。带宽 $B$ 为5.5 kHz，系统采样频率 ${f_s}$ 为100 kHz，码元宽度 ${T_{sym}}$ 为8 ms，编码速率为1/2，信道交织采用基于比特块交织的方式，交织器的参数为(56,30)。

跳频方式选择素数跳频序列，跳频点设置如表2所示。

多径衰落信道采用第1节中给出的实测信道，信道 $SNR$ 与 $Eb/N_0$ 转换方式如下：

$ SNR = Eb/N_0 - 10{\log _{10}}\left(\frac{{{T_{sym}} \cdot {f_s}}}{2}\right) 。$

(13)

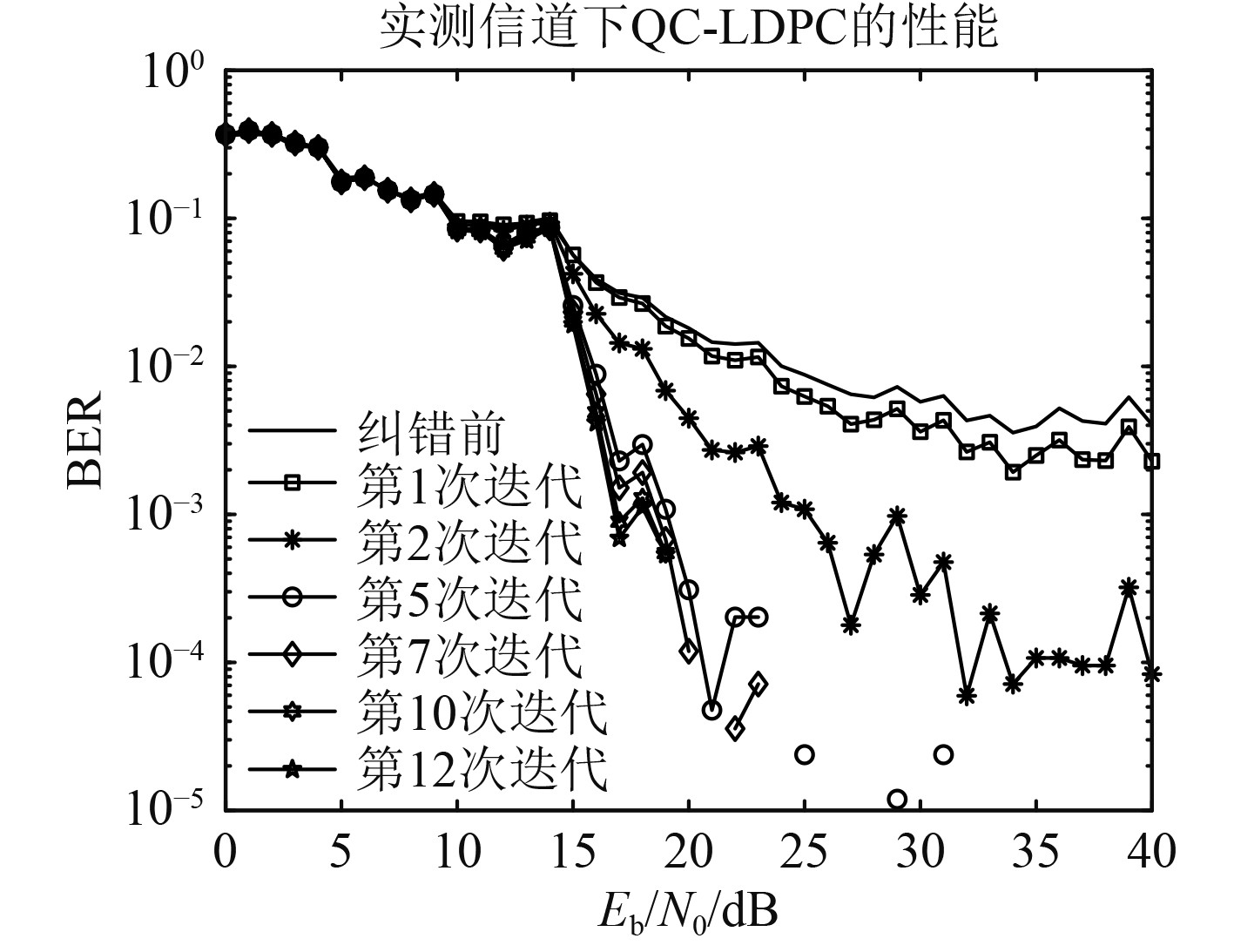
图4为QC-LDPC码在实测信道下的误码率性能曲线。

可以看出，在 $Eb/N_0 \geqslant 15\;{\rm{dB}}$ 时，编码带来的增益逐渐显现出来。随着迭代次数的增加，误码率性能不断提升。第2~5次迭代使误码率急剧下降到 ${10^{ - 4}}$ 量级，其中在迭代5次、 $Eb/N_0 \geqslant 30\;{\rm{dB}}$ 时，误码率出现 ${10^{ - 5}}$ 量级甚至零误码，但误码率仍有波动发生。第2次迭代误码率性能提升最为显著。第5~10次迭代时，高信噪比的误码率缓慢收敛至 ${10^{ - 5}}$ 以下，直至第10次迭代后，在 $Eb/N_0 \geqslant 20\;{\rm{dB}}$ 时，误码率均降至 ${10^{ - 5}}$ 以下，且实现零误码，产生零误码的原因是仿真帧数有限。而在迭代次数超过10次后，误码率性能并无明显提升。

3.2 Turbo码在实测信道下的仿真

Turbo编码时，分量码采用生成多项式为(7,5)的(2,1,3)递归系统卷积码，并且进行删余操作，删余矩阵为 ${\text{P}} = [1,0;0,1]$ ，以保证Turbo码的编码速率为1/2，数据帧长度取840 ${\rm{bit}}$ ，相应的Turbo码编码交织器深度为1680 ${\rm{bit}}$ ，交织方式为伪随机交织。信道交织参数与上文相同。

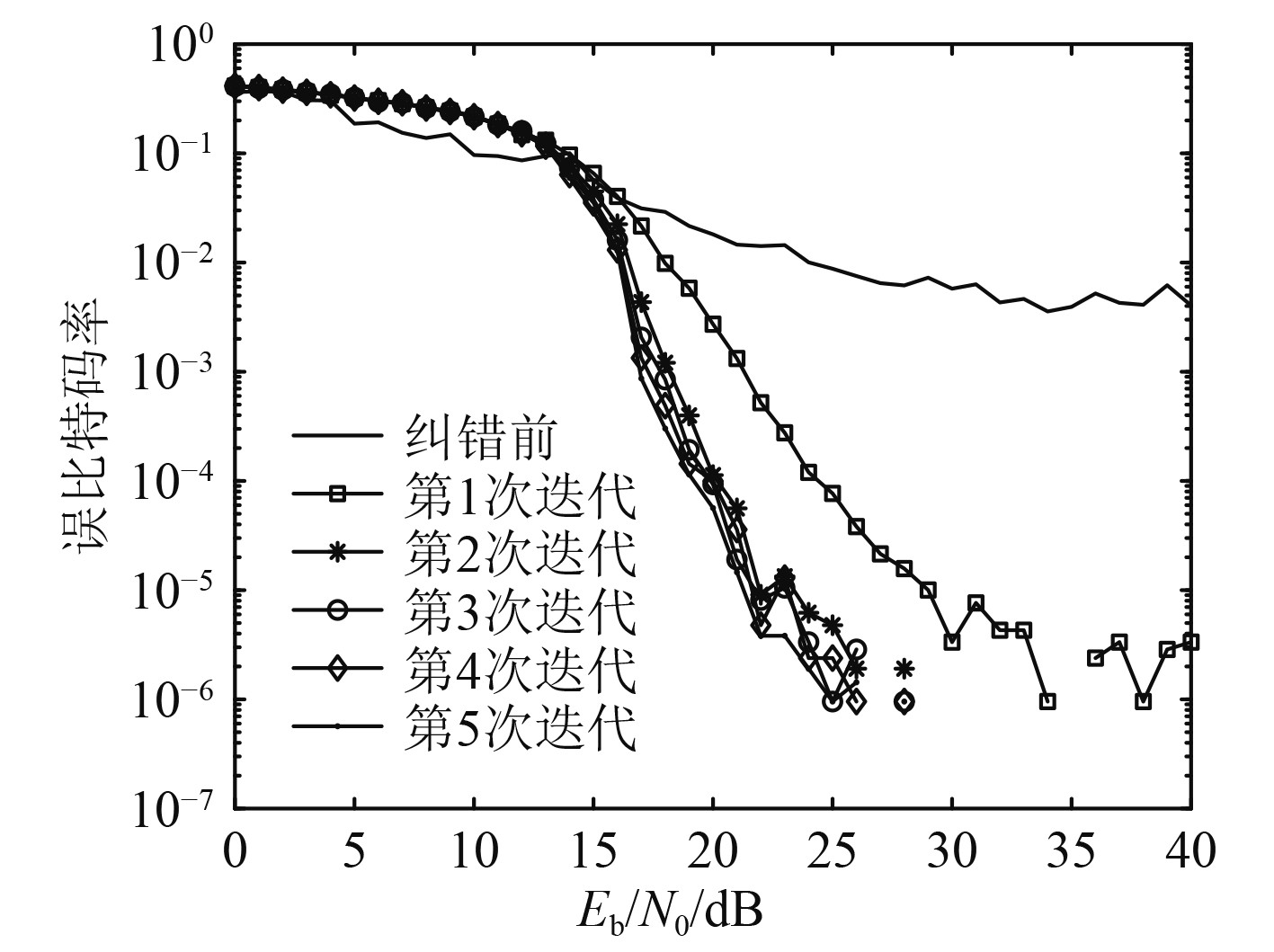
从图5可以看出，采用SOVA译码算法的Turbo码，在 $Eb/N_0 \geqslant 15\;{\rm{dB}}$ 时，编码获得的增益逐渐显现出来。随着迭代次数的增加，误码率性能不断提升。前两次迭代的增益最为明显，其中第1次迭代的误码率性能提升最为显著。而第3~5次迭代的误码率性能并未出现大幅度改善。当迭代次数为5次且 $Eb/N_0 \geqslant 22\;{\rm{dB}}$ 时，可达获得 ${10^{ - 5}}$ 级以下的误码率性能。

4 结　语

本文将Turbo码和QC-LDPC码应用在MC-FH/DPSK水声通信系统中，通过计算机仿真研究了2种纠错编码在实测水声信道中的纠错性能。

仿真结果表明：

1）相同码率的情况下，2种编码在一定条件下均能达到 ${10^{ - 5}}$ 级误码率性能；

2）QC-LDPC码在 $Eb/N_0 \geqslant 20\;{\rm{dB}}$ 时，误码率降至 ${10^{ - 5}}$ 级以下，甚至实现零误码。而Turbo码在 $Eb/N_0 \geqslant 22\;{\rm{dB}}$ 时，误码率才可降至 ${10^{ - 5}}$ 以下。因此在本文实测信道条件下，QC-LDPC码比Turbo码纠错能力更强，有2 dB的编码增益。