近年来,电力推进技术在各类船舶中得到广泛应用,采用电力推进的舰船数量不断增加[1]。由于实际船体、电机、螺旋桨的生产、匹配以及试验的运维成本较高,主要通过软件仿真研究船舶电力推进系统的外部特性。然而,船舶电力推进系统模型复杂计算量巨大,在确保仿真结果准确性的前提下提高仿真效率尤为重要。
船舶电力推进系统要求推进电机既能在低速时提供高扭矩,又能在恒功率条件下具有较宽的调速范围[2],但由于传统三相感应电机构成的交流传动系统调速范围有限[3],若只是简单地采用更大功率电机和大容量变频器,会导致电机体积和功率器件的容量都要增大,造成经济和能源上的浪费[4-6]。相比于同等容量的三相电机,多相电机结构简单、造价低、控制自由度多[3]、功率密度高、容错能力强 [7-8],可以使用低功率等级器件实现大功率传动[9]。因此现代船舶电力推进系统的推进电机大多采用多相电动机[10]。
二极管中点钳位(Neutral-Point Clamped,NPC)型三电平逆变器具有效率高,谐波含量少,开关频率低,开关管承受电压低,输出波形正弦度高等优点[11],适用于高电压大功率场合,如多相电机的驱动等。但该结构控制复杂,所用功率器件较多,相应的开关状态也较多,导致计算量巨大,成倍拖慢船舶电力推进系统整体仿真速度,使得时间长度为几分钟的仿真所花费的时间动辄达数小时。
目前NPC型逆变器的技术已较为成熟,但暂时还没有通过简化其结构或减少计算量来提高仿真速度的可靠方法。为提高船舶电力推进系统的整体仿真速度,本文对一种由NPC型三电平逆变器向十二相感应电机供电的船舶电力推进系统建模仿真,经分析验证,提出由受控电压源替代逆变器的仿真优化策略。
1 船舶电力推进系统 1.1 主要结构图1为一种船舶电力推进系统的结构图,4000 V直流母线经NPC型三电平逆变器向十二相感应电动机供电,单台电机额定相电压峰值为3450 V,采用双机双桨模式,即2台电机经以同轴串联的方式带动螺旋桨负载。
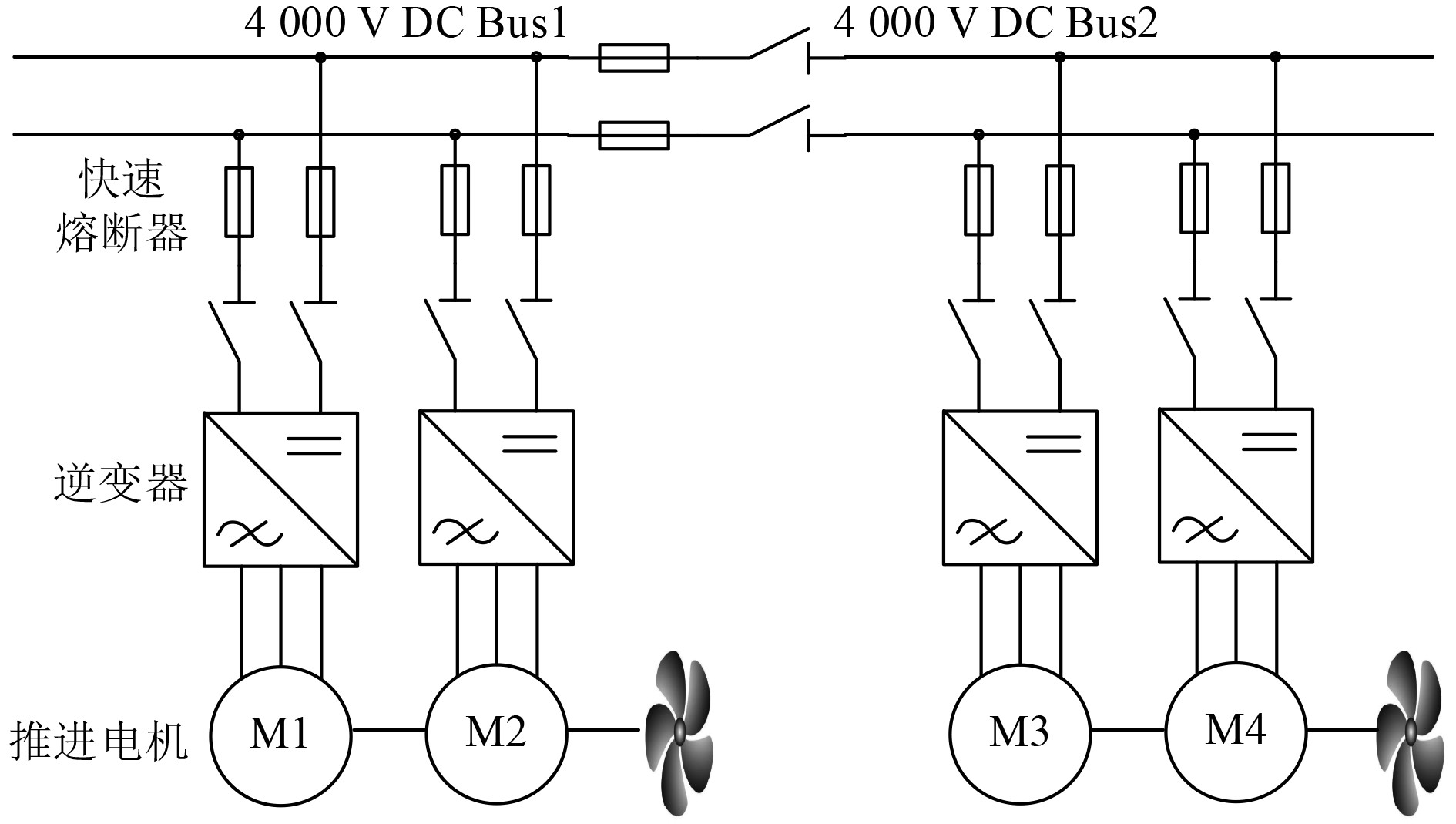
|
图 1 舶电力推进系统结构图 Fig. 1 Structure diagram of the marine electric propulsion system |
图2为逆变器拓扑结构。由三电平中点钳位型(NPC)H桥构成4组结构相同的三相逆变器单元,各相输出与中性点间电阻R1阻值为1 MΩ,每组逆变器单元依次延后15°,输出最大相电压峰值可达4000 V,可满足电机驱动的要求。采用回馈制动,制动电阻R2的阻值为7 Ω。当某一个电容器上电压超过2240 V时,相应的电阻回路导通,投入制动电阻,以消耗回馈的能量,电压下降到2190 V时开关断开,切除制动电阻。
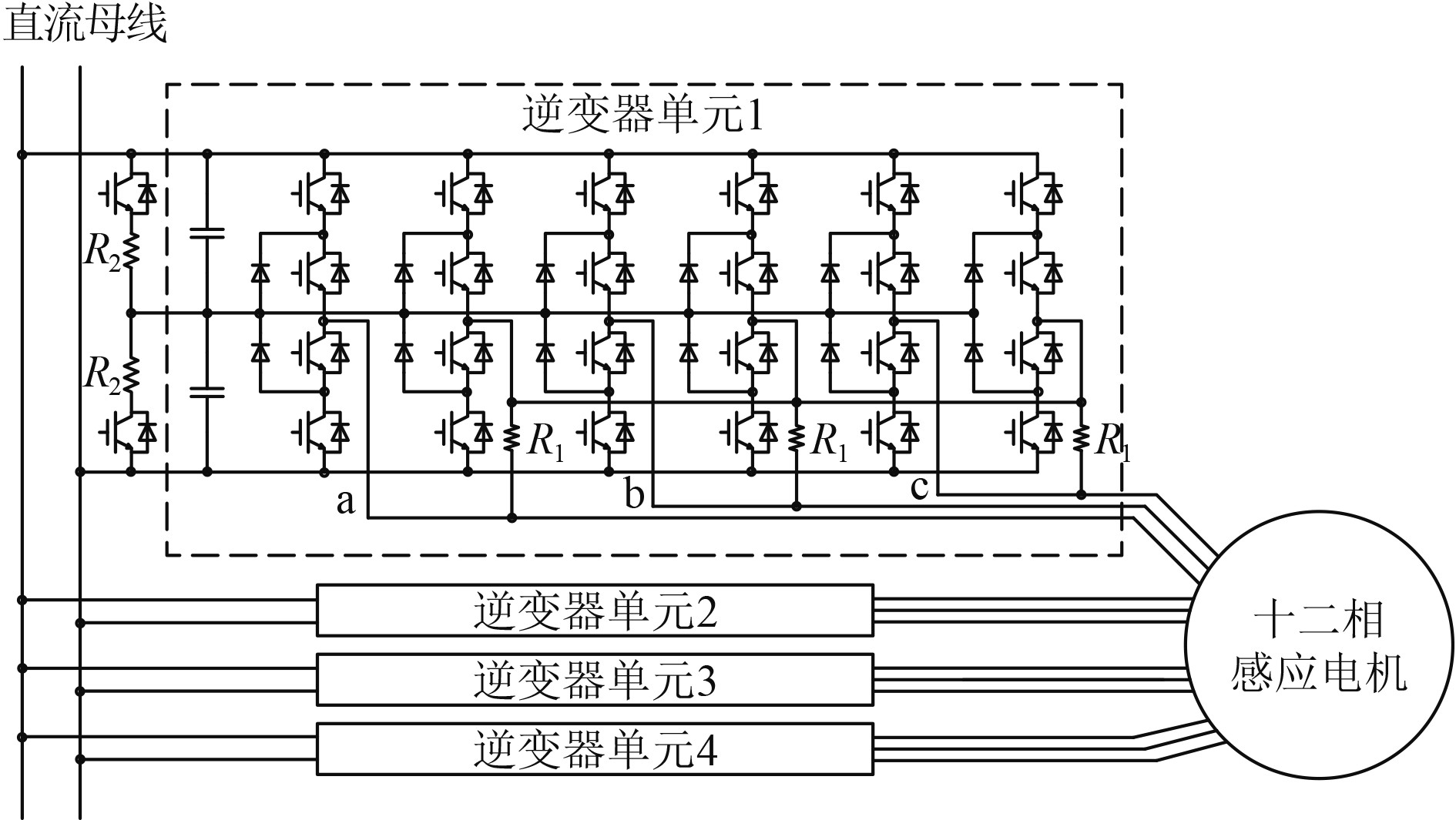
|
图 2 逆变器拓扑结构 Fig. 2 Topology of the inverter |
图3为单相NPC型逆变器拓扑结构,功率开关器件Sa1,Sa2,Sa3,Sa4采用IGBT,分别与二极管VDa1,VDa2,VDa3,VDa4反并联,每个半桥臂的中点由二极管VD1,VD2钳位于支撑电容C1,C2的中点m。
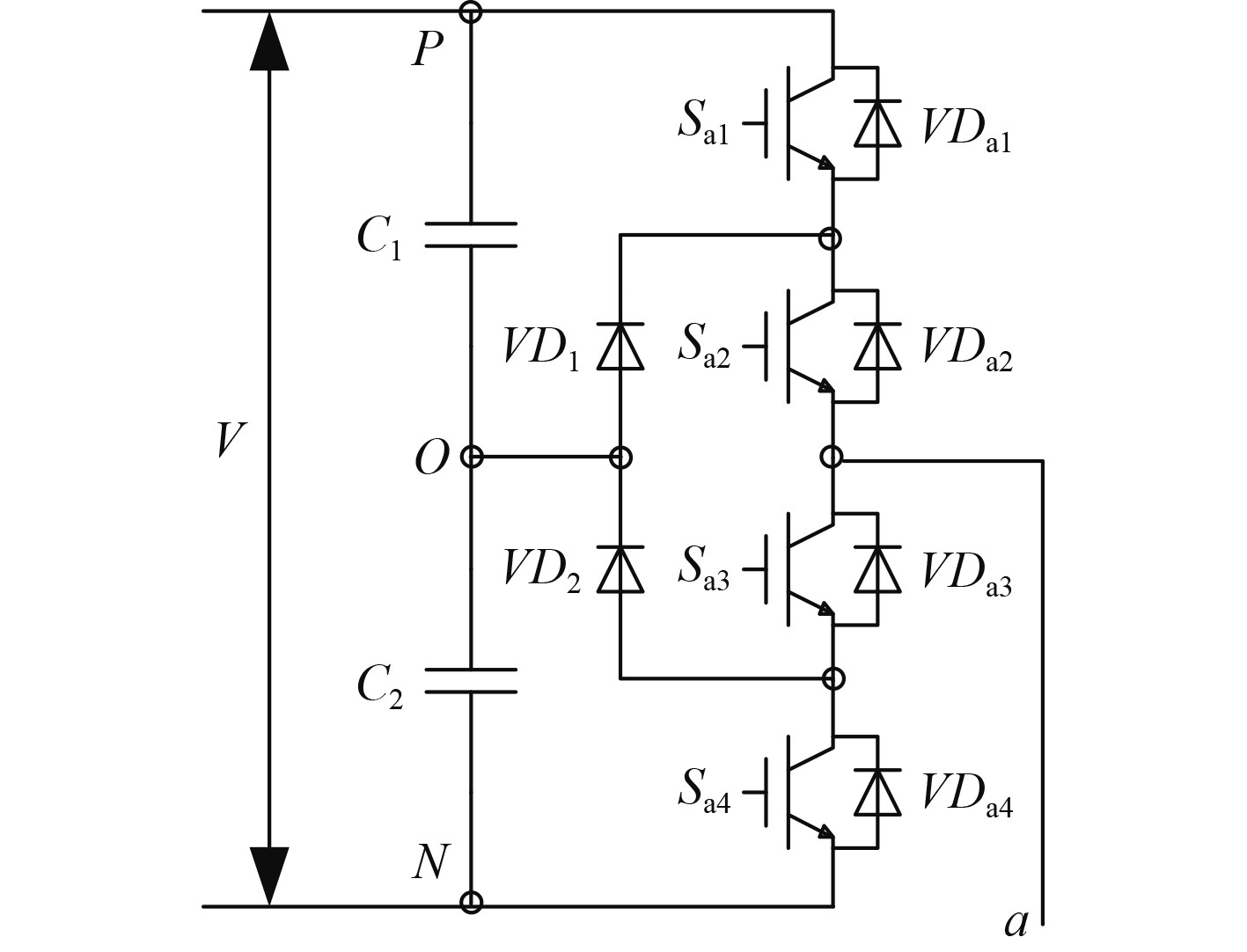
|
图 3 NPC型逆变器单相拓扑结构 Fig. 3 The single-phase topology of NPC inverter |
Sa1,Sa2导通,Sa3,Sa4断开时,电流由P点经Sa1 ,Sa2流向a点,a点电位为+V/2,若电流反向,则经VDa1,VDa2流向P点,a点电位仍为+V/2;Sa1,Sa2断开,Sa3,Sa4导通时,电流由N点经Sa3,Sa4流向a点,a点电位为-V/2,若电流反向,则经VDa3,VDa4流向N点,a点电位仍为-V/2;Sa1,Sa4断开,Sa2,Sa3导通时,电流由O点经VD1 ,Sa2流向a点,a点电位为0,若电流反向,则经VD2,Sa3流向O点,a点电位仍为0。
1.3 十二相感应电动机模型十二相感应电机绕组结构如图4所示。定子绕组分为abc,def,ghi,jkl等4套星型联结的三相对称绕组,每套绕组相角差为15°,组内相角差为120°转子为标准鼠笼型绕组。
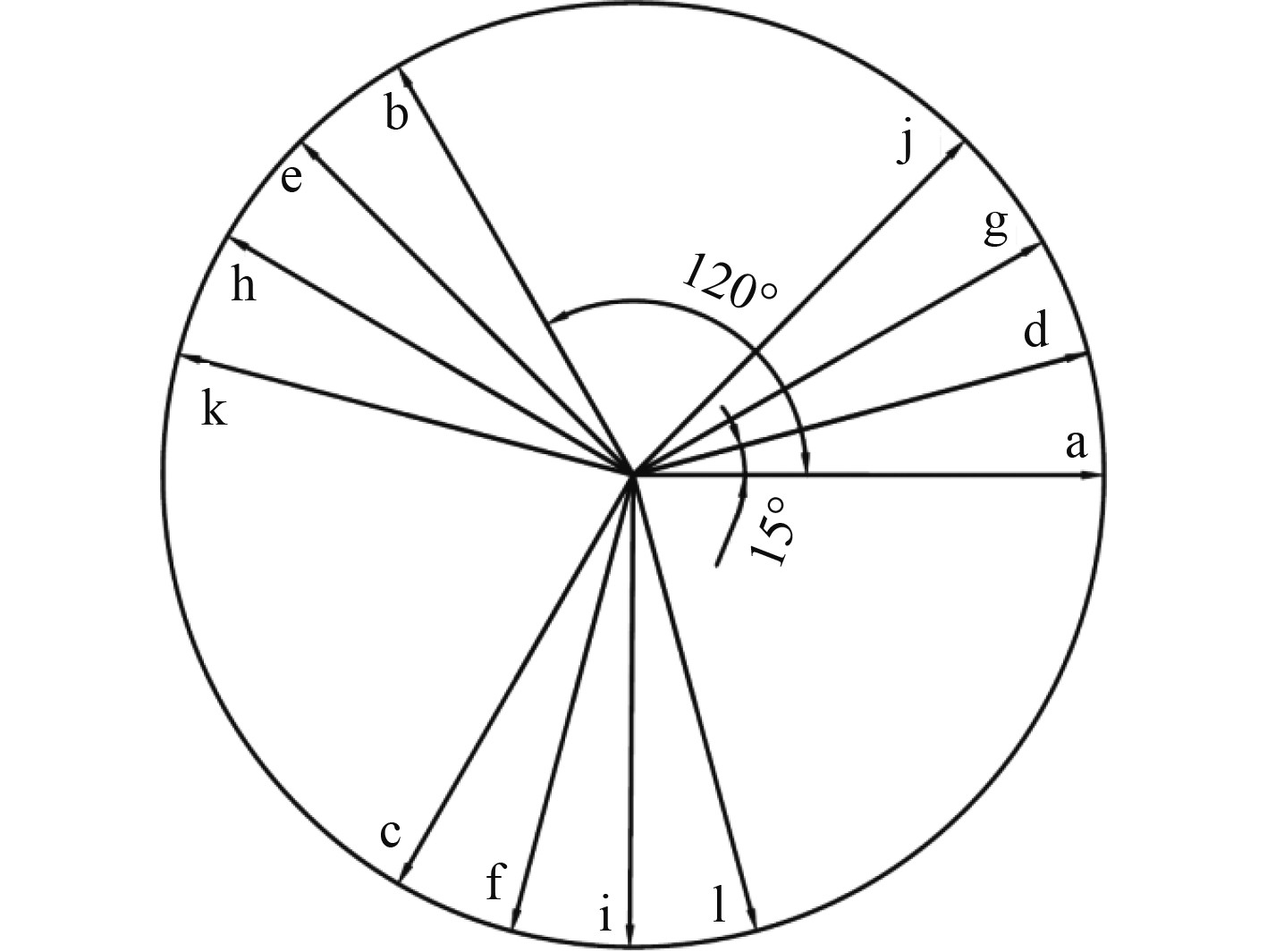
|
图 4 十二相电机绕组结构 Fig. 4 Winding structure of twelve-phase induction motor |
其数学模型如下:
磁链方程
| $ \left\{ \begin{gathered} {{\psi }_{s}}{ = }{{L}_{{ss}}}{{i}_{s}}{ + }{{L}_{{sr}}}{{i}_{r}} ,\\ {{\psi }_r}{ = }{{L}_{{rr}}}{{i}_{r}}{ + }{{L}_{{rs}}}{{i}_s}。\\ \end{gathered} \right. $ | (1) |
式中:
电压方程
| $\left\{\begin{array}{l}{{U}}_{{s}}={{R}}_{{s}}{{i}}_{{s}}+p{\psi}_{{s}},\\ {{U}}_{{r}}={{R}}_{{r}}{{i}}_{{r}}+p{\psi}_{r}。\end{array} \right.$ | (2) |
式中:
转矩方程
| $ {T_{e}} = \frac{1}{2}{n_{p}}\left( {{i}_{r}^T\frac{{{\rm{d}}{{L}_{{rs}}}}}{{{\rm{d}}{\theta _{r}}}}{{i}_{s}} + {i}_{s}^T\frac{{{\rm{d}}{{L}_{{sr}}}}}{{{\rm{d}}{\theta _{r}}}}{{i}_{r}}} \right)。$ | (3) |
式中:
运动方程
| $ \frac{J}{{{n_{p}}}}\frac{{d{\omega _{r}}}}{{{\rm{d}}t}} = {T_{e}} - {T_{L}} 。$ | (4) |
式中:
电力推进船舶中,螺旋桨为电动机的主要负载,所采用螺旋桨的转矩表达式:
| $ M = {K_M}'\rho {D^3}(v_p^2 + {n^2}{D^2})。$ | (5) |
式中:
螺旋桨推力系数
| $ {K_M}' = {K_M}'({J'}),$ | (6) |
式中,
| $ {J'} = \frac{{{v_p}}}{{\sqrt {v_p^2 + {n^2}{D^2}} }} 。$ | (7) |
由螺旋桨的转矩表达式可知,当螺旋桨进速一定时,转矩可近似看作与转速的几平方成正比。
2 推进电机的磁场定向控制建模船舶推进电机要求具有较大调速范围,故选用磁场定向控制。根据磁动势不变的原理,将自然坐标系上的十二相电压、电流变换到旋转的MT坐标系,转子磁链方向定为与M轴同向,T轴与M轴正交,从而转子磁链大小与其M轴分量大小相等,转子磁链T轴分量为0,如下式:
| $ \left\{ \begin{gathered} {{\psi }_{{{rM}}}}{ = }{{\psi }_{{r}}}{ = }{{L}_{{m}}}{{i}_{{s}{{M}}}}{ + }{{L}_{r}}{{i}_{{r}{{M}}}} ,\\ {{\psi }_{{{rT}}}}{ = 0 = }{{L}_{{m}}}{{i}_{{{st}}}}{ + }{L_r}{{i}_{{{rT}}}}. \end{gathered} \right. $ | (8) |
式中:
进一步推得按转子磁场定向下的转子磁链表达式:
| $ {{\psi }_{\text{r}}} = \frac{{{{L}_{\text{m}}}}}{{{{T}_{r}}p + 1}}{{i}_{{s}{\text{M}}}},$ | (9) |
式中,
| $ {T_{e}} = {n_{p}}\frac{{{{L}_{{m}}}}}{{{{L}_{\text{r}}}}}{{\psi }_r}{{i}_{{s}{{T}}}}。$ | (10) |
可见转子磁链仅受定子电流的M轴分量影响,控制转子磁链一定时,转矩仅由定子电流的T轴分量决定,从而实现对磁链和转矩的单独控制。
图5为磁场定向控制的原理图。将给定转速与实际转速的偏差输入转速外环的PI调节器,得到转矩参考值,进而计算出定子电流的转矩分量参考值IsT*。转速经函数发生器得到磁链参考值,进而计算出定子电流的磁链分量参考值IsM*。测得逆变器输出的各相定子电流的实际值Isa,Isb,…Isl,经坐标变换得到电流实际值的转矩分量IsT、磁链分量IsM,分别与各自参考值做偏差,输入内环的电流PI调节器,输出定子电压的参考值VM*和VT*,经过坐标反变换得到各相电压值Va*,Vb*,…Vl*,经SPWM算法得到NPC型三电平逆变器的门极驱动信号,输入逆变器。
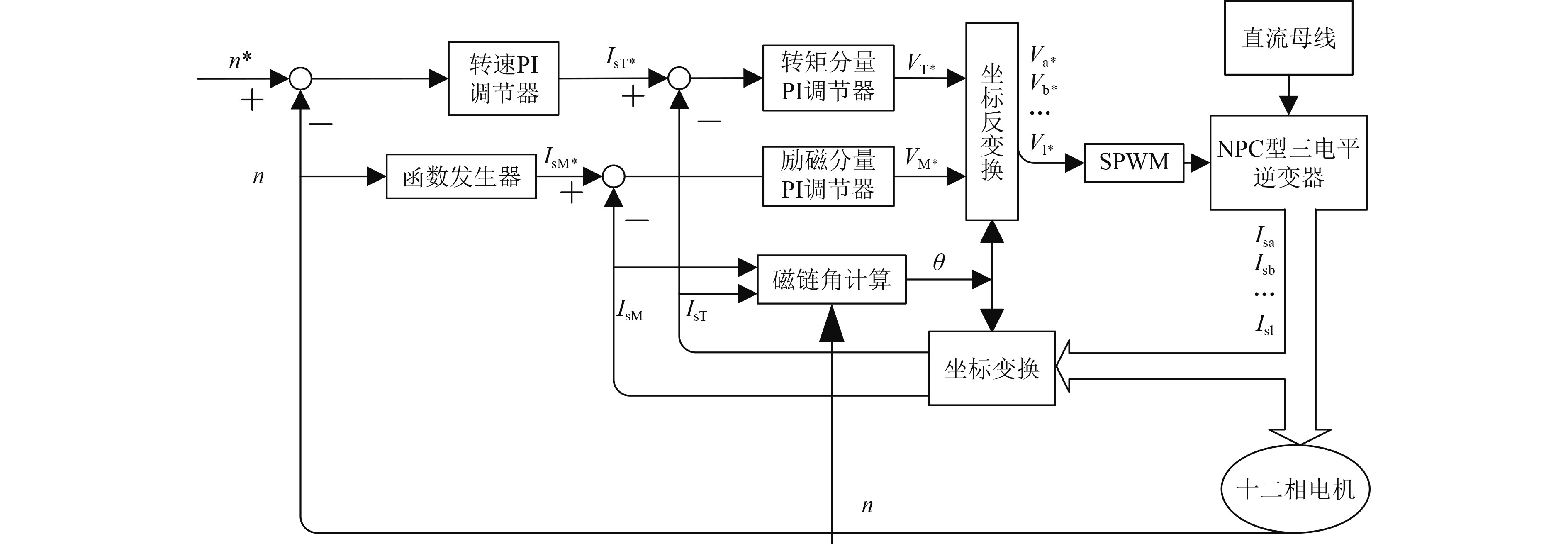
|
图 5 磁场定向控制原理图 Fig. 5 Schematic diagram of field oriented control |
原模型结构复杂,计算量大,为提高仿真运行速度,提出一种仿真优化策略,即用Matlab/Simulink中受控电压源模块替换逆变器,该模块响应迅速,无滞后环节,谐波少,输出波形稳定,随动性良好,可即时获得所需电压。图6为优化模型的拓扑结构图,将磁场定向控制获得的各相电压的参考值Va*、Vb*、···Vl*作为各受控电压源的输入,输出电压完美跟随参考值,受控电压源“星”接后连至电机的各相。通过受控电流源接入制动回路等效回馈电能的过程:用测得的电动机瞬时功率P除以直流侧电压,按相应比例折算为受控电流源输出电流值。同样地,由电容电压控制电阻回路的通断。相对来说,这种优化策略计算量较少,响应快,可将仿真时间大幅减少,外特性也略有提高。
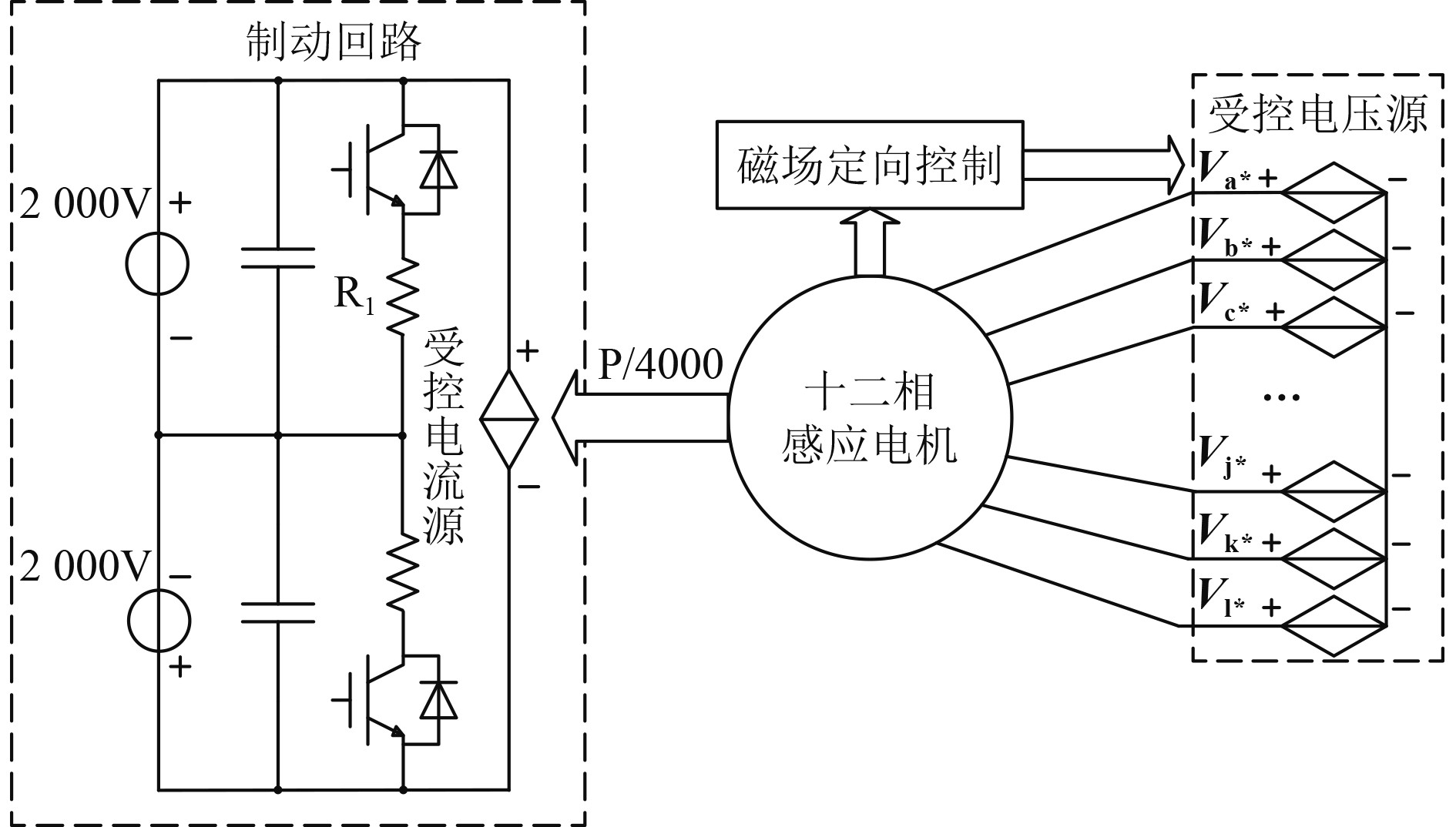
|
图 6 优化模型拓扑结构图 Fig. 6 Topology of the optimization model |
在Matlab/Simulink中对模型进行仿真,仿真时间长度设置为1 min,原模型仿真用时为3619.93 s,优化模型仿真用时为93.12 s,和原模型相比,优化模型仿真时间缩短了近40倍,速度和效率有显著提升。
4.1 转速响应对电机充磁5 s后给电机180 r/min指令,20 s时指令变更为−130 r/min,40 s时控制信号变为150 r/min。由于实际转速不会突变,将转速指令变化的最大速率限定为18 r/min。
图7为原模型与优化模型对不同转速指令的转速响应。从5 s开始输入转速指令,15 s时,转速给定到达180 r/min,原模型于15.8 s转速达到180 r/min,优化模型于15.57 s转速达到180 r/min;20 s开始减速并反向加速,37.22 s时,转速给定达到−130 r/min,原模型在37.79 s达到稳定转速−129.6 r/min,优化模型在37.77 s转速达到−130 r/min;40 s开始升速,55.55 s时,转速给定上升至150 r/min,原模型56.2 s达到稳定转速149.6 r/min,优化模型56.3 s转速达到150 r/min。总体来看,优化模型与原模型转速响应基本一致,差异主要来源于两模型PI参数不同。其次,由于逆变器中纹波的存在导致原模型的转速响应存在微小波动。
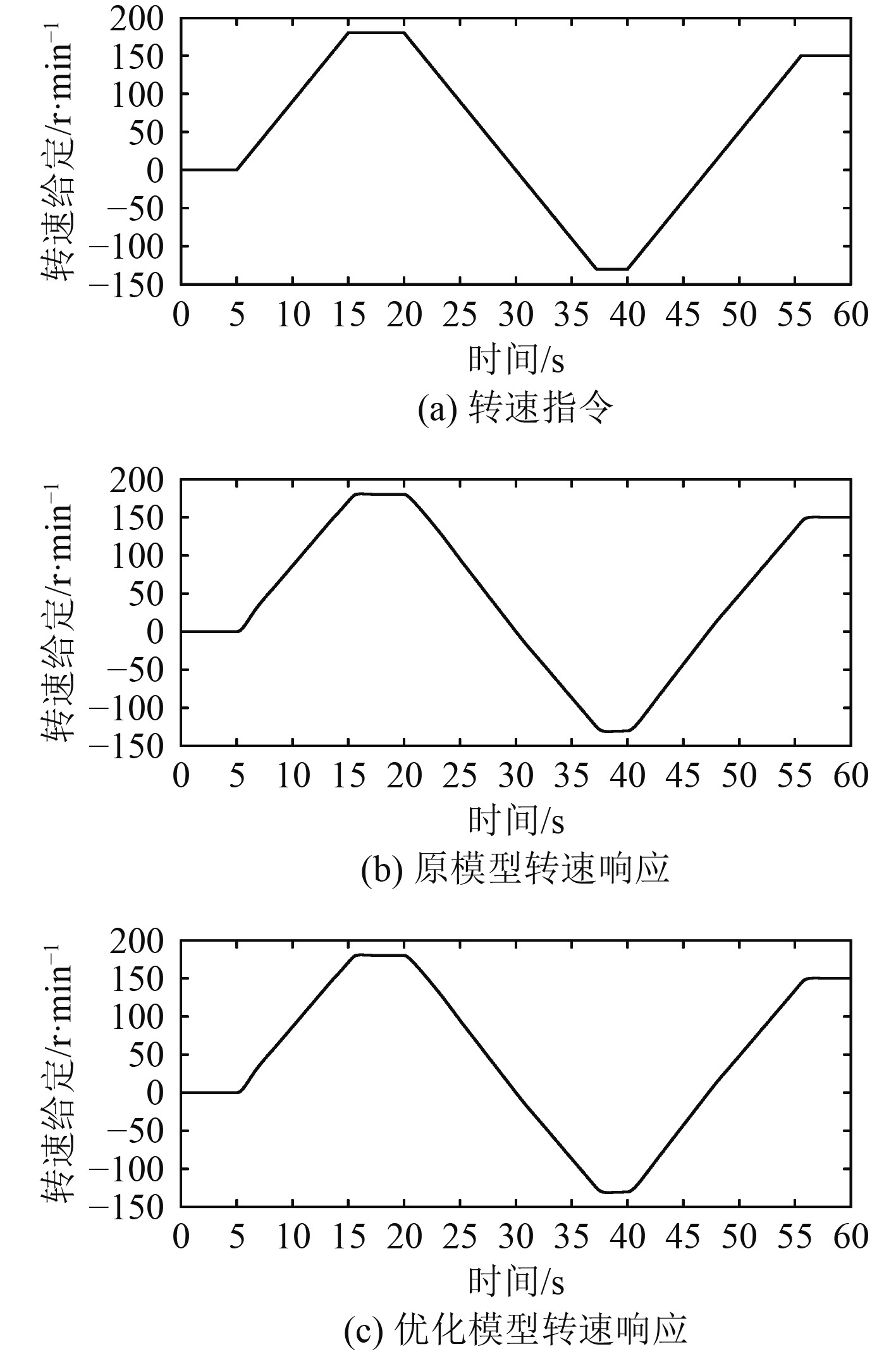
|
图 7 转速特性曲线 Fig. 7 Curve of the speed performance |
图8为两模型加速过程的电流对比,可以看出,优化模型与原模型电流特性基本一致,偏差较小,约为1.4%,两模型在转速指令3次变动中均出现超调。由于优化模型中受控电压源较稳定,不存在开关损耗、中性点偏移和谐波等影响故在运行过程中特性较“硬”,超调较大,响应稍快,电流略低,可调节PI参数满足不同的仿真分析需求。
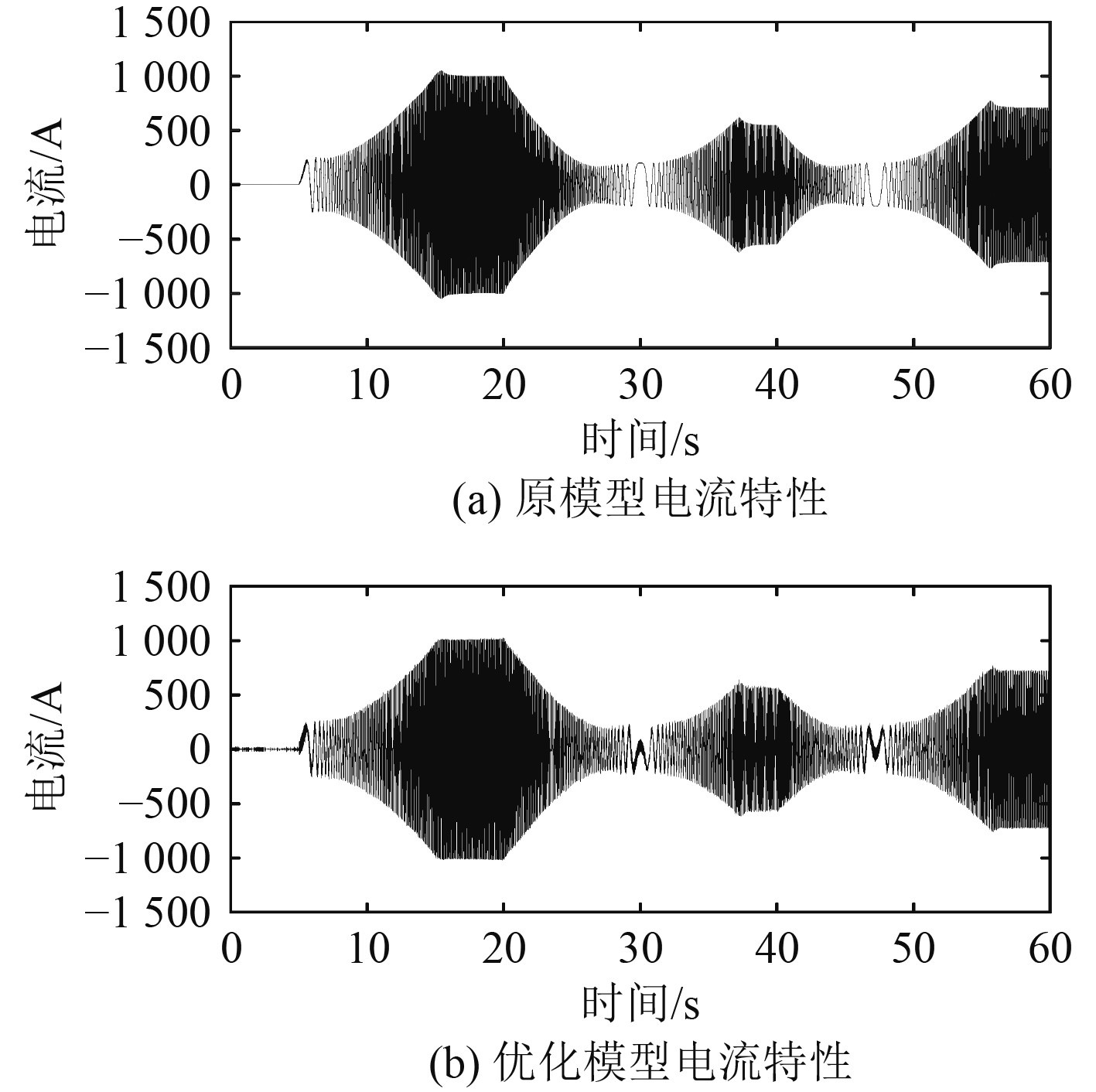
|
图 8 电流特性曲线 Fig. 8 Curve of the current performance |
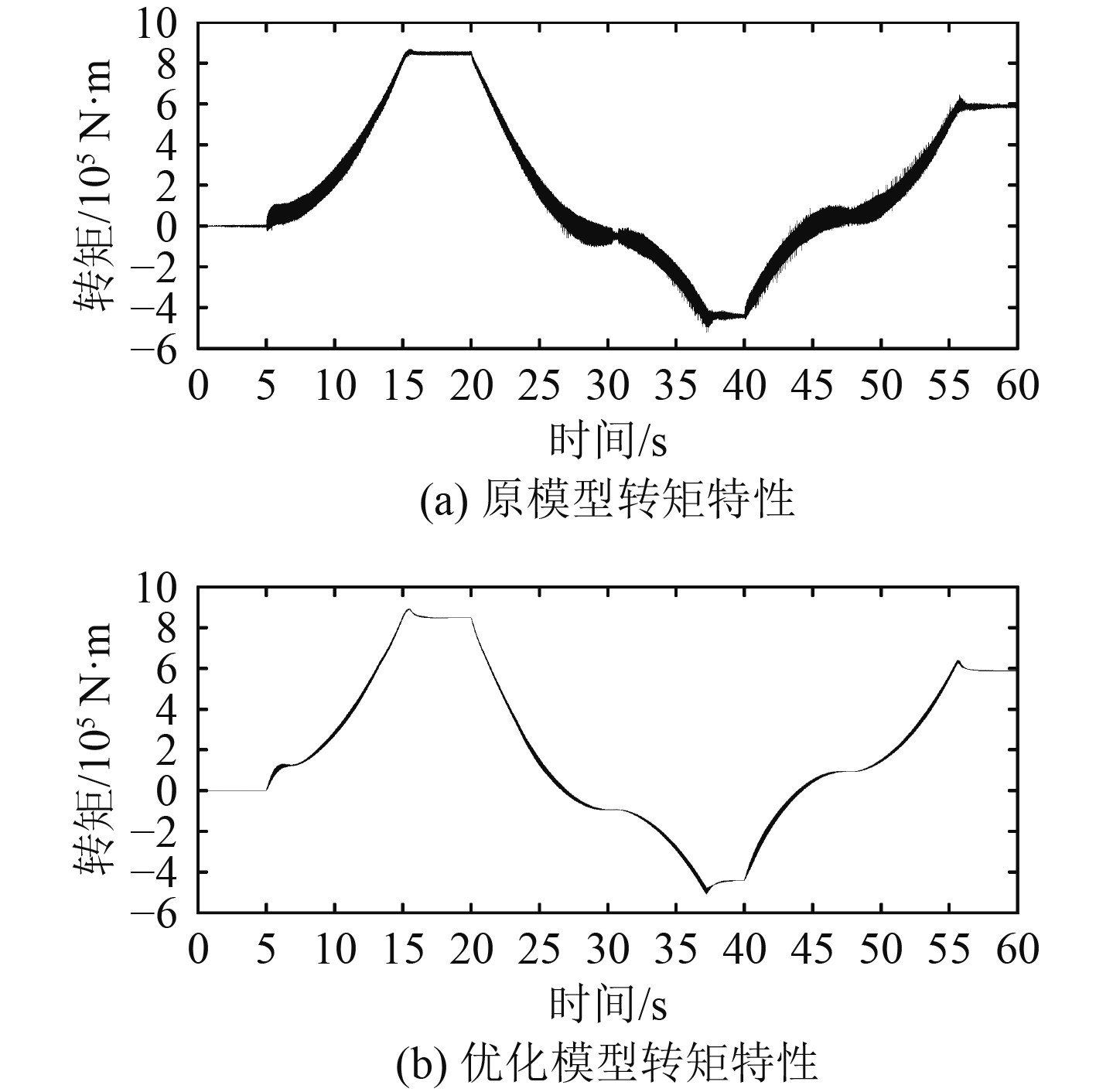
图9为原模型与优化模型在整个过程中的转矩波形图。由式(10)可知,磁场定向控制中,电动机转子磁链保持一定时,电磁转矩正比于电流的转矩分量,相应的,转矩幅值的变化与电流幅值的变化基本一致。从图中可以看出,在运行过程中优化模型转矩较大,转速到达稳态的时间稍快。这是由于优化模型中的转矩脉动主要由电机产生,谐波含量少,脉动幅值小,而原模型除了电机引起的转矩脉动,主要由于逆变器开关状态较多以及中性点电压不均衡导致谐波含量多,因此转矩脉动较大,有明显纹波,响应稍慢,原模型转矩脉动幅值高于优化模型最大约3.7%,此差异影响甚微。
|
图 9 转矩特性曲线 Fig. 9 Curve of the torque |
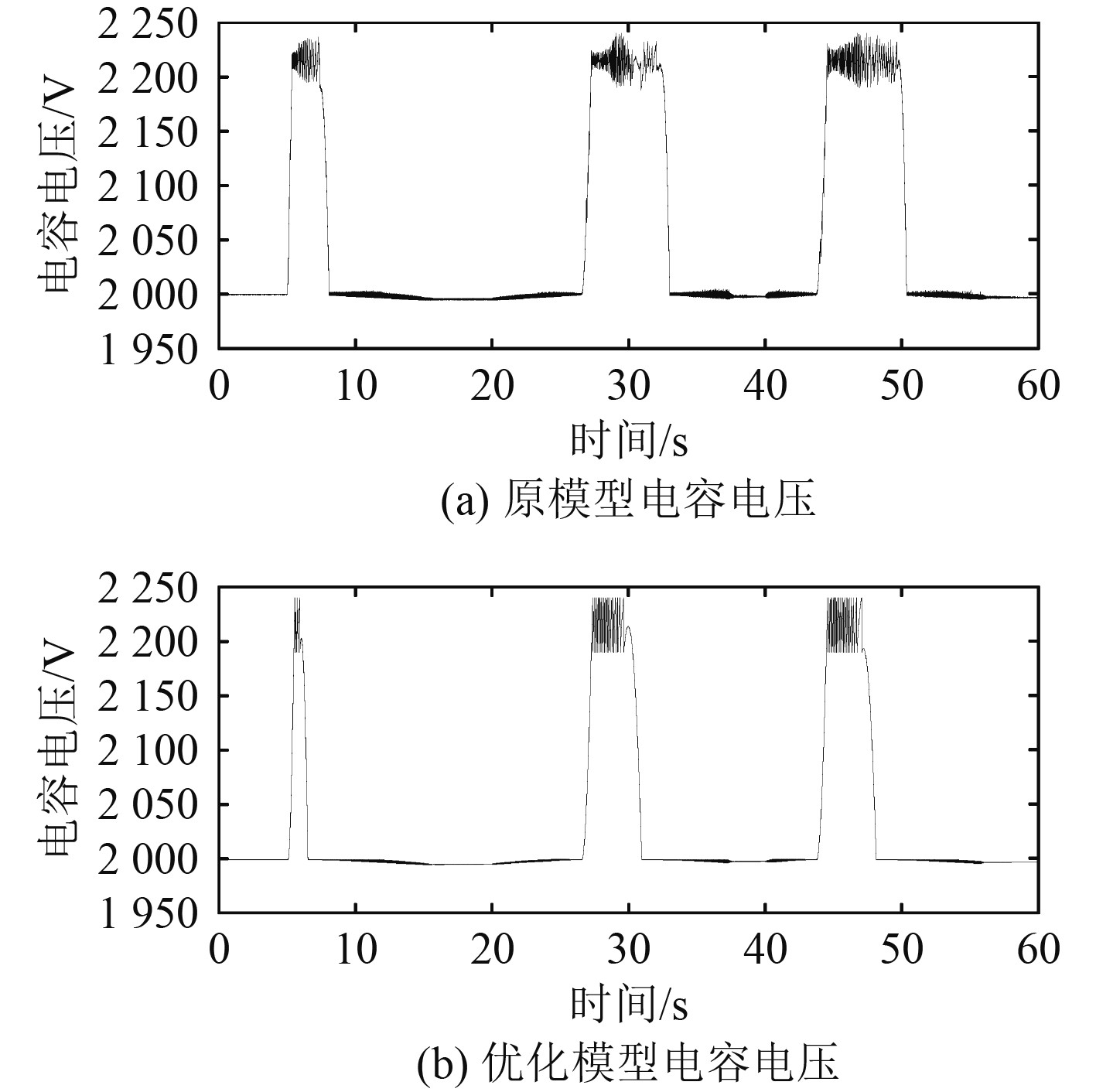
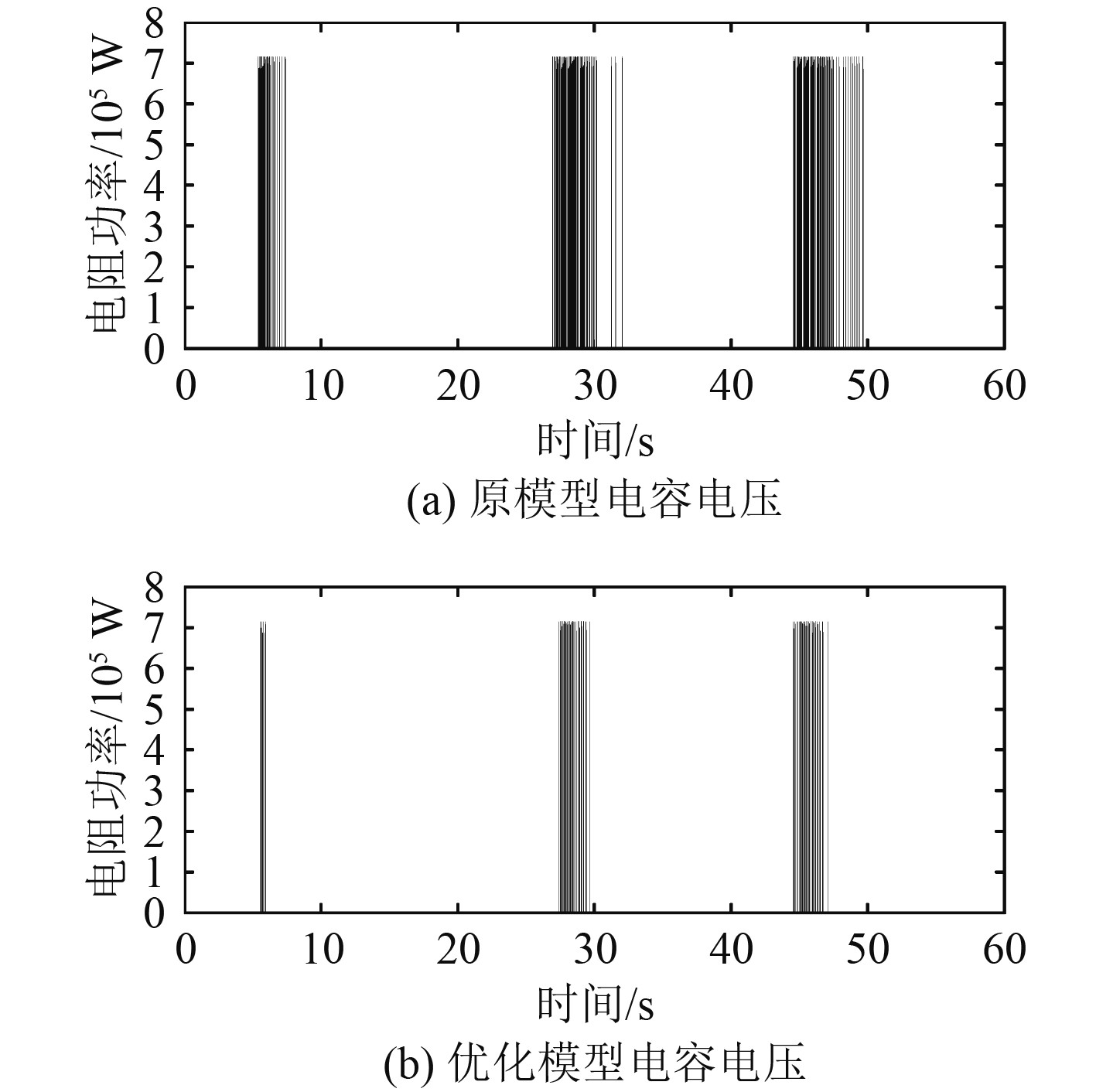
制动过程的电容电压与制动电阻功率的仿真结果如图10与图11所示。两模型电容电压基本一致,制动电阻上的瞬时功率大致相同,但原模型电阻放电时间略长于优化模型,相应的回馈更多电能。可以看到在5 s处由于电机启动导致电容电压升高,电机回馈电能,正转制动和反转制动至速度接近0时,泵升电压达到2240 V,制动电阻出现2次放电。
|
图 10 电容电压特性曲线 Fig. 10 Curve of the capacitor voltage |
|
图 11 制动电阻功率特性曲线 Fig. 11 Curve of the brake resistance power |
结合图8电机转矩波形可以看出,在减速至接近0时,由于转矩脉动,导致转矩过零,与转速反向,工作在发电状态,电机回馈电能。而原模型比优化模型放电时间略长,这时由于原模型中转矩脉动较大、直流侧两电容电压存在不均衡造成单侧电压升高、原模型控制特性较软导致定子电压略高等原因导致的。
5 结 语1)本文分析一种由NPC型三电平逆变器向十二相感应电机供电的船舶电力推进系统结构及控制原理,基于Matlab/Simulink建立其仿真模型。
2)提出一种优化策略,即使用受控电压源替换模型中的NPC型三电平逆变器,用以优化该模型,将仿真耗时缩短数十倍。
3)对比仿真结果,优化模型与原模型在系统的转速响应、转矩及电流特性上基本一致,它们之间存在的微小差异主要由逆变器本身带来的纹波、PI参数不同等因素引起。简化的电压源模型纹波更小、不存在直流侧两电容电压不均等问题。制动性能上由于逆变器损耗、拓扑本身导致的电压不均,包括外环控制稍差等因素,造成过冲电压存在一定差异,回馈的能量不尽相同。但误差也保持在较小的范围内,同理论分析相一致。
4)本文所提出的船舶电力推进系统仿真优化策略,利用受控电压源代替复杂的NPC型三电平逆变器,在各项性能都保持基本一致的前提下,将动辄数小时的实际仿真时长缩短数十倍,同时也减少分析过程中由逆变器产生的不必要干扰,可用于提升船舶电力推进系统整体在诸多工况下的仿真速度。对优化模型的准确性做出了验证,分析优化模型与原模型的性能差异,可用于快速预估船舶电力推进系统的仿真结果,对于解决不同工况中出现的问题,具有一定的参考意义,这种优化策略也可推广至其他异步电机的调速仿真中。
| [1] |
黄泽森, 谢卫, 杜彦清. 船用五相感应电动机的矢量控制研究[J]. 微特电机, 2019, 47(6): 73-77. HUANG Z S, XIE W, DU Y Q. Analysis of vector control for marine five-phase induction motor[J]. Small & Special Electric Machines, 2019, 47(6): 73-77. DOI:10.3969/j.issn.1004-7018.2019.06.016 |
| [2] |
RATNAYAKE K R M N, MURAI Y, WATANABE T. Novel PWM scheme to control neutral point voltage variation in three-level voltage source inverter[C]//Conference Record of the 1999 IEEE Industry Applications Conference. Thirty-Forth IAS Annual Meeting (Cat. No. 99CH36370), Phoenix, AZ, USA: IEEE, 1999: 1950–1955.
|
| [3] |
杨家强, 高健, 金玉龙, 等. 基于矢量控制的多相感应电机电子变极调速技术[J]. 电工技术学报, 2014, 29(3): 96-102. YANG J Q, GAO J, JIN Y L, et al. Electronic pole-changing speed adjusting technology of multiphase induction motors based on vector control[J]. Transactions of China Electrotechnical Society, 2014, 29(3): 96-102. DOI:10.3969/j.issn.1000-6753.2014.03.013 |
| [4] |
SWAMY M M, KUME T J, MAEMURA A, et al. Extended high-speed operation via electronic winding change method for AC motor[J]. IEEE Transactions. on Industry Applications, 2006, 42(3): 742-752. DOI:10.1109/TIA.2006.873657 |
| [5] |
LEVI E, JONES M, VOKOSAVIC S N, et al. A novel concept of a multiphase, multimotor vector controlled drive system supplied from a single voltage source inverter[J]. IEEE Transactions on Power Electronics, 2004, 19(2): 320-335. DOI:10.1109/TPEL.2003.823241 |
| [6] |
KUME T, SWAMY M, SAWAMURA M, et al. A quick transition electronic winding changeover technique for extended speed ranges[C]//2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No. 04CH37551). Aachen, Germany: IEEE, 2004: 3384–3389.
|
| [7] |
LEVI E. Multiphase electric machines for variable speed applications[J]. IEEE Transactions on Industrial Electronics, 2008, 55(5): 1893-1909. DOI:10.1109/TIE.2008.918488 |
| [8] |
LEVI E, BOJOI R, PROFUMO F, et al. Multiphase induction motor drives-a technology status review[J]. IET Electric Power Applications, 2007, 1(4): 489-516. DOI:10.1049/iet-epa:20060342 |
| [9] |
黄启岚, 康敏, 卞韩斌. 多相电机驱动控制系统的设计与实现[J]. 工业仪表与自动化装置, 2021(4): 58-63. DOI:10.3969/j.issn.1000-0682.2021.04.012 |
| [10] |
张亚杰, 赵峰. 用于推进电机的三相变五相电源变压器初步研究[J]. 变压器, 2020, 57(12): 7-9+13. DOI:10.19487/j.cnki.1001-8425.2020.12.002 |
| [11] |
王帅, 解伟, 林晓刚, 等. 基于矢量控制的定子笼型十二相感应电机极对数切换策略[J]. 电机与控制应用, 2021, 48(8): 1-7. WANG S, XIE W, LIN X G, et al. Pole-pair switching strategy of stator cage twelve-phase induction motor based on vector control[J]. Electric Machines & Control Application, 2021, 48(8): 1-7. |
 2023, Vol. 45
2023, Vol. 45
