2. 武汉理工大学 交通与物流工程学院,湖北 武汉 430063;
3. 国家水运安全工程技术研究中心 可靠性工程研究所,湖北 武汉 430063
2. School of Transportation and Logistics Engineering, Wuhan University of Technology, Wuhan 430063, China;
3. Reliability Engineering Institute, National Engineering Research Center for Water Transport Safety, Wuhan 430063, China
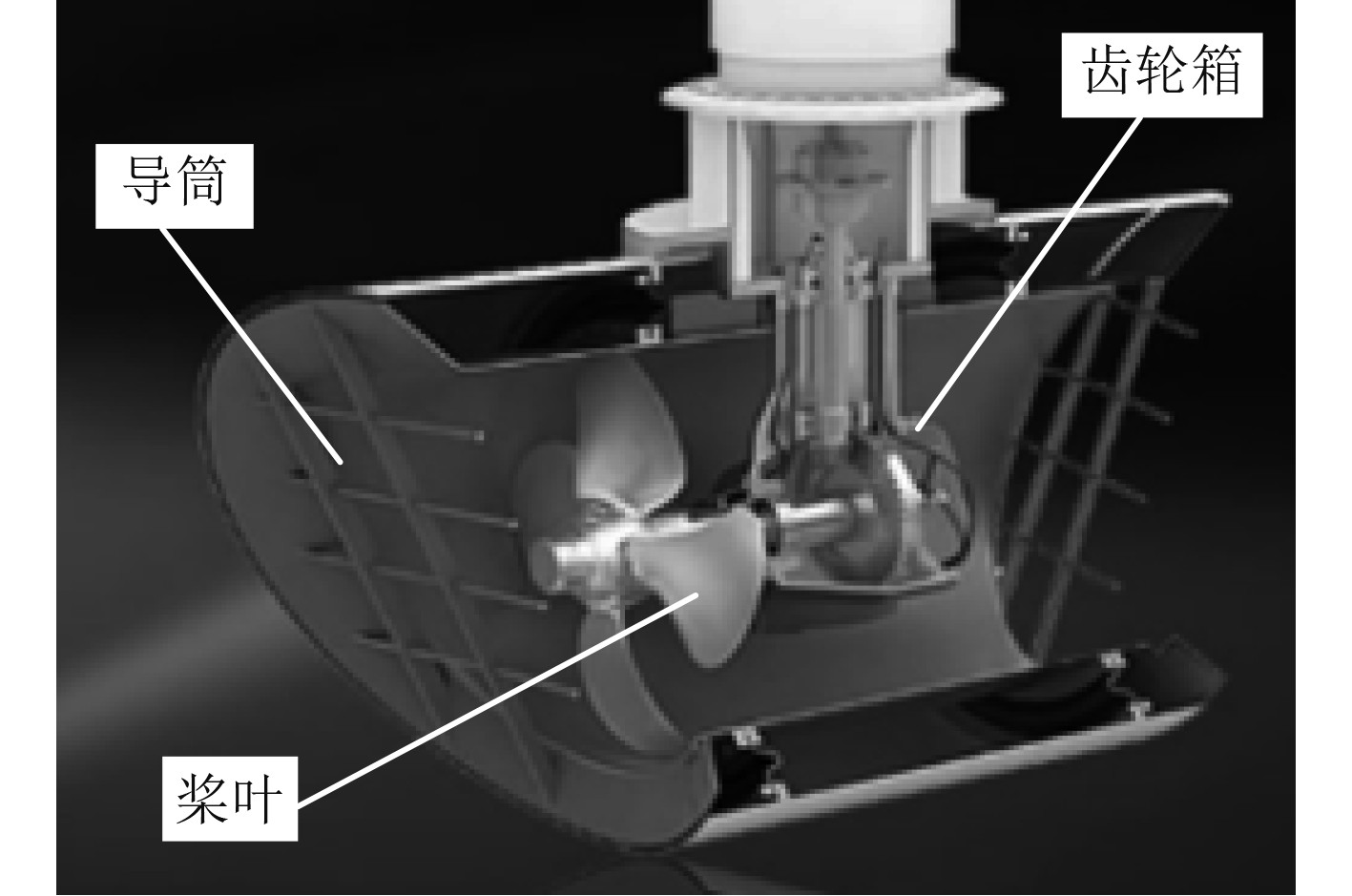
船舶侧推器是一种船舶辅助设备,其结构如图1所示。常规侧推器由导筒、齿轮箱和螺旋桨等部件组成,这些部件占据了导筒通道大量的空间,造成了流体流动附加阻力,同时影响侧推器的射流速度,而且振动和噪声较大、结构复杂、安装繁琐。
|
图 1 常规侧推器 Fig. 1 Conventional thruster |
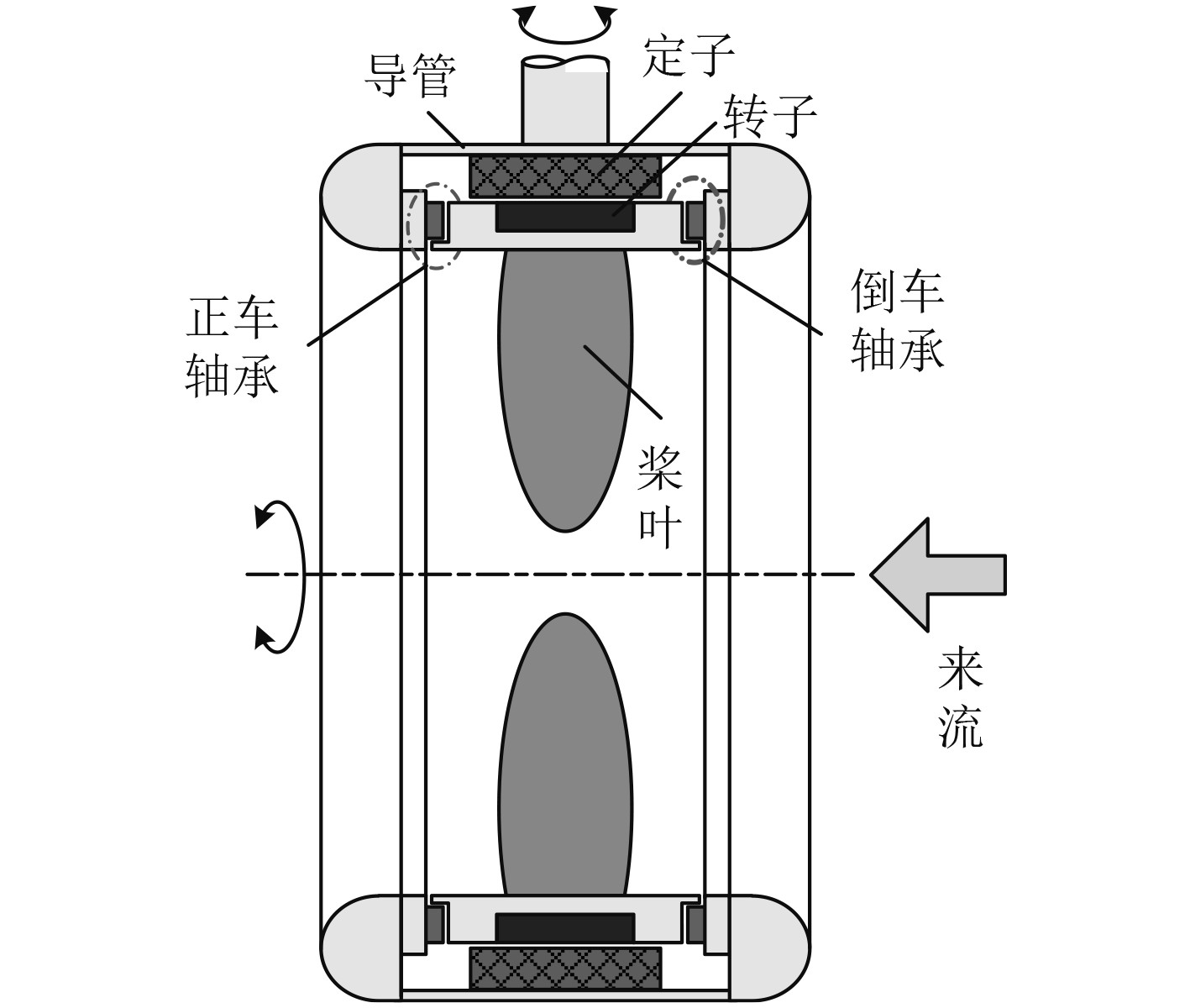
无轴轮缘推进器(Rim-Driven Thruster,RDT)是一种高度集成的电力推进系统,如图2所示,它省略了传动轴系,采用电机与螺旋桨一体化设计,实现了电力直驱[1]。这种设计非常适合用于侧推器,一方面,无齿轮箱等部件可最大限度减少流动阻力,无机械传动可减小振动和噪声;另一方面,如果采用对称的螺旋桨叶型设计,通过电机的正反转,一套无轴侧推进器即可实现双向推力。与同时配备2个传统侧推器实现船舶左右运动的常见形式相比,无轴侧推进器具有明显优势,因此开展无轴侧推器性能研究具有重要意义。
|
图 2 无轴轮缘推进器 Fig. 2 Shaftless rim thruster |
目前,学者们针对常规侧推器[2-3]及无轴推进器的电机[4]、轴承[5]和转子环等水力部件[6]进行了一些研究。无轴侧推进器的研究报道较少,其自身特性及其结构的优化设计有待研究。
本文以无轴轮缘侧推器为研究对象,建立船首−导筒−侧推器流体动力学模型,从流体域建立,网格划分,湍流模型的选取和计算参数设置等几个方面介绍侧推器水动力性能的数值计算过程,研究无轴侧推器水动力性能变化规律,并通过改变桨叶结构参数,对无轴侧推器水动力性能进行优化分析。
1 数学模型 1.1 基本控制方程和湍流模型无轴轮缘侧推器工作时,周围流体的运动状态,受到流体力学基本控制方程的约束。对侧推器水动力性能进行CFD求解时,需遵循基本控制方程中的连续性方程和动量守恒方程,如下式[7]:
| $ \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0 ,$ | (1) |
| $\begin{split} & \rho \frac{{\partial {u_i}}}{{\partial t}} + \rho \frac{{\partial {u_i}{u_j}}}{{\partial {x_j}}} = - \frac{{\partial p}}{{\partial {x_j}}} + \nu \frac{\partial }{{\partial {x_j}}}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) + \\ & \quad\quad \frac{\partial }{{\partial {x_j}}}\left( { - \rho \overline {{{u'}_i}{{u'}_j}} } \right) 。\end{split}$ | (2) |
其中:t为流动时间;ui, uj(i, j=1,2,3)为平均速度分量;ρ为水的密度;P为压强;ν为水的动态粘度;
本文采用的湍流模型为RNG k−ε,RNG k−ε湍流模型是将RNG的基本方法应用于N−S方程,并引入湍流动能K以及耗散率ε,方程形式如下:
| $\begin{split} &\frac{\partial }{{\partial t}}(\rho k) + \frac{\partial }{{\partial {x_i}}}(\rho k{u_i}) = \frac{\partial }{{\partial {x_j}}}\left[ {{\alpha _k}{\mu _{eff}}\frac{{\partial k}}{{\partial {x_j}}}} \right] +\\ & {G_k} + {G_b} - \rho \varepsilon - {Y_M} + {S_k},\end{split}$ | (3) |
| $ \begin{split} &\frac{\partial }{{\partial t}}(\rho \varepsilon ) + \frac{\partial }{{\partial {x_i}}}(\rho \varepsilon {u_i}) = \frac{\partial }{{\partial {x_j}}}\left[ {{\alpha _\varepsilon }{\mu _{eff}}\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] +\\ & {C_{1\varepsilon }}\frac{\varepsilon }{k}\left( {{G_k} + {G_{3\varepsilon }}{G_b}} \right) - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k} - {R_\varepsilon } + {S_\varepsilon }。\end{split} $ | (4) |
侧推器螺旋桨在运转时几乎不存在传统的进速。侧推力主要由螺旋桨的推力和船体两侧产生的压力差构成,因此其水动力性能可以用螺旋桨推力系数CT、扭矩系数CQ以及船体两侧的压差系数CF表达[3,8]:
| $ \left\{ {\begin{aligned} & {{C_T} = \frac{T}{{\rho {n^2}{D^4}}}},\\ &{{{\text{C}}_{Q}} = \frac{{\text{Q}}}{{\rho {n^2}{D^5}}}} ,\\ & {{{\text{C}}_{F}} = \frac{{\text{F}}}{{\rho {n^2}{D^4}}}} 。\end{aligned}} \right. $ | (5) |
式中:T为轴向推力;Q为扭矩;F为船体两侧受到压力差;ρ为水的密度;D为螺旋桨的直径;n为转速。
2 侧推器水动力性能仿真 2.1 三维模型与计算域无轴侧推器采用的螺旋桨为Ka型桨,主要桨叶参数如表1所示。
|
|
表 1 无轴侧推器桨叶参数 Tab.1 Parameters of shaftless thruster blades |
Ka型桨叶模型采用坐标转化法建立。无轴轮缘侧推器的桨叶与传统桨有明显的差异,传统螺旋桨叶根与桨毂连接,由轴带动桨叶旋转,为了满足强度要求,叶根至叶梢的叶截面厚度是逐渐减小的。无轴侧推器是由转子环带动桨叶旋转,故与传统桨叶截面厚度相反,根据实际情况,叶根剖面几何形式可以灵活变动,处理之后的桨叶截面如图3所示[9-10]。

|
图 3 桨叶剖面示意图 Fig. 3 Schematic diagram of blade section |
无轴侧推器结构如图4所示。运用三维软件建立船首−导筒−螺旋桨三维模型,并把尾部进行光顺处理,经过适当比例缩放后,船首模型总长为1.8 m,最宽1.7 m,吃水深度0.55 m,导筒最短长度为0.7 m,侧推器中心距离水位线0.3 m。

|
图 4 无轴轮缘侧推器结构 Fig. 4 Structure of shaftless wheel rim thruster |
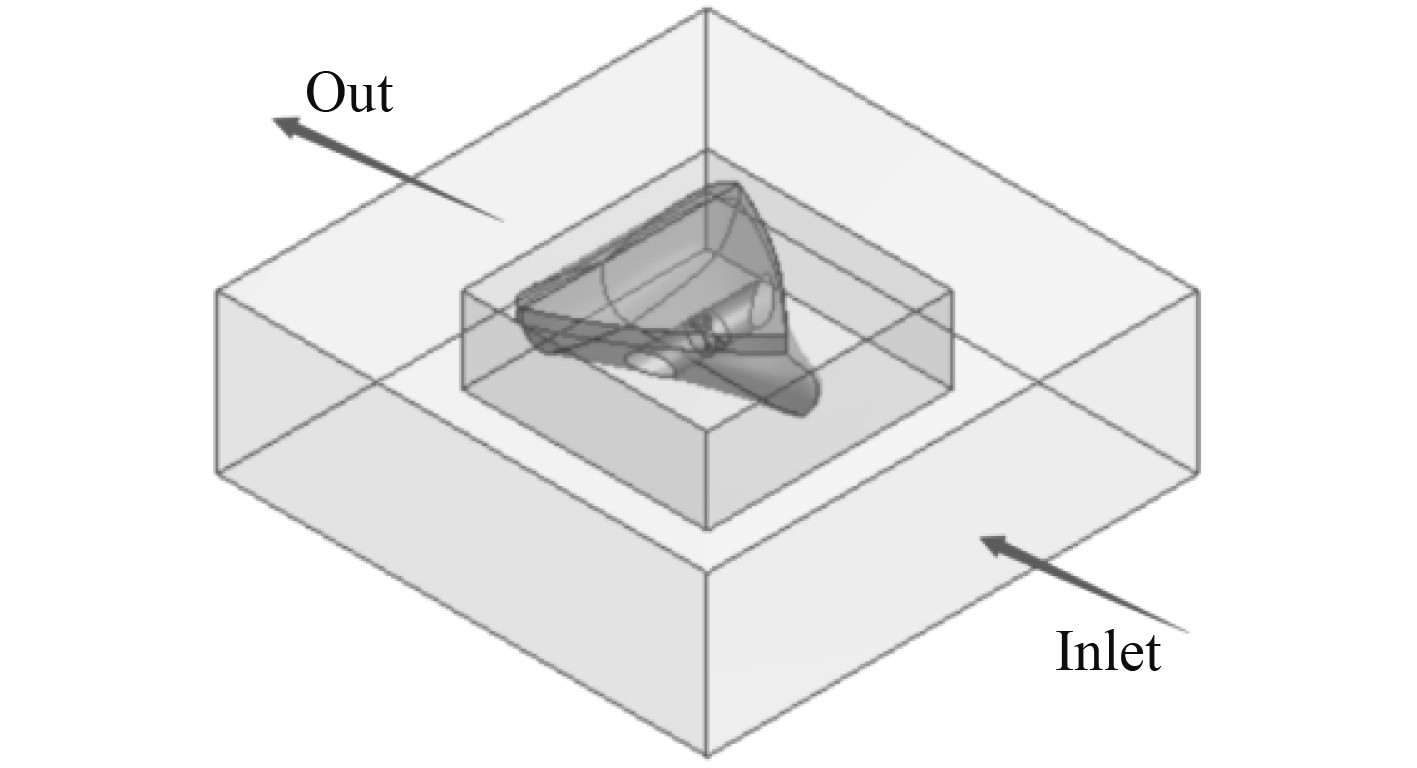
计算域分为外域、中域和内域,外域的高度为5 D,长度和宽度为16 D,进口距离桨中心8 D,出口距离桨中心8 D;中域包含船首,高度为3 D,长度和宽度为8 D,建立中域可以起到对船首部分进行局部加密的作用,并不是实际流域;内域包含螺旋桨,为一个直径1 D,长0.4 D的小圆柱体。外域为静止域,内域为旋转域,计算域模型如图5所示。
|
图 5 计算域示意图 Fig. 5 Schematic diagram of computational domain |
采用多面体网格划分无轴侧推器,多面体网格不仅质量高,而且网格数量少,具体网格划分情况如图6所示。

|
图 6 网格划分情况 Fig. 6 Grid division |
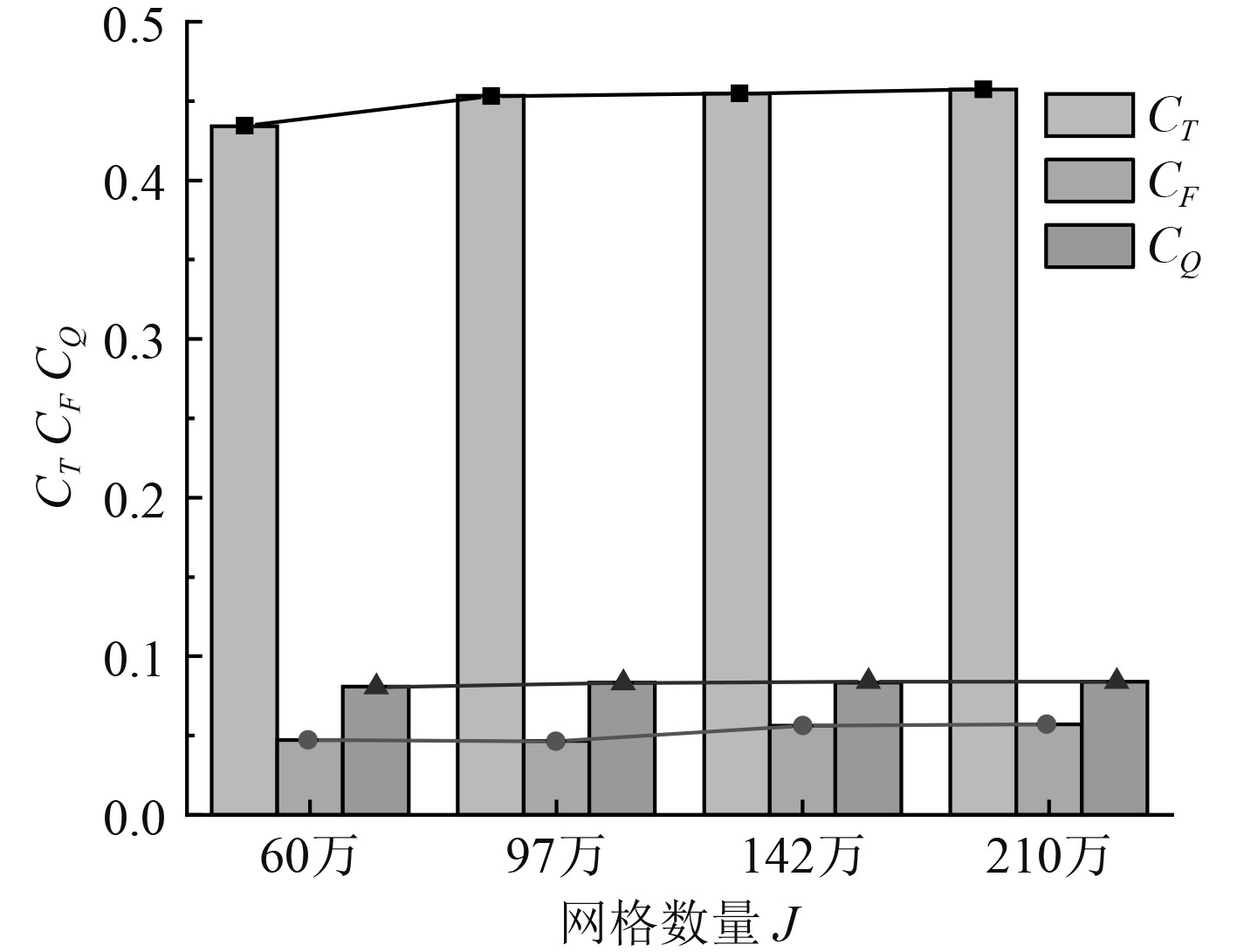
为了确保网格的质量,对网格进行无关性检验。采用全局尺度控制的方法,修改网格参数,计算设置参数保持不变,其结果如图7所示。
|
图 7 不同网格数量的影响 Fig. 7 Effect of different grid numbers |
可以看出,随着网格数量的增加,无轴侧推器的推力系数与扭矩系数都有所变化,各套网格之间的计算结果相差在5%之内,螺旋桨推力系数在142万之后误差较小,考虑到计算效率及精度的需求,采用142万网格数量进行数值计算。
计算域的边界条件为:进口采用速度入口边界条件,出口采用压力出口边界条件,不同流域的交界面设为Interface面,计算外域所有侧面均设为对称面,螺旋桨和船首表面设置为固壁面。内域为旋转域,转速设置为1 000 r/min,绕Z轴旋转。动量、湍流动能和湍流耗散率的空间差分均采用二阶迎风格式。
3 计算结果与讨论 3.1 无轴侧推器水动力性能变化规律选取航速分别为0.5 m/s,1 m/s,1.5 m/s,2 m/s,3 m/s等5组,计算在这些航速下无轴侧推器的推力系数和扭矩系数,计算结果如表2和图8所示。
|
|
表 2 航速对无轴侧推器的影响 Tab.2 Influence of speed on shaftless thruster |
|
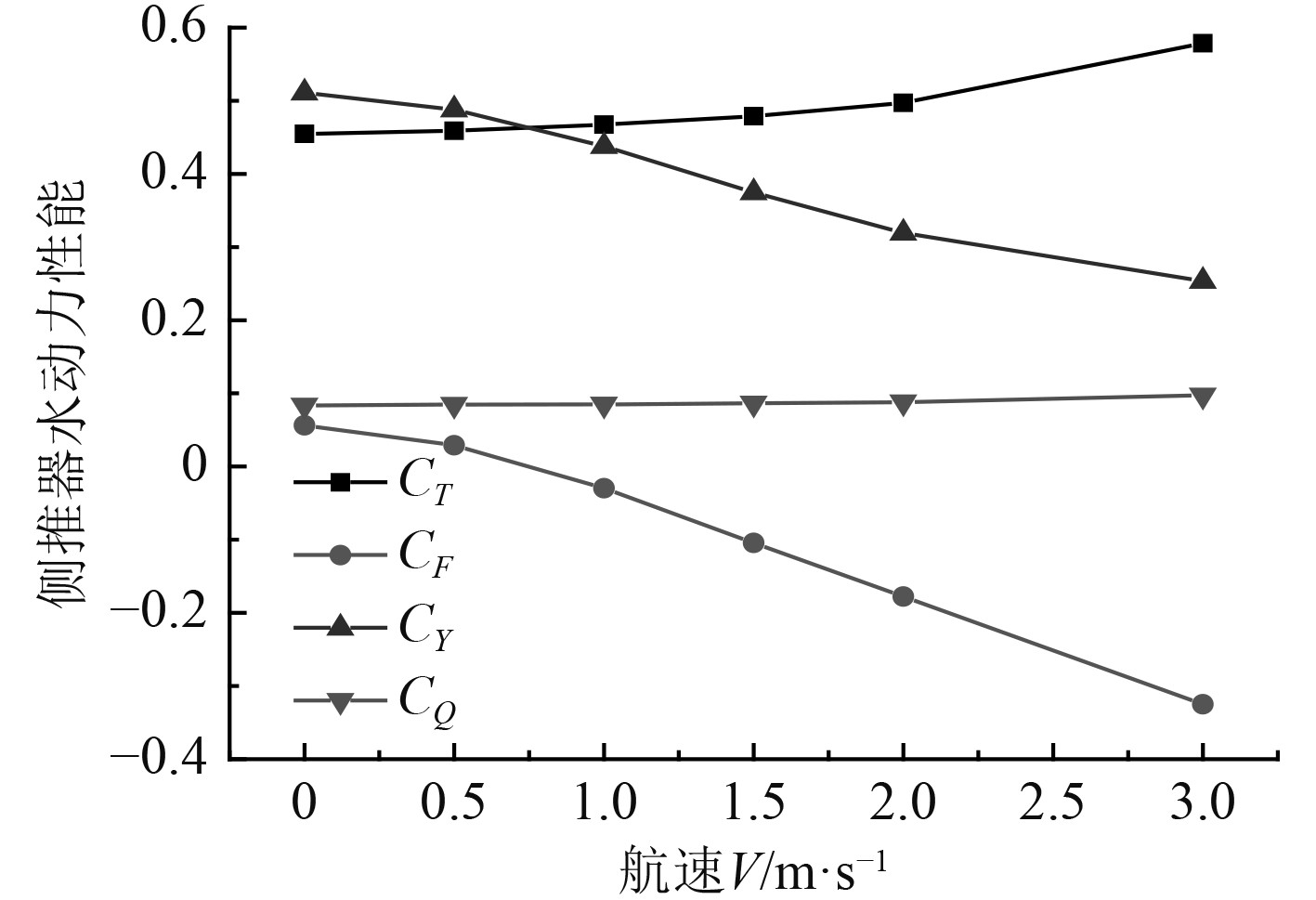
图 8 侧推器水动力性能变化规律 Fig. 8 Variation law of hydrodynamic performance of thruster |
由表2可知,螺旋桨的推力系数CT和扭矩系数CQ随着航速的增加而增大。主要是由于船首存在一定倾斜度,当来流经过船首表面时,会产生与侧推器进口速度相反的速度分量,这一分量使流体沿侧推器轴向方向上的进速降低,螺旋桨的推力系数增加。
船身两侧压力差CF随着航速的增加而减小,与轴向推力方向相同,在航速达到1 m/s时,CF变为负值,与桨推力方向相反,随着航速增加,反向推力变大,致使总推力系数CF在航速增加时,逐渐减小。
为了观察无轴侧推器流场的变化,这里分别选取静水工况和航速为3 m/s时无轴侧推器各部件的流场性能进行分析。
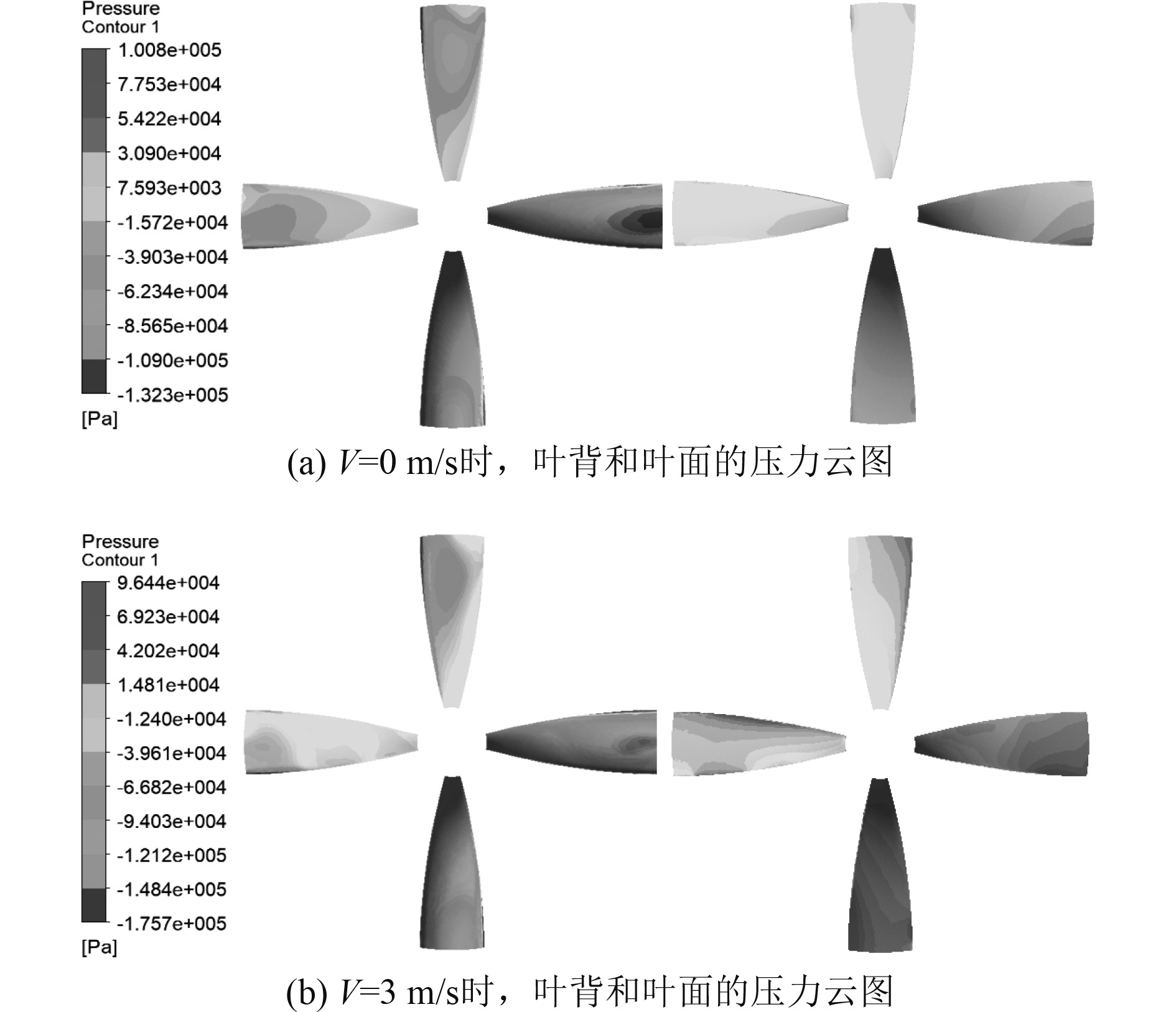
从图9可以看出,桨叶面上的压力分布不均匀。这是由于船首存在倾斜角,导致流体并非沿侧推器轴向方向流经桨叶。此外,在导筒进口处还存在低压涡流区域,致使叶背上有明显的梢涡存在。航速为3 m/s时,叶背的负压大于静水时桨叶背负压,而最大正压相差不大,因而产生的桨叶推力比静水中大。
|
图 9 不同航速时桨叶压力云图 Fig. 9 Cloud map of blade pressure at different speeds |
图10为无轴侧推器在船首位置进口和出口的压力云图。静水时,进口处存在低压区,而出口压力变化不明显。进口低压区产生的吸力与桨推力方向相同,而出口则与桨推力方向相反,无航速时船身两端压力差很小,此时船身受到侧向力与推力相同,操纵性能最好。

|
图 10 进出口压力云图 Fig. 10 Cloud map of import and export pressure |
航速为3 m/s时,进口低压区范围较小。在来流与侧推器喷流共同作用下,出口区域的低压区范围明显扩大,致使船首两侧的压力差变大,产生与桨推力方向相反的作用力,抵消了部分桨的推力,侧推器性能下降。随着航速的增加,该现象会愈加明显,最后侧推器作用失效。
3.2 结构参数影响分析在无轴侧推器原型桨的基础上,改变桨叶的结构参数,研究无轴侧推器的水动力性能变化规律,为无轴侧推器结构优化做好铺垫。
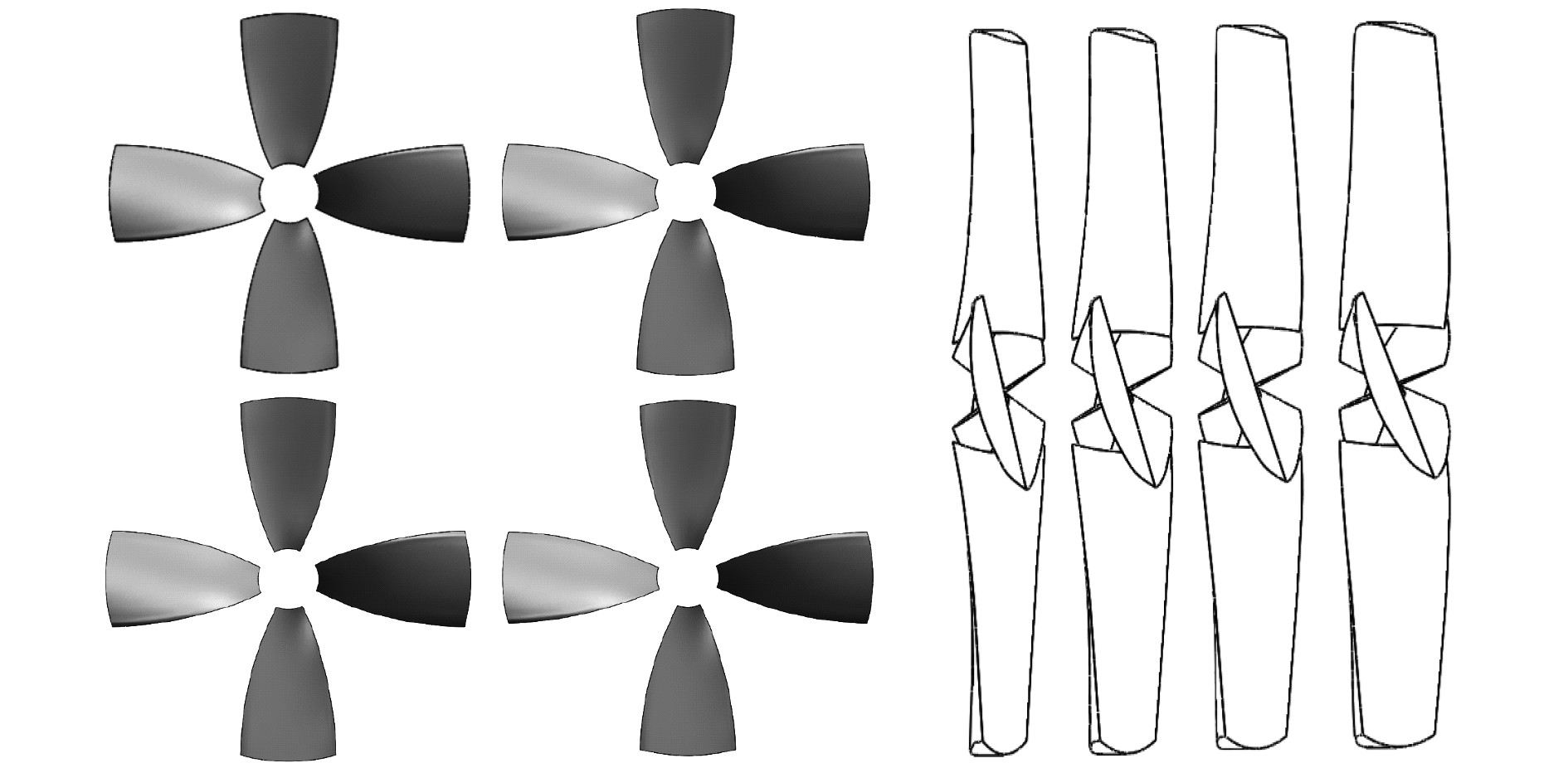
3.2.1 螺距比影响根据Ka型桨型值表,分别选取螺距比为0.7,0.9,1.0,1.2四个参数,并配以相同的盘面比0.5建立模型,桨叶模型如图11所示。
|
图 11 螺距比改变模型(从左至右0.7,0.9,1.0,1.2) Fig. 11 Pitch ratio change model (0.7, 0.9, 1.0, 1.2 from left to right) |
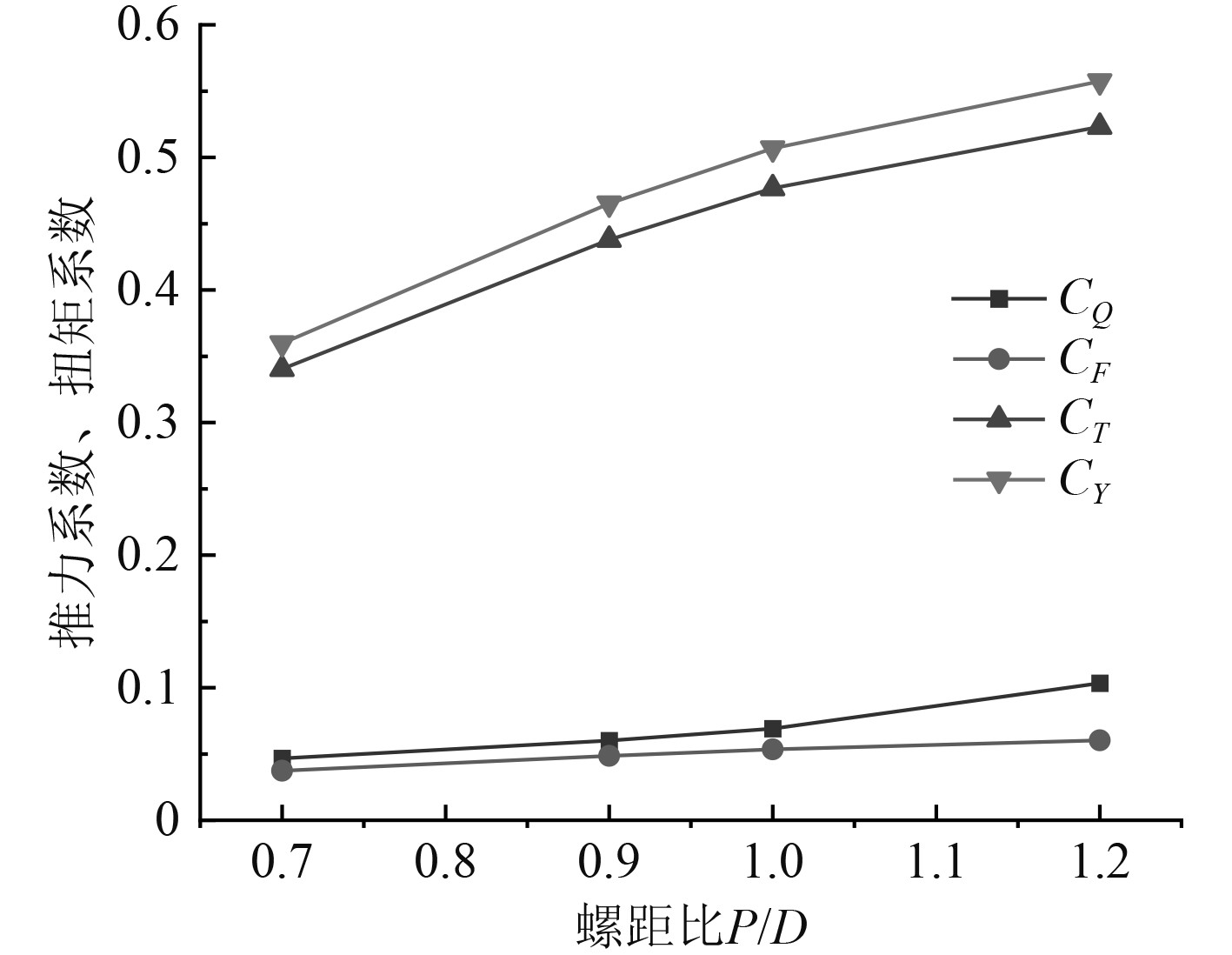
采用船首模型,螺旋桨转速为1000 r/min,计算无轴侧推器的敞水性能曲线,如图12所示。
|
图 12 螺距比对侧推器敞水性能的影响 Fig. 12 Influence of pitch ratio on open water performance of thruster |
可知,螺距比在0.7~1.2范围内,无轴侧推器的推力系数和扭矩系数随着螺距比的增加而增大,其中桨叶的推力系数CT变化超过10%,扭矩系数先缓慢增加后逐渐变快,而船首两侧压力差CF变化较小,但整体呈上升趋势。因此可以选择较大的螺距比设计无轴侧推器,高螺距比可以提高无轴推进器的推进效率。
图13为不同螺距比时船艏横向截面的压力云图。可以看出,随着螺距比的增加,导筒进口处的负压区域越来越明显,出口压力也越来越大,整个导筒压力升高。这是因为随着螺距比的增加,桨产生的推力越来越大,通过桨叶的流速增大,导致进口负压增大,出口动压增大。

|
图 13 不同螺距比时截面压力云图 Fig. 13 Sectional pressure cloud diagram for different pitch ratios |
选取盘面比分别为0.3,0.5,0.7,0.9四个参数,并配以相同的螺距比1.2,模型如图14所示。其他条件跟上文保持一致,计算结果如图15所示。

|
图 14 盘面比改变模型 Fig. 14 Model for changing the disk surface ratio |
|
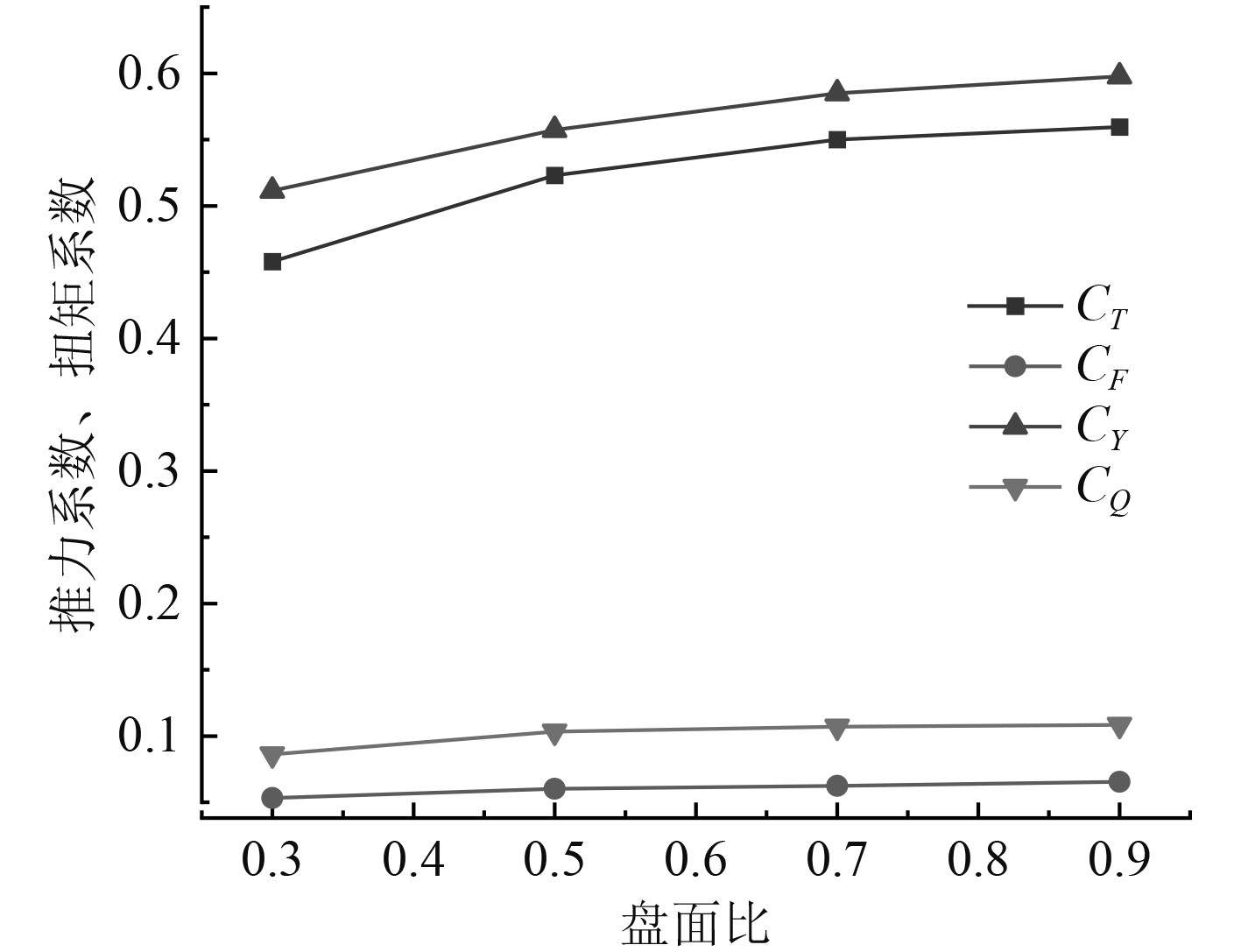
图 15 盘面比对侧推器敞水性能的影响 Fig. 15 The influence of the disk surface ratio on the open water performance of the thruster |
可知,盘面比在0.3~0.9范围内,随着盘面比的增大,侧推器的推力系数和扭矩系数均会增加,推力系数增长幅度在5%左右,但是盘面比对扭矩系数的影响较小,扭矩系数变化幅度小于2.5%。对推力系数而言,当盘面比大于0.5时,侧推器推力系数增加的幅度将会减小,说明在大盘面比下,通过改变盘面比优化侧推器的敞水性能的潜力有限。
图16分别为盘面比0.3,0.5,0.7,0.9时的船首横向截面的压力云图。可以看出,最大压力的增幅在100~200 Pa之间,增幅较小,导筒进口处的压力变化趋势大致相同,压力变化不明显,因此盘面系数的变化对整体侧推器的性能影响不大,而且大的盘面系数反而会增加阻力,一般来说五叶片和六叶片形式则可能需要较大的盘面系数。

|
图 16 不同盘面比时截面压力云图 Fig. 16 Sectional pressure cloud diagram for different disk surface ratios |
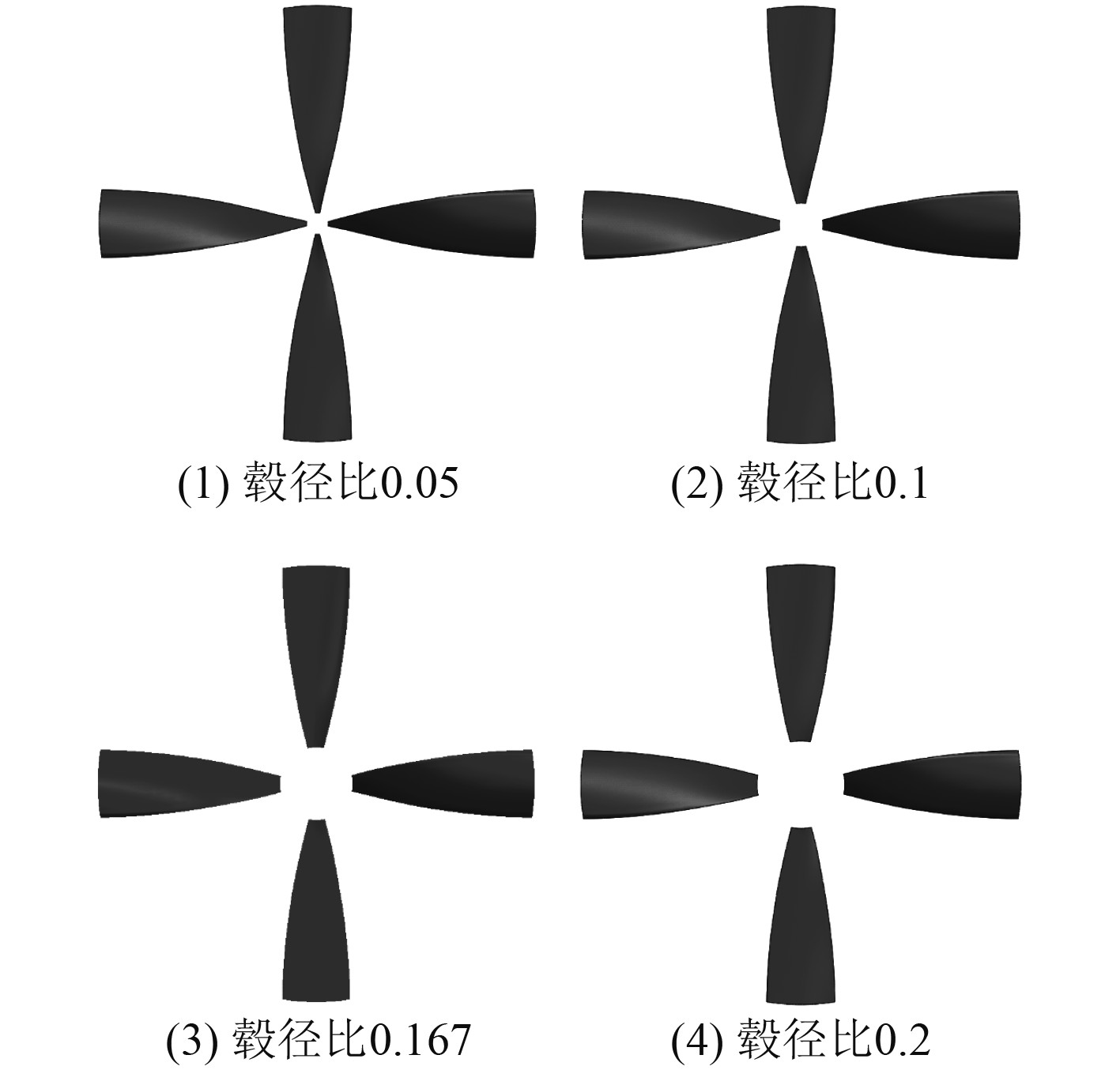
毂径比指轮毂直径与螺旋桨直径的比值,虽然无轴侧推器没有毂,但同样遵循毂径比的定义,毂径比的变化会导致叶根处做功能力不同,进而影响无轴侧推器的水动力性能。毂径比为0.167的模型已计算完成,另外建立毂径比0.05,0.1,0.2,螺距比1.2,盘面比为0.3,直径为0.25 m的无轴螺旋桨,建立的模型如图17所示。
|
图 17 不同毂径比桨模型 Fig. 17 Models of propellers with different hub diameter ratios |
同样配以相同的船首模型,计算条件跟上文保持一致,计算结果如图18所示。

|
图 18 毂径比对推理系数、扭矩系数的影响 Fig. 18 Influence of hub diameter ratio on inference coefficient and torque coefficient |
可以看出,无轴侧推器的桨推力系数,船身推力系数和总推力系数随毂径比的增加而减小,但变化量较小。毂径比的变化导致桨叶面积随之变化,叶面受力大小随着桨叶面积减小而减小,故推力系数也减小,总体来说毂径比对无轴侧推器的影响不明显。
4 结 语本文基于CFD方法,研究船舶无轴轮缘侧推器水动力性能规律和流场分布,并分析了结构参数对侧推器水动力性能的影响,结论如下:
1)当航速增加时,无轴侧推器的推力系数和转矩系数会随之增大,而船身两侧压力差先逐渐减小至零,之后再反向增大,在横向上,船体受到的总推力会随航速的增加而逐渐减小。
2)在静水和航行状态下桨叶面上的压力均呈不均匀分布,航行状态下产生的桨叶推力以及导筒壁面上低压涡流区域均比静水中的要大,但由于船首两侧的压力差变大,产生了与桨推力方向相反的作用力,抵消了部分桨的推力,导致侧推器性能下降。
3)螺距比增大,无轴侧推器的推力系数和扭矩系数也随之增大,且影响效果比较明显,推力系数增加幅度超过10%;盘面比的影响相对螺距比较小,但推力系数和扭矩系数总体呈上升趋势,扭矩系数变化幅度小于2.5%;毂径比对无轴侧推器水动力性能影响较小。
| [1] |
YAN X P, LIANG X X, OUYANG W, et al. A review of progress and applications of ship shaft-less rim-driven thrusters[J]. Ocean Engineering, 2017, 144: 142-156. DOI:10.1016/j.oceaneng.2017.08.045 |
| [2] |
魏跃峰, 詹明珠, 孟阳, 等. 球鼻艏船型船首侧推器推力减缩数值分析[J]. 中国造船, 2020, 61(S2): 222-230. DOI:10.3969/j.issn.1000-4882.2020.z2.024 |
| [3] |
刘辉, 代燚, 冯榆坤, 等. 船舶艏侧推器推力减缩试验与数值计算研究[J]. 中国造船, 2017, 58(4): 1-13. DOI:10.3969/j.issn.1000-4882.2017.04.001 |
| [4] |
LI Y K, SONG B W, MAO ZH Y, et al. Analysis and optimization of the electromagnetic performance of a novel stator modular ring drive thruster motor[J]. Energies, 2018, 11(6): 1598-1-23. DOI:10.3390/en11061598 |
| [5] |
LIANG X X, YAN X P, OUYANG W, et al. Thermo-Elasto-Hydrodynamic analysis and optimization of rubber- supported water-lubricated thrust bearings with polymer coated pads[J]. Tribology International, 2019, 138: 365-379. DOI:10.1016/j.triboint.2019.06.012 |
| [6] |
JIANG H , OUYANG W, SHENG C X, et al. Bucknall Richard. Numerical investigation on hydrodynamic performance of a novel counter-rotating shaftless rim-driven thruster[J]. Applied Ocean Research 2021, 118: 1–13.
|
| [7] |
SONG B W, WANG Y J, TIAN W L. Open water performance comparison between hub-type and hubless rim driven thrusters based on CFD method[J]. Ocean Engineering, 2015, 103: 55-63. DOI:10.1016/j.oceaneng.2015.04.074 |
| [8] |
郁程. 侧推器水动力性能与设计方法研究[D] . 上海: 上海交通大学, 2017.
|
| [9] |
吴利红, 董连斌, 许文海. 基于Matlab和ProE的螺旋桨三维建模[J]. 大连海事大学学报, 2011, 37(2): 17-20. DOI:10.16411/j.cnki.issn1006-7736.2011.02.028 |
| [10] |
兰加芬. 对转无轴轮缘推进器水动力性能分析及优化研究[D] . 武汉: 武汉理工大学, 2019.
|
 2023, Vol. 45
2023, Vol. 45
