2. 上海船舶设备研究所,上海 210030
2. Shanghai Marine Equipment Research Institute, Shanghai 210030, China
舰船作为海上主要作战平台,在服役期间无法避免遭遇各种复杂的冲击环境,尤其是受到水中非接触爆炸造成的冲击破坏更为严重[1]。推进轴系是船舶动力系统的核心部分之一,而中间轴承作为推进轴系的支撑单元,其抗冲击性能的好坏将直接影响到推进轴系的安全运转。中间轴承受到冲击破坏,其承载能力将会下降,导致轴系的校中性能下降、轴承与轴径的磨损加剧,从而使得轴系运转效率降低,甚至影响到舰船的正常航行。因此,开展中间轴承抗冲击性能分析,研究中间轴承抗冲击薄弱结构对保障舰船的安全航行,增强舰船生命力与战斗力具有重大意义。
国内学者从数值模拟、理论研究等方面对舰船推进轴系在复杂冲击环境下的抗冲击能力进行了大量的研究。马炳杰等[2]将各轴承简化为无质量的弹簧单元,采用时域模拟法对轴系抗冲击性能进行分析,指出了薄弱环节。李磊[3]将尾轴承简化为形状简单的轴套形式,采用时域法和频域法对尾轴承进行了抗冲击仿真计算,得到了相应的位移和应变值。李增光等[4]采用线性弹簧模拟轴承,分析了舰船推进轴系在多支点不同激励下的冲击响应。张晓阳等[5]在存在接触应力条件下,对舰船轴系液压螺栓采用了时域法和频域法对其进行抗冲击仿真计算,得到不同冲击载荷下的应力响应分布。吴晖等[6]采用时域法和频域法对法兰式液压联轴器进行抗冲击特性研究,得到其在冲击载荷下的应力分布。刘学斌等[7]采用线性弹簧单元模拟轴承的方式研究了推力轴承的冲击响应,通过改变轴承位置、支撑刚度等方法使轴承位移响应符合抗冲击规范要求。姚胜昶[8]将轴段简化为均质元件,轴承简化为弹簧元件,对舰船推进轴系进行了抗冲击仿真分析。姜克达[9]将轴系与船体进行耦合,将轴承简化刚性和弹性连接单元,通过仿真计算分析了推进轴系的响应特性。侯淑芳等[10]简化了轴承支撑,采用梁单元模型对轴系进行冲击计算,提高了轴系模拟仿真的计算效率。上述对舰船推进轴系抗冲击性能的研究,都是针对传动轴、联轴器及轴系附件所开展的,对于结构复杂的中间轴承,仅采用简化的弹簧单元模拟,没有考虑中间轴承实际结构的冲击响应特性。舰船推进轴系往往是由船体通过支撑轴承传递冲击载荷,所以安装于船体的中间轴承受冲击载荷作用情况更为恶劣。
本文以某型滑动式中间轴承为研究对象,建立基于时域法的抗冲击数值模型,分析中间轴承在各方向时域冲击载荷作用下的响应特点。根据计算结果的分析,进一步针对薄弱环节开展结构优化设计,对比分析结构优化后的响应特性。本文研究成果于为舰船滑动式中间轴承以及冷却盘管的结构设计与优化提供参考。
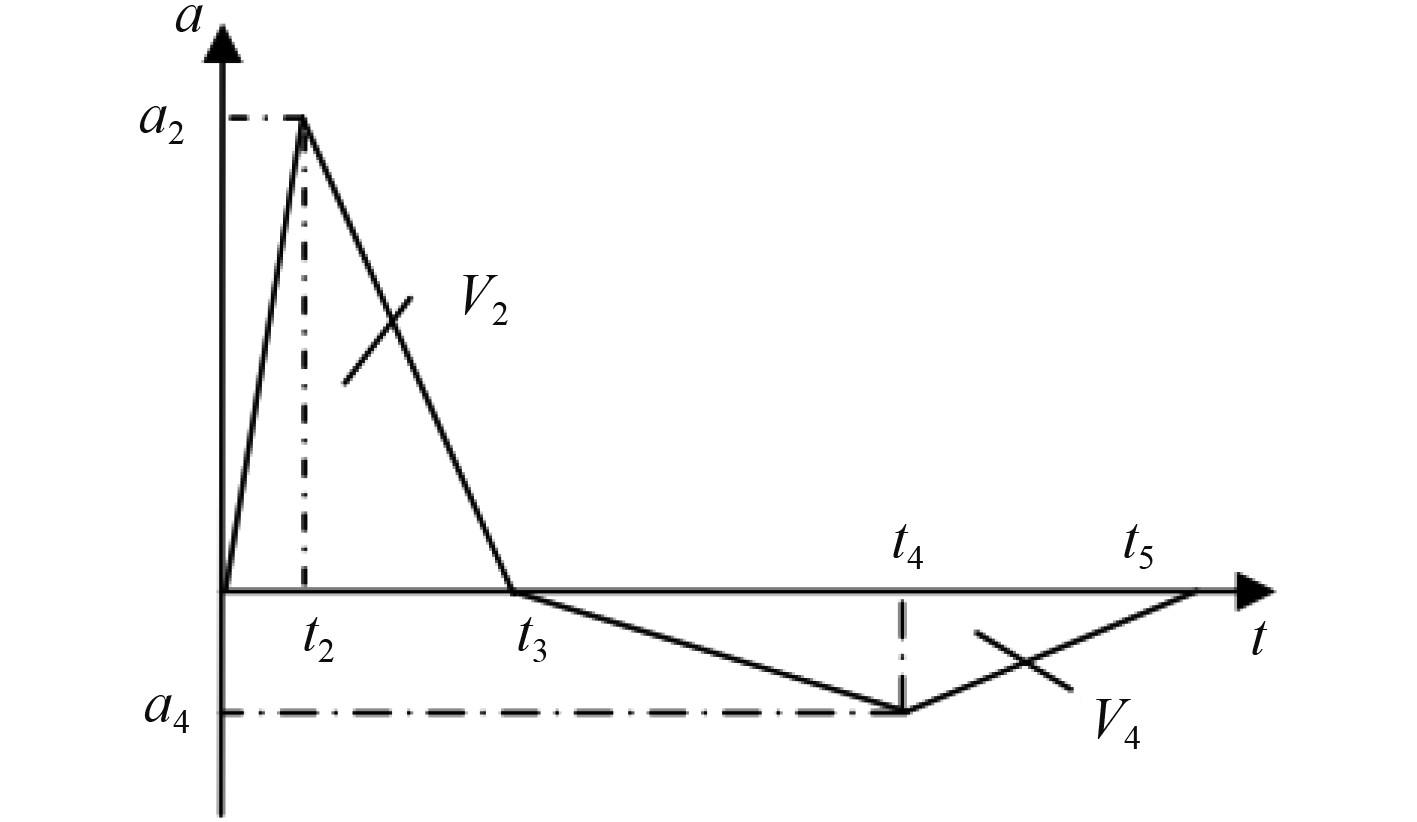
1 基础理论时域模拟法是采用时间历程曲线作为冲击输入载荷,在时间域上对舰船设备进行瞬态分析,可以考虑设备的结构非线性以及非线性破坏,应用时域法对舰船设备进行抗冲击分析最关键的就是冲击载荷谱的形式。联邦德国国防军舰艇建造规范BV043/85规定了冲击响应谱转化成正负三角波形式的时间历程曲线的方法,如图1所示,实现了从频域到时域冲击载荷谱的转化[11]。根据设备不同的安装区域,BV043/85规范中给出了等加速度谱、等速度谱、等位移谱数据参数,如表1所示,其为最严峻的冲击环境数据。
|
图 1 组合正负三角波时间历程输入曲线 Fig. 1 Time history input curve of combined positive and negative triangular wave |
|
|
表 1 冲击环境数据 Tab.1 Shock environmental data |
根据BV043/85规范的要求,第1个正三角形的加速度峰值a2约为最大加速度A0的0.6倍,面积约为最大速度V0的3/4;为了使最终的速度等于0,第2个负三角形的面积等于第1个正三角形的面积,即V2=V4;将加速度-时间历程曲线进行2次积分后可得到位移参数,同时根据实船试验的经验数据可以使t2=0.4t3,t4–t3=0.6(t5–t3),最终可以得到组合三角波时间历程曲线中各参数计算公式为:
| $ \left\{ \begin{gathered} {a_2} = 0.6{A_0},\\ {t_3} = \frac{{2{V_2}}}{{{a_2}}} = \frac{{2 \times 3/4{V_0}}}{{{a_2}}} ,\\ {t_2} = 0.4{t_3} ,\\ {t_5} = \frac{{6.3{D_0} - 1.6{a_2}t_3^2}}{{1.6{a_2}{t_3}}} + {t_3},\\ {t_4} = 0.6({t_5} - {t_3}) + {t_3} ,\\ {a_4} = - \frac{{{a_2}{t_3}}}{{{t_5} - {t_3}}} 。\\ \end{gathered} \right. $ | (1) |
当设备的质量大于5 t时,则折减换算如下式:
| $ \left\{ \begin{gathered} \frac{A}{{{A_0}}} = {\left( {\frac{{{m_i}}}{{{m_0}}}} \right)^{ - 0.537}},\\ \frac{V}{{{V_0}}} = {\left( {\frac{{{m_i}}}{{{m_0}}}} \right)^{ - 0.4}}。\\ \end{gathered} \right. $ | (2) |
式中:A为折减后的等加速度谱值;V为折减后的等速度谱值;mi为所分析的设备的质量;m0为临界质量,取值为5 t。
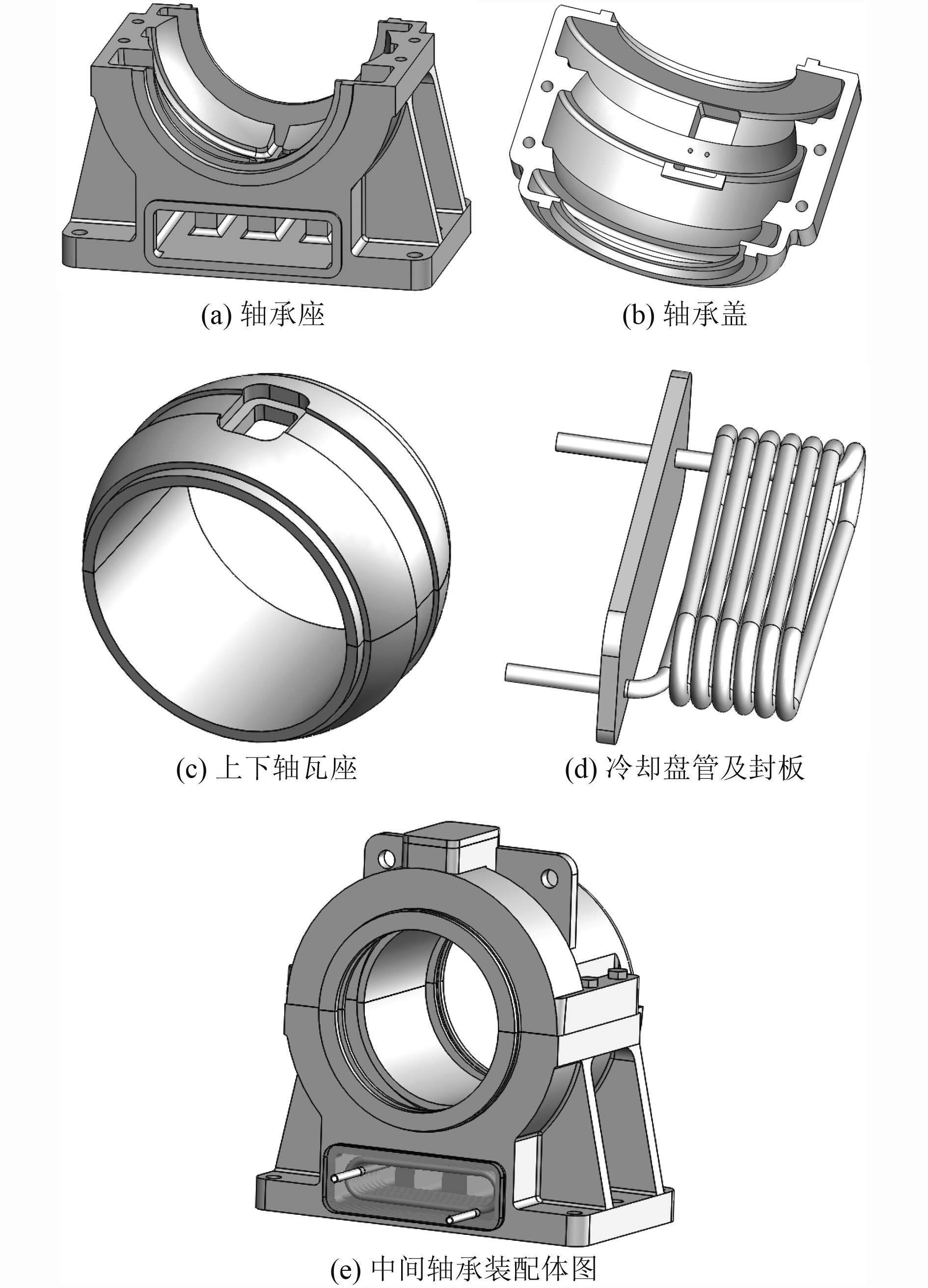
2 数值建模 2.1 几何模型滑动式中间轴承主要由轴承座、轴承盖、轴瓦座以及冷却盘管等部件组成,冷却盘管用于对轴承座底部储油池内的滑油进行冷却,是中间轴承重要的冷却部件。本文以某型船用滑动式中间轴承为研究对象,采用CAD软件建立各部件1∶1三维几何模型,并根据装配关系建立中间轴承装配体模型,如图2所示。
|
图 2 滑动式中间轴承三维几何模型 Fig. 2 3D geometric model of sliding intermediate bearing |
由于中间轴承各部件形状复杂,基于“适用性”原则对不同部件分别选用合适的网格类型进行网格划分。对于封板、压盖等形状规则的部件,采用六面体网格单元C3D8R进行网格划分;对于轴承座、轴承盖等形状复杂的部件,采用修正的二次四面体网格单元C3D10M进行网格划分;对于冷却盘管薄壳复杂部件,采用四边形壳单元SR4进行网格划分。同时,在各部件所关心的应力集中部位以及相互接触的关键部位进行适当网格细化。最终,建立中间轴承装配体的网格模型,如图3所示,主要部件网格信息如表2所示。

|
图 3 滑动式中间轴承三维网格模型 Fig. 3 3D mesh model of sliding intermediate bearing |
|
|
表 2 中间轴承主要部件网格信息统计表 Tab.2 Grid information statistics table of main parts of intermediate bearing |
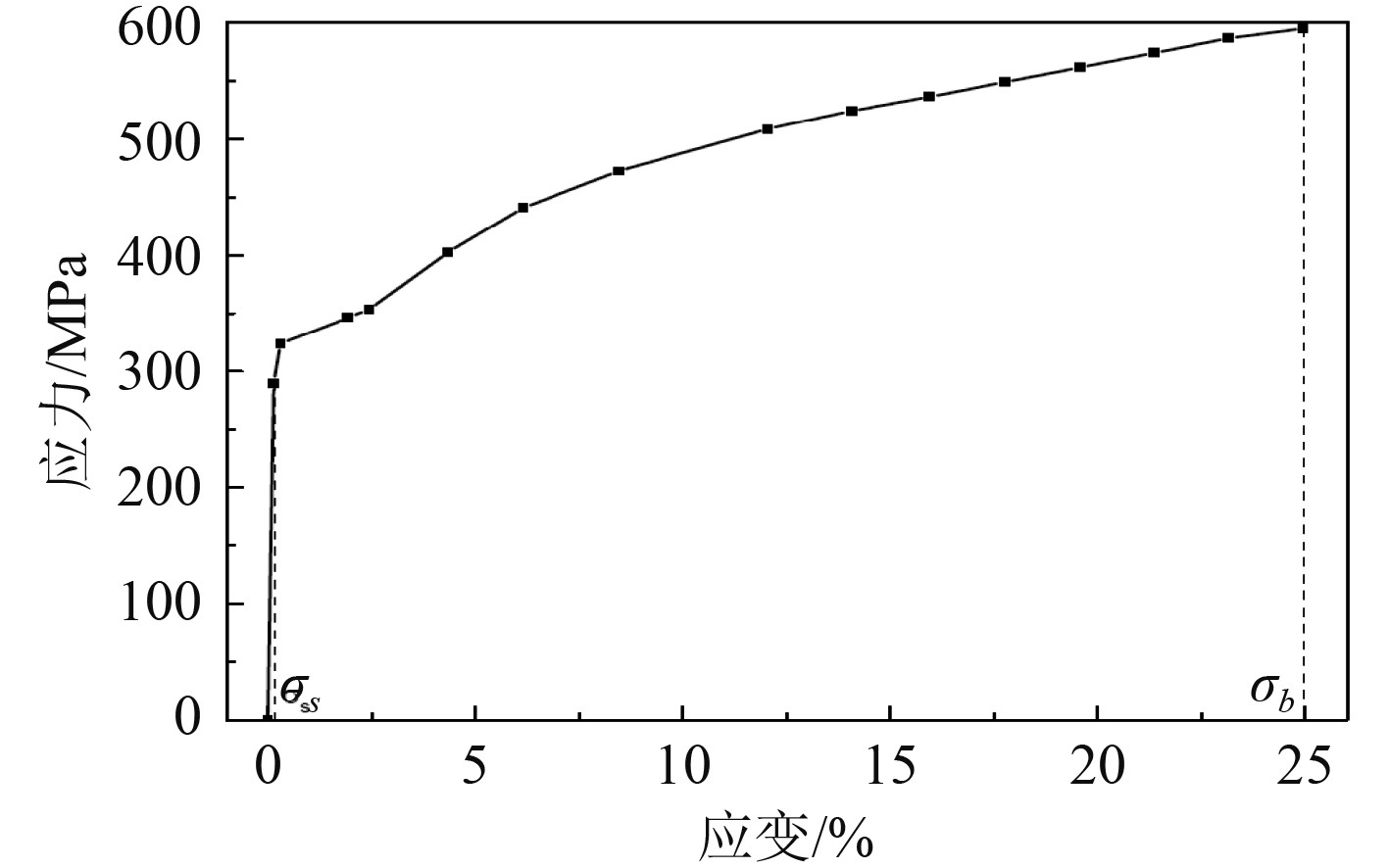
中间轴承各部件的材料属性参数如表3所示。其中,冷却盘管为铜基材料,采用弹塑性设计,抗拉强度为595 MPa,材料的本构关系参数如图4所示。
|
|
表 3 中间轴承各部件材料属性参数 Tab.3 Material property parameters of each component of the intermediate bearing |
|
图 4 冷却盘管弹塑性本构关系 Fig. 4 Elastoplastic constitutive relation of cooling coil |
根据中间轴承各部件实际安装关系,在计算模型中设置边界条件如下:
1)轴承座与轴承盖接触面、上下轴瓦座接触面、连接螺栓与螺栓孔、冷却盘管与封板安装面之间不允许发生相对运动,采用绑定(Tie)约束将这些区域绑定在一起。
2)考虑到冷却盘管在受冲击载荷作用期间会发生自接触,设置通用接触(general contact)关系用于模拟盘管间的相互作用关系;轴承座与下轴瓦座接触面、轴承盖与上轴瓦座接触面之间也设置接触关系,允许接触面之间发生挤压、滑移。
3)对轴承座底部安装表面6个自由度方向的位移实施固定约束。载荷谱施加于轴承座的底部表面,在进行时域垂向、横向或纵向冲击时就将该方向的位移自由度释放。根据前述的时域转化方法,计算得到各方向的时域冲击载荷谱如表4所示。
|
|
表 4 时域冲击载荷谱 Tab.4 Time-domain shock load spectrum |
基于BV043/85规范要求,对滑动式中间轴承进行垂向、横向和纵向3个方向上的抗冲击计算,得到主要部件在各冲击方向上的最大应力值如表5所示。对于中间轴承轴承座、轴承盖以及轴瓦座等主体部件,其受纵向冲击载荷时响应最大,横向次之,垂向最小,尤其是轴承座在垂向冲击下的最大应力值要远小于另外2个冲击方向。虽然时域垂向冲击环境是各冲击方向中最为严酷的,载荷谱的冲击加速度幅值更大,冲击时间更长,但是由于轴承座、轴承盖、轴瓦座在垂向上的结构刚度较大,导致部件产生的冲击应力与变形均较小。因此,相对于时域冲击载荷谱,设备的结构设计特点对其受冲击载荷后的动态响应影响程度更大。
|
|
表 5 不同冲击方向下中间轴承主要部件最大应力值(MPa) Tab.5 The maximum stress value of the main components of the intermediate bearing under different impact directions(MPa) |
图5为轴承座、轴承盖、轴瓦座在纵向和横向冲击载荷作用下的最大应力云图。可以看出,轴承座在纵向和横向冲击下均有应力集中现象,最大应力值分别出现在腰部过渡圆角处和肋板顶部连接处。轴承盖受纵向冲击载荷作用时在安装座夹角处会产生应力集中,出现最大应力;在横向冲击下最大应力出现在端面开口薄板处。轴瓦座在纵向和横向冲击下最大应力均位于和轴承座相互接触的表面上。轴承座、轴承盖以及轴瓦座在纵向和横向冲击下均会产生较为剧烈的响应,出现相对较大的应力值。因此,在进行滑动式中间轴承的设计工作时,应重点关注上述出现最大应力值的部位,避免中间轴承在冲击载荷作用下因应力集中发生破坏。

|
图 5 纵向、横向冲击载荷作用下中间轴承主体部件最大应力云图 Fig. 5 The maximum stress cloud diagram of the main part of the intermediate bearing under the action of longitudinal and transverse impact loads |
与其他部件响应规律相反,冷却盘管在垂向冲击下响应最大,横向次之,纵向最小,并在3个方向冲击载荷作用下最大应力均已超过了屈服强度,发生了塑性变形,但最大应力没有超过抗拉强度,冷却盘管在3个方向冲击下的最大应力云图如图6所示。根据冷却盘管的冲击响应过程可知,由于悬臂安装以及自身的结构特点,冷却盘管的运动要滞后于轴承座的运动。在垂向冲击过程中,冷却盘管不同时刻的形状图如图7所示。可知,由于惯性作用,冷却盘管先与储油池底面发生碰撞并产生较大的应力,之后向上运动并与储油池上部凸台结构发生剧烈碰撞,产生最大应力值,未与凸台发生碰撞的盘管在惯性作用下继续向上运动,盘管之间的晃动幅度也越来越大。同时,在整个垂向冲击过程中冷却盘管与封板连接处的应力值也处于较高的水平。在横向和纵向冲击过程中,冷却盘管运动幅度相对较小,没有与轴承座壁面发生接触。横向冲击时,最大应力值位于冷却盘管与封板连接处;纵向冲击时,盘管之间会发生相互碰撞,最大应力值位于第1道盘管与第2道盘管碰撞处。相比于另外2个方向的冲击,冷却盘管在垂向冲击下的晃动幅度较大,工作状况更为恶劣,这主要是由于冷却盘管在垂向上的结构刚度最小,抗弯能力最弱,变形最大,平衡稳定性最差,受冲击作用的影响最明显。因此,冷却盘管在受垂向冲击载荷作用时会产生剧烈的响应,工作状况恶劣,需进行结构上的优化设计。

|
图 6 不同冲击载荷作用下冷却盘管最大应力云图 Fig. 6 The maximum stress cloud diagram of the cooling coil under different impact loads |

|
图 7 垂向冲击过程中冷却盘管形状变化图 Fig. 7 Diagram of cooling coil shape change during vertical impact |
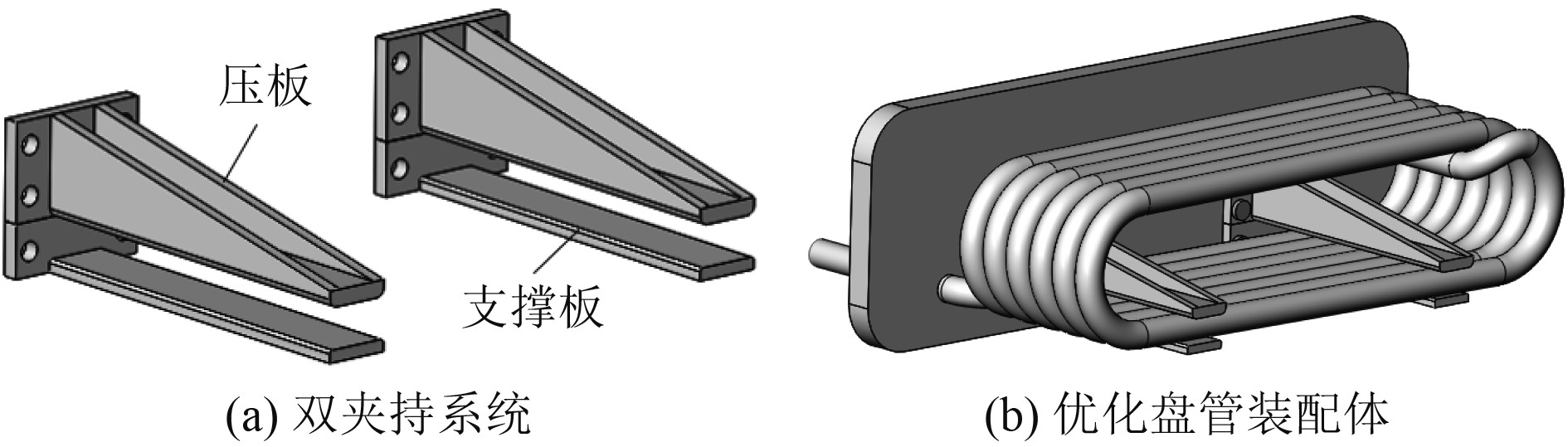
为了避免冷却盘管在垂向冲击下与轴承座结构发生剧烈碰撞产生噪声与冲击破坏,需要对冷却盘管整体结构进行优化设计,提高冷却盘管结构在垂向的刚度和稳定性。本文设计双夹持机构用于冷却盘管的垂向支撑,如图8所示。单个夹持机构主要包括阻碍盘管惯性运动的压板以及底面贴于轴承座上用于支撑冷却盘管的支撑板,压板和支撑板均通过螺钉固定在封板上。
|
图 8 冷却盘管优化几何模型 Fig. 8 Cooling coil optimized geometric model |
为了节省计算时间和计算资源,将优化后的冷却盘管结构单独进行抗冲击计算,冲击载荷谱施加于封板与轴承座安装接触表面,载荷谱与表4相同。双夹持机构各部件均采用六面体单元进行网格划分,网格模型如图9所示,总网格数约为27万。双夹持机构中各部件材料属性如表6所示。

|
图 9 优化盘管装配体网格模型 Fig. 9 Optimized coil assembly mesh model |
|
|
表 6 双夹持结构材料属性参数 Tab.6 Material property parameters of double clamp structure |
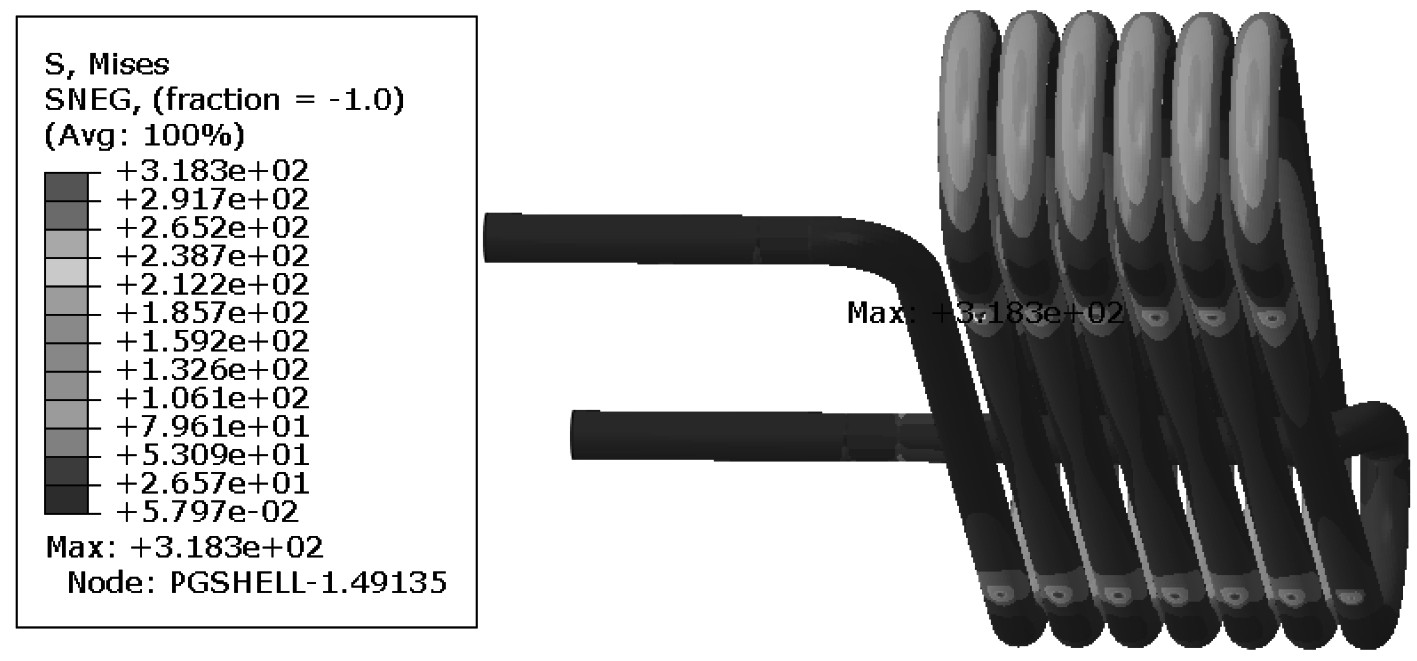
基于BV043/85规范要求,对冷却盘管结构进行3个方向上的抗冲击计算,得到主要部件在各冲击方向上的最大应力值如表7所示。可知,优化后的冷却盘管在垂向冲击作用下的最大应力为318.3 MPa,下降了30.29%。而在横向与纵向冲击下最大应力变化较小,这与双夹持机构的设计有关。图10为冷却盘管在垂向冲击下的最大应力云图。可以看出,最大应力出现在盘管与支撑板相互作用的位置,并且在冲击过程中冷却盘管与封板连接处的最大应力只有141.8 MPa,该处未发生塑性变形,受力情况得到明显改善。图11为垂向冲击15.204 ms时刻优化前后的冷却盘管变形对比图。与优化之前相比可知,垂向冲击过程中冷却盘管的晃动幅度明显减小,受力情况得到明显改善。这主要是由于双夹持机构极大地限制了冷却盘管在垂向冲击过程中的惯性运动,既避免了冷却盘管与轴承座发生剧烈碰撞的现象,又缓解了冷却盘管与封板连接处的受力情况。
|
|
表 7 不同冲击方向下冷却盘管主要部件最大应力值(MPa) Tab.7 The maximum stress values of the main components of the cooling coil under different impact directions(MPa) |
|
图 10 垂向冲击下冷却盘管最大应力云图 Fig. 10 The maximum stress cloud diagram of the cooling coil under vertical impact |

|
图 11 垂向冲击15.204 ms时刻优化前后冷却盘管形状对比图 Fig. 11 Comparison of cooling coil shapes before and after optimization at 15.204 ms vertical impact |
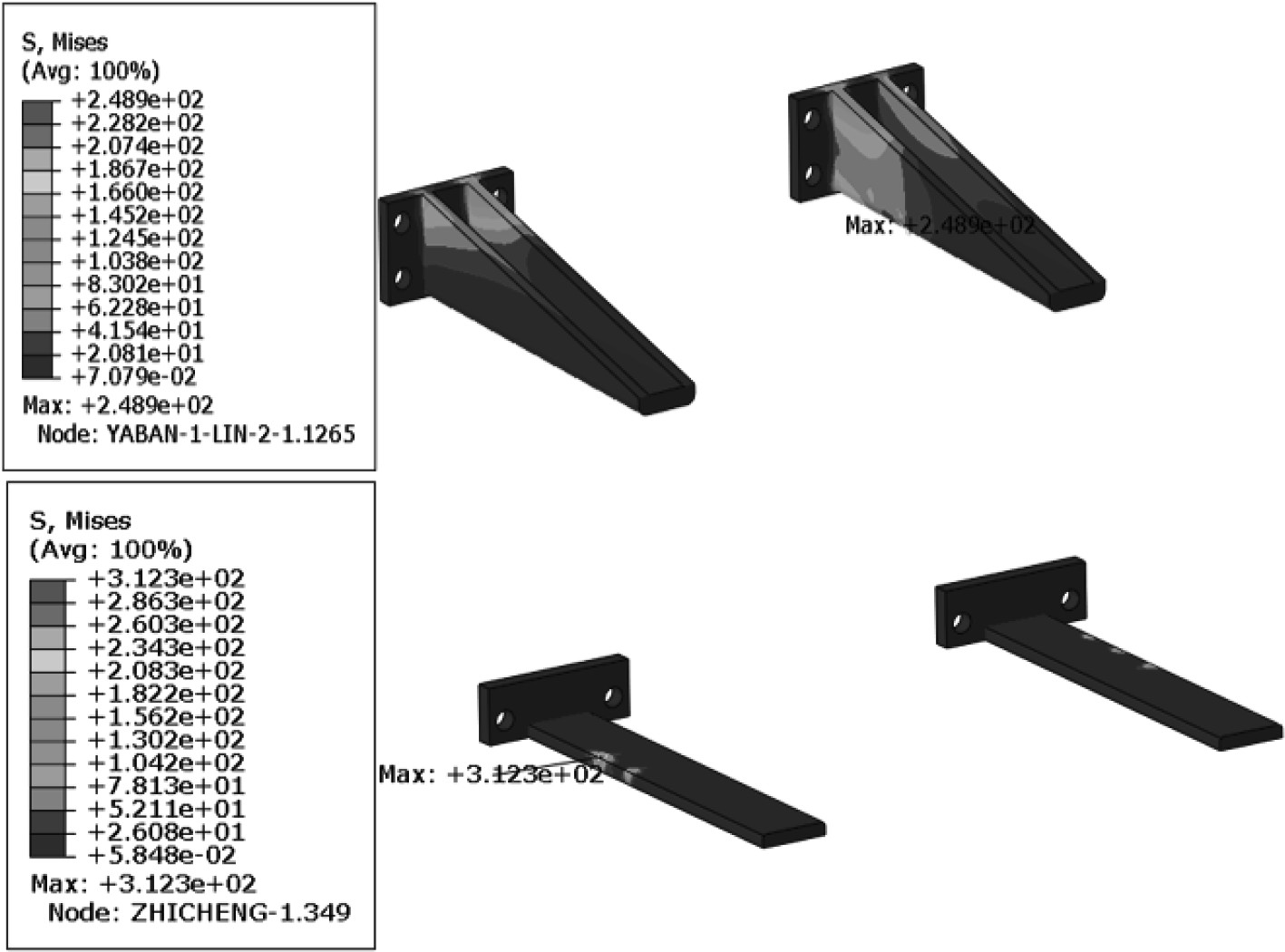
压板和支撑板在横向冲击时的最大应力要明显大于另外2个冲击方向,压板最大应力为248.9 MPa,支撑板最大应力为312.3 MPa,应力云图如图12所示,最大应力均产生在与冷却盘管接触的位置。根据冲击响应过程可知,在垂向冲击下,支撑板主要起支撑作用,压板阻碍了冷却盘管的惯性运动从而承受了冷却盘管的惯性载荷。在横向冲击下,由于冷却盘管受力的不对称性,其与压板和支撑板会发生挤压现象,且支撑板受挤压作用会更大,产生较大的应力;在纵向冲击下,冷却盘管也会与压板和支撑板发生挤压,但相比于横向冲击挤压作用较小。
|
图 12 横向冲击下压板、支撑板最大应力云图 Fig. 12 The maximum stress cloud diagram of the lower pressure plate and support plate under lateral impact |
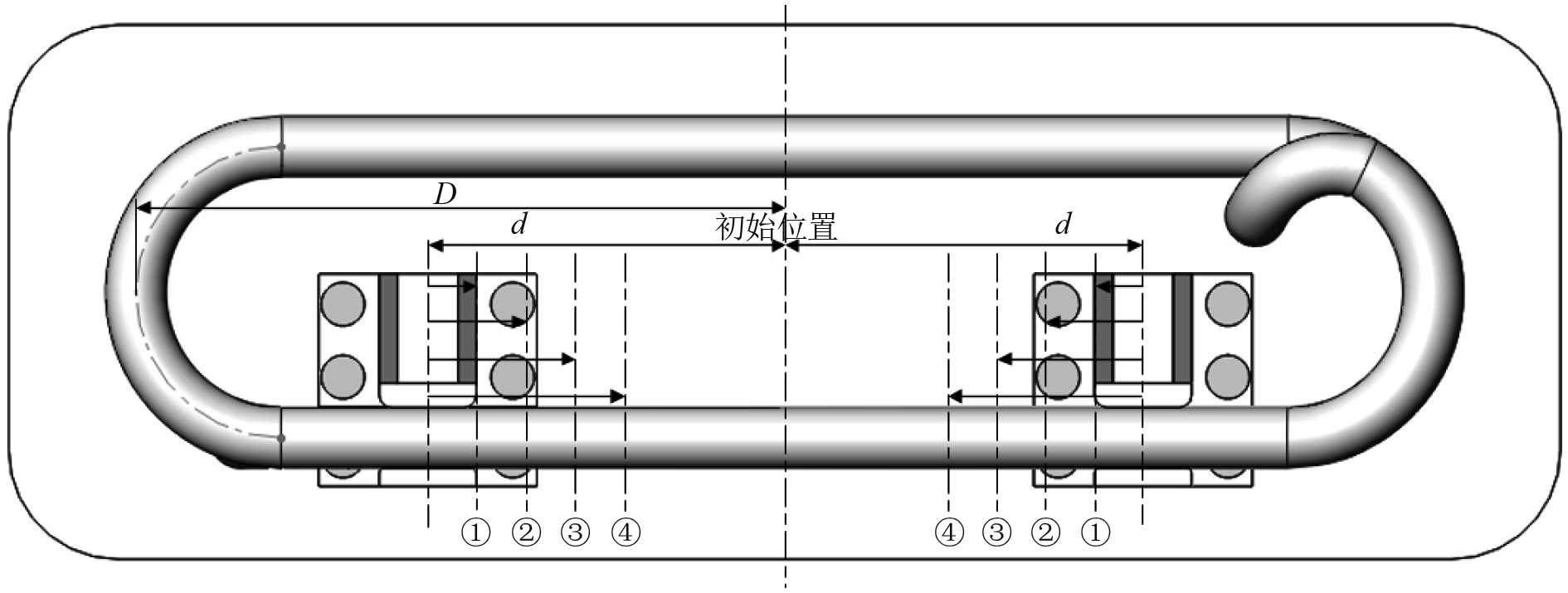
双夹持机构对称安装于冷却盘管中心线两侧,如图13所示。为了进一步评估双夹持机构安装位置对冷却盘管的支撑效果,引入安装系数μ,其表达式为
|
图 13 双夹持结构移动位置示意图 Fig. 13 Moving position diagram of double clamping structure |
| $ \mu = d/D ,$ | (3) |
式中:d为双夹持机构中心线与冷却盘管中心线之间的距离;D为冷却盘管的半长。
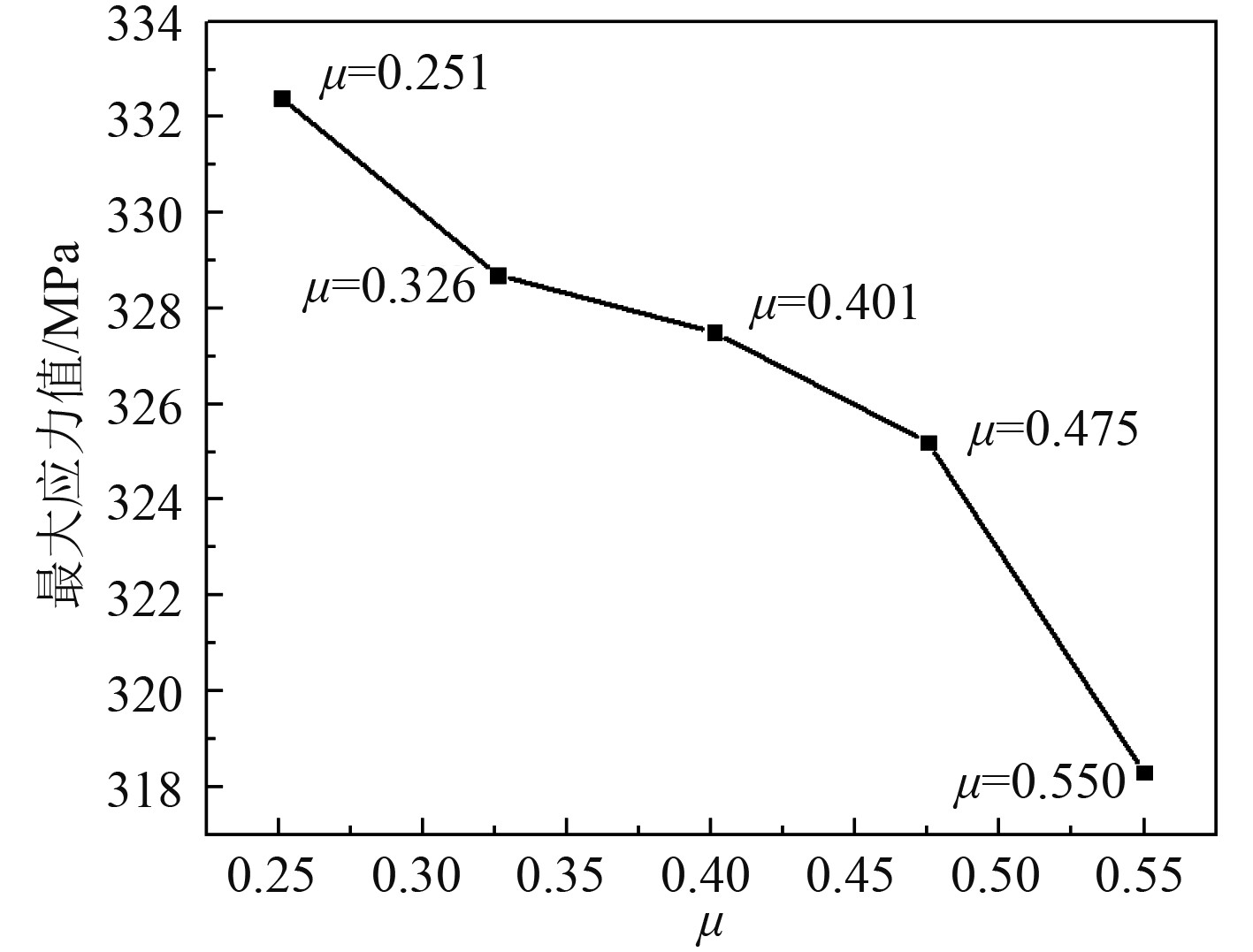
初始安装位置为μ=0.550,将两侧夹持机构同时向中心移动,分别取μ=0.475、μ=0.401、μ=0.326、μ=0.251等4种不同安装位置。保持材料属性、网格模型及边界条件等不变,进行3个方向上的抗冲击计算,得到各部件最大应力值如表8所示。可知,在垂向冲击载荷作用下双夹持机构安装位置对冷却盘管最大应力的影响较大,最大应力均产生于冷却盘管与支撑板相互作用处。如图14所示,随着左右两侧夹持机构从初始位置同时向冷却盘管中心对称移动,在垂向冲击载荷作用下冷却盘管最大应力呈增大的变化趋势,这是因为夹持机构越靠近中心线位置,其对冷却盘管的整体支撑效果越差。与此同时,安装位置对夹持机构自身压板和支撑板的应力响应也会产生一定的影响。随着夹持机构向冷却盘管中心移动,在垂向冲击下压板和支撑板最大应力整体呈增大的变化趋势,但是均没有超出屈服强度,满足设计要求。
|
|
表 8 夹持机构不同安装位置时各部件最大应力值(MPa) Tab.8 Maximum stress value of cooling coil when clamping mechanism is installed at different positions(MPa) |
|
图 14 垂向冲击下冷却盘管最大应力变化图 Fig. 14 Maximum stress variation diagram of cooling coil under vertical impact |
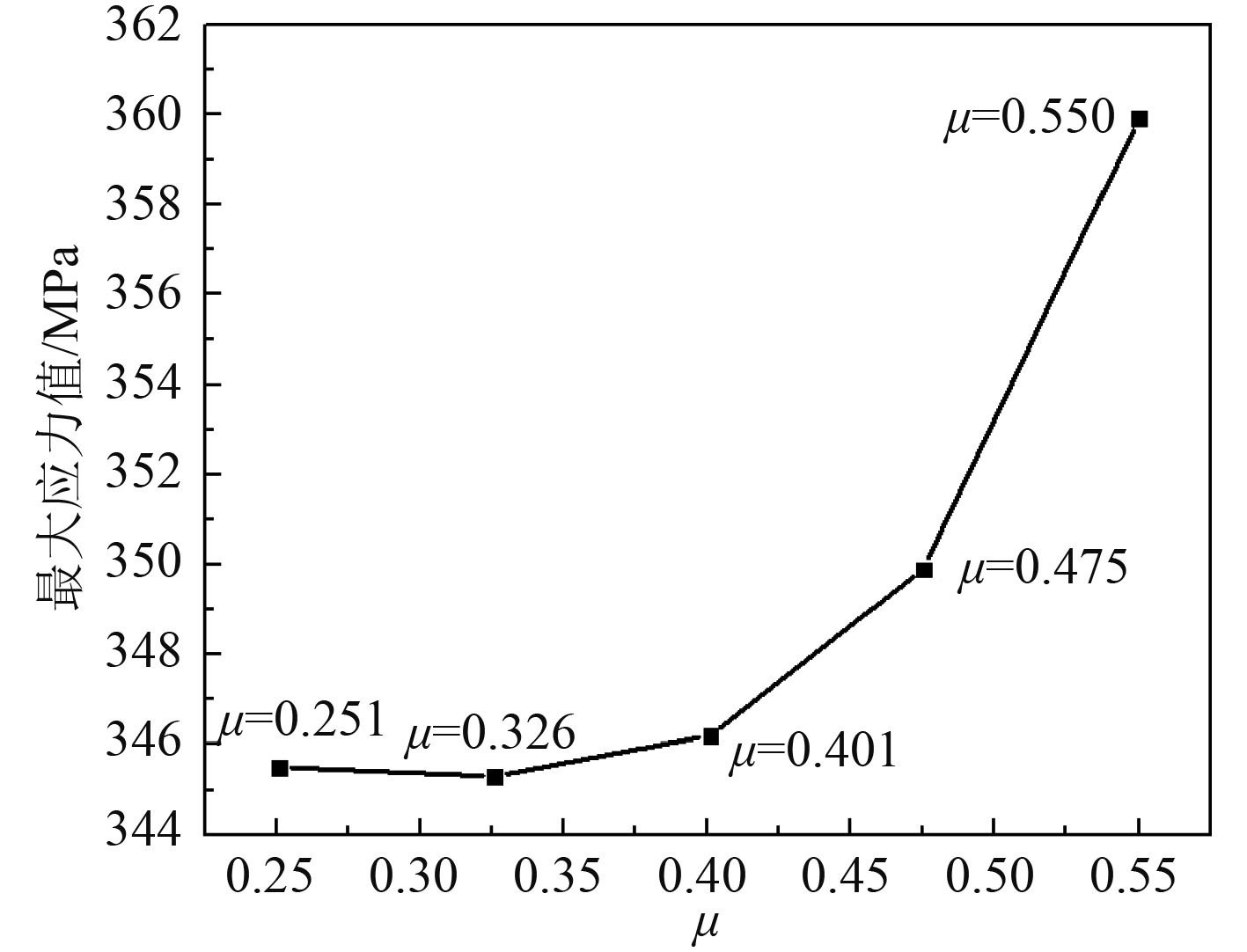
在横向和纵向冲击载荷作用下,冷却盘管最大应力产生在与封板连接处,随着夹持机构位置的改变最大应力变化较小。但是由于冷却盘管受力的不对称性,冷却盘管与压板和支撑板挤压处也会产生较大的应力,发生了塑性变形,并且随着夹持机构位置的改变该处应力变化较大,如图15和图16所示。可知,在横向和纵向冲击下冷却盘管与压板和支撑板挤压处最大应力均随夹持机构向中心移动而呈减小的趋势。这是因为夹持机构越靠近中心位置,与冷却盘管挤压产生的作用力越小。与此同时,随着夹持机构向冷却盘管中心移动,在横向和纵向冲击下压板和支撑板最大应力整体呈减小的变化趋势,并且最大应力均在设计允许范围内。
|
图 15 横向冲击下冷却盘管与夹持机构挤压处最大应力变化图 Fig. 15 Maximum stress variation diagram at the extrusion of cooling coil and clamping mechanism under transverse impact |
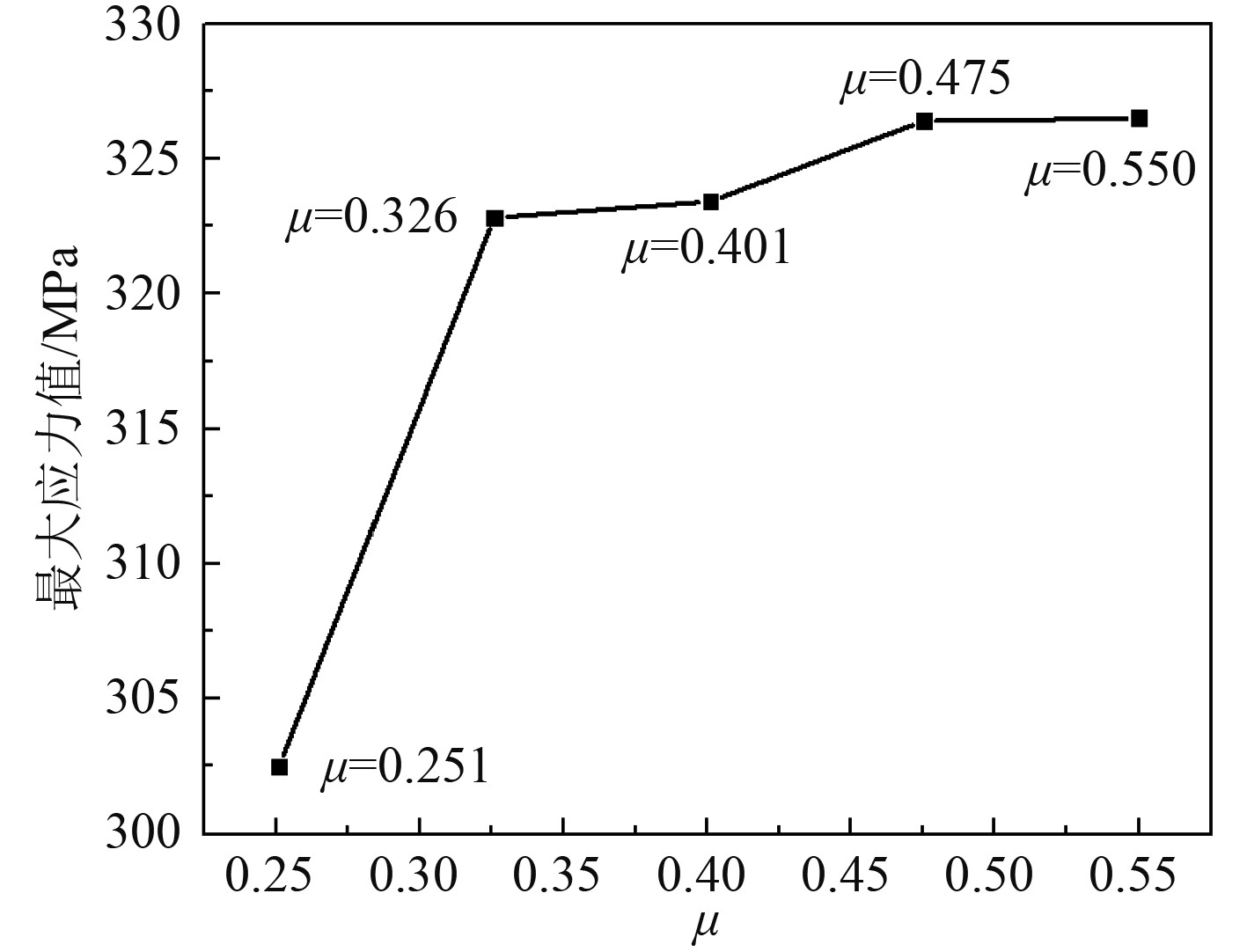
|
图 16 纵向冲击下冷却盘管与夹持机构挤压处最大应力变化图 Fig. 16 Maximum stress variation diagram at extrusion of cooling coil and clamping mechanism under longitudinal impact |
根据上述分析结论可知,夹持机构的安装位置既不能太靠近盘管两端也不能太靠近中心线位置,当安装系数μ小于0.48时,在垂向冲击下冷却盘管最大应力较大,当安装系数μ取0.48~0.55之间时,在横向冲击下冷却盘管与压板和支撑板挤压处最大应力减小趋势明显。因此,当夹持机构安装系数为0.48~0.55时,冷却盘管综合受力状况较好。
5 结 语本文以某型滑动式中间轴承为研究对象,采用时域法对其进行在垂向、横向以及纵向冲击载荷作用下的抗冲击性能分析。根据计算结果,进一步对冷却盘管这一薄弱环节进行了结构优化设计。采用双夹持机构的改进设计,提高了冷却盘管的抗冲击性能,并且分析了其安装位置对冷却盘管冲击响应的影响规律,得到以下主要结论:
1)中间轴承主体部件轴承座、轴承盖以及轴瓦座受纵向冲击载荷时响应最大,横向次之,垂向最小,尤其是轴承座在纵向和横向冲击时会产生较明显的应力集中部位,在设计时需要特别注意这些部位过渡圆角的控制。
2)由于冷却盘管在垂向上刚度小、稳定性差,导致其在垂向载荷谱冲击下响应最大,受惯性作用明显,在冲击过程中会与轴承座发生剧烈碰撞而产生很大的应力值,发生严重的塑性变形,工作状况恶劣。因此,对于悬臂安装的冷却盘管,需要进行改进设计,提高冷却盘管在垂向上的结构刚度,减小变形。
3)采用双夹持机构进行支撑能有效减弱冷却盘管在垂向载荷谱冲击下的响应,使冷却盘管的工作状况得到明显改善。冷却盘管与压板和支撑板在各方向冲击下会发生挤压现象,本文研究了夹持机构不同安装位置对冷却盘管冲击响应的影响,得到了较佳的安装位置范围。
| [1] |
汪玉, 王官祥. 舰船系统和设备的抗冲击性能动力学仿真[J]. 计算机仿真, 1999(1): 29-31. |
| [2] |
马炳杰, 王志刚, 姚辉. 船舶推进轴系冲击性能预估和影响因素分析[J]. 大连海事大学学报, 2011, 37(4): 13-16. DOI:10.16411/j.cnki.issn1006-7736.2011.04.021 |
| [3] |
李磊. 基于有限元方法的船舶推进轴系抗冲击性能研究[D]. 武汉: 武汉理工大学, 2012.
|
| [4] |
李增光, 马忠俊. 多支点处不同冲击作用下的舰船推进轴系冲击计算及分析[J]. 武汉理工大学学报(交通科学与工程版), 2013, 37(3): 566-569. |
| [5] |
张晓阳, 陈汝刚, 解忠良, 等. 舰船轴系用液压螺栓抗冲击性能的数值仿真[J]. 噪声与振动控制, 2015, 35(4): 149-152+158. |
| [6] |
吴晖, 周少伟. 法兰式液压联轴器抗冲击性能分析[J]. 舰船科学技术, 2015, 37(7): 38-42. WU Hui, ZHOU Shaowei. Analysis of the anti-shock performance for flanged hydraulic coupling[J]. Ship Science and Technology, 2015, 37(7): 38-42. DOI:10.3404/j.issn.1672-7649.2015.07.009 |
| [7] |
刘学斌, 徐伟, 何江洋. 舰船弹性支撑推力轴承抗冲击特性研究[J]. 船舶工程, 2016, 38(11): 58-61. DOI:10.13788/j.cnki.cbgc.2016.11.058 |
| [8] |
姚胜昶. 基于有限元分析的舰船推进轴系抗冲击性能研究[J]. 舰船科学技术, 2017, 39(22): 61-63. YAO Shengchang. Research on anti shock performance of ship propulsion shafting based on finite element analysis[J]. Ship Science and Technology, 2017, 39(22): 61-63. |
| [9] |
姜克达. 非接触爆炸下舰船推进轴系的冲击动响应研究[D]. 哈尔滨: 哈尔滨工程大学, 2019.
|
| [10] |
侯淑芳, 周志军, 肖能齐. 舰船推进轴系动力学建模及冲击响应分析研究[J]. 三峡大学学报(自然科学版), 2020, 42(4): 94-100. DOI:10.13393/j.cnki.issn.1672-948x.2020.04.016 |
| [11] |
联邦德国国防装备部. 联邦德国国防军舰艇建造规范-冲击安全性: BV043/85[S]. 中国舰船研究院, 译. 北京: 中国舰船研究院, 1998.
|
 2023, Vol. 45
2023, Vol. 45
