船舶在航运过程中的污染排放对环境有着很大的影响,针对我国目前提出的能源转型,推动能源系统逐步向清洁化、绿色化、低碳化方向转型。为了减少船舶的污染排放,目前燃料电池系统是最有前途应用于船舶的技术之一[1]。目前为止,大多数现有的燃料电池船都由质子交换膜燃料电池(PEMFC)驱动,因为它的零排放、相对较高的功率密度和快速启动[2]。适用于低功率船,如小型游艇或客船等。另一方面,与混合动力汽车相比,船舶可以提供更大的储能空间,因此可以在船上安装更大容量的电池。为了满足船舶功率需求,采用燃料电池和锂电池并联的混合动力系统。
对于混合动力船舶需要采用能量管理策略(EMS)高效分配燃料电池和锂电池的输出功率,Nelson等[3]提出了基于逻辑阈值的混合系统控制策略,目的是对多种能源进行能量管理。彭东恺等[4]采用燃料优化能量管理策略对经典船舶循环工况进行优化计算,得到了燃料电池混合动力系统最优能量分配策略。Erdinc等[5]采用小波模糊逻辑控制策略对混合动力系统进行功率分配,保证系统的稳定性。Li等[6]提出了一种非线性模型预测控制策略来提高混合动力电动客车的燃油经济性。Hou等[7]提出了一种自适应模型预测控制,在线参数辨识用于减轻参数不确定性,模型预测控制用于最优功率分配、处理约束和实现期望的动态响应。综上,为了解决混合动力系统的能量管理问题,提出一种基于功率解耦的外部能效最大化策略(改进EEMS),并与双闭环PI控制和外部能效最大化策略(EEMS)进行对比分析。
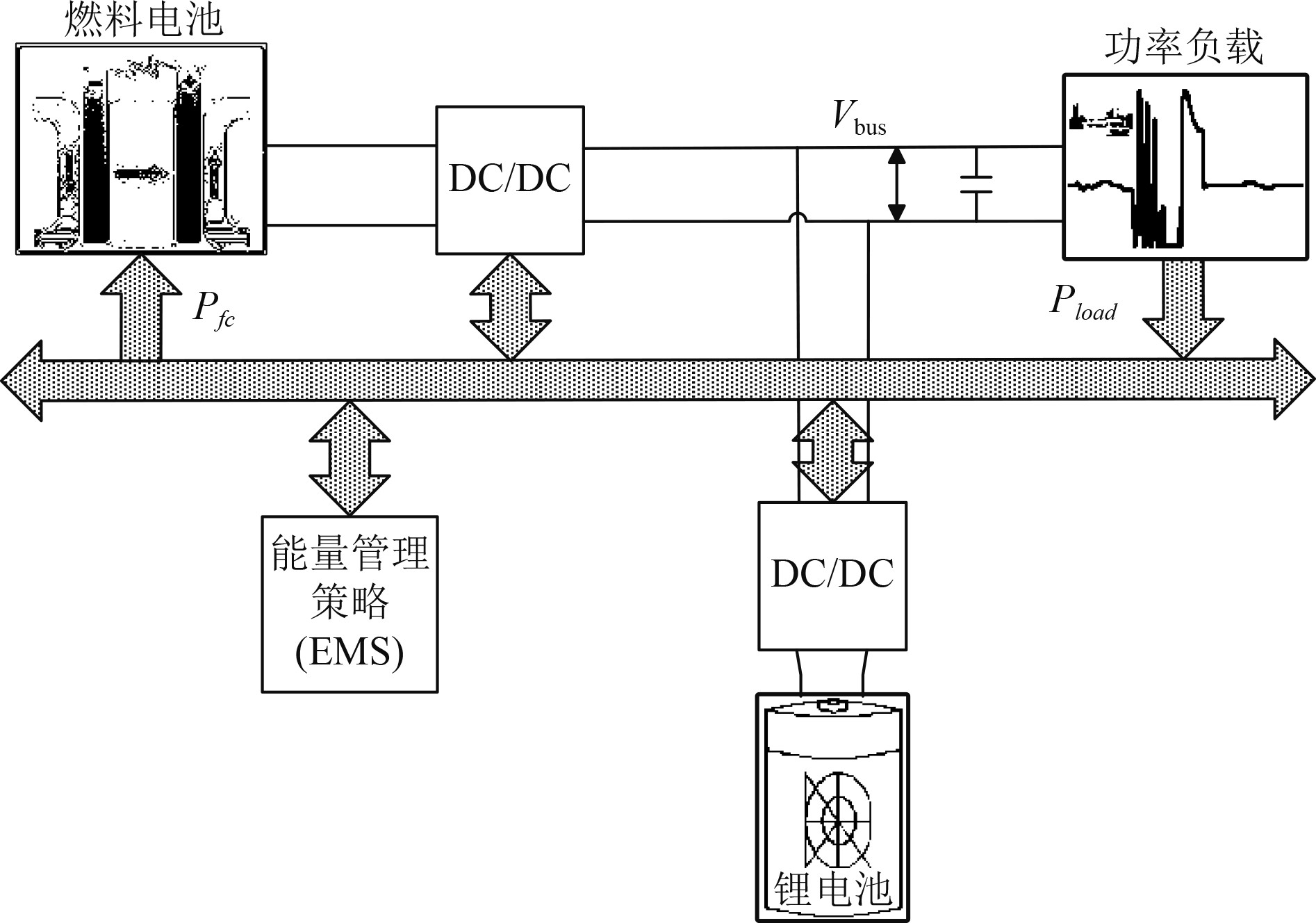
1 燃料电池船混合动力系统设计的燃料电池船混合动力系统采用的是燃料电池和锂电池作为动力源,同时为负载提供能量,并且在母线端并联电容器,以提高电源的瞬时功率和提高母线电压质量。燃料电池和锂电池的能量控制,分别是由单相Boost变换器和双向DC-DC变换器连接到母线上,系统的拓扑结构如图1所示。
|
图 1 混合动力系统拓扑结构图 Fig. 1 Topology diagram of hybrid power system |
图中
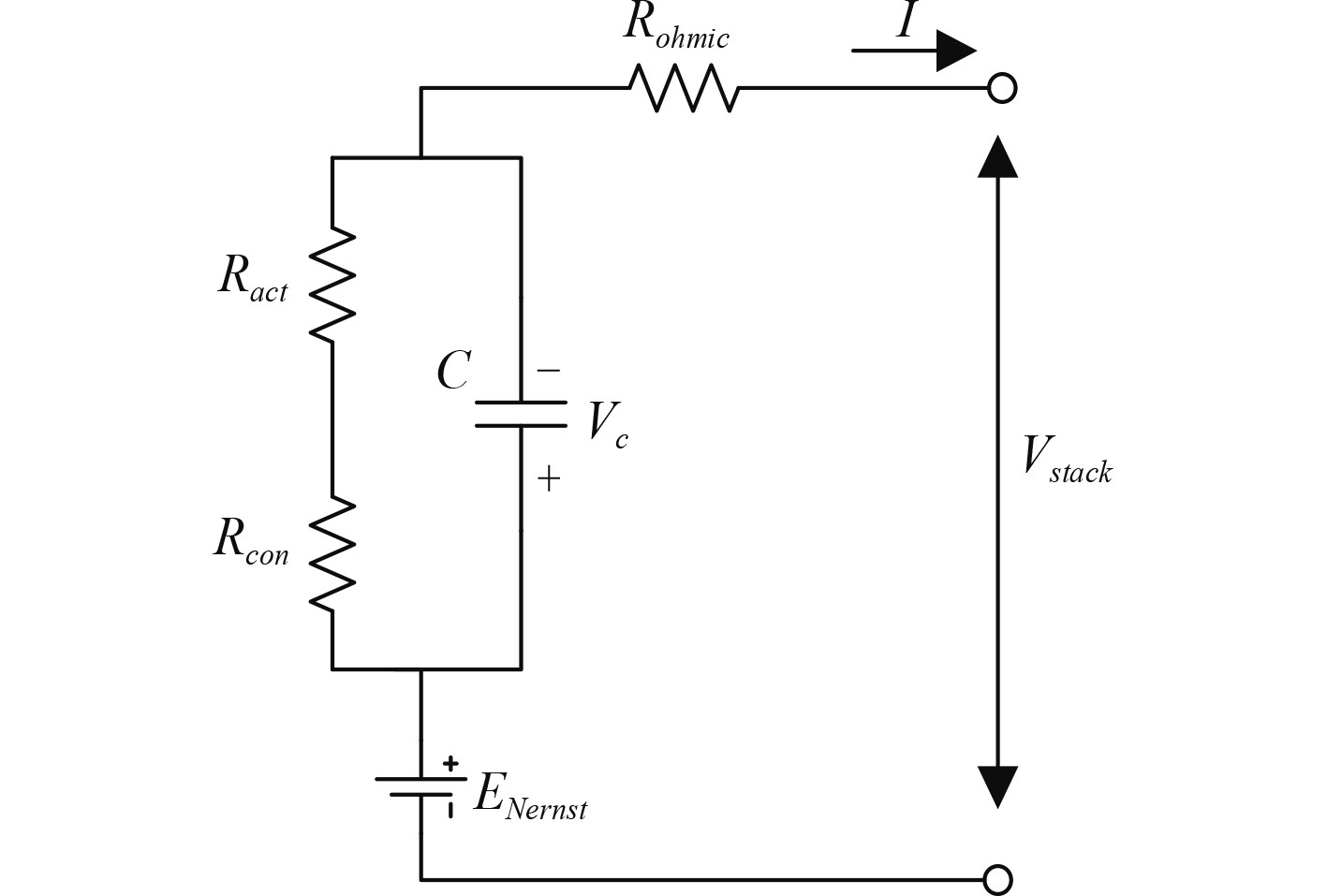
由于燃料电池是一个复杂的非线性系统,具有许多参数和依赖关系,因此需要根据具体的目的和目标建立模型。根据燃料电池的建模方法,模型可以分为机械的(理论的)、经验的(分析的)和半经验的。基于Amphlett等[9]提出的半经验模型模拟燃料电池在不同运行条件下的稳态伏安特性。该模型由理论推导的公式组成,其中参数根据测试结果估算。通常对该模型进行扩展,使其适用于燃料电池堆的建模,并考虑了浓度损耗。基于半经验模型并通过相应的公式进行扩展,燃料电池的数学模型如图2所示。
|
图 2 燃料电池数学模型 Fig. 2 Mathematical model of fuel cell |
燃料电池堆电压的计算公式为:
| $ {V_{stack}} = n \cdot {V_{cell}}, $ | (1) |
| $ {V_{stack}} = n \cdot \left( {{E_{N{\text{er}}nst}} + \Delta {E_{act}} + \Delta {E_{ohmic}} + \Delta {E_{con}}} \right)。$ | (2) |
式中:
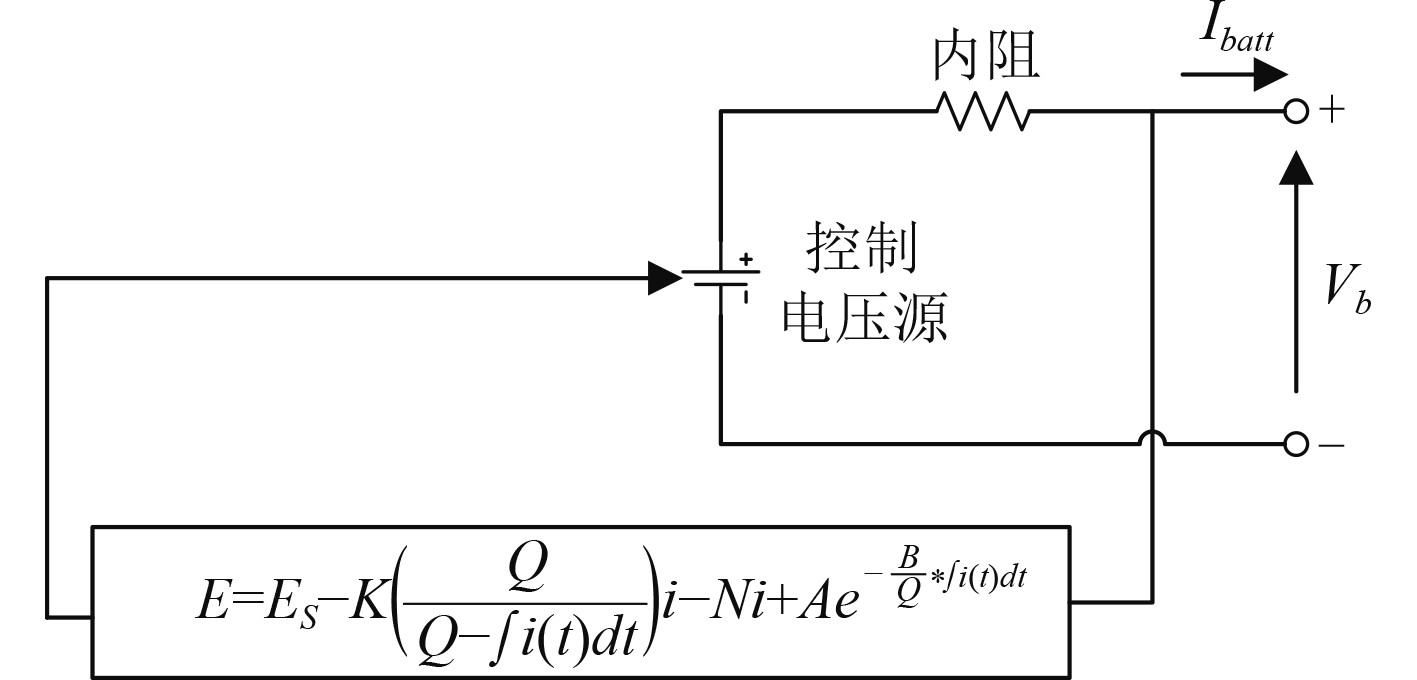
在Shepherd模型中,通过考虑非线性电压特性和串联内阻,电池被描述为类似于Rint模型。这个稳态模型有一个通用的建模方法,并且不限于特定的电池类型。Tremblay[10]改进了Shepherd模型,即电池内部的电压完全取决于当前的SOC。因此,开路电压随着SOC的减少而不断减小,并且与电流无关。得到的模型如图3所示。
|
图 3 锂电池模型 Fig. 3 Lithium battery model |
模型中参数E表示开路电压。
| $ E = {E_S} - K\left( {\frac{Q}{{Q - \int {{i}\left( t \right){\rm{d}}t} }}} \right)i - Ni + A{e^{ - \frac{B}{Q} * \int {i\left( t \right){\rm{d}}t} }} 。$ | (3) |
电池的端电压通过下式计算:
| $ {V_{batt}} = E - {I_{batt}} \cdot {R_{{int} }}。$ | (4) |
式中:
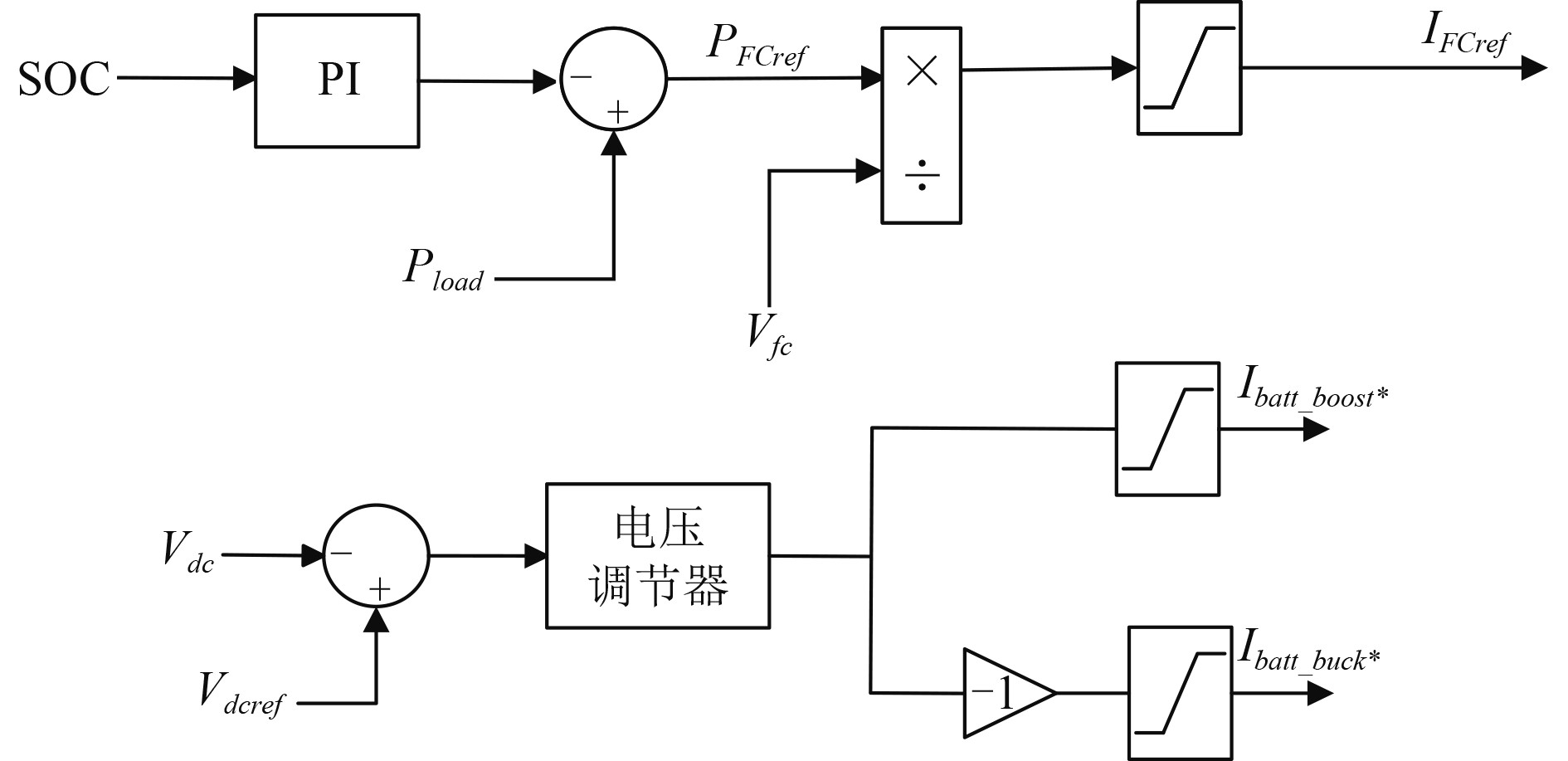
燃料电池采用双闭环PI控制,使输出功率保持着动态平衡。优点是很好解决了对于燃料电池承担功率突变的问题,使得燃料电池功率变化平稳,满足其较慢的动态响应速度。外环是基于锂电池SOC的闭环控制,能够有效控制锂电池过充过放,燃料电池会在适当的时候选择对其充电或者让其优先放电,整体控制策略如图4所示。
|
图 4 双闭环PI控制策略结构 Fig. 4 Double closed-loop PI control strategy structure |
确定锂电池SOC的常用方法是库仑计数法。当前SOC的计算方法如下[11]:
| $ SOC\left( t \right) = SO{C_0} + \Delta SOC = SO{C_0} - {\eta _{b,col}} \text{×} \frac{{\displaystyle\int _0^\tau {I_{{\text{b}}at}}\left( t \right){\rm{d}}t }}{Q} \text{×} 100 。$ | (5) |
式中:
外部能效最大化策略(EEMS)旨在最大限度地减少氢燃料消耗,通过在SOC正常范围内提高锂电池能量利用率,这种方法的主要优点是成本函数不需要评估等效电池能量,成本函数是在给定的间隔时间内外部能源提供的能量。控制策略结构如图5所示。
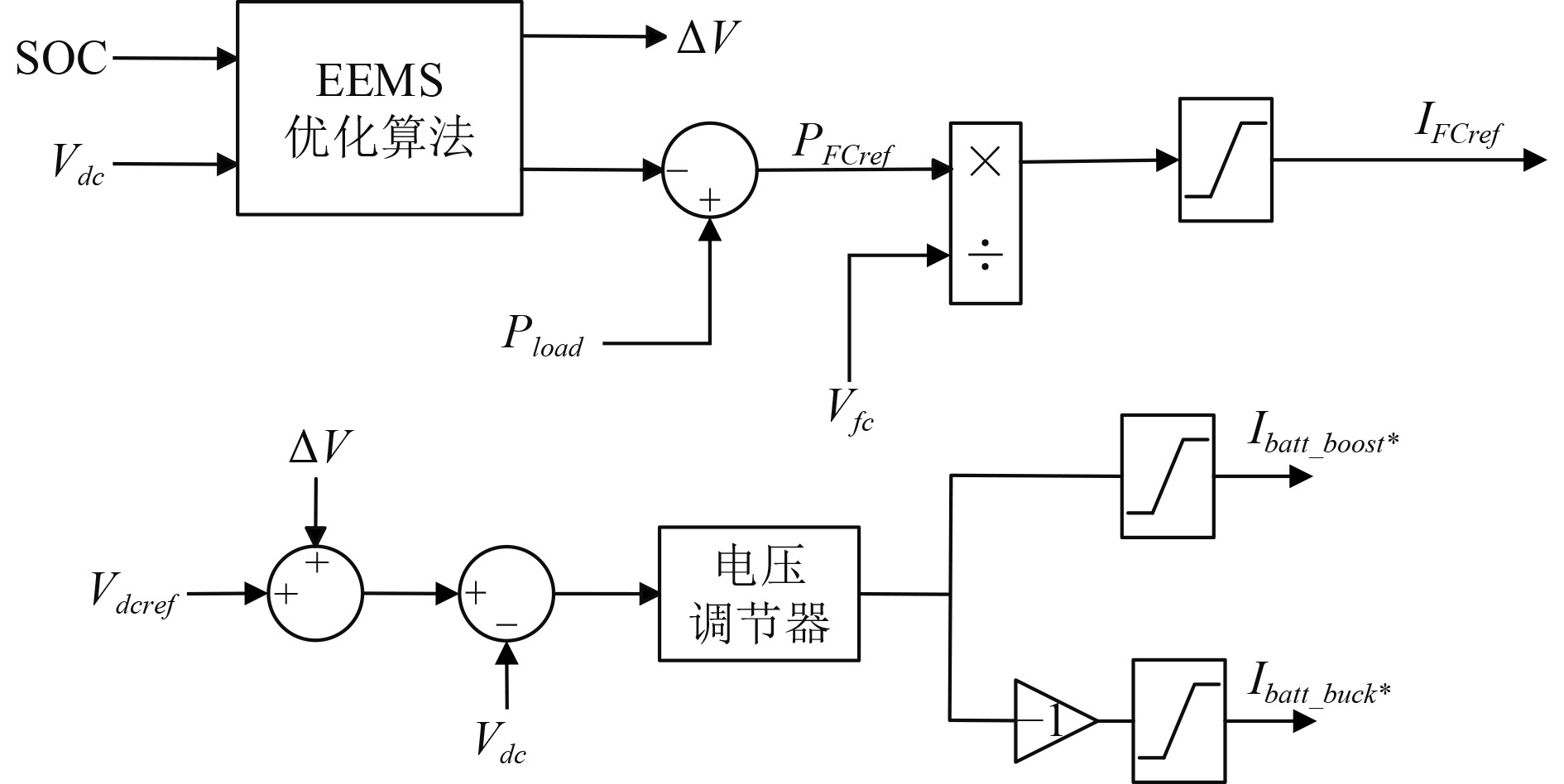
|
图 5 外部能效最大化策略结构 Fig. 5 External energy efficiency maximization strategy structure |
优化问题定义如下:
成本函数求解的不等式范围:
| $ {P_{FC}}\Delta T \leqslant \left( {SOC - SO{C_{\min }}} \right){V_{FC{\text{r}}}}{Q_{FC}}, $ | (6) |
边界条件:
| $ {P_{FC\min }} \leqslant {P_{FC}} \leqslant {P_{FC\max }} ,$ | (7) |
| $ {V_{dc\min }} - {V_{dc}} \leqslant \Delta V \leqslant {V_{dc\max }} - {V_{dc}}。$ | (8) |
式中:
设计的混合动力系统在母线端并联电容器,目的是抑制母线电压的瞬时波动,同时也有效提高电源的瞬时功率,使得整个系统更加稳定,所以为了更加准确得出燃料电池的参考功率,提出基于功率解耦的外部能效最大化策略(改进EEMS),在外部能效最大化策略优化算法上根据设计的混合动力系统特点进行了优化,增加了功率解耦,整体策略如图6所示。
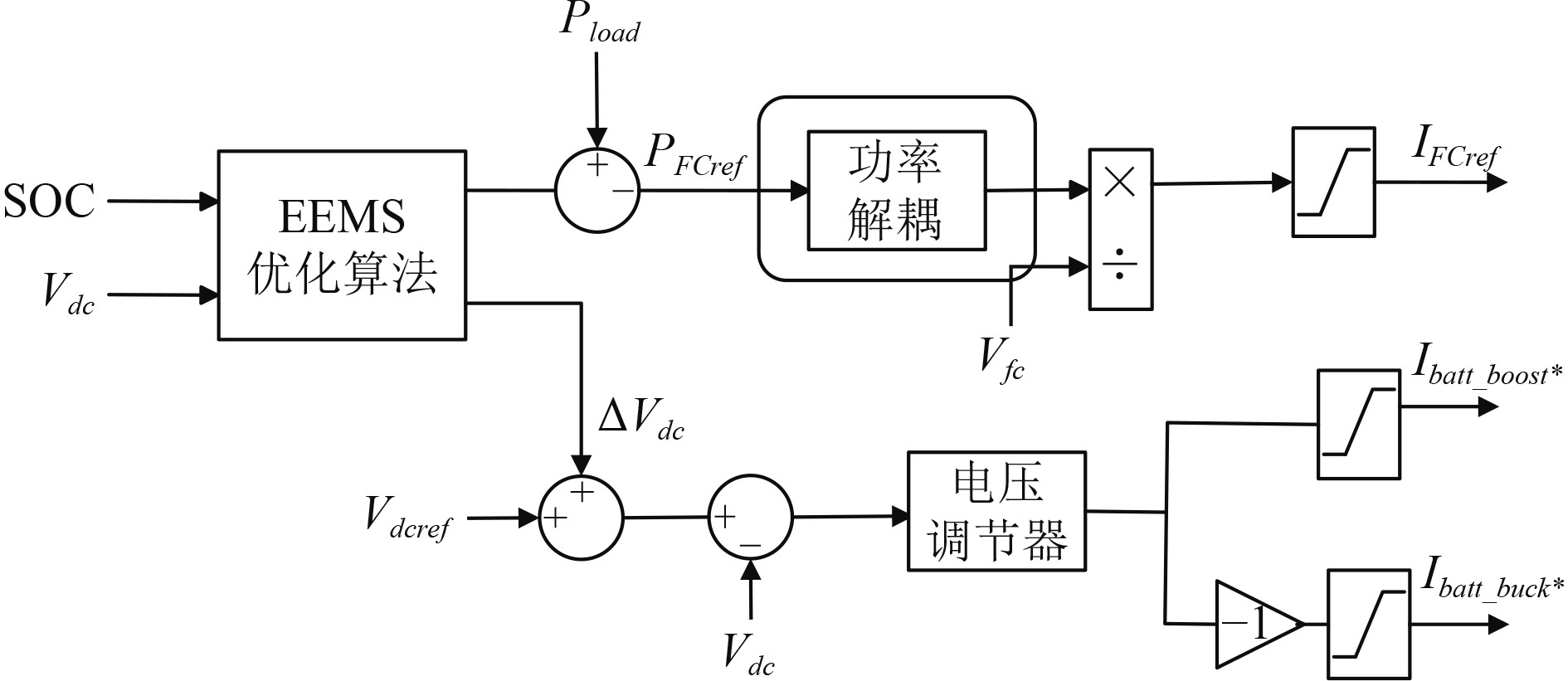
|
图 6 改进外部能效最大化策略结构 Fig. 6 Improve the external energy efficiency maximization strategy structure |
为了比较本文方案在燃料经济性方面的性能,Bernard等[13]开发了一种离线优化算法。该算法给出了在给定负载曲线下可以实现的最小燃料消耗,同时保持电池SOC在其限制范围内,如图7所示。
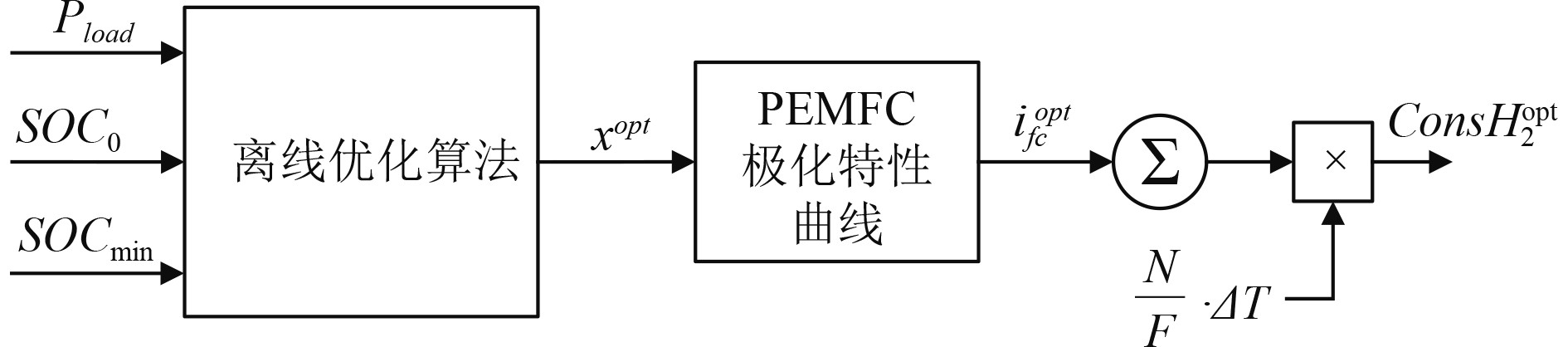
|
图 7 离线优化算法 Fig. 7 Off-line optimization algorithm |
该算法以电池SOC的初始值和最小值作为负载曲线的输入,输出是所需的最低燃料消耗。优化问题的定义如下:
求最优解
| $ H = \sum\limits_{k = 1}^n {{P_{fc}}\left( k \right) \cdot } \Delta T ,$ | (9) |
不等式约束条件(k=1,2,3,...,n):
| $ y = \left( {k + 1} \right) \leqslant \left( {SO{C_0} - SO{C_{\min }}} \right){V_{battr}}Q, $ | (10) |
| $ \sum\limits_{k = 1}^n {{P_{fc}}\left( k \right)} \geqslant n \cdot {P_{fc\min }}, $ | (11) |
| $ y\left( {k + 1} \right) = y\left( k \right) + \left( {{P_{load}}\left( k \right) - {P_{fc}}\left( k \right)} \right)\Delta T ,$ | (12) |
边界条件:
| $ {P_{fc\min }} \leqslant {P_{fc}} \leqslant {P_{fc\max }}。$ | (13) |
式中:
离线优化算法输出最优燃料电池功率(
| $ ConsH_2^{opt} = \frac{N}{F}\sum\limits_{k = 1}^n {i_{fc}^{opt}} \left( k \right) \cdot \Delta T 。$ | (14) |
式中:
在Matlab/Simulink仿真环境中,搭建由燃料电池和锂电池组成的混合动力系统,在满足船舶负载波动下,对3种不同控制策略进行对比分析验证控制策略的有效性,仿真参数如表1所示。将改进的外部能效最大化策略与双闭环PI控制和外部能效最大化策略进行对比,仿真结果如图8~图10所示。
|
|
表 1 仿真参数 Tab.1 Simulation parameters |
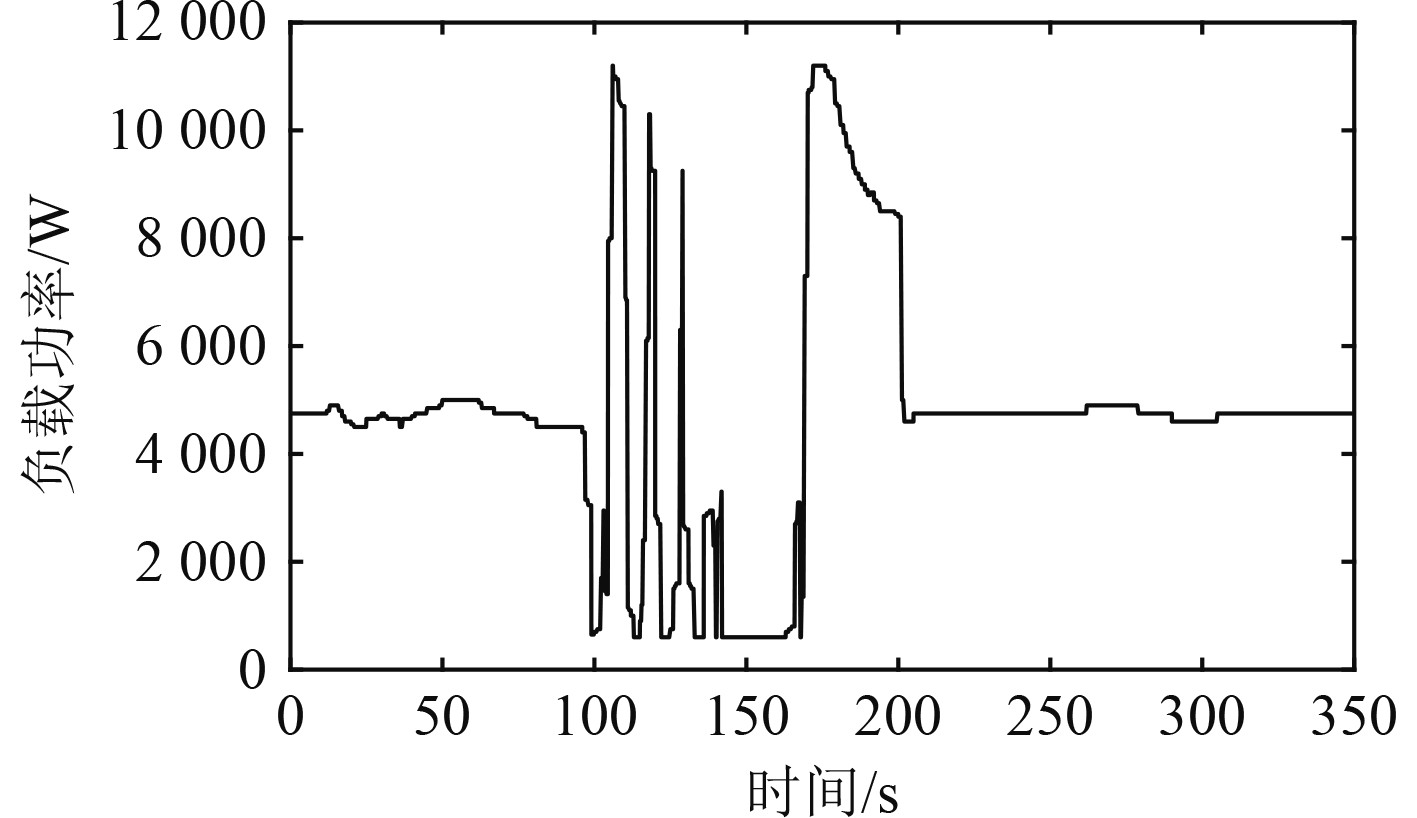
|
图 8 船舶典型工况 Fig. 8 Typical ship condition |
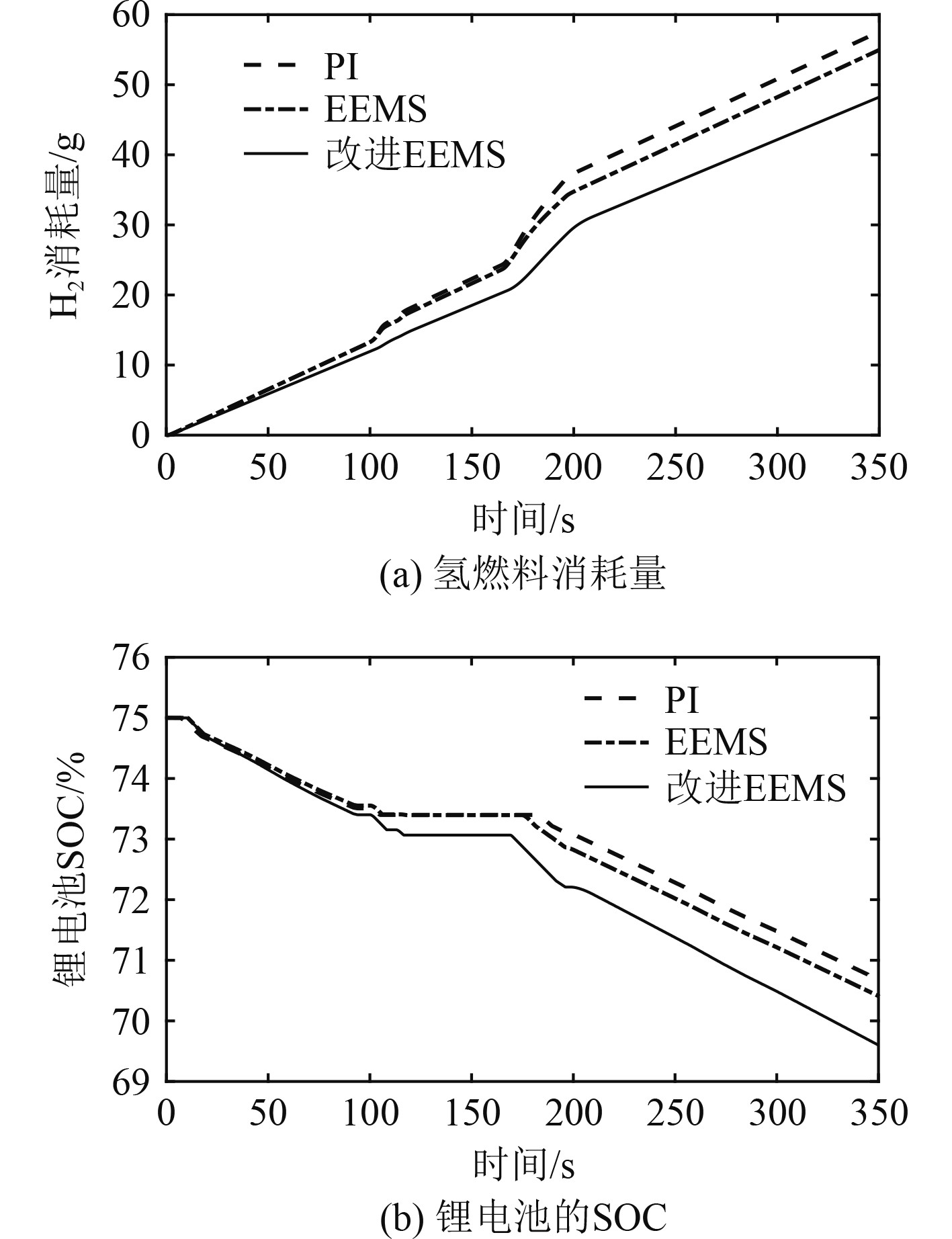
|
图 10 动力源的能量消耗 Fig. 10 Energy consumption of power source |
负载的仿真如图8所示。在第1阶段(0~100 s)和最后一个阶段(200~350 s)船舶为正常航行,第2阶段(100~142 s)为船舶靠港,此时负载功率在0~1 MW之间波动剧烈,第3阶段(142~170 s)是船舶靠岸接送乘客,只是维持基本的系统运行负载消耗较少,第4阶段(170~200 s)为船舶离港,推进系统使船舶加速至航行速度,负载功率到达峰值。
从图9 可以看出,在满足负载条件下,3种控制策略都能够有效控制能量分配,同时在停港和离港时负载波动剧烈。为了能够有效补偿负载的峰值功率和提高电源的瞬时功率,在靠岸时系统负载功率较小,此时燃料电池的输出功率能为锂电池进行充电,储存过剩的能量。通过对比可知,改进EEMS比双闭环PI控制和EEMS得到的燃料电池输出功率波动更小,曲线更平滑。
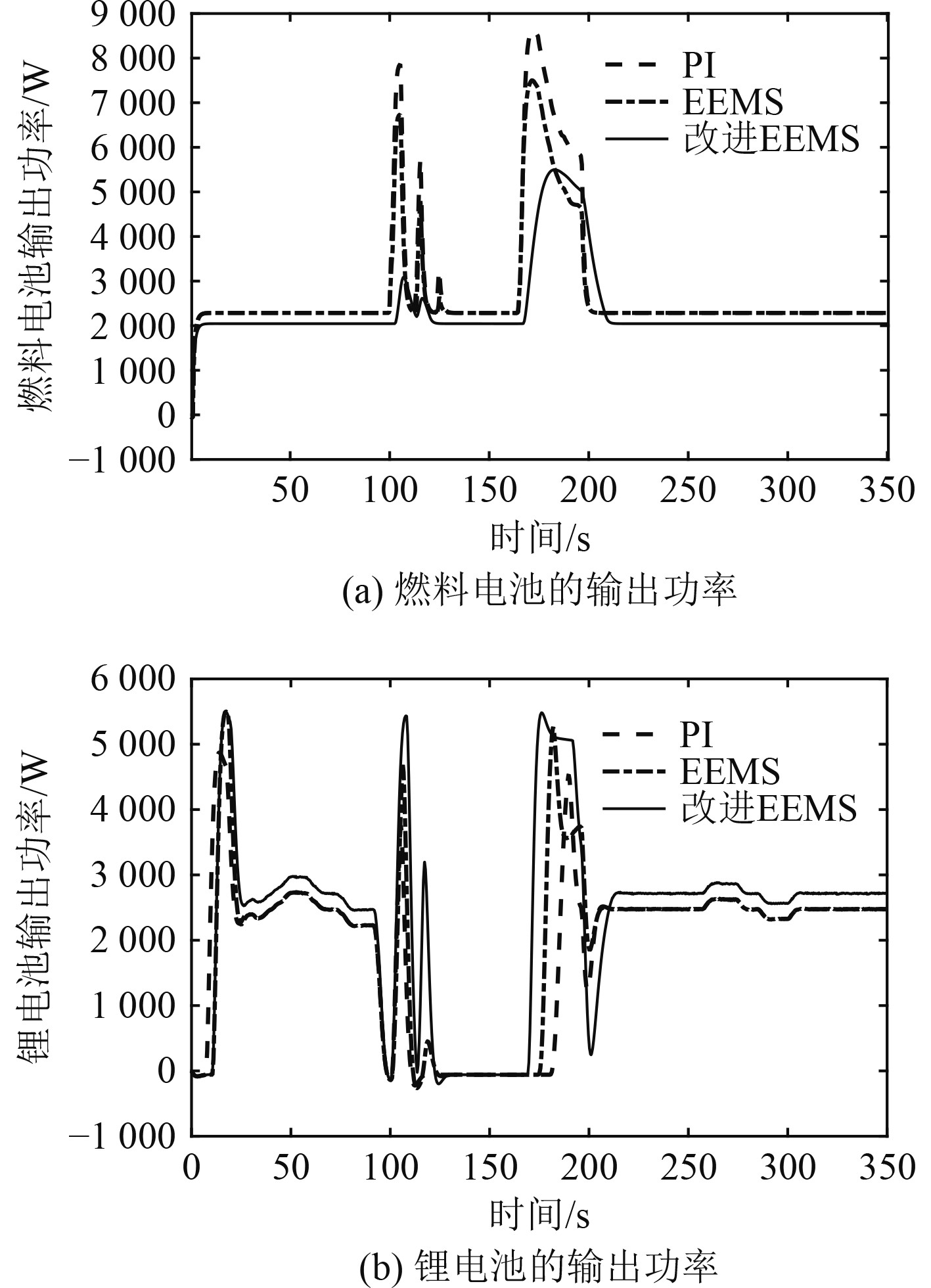
|
图 9 动力源的输出功率 Fig. 9 Power output of the power source |
从图10 (a)可以看出,在相同条件下,船舶的整个航行过程在不同控制策略下的燃料电池氢燃料消耗量和锂电池荷电状态的变化范围。双闭环PI控制、EEMS和改进EEMS等3种控制策略下氢燃料的消耗量分别为57.97 g,55.02 g,48.92 g。对于锂电池的荷电状态,从图10 (b)可以看出,锂电池经过整个循环工况后,电池的荷电状态仍可保持在合理范围内,并且船舶在靠岸时可使用岸电来为锂电池充电。通过对比可知,改进EEMS在保证混合动力系统稳定的同时能够使得辅助电源出力最大化和改善系统的鲁棒性,从而有效利用混合动力系统的特点,提高了氢燃料经济性。
4 结 语为了合理管理多动力源耦合系统,协调机电推进,保证船舶安全航行,提出了一种基于功率解耦的外部能效最大化策略,应用于燃料电池船舶混合动力系统,该策略能够优化能量分配,并对船舶典型工况下的负载功率变化具有更强的鲁棒性。通过建模仿真和对比分析,本文提出的策略分别比双闭环PI控制策略和外部能效最大化策略在氢燃料利用率上提升了15.61%和11.09%,提高了系统氢燃料经济性,使得燃料电池船舶混合动力系统能够总体高效运行。
由于本文只采用了燃料电池船舶的典型工况进行分析,但实际船舶的航行工况更为复杂,后续研究应在不同船舶工况下进行验证分析。
| [1] |
杨发财, 李世安, 沈秋婉, 等. 绿色航运发展趋势和燃料电池船舶的应用前景[J]. 船舶工程, 2020, 42(278): 46-52. DOI:10.13788/j.cnki.cbgc.2020.04.01 |
| [2] |
HAN J, CHARPENTIER J F, TANG T. An energy management system of a fuel cell/battery hybrid boat[J]. Energies, 2014, 7(5): 2799-2820. DOI:10.3390/en7052799 |
| [3] |
NELSON D B, NEHRIR M H, WANG C. Unit sizing and cost analysis of stand-alone hybrid wind/PV/fuel cell power generation systems[J]. Renewable Energy, 2006, 31(10): 1641-1656. DOI:10.1016/j.renene.2005.08.031 |
| [4] |
彭东恺, 朱礼斯, 韩金刚, 等. 船舶燃料电池-蓄电池混合动力系统能量管理策略及仿真分析[J]. 系统仿真学报, 2014, 26(11): 2797-2802. DOI:10.16182/j.cnki.joss.2014.11.043 |
| [5] |
ERDINC O, VURAL B, UZUNOGLU M. A wavelet-fuzzy logic based energy management strategy for a fuel cell/battery/ultra-capacitor hybrid vehicular power system[J]. Journal of Power Sources, 2009, 194(1): 369-380. DOI:10.1016/j.jpowsour.2009.04.072 |
| [6] |
LI L, ZHANG YB, YANG C, et al. Model predictive control-based efficient energy recovery control strategy for regenerative braking system of hybrid electric bus[J]. Energy Convers Manage, 2016,111: 299–314.
|
| [7] |
HOU J, SONG Z, HOFMANN H, et al. Adaptive model predictive control for hybrid energy storage energy management in all-electric ship microgrids[J]. Energy Conversion and Management, 2019, 198: 111929. DOI:10.1016/j.enconman.2019.111929 |
| [8] |
张泽辉, 高海波, 管聪, 等. 典型工况下的燃料电池船舶复合储能系统设计[J]. 船舶工程, 2018, 40(8): 103-108. DOI:10.13788/j.cnki.cbgc.2018.08.100 |
| [9] |
AMPHLETT J C, BAUMERT R M, MANN R F, et al. Performance modeling of the Ballard Mark IV solid polymer electrolyte fuel cell: I. Mechanistic model development[J]. Journal of the Electrochemical Society, 1995, 142(1): 1. DOI:10.1149/1.2043866 |
| [10] |
TREMBLAY O, DESSAINT L A, DEKKICHE A I. A generic battery model for the dynamic simulation of hybrid electric vehicles[C]//2007 IEEE Vehicle Power and Propulsion Conference. IEEE, 2007: 284−289.
|
| [11] |
ZHANG Y, SONG W, LIN S, et al. A novel model of the initial state of charge estimation for LiFePO4 batteries[J]. Journal of Power Sources, 2014, 248: 1028-1033. DOI:10.1016/j.jpowsour.2013.09.135 |
| [12] |
MOTAPON S N, DESSAINT L A, AL-HADDAD K. A robust H2-consumption-minimization-based energy management strategy for a fuel cell hybrid emergency power system of more electric aircraft[J]. IEEE Transactions on Industrial Electronics, 2014, 61(11): 6148-6156. DOI:10.1109/TIE.2014.2308148 |
| [13] |
BERNARD J, DELPRAT S, BUECHI F, et al. Global optimisation in the power management of a fuel cell hybrid vehicle (FCHV)[C]//2006 IEEE Vehicle Power and Propulsion Conference. IEEE, 2006: 1−6.
|
 2023, Vol. 45
2023, Vol. 45
