2. 中国舰船研究设计中心,湖北 武汉 430064
2. China Ship Development and Design Center, Wuhan 430064, China
无人艇作为一种具有环境感知、自主航行能力的小型智能化水面平台,在水面测绘、水体检测、监视侦察、扫雷反潜等民用和军用领域均有广泛应用。无人艇通常由大型母船携带并布放回收,在回收时需要以一定的航速逼近母船。在回收过程中,受航速、尾流以及波浪等因素影响,无人艇各方向自由度会发生不同程度的变化,其运动响应特性直接影响到无人艇回收的成功率和安全性。因此,开展无人艇回收过程动态特性研究对保证无人艇的正常回收,提高无人艇回收成功率均具有重要意义。
2010年,王金宝等[1]以商用软件Fluent为平台,以KVLCC2M算例为对象,进行了低速肥大船舶尾流场的数值模拟和阻力性能预报。通过将计算结果与实船实验结果比较,确定了工程上适用的计算方法,并将该计算方法应用于多艘船舶的尾流场模拟和阻力性能预报。杨勇[2]采用CFD模拟船体周围的粘性流场,计算船体所受的水动力,并分析了非定常操纵运动船体周围流场的特点。钱小斌等[3]对不规则波扰动进行建模并研究其对船舶运动的影响,同时对比了长短峰波的波面形状及其产生的力矩和波浪力,研究表明短峰不规则波会对船舶的运动产生较大影响。邓锐等[4]对RANS,LES,DES,URANS及混合RANS-LES等模型的特点进行了逐一探讨,并给出了各种湍流模型在船舶与海洋工程计算流体力学方面的一些应用实例。苑洋等[5]以“育鹏”轮为研究对象,对该船的直航和斜航运动水动力进行数值计算,并将结果与水池试验数据进行比较,验证了计算方法的可行性。陶志奇等[6]采用重叠网格及RANS方法对船模在顶浪条件下的运动进行了数值模拟,比较了规则波、白噪声波谱以及双参数谱3种计算方法的效果,并对造波参数进行了讨论。杜一豪等[7]采用统计学方法对不规则波作用下船舶运动幅值和响应周期的分布规律进行了深入探讨,结合傅里叶变换对运动响应进行了频谱特征分析,研究表明船舶在升沉和纵摇方向与横摇方向的随机运动响应特征有着显著差异。
本文以某型无人艇为研究对象,建立无人艇回收过程动态仿真数值模型,通过加载4级海况不规则波,分析在海浪及尾流共同作用下无人艇在逼近母船过程中横荡、垂荡、横摇角、纵摇角4个自由度的响应特性。对比分析回收速度、偏移距离及前方有无母船等因素对无人艇回收过程动态特性的影响规律,为后续无人艇回收条件的确定及回收过程的运动控制提供指导。
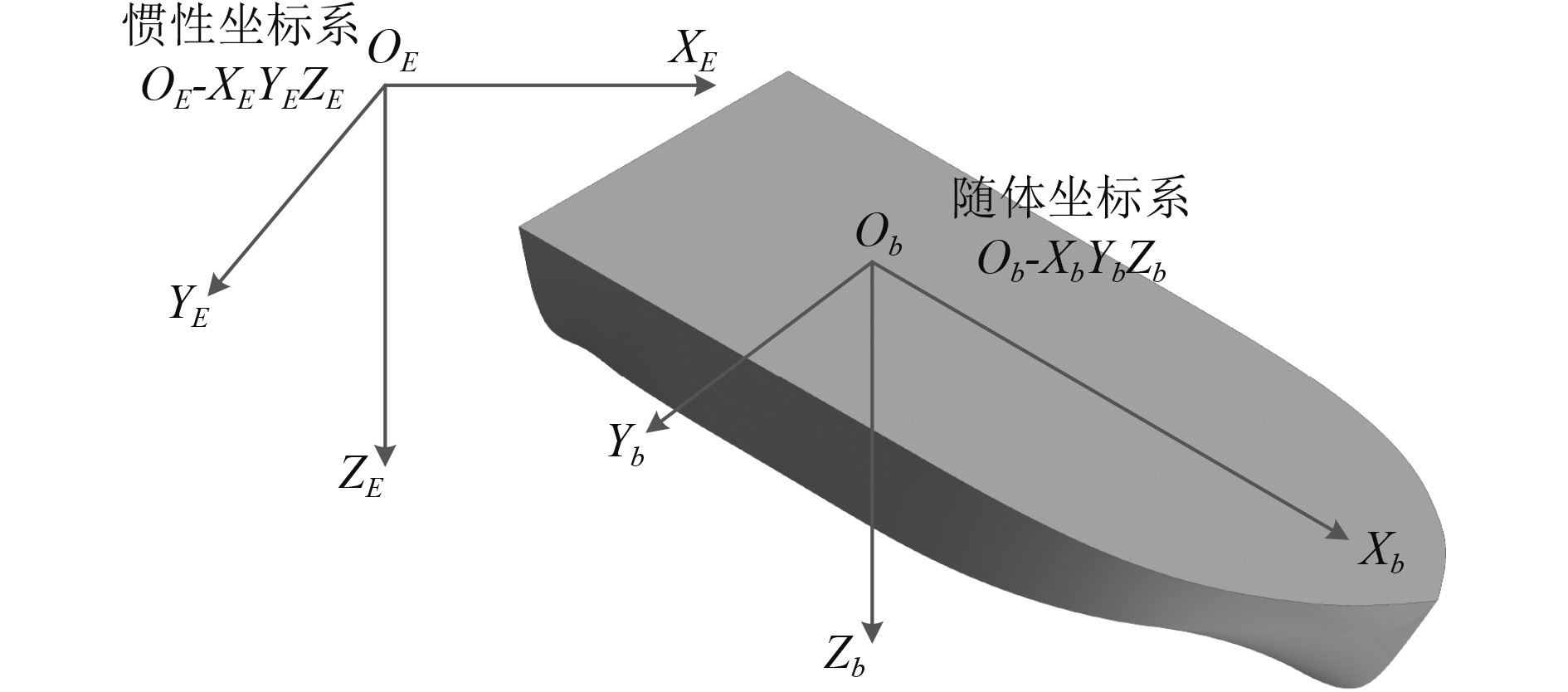
1 计算理论基础 1.1 无人艇运动模型无人艇航行时的运动可以分解为6个自由度,而描述无人艇的空间运动通常采用2种三维直角坐标系,即惯性坐标系OE-XEYEZE和随体坐标系Ob-XbYbZb,这2种坐标系均遵守右手法则,如图1所示。
|
图 1 无人艇坐标系 Fig. 1 Coordinate system of USV |
惯性坐标系OE-XEYEZE用于描述无人艇的位姿,其原点OE固定于水面上某点,OEZE轴以指向地心为正。随体坐标系Ob-XbYbZb用于描述无人艇的速度和受力,坐标原点Ob通常取在无人艇的重心G处,ObXb,ObYb,ObZb分别以指向艇首、右舷和向下为正[8-10]。
无人艇6个自由度中的横摇、纵摇和首摇用来确定无人艇姿态,统称为欧拉角,以随体坐标系Ob-XbYbZb相对于惯性坐标系OE-XEYEZE的3个姿态角[φ θ ψ]T表示,即将随体坐标系依次绕随体坐标系的坐标轴ObZb,ObYb,ObXb旋转ψ,θ,φ角度(旋转是指先绕ObZb轴旋转,再绕新的ObYb轴旋转,最后绕新的ObXb轴旋转)后有OEZE轴和ObZb轴平行、OEYE轴和ObYb轴平行、OEXE轴和ObXb轴平行。纵荡、横荡和垂荡确定无人艇位置,以随体坐标系Ob-XbYbZb原点Ob在惯性坐标系中的3个坐标分量[x y z]T表示。无人艇运动描述的相关符号及定义均采用造船与轮机工程师学会和国际拖曳水池会议推荐的符号体系,如表1所示。
|
|
表 1 无人艇运动符号定义 Tab.1 USV movement symbol definition |
根据惯性坐标系与随体坐标系之间的旋转与平移变换关系,可推导出两坐标系间的线速度运动量变换关系如下式:
| $\begin{split} \left[ \begin{aligned} {\dot x} \\ {\dot y} \\ {\dot z} \end{aligned} \right] = \;& \left[ {\begin{array}{*{20}{c}} {\cos \psi \cos \theta }&{ - \sin \psi \cos \phi + \cos \psi \sin \theta \sin \phi }\\ {\sin \psi \cos \theta }&{\cos \psi \cos \phi + \sin \psi \sin \theta \sin \phi }\\ { - \sin \theta }&{\cos \theta \sin \phi } \end{array}} \right.\\ &\left. {\begin{array}{*{20}{c}} {\sin \phi \sin \psi + \cos \psi \sin \theta \cos \phi }\\ { - \cos \psi \sin \phi + \sin \psi \sin \theta \cos \phi }\\ {\cos \theta \cos \phi } \end{array}} \right] \left[ \begin{aligned} u \\ v \\ w \end{aligned} \right] 。\end{split}$ | (1) |
而惯性坐标系与随体坐标系间的角速度运动量变换关系如下式:
| $ \left[ \begin{gathered} {\dot \phi } \\ {\dot \theta } \\ {\dot \psi } \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} 1&{\tan \theta \cos \phi }&{\tan \theta \cos \phi } \\ 0&{\cos \phi }&{ - \sin \phi } \\ 0&{\sec \theta \sin \phi }&{\sec \theta \cos \phi } \end{array}} \right]\left[ \begin{gathered} p \\ q \\ r \\ \end{gathered} \right] ,$ | (2) |
根据沿无人艇质心的动量定理和绕质心的动量矩定理,可得无人艇六个自由度运动方程如下式:
| $ \left\{ \begin{gathered} m\left( {\dot u - vr + wq} \right) = X ,\\ m\left( {\dot v + ur - wp} \right) = Y ,\\ m\left( {\dot w - uq + vp} \right) = Z ,\\ {J_{xx}}\dot p + \left( {{J_{zz}} - {J_{yy}}} \right)qr = K ,\\ {J_{yy}}\dot q + \left( {{J_{xx}} - {J_{zz}}} \right)rp = M ,\\ {J_{zz}}\dot r + \left( {{J_{yy}} - {J_{xx}}} \right)pq = N 。\\ \end{gathered} \right. $ | (3) |
式中:m为无人艇质量;Jxx,Jyy,Jzz分别为无人艇相对于随体坐标系ObXb,ObYb,ObZb等3个轴的转动惯量;X,Y,Z分别表示作用在无人艇3个方向上的合外力;K,M,N分别表示作用在无人艇3个方向上的合外力矩。
1.2 海况及其波浪表示在实际航行过程中,无人艇及其母船往往会遭遇不同等级的海况,为了模拟无人艇在真实环境中回收过程的动态特性,在数值模型中加载了4级海况条件,其相关参数如表2所示。
|
|
表 2 四级海况参数 Tab.2 Parameters of level 4 sea condition |
波浪是决定海况等级的主要因素,在工程上常用不规则波波浪谱来模拟波浪,采用JONSWAP波浪谱对实际波浪进行模拟,其表达式如下式:
| $ {S_J}(\omega ) = {A_\gamma }{S_{PM}}(\omega ){\gamma ^{\exp \left( { - 0.5{{\left( {\frac{{\omega - {\omega _p}}}{{\sigma {\omega _p}}}} \right)}^2}} \right)}} 。$ | (4) |
式中:SPM(ω)为Pierson-Moskowitz波浪谱;Aγ=1−0.287ln(γ)为归一化因子;γ为无量纲峰形参数,取平均值3.3;ωp表示波谱峰值频率,根据谱峰周期Tp计算得到,ωp=2π/Tp;σ为频谱宽度参数,ω≤ωp时取为σa,其均值为0.07,ω>ωp时取为σb,其均值为0.09。
2 数值建模 2.1 几何建模无人艇回收过程动态特性仿真所涉及的几何模型包括无人艇、母船及计算水域三部分。其中,无人艇及母船主要特征参数如表3所示。
|
|
表 3 船体相关几何参数 Tab.3 Hull related geometric parameters |
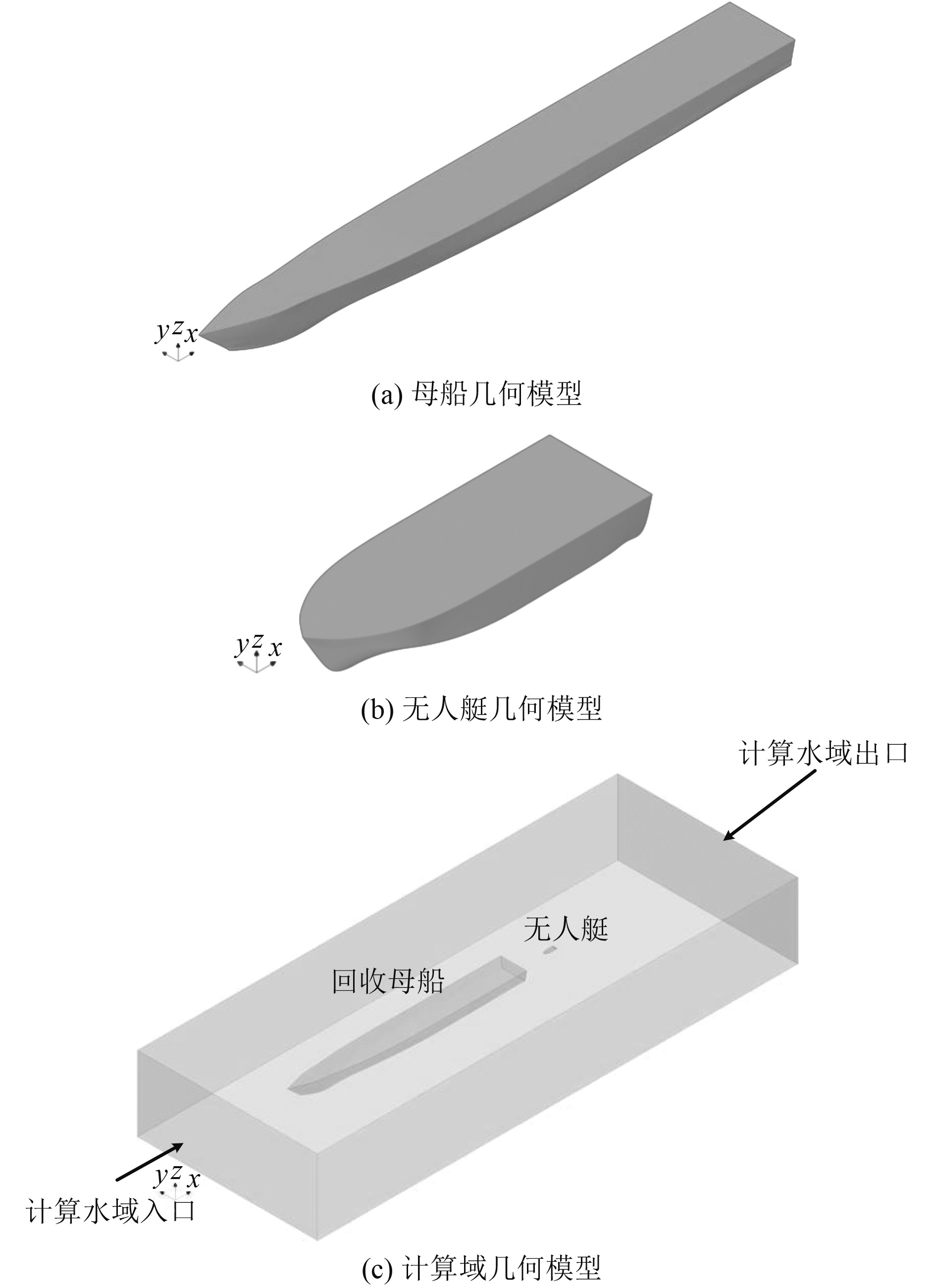
本文重点研究无人艇在回收过程中的运动响应,对无人艇及母船水线以上的几何外形进行适当简化。为消除计算域出口边界处回波的反射干扰,将无人艇和计算水域出口之间的距离适当加大,计算水域取值为长320 m、宽120 m、高50 m。无人艇及母船按照吃水深度布置在计算水域水平面相应位置,无人艇、母船及计算域几何模型如图2所示。
|
图 2 几何模型 Fig. 2 Geometric model |
采用切割体网格单元对计算域进行网格划分,并将切割体网格与自由表面对齐以确保对自由表面能进行正确求解。船体的运动过程采用重叠网格法实现,即建立一个长方体运动区域(重叠区域)将船体包裹起来,该长方体边界作为重叠边界与外部计算水域(背景区域)进行耦合并交换数据,从而实现船体的动态运动过程,背景区域和重叠区域的基础网格尺寸根据整个计算水域以及母船和无人艇的几何尺寸确定。
为了精确捕获不规则波及母船尾流对无人艇的作用力,对计算水域水平面附近及母船后方网格进行加密,使用精细的网格来解析小型波。同时在远离水平面及远离船体方向上逐级增加网格尺寸来减小计算压力。
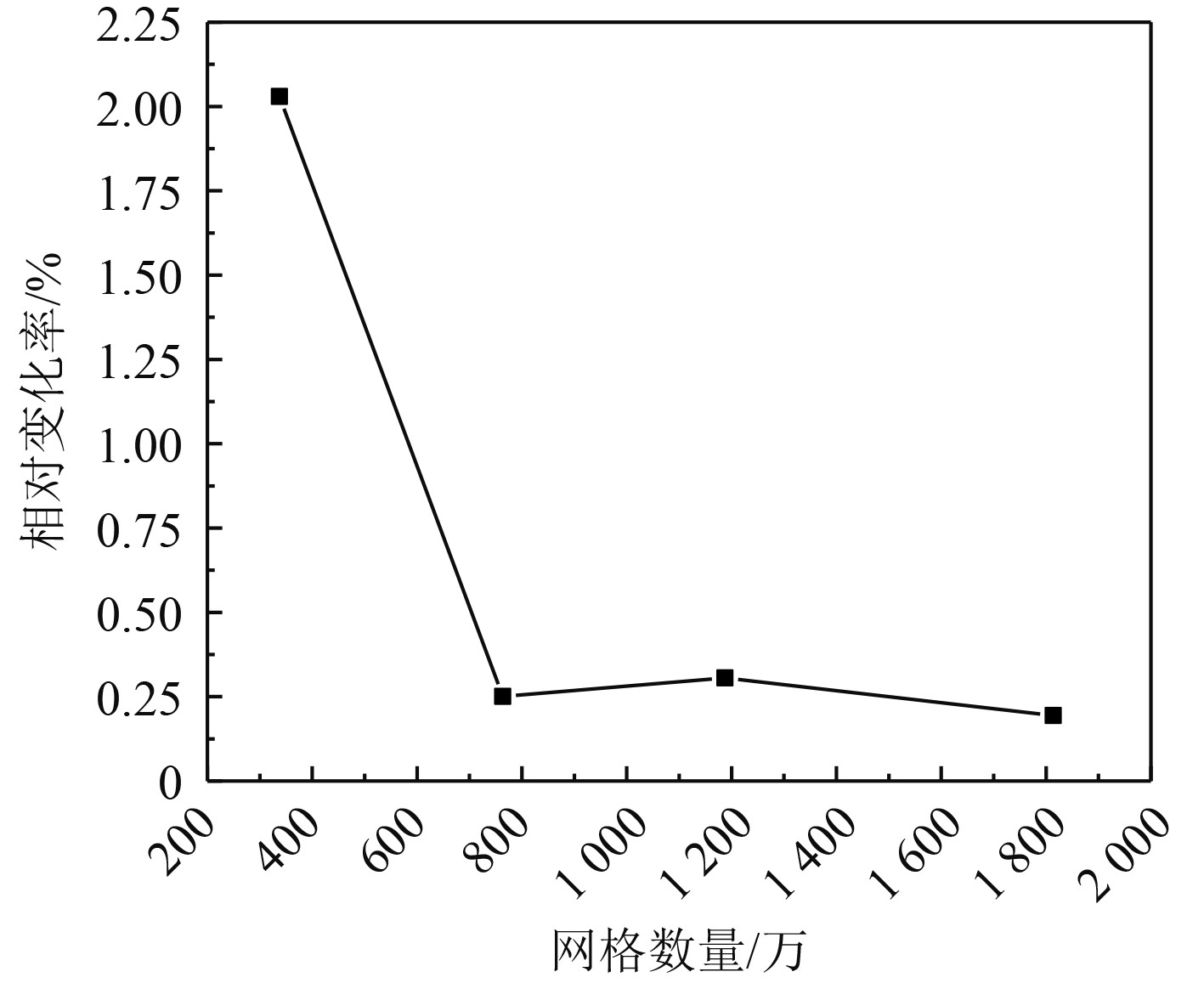
不同的网格密集程度对求解速度和计算精度有很大影响,为了确保所划分的网格能够在保持计算精度的同时有较快的计算速度,将无人艇放置于初始回收位置,仅保留其纵摇和垂荡方向自由度的运动,在计算域中施加方向与ObXb轴相反、大小为2 m/s的流速和风速以模拟无人艇的拖曳试验,并以ObYb轴力矩平衡状态下的无人艇阻力为参考对象,通过修改网格基础尺寸来改变网格数量以验证网格无关性,不同网格数量下的无人艇阻力及相对变化率如表4所示,无人艇阻力变化曲线如图3所示。
|
|
表 4 不同网格数量下无人艇阻力及相对变化率 Tab.4 USV resistance and relative variation ratio under different grid numbers |
|
图 3 无人艇阻力相对变化率曲线 Fig. 3 Curve of USV′s relative variation ratio of resistance |
根据表4和图3,当网格数量达到338万以上时,无人艇阻力与网格密集程度无关。最终对网格进行划分后背景区域网格数量为1911418,节点数为2018462,重叠区域网格数量为1464505,节点数为1533407,图4为母船和无人艇在计算水域中的网格剖面图。

|
图 4 网格剖面图 Fig. 4 Mesh section |
本文湍流模型采用K-Epsilon两层模型,相应地使用了2层全y+的壁面处理方法,以混合壁面函数对湍流边界层内层主物理量(湍流量、速度、温度)进行代数逼近,混合壁面函数是覆盖湍流边界层3个子层的连续函数,通过恰当地混合粘性子层和对数层来表示缓冲层。
计算为隐式非定常类型,使用二阶时间离散精度,时间步长设置为0.0025 s,足够小的时间步长能确保无人艇在每个时间步长内的位移不超过半个网格单元长度,从而避免使用二阶时间离散化的模拟出现发散的情况。每个时间步的内迭代次数设置为10,以保证计算的精度和稳定性。
为了模拟4级海况的影响,采用VOF波模型用于模拟空气域和水域交界面上的表面重力波,选用不规则波类型,参数设置如表5所示。
|
|
表 5 不规则波参数 Tab.5 Parameter of irregular wave |
整个计算域中的两相流体分别是空气和水,其材料属性参数如表6所示。
|
|
表 6 流体物性参数 Tab.6 Physical parameter of fluid |
在模拟不规则波的过程中,需要采取适当的措施避免波的反射。波的反射有2个来源:1)由于突兀的网格过渡所造成的波反射,可通过在网格稠密区域和网格稀疏区域之间采用多个过渡层来解决;2)来自边界的波反射。为了消除边界造成的波反射,需要在计算水域中激活阻尼选项,阻尼将垂直阻力引入垂直运动,从而在边界处对传播过来的波起到一定的衰减作用,避免其在边界处反射。VOF波阻尼长度一般设置为至少一个波长,本文将VOF波阻尼长度设置为30 m,并将计算水域的出口及左右两侧开启VOF波阻尼,同时加大母船后方计算域长度作为消波区。整个计算模型边界条件设置如表7所示。
|
|
表 7 边界条件 Tab.7 Boundary Conditions |
对于采用尾滑道回收装置进行回收的无人艇来说,为了回收时的平稳性,母船和无人艇通常在迎浪条件下进行回收,这样能够在最大程度上避免横向和斜向波浪对回收的影响,同时无人艇应尽量保持直线运动驶向母船。因此,在回收过程中无人艇的运动可简化为四自由度操纵运动,即认为无人艇在惯性坐标系XEOEYE水平面上保持恒定的速度和方向,纵荡和首摇方向运动幅值变化率恒定,只考虑无人艇横荡、垂荡、纵摇及横摇方向上的运动幅值随着无人艇回收过程的变化,且波浪方向设置为与无人艇航行方向相反以实现迎浪条件。
3.1 标准工况标准工况下,将无人艇放置在母船正后方20 m,无人艇与母船中心线重合,母船航速设定为5 m/s,无人艇航速设定为10 m/s,波浪前进方向与无人艇航行方向成180°。
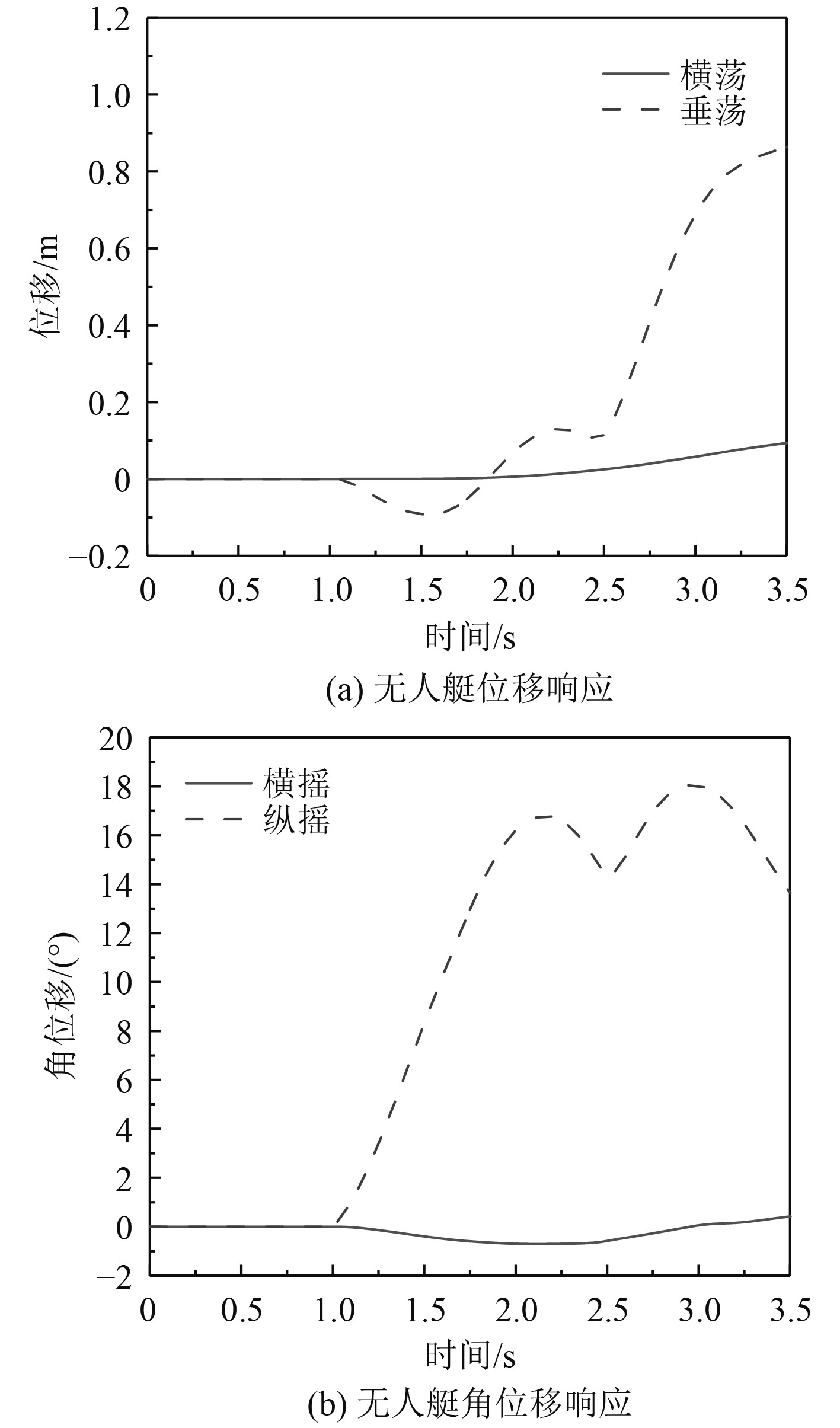
由于不规则波的传递需要一定的时间,在进行非定常仿真时,对无人艇设定1.0 s的延迟时间,以便加载的不规则波能充分发展并作用于母船产生尾流。因此,无人艇实际运动时间将从1.0 s开始,总计算时长为3.5 s。在此过程中无人艇运动响应及自由液面云图如图5和图6所示。
|
图 5 标准工况运动响应 Fig. 5 Motion response in standard conditions |

|
图 6 标准工况自由液面云图 Fig. 6 Free liquid surface cloud diagram under standard conditions |
可知,t=1.0 s时,不规则波已充分发展并作用于母船产生尾流,无人艇以5 m/s相对速度由母船正后方逼近。在此过程中,受母船尾流及不规则波的影响,无人艇纵摇角发生明显上升,并在一定区间内波动,无人艇垂荡位移也随着水面波动发生明显变化。由于标准工况下无人艇与母船中心线重合,无人艇两侧受力基本均衡,在回收过程中无人艇横摇角和横荡位移变化均不大。通过上述分析可知,标准工况下无人艇沿母船中心线以10 m/s的航速运动,在正面4级海况及母船尾流的综合作用下仍能保持相对平稳的运动。因此,可将该工况作为该型无人艇安全回收的标准工况。
此外,通过观察标准工况下自由液面不规则波传播云图可知,不规则波并没有在两侧以及出口处产生波的反射。
3.2 变速工况为分析不同回收速度对无人艇运动特性的影响,在标准工况基础上将无人艇航速由原来的10 m/s分别调整为7.5 m/s,12.5 m/s和15 m/s,其余条件不变。不同回收速度工况下,无人艇运动响应如图7所示。

|
图 7 变速工况运动响应 Fig. 7 Motion response in variable speed conditions |
与标准工况相比,当无人艇航速降低至7.5 m/s时,横荡、垂荡及横摇方向上的运动幅值改变不大且变化更加平缓。而在纵摇方向上尽管最大幅值超过了标准工况,但与标准工况相比差值不大且到达峰值后较快下降。当无人艇航速提升至12.5 m/s时,该工况下计算仅进行了2.2 s,因为此时无人艇纵摇角急剧上升,并超过了30°,同时垂荡方向峰值位移也超过2 m,已经超过了无人艇的安全极限。当无人艇航速进一步提升至15 m/s时,计算进行到2.17 s时,无人艇纵摇角已急剧上升超过40°,垂荡位移也急剧上升接近4 m。
由此可见,在回收过程中如果增加无人艇的航速,则无人艇将会有倾覆的风险。因此,在4级海况及母船尾流综合作用下,无人艇回收航速应控制在一定范围内,必要时甚至减速,避免因纵摇和垂荡运动幅值过大而导致无人艇的倾覆。
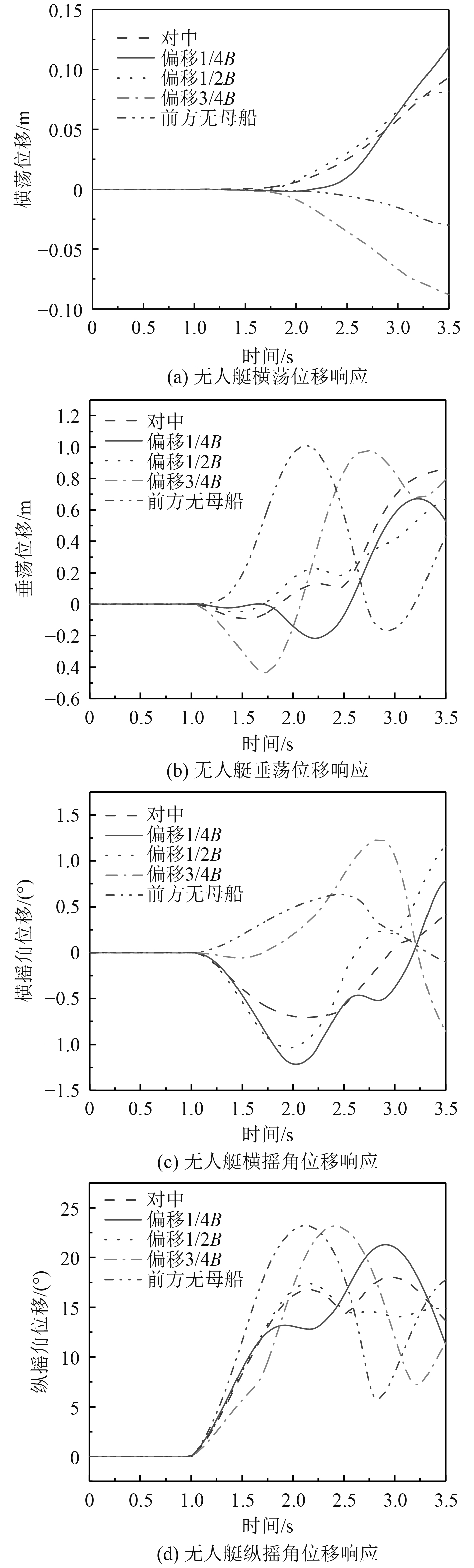
3.3 偏移工况为分析无人艇与母船轴线不对中存在偏移时,对无人艇运动特性的影响,将无人艇沿OEYE方向分别偏移1/4母船型宽(4.35 m)、1/2母船型宽(8.7 m)和3/4母船型宽(13.05 m),其余条件不变。特别地,当无人艇偏移母船较远时,可视为无人艇前方无母船。不同偏移工况下,无人艇运动响应如图8所示。
|
图 8 偏移工况运动响应 Fig. 8 Motion response in migration conditions |
可知,当无人艇与母船之间的偏移距离控制在母船1/2型宽及其以内时,无人艇的纵摇角和垂荡位移处于一个较安全的区间且波动较为平缓,而横摇角和横荡位移幅度均不大。因此,在实际回收过程中,应尽量将无人艇与母船的偏移距离控制在一定范围内,这样无人艇的运动响应较小,有利于无人艇的平稳回收。
当无人艇与母船之间的偏移距离进一步增大,达到3/4母船型宽,或前方无母船时,无人艇将直接与4级海浪迎面遭遇,在回收过程中无人艇纵摇角和垂荡位移发生明显上升,且波动更加剧烈,无人艇运动状态变得不稳定。
由此可见,当无人艇在回收航行过程中正面遭遇波浪时,无人艇的运动状态将会出现较大波动,需要降低航速,并通过自动航行系统稳定航向,确保无人艇的航行安全。此外,在回收过程中当无人艇接近母船后方时,由于前方母船的遮挡作用,4级海浪对无人艇的正面作用大大减小,尽管此时受到母船的尾流影响,但综合来看前方有母船时无人艇的运动状态会更加平稳,有利于回收。
4 结 语本文以某型无人艇为研究对象,建立无人艇回收动态仿真数值模型,对标准工况下无人艇回收过程的运动响应特性进行数值分析。在此基础上,对比分析了不同回收航速及偏移距离等因素对无人艇回收运动响应特性影响规律,得到主要结论如下:
1)标准工况下,该型无人艇的回收航速及航行路线能够保证无人艇回收的稳定性,确保回收过程的快速性和安全性。
2)如果在标准工况的基础上提高无人艇的回收航速,将引起无人艇纵摇角及垂荡位移急剧上升,给无人艇带来倾覆的风险。
3)在正面遭遇波浪时,若无人艇前方有母船,尽管此时无人艇受到母船尾流及周围波浪的综合影响,但相比于前方无母船直接遭遇波浪的情况,此时无人艇的航行稳定性仍然要更好。因此,在无人艇的回收过程中,若周围海况条件不佳,波浪较大时,应选择跟随在回收母船后方,再根据实际航行状态对无人艇进行回收的回收策略。
4)无人艇在实际回收过程中并不会像标准工况那样完全沿母船中心线回收,而是存在一定的偏移距离。在这种情况下,只要偏移距离不超过一定范围,无人艇的航行稳定性就和标准工况下较为接近,仍然满足无人艇回收的稳定性条件。
| [1] |
王金宝, 于海, 张越峰, 等. 低速肥大船舶尾流场数值模拟及阻力性能预报[J]. 水动力学研究与进展A辑, 2010, 25(5): 648-654. WANG J B, YU H, ZHANG Y F, et al. Numerical simulation of viscous wake field and resistance prediction around slow-full ships[J]. Journal of Hydrodynamics, 2010, 25(5): 648-654. |
| [2] |
杨勇. 非定常操纵运动船体水动力数值计算[D]. 上海: 上海交通大学, 2011.
|
| [3] |
钱小斌, 尹勇, 张秀凤, 等. 海上不规则波浪扰动对船舶运动的影响[J]. 交通运输工程学报, 2016, 16(3): 116-124. QIAN X B, YIN Y, ZHANG X F, el. Influence of irregular disturbance of sea wave on ship motion[J]. Journal of Traffic and Transportation Engineering, 2016, 16(3): 116-124. DOI:10.3969/j.issn.1671-1637.2016.03.014 |
| [4] |
邓锐, 高子予, 李裕龙, 等. 湍流模型的研究现状与最新进展[J]. 船舶力学, 2019, 23(3): 360-376. DENG R, GAO Z Y, LI Y L, et al. Development and research status of turbulence model[J]. Journal of Ship Mechanics, 2019, 23(3): 360-376. DOI:10.3969/j.issn.1007-7294.2019.03.009 |
| [5] |
苑洋, 张秀凤, 周佳其, 等. “育鹏”轮斜航水动力数值计算及运动仿真[J]. 大连理工大学学报, 2019, 59(6): 610-616. Yuan Y, ZHANG X F, ZHOU J Q, et al. Numerical calculation of oblique navigation hydrodynamics and motion simulation of YU PENG[J]. Journal of Dalian University of Technology, 2019, 59(6): 610-616. |
| [6] |
陶志奇, 王慧, 徐伟光, 等. 船舶在顶浪不规则波中的运动响应数值分析[J]. 船舶力学, 2020, 24(9): 1134-1141. TAO Z Q, WANG H, XU W G, el. Numerical analysis of ship motion responses in head irregular waves[J]. Journal of Ship Mechanics, 2020, 24(9): 1134-1141. DOI:10.3969/j.issn.1007-7294.2020.09.005 |
| [7] |
杜一豪, 纪翀, 姜胜超, 等. 不规则波下船舶运动响应特征数值分析[J]. 海洋工程, 2021, 39(3): 31-41. DU Y H, JI C, JIANG S C, el. Numerical analysis of ship motion response characteristics in irregular waves[J]. The Ocean Engineering, 2021, 39(3): 31-41. |
| [8] |
张显库, 陈秀嘉, 陆禹, 等. 航海模拟器目标船数学模型[J]. 中国造船, 2014(3): 125-130. ZHANG X K, CHEN X J, LU Y, et al. Mathematical model of target ships in maritime simulator[J]. Shipbuilding of China, 2014(3): 125-130. DOI:10.3969/j.issn.1000-4882.2014.03.014 |
| [9] |
郑烈心. 水面无人艇建模与运动控制系统设计[D]. 广州:华南理工大学, 2016.
|
| [10] |
廖煜雷. 水面机器人航行控制技术[M]. 北京:科学出版社, 2020: 27–29.
|
 2023, Vol. 45
2023, Vol. 45

