0 引　言

三体船是一种新兴的多体船型，兼具单体船和双体船的优点，具有较优的耐波性和快速性，是当前船舶领域的研究热点。多体船的片体对水体扰动强，与单体船型相比流场更加复杂，因此数值计算的难度更大。

目前多体船的参考规范和船型资料较少，传统的经验公式对多体船难以实现准确的阻力预报，但是研究表明借助计算流体动力学(computational fluid dynamics, CFD)技术可以有效提升预报准确度。张磊等^[1]详细讲解了应用CFD技术预报船体阻力与运动响应的流程。陈康等^[2]将仿真结果与实验结果比对，验证了仿真结果的可信度。谢云平等^[3]利用CFD方法计算某三体船模的阻力，经试验验证计算方法的准确性后，对不同侧体型线方案进行计算和比对。张明霞等^[4]基于试验数据对比分析了仿真中船体周围网格加密尺寸、边界层首层网格节点高度、湍流模型等因素对计算准确度的影响。周广利等^[5]研究了三体船侧体排水量占总排水量比例对船体阻力的影响，并通过试验验证了数值仿真的准确性。付丽宁等^[6]针对某双体船提出了多种船型优化方案，并使用CFD商业软件对阻力优化效果进行仿真评估。李志君等^[7]从主侧体主尺度和主侧体布局2个角度出发，对船体阻力进行仿真和优化。金梦显等^[8]针对某三体船设计了多种侧体布局方案，并根据阻力仿真计算进行选优，结果表明侧体位于船尾对阻力性能有利。

为准确预报项目研发的无人艇阻力，探讨中低速三体船的水动力特性，为船体的快速性优化积累经验，本文利用STAR-CCM+软件对该无人艇进行流体仿真，考虑侧体布置和侧体型线2种因素设置不同的计算方案，对比其阻力计算结果并分析流场特征，为后续的船体研究提供参考。

1 数值计算方法 1.1 数学模型

在粘性流动的范畴内，湍流是一种非线性的复杂流体运动，具有不规则脉动、三维有旋等特征。目前湍流的数值模拟方法主要有直接数值模拟(direct numerical simulation, DNS)、雷诺平均法(Reynolds average Navier-Stokes, RANS)和大涡模拟(large eddy simulation, LES)，其中RANS方法可以模拟高雷诺数流动，计算量较小，能对绝大多数工程问题进行求解，因此得到广泛应用。本文采用RANS方法模拟数值拖曳水池，假设流体为不可压缩粘性流，平均流动的连续方程和雷诺方程分别如下：

$ \frac{{\partial \overline {\mathop u\nolimits_i } }}{{\partial \mathop x\nolimits_i }} = 0 ，$

(1)

$ \rho \left[\frac{{\partial \overline {\mathop u\nolimits_i } }}{{\partial t}} + \overline {\mathop u\nolimits_j } \frac{{\partial \overline {\mathop u\nolimits_i } }}{{\partial \mathop x\nolimits_j }}\right] = \rho \overline {\mathop g\nolimits_i } - \frac{{\partial \overline p }}{{\partial \mathop x\nolimits_j }} + \mu \mathop \nabla \nolimits^2 \mathop u\nolimits_i - \rho \frac{{\partial \overline {\mathop u\nolimits_i' \mathop u\nolimits_j' } }}{{\partial \mathop x\nolimits_j }} 。$

(2)

式中： $\overline {\mathop u\nolimits_i } $ 和 $\overline {\mathop u\nolimits_{\text{j}} } $ 为流体时间平均速度在直角坐标系下分量； $ \overline p $ 为时间平均压强； $ \ \mu $ 为流体的动力粘度； $\ \rho \overline {\mathop u\nolimits_i' \mathop u\nolimits_j' } $ 为雷诺应力项。由于方程右边多了雷诺应力项，未知量数多于方程数，需要引入湍流模型来封闭方程组。湍流模型通常不再经由质量或能量守恒原理推出，而是经验或半经验公式。常用的湍流模型有基于Boussinesq近似原理的零方程模型、一方程模型和二方程模型，本文使用二方程模型中的SST k-ω模型计算RANS方程。

自由液面的处理采用VOF多相流模型，该模型根据不同位置处每个物相的体积分数追踪气液交界面的相位置和相分布。某一相i的体积分数定义如下：

$ \mathop \alpha \nolimits_{\text{i}} = \frac{{\mathop V\nolimits_i }}{V} ，$

(3)

$ \sum\limits_{i = 1}^N {\mathop \alpha \nolimits_i } = 1 。$

(4)

式中： $\mathop V\nolimits_i $ 为网格单元中相i的体积； $V$ 为单元总体积；N为相数。

根据体积分数可以确定某网格单元中流体的状态：

$ \left\{\begin{array}{l}{\alpha }_{i}=0\text{，}单元中没有相i，\\ {\alpha }_{i}=1\text{，}单元由相i完全填充，\\ {0 < \alpha }_{i} < 1\text{，}单元中存在交界面。\end{array}\right. $

(5)

根据质量守恒原理得出相的连续性方程如下：

$ \frac{\partial }{{\partial t}}\left( {\int_V {\rho {\rm{d}}V} } \right) + \oint_A {\rho v{\rm{d}}} a = \int_V {S{\rm{d}}V} 。$

(6)

其中， $S = \sum\nolimits_{{i}} {\mathop S\nolimits_{\mathop \alpha \nolimits_i } } \mathop \rho \nolimits_i$ ，为质量源项。

1.2 数值拖曳水池

计算模型为穿浪三体船型，采用深V型舭部和方尾设计，建模比例为1∶1，侧体布置于主体两侧中部偏后位置，如图1所示。以主侧体的中纵剖面为基准定义片体的横向跨距为a，以主侧体尾柱间距表示侧体纵向位置为b。原船型全长4.75 m，主体宽(图1中c)0.52 m，吃水0.36 m，排水量380 kg，侧体长2.5 m，宽(图1中d)0.3 m。船体模型由CAID软件建立，经ANSA进行面网格优化后可直接导入STAR-CCM+进行计算域划分。船体静水力参数由Maxsurf软件进行核算。

计算域为长方形，如图2所示。计算模型具有对称性，为减少计算量采用半船计算。L为船总长，上游距船首1 L，下游距船尾4 L，侧壁距对称面1 L，上下边界分别距水线面1 L和2 L。上游为入口并设置流体速度分量，下游为压力出口，侧壁和对称面均设置为对称边界条件，船壳设置为无滑移壁面条件。使用STAR-CCM+的Surface Remesher，Automatic Surface Repair，Prism Layer Mesher，Trimmed Cell Mesher生成面网格和体网格。在船体舷侧表面设置面网格加密，对船体附近、自由液面附近、船行波区域设置3层体网格过渡加密，以捕捉船体周围流场和尾流信息。根据文献[1，9，10]的结论调整船体舷侧边界层厚度，使数值模拟所关注区域的y+值保持在200万左右。

2 计算方案设置及结果分析 2.1 单个片体阻力分析

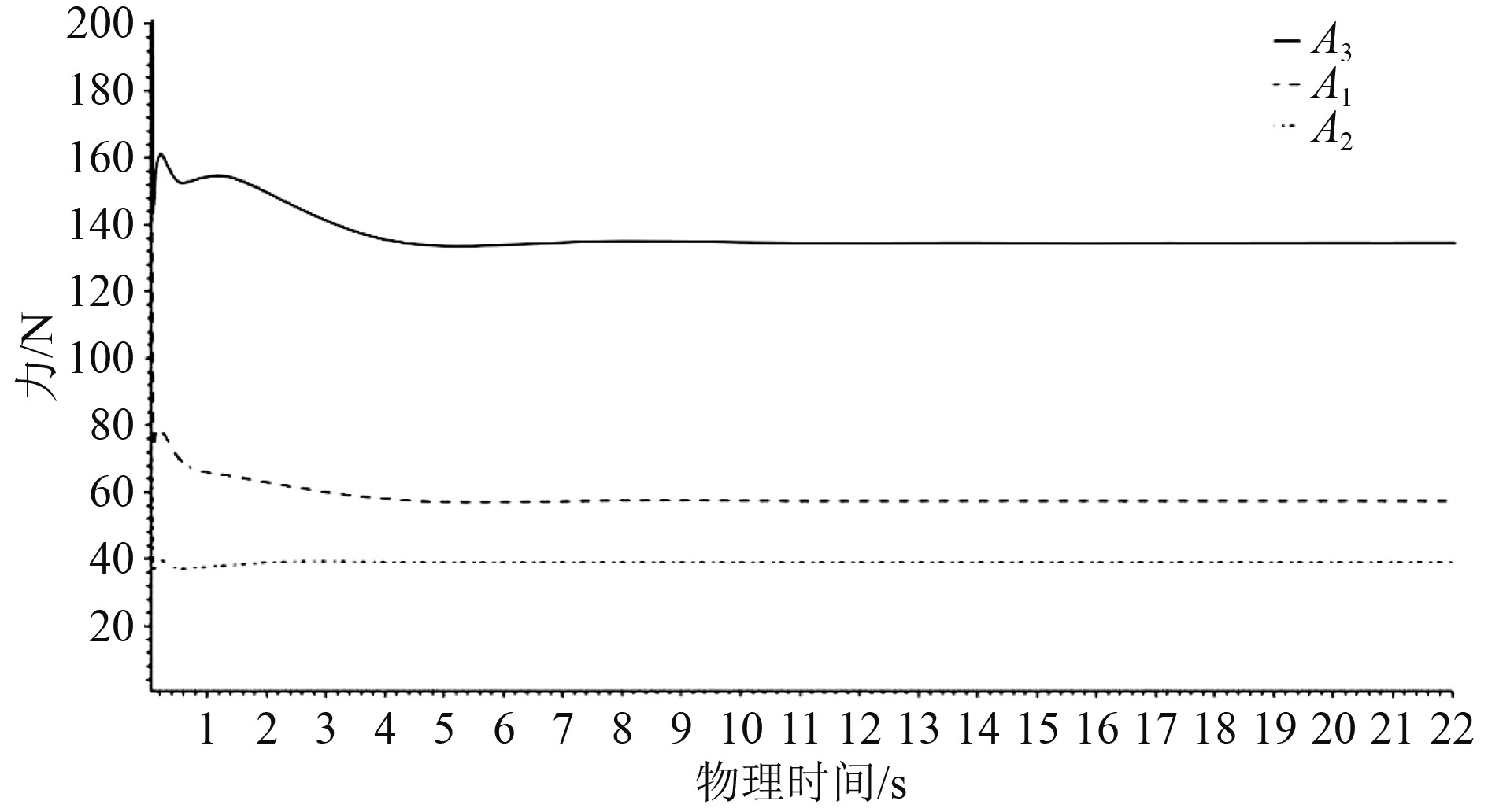
根据无人艇的设计指标指定水流速度为2.572 m/s，原船型在额定载况下的主体水线长约4.7 m，设计航速下Fr=0.38，傅汝德数较小说明该无人艇属于中低速船。通常船体阻力可分为摩擦阻力和压阻力，为了确定该船在设计航速下各阻力成分的占比，针对主体、侧体、三体船3种工况进行计算。分别建立主体、侧体和三体船的计算模型，并通过仿真软件监测船体的摩擦阻力、压阻力和总阻力，绘制阻力随物理时间变化的曲线如图3所示，计算结果稳定无发散。

各计算方案依次编号为A₁～A₅，汇总的计算结果如表1所示。可以看出三体船组合前后同一片体的摩擦阻力基本不变，组合后片体间兴波扰动会导致主体压阻力减小和侧体压阻力增大，且两者变化幅度相近。对单个片体的阻力成分进行分析后可以发现，主体的压阻力约占其总阻力的52.7%，侧体的压阻力约占53.0%，两片体的压阻力占比均较大。

2.2 侧体纵向位置对阻力的影响

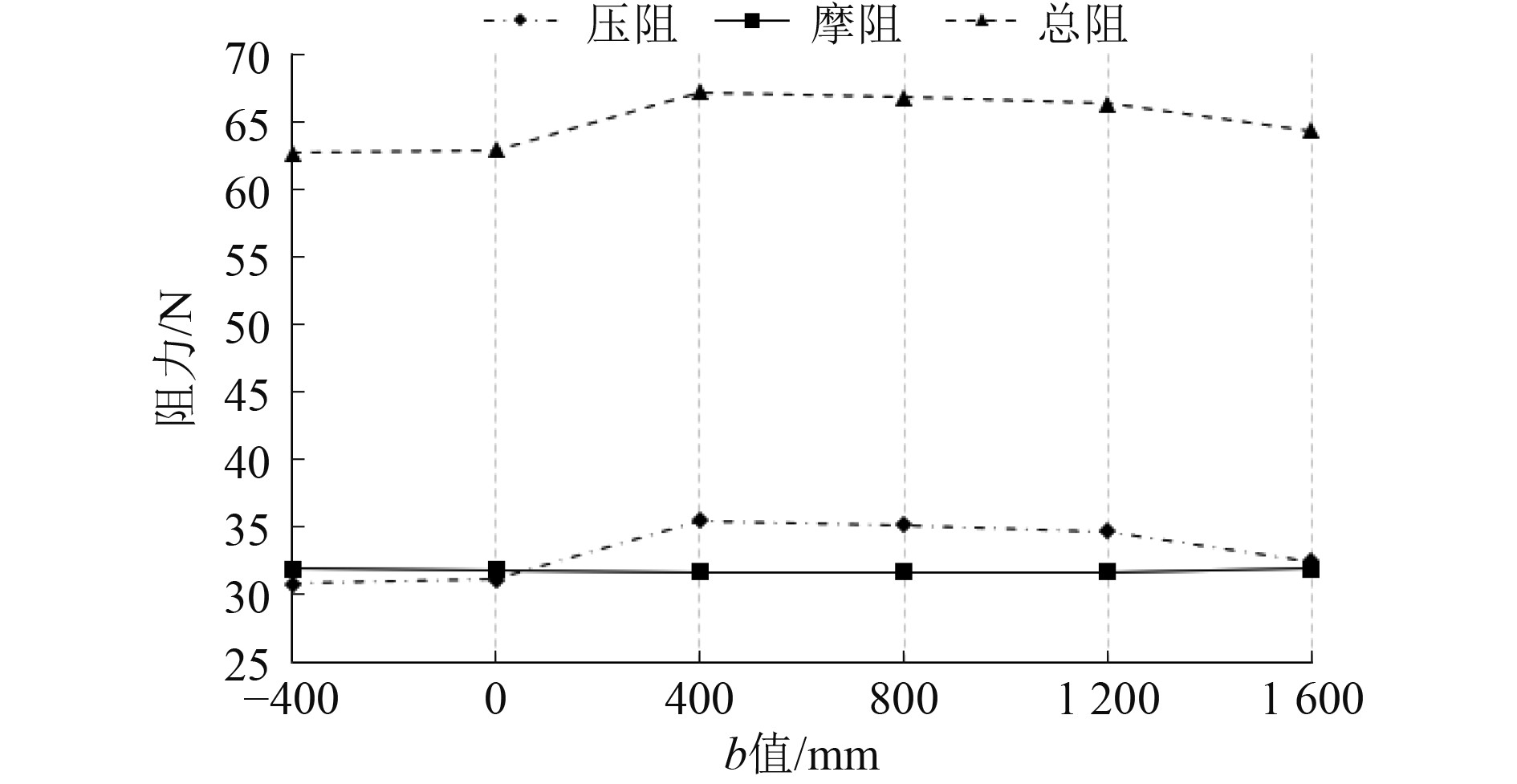
根据已有的三体船阻力研究，侧体纵向位置是影响阻力的重要因素^[11]。本文针对侧体纵向布局设置了多组计算方案，各方案的b值及计算结果如表2所示。b为负值表示侧体尾部在主体尾部之后。随着侧体位置从后向前移动，船体阻力先增大后减小，最小阻力值出现在方案B₁处，与原船型相比阻力降低约6.7%。从图4可以看出，随着侧体位置后移船体摩擦阻力曲线基本保持水平，说明侧体纵向位置变动对摩擦阻力影响不明显；压阻力与总阻力的变化趋势相同，说明总阻力的变化主要受压阻力的影响。

从图5可以看出，B₁～B₃船体周围流场趋向复杂，液面等高线更密集，波形更复杂，片体间的兴波扰动更明显，同时波峰升高。上述流场变化导致船体兴波阻力增大。

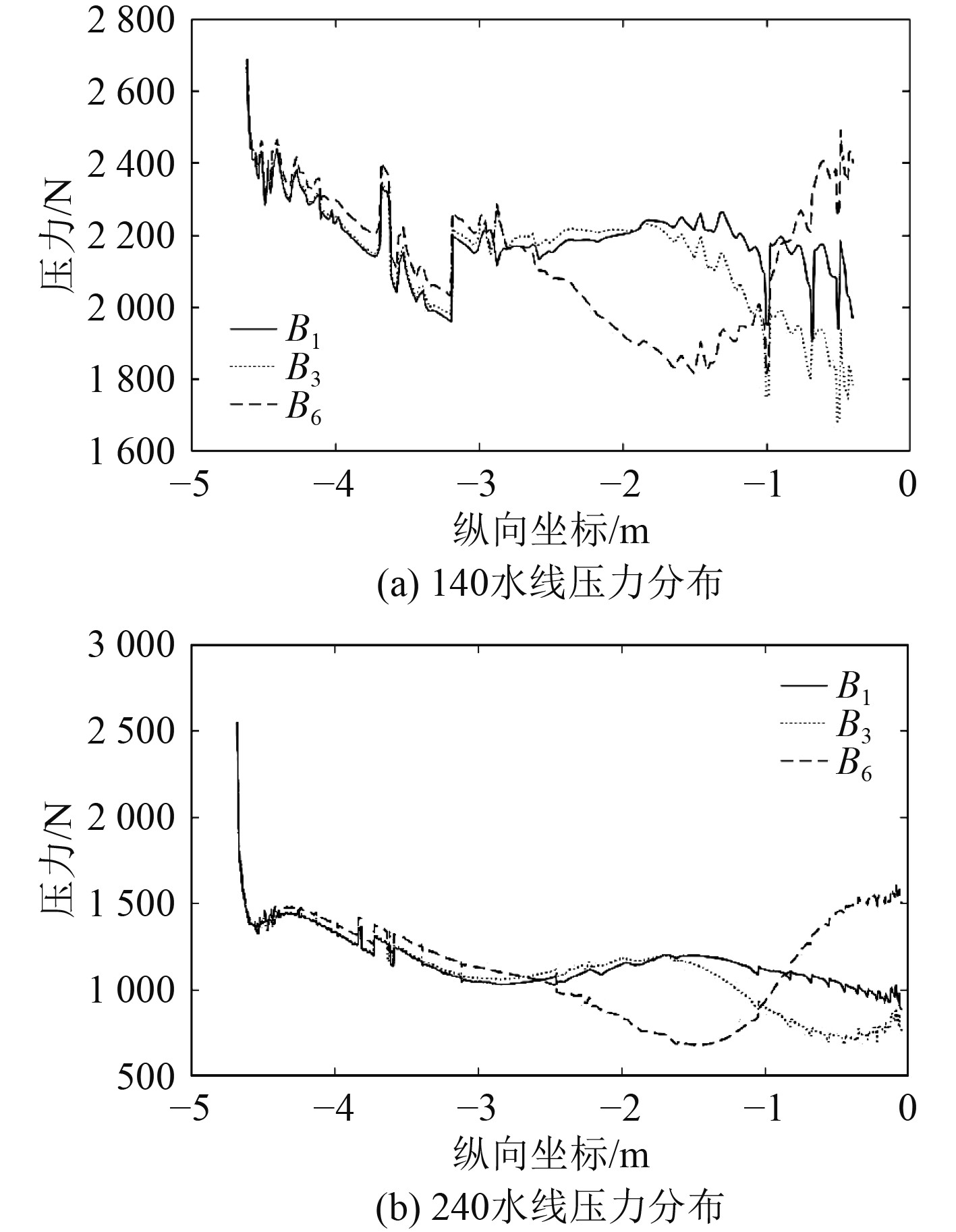
图6为各方案的艇底压力分布图。可以看出从B₁～B₃随着侧体位置前移，艇尾底部区域的压力逐渐减小，艇首底部区域的压力逐渐增大，主体的首尾压力差增大。B₃和B₄的艇底压力分布较为接近。从B₄～B₆艇尾底部压力逐渐增大，艇首底部压力逐渐减小，首尾压力差减小。为对比艇底压力的纵向分布，对B₁，B₃，B₆分别沿140水线和240水线提取压力值，汇总并绘制曲线如图7所示。其中横坐标的零点位于尾柱，向船首方向为负。可以看出两图的压力变化规律大致相同，B₃比B₁的艇尾压力小，而B₆的艇中后部压力较低，尾端压力明显高于B₁和B₃，艇首压力略高于前两者。

2.3 侧体型宽对阻力的影响

原船型的侧体宽0.296 m，长宽比约为8.4，半进流角约为8.2°，在保持侧体总长和三体船排水量不变的基础上，减小侧体型宽，以增大侧体长宽比并减小侧体半进流角，改善侧体周围流场以减小压阻。根据外观、稳性等方面的设计要求，设置了3种不同的方案，具体侧体船型参数如表3所示。

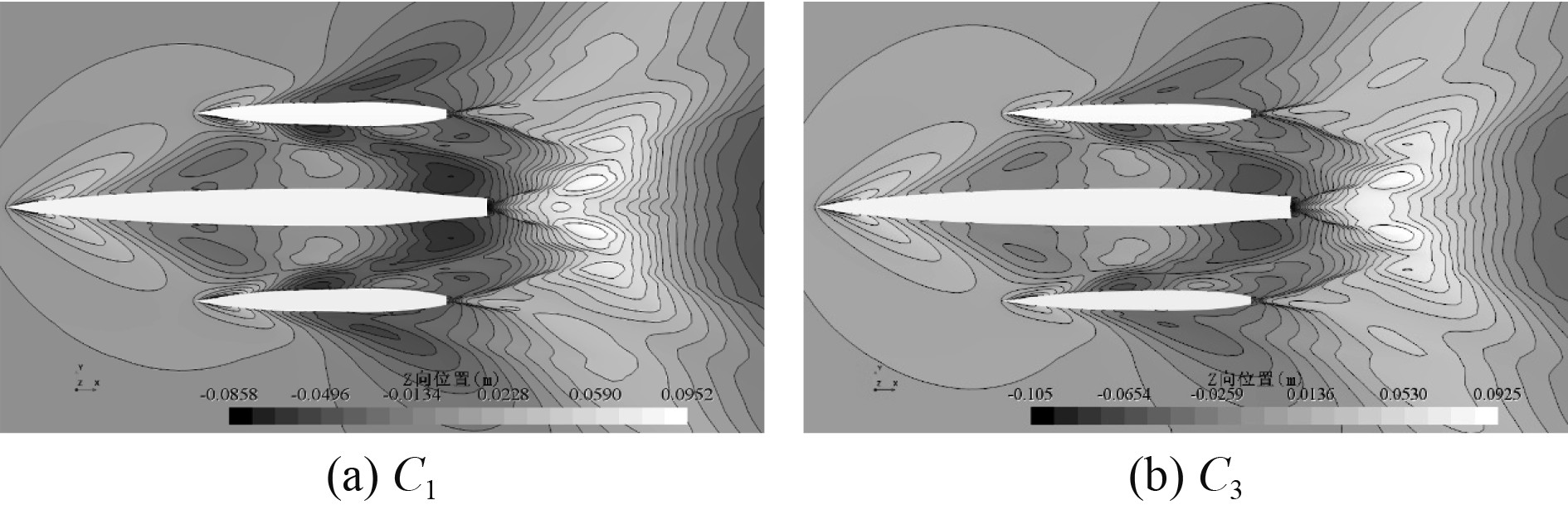
各方案的计算结果汇总如表4所示。可以看出，b值为0 m时侧体型宽对船体阻力的影响很小，其中C₄，C₅的压阻力结果相近，C₆的压阻力较低，但是吃水增大导致摩擦阻力升高，因此总阻力基本不变。b值为0.4 m时三种船型的阻力差距稍明显，C₃相对于C₁阻力降低1.3%，其中压阻力降低约4.5%，摩擦阻力升高约2.2%。绘制船体兴波高程图，取C₁和C₃方案的兴波高程作对比如图7所示。可以看出，C₃的舷侧兴波减小，等高线变疏，主体尾部兴波幅度也有些许降低，“鸡尾波”波峰高度由0.0952 m降至0.0925 m。

3 结　语

本文对某型三体船在黏性流中的静水阻力进行数值仿真，对比多种方案的计算结果后得出如下结论：

1)该三体无人艇航速较低，片体间兴波扰动较小，船体兴波幅度较低，最大波峰不超过0.1 m。船体的摩擦阻力占比较大，达总阻力的一半以上。

2)侧体靠后布置可明显改善流场，减小兴波幅度，有利于降低阻力，最大减阻率约为6.7%。

3)减小侧体型宽可以小幅度降低三体船压阻，但由此导致的吃水变化会增大摩阻，船体总阻力降低约1.3%。