2. 西南科技大学,四川 绵阳 621000;
3. 西北工业大学,陕西 西安 710072
2. Southwest University of Science and Technology, Mianyang 621000, China;
3. Northwestern Polytechnical University, Xi′an 710072, China
水空两栖多旋翼飞行器具有传统的空中飞行器以及水下航行器的优点,同时具有良好的工作环境适应性和活动范围大等特点。
2012年,MIT林肯实验室的Fabian等[1]设计了一款仿鲣鸟微小型两栖无人飞行器。该样机多次成功实现了空-水介质转换(入水),验证了溅落方式入水的可行性。2014年,Drews等[2]考虑跨越细节,将跨越过程分空中和水下2个阶段;根据建立的动力学模型设计了比例-微分(PD)控制器,初步验证了该结构实现跨介质过程的可行性。2015年,Neto等[3]采用切换方式完成跨介质过程。提出用于空气和水下介质控制的鲁棒控制器。由于缺乏考虑附加质量变化和浮动变化,无法实现无缝跨介质过程。2015年,Chen等[4]在已有样机RoboBee的基础上提出了一种仿昆虫的扑翼式水空两栖跨介质无人飞行器样机。通过3D-CFD仿真计算和仿生样机实验发现,采用扑翼推进方式在水下和空中都可以实现比较好的俯仰控制,同时验证了RoboBee在水下环境开环控制的游动能力,并实现了其从空气介质到水体介质的转换。2015年,余宗金等[5]设计了一种模拟水空跨介质航行器的对称圆柱航行器物理模型用于研究水空跨介质航行器出水运动的规律。2015年,徐宝伟等[6]提出通过变形实现水空跨介质的变体无人机,并通过共形半环翼变体无人机论述了外形设计、气动水动特性、出水入水受力特性等待研究的问题。2017年,Siddall等[7]设计了一款桨式推进仿鲣鸟两栖飞行器。该飞行器采用仿飞乌贼喷射方式起飞,成功实现了从水下到空中的过渡。2019年,谭骏怡等[8]基于一种可变体的水空跨介质航行器的水下构型,利用CFD流体仿真软件,对其斜出水过程进行数值仿真,研究结果对跨介质问题提供了研究思路和理论参考。2020年,颜奇民等[9]针对跨介质航行器的水空跨越问题,设计了基于RBF神经网络实时整定参数的PID控制器。该控制器在姿态角控制上较传统PID控制器有更好的鲁棒性。2022年,聂星宇等[10]设计了一种倾转四旋翼跨介质飞行器构型。在控制策略上,设计了水面垂直起飞流程以及切换控制策略。
本文在国内外学者研究的基础上,针对前期搭建的水空两栖多旋翼飞行器样机,提出分段变参数PID跨介质出水控制方法,并结合遗传算法进行参数整定,对后续深入开展水空多旋翼飞行器跨介质整体样机的控制研究具有重要意义。
1 运动学和动力学建模本文研究对象为自主研制的一种水空两栖六旋翼飞行器样机。该飞行器在空中和水下的动力均由旋翼提供。其中飞行器实物样机参数如表1所示。
|
|
表 1 水空多旋翼飞行器样机参数 Tab.1 Parameters of water-air multi-rotor vehicle prototype |
表中,
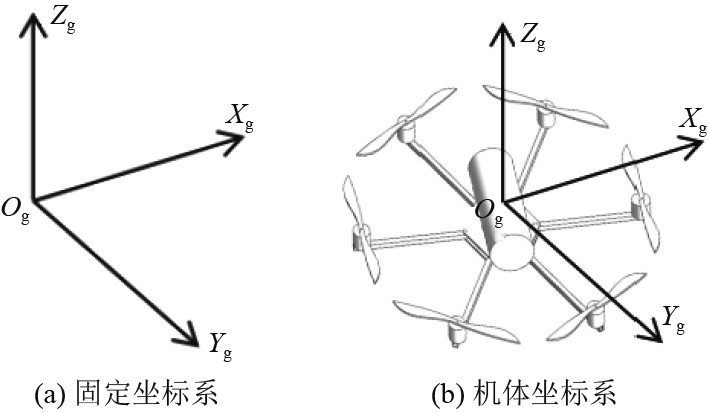
飞行器坐标系示意图如图1所示。
|
图 1 水空六旋翼飞行器坐标系示意图 Fig. 1 Diagram of coordinate system of water - air six-rotor aircraft |
固定坐标系转换至机体坐标系的转换矩阵为:
| $ \begin{split}{{\boldsymbol{R}}_{gb}} =& \left[ {\begin{array}{*{20}{c}} {\cos \theta \cos \psi } \\ {\sin \varphi \sin \theta \cos \psi - \cos \varphi \sin \psi } \\ {\cos \varphi \sin \theta \cos \psi + \sin \varphi \sin \psi } \end{array}} \right.\\ &\left. {\begin{array}{*{20}{c}} {\cos \theta \sin \psi }&{ - \sin \theta } \\ {\sin \varphi \sin \theta \sin \psi + \cos \varphi \cos \psi }&{\sin \varphi \cos \theta } \\ {\cos \varphi \sin \theta \sin \psi - \sin \varphi \cos \psi }&{\cos \varphi \cos \theta } \end{array}} \right] 。\end{split}$ | (1) |
式中:
机体坐标系转换至固定坐标系的转换矩阵为固定坐标系转换至机体坐标系的转换矩阵的逆。
将水空多旋翼飞行器的整个出水过程分为3个阶段,分别为水下航行阶段、水空跨越阶段以及空中飞行阶段。
为方便分析水空多旋翼飞行器的运动及受力情况,提出以下6点假设:1)水空多旋翼飞行器机体严格对称,且可看作一质量均匀分布的刚体;2)水空多旋翼飞行器机体的中心和重心都与机体坐标系的原点重合;3)重力加速度(系数)不变;4)忽略飞行器在空中时其旋翼对周围空气流动的影响;5)飞行器可近似为柱体;6)飞行器所在水域流速为零且流体不可压缩。
在建模前,对涉及到的物理量,包括在运动坐标系下的线速度和角速度,力和力矩,在固定坐标系下的位置、线速度、欧拉角等的符号进行定义,如表2所示。
|
|
表 2 本文涉及的物理量符号表示 Tab.2 Symbolic representations of the physical quantities involved in this paper |
根据牛顿欧拉公式,水空多旋翼飞行器空中飞行阶段动力学模型为[11,15]:
| $ \left\{ {\begin{aligned} & {m{{\ddot x}}= \left( {\sin \theta \cos \varphi \cos \psi + \sin \varphi \sin \psi } \right)\sum\limits_{i = 1}^6 {F_i^b} - {K_{Dx}}\mathop {{\rm{\dot x}}} },\\ & {m{{\ddot y}} = \left( {\sin \theta \cos \varphi \sin \psi - \sin \varphi \cos \psi } \right)\sum\limits_{i = 1}^6 {F_i^b - {K_{Dy}}\mathop {{\rm{\dot y}}}} },\\ & {m{{\ddot z}}= \cos \varphi \cos \theta \sum\limits_{i = 1}^6 {F_i^b - {K_{Dz}}\mathop {{\rm{\dot z}}} + mg} },\\ & {{I_x} {\dot{\omega _x}}= - \left( {{I_z} - {I_y}} \right){\omega _z}{\omega _y} + l\left( {F_4^b - F_2^b} \right)},\\ & {{I_y} {\dot{\omega _y}} = - \left( {{I_x} - {I_z}} \right){\omega _x}{\omega _z} + l\left( {F_3^b - F_1^b} \right)},\\ & {{I_z} {\dot{\omega _z}} = - \left( {{I_y} - {I_z}} \right){\omega _x}{\omega _y} + \left( { - M_1^b + M_2^b - M_3^b + M_4^b} \right)}。\end{aligned}} \right. $ | (2) |
式中:
根据刚体动量定理以及刚体动量矩定理,并假设重心与机体坐标原点重合,水空多旋翼飞行器水下航行阶段及水空跨越阶段的动力学模型为[12]:
| $ \left\{ \begin{gathered} X = m\left( {\dot u - rv + wq} \right), \\ Y = m\left( {\dot v - wp + ur} \right), \\ Z = m\left( {\dot w - uq + vp} \right), \\ K = {I_x}\dot p+ \left( {{I_z} - {I_y}} \right)qr, \\ M = {I_y}\dot q + \left( {{I_x} - {I_z}} \right)rp , \\ N = {I_z}\dot r + \left( {{I_y} - {I_x}} \right)pq 。\\ \end{gathered} \right. $ | (3) |
水空多旋翼飞行器在水中做空间运动时,会受到水流在飞行器表面产生的水动力
| $ \begin{split} {{\tau }_{{RB}}} =& {{\tau }_{H}}{ + }{{\tau }_{S}}{ + }{{\tau }_{p}}{ + \Delta \tau } =\\ &{\left[ {\begin{array}{*{20}{c}} X&Y&Z&K&M&N \end{array}} \right]^{\text{T}}} , \end{split} $ | (4) |
其中,飞行器在水下受到的水动力主要为惯性水动力
| $ {{\tau }_{H}}{ = }{{\tau }_{A}}{ + }{{\tau }_{D}} ,$ | (5) |
水空多旋翼飞行器在水中航行时,其周围的水由于飞行器的运动而产生运动,因为水有一定的惯性,所以飞行器会受到流体惯性力
刚体在水下的附加质量只与刚体形状、刚体所处流体密度以及机体坐标系有关。假设该飞行器对称,且近似成圆柱,则附加质量矩阵可简化为式(6),并由式(7)进行计算。
| $ {{M}_{A}} = - {\rm{diag}}\left[ {\begin{array}{*{20}{c}} {{m_{11}}}&{{m_{22}}}&{{m_{33}}} & {{m_{44}}}&{{m_{55}}}&{{m_{66}}} \end{array}} \right] 。$ | (6) |
其中:
| $ \left\{ \begin{gathered} {m_{11}} = - 0.1m, \\ {m_{22}} = {m_{33}} = - \text{π} {\rho _i}{R^2}L , \\ {m_{44}} = 0, \\ {m_{55}} = {m_{66}} = - \frac{\text{π} }{{12}}{\rho _i}{R^2}{L^3}。\\ \end{gathered} \right. $ | (7) |
由于流体粘性的存在,刚体在其中运动时会受到流体产生的阻尼作用,即粘性力
对于水空多旋翼飞行器受到的粘性水动力,通过Fluent流体力学仿真计算获取。假设飞行器是沿着z轴以0~1 m/s的速度移动,则沿z轴方向的速度与粘性水动力(力矩)之间的关系如表3和表4所示。
|
|
表 3 粘性水动力测试表 Tab.3 Viscous hydrodynamic test table |
|
|
表 4 粘性水动力力矩测试表 Tab.4 Test table of viscous hydrodynamic torque |
根据仿真结果,可认为水空多旋翼飞行器只在z轴方向上受到粘性水动力,其他方向上的力和力矩均可忽略。将仿真数据进行拟合,得到速度
| $ {\tau _D} = 37.643\,1{w^2} + 0.367\,2w - 0.027\,1。$ | (8) |
飞行器在水下运动所受的静力包括重力
| $ {r}_{G}^{b} = {\left[ {\begin{array}{*{20}{c}} 0&0&0 \end{array}} \right]^{\text{T}}}, $ | (9) |
| $ {r}_{B}^{b} = {\left[ {\begin{array}{*{20}{c}} 0&0&{{z_B}} \end{array}} \right]^{\text{T}}}, $ | (10) |
在固定坐标系下,水空多旋翼飞行器的静力矩阵(相对于机体坐标系)为:
| $ {{{\boldsymbol{\tau}} }_{S}} = \left[ {\begin{array}{*{20}{c}} {\left( {G - B} \right)\sin \theta } \\ { - \left( {G - B} \right)\cos \theta \sin \varphi } \\ { - \left( {G - B} \right)\cos \theta \cos \varphi } \\ { - {z_B}B\cos \theta \sin \varphi } \\ { - {z_B}B\sin \theta } \\ 0 \end{array}} \right] 。$ | (11) |
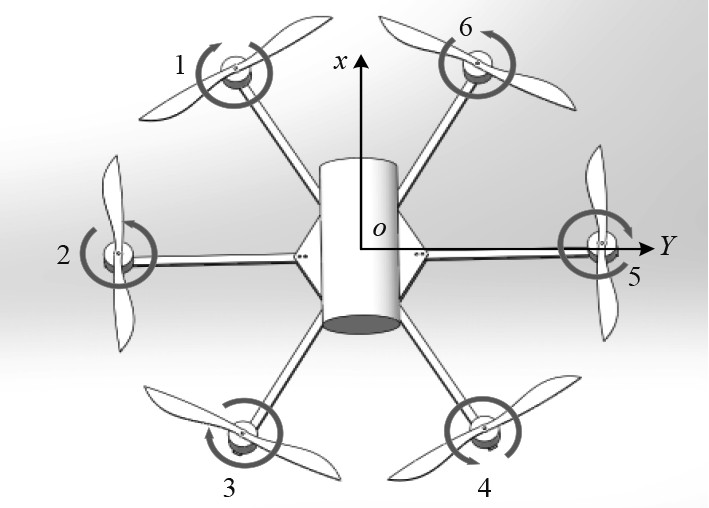
6个电机分布如图2所示。假设在工作时,转速分别为
|
图 2 水空多旋翼飞行器电机分布 Fig. 2 Motor distribution of water - air vehicle |
| $ {\tau}_{\text{p}}=\left[ \begin{array}{c} {\tau }_{pX}\\ {\tau }_{pY}\\ {\tau }_{pZ}\\ {\tau }_{pK}\\ {\tau }_{pM}\\ {\tau }_{pN}\end{array} \right]=\left[ \begin{array}{c}0\\ {\displaystyle\sum }_{m=1}^{6}{f}_{m}\\ b\mathrm{cos}{60}^{^\circ}\left[\left({f}_{1}+{f}_{3}\right)-\left({f}_{4}+{f}_{6}\right)\right]+b\left({f}_{2}-{f}_{5}\right)\\ b\mathrm{sin}{60}^{^\circ}\left[\left({f}_{1}+{f}_{6}\right)-\left({f}_{3}+{f}_{4}\right)\right]\\ \left({T}_{1}+{T}_{3}+{T}_{5}\right)-\left({T}_{2}+{T}_{4}+{T}_{6}\right)\end{array} \right] ,$ | (12) |
| $ {f_m} = {K_F}{\rho _i}n_m^2D_a^4(m = 1,2,3,4,5,6), $ | (13) |
| $ {T_m} = {K_T}{\rho _i}n_m^2D_a^4(m = 1,2,3,4,5,6)。$ | (14) |
式中:
采用PID控制算法[16-17]进行水空两栖多旋翼飞行器的出水控制研究,并在此基础上提出分段变参数控制方法。利用智能寻优算法对PID参数进行整定,形成自适应PID控制器。
目前,常用的智能寻优算法有粒子群优化算法[18]、蚁群算法[19]和遗传算法[20]等,本文选用遗传算法对PID参数进行整定,完成基于自适应PID的水空多旋翼飞行器出水控制研究。
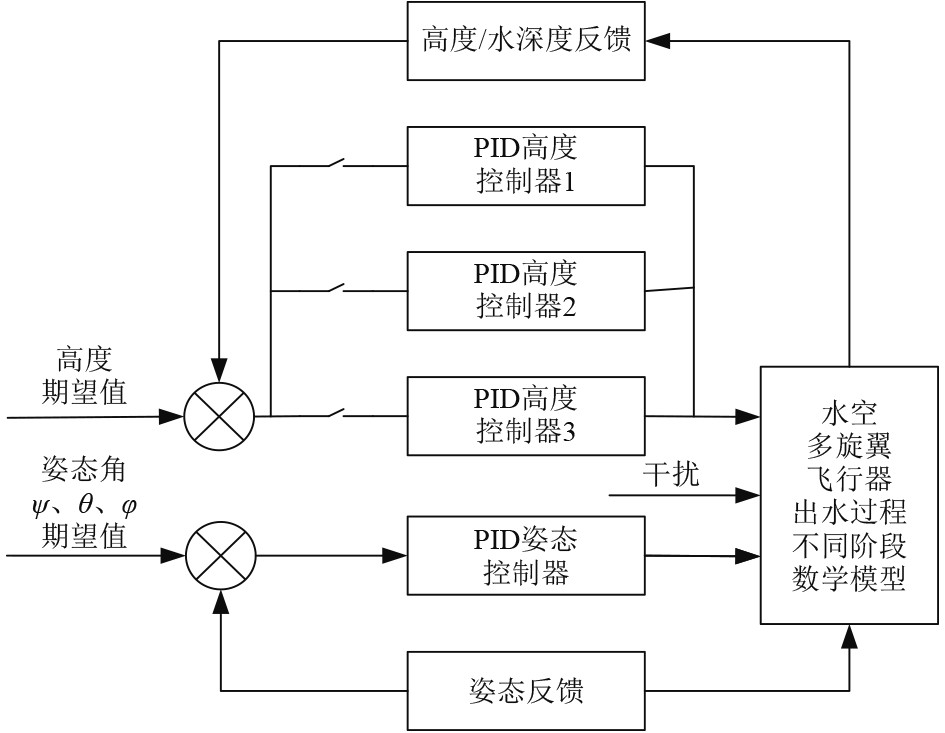
3.1 跨介质控制器搭建在出水过程中,假设只考虑水空多旋翼飞行器的垂直运动和姿态变化,则可以将飞行器常用的串级控制器简化为图3所示的单级控制器。水空多旋翼飞行器的姿态控制和高度控制被分解为2个独立的模块,在水空多旋翼飞行器的整个出水过程中,可以将飞行器的飞行高度以及姿态角进行分别控制。其中,由于水、空气2种介质物理性质相差巨大,在跨介质过程中(水下航行、水空跨越以及空中飞行),水空多旋翼飞行器的运动学、动力学模型将在某一瞬间产生突变。而PID控制器自适应能力较差,在上述3种情况下,单一PID控制器难以达到最优的控制效果。因此,提出分段变参数PID跨介质出水的控制方法,3个高度控制器分别作用于水下航行、水空跨越以及空中飞行3种状态。
|
图 3 飞行器出水过程不同阶段通用控制框图 Fig. 3 General control block diagram of different stages of aircraft outlet process |
最终在Matlab/Simulink中搭建的仿真模型。
3.2 基于遗传算法的PID参数整定选取遗传算法对跨介质控制器进行参数寻优,算法流程如图4所示。该方法是一种不需要任何初始信息并可以寻求全局最优解的、高效的优化组合方法[21]。

|
图 4 遗传算法流程图 Fig. 4 Flow chart of genetic algorithm |
引入遗传算法对PID参数进行整定,整定过程如图5所示。

|
图 5 引入遗传算法PID流程图 Fig. 5 Introduce genetic algorithm PID flow chart |
按照水空多旋翼飞行器跨介质的理想控制效果,跨介质控制器参数寻优问题可转化为:在满足姿态稳定的情况下,控制的超调量尽可能小,用最短的时间到达目标,用适应度函数将上述要求进行综合。该优化问题的数学模型为:
| $ \left\{ \begin{gathered} X = \left\{ {P,I,D} \right\}, \\ {\rm{s.t.}}\;\min (f), \\ X \in \left[ {{X_L},{X_U}} \right], \\ \end{gathered} \right. $ | (15) |
| $ f = 1/J。$ | (16) |
式中:
综合目标函数
快速性、准确性和稳定性是衡量控制系统的3个指标。为了得到好的控制效果,对控制量、误差和上升时间进行约束。当确定了综合目标函数
为得到满意的控制系统指标,主要采用加权误差绝对值对时间进行积分作为最小目标函数。为防止控制能量过大,在目标函数中还加入了控制器输入的平方项,则参数选取的最优指标为:
| $ J = \int_0^\infty {({w_1}\left| {e(t)} \right| + {w_2}{u^2}(t)){\text{d}}t} + {w_3} \cdot {t_u}。$ | (17) |
式中:
为进一步抑制系统超调,增加“惩罚功能”,即当系统产生超调时,目标函数会把超调量作为指标中很重要的一项,此时最优指标为:
| $ J = \int_0^\infty {({w_1}\left| {e(t)} \right| + {w_2}{u^2}(t) + {w_4}\delta (e(t))){\text{d}}t} + {w_3} \cdot {t_u} 。$ | (18) |
其中:
| $ \delta (e(t)){\text{ = }}\left\{ {\begin{array}{*{20}{c}} {1,e(t) \gt 0\;}, \\ {0,e(t) \leqslant 0。\;} \end{array}} \right. $ |
式中,
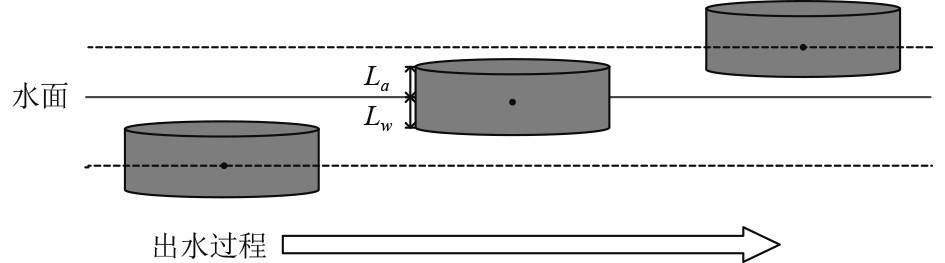
在仿真过程中,采用等效密度的方式处理出水过程中水空多旋翼飞行器受力的改变。假设水空交界始终保持静止,飞行器看做圆柱(见图6),其处于空气中和浸没在水中部分的长度分别为
|
图 6 水空多旋翼飞行器垂直出水等效示意图 Fig. 6 Equivalent schematic diagram of vertical outlet of water-air multi-rotor aircraft |
| $ {\rho _t} = {\rho _a}\frac{{{L_a}}}{L} + {\rho _w}\frac{{{L_w}}}{L} 。$ | (19) |
经过反复实验尝试,人工整定得到的飞行器在水下阶段、水空跨越阶段以及空中阶段的PID参数如表5所示(固定坐标系建立在水下2 m处,在介质跨越过程中考虑了飞行器的高度)。
|
|
表 5 分段PID控制参数 Tab.5 Piecewise PID control parameters |
得到的水下,水、空介质过渡,空中3个阶段的控制效果分别如图7~图9所示。
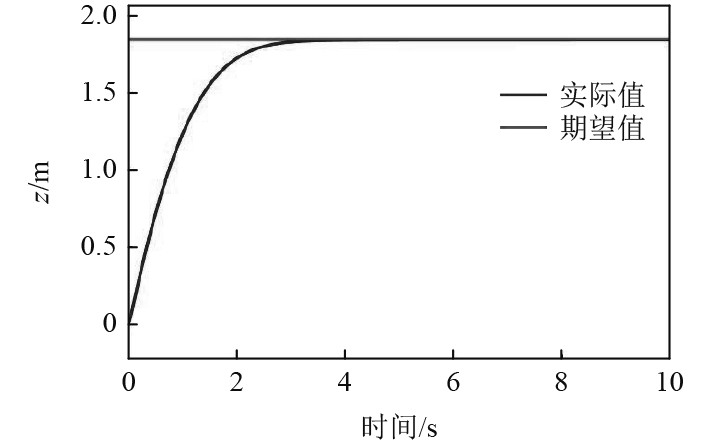
|
图 7 水下阶段系统响应曲线图 Fig. 7 System response curve in underwater phase |
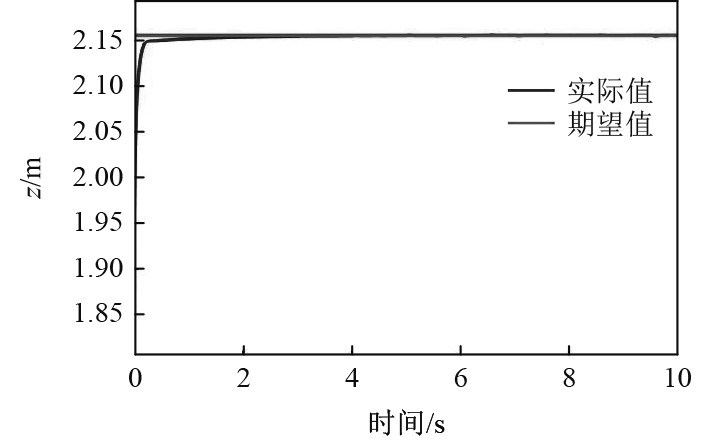
|
图 8 水-空过渡阶段系统响应曲线图 Fig. 8 System response curve of water-air transition stage |

|
图 9 空中阶段系统响应曲线图 Fig. 9 Aerial phase system response curve |
针对水下航行阶段,水空多旋翼飞行器大约3 s便可从水下到达水面,过程平稳且最终无静态误差;在水空跨越过程中,水空多旋翼飞行器的快速性极好,但存在较长时间的静态误差。对于空中飞行过程,人工经验得到的空中效果较差,大约4 s到达目标高度,且后续还存在周期性振荡。
本文提出的分段变参数PID控制方法更加贴合实际跨介质过程,可行性高。
4.2 遗传算法整定PID参数遗传算法寻优PID参数遵循以下原则:
1)快速性好;2)超调量小,无振荡、静态误差;3)介质跨越过程平缓。最终设置的遗传算法参数如表6所示。
|
|
表 6 遗传算法参数设置表 Tab.6 Genetic algorithm parameter setting table |
其中,参数
|
|
表 7 遗传算法参数设置 Tab.7 Genetic algorithm parameter Settings |
针对水空多旋翼飞行器跨介质的3个过程,遗传算法整定参数过程如图10所示。
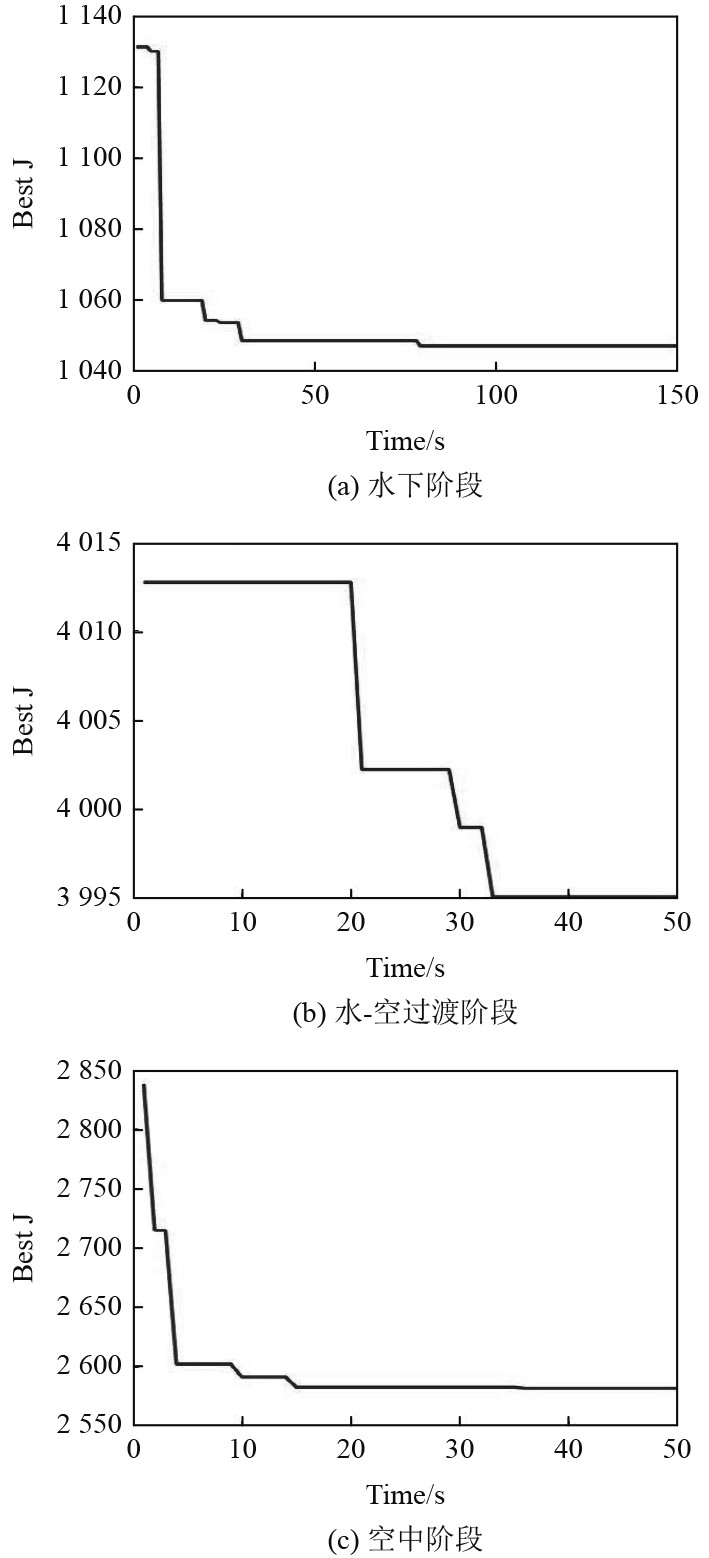
|
图 10 优化过程 Fig. 10 Optimization process |
在表7参数条件下,经过遗传算法寻优整定后得到的水下、水-空过渡、空中的最优PID参数分别为:Kp= 150.1,Ki= 12.189 0,Kd= 50.075 8;Kp= 13.1,Ki= 2 412.3,Kd= 150.3;Kp= 71.041 6,Ki= 37.981 7,Kd= 35.075 6。
同样,经过遗传算法整定后3个阶段的PID参数差异巨大,这再次反映出了水、空环境突变对PID控制算法影响巨大,有必要开展分段PID控制。
4.3 引入遗传算法前后仿真结果对比分析将上述寻优结果的参数放入搭建的模型当中,引入遗传算法前后的水空多旋翼飞行器出水过程的3个阶段的控制仿真系统响应曲线对比如图11~图13所示。
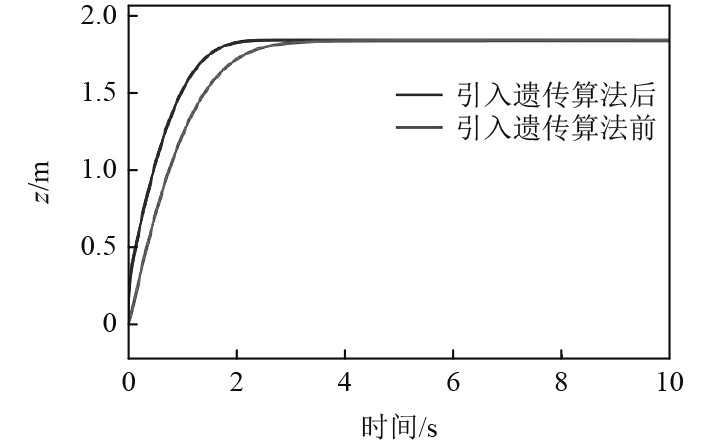
|
图 11 引入遗传算法前后水下阶段系统响应曲线图 Fig. 11 System response curve of underwater stage before and after genetic algorithm was introduced |
|
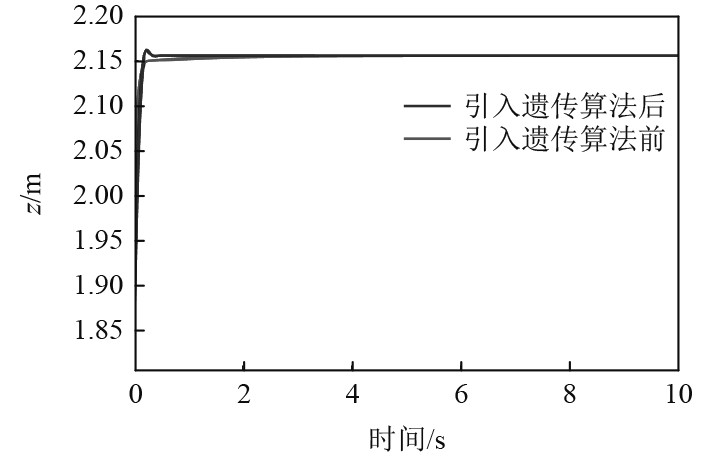
图 12 引入遗传算法前后水-空过渡阶段系统响应曲线图 Fig. 12 System response curve of water-air transition stage before and after genetic algorithm was introduced |
|
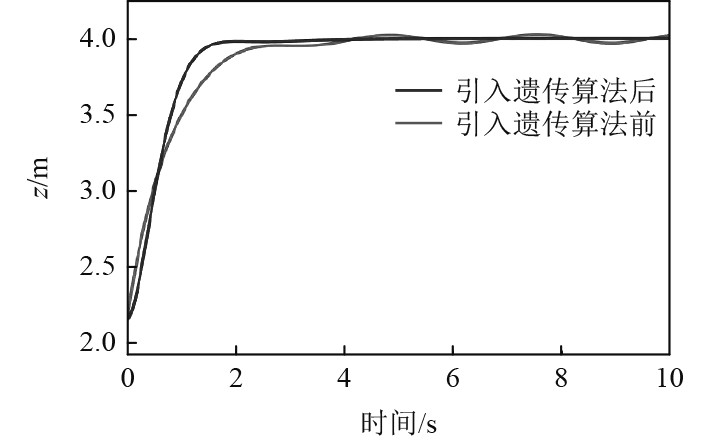
图 13 引入遗传算法前后空中阶段系统响应曲线图 Fig. 13 Response curves of airborne phase system before and after the introduction of genetic algorithm |
分析可知:
1)针对水下航行过程,在引入遗传算法整定参数后,水空多旋翼飞行器由水下到达水面的时间从大约3 s缩短至大约2 s,提高了水空多旋翼飞行器在出水过程中的快速性。
2)在水空过渡阶段,引入遗传算法后,静态误差得到了一定的抑制,但引入了微小的超调,快速性也没有得到进一步提升。从总体上来看,水空过渡阶段的性能还是得到了一定提升。
3)对于空中飞行阶段,通过遗传算法优化后,消除了人工整定参数存在的振荡问题,同时提高了空中飞行过程的快速性,时间从大约4 s缩短至大约2 s。
综上,引入遗传算法后,水空多旋翼飞行器在整个跨介质过程中得到了更好的控制性能,更符合飞行器在水空跨越过程的实际情况,飞行器更稳定。
5 结 语本文以自主搭建的水空多旋翼飞行器样机为研究对象,针对水空多旋翼飞行器在水空跨越过程的不同阶段,建立了对应的动力学和运动学模型。运用Fluent对飞行器在水下受到的粘性水动力进行流体力学分析,进而得到其与速度之间的多项式函数关系。最后,利用Matlab搭建了简化的控制器系统,对飞行器的出水过程进行控制仿真,并将引入遗传算法前后的仿真结果进行对比,最终验证了分段变参数PID算法在水空多旋翼飞行器出水控制中的必要性,同时也证明了遗传算法整定PID参数的优越性。
| [1] |
FABIAN A, FENG Y F, SWARTZ E, et al. Hybrid aerial underwatervehicle[R]. Lexington, USA: MIT Lincoln Lab, 2012.
|
| [2] |
DREWS J R P, NETO A A, CAMPOS M F M. Hybrid unmanned aerial underwater vehicle: modeling and simulation [C]//2014 IEEE RSJ International Conference on Intelligent Robots and Systems(IROS). Chicago: IEEE, 2014: 4637–4642.
|
| [3] |
NETO A A, MOZELLI L A, DREWS P L J, et al. Attitude control for an hybrid unmanned aerial underwater vehicle: A robust switched strategy with global stability[C]//2015 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2015: 395–400.
|
| [4] |
CHEN Y, HELBLING E F, GRAVISH N, et al. Hybrid aerial and aquatic locomotion in an at-scale robotic insect[C]//2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2015: 331–338.
|
| [5] |
余宗金, 冯金富, 胡俊华, 等. 水空跨越航行器出水运动建模[J]. 计算机仿真, 2015, 32(11): 101–105.
|
| [6] |
徐保伟, 冯金富, 廖保全, 等. 介质跨越变体无人机及其跨越动力学研究[J]. 飞航导弹, 2015, 32(12): 50-53. |
| [7] |
SIDDALL R, ORTEGA A A, KOVAC M. Wind and water tunnel test-ing of a morphing aquatic micro air vehicle[J]. Interface Focus, 2017, 7(1): 1-5. |
| [8] |
谭骏怡, 胡俊华, 陈国明, 等. 水空跨介质航行器斜出水过程数值仿真[J]. 中国舰船研究, 2019, 14(6): 104-121. |
| [9] |
颜奇民, 胡俊华, 陈国明, 等. 双层四旋翼跨介质航行器水空跨越建模与控制[J]. 飞行力学, 2020, 38(5): 50-56. |
| [10] |
聂星宇, 胡志强, 孙浩添, 等. 倾转四旋翼跨介质飞行器水面垂直起飞策略研究[J]. 舰船科学技术, 2022, 44(4): 66-71. |
| [11] |
王术波, 韩宇, 陈建, 等. 基于ADRC迭代学习控制的四旋翼无人机姿态控制[J]. 航空学报, 2020, 41(12): 319-331. |
| [12] |
LI J, CHEN S, GUO M, et al. Underwater Dynamics Modeling and Simulation Analysis of Trans-media Multicopter[C]// 2021 5th International Conference on Robotics and Automation Sciences (ICRAS). IEEE, 2021: 116–122.
|
| [13] |
WANG Y, LI J, HUO J, et al. Analysis of the hydrodynamic performance of a water-air amphibious trans-medium hexacopter[C]//2020 Chinese Automation Congress (CAC). IEEE, 2020: 4959–4964.
|
| [14] |
CHEN Y, LIU Y, MENG Y, et al. System modeling and simulation of an unmanned aerial underwater vehicle[J]. Journal of Marine Science and Engineering, 2019, 7(12): 444. DOI:10.3390/jmse7120444 |
| [15] |
陈彦民, 何勇灵, 孔令博, 等. 四旋翼飞行器分散PID神经元网络控制[J]. 中国惯性技术学报, 2014, 22(2): 185–190.
|
| [16] |
胡志强, 周焕银, 林扬, 等. 基于在线自优化PID算法的USV系统航向控制[J]. 机器人, 2013, 35(3): 263-268+275. DOI:10.3724/SP.J.1218.2013.00263 |
| [17] |
彭程, 白越, 乔冠宇, 等. 四旋翼无人机的偏航抗饱和与多模式PID控制[J]. 机器人, 2015, 37(4): 415-423. DOI:10.13973/j.cnki.robot.2015.0415 |
| [18] |
冯茜, 李擎, 全威, 等. 多目标粒子群优化算法研究综述[J]. 工程科学学报, 2021, 43(6): 745-753. |
| [19] |
乔东平, 裴杰, 肖艳秋, 等. 蚁群算法及其应用综述[J]. 软件导刊, 2017, 16(12): 217-221. |
| [20] |
李岩, 袁弘宇, 于佳乔, 等. 遗传算法在优化问题中的应用综述[J]. 山东工业技术, 2019, 290(12): 242-243+180. |
| [21] |
刘延飞, 彭征, 王艺辉, 等. 基于改进的遗传算法的有刷直流电机PID参数整定[J]. 计算机应用, 2022, 42(5): 1634-1641. |
 2023, Vol. 45
2023, Vol. 45
