0 引　言

船舶货物吊装的工作场景包括：

1）海上作业平台的货物转运

海洋蕴藏丰富的石油、天然气资源，为了开发这些资源，建立了多种用途的海上作业平台，如钻井平台等，这些资源开采后通过大型船舶运输至陆地，转运过程需要借助大吨位吊机进行货物转运。

2）港口装卸货物

大型集装箱船的货物装卸需要借助港口吊机，货物在船舶甲板的搬运需要借助自身吊机。

船舶吊运货物通常使用吊运机械臂完成，当船体受到海浪冲击作用和海风干扰时，一方面，船体本身的纵摇、横摇运动会引起吊运机械臂基座的运动，这种非惯性运动使得机械臂承受更大的载荷，对机械臂和基座的强度带来了挑战；另一方面，由于吊运机械臂本身具有多自由度的运动，叠加船体自身的运动，机械臂与货物会产生更大幅度的晃动，影响货物吊运的安全性。当货物吊运过程出现碰撞等事故时，会对货物和船体造成严重的冲击。

为此，本文研究一种海浪环境下的船舶吊运机械臂运动补偿控制系统，该系统的关键作用是进行波浪环境下的吊运机械臂运动补偿，提高吊运机械臂的稳定性。

1 海浪环境下的船舶吊运机械臂运动建模

船舶吊运过程中影响最大的环境因素是海浪作用力，为了提高吊运机械臂的建模精度，对海浪特性进行详细研究。

海浪运动是一种不规则波运动，在进行海浪运动建模时可以只考虑单一方向上的海浪传播特性，将复杂的海浪运动分解为不同规则波的叠加。

建立海浪特性方程：

$\xi (t) = \sum\limits_{i = 1}^n {{\xi _0}(t)\cos ({w_0}t + \varphi )} \text{。}$

式中： ${\xi _0}(t)$ 为幅值； ${w_0}$ 为波浪角速度； $\varphi$ 为初始的相位^[1]。

建立能谱密度方程^[2]：

$E({\omega _0}) = \frac{{{k_1}}}{{{\omega _0}^3}}\exp (\frac{{ - {k_2}}}{{{\omega _0}^4}}) \text{。}$

式中：k₁为能谱密度系数，k₁=7.9×10⁻³ g²； ${k_2} = \displaystyle\frac{{3.09}}{{{h_0}^2}}$ ； ${h_0}$ 为波高。

将波浪的速度场在2个方向上分解，可以得到：

$\begin{gathered} {E_x}{\text{ = }}\frac{\text π }{2}{\varphi _0}{\theta ^{kt}}\cos \left( {kx - {w_0}t} \right), \\ {E_y} = \frac{1}{2}{\varphi _0}{\theta ^{kt}}\sin \left( {kx - {w_0}t} \right)。\\ \end{gathered}$

式中， ${\theta ^{kt}}$ 为波浪的速度势。

建立船舶吊运机械臂在海浪环境下的运动坐标系如图1所示。

根据图1坐标系，建立吊运机械臂的力矩方程^[3]为：

${I_z}\frac{{{\rm{d}}{w_z}}}{{{\rm{d}}t}} = {M_z} + {M_{sp}} \text{。}$

式中： ${I_z}$ 为机械臂沿z轴的转动惯量； ${w_z}$ 为绕z轴的转动角速度； ${M_z}$ 为干扰力矩； ${M_{sp}}$ 为附加力矩。

建立机械臂的运动学方程如下式：

$\begin{aligned} & {m\frac{{{\rm{d}}v}}{{{\rm{d}}t}} = P\cos \left( {\alpha + \theta } \right) - Q - mg\sin \theta } ,\\ & {m\frac{{{\rm{d}}\theta }}{{{\rm{d}}t}} = P\sin \left( {\alpha + \theta } \right) - mg\cos \theta }, \\ & {{I_z}\frac{{{\rm{d}}{w_z}}}{{{\rm{d}}t}} = {M_z} + {M_{sp}}} ,\\ & {\frac{{{\rm{d}}x}}{{{\rm{d}}t}} = v\cos \theta }, \\ & {\frac{{{\rm{d}}h}}{{{\rm{d}}t}} = v\sin \theta } \text{。} \end{aligned}$

式中： $P$ 为机械臂电机驱动力； $\theta$ 为机械臂转运角度； $h$ 为机械臂距离甲板的垂直高度； $v$ 为货物吊运的速度。

建立瞬时运动速度模型为：

$\begin{gathered} X(t) = \sum\limits_{i = 1}^n {\left[ {{h_x}/n \cdot \cos \left( {{\omega _i}t + {\gamma _{xi}}} \right)} \right]}, \\[2.5pt] Y(t) = \sum\limits_{i = 1}^n {\left[ {{h_y}/n \cdot \cos \left( {{\omega _i}t + {\gamma _{ji}}} \right)} \right]} , \\[2.5pt] Z(t) = \sum\limits_{i = 1}^n {\left[ {{h_z}/n \cdot \cos \left( {{\omega _i}t + {\gamma _{zi}}} \right)} \right]}。\\ \end{gathered}$

式中： ${\omega _i}$ 为船舶角速度， $\left[ {{h_x}/{h_y}/{h_z}} \right]$ 为船舶3个方向的相位； $\left( {{\gamma _{xi}}/{\gamma _{zi}}/{\gamma _{ji}}} \right)$ 为船舶3个方向的幅值。

3个坐标轴的角度模型为：

$\begin{gathered} \gamma = \sum\limits_{i = 1}^n {\left[ {{A_r}/n \cdot \sin \left( {{\omega _r}t + {\varphi _r}} \right)} \right]}, \\[2.5pt] \theta = \sum\limits_{i = 1}^n {\left[ {{A_\theta }/n \cdot \sin \left( {{\omega _\theta }t + {\varphi _\theta }} \right)} \right]}, \\[2.5pt] \psi = \sum\limits_{i = 1}^n {\left[ {{A_\psi }/n \cdot \sin \left( {{\omega _\psi }t + {\varphi _\varphi }} \right)} \right]}。\\ \end{gathered}$

式中： $\left( {\gamma /\theta /\psi } \right)$ 分别为横摇角，纵倾角和航向角； $\left( {\varphi _r}/ {\varphi _\theta }/ {\varphi _\varphi } \right)$ 为3个角度方向的相位； $\left( {{A_r}/{A_\theta }/{A_\psi }} \right)$ 为幅值； $\left( {{\omega _r}/{\omega _\theta }/{\omega _\psi }} \right)$ 为角速度。

2 船舶吊运机械臂海浪环境下的运动补偿控制系统开发 2.1 PID控制器原理

针对船舶吊运机械臂的运动补偿控制器，利用PID控制器建立一种自适应控制系统。

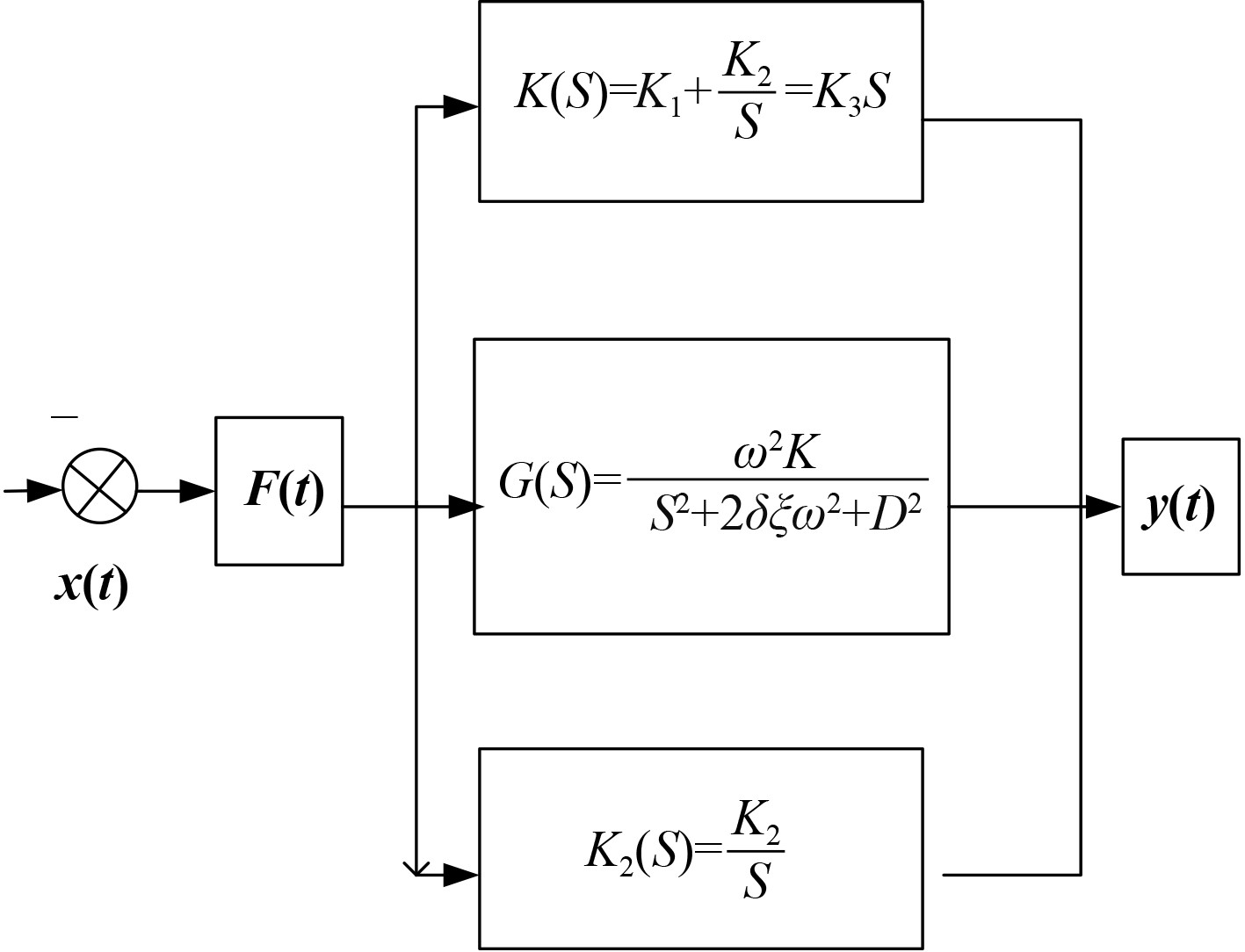
PID控制器是一种应用广泛、可靠性高的反馈控制器，包括积分控制、微分控制和比例控制3部分，对于改善系统的稳态误差、非线性误差等效果明显，图2为PID控制器的原理。

PID控制器的工作流程包括：

1） 确定被控系统的信号采集周期；

2）利用比例控制和阶跃响应信号，确定PID控制器的比例放大系数 ${K_1}$ ；

3）利用积分和微分控制环节，调节被控系统的信号超调量。

PID控制器的数学模型为：

$K(S) = {K_1} + \frac{{{K_2}}}{S} + {K_3}S \text{。}$

式中： ${K_1}$ 为放大系数； ${K_2}$ 为超调量系数； ${K_3}$ 为微分系数。

PID控制器的传递函数为：

$G(S) = \frac{{{\omega ^2}K}}{{{S^2} + 2\delta \xi {\omega ^2} + {D^2}}} \text{。}$

式中： $\xi$ 为系统阻尼比； $K$ 为增益系数。

2.2 PID控制器的吊运机械臂电动机控制研究

针对船舶机械臂的运动补偿，设计一种六自由度补偿机构，通过电机控制补偿机构上下平台的偏移量实现波浪运动的补偿。

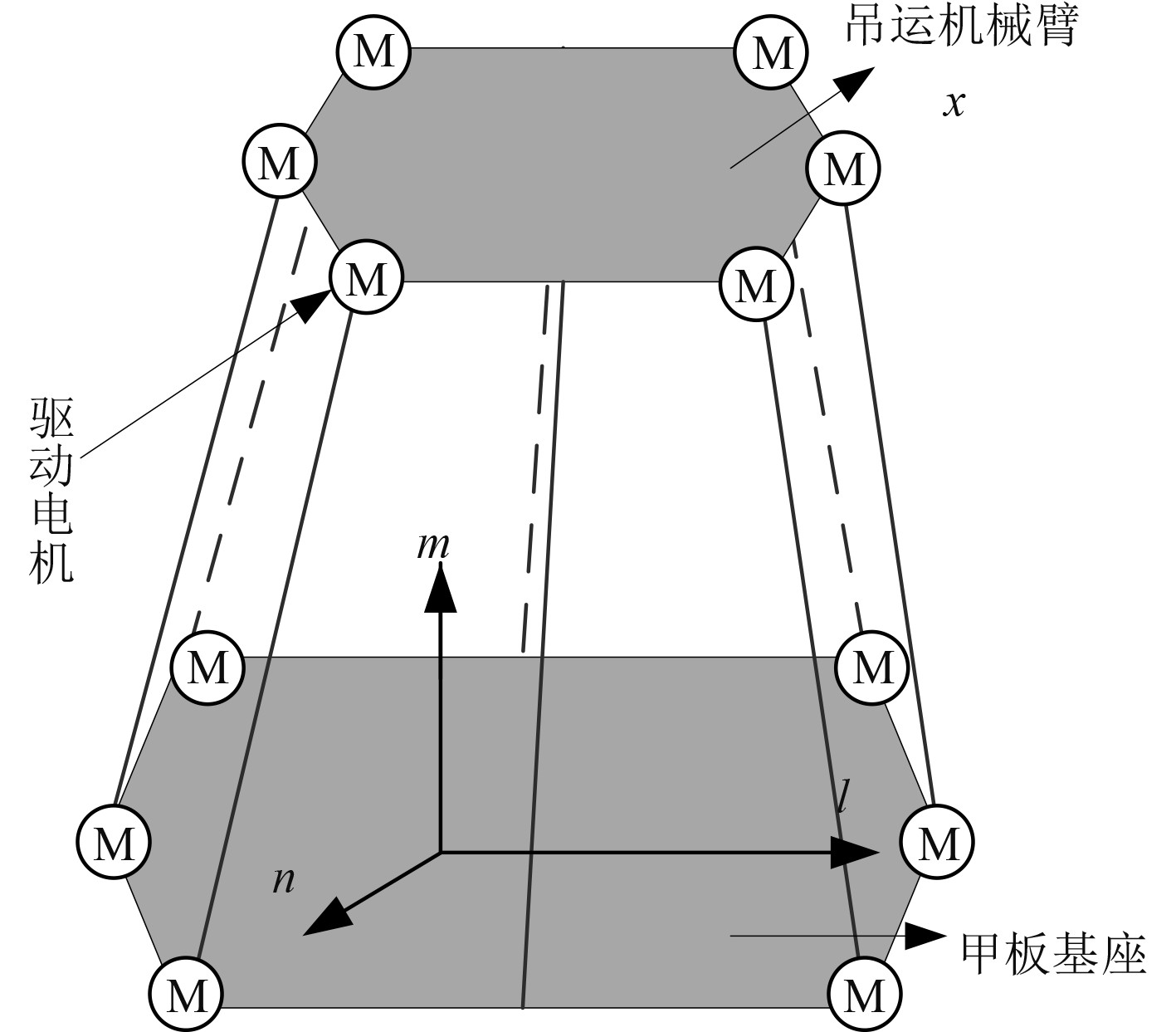
图3为吊运机械臂运动补偿机构的原理图。

六自由度补偿机械的关键控制环节是机械的电机伺服控制，本文使用三相永磁同步电机作为波浪补偿结构的动力来源。

建立三相永磁同步电机的电压方程如下：

$\left[ {\begin{array}{*{20}{l}} {{u_a}} \\ {{u_b}} \\ {{u_c}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{R_s}}&0&0 \\ 0&{{R_s}}&0 \\ 0&0&{{R_s}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{i_a}} \\ {{i_b}} \\ {{i_c}} \end{array}} \right] + p\left[ {\begin{array}{*{20}{c}} {{\varphi _a}} \\ {{\varphi _b}} \\ {{\varphi _c}} \end{array}} \right] \text{。}$

式中： ${u_a}$ ， ${u_b}$ ， ${u_c}$ 为三相电机定子的三相电压； ${R_s}$ 为电机定子的等效电阻； ${i_a}$ ， ${i_b}$ ， ${i_c}$ 为定子的三相电流； ${\varphi _a}$ ， ${\varphi _b}$ ， ${\varphi _c}$ 为电机的三相磁链； $p$ 为电机磁链系数。

磁链方程为：

$\left[ {\begin{array}{*{20}{c}} {{\varphi _a}}\\ {{\varphi _b}}\\ {{\varphi _c}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{L_{aa}}}&{{M_{ab}}}&{{M_{ac}}}\\ {{M_{ba}}}&{{L_{bb}}}&{{M_{bc}}}\\ {{M_{ca}}}&{{M_{cb}}}&{{L_{cc}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{i_a}}\\ {{b_b}}\\ {{i_c}} \end{array}} \right] + {\varphi _r}\left[ {\begin{array}{*{20}{c}} {\cos \theta }\\ {\cos \left( {\theta - 120^\circ } \right)}\\ {\cos \left( {\theta + 120^\circ } \right)} \end{array}} \right]。$

式中： ${L_{aa}}$ ， ${L_{bb}}$ ， ${L_{cc}}$ 为绕组的自感； ${M_{ij}},i = a,b,c;j = a,b,c$ 为三相绕组之间的互感。

本文使用的电机参数如表1所示。

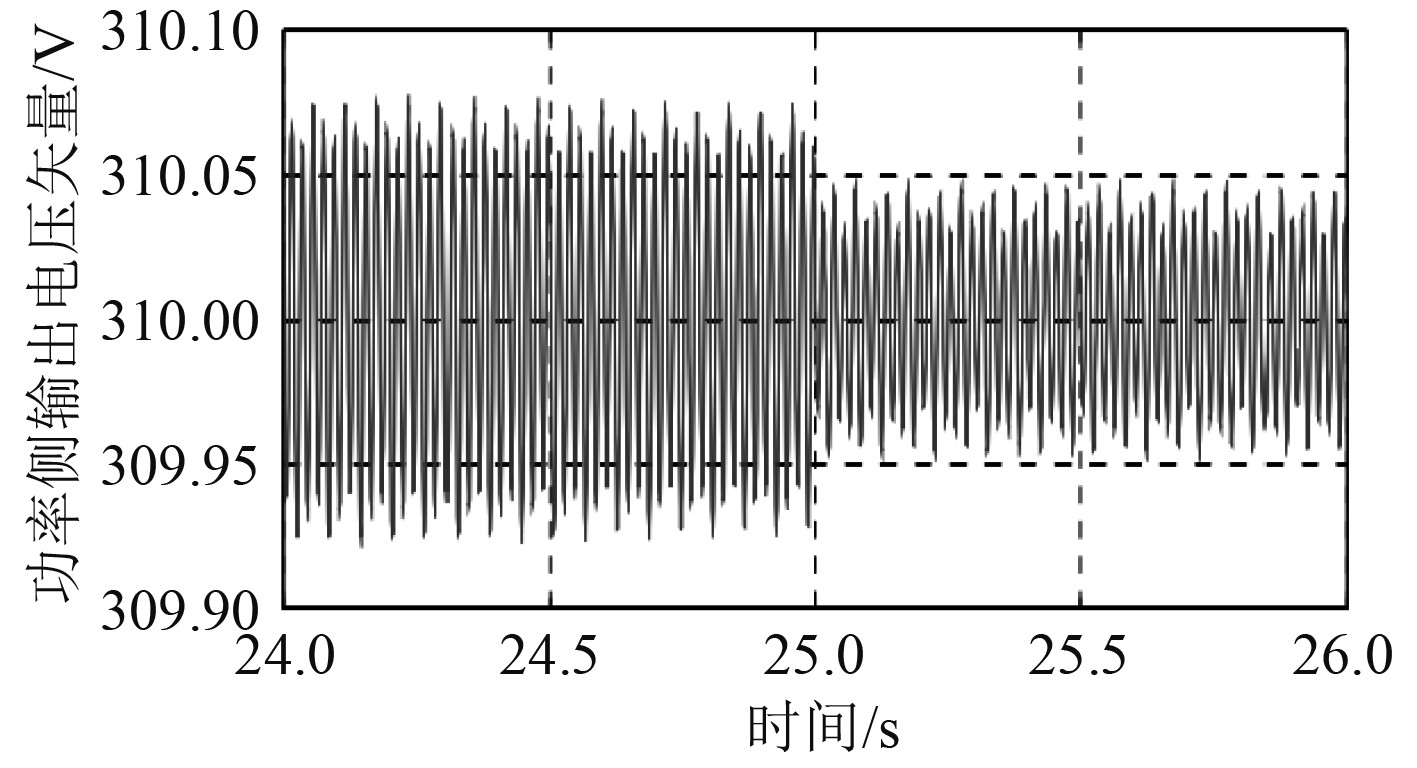
图4为波浪补偿机构电机输出电压矢量图。

2.3 船舶吊运机械臂波浪补偿控制系统的搭建

结合PID控制器，针对船舶吊运机械臂的波浪补偿控制进行开发，吊运机械臂的波浪补偿控制系统原理图如图5所示。

可知，波浪补偿控制器基于PID控制原理，接收运动模型的参数，控制电动机的转矩信号，然后通过执行器进行补偿平台的控制。同时，系统位置传感器采集吊运机械臂和船体的横摇等运动参数，作为负反馈信号输入PID控制器中^[4]。

建立三相永磁同步电机的控制信号为：

$\begin{aligned} & {{u_a}{\text{ = }}{U_0}\cos wt}, \\ & {{u_b} = {U_0}\left( {\cos wt - {\raise0.7ex\hbox{${2{\text π} }$} \mathord{\left/ {\vphantom {{2{\text π} } 3}}\right.} \lower0.7ex\hbox{$3$}}} \right)}, \\ & {{u_c} = {U_0}\left( {\cos wt + {\raise0.7ex\hbox{${2{\text π} }$} \mathord{\left/ {\vphantom {{2{\text π} } 3}}\right.} \lower0.7ex\hbox{$3$}}} \right)}。\end{aligned}$

根据PID控制器原理，确定永磁同步电动机的控制精度为 $\delta = \displaystyle\frac{{\left( {{x_{\min }}\sim{x_{max}}} \right)}}{{{2^L} - 1}}$ 。

确定PID控制器的放大系数 ${K_1}$ ，超调量系数 ${K_2}$ 和微分系数 ${K_3}$ 。

最后，结合位置传感器的信息实现吊运机械臂的运动补偿控制。

本文在Simulink中进行波浪补偿前后的吊运机械臂位移量仿真，得到曲线如图6所示（曲线1为补偿前，曲线2为补偿后）。

3 结　语

船舶吊运机械臂的稳定性对于货物与船体的安全十分重要，因此，在进行船舶吊运机械臂设计时，有必要考虑船体的波浪补偿控制。本文介绍吊运机械臂的力学特性，建立一种六自由度运动补偿机制，针对系统的电机控制引入PID控制技术，取得了良好的效果。