2. 天津航海仪器研究所九江分部,天津 300131
2. Jiujiang Division, Tianjin Navigation Instruments Research Institute, Tianjin 300131, China
船舶在海上航行时,海浪的一阶波浪力会造成船舶航向的高频振荡,若直接将此信号反馈给自动舵系统,航向控制器会输出相应的高频舵角指令。然而由于船舶是一个大惯性系统,其航向运动的响应频率较小,当船舶的舵机系统接收到高于船舶航向响应频率的舵角指令时,无论采取多大舵角,船舶的运动状态都不会响应,这种操舵被称为无效操舵[1]。
在自动舵系统中,解决无效操舵现象的通常做法是对海浪高频干扰下的航向信号进行滤波,常用的滤波方法有均值滤波、低通滤波、带通滤波与陷波滤波等[2],但这几种滤波方法会产生信号的相位滞后,这种滞后会恶化航向控制器的控制效果。为解决相位滞后问题,樊冀生等[3]在陷波滤波器基础上进行改进,通过扩张一个状态量对陷波滤波器的滞后进行补偿,解决了陷波滤波器的滞后问题,但这种方法无法同时对船舶的速度状态量进行重构。李杨等[4]通过分析海浪高频模型,在潜艇线性化模型基础上加入海浪高频模型,通过状态观测器的方法将航向信号中高频与低频信号进行分离,并对低频的航向角速度信号进行重构,有效减少了无效舵问题。但这种方法在风、流与海浪二阶漂移力的情况下观测结果会存在静差,进而影响了航向控制器的控制效果。
本文针对海浪干扰下船舶控制系统存在的无效舵问题以及风、流干扰下观测器存在的静差问题,提出一种基于扩张状态卡尔曼滤波的海浪滤波算法,并结合传统的PID控制器验证了该算法的优势。
1 船舶Nomoto模型与参数辨识船舶的MMG分离模型[5]描述如下:
| $ \left\{ \begin{gathered} \dot x = u\cos \psi - v\sin \psi ,\\ \dot y = u\sin \psi + v\cos \psi ,\\ \dot \psi = r ,\\ \dot u = \frac{{\left( {m + {m_y}} \right)vr + {X_H} + {X_P} + {X_R} + {X_{disturb}}}}{{m + {m_x}}} ,\\ \dot v = \frac{{\left( {m + {m_x}} \right)ur + {Y_H} + {Y_P} + {Y_R} + {Y_{disturb}}}}{{m + {m_y}}} ,\\ \dot r = \frac{{{N_H} + {N_P} + {N_R} + {N_{disturb}}}}{{{I_{zz}} + {J_{zz}}}}。\\ \end{gathered} \right. $ | (1) |
式中:
由于船舶MMG模型结构复杂,水动力参数居多,不能直接用于状态观测器与控制器的设计,且由于船舶在大洋航行时主要关注航向、航向角速度等状态的信息,因此以Nomoto模型[6]代替MMG模型进行状态观测器的设计,一阶线性Nomoto模型如下式:
| $ T\dot r + r = K\delta + d\;。$ | (2) |
式中:
为了对Nomoto模型的
| $ \begin{split} & \frac{{T\dot \psi (k) - T\dot \psi (k - 1)}}{{T{}_s}} + \frac{{\psi (k) - \psi (k - 1)}}{{{T_s}}} = k\delta (k - 1) ,\\ & \frac{{T\psi (k) - T\psi (k - 1)}}{{{T_s}}} - \frac{{T\psi (k - 1) - T\psi (k - 2)}}{{{T_s}}}+\\ & \psi (k) - \psi (k - 1) = {T_s}K\delta (k - 1) ,\\ & T\psi (k) - T\psi (k - 1) - T\psi (k - 1) + T\psi (k - 2)+\\&{T_s}\psi (k) - {T_s}\psi (k - 1) = T_s^2K\delta (k - 1) ,\\ & (T + {T_s})\psi (k) - (2T + {T_s})\psi (k - 1) + T\psi (k - 2) = T_s^2K\delta (k - 1) ,\\ &\psi (k) = \frac{{2T + {T_s}}}{{(T + {T_s})}}\psi (k - 1) - \frac{T}{{(T + {T_s})}}\psi (k - 2) +\\ & \frac{{T_s^2}}{{(T + {T_s})}}K\delta (k - 1) 。\\[-15pt] \end{split} $ | (3) |
式中
将离散化的Nomoto方程转化为参数估计的形式:
| $ \psi (k) = {\phi ^{\rm{T}}}(k - {\text{1}})\theta \;。$ | (4) |
式中:
| $ \begin{gathered} {\phi ^{\rm{T}}}(k - 1) = \left[ {\psi (k - 1),\psi (k - 2),\delta (k - 1)} \right],\\ {\theta ^{\rm{T}}} = \left[ {{\theta _1},{\theta _2},{\theta _3}} \right] \;。\\ \end{gathered} $ |
基于船舶巡航航速下的Z型实验数据采用带有遗忘因子的最下二乘算法[7]对式(4)进行参数估计,如下式:
| $ \left\{ \begin{gathered} K\left( k \right) = \frac{{P\left( {k - 1} \right)\phi \left( {k - 1} \right)}}{{\lambda + {\phi ^T}\left( {k - 1} \right)P\left( {k - 1} \right)\phi \left( {k - 1} \right)}} ,\\ \theta \left( k \right) = \theta \left( {k - 1} \right) + K\left( k \right)\left[ {\psi \left( k \right) - {\phi ^T}\left( k \right)\theta \left( {k - 1} \right)} \right],\\ P\left( k \right) = \frac{1}{\lambda }\left[ {I - K\left( k \right){\phi ^T}\left( {k - 1} \right)} \right]P\left( {k - 1} \right) 。\end{gathered} \right. $ | (5) |
式中:
最终可求得船舶的
| $\begin{split} &T=\frac{{\theta }_{1}-1}{2-{\theta }_{1}}{T}_{s},\\ & K=\frac{{\theta }_{3}\left(T+{T}_{s}\right)}{{T}_{s}^{2}}。\end{split}$ | (6) |
海浪对于航行中船舶的作用力分为一阶波浪力与二阶波浪力。其中,二阶波浪力为漂移力,其作用可使船舶偏离原航向;一阶波浪力为高频作用力,其作用会使船舶航向高频摆动。由Fossen[8]的研究成果可知,一阶海浪力对船舶航向产生的高频摆动运动可由如式(7)所示的二阶传递函数表示。
| $ {\psi _H}(s) = \frac{{{K_\omega }s}}{{{s^2} + 2\zeta {\omega _n}s + {\omega _n}^2}}{w_H}(s) \;。$ | (7) |
式中:
将式(7)所示的二阶传递函数以状态方程的形式表示,如下式:
| $\begin{split} &{{\dot \xi }_H}{\text{ = }}{\psi _H} ,\\ &{{\dot \psi }_H}{\text{ = }} - 2\zeta {\omega _n}{\psi _H} - {\omega _n}^2{\xi _H} + {K_w}{w_H} \; 。\end{split} $ | (8) |
由船舶上的罗经设备测得的航向角可认为是由操舵产生的航向角、一阶海浪力产生的航向角和测量干扰叠加而成,如下式:
| $ \psi = {\psi _L} + {\psi _H} + {\upsilon _H},$ | (9) |
式中,
根据船舶的Nomoto响应性模型与海浪造成的船舶航向高频运动状态方程(8),可得到海浪干扰和操舵联合作用下的船舶航向运动状态方程:
| $ \begin{split} \left[ {\begin{array}{*{20}{c}} {{{\dot \psi }_L}} \\ {{{\dot r}_L}} \\ {{{\dot \xi }_H}} \\ {{{\dot \psi }_H}} \end{array}} \right] =\;& \left[ {\begin{array}{*{20}{c}} 0&1&0&0 \\ 0&{\dfrac{{ - 1}}{T}}&0&0 \\ 0&0&0&1 \\ 0&0&{-2\zeta {\omega _n}}&{{\omega _n}^2} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\psi _L}} \\ {{r_L}} \\ {{\xi _H}} \\ {{\psi _H}} \end{array}} \right]+\\ & \left[ {\begin{array}{*{20}{c}} 0 \\ {\dfrac{K}{T}} \\ 0 \\ 0 \end{array}} \right]\delta + \left[ {\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \\ {{K_w}} \end{array}} \right]{w_H} \; 。\end{split}$ | (10) |
由于船舶在航行过程中会受到风、流、浪的二阶干扰力影响,Nomoto模型中环境与未建模的综合干扰项d会使状态观测的结果存在误差。因此综合干扰项作为扩张状态加入到运动状态方程(10)中,补偿状态观测误差。扩张后的状态方程如下式:
| $ \begin{split} \begin{bmatrix} {{{\dot \psi }_L}} \\ {{{\dot r}_L}} \\ {{{\dot \xi }_H}} \\ {{\dot \psi }_H} \\ {\dot d} \end{bmatrix} = & \underbrace {\begin{bmatrix} 0&1&0&0&0 \\ 0&{ - 1/T}&0&0&1 \\ 0&0&0&1&0 \\ 0&0&{{{ - }}2\zeta {\omega _n}}&{{\omega _n}^2}&0 \\ 0&0&0&0&0 \end{bmatrix}}_A\underbrace{\begin{bmatrix} {{\psi _L}} \\ {{r_L}} \\ {{\xi _H}} \\ {\psi _H} \\ d \end{bmatrix}}_X + \underbrace{\begin{bmatrix} 0 \\ {K/T} \\ 0 \\ 0 \\ 0 \end{bmatrix}}_B\underbrace \delta _U ,\\ \underbrace \psi _Z =\; & \underbrace {\left[ {\begin{array}{*{20}{c}} 1&0&0&1&0 \end{array}} \right]}_CX 。\\[-15pt] \end{split} $ | (11) |
使用后向差分方法对扩张状态的状态空间表达式进行离散化处理,离散化后的表达式如下式:
| $ \left\{ \begin{gathered} {X_k} = {A_d}{X_{k - 1}} + {B_d}{U_{k - 1}} ,\\ {Z_k} = {C_d}{X_k} 。\\ \end{gathered} \right. $ | (12) |
式中:
基于卡尔曼滤波原理[9]根据船舶航行时的实时输入输出数据重构运动状态信息。卡尔曼滤波的递推过程如下:
1)确定过程噪声方差Q、测量噪声方差R、初始状态X0以及初始协方差矩阵P0。
2)根据前一时刻的状态估计值推算当前时刻的状态先验估计值,如下式:
| $ {X_{k - 1|k}} = {A_d}{X_{k - 1}} + {B_d}{U_{k - 1}} ,$ | (13) |
| $ {P_{k - 1|k}} = {A_d}{P_{k - 1}}A_d^T + Q \;。$ | (14) |
3)计算卡尔曼增益,如下式:
| $ {K_k} = {P_{k - 1|k}}C_d^T{\left( {{C_d}{P_{k - 1|k}}C_d^T + R} \right)^{ - 1}}\;。$ | (15) |
4)根据测量值与先验估计值计算状态后验估计值与误差协方差后验估计值,如下式:
| $ {X_k} = {X_{k - 1|k}} + {K_k}\left( {{Z_k} - {C_d}{X_{k - 1|k}}} \right),$ | (16) |
| $ {P_k} = \left( {I - {K_k}{C_d}} \right){P_{k - 1|k}} \;。$ | (17) |
为了验证本文所设计的海浪滤波算法的有效性,以47.4 m长的执法船海巡0208轮作为仿真对象进行算法验证。
设置船舶航行速度为12 kn,在无环境干扰的工况下进行Z型试验,仿真结果如图1所示。
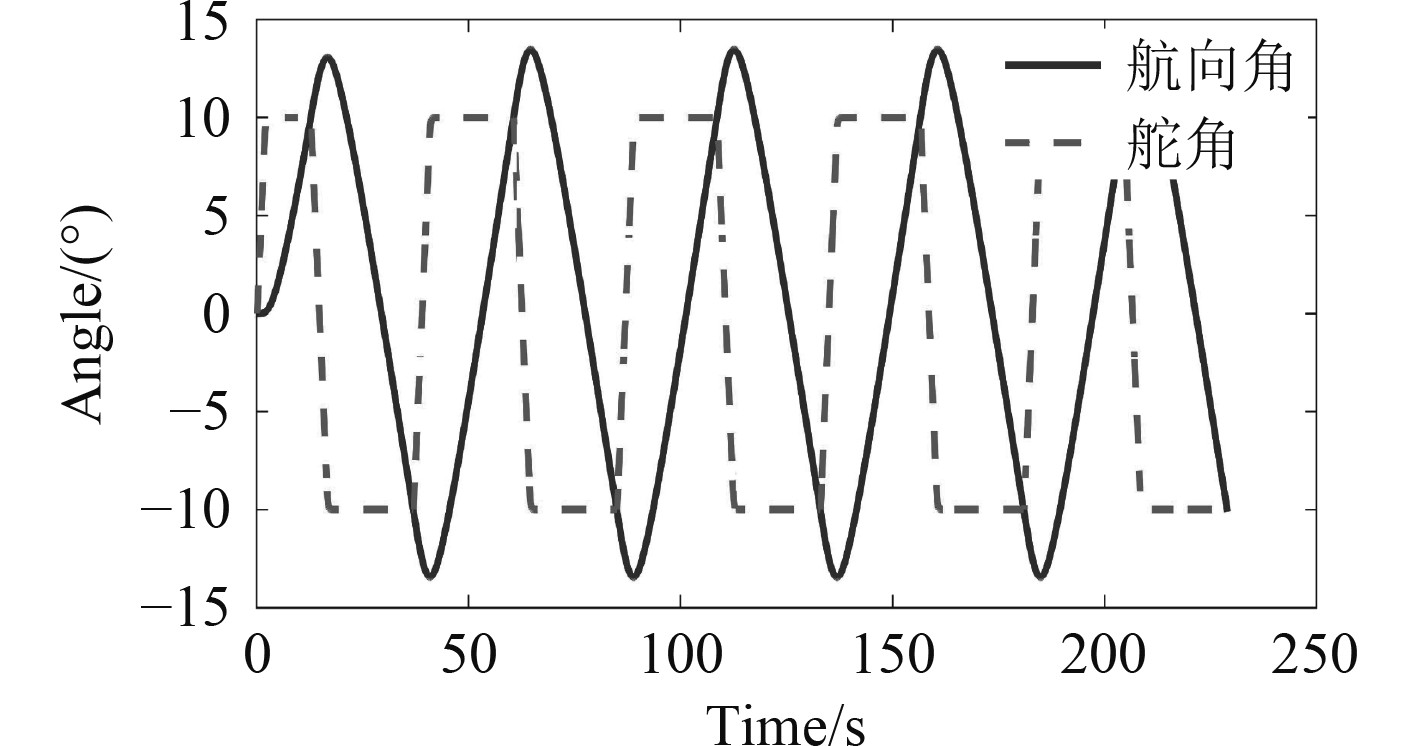
|
图 1 Z型试验仿真结果 Fig. 1 Simulation result of Z−type test |
以所设计的基于遗忘因子最小二乘的参数辨识算法进行K和T参数的辨识,辨识结果如图2所示。
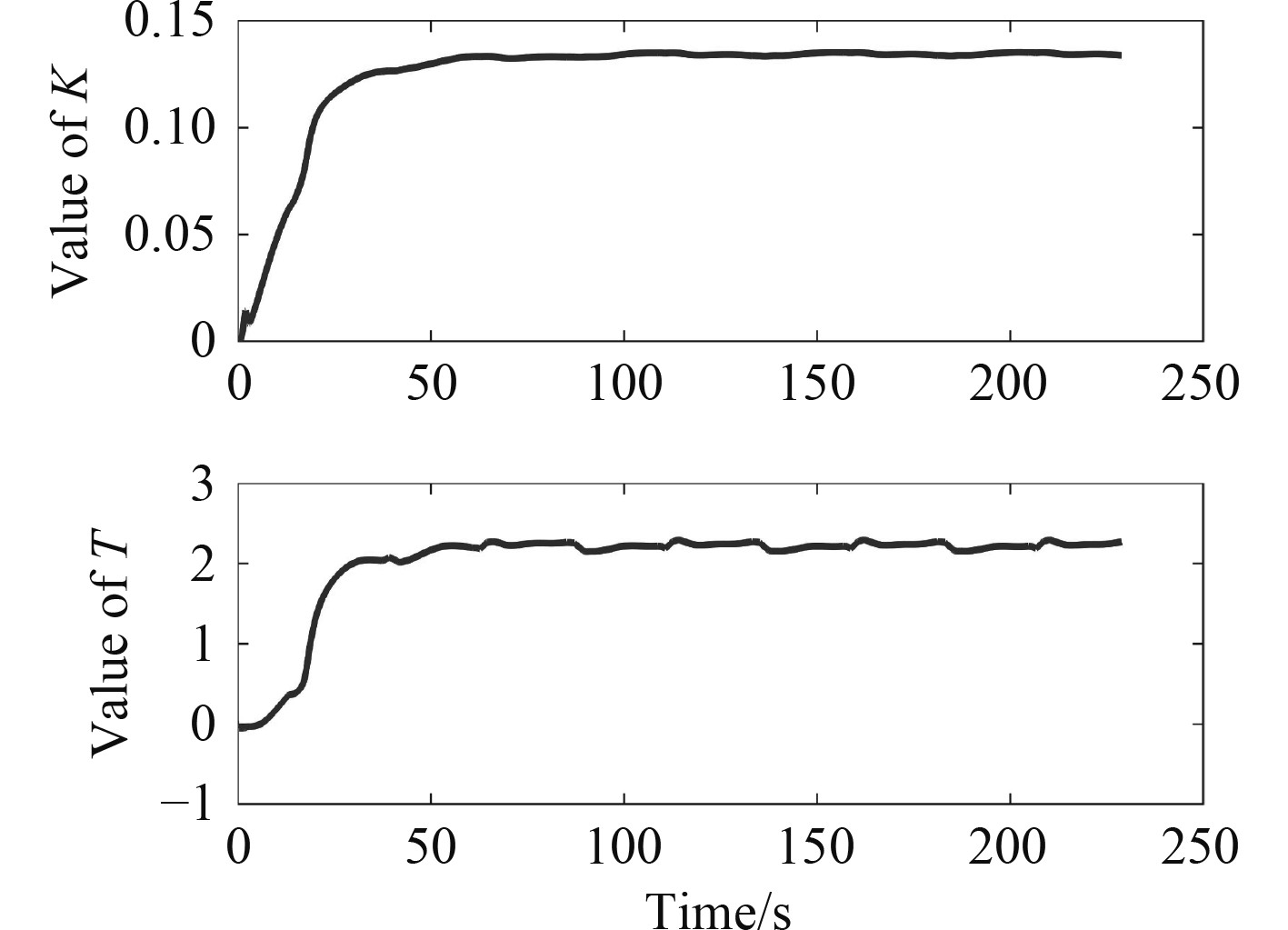
|
图 2 K,T参数辨识结果 Fig. 2 Identification results of K and T parameters |
从K和T参数的辨识结果中可以看出,2个参数在50 s后趋于稳定。为了准确的求解K和T参数,对100 s后的数据求取平均值,最终求解出的K和T参数为:
| $ K=0.1249,T=2.0187 。$ |
为了验证本文设计海浪滤波器的无差观测能力,在风向为90°的5级风、无海浪干扰环境下进行变向控制试验,控制器选用传统的PID控制器,对比分别以四阶状态方程(10)与五阶状态方程(11)设计观测器的观测效果,仿真结果如图3与图4所示。
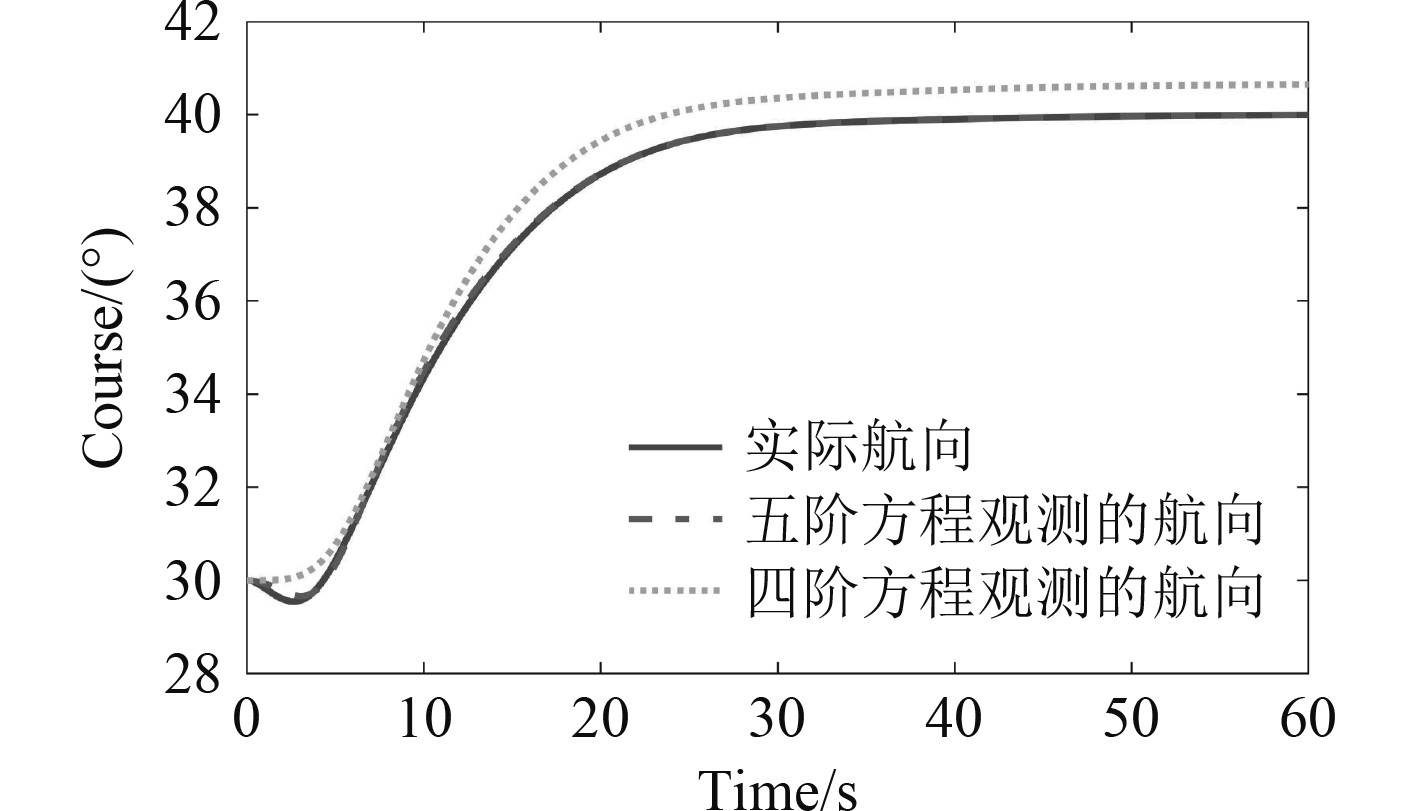
|
图 3 航向观测结果对比图 Fig. 3 Comparison of course observation results |
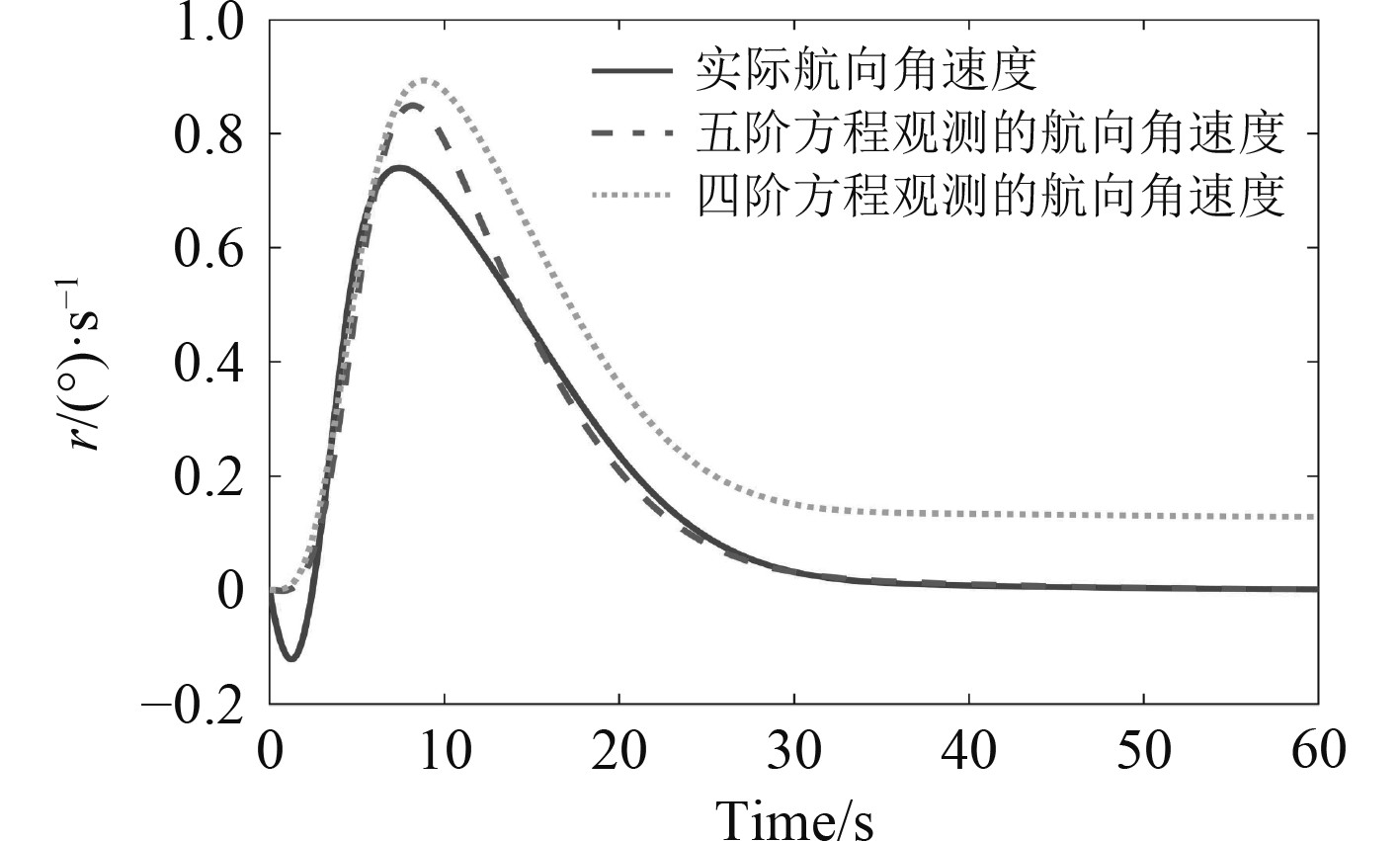
|
图 4 航向角速度观测结果对比图 Fig. 4 Comparison of course velocity observation results |
可以看出,五阶状态方程观测出与实际航向、航向角速度稳定值基本重合,而四阶状态方程观测出的航向值稳定后存在0.6°的静差,航向角速度值稳定后存在0.12°/s的静差,证明本文设计的海浪滤波算法能够在干扰环境下准确的估计出船舶的运动状态。
为了验证本文设计海浪滤波器的航向高频信号滤波能力与无效舵抑制能力,在4级海况下进行定向控制试验,控制器选用传统的PID控制器,航行速度设置为12 kn,500 s时开启海浪滤波器,仿真结果如图5与图6所示。
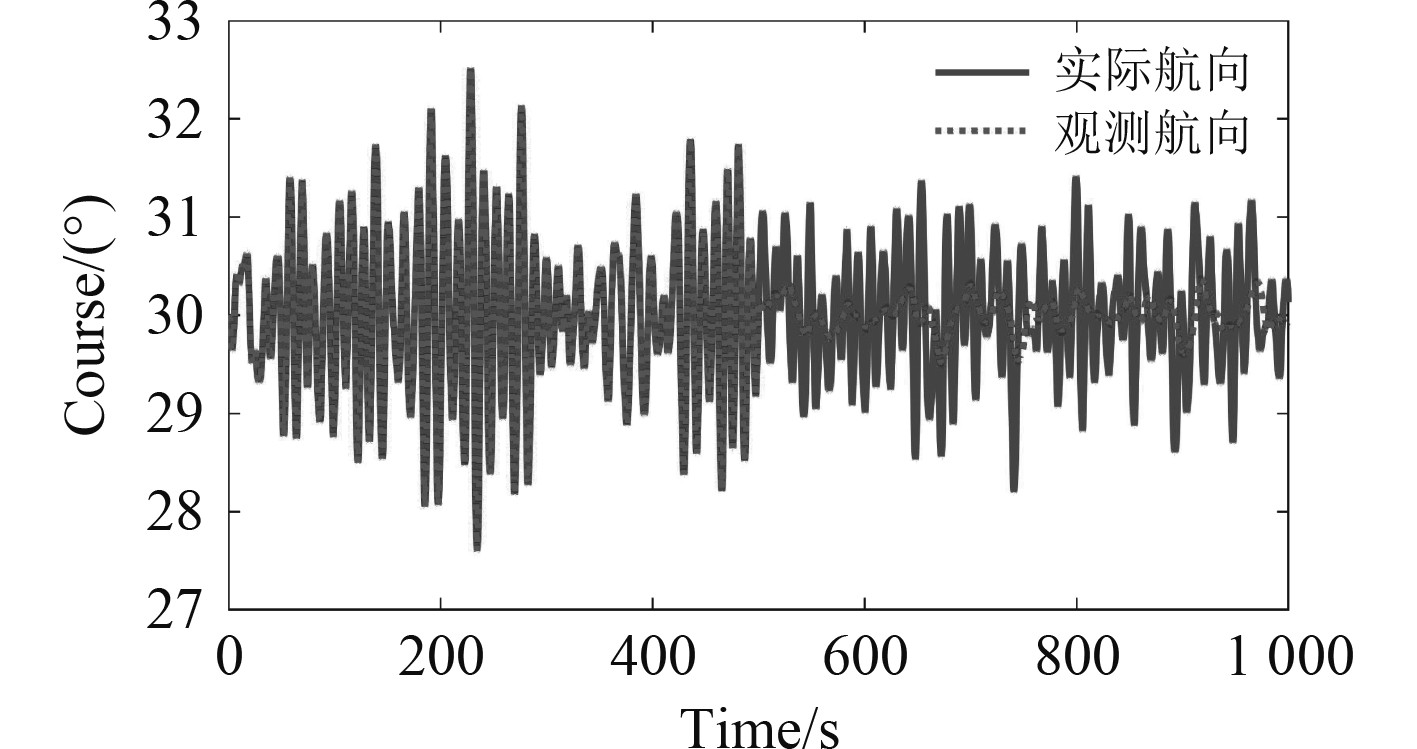
|
图 5 航向角仿真曲线 Fig. 5 Simulation curve of course |
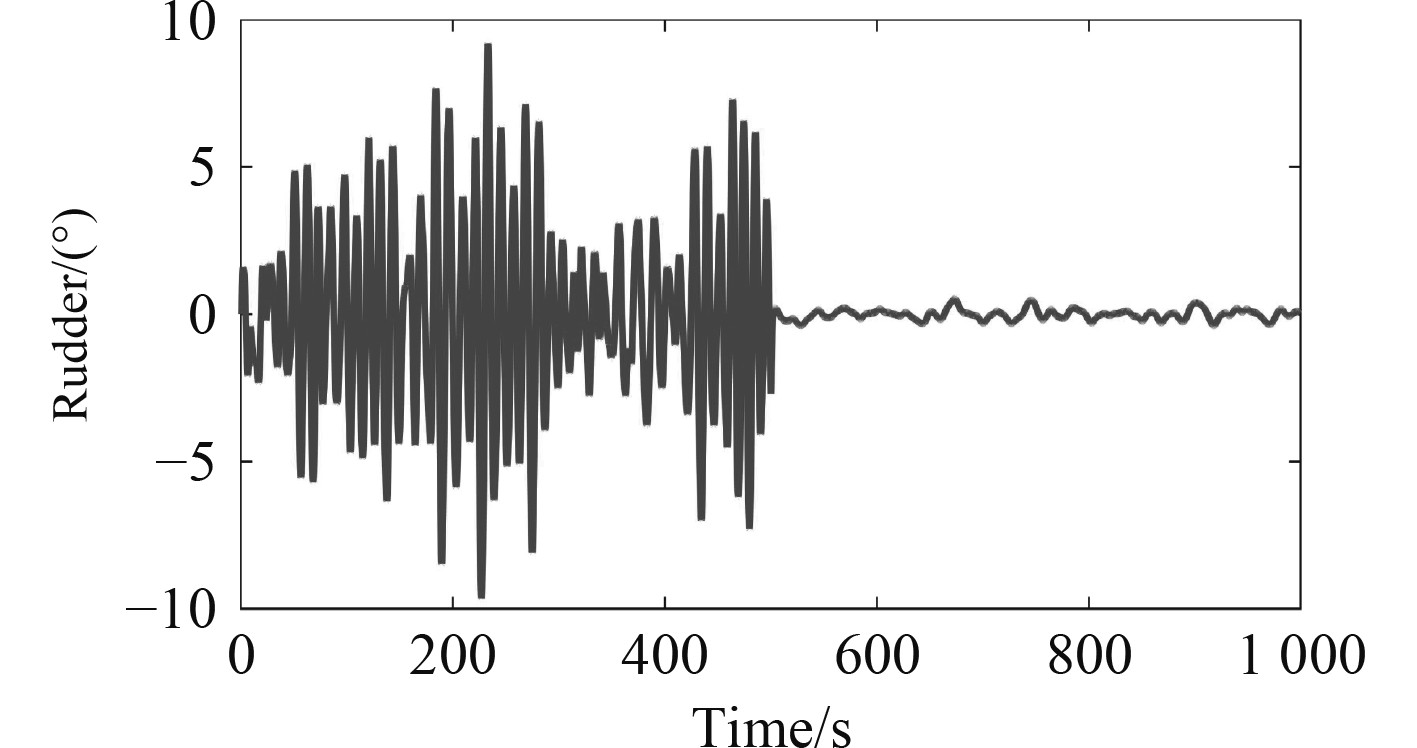
|
图 6 舵角仿真曲线 Fig. 6 Simulation result of rudder |
从图5可以看出,500 s开启海浪滤波器后观测航向的频率与幅度明显降低,达到了航向中由海浪一阶力造成的高频干扰滤除的目的;从图6可以看出,500 s开启海浪滤波器后控制器输出舵角指令的频率与幅度均有明显降低,舵角的均方根由3.28°降为0.19°,证明该方法能够有效地降低控制器产生的无效舵现象。结合图5实际航向仿真曲线可以看出,在无效舵降低的同时航向的控制精度并未发生变化。
4 结 语本文针对海浪干扰下船舶控制系统存在的无效舵问题以及风、流干扰下观测器存在的静差问题,设计一种基于扩张状态卡尔曼滤波的波浪滤波算法,通过构建的五阶扩张状态方程与卡尔曼滤波器结合,同时完成运动状态的误差估计与海浪高频干扰信号的滤除。仿真结果表明,该算法能够有效滤除船舶航向的高频信号并正确的估计出船舶的运动状态,并显著减少了船舶航行时的无效舵问题。
| [1] |
彭秀艳, 胡忠辉. 带有海浪滤波器的船舶航向反步自适应输出反馈控制[J]. 控制理论与应用, 2013, 30(7): 863-868. DOI:10.7641/CTA.2013.21104 |
| [2] |
王元慧, 边信黔, 施小成. 海浪噪声的仿真与滤波[J]. 计算机仿真, 2007, 24(4): 318-321. DOI:10.3969/j.issn.1006-9348.2007.04.086 |
| [3] |
樊冀生, 袁伟, 李文娟. 船舶动力定位自适应滤波器设计[J]. 舰船科学技术, 2017, 39(10): 79-83. DOI:10.3404/j.issn.1672-7649.2017.10.015 |
| [4] |
李杨, 徐雪峰, 赵光. 基于扩展状态观测器的海浪滤波算法及仿真[J]. 中国舰船研究, 2020, 15(1): 1-5. DOI:10.19693/j.issn.1673-3185.01651 |
| [5] |
DO K D, JIANG Z P, PAN J. Global robust adaptive path fllowing of underactuated ships[J]. Automatica, 2006, 42(10): 1713-1722. DOI:10.1016/j.automatica.2006.04.026 |
| [6] |
李奕. 无人艇航向运动控制技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2018.
|
| [7] |
周怡, 王俊雄. 自适应粒子群算法在AUV水动力参数识别中的应用[J]. 舰船科学技术, 2021, 43(11): 90-95. |
| [8] |
FOSSEN T I, PEREZ T. Kalman filtering for positioning and heading control of ships and offshore rigs[J]. IEEE Control Systems, 2009, 29(6): 32-46. DOI:10.1109/MCS.2009.934408 |
| [9] |
FOSSEN T I. Guidance and control of ocean vehicles[M]. Chichester: John Wiley & Sons, 1994.
|
 2023, Vol. 45
2023, Vol. 45
