0 引　言

航行中的船舶在海流、海浪等外界因素的扰动下，船体会发生各种摇荡运动。其中，横摇运动对船舶的安全性、稳定性造成的影响最大，当横摇运动的剧烈程度超过船舶自身的平衡位置时，船体就会出现侧翻、倾覆等严重事故。因此，解决船舶在风浪条件下的稳态特性非常重要。减摇设备作为一种船舶主动提高稳定性的装置，目前在各类船舶上获得了广泛应用，当前使用量最大的减摇设备是减摇鳍，减摇鳍的工作原理基于流体动力学特性，当减摇鳍与流体之间发生相对运动时，流体在减摇鳍表面形成压力差，给减摇鳍一个反向力和力矩，从而抵抗来自海浪和洋流的干扰力^[1]。

减摇鳍尽管应用广泛，但也存在一定的局限性。当船舶在静止或者航速较低的情况下，减摇鳍产生的抵抗力矩非常小，减摇效果不明显。本文针对这一问题进行研究，通过分析减摇鳍的工作原理，采用一种基于嵌入式控制技术的主动式减摇鳍，结合控制理论实现了减摇鳍的主动控制，具有重要的应用价值。

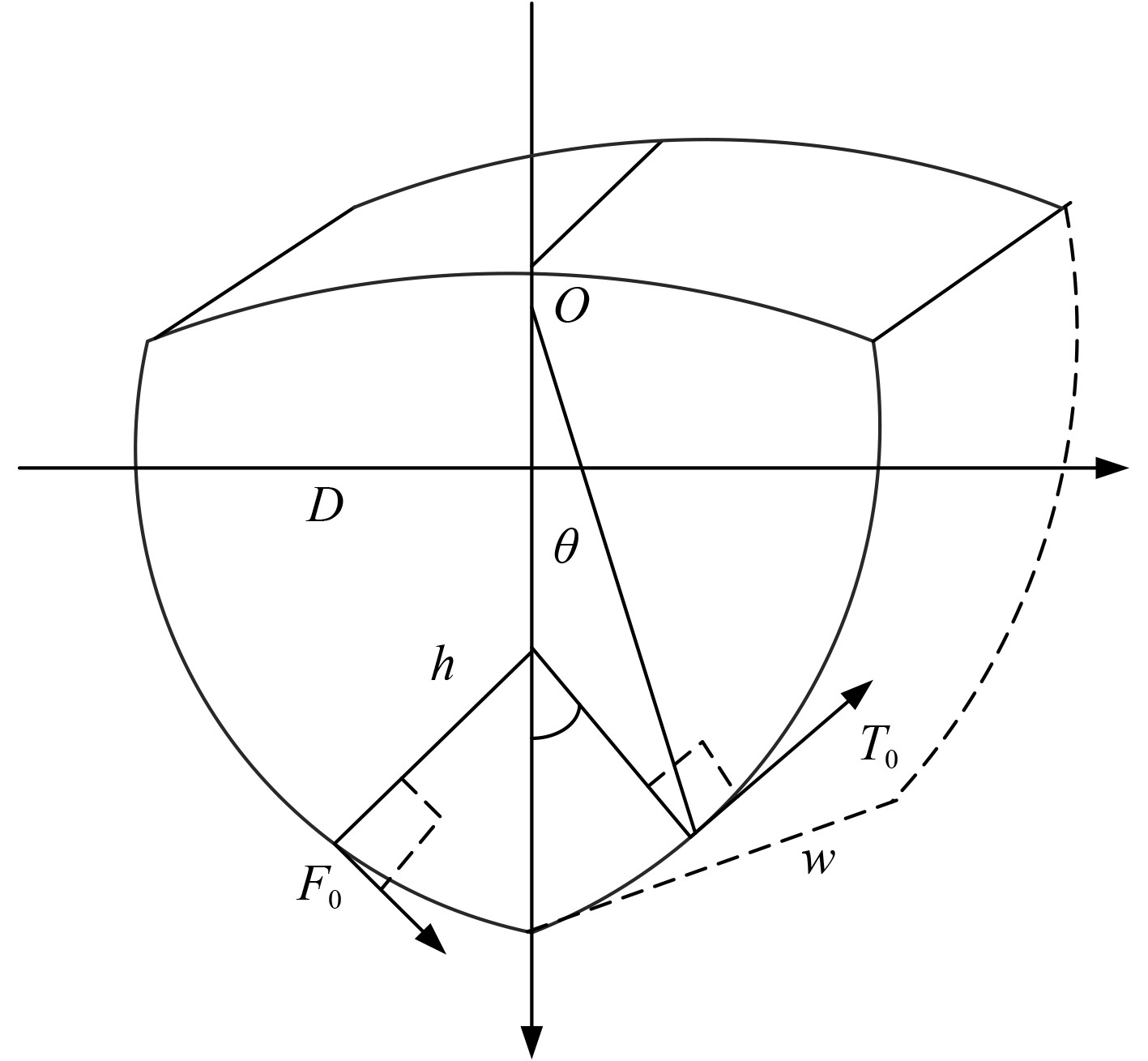
1 船舶横摇运动数学建模与减摇原理分析

船舶的减摇特性与其流体动力学特性密切相关，因此，首先对船舶的横摇运动、力学边界等方面进行研究，建立船舶的力学模型如图1所示。

首先建立船舶运动方程：

$ \left\{ {\begin{aligned} & {\left( {{J_{}} + \Delta {J_{}}} \right)w + 2\kappa w + \frac{1}{2}Dh\theta = {T_0}} \text{，}\\ & {M\dot v\sin \theta + M\dot u\cos \theta = {F_0}} \text{。} \end{aligned}} \right. $

式中：M为船舶质量； $ \dot u $ 和 $ \dot v $ 分别为2个方向的加速度； $ w $ 为船舶角速度； $ \theta $ 为横摇角度； $ h $ 为吃水深度； $ {T_0} $ 为受到的干扰转矩； $ {F_0} $ 为受到的干扰力； $ J $ 为转动惯量； $ \Delta J $ 为附加转动惯量^[2]； $ \kappa $ 为流体阻尼系数； $ D $ 为船宽。

船舶横摇运动的周期按下式计算：

$ T = \sqrt 2 {\text π} \sqrt {\frac{{w + \Delta w}}{{D\sin \theta }}} 。$

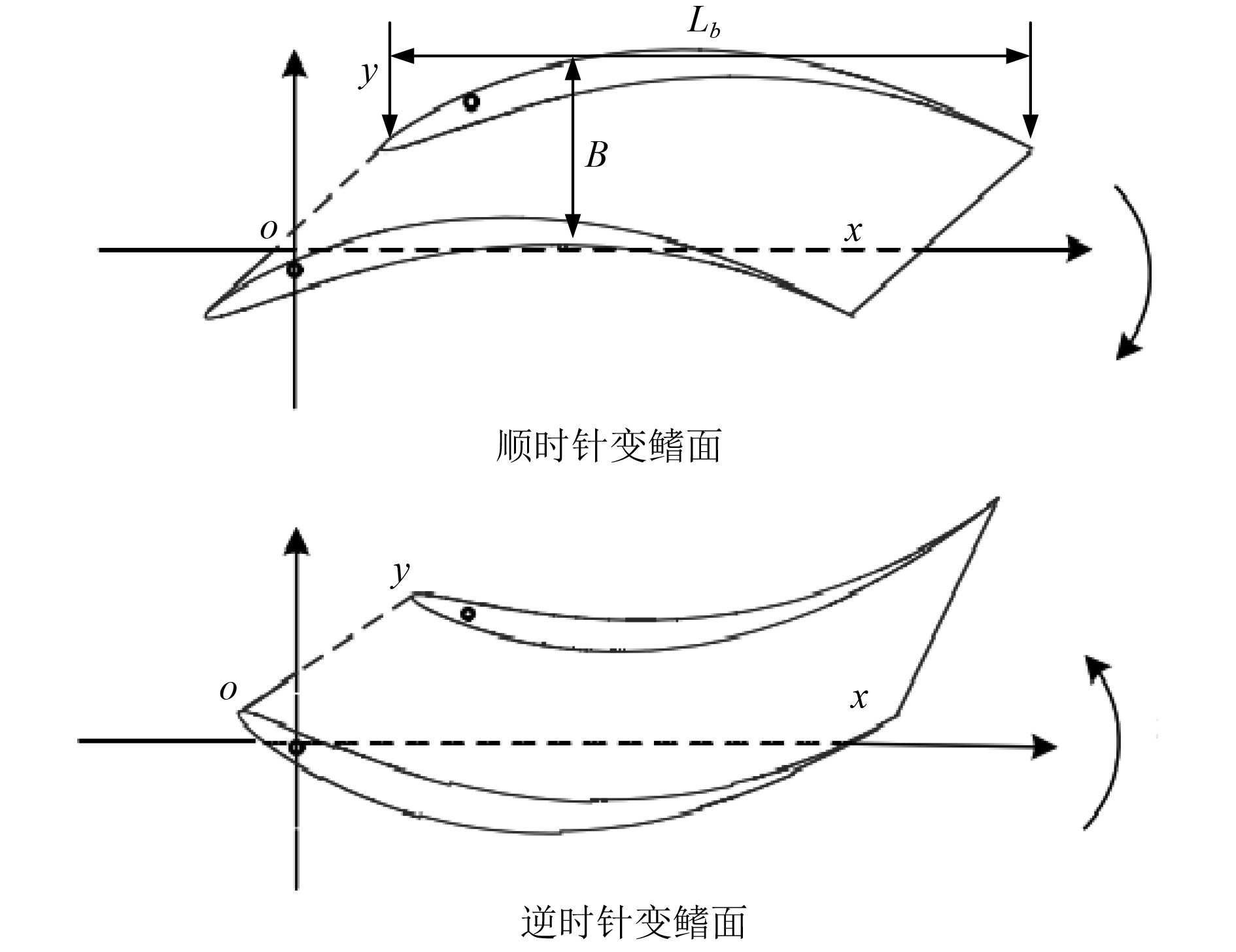
建立减摇鳍的力学模型如图2所示。

减摇鳍受到的波浪弯矩为：

$ {M_o} = \frac{1}{2}{k_1}{k_2}L_b^2B(\delta + 0.8) \cdot {10^{ - 2}}\;{\rm{kN}} \cdot {\rm{m}} \text{。} $

式中： $ L_b^{} $ 为减摇鳍弦长； $ B $ 为宽度； $ \delta $ 为减摇鳍的载重系数， $ \delta \approx 0.5 $ ； $ {k_1} $ ， $ {k_2} $ 为弯矩系数，按照下式计算：

$ {k_1} = 4.5{\left( {\frac{{{L_b}}}{{980}} - 0.2} \right)^2} + 0.82 \text{，} {k_2} = 9 - 0.96{\left( {\frac{{300 - {L_b}}}{{100}}} \right)^2} 。$

减摇鳍受到的扭矩为：

$ {M_n} = {e^{ - 0.00023}}\frac{{{L_b}{B^2}{C_t}}}{{10000}}\left( {1.7 + 1.5\frac{\alpha }{{{h_0}}}} \right) 。$

式中： $ \alpha $ 为扭转角度； $ {C_t} $ 为扭矩系数， $ {C_t} = 0.26 $ ； $ {h_0} $ 为重心位置的深度。

减摇鳍在工作过程中必须要产生与干扰力大小一样，方向相反的效果，定义船舶的速度为 $ {V_1} $ ，海水密度 $ {\rho _0} $ ，由上述力学模型可知，减摇鳍需要产生的反作用力^[3]为：

$ - {F_0} = {F_k} = \frac{1}{2}{\rho _0}S \cdot \delta {V_1}^2 。$

式中： $ S $ 为比表面积； $ \delta $ 为减摇鳍的升力系数，升力系数的大小与减摇鳍的形状和材料有关。

减摇鳍在流体中需要产生的抵抗力矩为：

$ - {T_0} = \sqrt {\left( {{M_0}^2 + {M_n}^2} \right)} = \frac{1}{2}h\sin \theta {F_s}\cos \alpha \text{。} $

2 基于嵌入式控制技术的减摇鳍自适应控制器开发 2.1 嵌入式控制系统设计

传统的减摇鳍是一种被动式的减摇，对船舶速度等因素有较高的要求，针对这一局限性，本文引入一种嵌入式控制的自适应减摇鳍系统，其最大的优势在于通过嵌入式控制器，实现减摇鳍角度和鳍面的变化，调整减摇鳍产生的减摇力和力矩。

图3为基于嵌入式控制技术的减摇鳍自适应控制系统原理。

减摇鳍自适应控制系统的关键组成包括测量元件、控制器、随动系统和辅助部分等。

1）测量元件

测量元件以传感器为主，在船舶减摇控制过程中，为了合理控制减摇鳍鳍面与角度，需要采集船舶的航行速度、加速度、横摇角速度等信号，通常采用角速度陀螺仪等设备^[4]。测量元件采集的信号是减摇鳍嵌入式控制系统的输入信号，信号需要通过积分、噪声过滤等环节。加速度仪具有体积小、精度高的优点，使用加速度仪可以采集船舶横摇运动、航向运动的加速度信号。

除了角速度传感器外，航行速度信号由计程仪设备采集，航行速度信号同样也是减摇鳍嵌入式控制系统的输入信号。

2）嵌入式控制器

嵌入式控制器是系统的核心，通过采集测量元件的信号获取船舶的横摇运动状态，结合内部的控制逻辑与传递函数，得到船舶减摇鳍的最佳控制策略，然后将控制信号发送至船舶减摇鳍随动系统，由电液控制器驱动减摇鳍进行鳍面的变换。

3）随动系统

随动系统是指减摇鳍自适应控制系统的信号前处理和后处理单元，包括测量信号的功率放大、信号噪声滤波等，随动系统必须具有高效、准确的特点，从而保障嵌入式控制器发出的控制指令能够准确和快速的传递至驱动模块，在船舶横摇运动失控之前，调整船舶减摇鳍的鳍面^[5]。

4）辅助部分

主要是指船舶减摇鳍控制系统的电源模块、液压控制回路等，辅助部分也是减摇鳍自适应控制系统不可缺少的部分。

嵌入式减摇鳍控制系统的各环节传递函数如下：

1）横摇运动传递函数

$ {G_\phi }(s) = \frac{{\phi (s)}}{{\alpha (s)}} = \frac{1}{{2.05{s^2} + 0.389s + 1}} \text{。} $

式中： $\phi (s)$ 为横摇角度； $ \alpha (s) $ 为波浪倾角。

2）测量元件传递函数

$ {G_o}(s) = \frac{{400s}}{{{s^2} + 80s + 4000}} 。$

3）随动系统传递函数；

$ {G_Q}(s) = \frac{{{K_Q}}}{{(30s + 1)(0.56s + 1)}} \text{，} $

式中： $ {K_Q} $ 为随动系统的增益。

4）嵌入式控制器的传递函数

$ {G_{qrs}}(s) = {K_p} + \displaystyle\frac{{{K_I}}}{{24.607s + 1}} + \displaystyle\frac{{0.064{K_D}s}}{{(0.064s + 1)(0.18s + 1)}}。$

式中： $ {K_p} $ 为嵌入式系统积分系数； $ {K_I} $ 为嵌入式系统比例系数； $ {K_D} $ 为嵌入式系统微分系数。

图4为嵌入式系统测量元件采集的一段时间内船舶横摇角度曲线。

2.2 主动式减摇鳍的形状设计及仿真

在减摇鳍嵌入式控制系统中，减摇鳍的表面积形状设计方程为：

$ {L^2} = \frac{{3.5\cdot{B_0}\cdot{D_0}}}{{{T^2}\cdot{V^2}}} \text{，} $

式中： $ {B_0} $ 为吃水线上的减摇鳍面宽度^[6]； $ L $ 为吃水线上的减摇鳍长度； $ {D_0} $ 为减摇鳍排水量； $ T $ 为运动周期； $ V $ 为与水流的相对速度。

结合软件程序进行减摇鳍自适应控制系统的性能仿真，采用的减摇鳍参数为B₀= 2.3 m，D₀取105 L，V取50 km/h和60 km/h。仿真边界条件如表1所示。

图5为仿真得到的 $ V $ 取50 km/h和60 km/h两种流体相对速度下的横摇角度控制曲线。从图中可以看出在60 km/h的速度下横摇角度控制更加平顺。

3 结　语

主动式减摇鳍具有更高的灵活性，在实际应用中减摇效果也更好。本文结合嵌入式控制技术，开发了 一种减摇鳍自适应控制系统，从减摇鳍工作原理、自适应控制器原理和仿真等方面进行详细研究。结果表明，该系统能够有效提高船舶横摇运动的稳定性。