助推过程中振动噪声一方面影响水下航行器的安全性,另一方面会影响航行器的水声设备正常工作。对助推过程中振动噪声特性的研究显得尤为重要,以振动特性为依据可以评估助推系统的振动性能[1]、研究振动机理[2]、研究振动控制方法[3-4]。最后可将这些研究结果应用于系统减振降噪以及其它方面的优化设计。
信号处理方法是研究振动特性的常用方法,通常包括时域分析方法、频域分析方法,以及时频分析方法。时频分析方法不仅能够获取振动信号的频谱成分,而且能够获取某一频率成分出现的时间点。常见的时频分析方法有短时傅里叶分析、小波变换、HHT变换、VMD等。VMD方法最早由 Konstantin Dragomiretskiy 等[5]在2014 年提出,大量实践表明该方法在处理非线性非平稳信号时能取得较好的结果。
李占龙等[6]采用VMD方法对含噪声、冲击和间断信号这3类典型的非平稳信号进行分解,并结合Teage算子对分解得到的IMF信号进行解调得到瞬时的时频图。结果表明VMD方法抗混叠性能较好。杨宗林等[7]利用GA-PSO算法对VMD算法中所需要预设的模态个数与惩罚因子进行了优化。柳絮等[8]结合HHT和VMD对某海上平台进行振动分析。刘长福等[9]结合VMD和FFT算法提取了颤振动特征。将VMD方法应用到助推过程并进一步分析振动源和振动传递等特性研究尚不充分。
本文基于变分模态分解方法结合希尔伯特黄变换[10]分析系统助推时振动信号的时频分布情况,基于时频分布结果进一步分析振动源类别、振动传递特性。以所得到的振动特性为依据,结合主动[11]或半主动方法[12]抑制振动,在振动传递过程中对振动进行控制[13-14]、对各低频[15-16]或高频振动源提出针对性强的控制方法,综合评估系统的振动性能。
1 变分模态分解理论变分模态分解方法是建立在维纳滤波、希尔伯特变换、解析信号、频率混合和外差解调基础上,在给定的变分模型下进行迭代从而将输入的实信号
实信号
基于以上理论,对于每个
| $ \begin{split}\mathop {\min }\limits_{\left\{ {{u_k}} \right\},\left\{ {{\omega _k}} \right\}} &\alpha \left\{ {\sum\limits_k {\left\| {{\partial _t}\left[ {\left( {\delta \left( t \right) + \frac{j}{{\pi t}}} \right) . {u_k}\left( t \right)} \right]{e^{ - j{\omega _k}t}}} \right\|_2^2} } \right\} +\\ &\left\| {f\left( t \right) - \sum\limits_k {{u_k}\left( t \right)} } \right\|_2^2 + \left\langle {\lambda \left( t \right),f\left( t \right) - \sum\limits_k {{u_k}\left( t \right)} } \right\rangle \end{split},$ | (1) |
| $ {\rm{s}}.{\rm{t}}.\sum\limits_k {{u_k} = f} 。$ | (2) |
式中,
对于
| $ \hat {u} _k^{n + 1}\left( \omega \right) = \frac{{{f\left( \omega \right) -\displaystyle {\sum}_{i \ne j} { {{\hat{u_i}}^{\left( \omega \right)}} + {\dfrac{{\lambda}}{2}} }} }}{{1 + 2\alpha {{\left( {\omega - {\omega _k}} \right)}^2}}} ,$ | (3) |
对于
| $ \omega _k^{n + 1} = \mathop {\arg \min }\limits_{{\omega _k}} \left\{ {\int_0^\infty {{{\left( {\omega - {\omega _k}} \right)}^2}} \left| {\mathop {{\hat{u_k}}\left( \omega \right)}\limits^ \wedge } \right|d\omega } \right\} ,$ | (4) |
| $ \omega _k^{n + 1} = \frac{{\displaystyle\int_0^\infty {\omega {{\left| {{{\mathop u\limits^ \wedge }_k}\left( \omega \right)} \right|}^2}{\rm{d}}\omega } }}{{\displaystyle\int_0^\infty {{{\left| {{{\mathop u\limits^ \wedge }_k}\left( \omega \right)} \right|}^2}{\rm{d}}\omega } }} ,$ | (5) |
| $ {\lambda ^{n + 1}} \leftarrow {\lambda ^n} + \tau \left( {f - \sum\limits_k {u_k^{n + 1}} } \right) ,$ | (6) |
迭代收敛的准则如下式:
| $ {{\sum\nolimits_k {\left\| {u_k^{n + 1} - u_k^n} \right\|} _2^2} \mathord{\left/ {\vphantom {{\sum\nolimits_k {\left\| {u_k^{n + 1} - u_k^n} \right\|} _2^2} {\left\| {u_k^n} \right\|}}} \right. } {\left\| {u_k^n} \right\|}}_2^2 < \varepsilon 。$ | (7) |
其中,
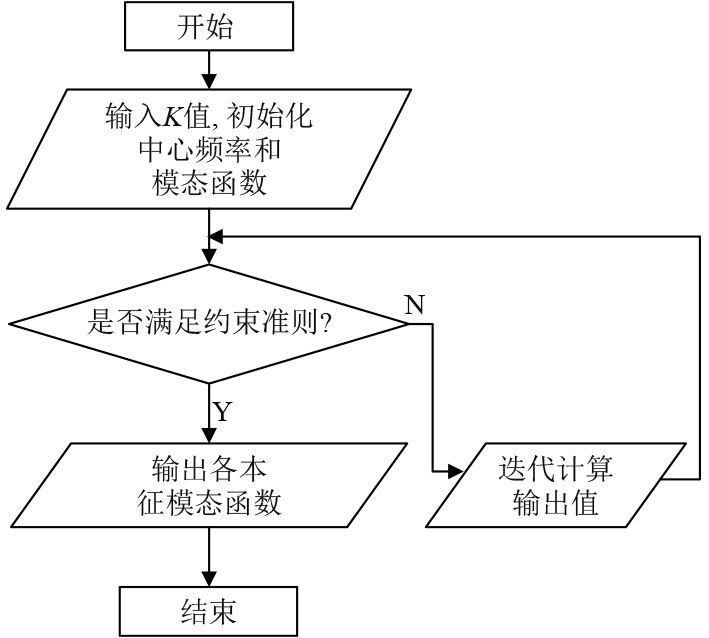
算法的主要流程为:初始化本征模态函数
|
图 1 VMD算法流程 Fig. 1 VMD algorithm flowchart |
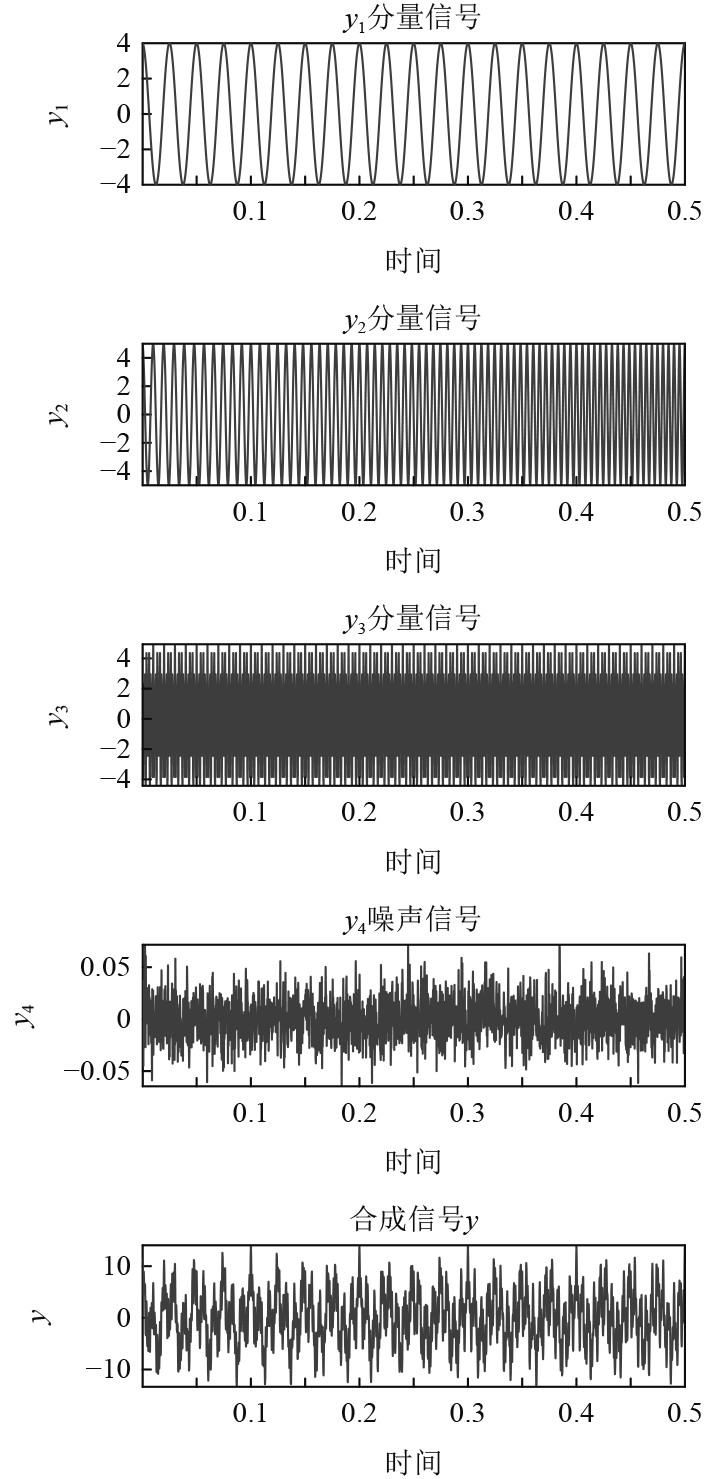
仿真信号由3个信号加上噪声组成:
|
图 2 仿真信号时域图形 Fig. 2 Simulation signal time domain graphics |
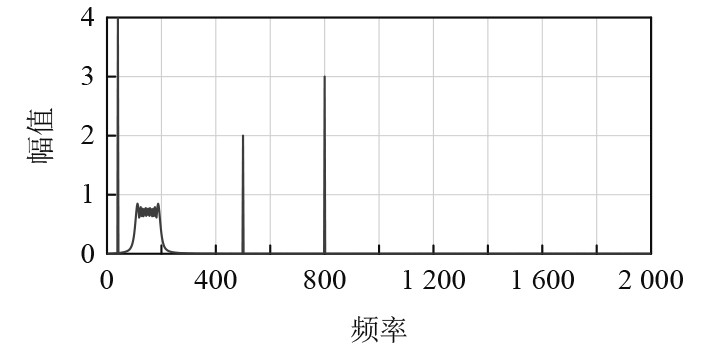
采用快速傅里叶变换方法对仿真信号
|
图 3 仿真信号fft频率-幅值图 Fig. 3 Frequency-amplitude diagram of simulation signal |
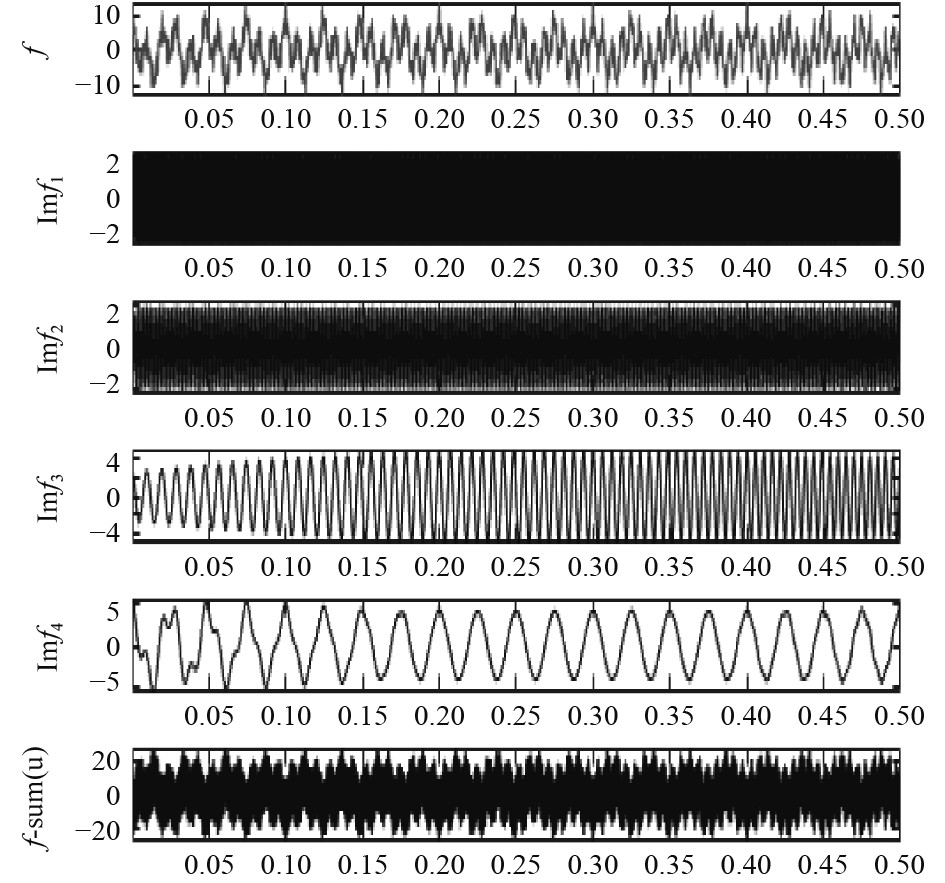
采用VMD方法对仿真信号进行分解,由图3可得仿真时模态数量
|
图 4 分解后的原始信号与本征模态函数信号 Fig. 4 Diagram of original signal and IMFs |
对分解后得到的各本征模态函数与原仿真信号做对比,imf1和imf2对应于分量信号
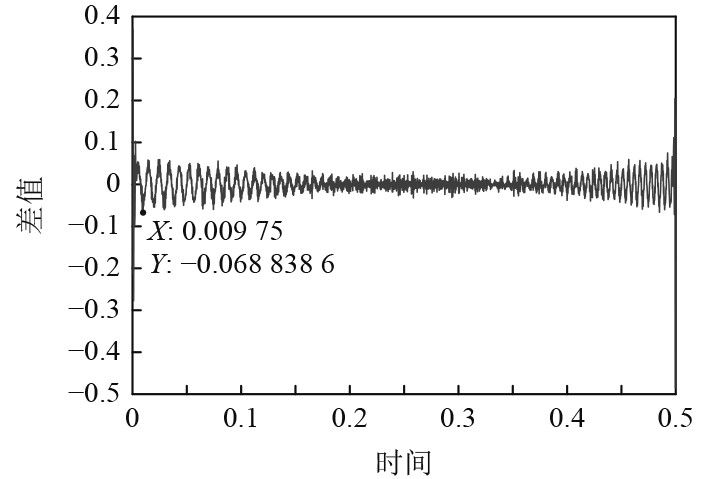
|
图 5 合成信号与原始信号误差 Fig. 5 Error between synthetic signal and original signal |
基于VMD方法对本征模态函数做HHT变换得到的时频分布如图6所示。
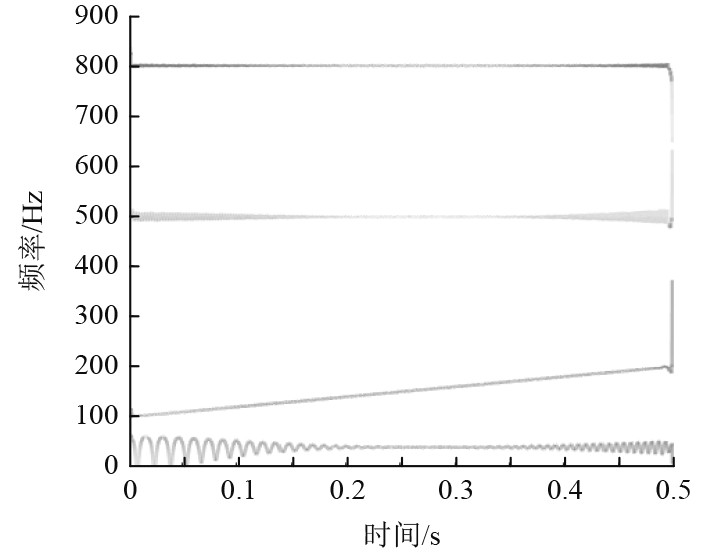
|
图 6 原始信号时频分布图 Fig. 6 Original signal time-frequency distribution |
实验系统组成如图7所示。实验时在保证其他条件一样的情况下,助推系统动力源提供的动力大小分别设置为3 MPa,5 MPa,7 MPa。
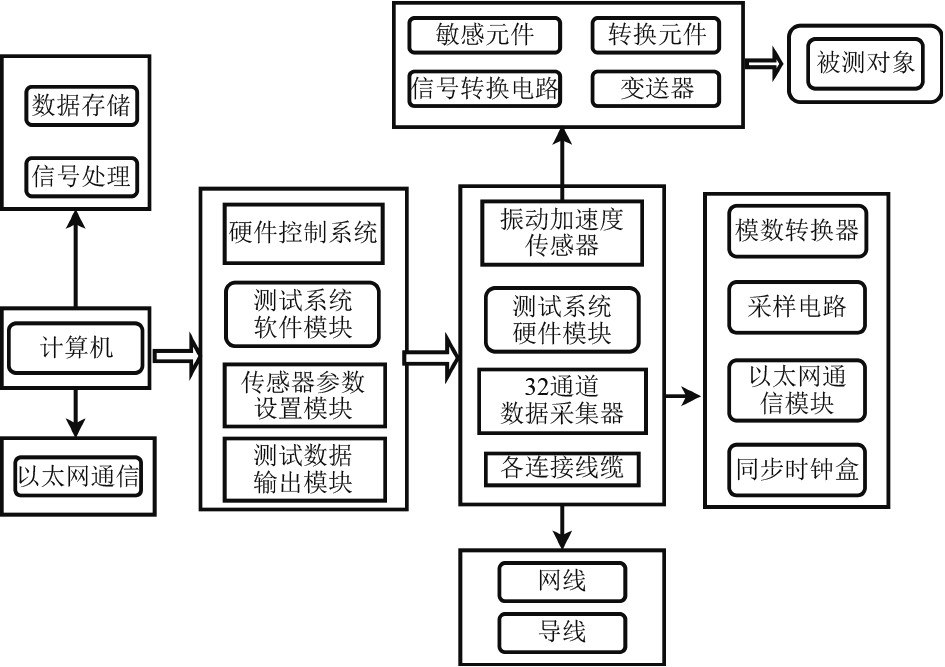
|
图 7 测试系统组成 Fig. 7 Test system composition |
实验获取了旋转机械1、减速器、旋转机械2、航行器器壁处振动信号。由于助推系统安装在航行器上,连接处的振动会经过航行器向外传递,实验时也测取了连接处的振动信号。
4 振动信号时频分布旋转机械1振动信号时频分布如图8所示。
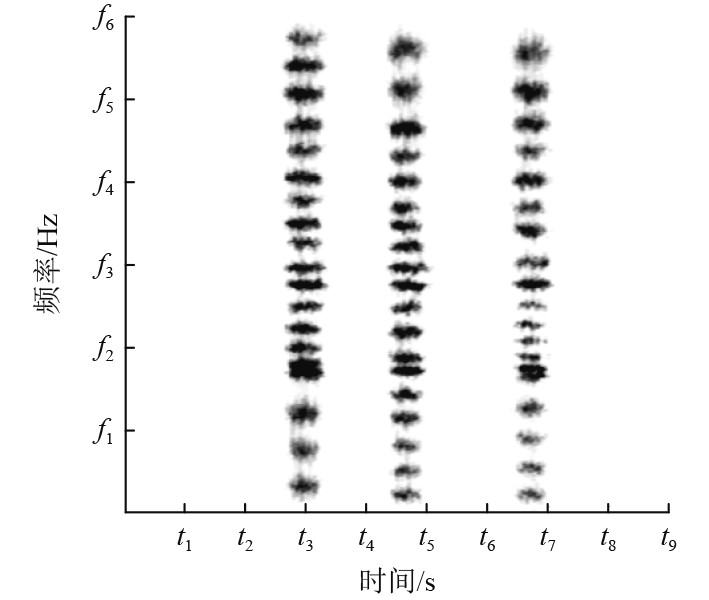
|
图 8 测试系统实物图 Fig. 8 Physical picture of the test system |
减速器振动信号时频分布如图9所示。
|
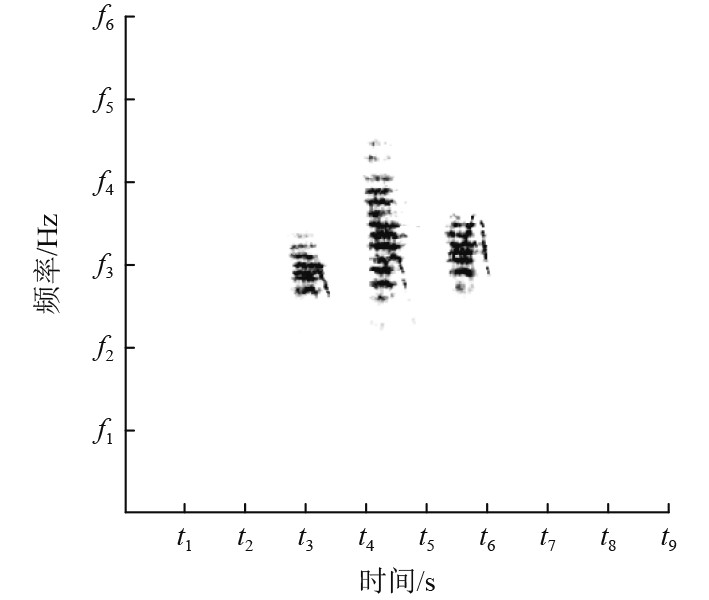
图 9 旋转机械1振动信号时频分布 Fig. 9 Time-frequency distribution of rotating machinery 1 vibration signal |
旋转机械2振动信号时频分布如图10所示。
|
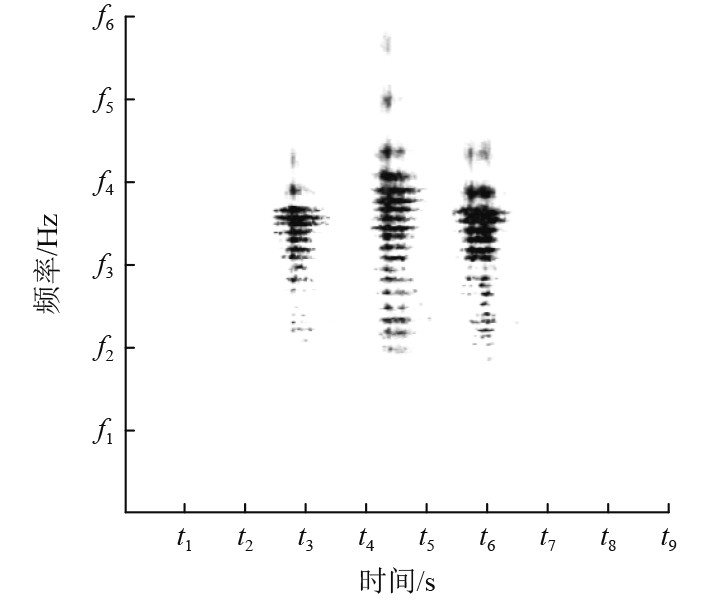
图 10 减速器振动信号时频分布 Fig. 10 Time-frequency distribution of reducer vibration signal |
助推系统与航行器连接处振动信号时频分布如图11所示。
|
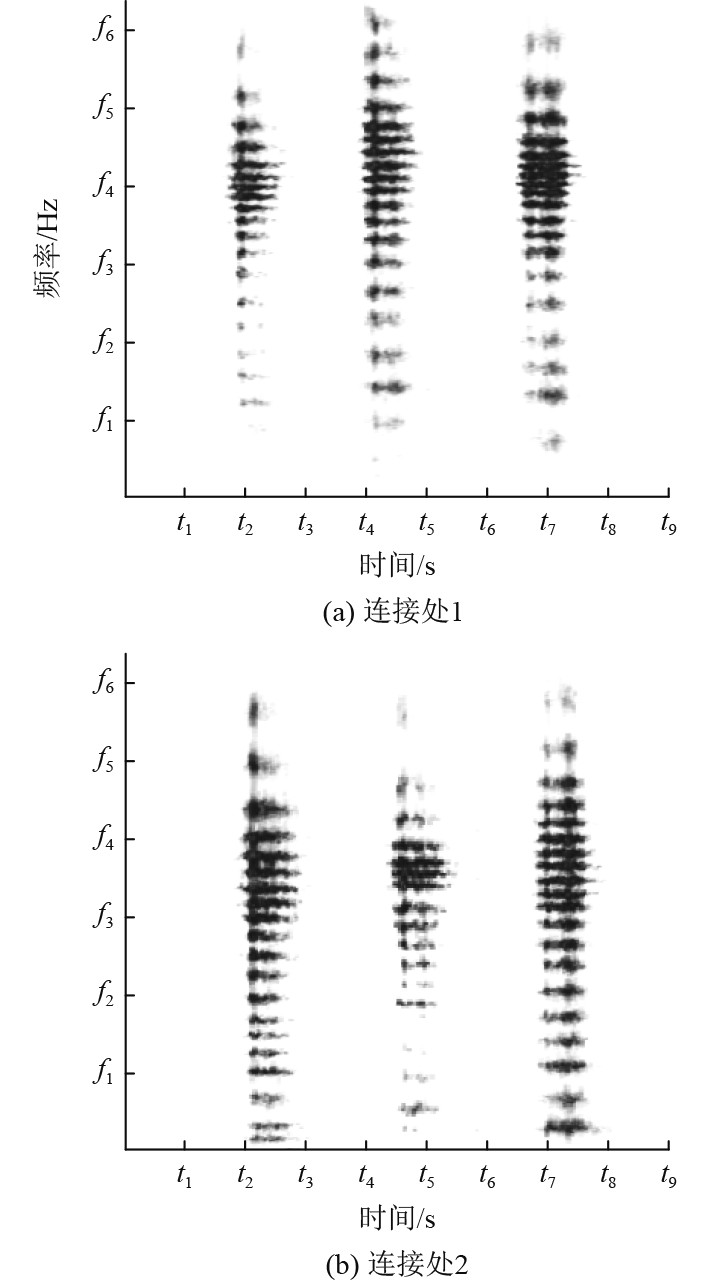
图 11 旋转机械2振动信号时频分布 Fig. 11 Time-frequency distribution of rotating machinery 2 signal |
|
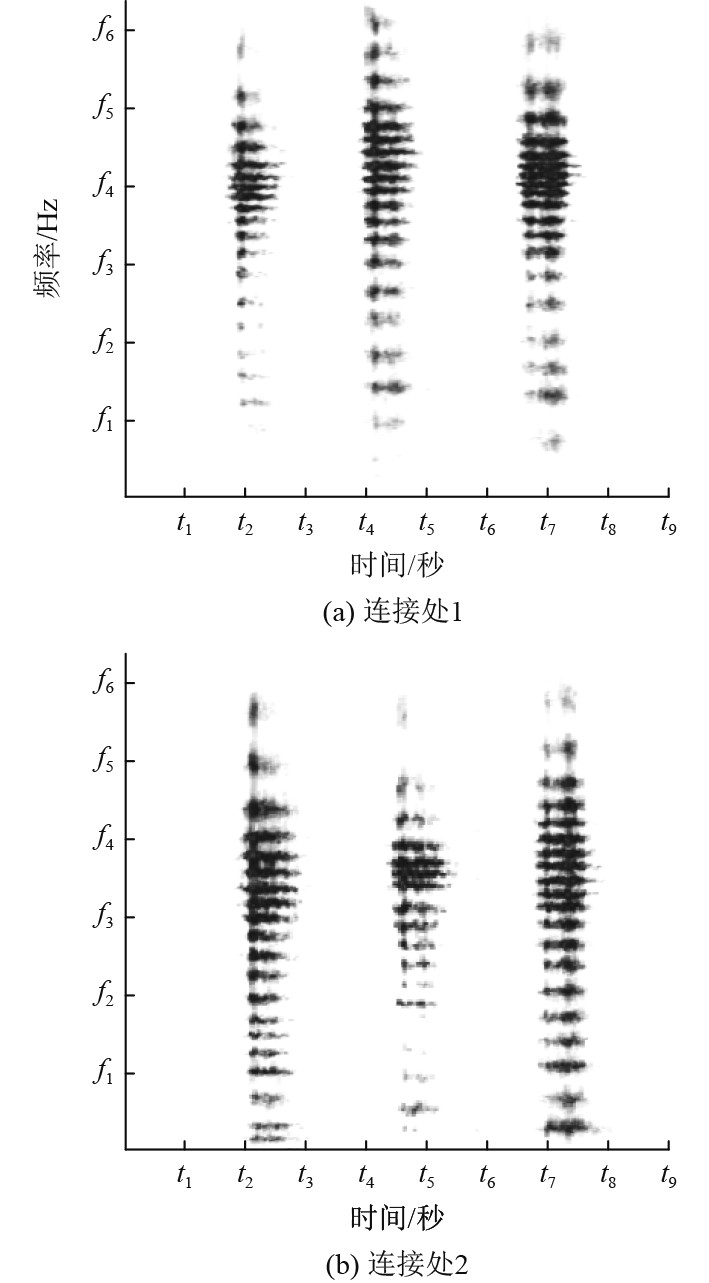
图 12 助推系统与航行器连接处振动信号时频分布 Fig. 12 Time-frequency distribution of signals at the connection between the boost system and the vehicle |
旋转机械1振动频率分布范围较广,主要集中在0~f6 Hz之间,低频成分主要集中在f1 Hz以下。频率较强的成分分布情况表1所示,从表中可以看出在所给出的3种工况下旋转机械1振动信号频率分布范围基本一致,较强的频率成分分布大体一致,相差较小。
|
|
表 1 旋转机械1较强频率成分分布表 Tab.1 Stronger frequency component distribution of rotating machinery 1 |
减速器振动信号频率主要集中在f2~f3 Hz之间,振动频率相对集中,频率较强的成分分布如表2所示。工况1和工况3下减速器振动信号频率分布范围较为接近,较强的频率成分分布也较为一致。工况2下减速器振动频率分布范围较广,主要分布在f2~f4之间,较强的频率成分值比工况1和工况3高。
|
|
表 2 减速器较强频率成分分布表 Tab.2 Stronger frequency component distribution of reducer |
旋转机械2振动信号频率主要分布在f2~f4之间,频率成分较强的分布在f3~f4之间,工况2下对应的最强振动频率值最大,不存在f1以下的低频信号。旋转机械2振动信号较强频率成分分布如表3所示。
|
|
表 3 旋转机械2较强频率成分表 Tab.3 Stronger frequency component distribution of rotating machinery 2 |
助推系统与航行器连接处1振动信号较强频率成分分布如表4所示,较强的频率成分主要分布在f4附近。从时频分布图中可以看出,工况压力与较强的频率值之间没有严格的对应关系,即助推时压力增大对应的最强的频率成分值不一定增大。
|
|
表 4 连接处1较强频率成分表 Tab.4 Stronger frequency component at joint 1 |
助推系统与航行器连接处2振动信号较强频率成分如表5所示。振动频率主要集中在0~f6之间,频率分布范围较广,存在较多的低频振动信号。7 MPa时的低频振动信号较5 MPa时更多。
|
|
表 5 连接处2较强频率成分表 Tab.5 Stronger frequency component at joint 2 |
由于低频振动衰减较慢,对振动源分析析时主要关心低频振动。从图8以及图11(b)可看出,f1以下的低频振动主要来源于旋转机械1以及航行器器壁振动。
旋转机械1等流体机械的振动主要有转子的不平衡带来的振动以及流致振动。流致振动主要由流体与壁面的结构耦合、回流、脱流、空化、流动失稳、流体对壁面的冲击等造成。从低频振动信号分布时间来看,转子转速较高,其造成振动的频率也较高,由此可知低频部分主要是由流致振动引起的。航行器器壁振动是低频振动的又一来源,主要由流体的冲击以及振动传递造成。
对f2~f4的中频振动,各子系统对该频段的振动均有贡献,但在该频段内各系统较强成分的有差别。对f5以上的高频振动,振动源主要为旋转机械1以及航行器器壁。
6.2 传递特性分分析实际系统中旋转机械1和减速器连接,从图9可看出,在减速器上未检测到相应的低频信号,主要是由于旋转机械1低频振动较弱。减速器上未检测到f5以上的高频信号,主要与高频信号的衰减速度有关。
从图11可以看出,连接处的低频振动主要由航行器器壁传递而来。其中7 MPa下低频振动最强。连接处高频振动一方面由旋转机械2传递而来,另一方面航行器器壁振动传递而来。
7 结 语本文首先基于变分模态分解和希尔伯特变换得到了助推系统中旋转机械1、减速器、旋转机械2、航行器连接处振动信号的时频分布情况。以振动信号时频分布情况为依据,进一步分析了助推系统的振动源构成情况、振动传递特性。
旋转机械1的振动频率最强的成分均分布在f3附近,最强振动频率之间差距较小在60 Hz内。旋转机械1是低频振动的重要来源,但是旋转机械1低频振动较弱,传播距离有限。减速器振动最强的频率成分集中在f3附近,工况1和工况3的最强振动频率值相差较小。
旋转机械2振动最强的频率成分集中在f4附近,不同工况之间相差50~591 Hz。旋转机械2与航行器连接处振动频率较强的成分集中在f3~f4附近。不同工况之间相差281~846 Hz。连接处2振动频率最强的成分主要集中在f3~f4之间,器壁的振动是低频振动的另一个来源。结合旋转机械1和器壁低频振动的传递路径上的测点振动信号来看,器壁的低频振动强度比旋转机械1的强。
同一子系统不同工况下对应的最强振动频率值有差别,但是总体上差别不大,最强的振动频率值差值在10~846 Hz之间。对同一子系统,助推压力增大时对应的最强振动频率值不一定增大。从振动源构成的角度讲,低频振动控制将重点放在旋转机械1和航行器器壁。从振动传递特性角度讲,需将减振降噪设计应用于如连接处这样振动传递效率较高的地方。
| [1] |
孟庆成, 何翰林, 张梦宇, 等. 高架候车厅车致振动特性及减振控制研究[J]. 噪声与振动控制, 2021, 41(1): 177–183.
|
| [2] |
宋超, 赵岩, 刘江涛, 等. 弹性支撑对多跨梁结构振动特性的影响[J]. 舰船科学技术, 2020, 42(10): 17-22. DOI:10.3404/j.issn.1672-7649.2020.10.004 |
| [3] |
赖俊杰, 浮洁, 白俊峰, 等. 精密加工平台隔振系统多频振动控制[J]. 振动与冲击, 2019, 38(10): 242–248.
|
| [4] |
廖锦鹏, 涂建维, 张家瑞, 等. 基于实时频率识别的调频 TMD竖向振动控制试验研究[J]. 武汉大学学报(工学版), 2021, 54(12): 1119-1125. |
| [5] |
KONSTANTIN D, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Pro-cessing, 2014, 62(3): 531-544. DOI:10.1109/TSP.2013.2288675 |
| [6] |
李占龙, 刘林霞, 李虹, 等. 基于 VMD-Teager 的非平稳振动时频特性研究[J]. 兵器装备工程学报, 2021, 42(1): 150-156. DOI:10.11809/bqzbgcxb2021.01.028 |
| [7] |
杨宗林, 熊继军. 参数优化VMD在爆破振动信号分析中的应用[J]. 中北大学学报(自然科学版), 2020, 41(5): 467-473. |
| [8] |
柳絮, 王坚, 李文. 集成变分模态分解和希尔伯特-黄变换的结构振动时频提取模型[J]. 武汉大学学报·信息科学版, 2021, 46(11): 1686-1692. DOI:10.13203/j.whugis20200646 |
| [9] |
刘长福, 朱立达, 仇健, 等. 基于 VMD 和 FFT 的变切深侧铣颤振特征提取方法[J]. 东北大学学报 (自然科学版). 2018, 39(8): 1154–1157.
|
| [10] |
HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[J]. Proceedings Mathematical and Engineering Science, 1998, 454(1971): 903-995. |
| [11] |
LAI Tao, LIU Jun-feng. Active vibration control of a ro-tor-bearing-actuator system using robust eigenvalue placement method[J]. Measurement and Control, 2020, 53(3): 531-540. |
| [12] |
邢昭阳, 申永军, 刘树勇, 等. 一种半主动负刚度动力吸振器[J]. 振动与冲击, 2021, 40(15): 124–136.
|
| [13] |
HE Shuilong, TANG Tao, Mingsong YE, et al. A multi-point iterative analysis method for vibration control of a steering wheel at idle speed[J]. IEEE Access 2017, 7: 88399–88417.
|
| [14] |
段勇, 郭君, 周凌波. 隔振技术在水下航行器推进轴系振动控制中的应用[J]. 水下无人系统学报, 2018, 26(1): 70–77.
|
| [15] |
王同梦, 柴凯, 刘树勇, 等. 准零度刚度隔振器设计及振动控制技术[J]. 船舶工程, 2022, 44(s01): 352-359. |
| [16] |
YAN Li-xun , GONG Xing-long. Experiment study of vibration isolation characteristics of a geometric anti-spring isolator[J]. Applied Science, 2017, 7(7): 1–20.
|
| [17] |
TIKHONOV A. N. Solution of incorrectly formulated problems and the regularization method[J]. Soviet Mathematics Doklady. 1963, 4: 1035–1038.
|
 2023, Vol. 45
2023, Vol. 45
