2. 英辉南方造船(广州番禺)有限公司,广东 广州 511431;
3. 上海船舶运输科学研究所,上海 200135
2. Afai Southern Shipyard(Panyu Guangzhou) Co., Ltd., Guangzhou 511431, China;
3. Shanghai Ship and Shipping Research Institute, Shanghai 200135, China
对于高速双体客船而言,其快速性对旅途时间(乘客体验)及造船成本(推进设备选型)有较大影响,是方案设计阶段船东最为关注的性能之一。设计方为了提高其自身竞争力,往往需要在短时间内完成多工况的航速预报计算,进而提供多套快速性配置方案供船东抉择。实船阻力预报的方法主要有水池模型试验、数值模拟和实船试航,相较于模型试验的巨大花费和时间成本以及实船试航结果样本的有限性,实尺度数值模拟计算的方便和迅捷得到了设计方的青睐,但其计算精度一度被大家怀疑。为了验证实尺度数值模拟计算在某高速双体客船应用的可行性,本文选取典型的试航工况,采用重叠网格和六自由度模型(DFBI)开展实尺度的数值模拟计算,并将计算结果分别与实船试航结果和水池模型试验结果对比,得到了预期结果。
1 获取实船阻力的方法 1.1 模型试验采用一定缩尺比的船体模型进行阻力拖曳试验获得模型阻力,利用传统的换算方法进行实船阻力换算是实船阻力预报的常用方法之一[1-2]。较为常用的换算方法有2种,分别是二因次换算法(又称傅汝德换算法)和三因次换算法(又称1+K法)[3]。
二因次换算法是基于傅汝德假设,将船舶总阻力划分为摩擦阻力和剩余阻力2个组成部分。这种方法认为船舶受到的摩擦阻力只与雷诺数有关,而剩余阻力仅与傅汝德数有关,这在理论上不太妥当,实际运用较少。三因次换算方法的主要观点是将粘压阻力与摩擦阻力合并称为船舶的粘性阻力,这种换算方法在业界得到广泛运用,其实船的阻力系数可表达为:
实尺度的数值模拟一直以来得到了业界的普遍重点关注,也是被公认为最有发展前景的技术方法之一。相较于传统拖曳水池的模型试验和模型尺度下的数值模拟,实尺度数值模拟能同时满足傅汝德数和雷诺数相等,避免了尺度效应,目前在理论上也暂时没发现明显缺陷,在集装箱船、散货船、油船等低速船上应用较广,对于高速船尤其是高速双体船而言,由于其傅汝德数较高,其实尺度计算比常规低速船要复杂一些。为了获得较为可观的计算精度,需格外注意网格质量(网格的数量及划分方式)、壁面函数(Y+)的设置和时间步长的选取。
1.3 实船试航为了验证新建造船舶的合同航速,船厂、船东、船检往往会开展设计装载状态下的实船试航。相较于静水条件,试航中真实的海况包含风、浪、涌等环境因素,这在一定程度上会影响实船试航结果。所以,需要对试航中的速度进行航速修正以便将实际海况中的试航航速修正到无环境风、无浪、无涌、无限水深的真实航速[4-7]。关于实船试航的航速修正方法,ISO 15016:2015[8] 是国际海事组织(IMO)指定的实船航速修正标准之一,也是目前业界接受且较为常用的修正方法。
2 计算实例本次算例的计算分别满足连续性方程和动量守恒定律。其中湍流模拟的方法采用常用的Reynolds平均法,湍流模式则采用经典的Realizable k-ε模型。计算期间,通过设置VOF模型对计算船型的自由液面进行精确捕捉。为了贴近实船航行的流场,提升计算输出数据的精度,通过设置重叠网格和六自由度模型(DFBI)实现对实船航行姿态和阻力的精确预报。
2.1 船舶信息及主要船型参数该船主要航行于我国沿海航区,为典型的高速双体船型。这种船型的主要特点:甲板面积较大(适合载客)、排水量小(快速性好)、吃水较浅(同时适用浅水航道),水线下的片体部分往往十分尖瘦、设计航速一般为30 kn以上,主要船型参数如表1所示。
|
|
表 1 船型参数 Tab.1 Ship form parameters |
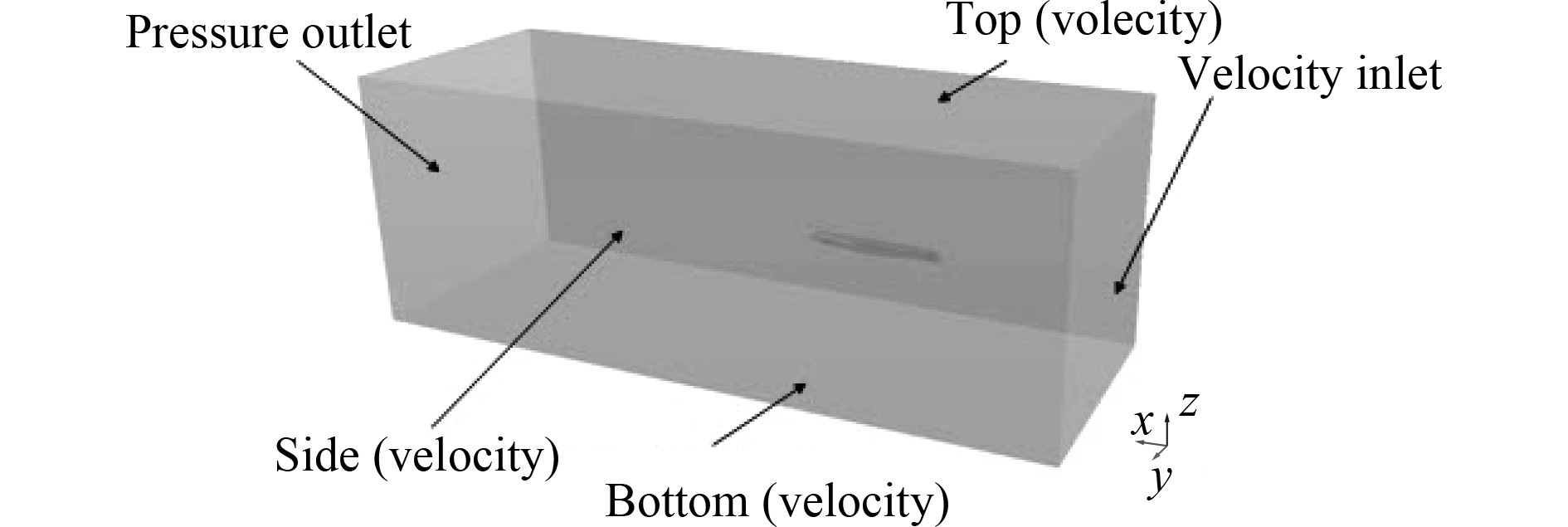
与低速船的流场相比,高速双体船的尾流较长,且需考虑计算干舷甲板以上部分的风阻,故在船尾以后(船长方向)和干舷甲板以上(型深方向)保留足够长度的计算域。本船的计算域为−1.5Lwl≤x≤5.0Lwl,0.0Lwl≤y≤1.5Lwl和 −1.5Lwl≤z≤2.0Lwl,计算域如图1所示。其中Velocity inlet,Top,Side,Bottom的边界条件为基于水气VOF组分的平坦波速度入口;Pressure outlet的边界条件为基于水气VOF组分的平坦波压力出口;船体及上层建筑部分的边界条件则为无滑移壁面。为了防止由于船舶航行过程中造成的自由表面兴波波形的反射,在计算域的Velocity inlet,Side,Pressure outlet边界分别设置了数值消波岸进行处理,以免影响计算精度或造成计算发散。
|
图 1 计算域 Fig. 1 Computing domain |
在实尺度数值模拟计算中,第1层边界层厚的选取往往对于计算精度产生较大影响。为了方便取值,通常采用用壁面函数(Y+)来进行计算:Y+=0.172ΔypRe0.9/L,其中L为特征长度,Re为雷诺数,由此可以快速计算出第1层边界层网格的厚度。对于高速双体船的实船计算而言,目前建议采用的Y+范围是30~300[9]。船壳处生成的边界层网格如图2所示。

|
图 2 边界层网格划分 Fig. 2 Boundary layer meshing |
数值计算中的网格是几何域的离散表现形式,良好的网格划分和网格质量是数值模拟的前提条件,也是提高计算精度的保证。采用STAR-CCM+对双体船的船体和上层建筑表面进行曲面重构(surface remesher),然后生成边界层网格(prism layer mesh)、切割体网格(trimmed mesh)和包面体网格(wrapped mesh)3种类型的体网格。为了更好捕捉空气与水的交界面,应用控制体积对凯尔文波系范围(19°28')内的域加密,如图3所示。

|
图 3 波形加密 Fig. 3 Waveform encryption |
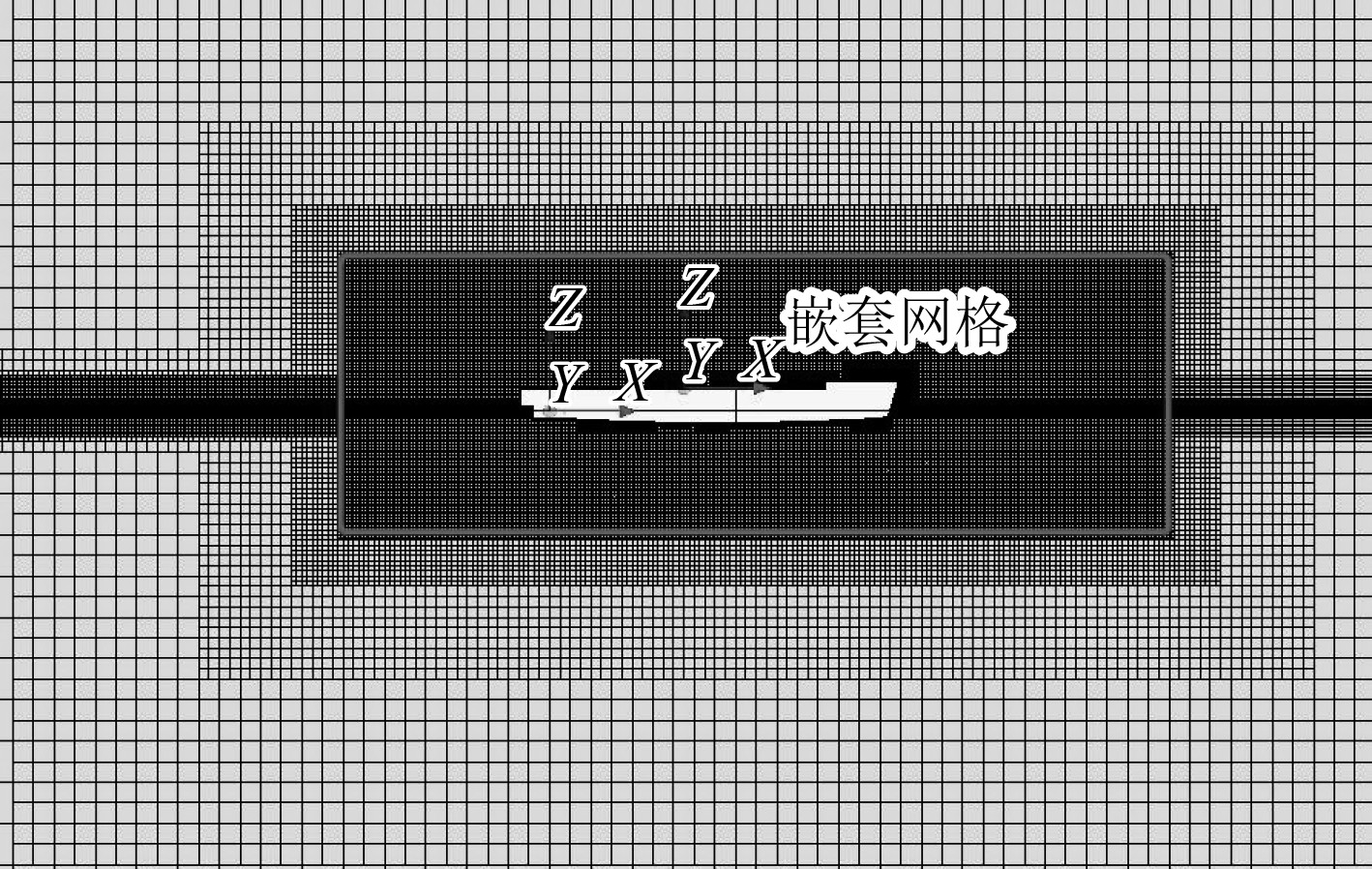
在自由度开放的计算条件下,高速双体船的运动幅度往往较大,若采用普通动网格会产生异常变形的情况,从而导致计算精度不高,严重的话还会出现计算发散的现象,对受船舶运动影响较大的区域采用嵌套网格设置则很好地解决了这个问题。对影响较大区域采用嵌套网格(Overset mesh)设置,这样的网格单元就可以分为激活网格单元、非激活网格单元、接受插值网格单元3个组成部分。其中被激活网格单元可以直接参与离散方程的求解,非激活网格单元则暂时不会参加离散方程求解。供体网格单元与受体网格单元统称为接受插值网格单元,分别处于背景网格单元边界与重叠网格单元的边界上,进行两部分网格之间的信息传递,这样既能节约计算资源,又能更好捕捉高速中的船舶运动,有效地提高计算效率和计算精度[10-11]。自由度开放下的嵌套网格如图4所示。最终,嵌套域与背景域生成的网格总数为800万左右。
|
图 4 嵌套网格 Fig. 4 Overset mesh |
在计算设置过程中,时间步长的选取与网格单元的尺寸相关,对数值计算也会产生较大影响,对傅汝德数较高的船来说,选取相对不合理的时间步长可能会导致计算发散。为了便于操作,一般通过库朗数(CFL)控制时间步长和网格尺寸,CFL= U∆t /∆x,其中U为计算速度,∆t为时间步长,∆x为网格单元尺寸。通常,根据船型尺寸确定最小网格尺寸的前提下,库朗数的取值应该≤1,在实尺度船舶阻力性能模拟中,目前普遍采用的时间步长范围控制在0.005 ~ 0.01 Lwl /U[12-14] 以内。
2.6 DFBI(dynamic fluid body interaction)模型双体船在高速航行时,运动姿态往往会不断调整直至达到动态平衡,一般纵倾和升沉的幅度会比较大,传统固定姿态的计算与实际航行情况有较大偏差,其计算结果也会出现一定的偏离[15]。本算例的傅汝德数较高,模拟运动中的纵摇和垂荡运动应用软件的DFBI(dynamic fluid body interaction)6-DOF模型进行模拟与求解。3个方向运动的转动惯量可用下式表示:
| $\begin{split} &\left[ {\begin{array}{*{20}{l}} {{I_x}}&0&0 \\ 0&{{I_y}}&0 \\ 0&0&{{I_z}} \end{array}} \right] = \\ & \left[ {\begin{array}{*{20}{c}} {m\left( {r_{g,x}^2 + y_G^2 + z_G^2} \right)}&0&0 \\ 0&{m\left( {r_{g,y}^2 + y_G^2 + z_G^2} \right)}&0 \\ 0&0&{m\left( {r_{g,z}^2 + y_G^2 + z_G^2} \right)} \end{array}} \right]\end{split}。$ |
式中:
| $ {F_{CGi}} = m\frac{{{\rm{d}}_{{x_{CGi}}}^2}}{{{\rm{d}}{t^2}}} \text{,} {L_{CGi}} = \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {{I_i}\frac{{{\rm{d}}{\theta _{CGi}}}}{{{\rm{d}}t}}} \right) ,$ |
纵荡:
横荡:
垂荡:
横摇:
纵摇:
首摇:
式中:
试验采用的模型缩尺比为1∶15,最大傅汝德数为1.034。所有试验数据的测试均符合国际拖曳水池会议(ITTC)推荐的规程要求。该船型为英辉南方造船(广州番禺)有限公司的成熟船型,先后为珠三角船东建造的数量超过10艘,每艘船都相应接受了CCS检验,并通过相关试航试验反复验证其性能指标,试航结果与实尺度计算及模型试验结果的对比如图5~图7所示。
|
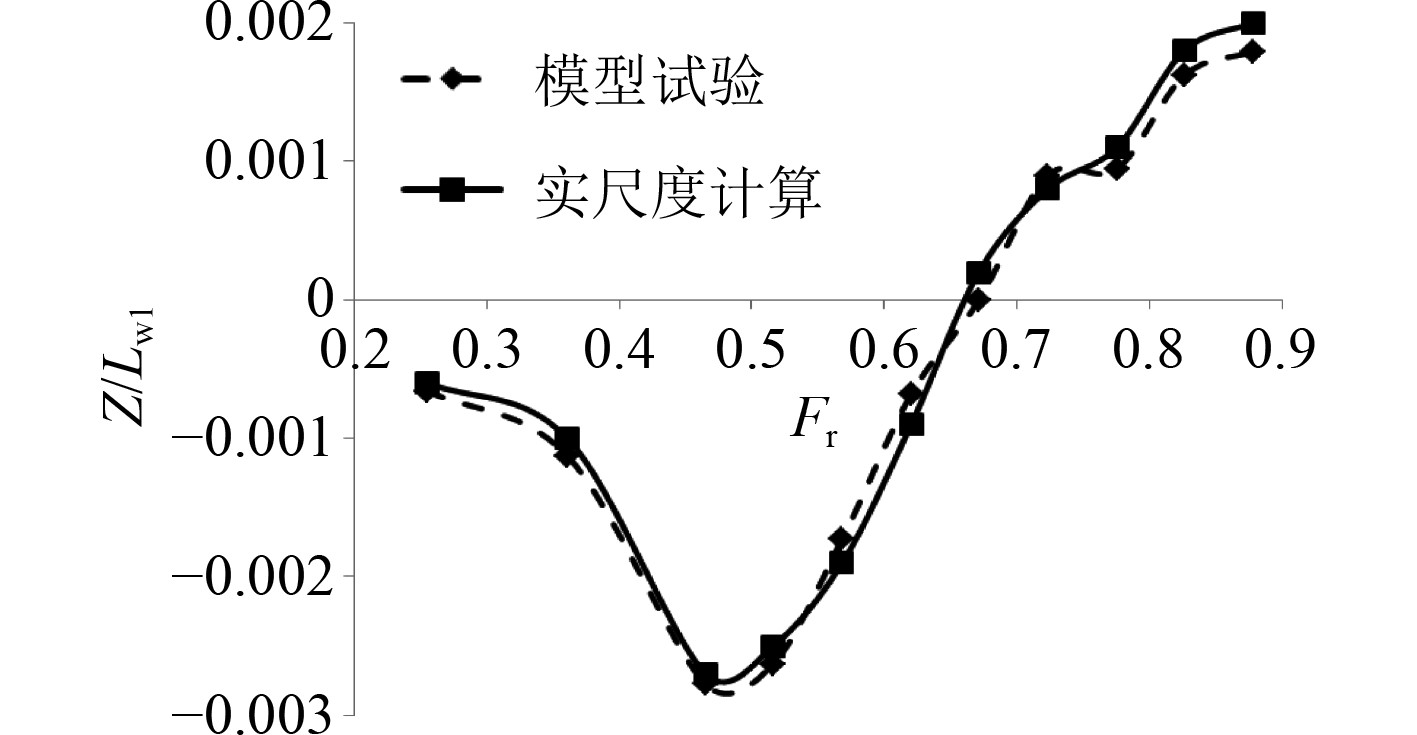
图 5 升沉结果对比 Fig. 5 Comparison of heave results |
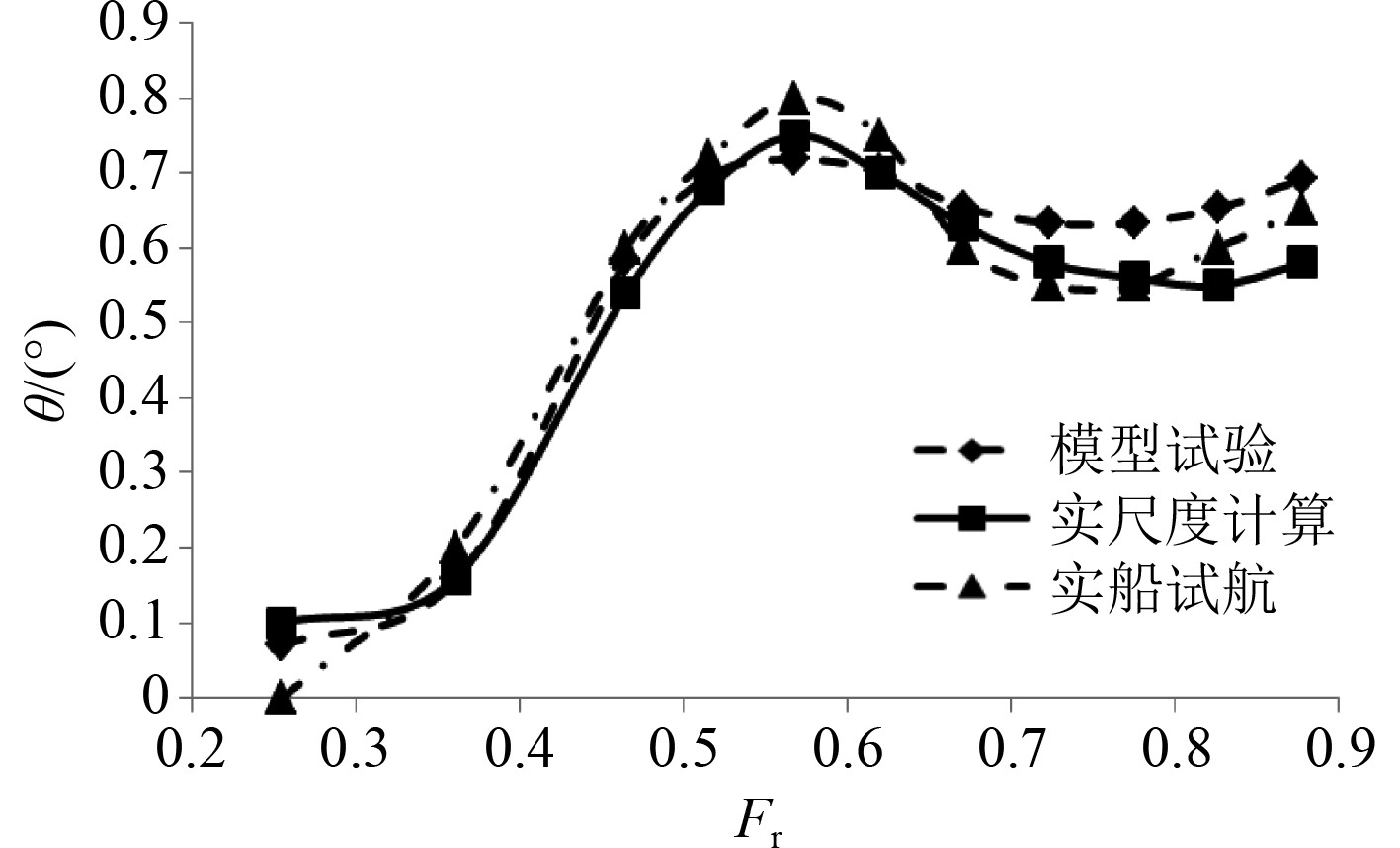
图5和图6分别为模型试验、实尺度计算、实船试航的升沉(z)结果对比和模型试验与实尺度计算的船舶纵倾(θ)结果对比。可知:模型状态的升沉幅度与实尺度计算的升沉幅度相对比较接近;实尺度下的船舶纵倾计算结果与模型试验、实船试航结果的趋势符合性良好,但在低速(Fr=0.26附近)和高速(Fr=0.8附近)实尺度的纵倾计算结果、模型试验结果与实船结果有一定的偏差。
|
图 6 纵倾结果对比 Fig. 6 Comparison of trim results |
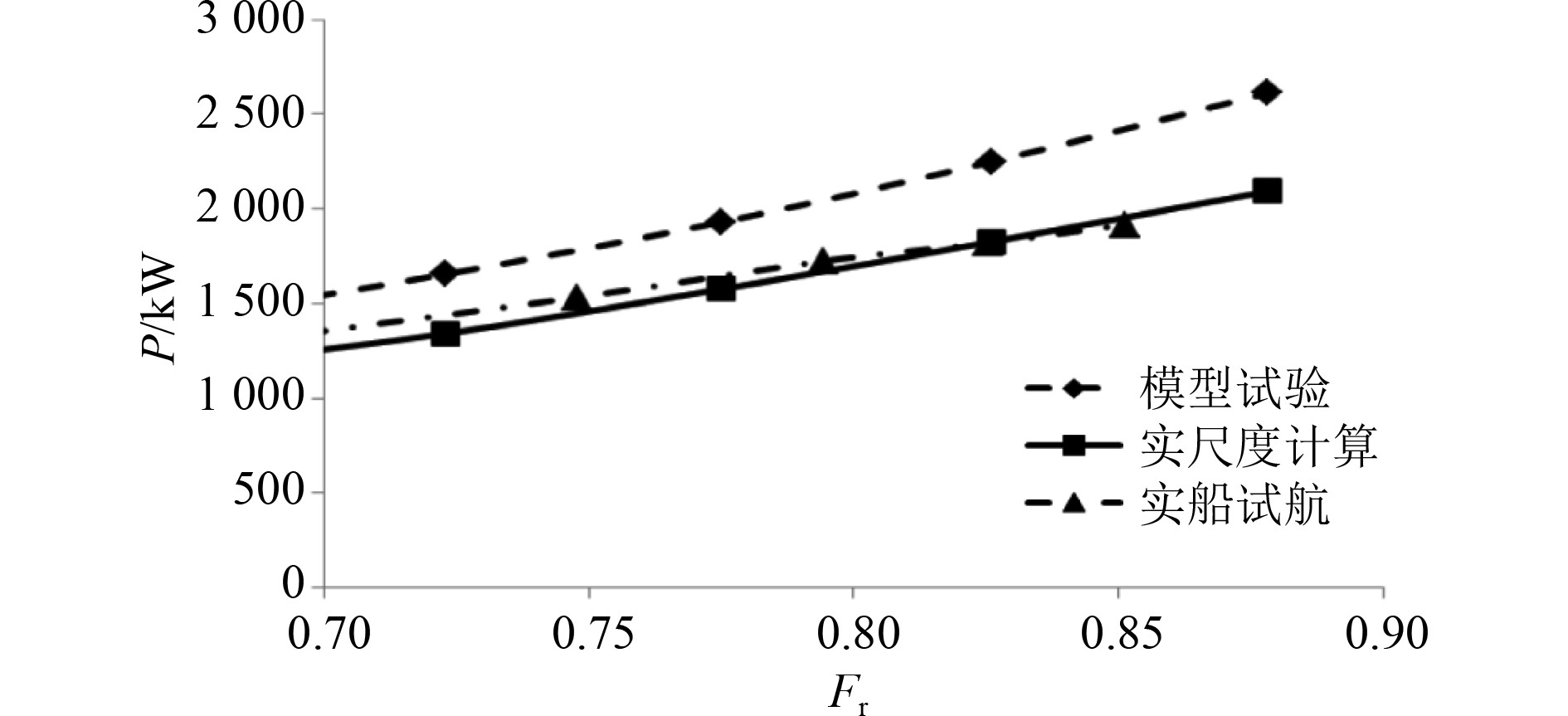
图7为模型试验、实尺度计算、实船试航的有效功率(P)结果对比。可知:实尺度计算结果与实船试航结果十分接近,最大偏差在3%左右,随着傅汝德数增加,偏差逐渐减小;模型试验结果与实船试航结果正偏离较大,最大偏差在20%左右且正偏差有随傅汝德数增大而增加的趋势。
|
图 7 有效功率结果对比 Fig. 7 Comparison of effective power results |
针对模型试验、实尺度计算、实船试航结果,产生上述差异的可能原因如下:
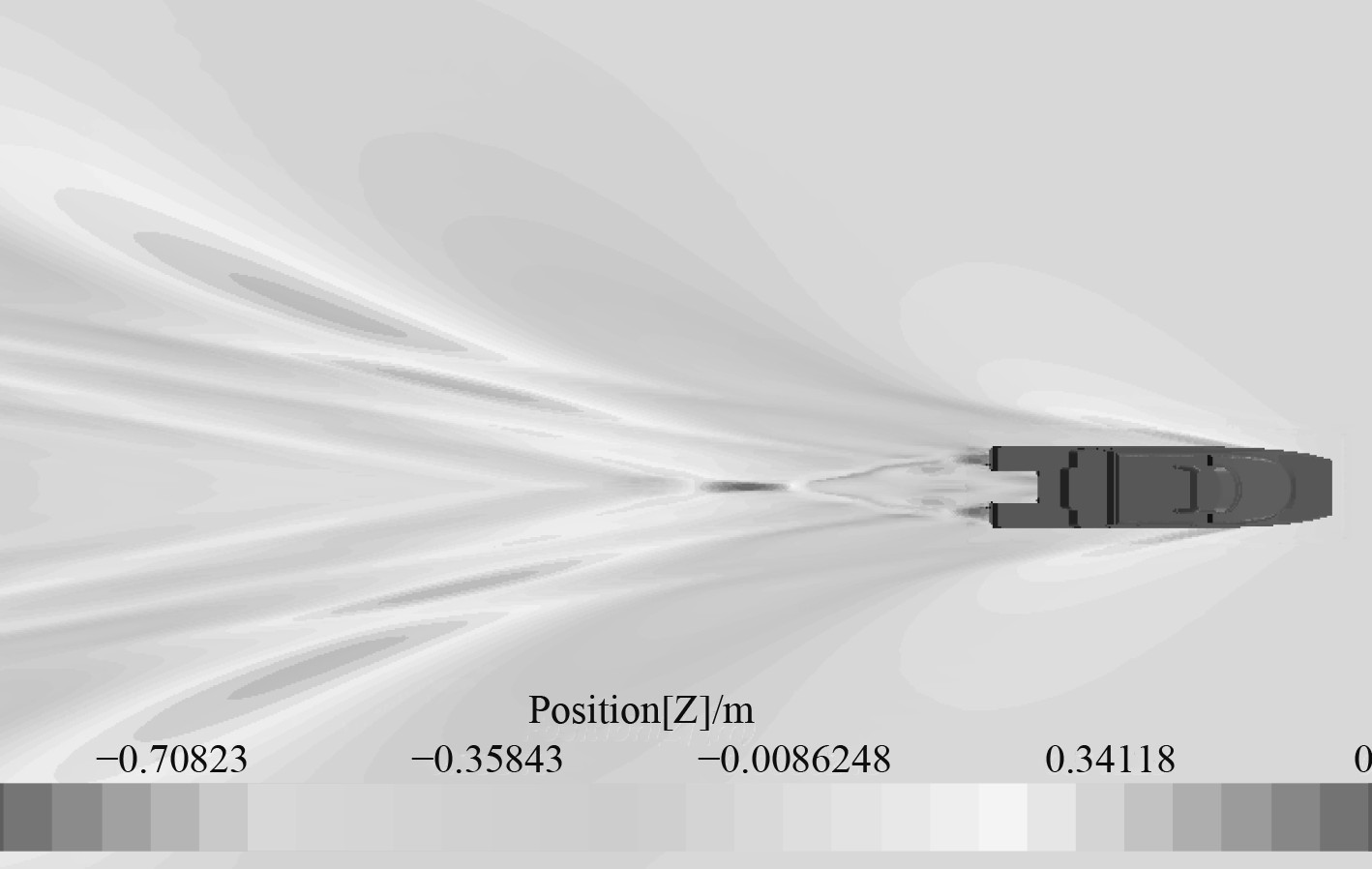
1)本高速双体船实尺度数值模拟的流场与实船的流场比较接近,包含完整的上层建筑部分的风阻模拟和船体部分的模拟,相关云图如图8和图9所示。
|
图 8 Fr=0.85自由液面波形 Fig. 8 Free surface waveform at Fr=0.85 |
2)高速双体船对模型试验的尺度效应比较敏感,模型试验的流场与实船相比有一定的偏差。
3)传统的模型试验换算方法对常规的低速船应用良好,对傅汝德数较高的高速双体船的应用有待进一步研究。
4)传统低速船的风阻在总阻力中的占比较低,几乎可以忽略,但对高速双体船的风阻可能需要单独考虑。

|
图 9 Fr=0.85上层建筑的压力云图与流线图 Fig. 9 Fr=0.85 free pressure cloud diagram and flow diagram of superstructure at Fr=0.85 |
本文对某高速双体客船开展实尺度(包含船体和上层建筑部分)数值模拟,并将其升沉、纵倾、有效功率结果分别与模型试验和实船试航结果进行对比,得到以下结论:
1)实尺度数值模拟结果与实船结果十分接近,纵倾结果与实船趋势一致且最大偏差在5%左右,高速段有效功率与实船的最大偏差在3%左右。
2)模型试验的升沉结果与实尺度数值模拟趋势一致且最大偏差在5%左右;纵倾结果与实船结果趋势一致且在高速段的偏差达到15%左右;高速段的有效功率与实船的最大偏差在20%左右且偏差有随傅汝德数增大而增加的趋势。
3)针对本常规高速双体客船而言,实尺度数值模拟的结果与实船试航修正后的结果十分接近,具有较高的工程应用价值,对于其他高速船型(比如单体船、穿浪双体船、三体船等)的应用有待进一步研究。
| [1] |
杨建民, 肖龙飞, 盛振邦. 海洋工程水动力学试验研究[M]. 上海: 上海交通大学出版社, 2008: 18-27.
|
| [2] |
周广利, 黄德波, 等. 三体船阻力性能的模型系列试验研究[J]. 哈尔滨工程大学学报, 2010, 31(5): 576-584. DOI:10.3969/j.issn.1006-7043.2010.05.006 |
| [3] |
李云波. 船舶阻力[M]. 哈尔滨: 哈尔滨工程大学出版社, 2006: 41-45.
|
| [4] |
张海华, 徐杰, 赵璐, 等. 某集装箱船实船试航与模型试验的数据分析[J]. 船舶工程, 2020, 42(6): 36-40. DOI:10.13788/j.cnki.cbgc.2020.06.08 |
| [5] |
王金宝, 吴琼, 于海. CFD技术在实船航速预报和试航修正中的研究综述[J]. 中国造船, 2020, 61(S2): 100-112. WANG Jinbao, WU Qiong, YU Hai. Comprehensive Review of CFD Technology in Speed-Power Prediction and Trial Correction[J]. Shipbuilding of China, 2020, 61(S2): 100-112. DOI:10.3969/j.issn.1000-4882.2020.z2.011 |
| [6] |
王楠, 周旭, 郑金伟, 等. ISO与ITTC方法在实船航速修正上的应用对比[J]. 船舶工程, 2020, 42(9): 59-63+98. DOI:10.13788/j.cnki.cbgc.2020.09.11 |
| [7] |
杨斌. 基于BSRA、ISO15016和STA-JIP航速修正方法研究[D]. 湛江: 江苏科技大学, 2019.
|
| [8] |
International Organization for Standardization. Ship and Marine Technology-Guidelines for the Assessment of Speed and Power Performance by Analysis of Speed Trial Data [S]. 2015.
|
| [9] |
苏玉民, 林健峰, 赵大刚, 等. 实尺度船舶快速性数值模拟方法综述[J]. 中国造船, 2020, 61(2): 229-239. SU Yumin, LIN Jianfeng, ZHAO Dagang. Review of Numerical Simulation Methods for Full-scale Ship Resistance and Propulsion Performance[J]. Shipbuilding of China, 2020, 61(2): 229-239. DOI:10.3969/j.issn.1000-4882.2020.02.022 |
| [10] |
胡光初, 夏立明. 嵌套网格CFD技术在水动力仿真测试的应用前景[A]. 中国造船工程学会船舶力学学术委员会测试技术学组. 聚焦应用 支撑创新——船舶力学学术委员会测试技术学组2016年学术会议论文集[C]. 中国造船工程学会船舶力学学术委员会测试技术学组: 中国船舶科学研究中心《船舶力学》编辑部, 2016: 6.
|
| [11] |
吴铁成. 船舶精细流场数值模拟及基于PIV的试验研究[D]. 哈尔滨: 哈尔滨工程大学, 2015.
|
| [12] |
李晓鹏. 实船尺度船舶水动力数值模拟和尺度效应分析研究[D]. 北京: 中国舰船研究院, 2019.
|
| [13] |
TEZDOGAN T, DEMIREL Y K, KELLETT P, et al. Full-scale unsteady RANS CFD simulations of ship behavior and performance in head seas due to slow steaming[J]. Ocean Engineering, 2015, 97: 186-206. DOI:10.1016/j.oceaneng.2015.01.011 |
| [14] |
邵汉东, 杨富茗, 田晓庆, 等. 基于CFD实尺2339 标准箱集装箱船的阻力分析和实船验证[J]. 船舶, 2018(3): 18-23. |
| [15] |
周广利, 艾子涛, 邓锐, 等. 高速三体船的阻力预报方法研究[J]. 船舶力学, 2016, 20(7): 805-815. ZHOU Guang-li, AI Zi-tao, DENG Rui, et al. Resistance prediction method research of high speed trimaran[J]. Journal of Ship Mechanics, 2016, 20(7): 805-815. DOI:10.3969/j.issn.1007-7294.2016.07.003 |
 2023, Vol. 45
2023, Vol. 45
