0 引　言

国际船模试验池会议ITTC (International Towing Tank Conference)推荐世界各国把不确定度分析应用于实验流体力学中。在当前船模阻力试验不确定度研究中，均仅限于模型的总阻力系数、剩余阻力系数、1+K值等的不确定度分析^[1-7]。而假设由船模向实船的换算不存在不确定度分量，由试验原理可知，这是不正确的。由于部分实船换算方程的灵敏度系数难以求解，以GUM(Guide to the expression of Uncertainty in Measurement)法为基础的ITTC推荐规范在实船换算不确定度分析中存在较大困难。蒙特卡罗仿真^[8-9]方法在测量不确定度的评定中被日渐重视和推广，其不仅能够给出试验结果的不确定度，而且能给出分布情况。本文对一艘4 m长模型的阻力试验实船换算进行蒙特卡罗仿真，给出了实船不同航速下有效功率的估计值及其不确定度。

1 船舶阻力试验实船换算方法

1+ $K$ 方法是目前ITTC推荐的方法。

旋涡阻力主要由水的粘性所引起，鉴于此傅汝德法把旋涡阻力（形状阻力）与兴波阻力归并成剩余阻力不尽合理，1+ $K$ 法将其与摩擦阻力归并在一起成为粘性阻力。

实船总阻力为：

$ {R_{ts}} = {R_{\upsilon s}} + {R_{ws}} + \Delta {R_s} + {R_{as}} 。$

(1)

式中： $ {R_{\upsilon s}} $ 为实船粘性阻力，N； $ {R_{ws}} $ 为实船兴波阻力，N； $ \Delta {R_s} $ 为实船附体阻力，N； $ {R_{as}} $ 为实船空气阻力，N。

实船粘性阻力 $ {R_{\upsilon s}} $ 由下式确定：

$ {R_{\upsilon s}} = \left( {\left( {1{\text{ + }}K} \right){C_{fs}}{\text{ + }}\Delta {C_{fs}}} \right) \cdot \frac{1}{2}{\rho _s} \cdot S{}_s \cdot {V_s}^2 。$

(2)

式中：1+ $K$ 为形状因子； ${C_{fs}}$ 为实船湿表面积摩擦系数； $\Delta {C_{fs}}$ 为实船湿表面积粗糙因子； ${\rho _s}$ 为实船所在水域水的密度， ${\rm{kg}}/{{\rm{m}}^3}$ ； $S{}_s$ 为实船湿表面积， ${{\rm{m}}^2}$ ； ${V_s}$ 为实船运行速度， ${\rm{m}}/{\rm{s}}$ 。

实船兴波阻力 $ {R_{ws}} $ 由下式确定：

$ {R_w}_s = {C_{ws}} \cdot \frac{1}{2}{\rho _s} \cdot S{}_s \cdot {V_s}^2 ，$

(3)

式中， ${C_{ws}}$ 为实船兴波阻力系数。

附体包括舵、舭龙骨、轴包架、轴和支架轴等，附体阻力 $\Delta {R_s}$ 常用附体系数(百分数) $k{}_{ap}$ 的形式表示，它是安装全部附体后较之裸体船所增加的阻力与裸船体阻力之比。

$ \Delta {R_s}{\text{ = }}k{}_{ap}({R_{vs}} + {R_{ws}}) ，$

(4)

空气阻力 ${R_{as}}$ 被单独计算，实船空气阻力 ${R_{as}}$ 由下式确定：

$ {R_a}_s = {C_{as}} \cdot \frac{1}{2}{\rho _a} \cdot {A_t} \cdot {V_a}^2 。$

(5)

式中： ${C_{as}}$ 为实船船体水线以上部分空气系数； ${\rho _a}$ 为实船船体水线以上部分所受到的迎风空气密度， ${\rm{kg}}/{{\rm{m}}^3}$ ； ${A_t}$ 为实船船体水线以上部分在横剖面上的投影面积， ${{\rm{m}}^{\text{2}}}$ ； ${V_a}$ 为实船与空气之间的相对速度，m/s。

由式(1)～(5)可得：

$ \begin{split} {R_t}_s =& (1 + k{}_{ap})(\left( {1{\text{ + }}K} \right){C_{fs}}{\text{ + }}\Delta {C_{fs}} + {C_{ws}}) \times \\ & \frac{1}{2}{\rho _s} \cdot S{}_s \cdot {V_S}^2 + {C_{as}} \cdot \frac{1}{2}{\rho _a} \cdot {A_t} \cdot {V_a}^2 ，\end{split} $

(6)

实船的裸船体总阻力系数 $ {C_{ts}} $ 为：

$ {C_{ts}} = \left( {{\text{1 + K}}} \right){C_{fs}} + \Delta {C_{fs}} + {C_w}_s 。$

(7)

1）摩擦阻力系数

实船摩擦阻力系数 ${C_{fs}}$ 和模型摩擦阻力系数 ${C_{fm}}$ ，计算式如下：

$ \left\{ \begin{gathered}{C_{fs}} = \frac{{0.075}}{{{{(\log {R_e} - 2)}^2}}} ，\\ {C_{sm}} = \frac{{0.075}}{{{{(\log {R_e} - 2)}^2}}}。\end{gathered} \right.$

(8)

式中： ${R_e}$ 为表征粘性的相似准数， ${R_e} = {{V{L_{WL}}} \mathord{\left/ {\vphantom {{V{L_{WL}}} \nu }} \right. } \nu }$ ， $ {L_{WL}} $ 为水线长， ${\rm{m}}$ ； $\nu $ 为水的动力粘性系数与密度的比值， ${{\rm{m}}^2}/{\rm{s}}$ 。

2）兴波阻力系数 $ {C_w} $

在傅汝德数相等时，实船和模型的兴波阻力系数相等，因模型具有“光滑表面”，所以不存在粗糙度问题，故实船兴波阻力系数：

$ {C_w}_s = {C_w}_m= {C_{tm}} - \left( {1{\text{ + }}K} \right){C_{fm}} 。$

(9)

式中： ${C_{tm}}$ 为模型湿表面积总系数； ${C_{fm}}$ 为模型湿表面积摩擦系数，由式(8)确定。

1+ $K$ 方法中 $K$ 系数的取值根据傅汝德数0.1～0.2范围内的试验结果采用Prohaska方法确定，即

$ \frac{{{C_{tm}}}}{{{C_{fm}}}} = (1 + K) + A\frac{{{F_n}^4}}{{{C_{fm}}}} 。$

(10)

式中： ${F_n}$ 为傅汝德数， ${F_n}$ = $ {{{V_m}} \mathord{\left/ {\vphantom {{{V_m}} {\sqrt {g{L_{WLm}}} }}} \right. } {\sqrt {g{L_{WLm}}} }} $ ， $ {L_{WLm}} $ 为模型水线长， ${\rm{m}}$ ； ${V_m}$ 为模型运行速度， ${\rm{m}}/{\rm{s}}$ 。

模型总阻力系数：

$ {C_{tm}} = \frac{{{R_m}}}{{\frac{1}{2}{\rho _m}{S_m}{V_m}^2}}。$

(11)

式中： $ {R_m} $ 为模型裸船体总阻力， ${\rm{N}}$ ； ${\rho _m}$ 为实船所在水域水的密度， ${\rm{kg}}/{{\rm{m}}^3}$ ； $S{}_m$ 为模型湿表面积， ${{\rm{m}}^2}$ 。

3） 实船粗糙度补贴 $ \Delta {C_{fs}} $

$ \Delta {C_{fs}} = \left\{ 105 \times \left( \frac{{{K_S}}}{{{L_{WLs}}}}\right)^{\frac{1}{3}} - 0.64 \right\} \times {10^{ - 3}} ，$

(12)

式中， ${K_S}$ 为实船粗糙度， ${K_S}$ = $1.5 \times {10^{ - 4}}$ m。

计算出实船的阻力之后，将计算结果换算成实船的有效功率：

$ {P_e} = \frac{{{R_{ts}} \times {V_s}}}{{735.{\text{5}}}} 。$

(13)

2 蒙特卡罗仿真 2.1 蒙特卡罗仿真的步骤

采用蒙特卡罗仿真对船舶阻力试验实船换算的步骤如下：1）建立船舶阻力试验实船换算仿真模型；2）确定阻力试验和实船换算中输入量（如阻力传感器测量值、试验速度等）及其分布规律；3）根据输入量的分布规律，构造相应的数学概率模型；4）将随机输入量的抽样值加载到仿真模型，得到输出量（实船阻力和实船有效功率）的估计值；5）重复n次步骤4；6）对输出量的结果进行处理，得到实船阻力和实船有效功率的统计特征值，如估计值(期望)、标准不确定度、95%概率包含区间的左端点和右端点。

2.2 蒙特卡罗仿真的输入量

试验速度和试验阻力如表1所示。试验速度的最大允许误差为±0.000 5 m/s，试验阻力的最大允许误差为±0.006 7 kg；其他输入量的量值(期望)与最大允许误差见表2，缩尺比λ视为真值，无偏差。以上均假设为均匀分布。仿真次数n=100000。

2.3 蒙特卡罗仿真的输出量

船舶阻力试验实船换算（实船阻力、实船有效功率）的蒙特卡罗仿真结果如表3和表4所示。

以实船速度13.50 kn为例，从表3和表4中可知，实船阻力估计值为357848 N，在95%概率包含区间为[354859, 360855]N，标准不确定度为1558 N；实船有效估计值为2518.97 kW，在95%概率包含区间为[2497.9, 2540.2]kW，标准不确定度为11 kW。随着实船速度的增加，实船阻力和实船有效功率的标准不确定度分别从455 N，1.42 kW逐步增加至1558 N，10.96 kW，相对标准不确定度为标准不确定度除以估计值的绝对值，由于仅考虑模型试验速度不确定度的尺度效应导致的实船速度不确定度，实船速度的不确定度是一个非常小的量级，造成了在不同速度下实船阻力和实船有效功率的相对标准不确定度几乎一致。随着实船速度的增加，实船阻力和实船有效功率的相对标准不确定度分别从1.56%，1.56%下降至0.44%，0.44%，表明基于1+K法的船舶阻力试验实船换算结果较为精确。

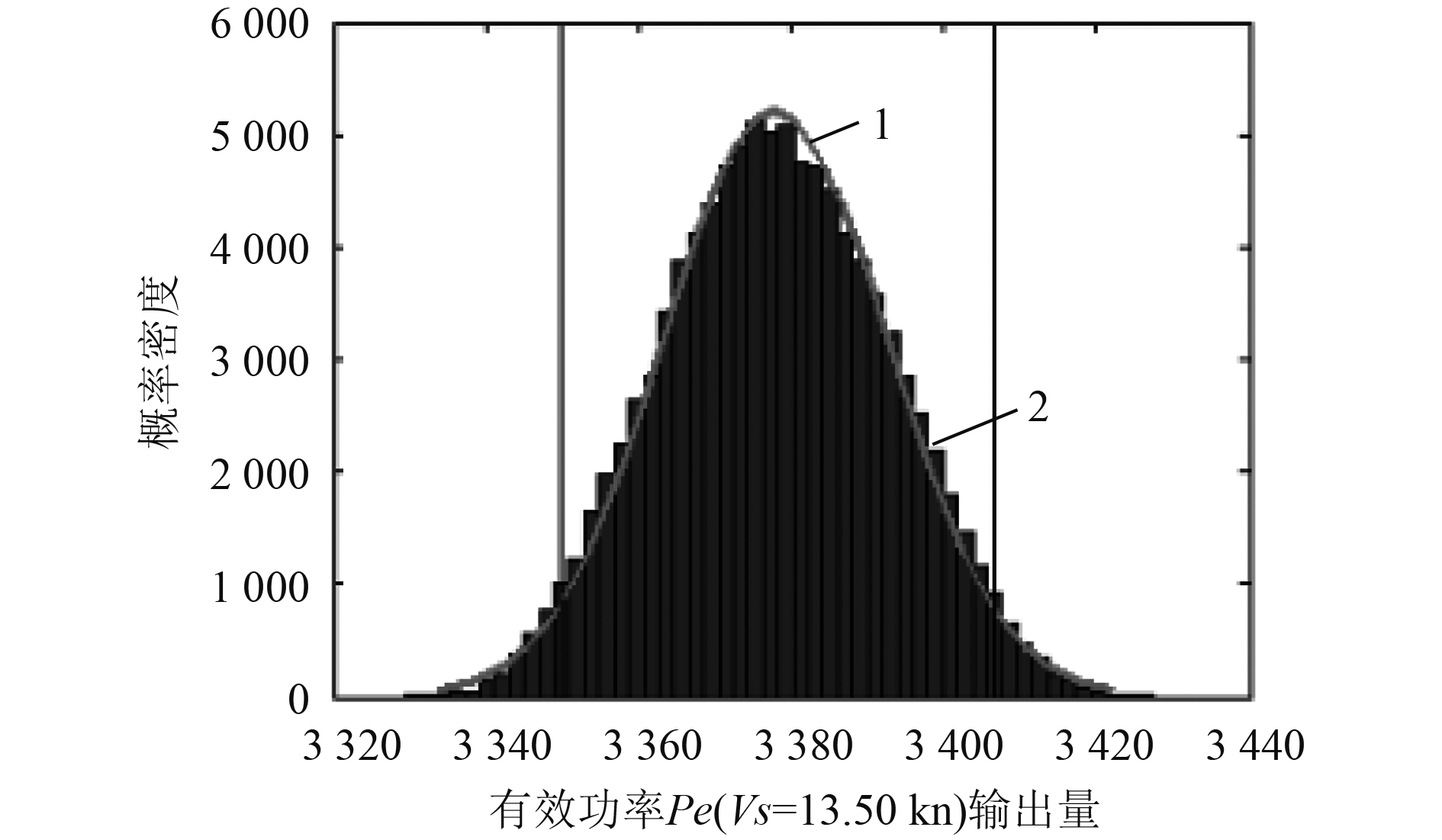
如图1所示，曲线1为正态分布曲线，区域2为质量M的概率密度直方图，两黑色垂直线为95%概率包含区间。在实船速度13.50 kn时，实船有效功率的仿真值分布左右对称，符合正态分布。其他速度下的实船阻力和实船有效功率亦有相同的趋势。

3 结　语

1）随着实船速度的增加，实船阻力和实船有效功率的标准不确定度分别从455 N，1.42 kW逐步增加至1558 N，10.96 kW，实船阻力和实船有效功率的相对标准不确定度却分别从1.56%，1.56%下降至0.44%，0.44%，表明基于1+K法的船舶阻力试验实船换算结果较为精确。

2）实船阻力和实船有效功率的蒙特卡罗仿真值分布左右对称，符合正态分布。