0 引　言

机械零部件故障是影响船舶运输安全的重要因素，对其进行寿命分析，估计其退化状态，对船用机械零部件进行及时维护以及确保船舶运行安全具有重要意义^[1-2]。

武滢等^[3]分析了机械零部件不同状态信号，获取其时频特征后采用经验模态分解（EMD）提取其时频域特征，通过计算皮尔逊相关系数完成特征向量选取，将其作为PSO-SVR寿命预测模型的输入，实现零部件剩余寿命估计，但该方法寿命估计效果不理想，其原因在于各状态信号通过经验模态分解后发生了混叠现象，影响了特征提取结果。陈云翔等^[4]在分析装备部件运行条件的基础上，选取参照部件，将其性能状态作为参照标准，在计算其与服役部件性能相似性后，确定剩余寿命结果。该方法的实用性较低，原因是该方法不能确定零部件退化的敏感特征。支持向量回归模型广泛应用于寿命预测领域，可通过对退化特征与剩余寿命的回归分析，达到剩余寿命估计目的，但该模型预测性能往往受模型参数影响较大。因此，本文提出基于改进支持向量回归的船用机械零部件寿命估计方法，实现船用机械零部件的智能化维护。

1 船用机械零部件寿命估计 1.1 船用机械零部件寿命特征提取 1.1.1 时域特征

机械零部件全寿命周期数据的时域特征是反映其运行状态的重要指标，二者具有对应关系，因此，可获取其时域特征，以此完成其寿命的估计。采用小波变换法对船用机械零部件全寿命周期数据作去噪处理后，将峭度、峰值、脉冲、波形、偏度、整流平均、峰峰值、均方根、标准差、频率峰值、均值、方差、边缘因子13个可以反映故障状态的时域指标作为船用机械零部件的时域特征。

1.1.2 频域特征

采用集合经验模态分解方法（EEMD）对全寿命周期数据进行分析，以获取频域特征，公式描述为：

$ x\left( t \right) = \sum\limits_{j = 1}^n {{c_j}} \left( t \right) + r\left( t \right) 。$

(1)

其中： $ x\left( t \right) $ 表示全寿命周期数据信号，通过对该信号进行分解可获得 $ n $ 个本征模态分量 $ {c_j}\left( t \right) $ 以及剩余分量 $ r\left( t \right) $ 。对于 $ {c_j}\left( t \right) $ ，其频域特征 $ {U_j} $ 表示为：

$ {U_j} = {\int_0^{ + \infty } {\left| {{c_j}\left( t \right)} \right|} ^2}{\rm{d}}t 。$

(2)

1.1.3 敏感特征

主成分分析法通过线性变换使得原本存在关联性的原始变量变成了一组相互独立变量，而原始变量中的重要信息均留存于首个变量中。通过下式实现数据信号的降维处理：

$ {X_{m \times 1}} = {L_{m \times s}}{U_{s \times 1}} = \left\{ \begin{gathered} {x_1}\left( t \right) = {l_{11}}{u_1} + {l_{12}}{u_2} + \cdots {l_{1s}}{u_s}，\\ {x_2}\left( t \right) = {l_{21}}{u_1} + {l_{22}}{u_2} + \cdots {l_{2s}}{u_s}，\\ \mathop {}\nolimits^{} \mathop {}\nolimits^{} \mathop {}\nolimits^{} \mathop {}\nolimits^{} \vdots \\ {x_m}\left( t \right) = {l_{m1}}{u_1} + {l_{m2}}{u_2} + \cdots {l_{ms}}{u_s}。\\ \end{gathered} \right. $

(3)

其中： $ U $ 为原始特征变量，其维度为 $ s $ ； $ L $ 为转换矩阵， $ m \leqslant s $ 。

通过主成分分析法对其作降维处理，以剔除其中的冗余内容等，结果用 $ S = \left\{ {\left( {{z_i},{y_i}} \right)} \right\} $ 表示，以此提取该数据集合中的敏感特征，最终提取到的特征用 $ {U'} $ 表示。

1.2 支持向量回归模型（SVR）

SVR是支持向量机的一个重要分支，能够在两变量关系不确定的情况下，通过某种函数关系实现输出变量的预测。

假设 $ S = \left\{ {\left( {{z_i},{y_i}} \right)} \right\} $ 表示输入样本数据， $ {z_i} \in {R^N} $ , $ {y_i} \in R $ ，回归函数通过下式进行确定：

$ f\left( z \right) = {w^{\rm{T}}} \cdot \varphi \left( z \right) + b。$

(4)

式中： $ \varphi \left( z \right) $ 为非线性映射函数； $ w $ 为SVR模型参数； $ b $ 为偏置， ${\rm{T }}$ 表示转置。本文将松弛变量 $ {\xi _i} $ 和 $ {\hat \xi _i} $ 添加到模型中，在使模型更具鲁棒性的同时，可以确保 $ f\left( z \right) $ 无限趋近于 $ y $ ，则SVR模型如下：

$ \mathop {\min }\limits_{w,b,{\xi _i},{{\hat \xi }_i}} \frac{{{{\left\| w \right\|}^2}}}{2} + C\sum\limits_{i = 1}^N {\left( {{\xi _i} + {{\hat \xi }_i}} \right)} ，$

(5)

$ \begin{gathered} {\rm{s.t.}}\mathop {}\nolimits^{} f\left( {{z_i}} \right) - {y_i} \leqslant \varepsilon + {\xi _i}，\\ \mathop {}\nolimits^{} \mathop {}\nolimits^{} {y_i} - f\left( {{z_i}} \right) \leqslant \varepsilon + {{\hat \xi }_i}，\\ \mathop {}\nolimits^{} \mathop {}\nolimits^{} {\xi _i} \geqslant 0,{{\hat \xi }_i} \geqslant 0,i = 1,2, \cdots N 。\\ \end{gathered} $

(6)

式中： $ C $ 为惩罚系数； $ \varepsilon $ 为不敏感损失系数； $ {y_i} $ 为寿命估计模型输出结果。采用拉格朗日乘子对式（5）进行求解，则有：

$ w = \sum\limits_{i = 1}^N {\left( {{\alpha _i} - {{\hat \alpha }_i}} \right)} \varphi \left( {{z_i}} \right) ，$

(7)

式中， $ {\alpha _i} $ 和 $ {\hat \alpha _i} $ 表示2个不同的拉格朗日乘子。

$ f\left( z \right) $ 可改写为：

$ f\left( z \right) = \sum\limits_{i = 1}^N {\left( {{{\hat \alpha }_i} - {\alpha _i}} \right)} K\left( {{z_i},z} \right) + b，$

(8)

其中， $\sigma = K\left( {{z_i},z} \right) = \varphi {\left( {{z_i}} \right)^{\rm{T}}}\varphi \left( z \right)$ 表示核函数。SVR模型的预测精度受其参数 $ C $ ， $ \sigma $ ， $ \varepsilon $ 等影响很大，故需对其进行改进处理，以实现船用机械零部件寿命的准确估计。

1.3 基于改进蚁狮优化算法的模型参数寻优

蚁狮优化算法（ALO）是受蚁狮猎食行为的启发而形成的智能寻优算法，优势在于可通过较少参数的调整实现寻优性能的大幅度提升，但该算法在搜索过程中容易陷入局部最优，因此在其基础上考虑莱维飞行机制，以此对其进行改进。利用改进后的算法实现模型参数寻优，实现船用机械零部件寿命的准确估计。莱维飞行机制是以随机游走方式来反映蚁狮的猎食行为，既能达到搜索空间变广的目的，又能使种群更具多样化。

假设 $ G_i^t $ 表示蚂蚁 $ t $ 时刻所在位置，利用莱维飞行机制对其位置进行修正后，结果为 $ G_i^{t + 1} $ ，则有：

$ G_i^{t + 1} = G_i^t + \beta \otimes Levy\left( s \right)。$

(9)

式中： $ s $ 为步长； $ \beta $ 为蚁狮优化算法参数。为使 $ s $ 满足莱维分布特性，其可描述为：

$ s = \frac{{u \cdot G_i^{t + 1}}}{{{{\left| v \right|}^{{\gamma ^{ - 1}}}}}} 。$

(10)

其中：莱维分布参数 $ u $ ， $ v $ 具有正态分布性； $ \gamma $ 为一个常数。参数 $ \beta $ 限制了改进蚁狮优化算法的寻优性能，故对其进行调整，以提高其动态适应能力，其公式描述为：

$ \beta = \exp \left( { - \left| {\frac{{s - t}}{s}} \right|} \right){\rm{sign}}\left( {rand - 0.5} \right)。$

(11)

其中： ${\rm{sign}}\left( \cdot \right)$ 表示符号函数， $ t $ 表示莱维分布特征参数， $ rand $ 表示(0.5,1]之间的一个随机数。

基于改进SVR模型的船用机械零部件寿命估计流程如下：

步骤1　获取船用机械零部件全寿命周期数据后，提取峭度等13个时域特征。对机械零部件全寿命周期数据作EEMD分解，确定若干个本征模态分量，获得各分量能量熵，实现频域特征的提取。

步骤2　获取船用机械零部件时域、时频域特征后，计算各特征与机械零部件剩余寿命间的互信息值，完成机械零部件寿命相关特征的选择，通过主成分分析法作降维处理，确定敏感特征 $ {U'} $ 。

步骤3　基于获得的敏感特征 $ {U'} $ 以及机械零部件寿命数据设计训练、测试样本，将训练样本作为船用机械零部件寿命估计模型的输入，完成模型训练后，利用其对测试样本进行机械零部件寿命估计。选取均方误差指标（ $ E $ ）、决定系数指标（ $ {R^2} $ ）对模型的能力进行评估，当轨迹结果无法满足预定条件时，则需对模型参数继续寻优，反之，输出寿命估计结果。 $ E $ 的计算公式为：

$ E = \dfrac{{{{\displaystyle\sum\limits_{i = 1}^N {\left( {{{\hat y}_i} - {y_i}} \right)}^2 }}}}{N} ，$

(12)

$ {R^2} = \dfrac{{{{\left( {N\displaystyle\sum\limits_{i = 1}^N {\hat y_i^{}y_i^{} - \displaystyle\sum\limits_{i = 1}^N {\hat y_i^{}\displaystyle\sum\limits_{i = 1}^N {y_i^{}} } } } \right)}^2}}}{{\left[ {N\displaystyle\sum\limits_{i = 1}^N {\hat y_i^2 - {{\left( {\displaystyle\sum\limits_{i = 1}^N {\hat y_i^{}} } \right)}^2}} } \right]\left[ {N\displaystyle\sum\limits_{i = 1}^N {y_i^2 - {{\left( {\displaystyle\sum\limits_{i = 1}^N {y_i^{}} } \right)}^2}} } \right]}}。$

(13)

式中， $ {\hat y_i} $ 表示船用机械零部件的实际剩余寿命。

2 实验分析

将船舶机械轴承作为研究对象，通过加速退化试验台采集其寿命周期数据，采用加速度传感器以22 kHz频率获取该轴承的全寿命周期数据，信号采样周期设定为10 s，时长为0.1 s。设置3种工况，工况1为3个轴承在4000 N荷载下以1900 rad/s转速运行；工况2为3个轴承在4300 N荷载下以1600 rad/s转速运行；工况3为1个轴承在4800 N荷载下以1500 rad/s转速运行。

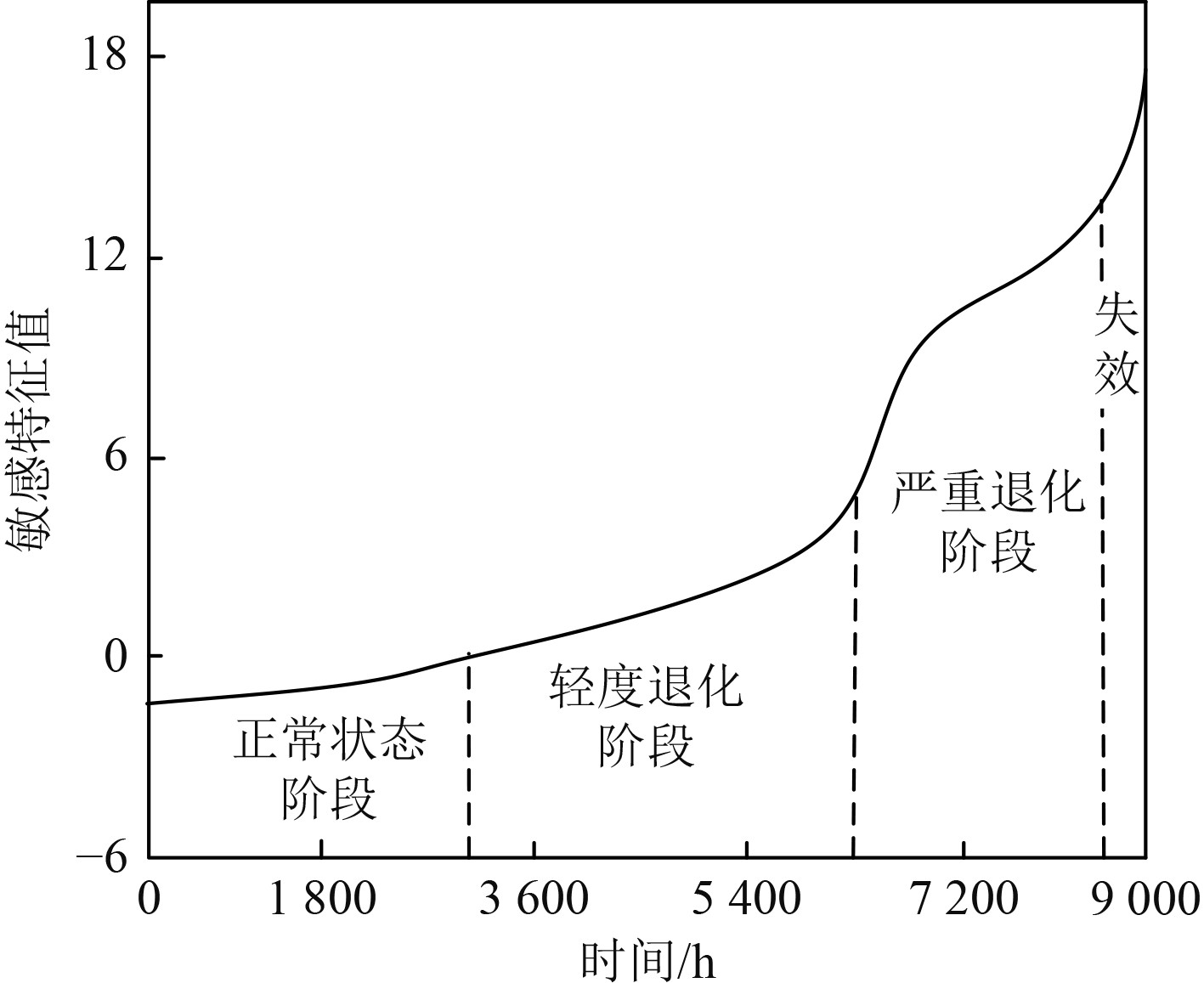
采用本文方法提取机械轴承退化的敏感特征，通过分析轴承退化过程中敏感特征值的变化分析轴承退化状态，实验结果如图1所示。

可知，船用轴承在退化过程中，其敏感特征值随时间的增加而逐渐增大。在船用轴承刚投入使用初期阶段，其运行状态最佳，敏感特征值低于0；轴承在使用过程中不断磨损，磨损程度越高，敏感特征值越大，当敏感特征值处于5 ～13之间时，轴承严重退化，当敏感特征值达到13后，轴承已退化至失效边缘。

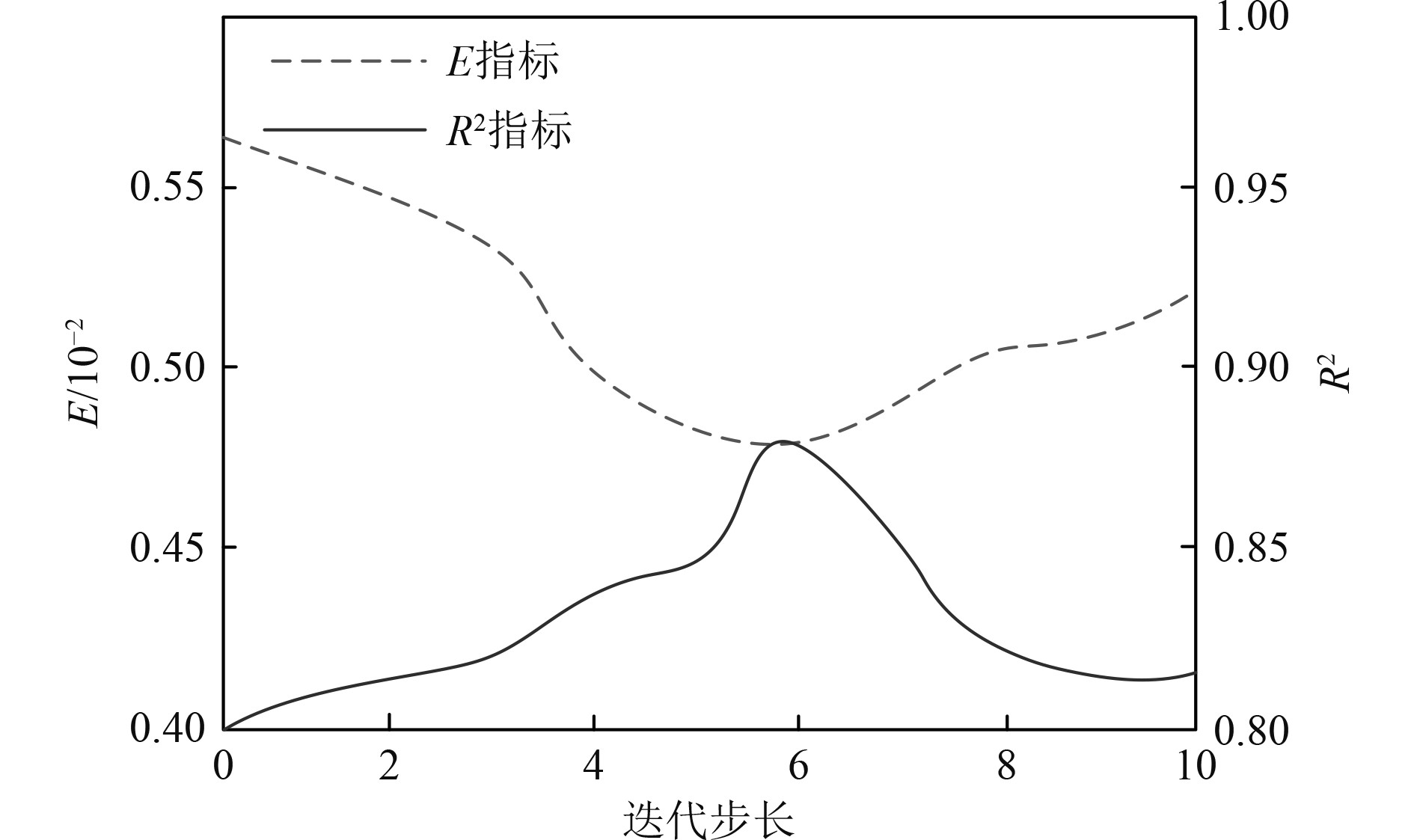
SVR参数对船用轴承寿命估计精度起决定性作用，通过对不同步长下 $ E $ 和 $ {R^2} $ 指标的变化分析本文方法的寿命估计效果，实验结果如图2所示。

可知，采用本文方法对船用机械零部件寿命估计模型参数进行优化后，随着迭代步长的不断增加， $ E $ 指标曲线呈先降后升趋势变化， $ {R^2} $ 指标曲线呈先升后降规律变化，当步长取值为6时， $ E $ 指标值最小，而 $ {R^2} $ 指标值最大，此时SVR可取得最佳寿命估计结果，因此可确定最佳迭代步长为6。

将迭代步长设置为6，应用本文方法对不同工况条件下的船用轴承寿命进行估计，实验结果如表1所示。

可知，采用本文方法可确定不同工况下各轴承的退化状态，并获得其寿命估计值，估计值与实际值更接近，寿命估计精度更高。

3 结　语

以船用轴承为实验对象，应用本文方法对其寿命进行估计，分别从数据信号去噪、特征提取以及寿命估计性能和估计结果方面验证本文方法的应用效果。实验结果表明，当步长为6时，寿命估计模型性能最优，实现不同工况下轴承剩余寿命估计，可以应用在船用机械零部件寿命估计领域。