在经济全球化发展大趋势下,国家之间贸易交流日益频繁,而大宗货物运输通常使用海运方式[1]。面对较为复杂多样的海洋航行环境以及海上运输线路存在交叉的问题,为船舶规划最优航行线路是海上运输行业重点研究方向[2]。当前也有很多学者研究船舶最优航线生成方法,王立鹏等[3]提出的船舶航线规划算法,该算法通过建立船舶航行时回转与降速模型得到船舶航线数据,再通过分析海图航线规划和陆地物标之间的关系,最后利用四叉树和不规则边界检测方式生成船舶航线。韩志豪等[4]提出深度强化学习的航线生成方法,该方法将电子海图上的航线作为初始数据,利用深度学习神经网络对电子海图上的航线进行采样处理后,输出船舶航行最优航线。但是上述2种方法生成的航线均存在无法规避较小障碍物、生成线路不是最佳线路问题,为此本文研究基于多维度数据挖掘的船舶最优航线生成方法。
1 船舶最优航线生成方法 1.1 基于多维度数据挖掘的初始航线生成挖掘官方电子海图(eiectronic navigational charts,ENCs)的海域港口、陆地物标(岛屿、礁石)等多维度坐标数据,并将每个港口、陆地物标看作一个节点,使用改进随机路径图(improved probabilistic roadmap,IPRM)方法生成船舶航行初始航线,详细过程如下:
从官方电子海图中挖掘到海域港口、陆地物标节点数据后,在船舶航行起点与目的地空间内选择
在一条航线上,可能存在2艘或者多艘船舶同目的地相同的情况。当线路生成不合理时,船舶出发或者到达目的地时潮汐较大或过小均影响船舶出入港,因此需从潮汐、船舶安全航行距离多个维度设置最优航线生成多维指标。
1)船舶航行安全距离指标
2艘或者多艘船舶向同一目的地航行时,相邻2艘船舶中,后一艘船舶的航速不得高于前一艘船舶。假设用
| $ t = \min ({D_i},{D_j}) 。$ | (1) |
式中:
2艘船舶航行速度满足如下条件:
| $ {V_j} \cdot (t' + t) \geqslant {V_i} \cdot t + 6{L_i}。$ | (2) |
式中:
由式(1)和式(2)综合可得到2艘船舶安全航行时间间隔
| $ t_{ij}' = \frac{{{X_{ij}} \cdot {V_i} \cdot \min ({D_i},{D_j})}}{{{V_j}}} - \frac{{{X_{ij}} \cdot {V_j} \cdot ({D_i},{D_j}) + 6{L_i}}}{{{V_j}}}。$ | (3) |
式中:
2)航线目的地潮汐时间指标
受潮汐运动影响,船舶无法实现全时间通航。为保障船舶到达港口附近时能高效进港,需要假设该港口入港航段为单向通航。假设船舶平均吃水为
| $ Z = {z_d} + k \cdot \frac{1}{{60}} \cdot \dot t 。$ | (4) |
式中:
由于船舶大多数均满载货物,其入港时吃水较深,入港时则需乘潮,其到达目的地进入港口潮汐时刻约束条件如下:
| $ \delta _p^s \leqslant \left[ {{Q_i} + Z + \varPhi G{C_p} + \varPhi B{H_{ip}} - 2\varPhi } \right] \leqslant \delta _p^f 。$ | (5) |
式中:
以船舶航线无向路径网络图
假设
| $ \begin{split} {H_M} =& \left[ \begin{array}{ll} {X^1}& f({X^1}) \\ {X^2}& f({X^2}) \\ {X^U}& f({X^U})\end{array} \right] \times \\ & \left[ {{Z_i} + \varPhi G{C_p} + \varPhi B{H_{ip}} - 2\varPhi } \right] \times t_{ij}' 。\end{split} $ | (6) |
式中:
| $ f(R) = \sum\limits_{i = 1}^{n - 1} {S({P_i},{P_{i + 1}})} 。$ | (7) |
式中:
在和声搜索算法内引入遗传算法,使用遗传算法在和声搜索记忆库内通过交叉航线、消除节点以及微调节点位置后,生成最优船舶航线,其过程如下:
从
| $ X_1^{new} = (x_1^1, \cdots ,x_i^1,{p_c},x_j^2, \cdots ,x_m^2),$ | (8) |
| $ X_2^{new} = (x_1^2, \cdots ,x_k^2,{p_c},x_l^1, \cdots ,x_n^1) 。$ | (9) |
将新生成的2条航线与未交叉前的原航线进行对比分析,将高质量的2条航线存储到记忆库内。将记忆库内所有航线均进行交叉操作后,对记忆库内航线进行节点消除和微调处理。假设
| $ x_{i1}^{new} = {x_{i1}} + {O_1},\left| {{O_1}} \right| < \zeta ,$ | (10) |
| $ x_{i2}^{new} = {x_{i2}} + {O_2},\left| {{O_2}} \right| < \zeta 。$ | (11) |
式中:
通过式(10)和式(11)生成新航线后,将新生成的航线与记忆库内适应度最差的航线进行比较,选择适应度数值最高的航线作为最优航线。
2 实验分析 2.1 初始航线生成测试以一艘船舶作为实验对象,使用本文方法生成其初始航线,结果如图1所示。
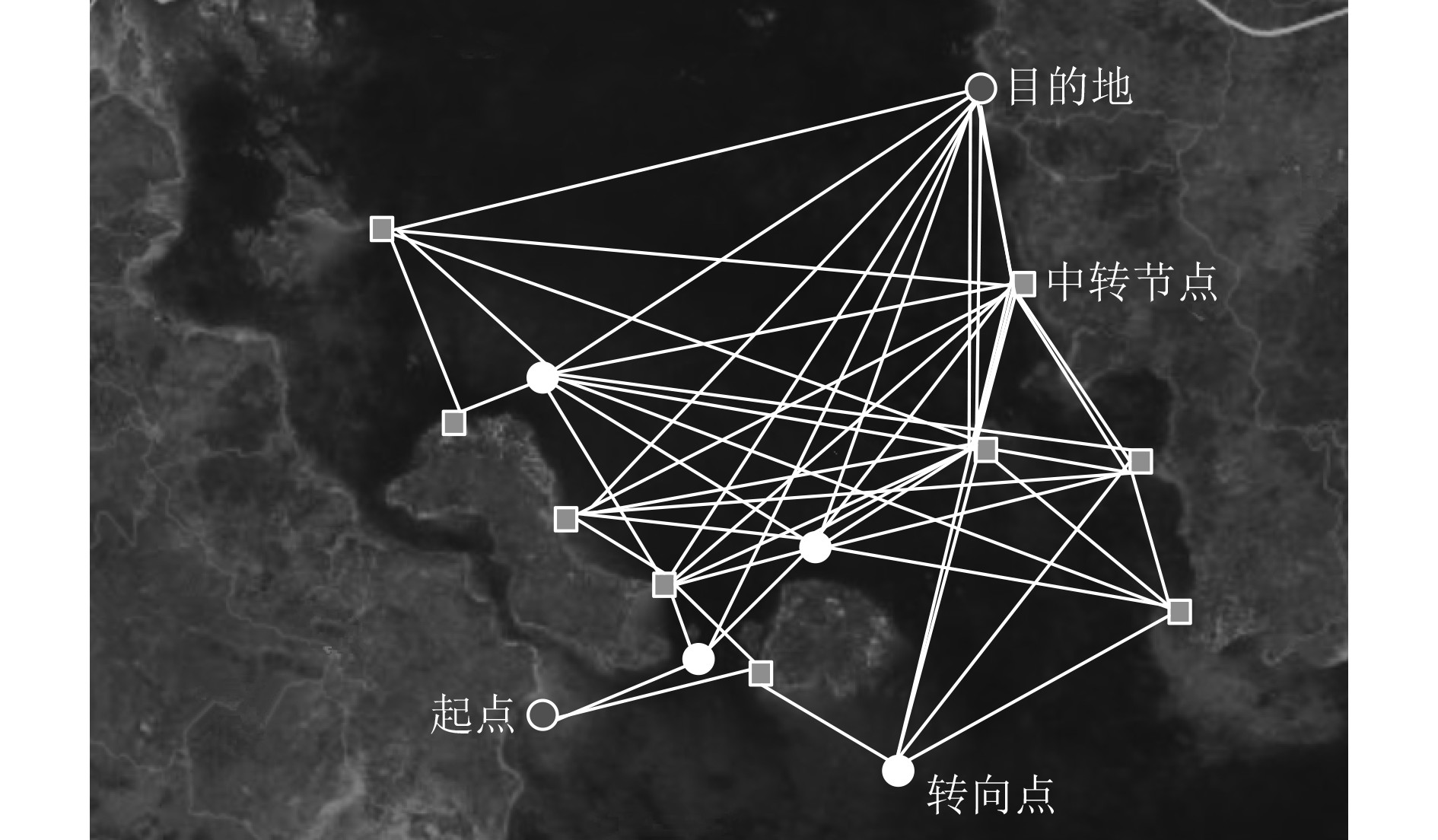
|
图 1 船舶初始航线生成结果 Fig. 1 Initial route generation results of ships |
可知,当该船需要从起点航行到目的地时,使用本文方法可生成若干条航线,且每条航线均可到达目的地,同时涵盖所有中转节点和转向点。该结果证明,使用本文方法可有效获取较为全面的船舶初始航线,也从侧面说明本文方法具备较好的航线生成能力。
2.2 最优航线生成测试以一般船舶为实验对象,使用本文方法生成其最优航线路线,结果如图2所示。
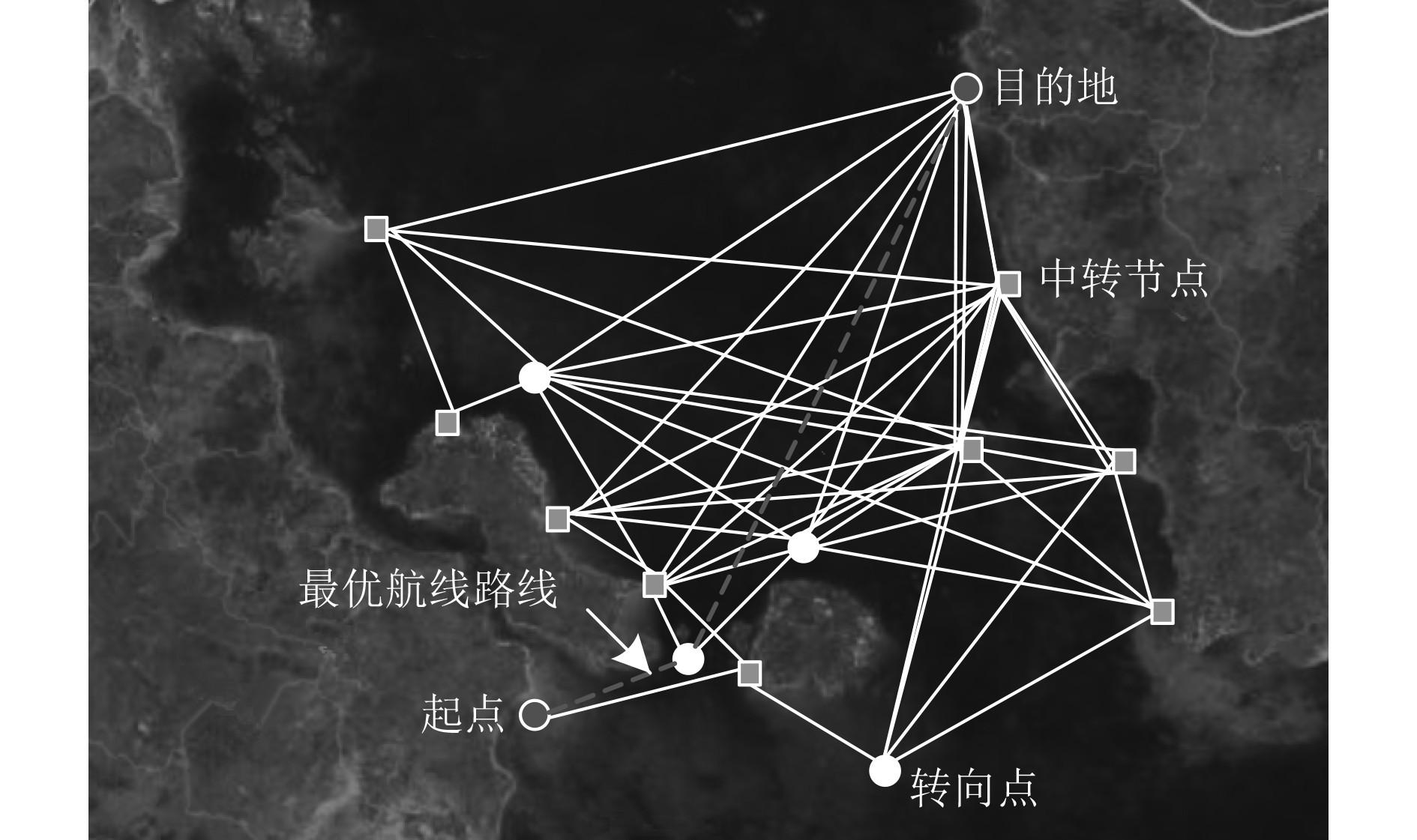
|
图 2 船舶最优航线路线生成结果 Fig. 2 Generation result of optimal ship route |
分析可知,使用本文方法可有效在初始航线中生成最优航线,且该路线在所有路线中航程最短,在该最优航线内,仅存在一个转向点,航线上无中转节点,可较大程度降低船舶航行耗时。综上结果,本文方法可有效生成最优航线。
以10艘船舶作为实验对象,使用本文方法生成这10艘船舶最优航线。将每条最优航线的适应度值作为衡量指标,测试本文方法生成最优航线能力,结果如图3所示。
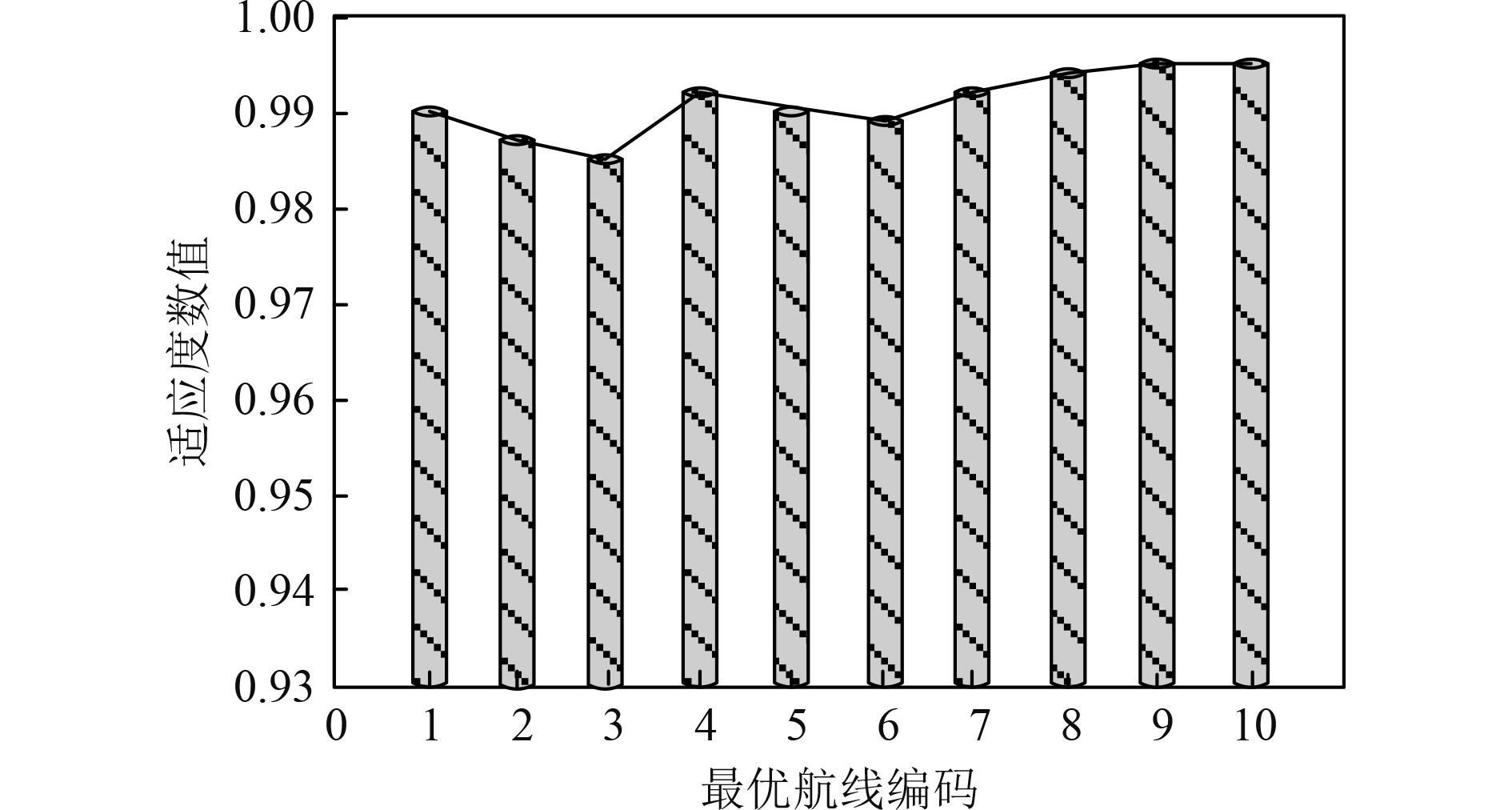
|
图 3 最优航线适应度值 Fig. 3 Optimal route line fitness value |
分析可知,本文方法生成的船舶航线适应度数值始终在0.985~0.995波动,说明本文方法生成航线较为准确,也是最优航线,应用效果较好。
3 结 语本文研究基于多维度数据挖掘的船舶最优航线生成方法,考虑船舶航行安全距离和港口潮汐时间多维度,并以其作为挖掘最优航线指标,最终生成最优航线。经过实验验证:本文方法可有效生成最优航线,且所生成的最优航线适应度数值较高,应用效果较好。
| [1] |
李忠美, 张猛, 李劲澎, 等. 基于大椭圆航线的船舶位置估算方法[J]. 大连海事大学学报, 2020, 46(4): 17-23. LI Zhongmei, ZHANG Meng, LI Jinpeng, et al. Ship position estimation method based on great ellipse route[J]. Journal of Dalian Maritime University, 2020, 46(4): 17-23. DOI:10.16411/j.cnki.issn1006-7736.2020.04.003 |
| [2] |
潘明阳, 刘乙赛, 李琦, 等. 基于改进A*算法的内河水网航线规划及应用[J]. 上海海事大学学报, 2020, 41(1): 40-45. PAN Mingyang, LIU Yisai, LI Qi, et al. Improved A* algorithm based route planning and its application for inland waterway network[J]. Journal of Shanghai Maritime University, 2020, 41(1): 40-45. |
| [3] |
王立鹏, 张智, 马山, 等. 考虑船舶操纵性约束得改进遗传算法航线规划[J]. 哈尔滨工程大学学报, 2021, 42(7): 1056-1062. WANG Lipeng, ZHANG Zhi, MA Shan, et al. Improved genetic algorithm-based ship route planning considering ship maneuverability constraints[J]. Journal of Harbin Engineering University, 2021, 42(7): 1056-1062. |
| [4] |
韩志豪, 汪益兵, 张宇, 等. 基于深度强化学习的船舶航线自动规划[J]. 中国航海, 2021, 44(1): 100-105. HAN Zhihao, WANG Yibing, ZHANG Yu, et al. Automatic ship route planning based on deep reinforcement learning[J]. Navigation of China, 2021, 44(1): 100-105. |
 2023, Vol. 45
2023, Vol. 45
