0 引　言

混合人工蜂群算法是通过观察蜜蜂的群体行为提出的一种优化算法，其核心是模拟蜂群中每个个体的寻优过程，实现全局寻优。混合人工蜂群算法相对于其他算法，具有算法简便、收敛速度快、抗干扰能力强等优点，在一些复杂问题寻优时被大量应用。

船舶通信网络随着计算机技术、无线通信的发展，通信质量、信号传输距离等不断提升，在船舶无线通信网络中，无线网络节点具有重要意义，每个无线网络节点与周围船舶构成一个小范围通信网络，节点既可以接收来自附近船舶终端的无线通信数据，又可以通过大功率信号收发机，向其他网络节点发送和接收无线通信数据，大量无线网络节点使得船舶无线网络系统能够保证足够大的覆盖范围。通常，船舶无线网络节点位于陆地的基站，有些海域内海上作业平台等也可以作为无线网络节点。

为保证海上船舶无线通信网络的正常工作，确保无线网络的覆盖率、节点之间的联通，无线网络节点的功率大、建造成本高，因此，必须要合理配置无线网络节点的位置和功能，既可以保证无线网络的覆盖率，使尽可能多的船舶实现高质量通信，又可以降低整体的运营成本。

本文利用混合人工蜂群算法，进行船舶无线通信网络的优化设计，重点是通过合理配置网络节点的位置，提高船舶无线网络的整体覆盖率。

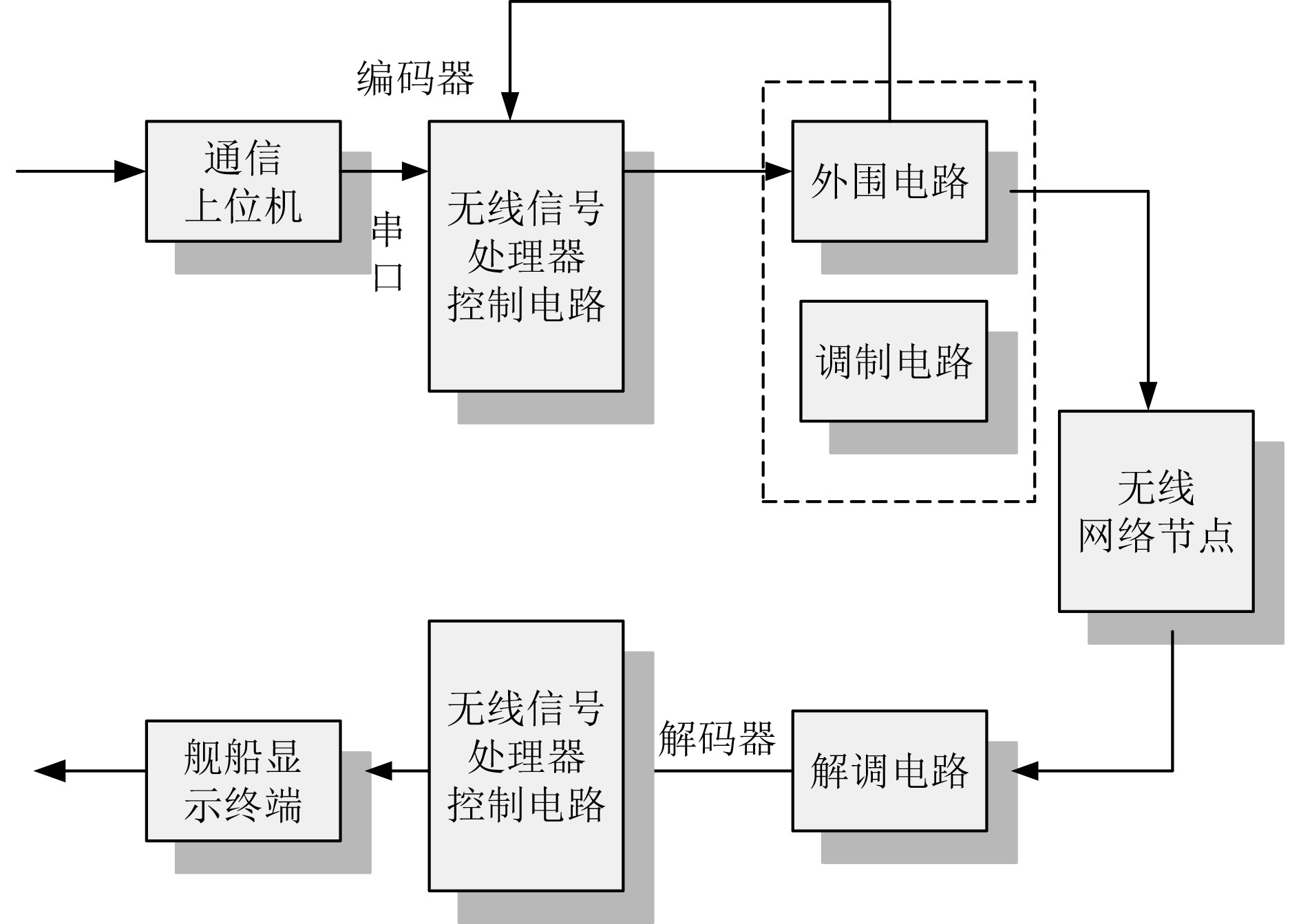
1 船舶无线通信网络研究

船舶无线通信传输过程包括信号编码、调制、传输、解调、信号分析等，图1为船舶无线通信网络的工作原理图。

组成船舶无线通信网络的关键硬件设备有通信上位机、调制电路、控制电路、解调电路和无线网络节点等。

1）通信上位机

船舶无线通信网络的上位机通常是PC终端，其主要作用包括：

① 打包和整理船舶无线通信网络中的待传输数据，并在PC终端显示器上显示数据收发的进程，用户可以通过通信上位机查询、存储无线通信网络数据，对通信指令进行实时的跟踪。

② PC终端上位机的串口可以接收和发送控制指令，通常采用的串口为RS-232C，无线信号处理器及控制电路接收来自上位机的指令后，将反馈信号通过串行接口返回上位机。

2）无线网络节点

无线网络节点是进行无线数据接收和发送的单元，对于船舶无线通信系统有重要意义，其功能包括：

① 信号收发功能。无线网络节点接收来自调制电路的编码信号，进行信号的初步分析和处理，根据信号中的地址编码等特征，将无线信号转发至网络中的其他船舶终端^[1]。

② 下游设备的控制功能。无线网络节点在进行组网时，一个网络节点按照覆盖范围接入了多个子节点，并能够对局域网络中的子节点和下游设备进行控制。

③ 自组织和独立运行。每个无线通信网络节点内部集成了嵌入式操作系统，一方面能够实现与上位机和下游设备的通信功能，另一方面网络节点具有相对独立性。

2 基于混合人工蜂群算法的船舶通信网络优化 2.1 混合人工蜂群算法

混合人工蜂群算法的核心是模拟蜂群的劳动分工和自组织特性，从而实现蜂群中的位置寻优。其中，自组织特性是一种内驱机制，自组织寻优的过程与个体之间的相互作用有关。

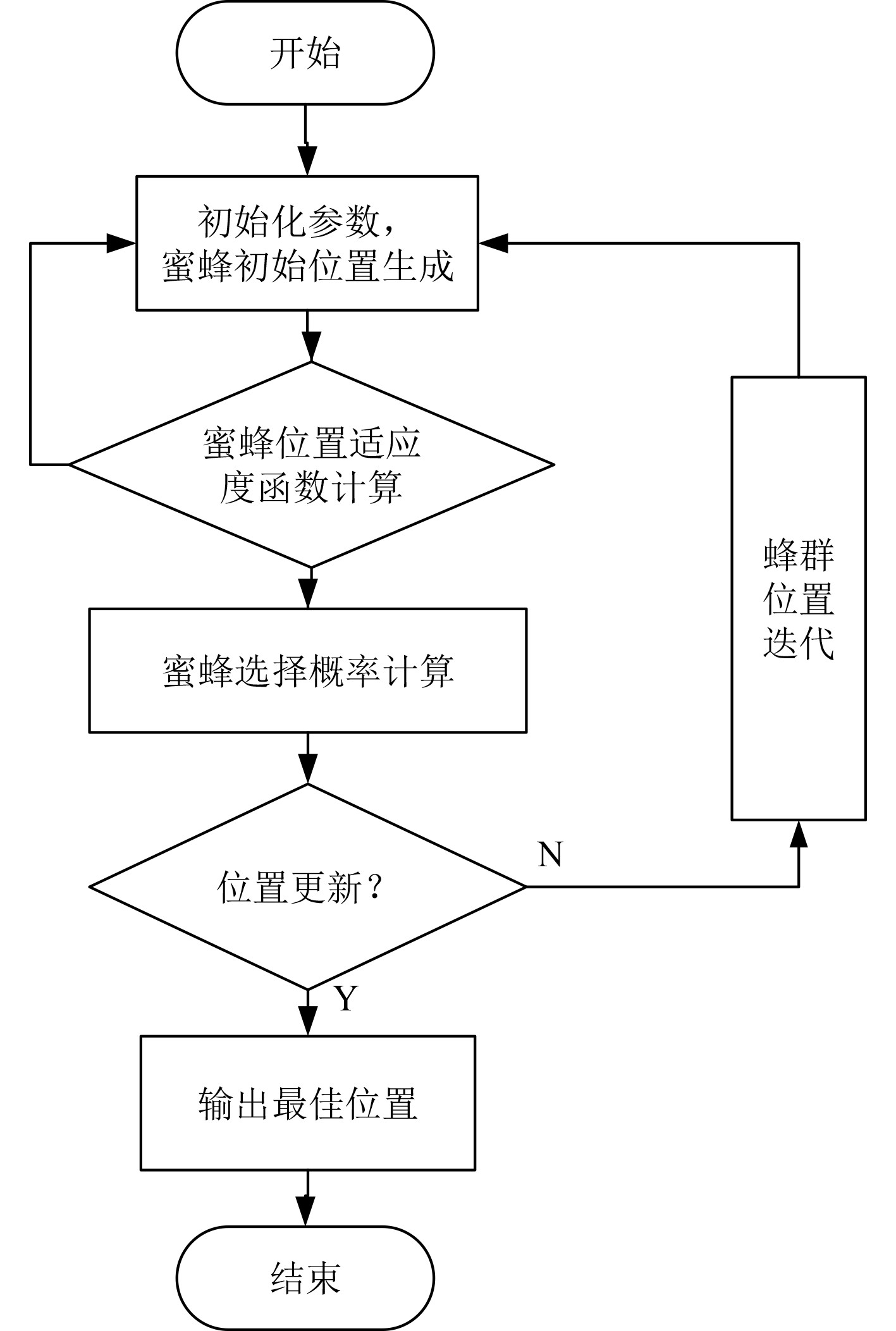
混合人工蜂群算法的基本流程如图2所示。

混合人工蜂群算法的关键要素包括正反馈、负反馈、波动性和容错性。

1）正反馈

混合人工蜂群算法的正反馈是一种检验法则，基于正反馈要素可以提高蜂群算法的高效性、优化算法的结构，比如蜜蜂在飞行路径留下的信息素、包含蜜源信息的舞姿等。

2）负反馈

负反馈要素有助于提高算法的稳定性，与正反馈相互抵消，混合人工蜂群中的负反馈行为包括食物短缺导致的蜂群繁殖减少等，负反馈机制也是限制混合蜂群算法的主要边界条件。

3）波动性

波动性是指混合人工蜂群算法的随机性，比如随机路径、蜂群中某个个体的随机行为等，波动性要素有助于提高系统的创造力，基于波动性的智能算法有助于最优解的产生和寻优。

4）容错性

容错性是混合人工蜂群算法的控制阈值，蜂群的自组织行为具有一定的容错空间，防止由于限制条件的影响导致优化算法不收敛^[2]。

蜂群中食物源的位置更新模型为：

$ {V_{ij}} = \frac{{{x_{ij}} + {R_i}_j\left( {{x_{ij}} - {x_{kj}}} \right)}}{K} 。$

(1)

式中： $ {V_{ij}} $ 为食物源的新位置； $ {x_{ij}} $ 为食物源当前位置； $ {x_{kj}} $ 为迭代过程的位置； $ K $ 为−1～1的随机数。

混合人工蜂群算法的适应度函数为：

$ {P}_{i}=\frac{{f}_{i}{t}_{i}}{{\displaystyle \sum _{i=1}^{S\text{N}}{f}_{i}}{t}_{i}} 。$

(2)

式中： $ S \text{N} $ 为种群的数量； $ {f_i}{t_i} $ 为第i个位置解求出的适应度函数值。

2.2 基于混合人工蜂群算法的无线通信覆盖区域优化

为了提高船舶无线通信网络的覆盖率，在保证每个无线网络节点的信号传输半径的同时，通过合理的布局无线网络节点的位置，可以实现覆盖区域的最大化^[3]。

在二维平面内，定义无线网络节点S的信号传输半径为 $ Rs $ ，节点位置为 $ \left( {{x_s},{y_s}} \right) $ ，目标船舶位置为 $ \left( {{x_p},{y_p}} \right) $ ，无线网络节点与目标位置之间的距离为：

$ d\left( {s,p} \right) = \sqrt {{{\left( {{x_s} - {x_p}} \right)}^2} + \left( {{y_s} - {y_p}} \right)} \text{。} $

(3)

网络节点能够覆盖船舶目标的概率表示为：

$ {C_p}(s) = \left\{ \begin{array}{*{20}{l}} {1,\;d\left( {s,p} \right) < {R_S}} \text{，}\\ {0,\;{\rm{else}}} \text{。} \end{array} \right. $

(4)

当网络节点与船舶之间的距离小于覆盖半径时，概率为1；当网络节点与船舶之间的距离大于覆盖半径时，概率为0。

由于船舶无线通信网络在实际工作过程中，信号的传输会受到电磁波干扰、气象条件干扰，且随着网络节点与船舶之间距离的增大，这种干扰现象越明显。因此，在进行无线通信网络感知概率建模时，将感知半径分为r和 $ {r_e} $ ，r为确定可感知的半径， $ {r_e} $ 为不确定可感知的半径，则感知概率更新为：

$ {C_p}(s) = \left\{ {\begin{array}{*{20}{c}} 0&{{\text{ if }} r + {r_e} \leqslant d(s,p)} \text{，}\\ {{e^{{{\left( { - {\lambda _2}{\lambda _1}} \right)}^\beta }}}}&{{\text{ if }} r - {r_e} < d(s,p) < r + {r_e}} \text{，}\\ 1&{{\text{ if }} d(s,p) \leqslant r - {r_e}} \text{。} \end{array}} \right. $

式中： $\ \beta $ 为分布因数； $ {\lambda _2}和{\lambda _1} $ 为概率检测参数。

无线网络节点的使用效率用所有节点的有效覆盖区域和全部覆盖区域的比值表示，定义为：

$ {p_{{w}}} = \frac{{\displaystyle\bigcup\limits_{i = 1,2,...,N} {{S_i}} }}{{\displaystyle\sum\limits_{i = 1}^N {{S_i}} }} 。$

(5)

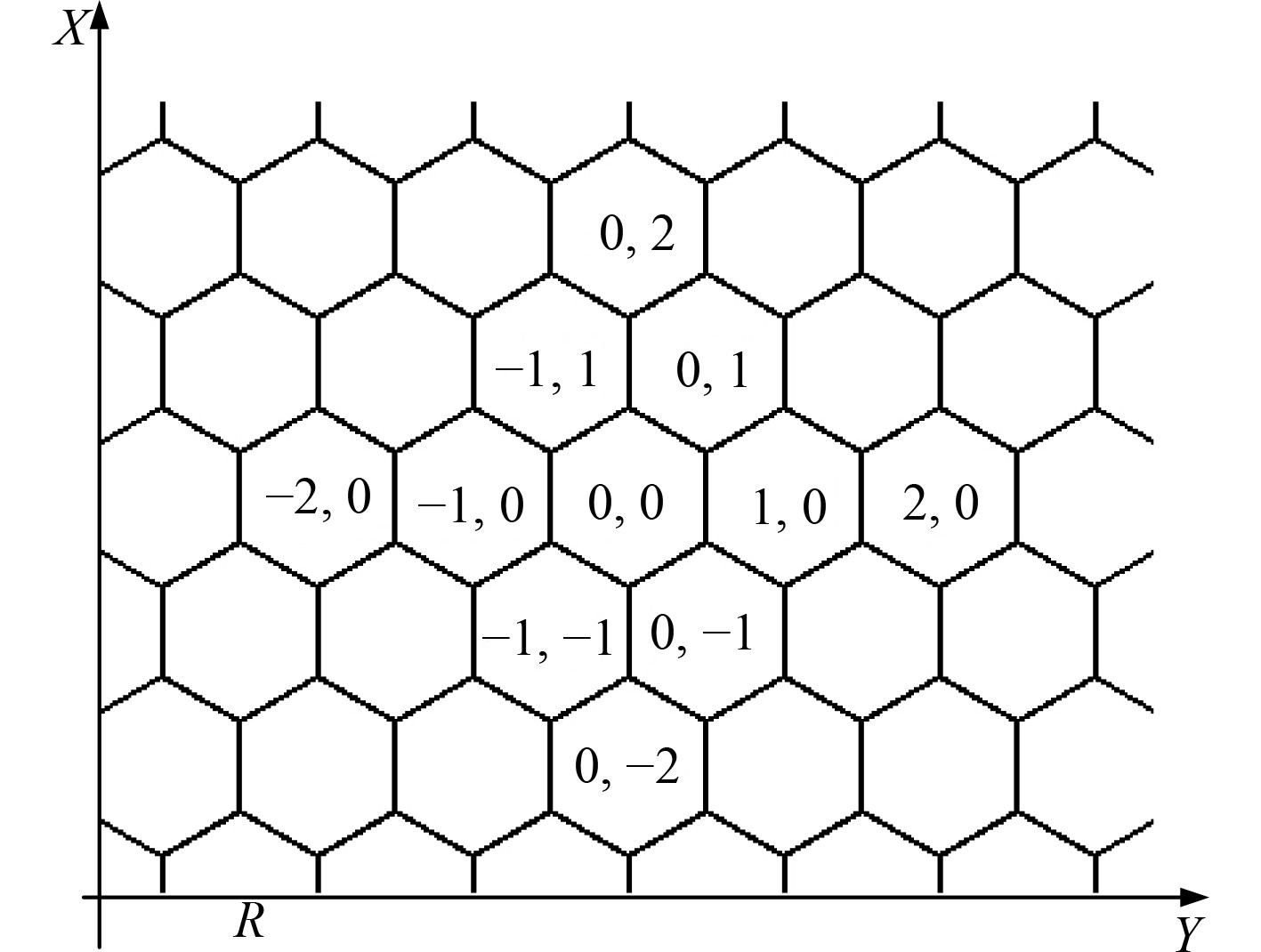
基于混合人工蜂群算法寻优，得到无线通信网络节点在正六边形节点分布时具有最大的覆盖面积，示意图如图3所示。

当无线网络节点按照六边形分布时有如下特点：

1）此时无线网络节点的覆盖面积利用率最高，有效半径 $ R > \sqrt 3 Rs $ ，且此时无线网络之间的联通特性最佳。

2）每个无线网络节点与相邻的6个节点保证信息畅通，信号传输具有冗余设计特点，抗干扰能力强。

3）采用正六边形的节点分布，能够降低无线通信网络整体的功率损耗，提高系统效率。

2.3 基于混合人工蜂群算法的船舶无线通信覆盖区域优化仿真

基于Matlab软件，使用Sphere函数^[4]作为优化算法的基本测试函数，测算混合人工蜂群算法对于船舶无线通信网络覆盖区域的优化效果。

Sphere函数的表达式为：

$ f\left( x \right) = \sum\limits_{i = 1}^m {{x_m}^2} \text{。} $

(6)

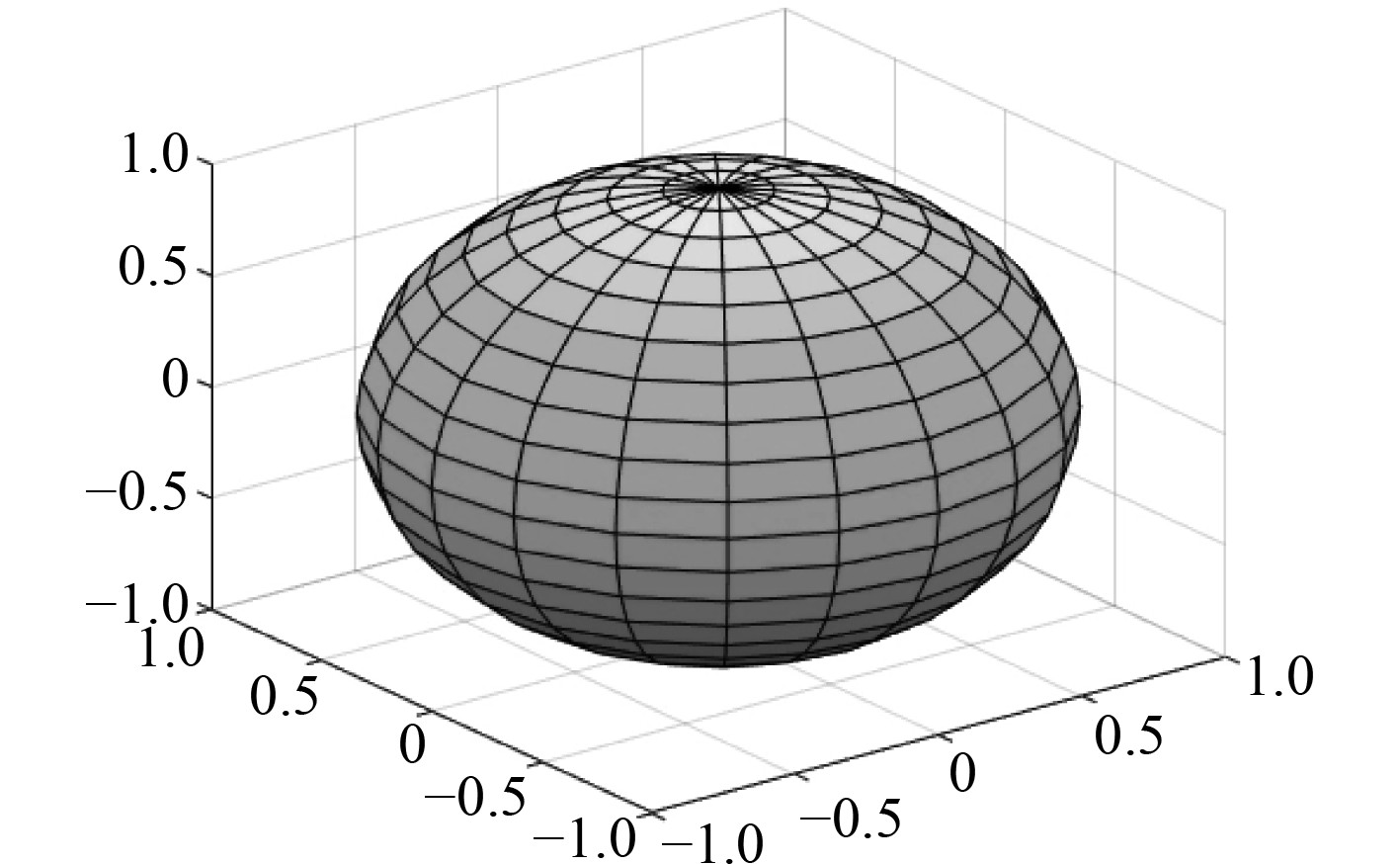
Sphere函数模型如图4所示。

在Matlab中建立混合人工蜂群算法模型时需要考虑以下几个维度：

1）多峰值特性

由于蜂群算法具有局部寻优和整体寻优功能，因此在迭代过程中包含多个局部极值点和整体极值点。

2）误导性

由于多峰值特性，在迭代优化时可能导致优化结果的误导。

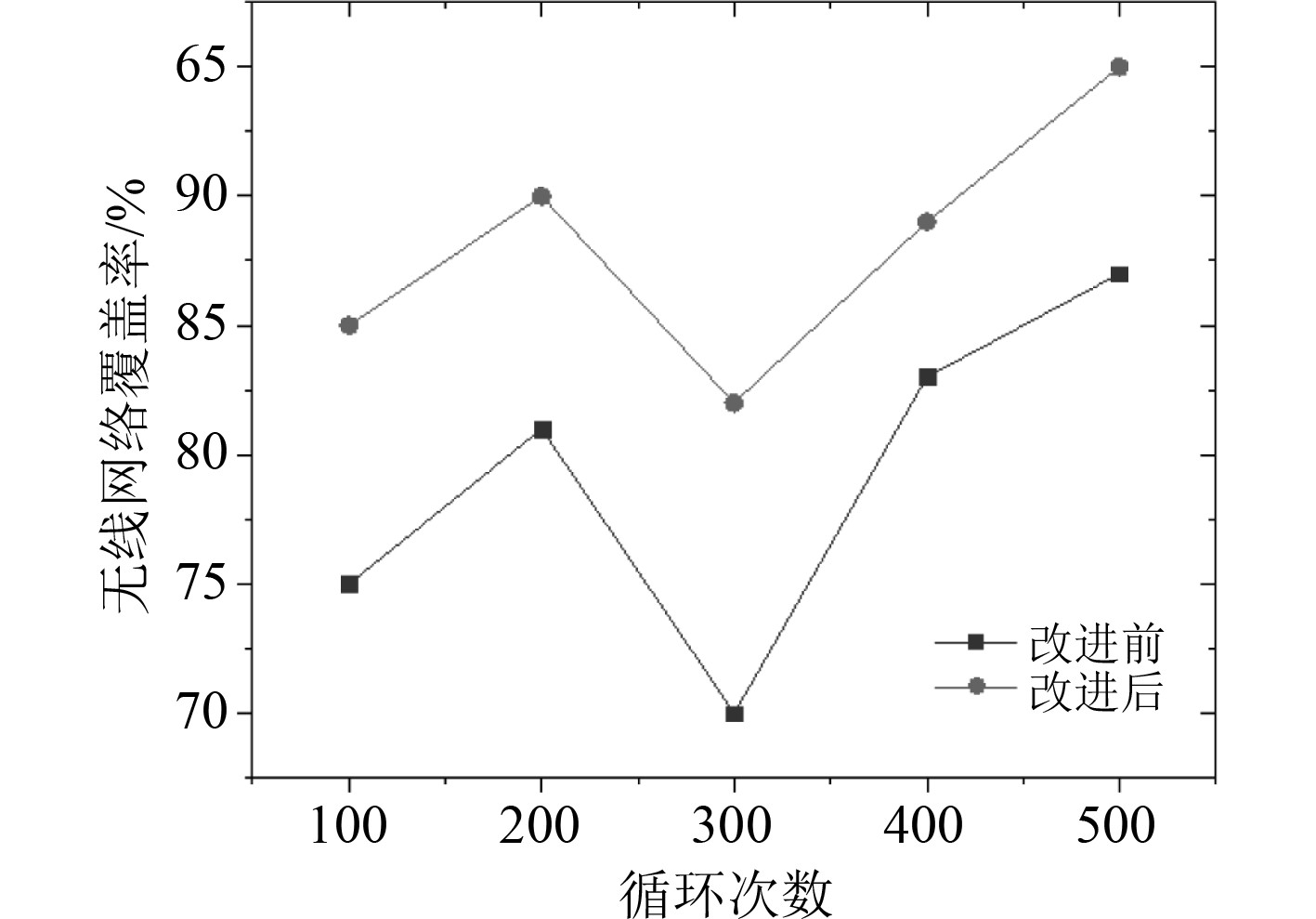
在测算时，将混合人工蜂群算法的循环次数分别定义为100，200，300，400，500，均测算出对应的网络节点覆盖率，图5为人工蜂群算法改进前后的无线网络节点覆盖率对比曲线。

3 结　语

为了提高船舶无线通信网络的有效覆盖率，利用混合人工蜂群算法对船舶无线网络节点的分布进行优化，并结合Sphere函数和Matlab软件进行无线网络节点覆盖率优化的测算，具有一定的实际应用价值。