混响指声波在传播过程中遇到墙壁等障碍物的反射和吸收作用所形成的物理现象。波束成形技术是一种基于传声器阵列测量的噪声源识别技术[1],可以对采集到的声场信息进行声源面的聚焦重构,通过加强目标声源的输出能量实现声源定位[2-3]。当在机舱等密闭的环境中进行声成像时,传感器除了接收到声源产生的声波信号外,还会接收到混响场中声波经过多次反射后的反射声波,并且随着反射的次数增加,接收到的信号能量也逐渐衰减,最终影响成像效果。
因此,对混响背景下的声学成像技术进行研究具有重要意义。
Bees[4]提出将去混响问题分两步实现,最小均方准则设计去混响逆滤波器。Sehr等[5]提出了一种基于语音特征参数域去混响的方法。Jiang[6]针对混响背景中声源定位不准的问题,提出了一种将深度融合和卷积神经网络相结合的新型算法。王小军[7]提出了一种基于混响时间感知的特征提取方法。孟维鑫等[8]提出了一种新的多通道联合去混响波束形成器。张宏宇[9]针对船舱中的混响环境,提出用房间脉冲响应函数代替自由空间格林函数,有效地抑制了混响的干扰。赵中华等[10]为了提高混响条件下时延算法的精度,提出了基于自适应特征值传播的时间延时算法。魏元泽[11]为了有效滤除噪声和混响抑制,提出了一种基于数学形态学和EMD法的声源定位方法。韩哲等[12]提出了一种新的分布式自适应去混响算法。
本文主要针对常规波束成形算法(CBF)、基于正交匹配追踪的反卷积波束成形算法(OMP-DAMAS)以及基于脉冲响应函数的自适应波束成形算法(RIR-SC-DAMAS)3种不同的声成像技术,模拟混响环境,通过对比定位精度、算法运行速度等,确定混响背景中进行声源定位的最佳方法。
1 波束成形波束成形是一种空间声场的可视化技术,在声源识别领域得到了广泛的研究和应用[13]。波束成形的核心思想是将声源面离散化形成聚焦网格点,利用传声器阵列采集声信号反向聚焦各网格点,并按聚焦点位置进行相位补偿后加和输出,真实声源所在聚焦点的输出量被加强,其他聚焦点的输出量被衰减,从而有效识别声源。
1.1 常规波束成形常规波束成形算法是利用多个阵元接收到的信号具有的相位差,通过在接收端进行延时求和、加权输出得到输出功率,确认波达方向。
在进行信号处理时,通常将信号从时域转到频域上进行处理,从而提高运行效率。阵列接收到的信号表达式为:
| $ X\left( t \right) = {\boldsymbol{A}} \cdot S\left( t \right) + N\left( t \right)。$ | (1) |
式中:
对式(1)进行加权后得到输出信号为:
| $ Y\left( t \right) = {{\boldsymbol{{\boldsymbol{\omega}} }} ^{\rm{H}}}X\left( t \right)。$ | (2) |
通过傅里叶变换,将输出信号转换至频域:
| $ Y\left( k \right) = {{\boldsymbol{{\boldsymbol{\omega}} }} ^{\rm{H}}}X\left( k \right) 。$ | (3) |
式中,
分别计算时域、频域的阵列输出平均功率:
| $ {P_t} = \frac{1}{L}{\left| {Y\left( t \right)} \right|^2} = {{\boldsymbol{{\boldsymbol{\omega}} }} ^{\rm{H}}}E\left[ {X\left( t \right){X^{\rm{H}}}\left( t \right)} \right]{\boldsymbol{{\boldsymbol{\omega}} }} = {{\boldsymbol{{\boldsymbol{\omega}} }} ^{\rm{H}}}{{\boldsymbol{R}}_t}{\boldsymbol{{\boldsymbol{\omega}} }},$ | (4) |
| $ {P_k} = \frac{1}{L}{\left| {Y\left( k \right)} \right|^2} = {{\boldsymbol{\omega}} ^{\rm{H}}}E\left[ {{\boldsymbol{X}}\left( k \right){{\boldsymbol{X}}^{\rm{H}}}\left( k \right)} \right]{\boldsymbol{\omega}} = {{\boldsymbol{\omega}} ^{\rm{H}}}{{\boldsymbol{R}}_k}{\boldsymbol{\omega}} 。$ | (5) |
式中:
| $ \mathop {\boldsymbol{R}} \limits^ \wedge = \frac{{X\times {X^{\rm{H}}}}}{L} ,$ | (6) |
最终得到声源面的声压值为:
| $ {P_{CBF}} = {{\boldsymbol{\omega}} ^{\rm{H}}}\mathop {\boldsymbol{R}}\limits^ \wedge {\boldsymbol{\omega}} 。$ | (7) |
反卷积波束成形算法主要以DAMAS[14-15]算法为代表,利用点扩散函数(PSF)以及高斯赛德尔迭代法逆向计算目标声源面的声压分布,从而识别声源。该算法较常规波束成形算法提高了空间分辨率以及定位精度。
首先将目标声源面划分为若干网格聚焦点,测量面上测得的声压可表示为:
| $ p = {\boldsymbol{G}}q 。$ | (8) |
式中:
声压互谱矩阵的表达式为:
| $ {\boldsymbol{C}} = p{p^{\rm{H}}} = {\boldsymbol{G}}q{q^{\rm{H}}}{{\boldsymbol{G}}^{\rm{H}}} ,$ | (9) |
当目标声源为不相干声源时,
各聚焦网格点的输出功率为:
| $ b = {{\boldsymbol{\omega}} ^{\rm{H}}}{\boldsymbol{C}}{\boldsymbol{\omega}} = {{\boldsymbol{\omega}} ^{\rm{H}}}{\boldsymbol{G}}q{q^{\rm{H}}}{{\boldsymbol{G}}^{\rm{H}}}{\boldsymbol{\omega}} = {\sum\limits_{}^N {\left| {{q_n}} \right|} ^2}{{\boldsymbol{\omega}} _n}^{\rm{H}}{{\boldsymbol{g}}_n}{{\boldsymbol{g}}_n}^{\rm{H}}{{\boldsymbol{\omega}} _n} ,$ | (10) |
式中:
记
| $ b = {\sum\limits_{}^N {\left| {{q_n}} \right|} ^2}psf 。$ | (11) |
在混响背景下,声波在传播时受到障碍物的反射和吸收,导致阵列接收到的信息复杂多样。而自适应波束成形算法可以依据自适应压缩采样重构算法(SAMP-COSAMP),能够自动搜索声源个数,将测得的声源信息进行加权处理,达到重构声源的目的。该算法较反卷积波束成形克服了稀疏度的限制,无需提前预知声源个数,但缺点是运行时间有所延长。
1.3.1 基于镜像源法的脉冲响应函数声波在传播过程中往往会受到壁面的反射和吸收作用,这就形成了一个复杂的混响场,当利用阵列接收传播信号时也会因为反射声波的干扰对最终目标声源的定位效果产生较大的影响,而为了在混响背景下仍然能够精准定位声源,首先要计算声波在混响场中的传递函数,即室内脉冲响应函数。
镜像源法是利用镜像的原理,计算声波的传播路程,再结合壁面对声波的吸收和反射作用,计算再传播过程中的能量衰减,得到室内脉冲响应函数:
| $\begin{aligned} & h\left( t \right) =\\ & \sum\limits_{p = 1}^8 {\sum\limits_{r = - \infty }^\infty {\beta _{x,1}^{\left| {{n_x} - q} \right|}} } \beta _{x,2}^{\left| {{n_x}} \right|}\beta _{y,1}^{\left| {{n_y} - j} \right|}\beta _{y,2}^{\left| {{n_y}} \right|}\beta _{z,1}^{\left| {{n_z} - k} \right|}\beta _{z,2}^{\left| {{n_z}} \right|}\frac{{\delta \left[ {t - \left( {\left| {{R_p} + {R_r}/c} \right|} \right)} \right]}}{{4{\text{π}} \left| {{R_p} + {R_r}} \right|}},\end{aligned} $ | (12) |
通过傅里叶变换,将其转换至频域:
| $ \begin{split} & H\left( {\boldsymbol{\omega}} \right) = \\ & \sum\limits_{p = 1}^8 {\sum\limits_{r = - \infty }^\infty {\beta _{x,1}^{\left| {{n_x} - q} \right|}} } \beta _{x,2}^{\left| {{n_x}} \right|}\beta _{y,1}^{\left| {{n_y} - j} \right|}\beta _{y,2}^{\left| {{n_y}} \right|}\beta _{z,1}^{\left| {{n_z} - k} \right|}\beta _{z,2}^{\left| {{n_z}} \right|}\frac{{{e^{i\frac{{\boldsymbol{\omega}} }{c}\left| {{R_p} + {R_r}} \right|}}}}{{4{\text{π}} \left| {{R_p} + {R_r}} \right|}}{e^{ - i{\boldsymbol{\omega}} t}}。\end{split} $ | (13) |
式中:
根据声波在混响场中的传递函数
| $ y(t) = \int_0^{ + \infty } {h\left( \tau \right)} x\left( {t - \tau } \right){\rm{d}}\tau + n\left( t \right) = h\left( t \right)\cdot x\left( t \right) + n\left( t \right),$ | (14) |
通过傅里叶变换,将输出信号转换至频域:
| $ Y\left( {\boldsymbol{\omega}} \right) = X\left( {\boldsymbol{\omega}} \right)H\left( {\boldsymbol{\omega}} \right) + N\left( {\boldsymbol{\omega}} \right) 。$ | (15) |
阵元接收到信号之后,利用自适应压缩采样重构算法对信号进行重构,该算法基本步骤为:
步骤1 令初始稀疏度
步骤2 根据
步骤3 若
步骤4 计算初始余量
步骤5 令初始估计信号
步骤6 根据步骤2计算相关系数,并按
步骤7 令
步骤8 当
步骤9 当
在混响场中,阵列接收信号也满足式(1),其中的传递函数
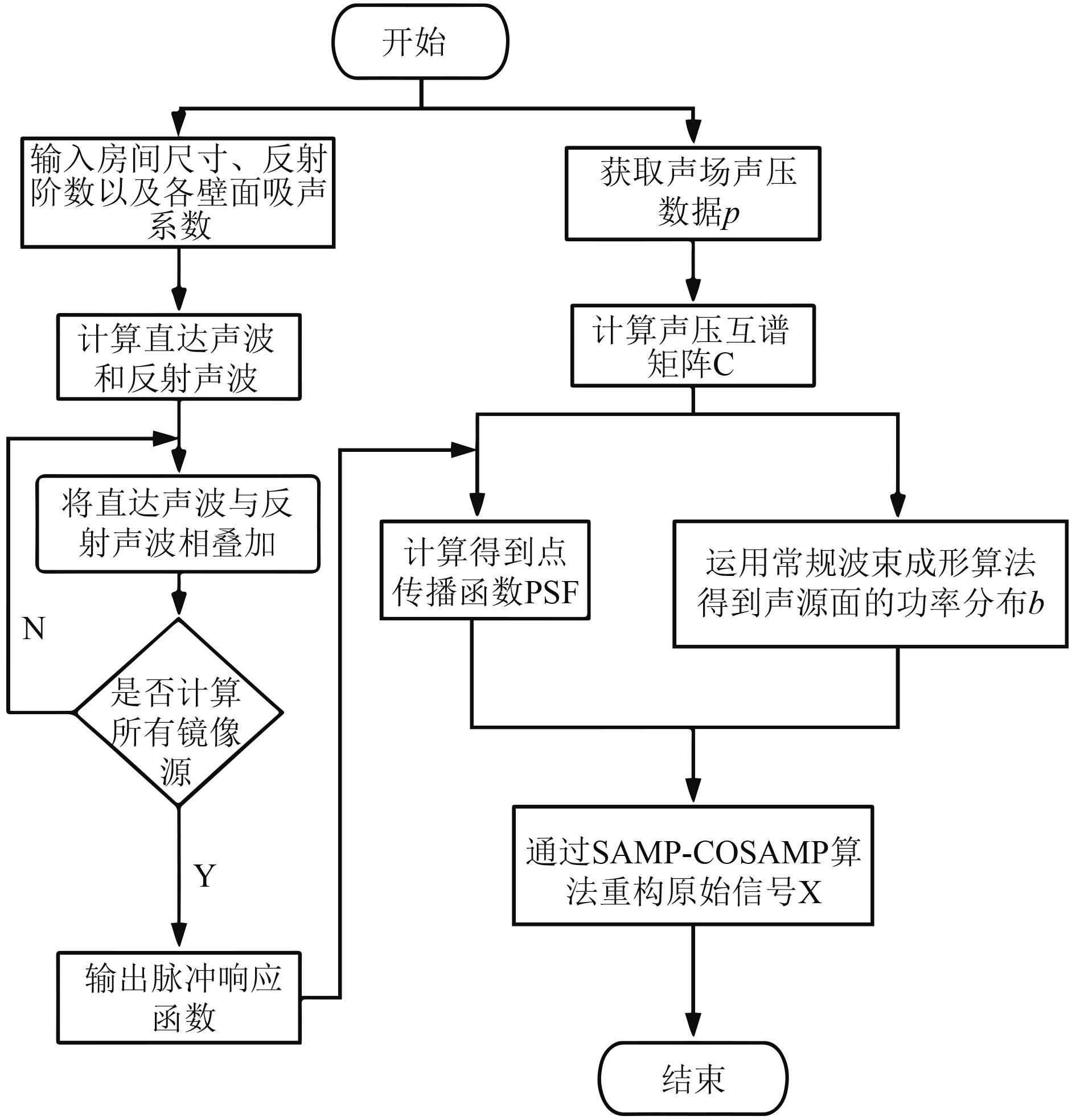
|
图 1 算法流程图 Fig. 1 Flow diagram of the algorithm |
常见机械故障特征频率分布在1800~4200 Hz频带内,故选取1000 Hz,2000 Hz,4000 Hz分别为低、中、高频进行仿真研究分析。利用Comsol Multiphysics对声场信息进行建模和仿真实验,其主要思路为:选择射线声学模块进行建模仿真,首先构建出混响场模型,选择射线从点释放作为声源,然后在距离声源面一定位置处添加测量阵列,用于捕捉声场信息,最后用上文3种波束成形算法对捕捉到的声压数据进行处理,完成声源定位工作,并与真实的声源位置进行对比,确定混响背景下最佳的声成像方法。
2.1 混响场模型首先在环境中构建一个3 m×4 m×3 m的长方体混响区域,将整个区域的介质设置为相对湿度为50%的空气,并将流体模型设置为大气衰减。然后在(1.5 m, 3 m, 1.5 m)的位置构建一点声源,设置总源功率为1 W,波矢空间射线数为100000。将阵列测量面设置在距离声源面1 m处,阵元数为11×11,阵元间距为0.1 m。构建的声场模型及阵列如图2和图3所示。

|
图 2 混响场模型 Fig. 2 Reverb-field model |
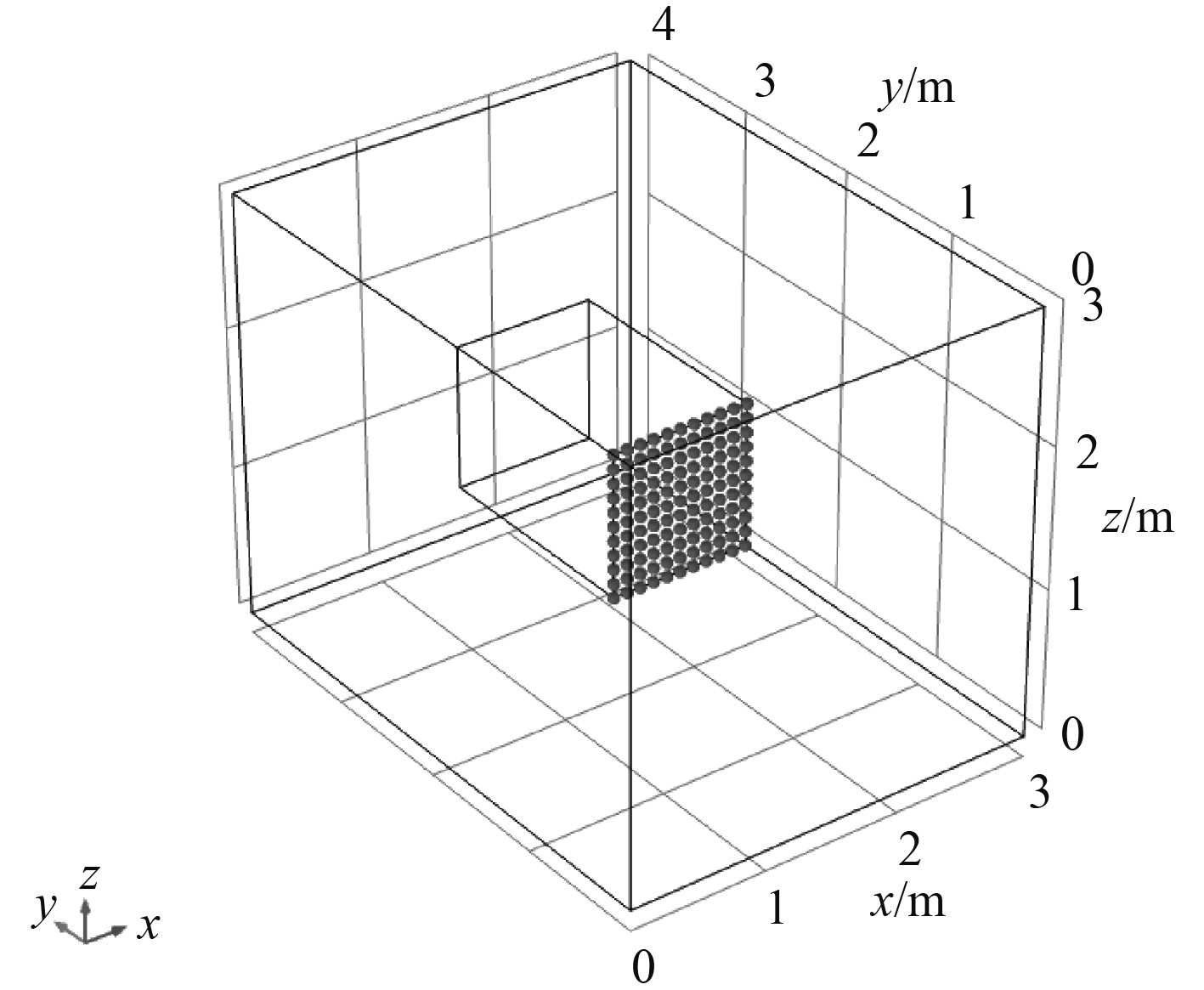
|
图 3 阵列位置示意图 Fig. 3 Schematic representation of the array position |
由于是混响环境,需要对各个壁面的吸声系数进行设置,整个长方体混响场的正面及左侧面材料为玻璃,右侧面及顶部为墙壁,地面材料为瓷砖,后侧面为上窗下柜,不同壁面材料在不同频率下的吸声系数如表1所示。
|
|
表 1 各壁面吸声系数 Tab.1 Sound absorption coefficient of each wall surface |
根据表1对各壁面进行设置,在进行Comsol研究时,以0.01 s为步长,停止时间为0.1 s进行参数化扫描,得到各频率下的声源射线轨迹点样式以及测量面的声压级分布。图4和图5分别为频率1000 Hz时仿真得到的射线轨迹和声压级分布图。

|
图 4 射线轨迹图 Fig. 4 Ray track diagram |

|
图 5 测量面声压级分布图 Fig. 5 Sound pressure level distribution diagram of the measurement surface |
利用Comsol仿真软件导出频率分别为1000 Hz,2000 Hz以及4000 Hz下的声压数据,将其分别利用常规波束成形算法(CBF)、基于OMP的反卷积波束成形算法(OMP-DAMAS)以及基于压缩感知的自适应波束成形算法(RIR-SC-DAMAS)进行处理,得到相应的声成像如图6~图8所示。3种算法在不同频率下的声源定位结果对比如表2所示。

|
图 6 1000 Hz下各算法声学成像图 Fig. 6 Acoustic imaging diagram of each algorithm at 1000 Hz |

|
图 7 2000 Hz下各算法声学成像图 Fig. 7 Acoustic imaging diagram of each algorithm at 2000 Hz |
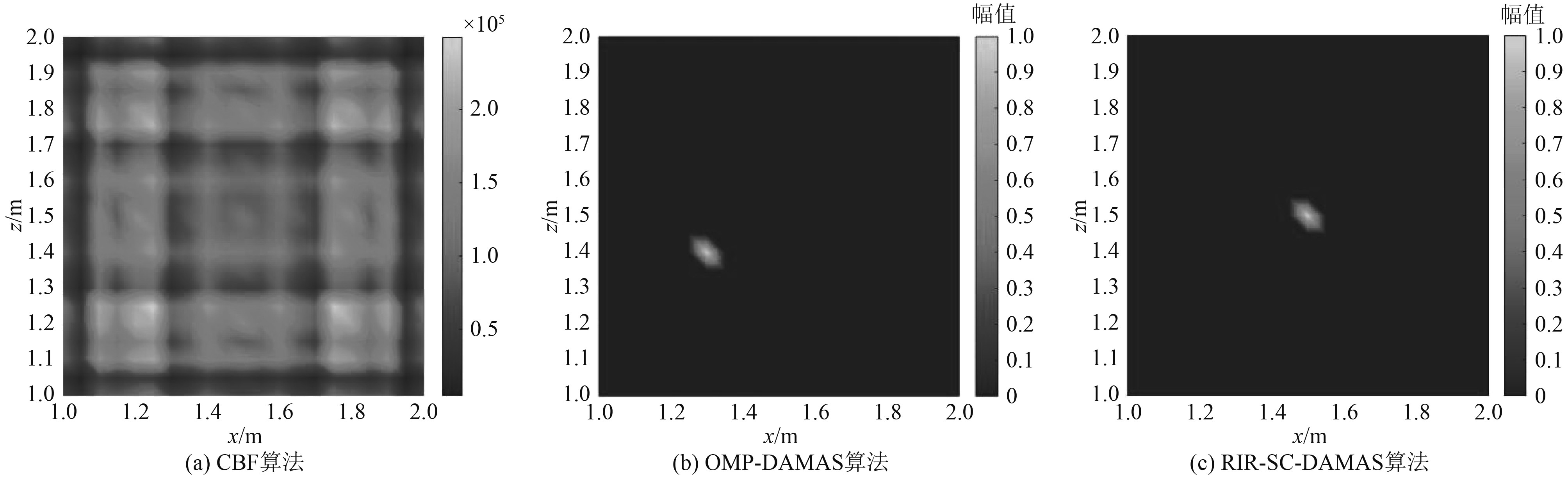
|
图 8 4000 Hz下各算法声学成像图 Fig. 8 Acoustic imaging diagram of each algorithm at 4000 Hz |
|
|
表 2 不同频率下成像结果对比表 Tab.2 Comparison table of the imaging results at different frequencies |
通过图6~图8及表2可知,在混响场中相同频率下CBF算法的定位结果旁瓣大,成像多,定位效果较差;OMP-DAMAS算法旁瓣小,但是只在中低频有较好的定位效果,高频下会影响定位精度;RIR-SC-DAMAS算法无论是在中低频还是高频下都有良好的定位效果。
各算法分别在不同频率下运行5次,5次运行时间的平均值如表3所示。
|
|
表 3 各算法运行时间表 Tab.3 Operation schedule of each algorithm |
可以看出,每种算法在不同频率下的运算时间相差不大,但不同算法在同一频率下的运算时间有很大的差别。其中CBF算法在运行时仅需普通的数据计算,所以其运行时间最短;OMP-DAMAS算法较CBF算法需要利用反卷积以及压缩感知对声源进行重构,大大增加了运行时间;RIR-SC-DAMAS算法在前两者的基础上还要模拟混响环境,重新构造室内脉冲响应函数,故运行时间较前两者有明显的增加。
为进一步比较3种算法在复杂环境下的成像精度,在混响场中加入snr为0的高斯白噪声,分别利用CBF,OMP-DAMAS以及RIR-SC-DAMAS算法对阵列接收的声场信息进行处理,得到不同频率下对应的声成像如图9~图11所示。
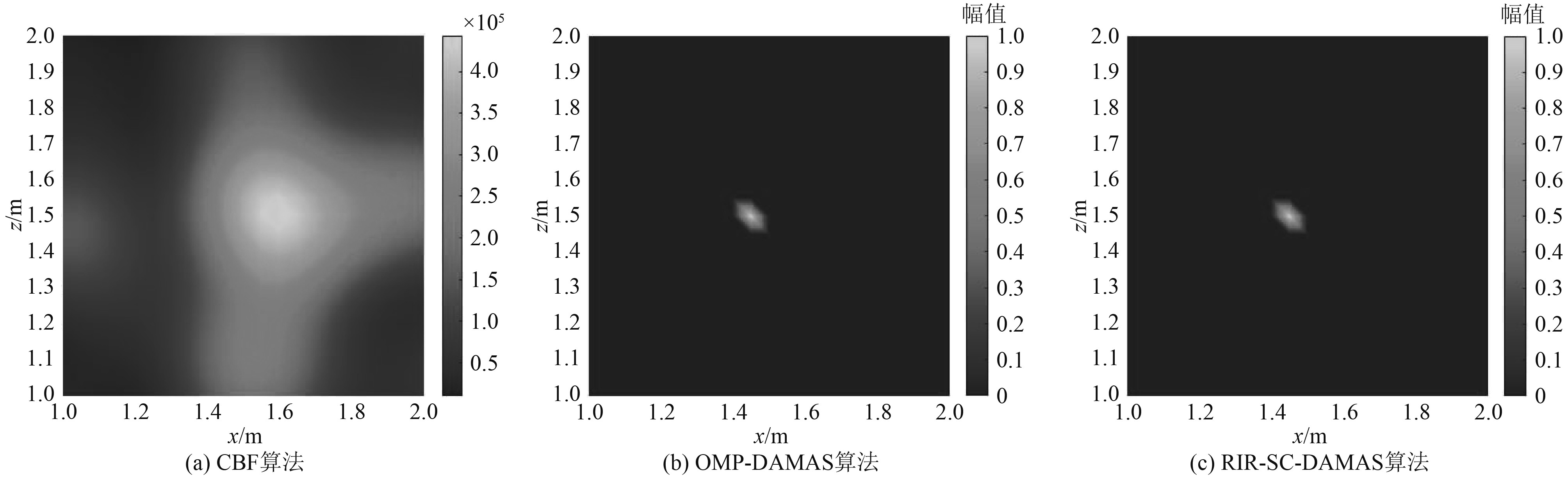
|
图 9 1000 Hz下各算法声学成像图(SNR=0) Fig. 9 Acoustic imaging diagram of each algorithm at 1000 Hz (SNR=0) |

|
图 10 2000 Hz下各算法声学成像图(SNR=0) Fig. 10 Acoustic imaging diagram of each algorithm at 2000 Hz (SNR=0) |
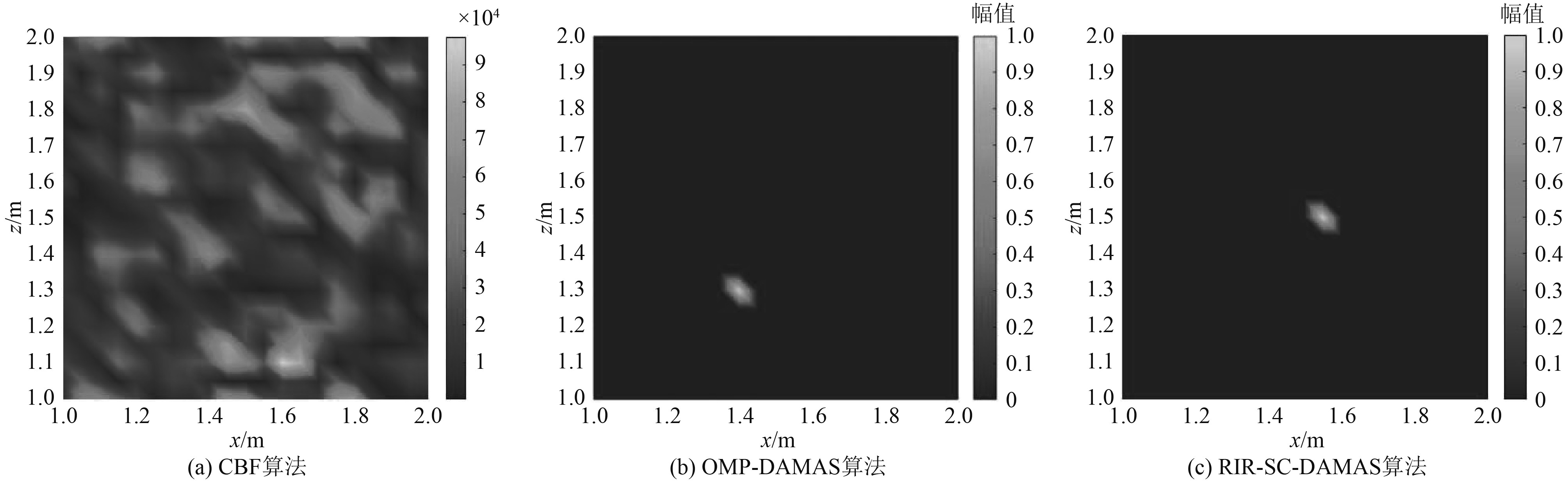
|
图 11 4000 Hz下各算法声学成像图(SNR=0) Fig. 11 Acoustic imaging of each algorithm at 4000 Hz (SNR=0) |
在加入SNR=0的高斯白噪声条件下各算法在不同频率下的声源定位结果对比如表4所示。
|
|
表 4 不同频率下成像结果对比表(SNR=0) Tab.4 Comparison table of imaging results at different frequencies (SNR=0) |
通过图9~图11及表4可知,在加入干扰噪声后,CBF算法的成像精度大大降低,并且在声成像图上出现大量干扰声源;OMP-DAMAS算法在中低频下受影响不大,但在高频下的声成像效果远远偏离了实际声源位置;RIR-SC-DAMAS算法在加入干扰噪声后受到的影响较小,仍能保持较高的成像精度。
计算各算法在加入干扰噪声后不同频率下的运行时间,取5次运行时间的平均值如表5所示。
|
|
表 5 各算法运行时间表(SNR=0) Tab.5 Operation schedule of each algorithm (SNR=0) |
表5与表3所得结论基本相同,在同一频率下,CBF算法用时最短,OMP-DAMAS算法次之,RIR-SC-DAMAS算法用时最长。
综上所述,在混响场中,CBF算法以及OMP-DAMAS算法只在中低频下具有一定的定位精度,而RIR-SC-DAMAS算法较前两者的定位精度有极大的精准度,特别是当干扰噪声存在时,该算法受到的影响较小,而另外2种算法基本无法准确定位. 但从运行时间来看,RIR-SC-DAMAS算法的运行时间远远超过其他2种算法。
3 结 语本文首先介绍了3种基于波束成形算法的声学成像技术,即常规波束成形法(CBF)、基于正交匹配追踪的反卷积波束成形算法(OMP-DAMAS)以及基于脉冲响应函数的自适应波束成形算法(RIR-SC-DAMAS),然后构建混响场模型,分别利用3种算法对不同频率下的目标声源进行声学成像,最后对仿真结果进行对比分析并得出结论,即在有干扰噪声存在的混响背景中,基于脉冲响应函数的自适应波束成形算法具有更好的定位精度和效果。
| [1] |
DOUGHERTY R P. Noise source imaging by beamforming[J]. SAE Paper, 2008, 2008-36-0518.
|
| [2] |
BATAL M, MARROQUIN M. Noise source location techniques simple to advanced applications[J]. Journal of Sound Andvibration, 2003, 37(3): 24-38. |
| [3] |
CHRISTENSEN J J, HALD J. Beamforming[J]. B& K Techni-cal Review, 2004(1): 1-31. |
| [4] |
BEES D, BLOSTEIN M, KABAL P. Reverberant speech enhancement using cepstralprocessing[C].// Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing. Toronto, Ontario, Canada, 1991, Ⅱ: 977-980.
|
| [5] |
SEHR A, KELLERMANN W. A new concept for feature-domain dereverberation forrobust distant-talking ASR[J]. IEEE Proceedings of ICASSP, 2007, IV: 369-372. |
| [6] |
JIANG Shilong , WU Lulu , YUAN Peipei , et al. Deep and CNN fusion method for binaural sound source localisation[J]. The Journal of Engineering, 2020(13): 511-516. |
| [7] |
王小军. 基于深度学习的语音去混响方法研究[D].太原: 太原理工大学, 2021.
|
| [8] |
孟维鑫, 厉剑, 郑成诗, 等. 复广义高斯分布多通道最大似然联合去噪去混响波束形成器[J]. 信号处理, 2022, 38:(4): 677-689.
|
| [9] |
张宏宇, 郭文勇, 韩江桂, 等. 基于镜像源方法抑制混响干扰的声全息算法改进[J]. 科学技术与工程, 2019, 19(33): 113-118.
|
| [10] |
赵中华, 李竞荣, 邓德迎. 基于倒谱分析的防混响时延估计算法[J]. 广西大学学报(自然科学版), 2021, 46(3): 703-713.
|
| [11] |
魏元泽. 低信噪比混响环境下声测定位方法的实现[D]. 成都: 电子科技大学, 2014.
|
| [12] |
韩哲, 郑成诗, 柯雨璇, 等. 分布式无线声传感网加权预测误差语声去混响方法 [J]. 应用声学, 2022, 41(1): 21-31.
|
| [13] |
褚志刚, 杨洋, 倪计民, 等. 波束形成声源识别技术研究进展[J]. 声学技术, 2013(5): 80-85. |
| [14] |
BROOKS T. F, HUMPHREYS W M.A deconvolution approach for the mapping of acoustic sources (DAMAS) determined from phased microphone arrays[J].Journal of Sound and Vibration, 2006, 294(4-5): 856-879.
|
| [15] |
BROOKS T F, HUMPHREYS W M. Extension of DAMAS phased array processing for spatial coherence determination (DAMAS-C) [C]// 12th AIAA/CEAS Aeroacoustics Conference, Massachusetts, 2006: 1-16.
|
 2023, Vol. 45
2023, Vol. 45
